A robust multi-objective bargaining methodology for inter-basin water resource allocation: a case study

Abstract

In this study, a new methodology is proposed to balance environmental and economic issues in water allocation under uncertainty. Two objective functions, including maximizing economic income (EI) and minimizing environmental pollution (EP), were considered as two groups of players to construct a deterministic multi-objective bargaining methodology (DMOBM). In the next step, it is enhanced to a robust multi-objective bargaining methodology (RMOBM), which is capable of incorporating the main uncertainties exist in the problem. A large-scale inter-basin water transfer case study was utilized to investigate the applicability of the developed model. The outputs of the models showed that Nash equilibrium provide a rather narrow range of solutions. According to the results, the required rounds to reach Nash equilibrium raised as the uncertainty level increased. In addition, higher levels of uncertainty lead to higher reduction in water allocating of receiving basin. Sensitivity analysis showed that economic income values are less sensitive to changes of uncertain parameters than the environmental objective function. The developed methodology could provide a framework to incorporate the behavior of different stakeholders. Furthermore, the proposed method can be reliable under the condition of facing water allocation uncertainties.

Introduction

Recently, water-shortage and high-demand of water on the one hand, and the existence of uncertain data on the other hand, leads the reliable water allocation to be a major challenge. In order to achieve the sustainable development approach, US Water Resource Council (1973) has suggested to consider national economic development and environmental quality as two crucial objectives in water resource schemes. However, over the past few decades, inter-basin water transfer schemes commonly have been constructed with major and minor emphasize respectively on economic and environmental aspects. Due to some negative environmental impacts of such projects, environmental aspects need to get more attention. Likewise, uncertainties of such schemes supposed to be taken into consideration.

Water transfer scheme, from a reach (donor) basin to a poor one (receiving), have been implemented as an alternative to balance the uneven distribution of water resources all over the world. In spite of having many benefits for the receiving basin, it may have negative impacts on the donor basin. Hence, it is imperative to justify such schemes to avoid expected conflicts. Since achieving to a balance between economic and environmental issues in such a case is more complicated, an inter-basin case study is considered. However, the methodology can be used for intra-basin water allocations schemes as well.

Some research have focused on the economic and environmental aspects of water transfer schemes. For example, Draper et al. (2003) utilized a model with economic objective function for main water supply system in California and confirmed its effectiveness for assessing the project. A framework that integrates ecological consequences into the economic assessment model was proposed by Matete and Hassan (2005), to ensure sustainable development. Karamouz et al. (2009) investigated the feasibility of two inter-basin water transfer schemes by applying an economic model. The outputs of their model were the value of economic gain of the donor basin to offset the loss of agricultural income and environmental costs.

To consider several conflicting objectives, conventional multi-objective approaches are often utilized. These approaches, which their solutions are obtained from an optimization view point, address the problem only as a single decision-making procedure. Such problems result in a set of optimal solutions, known as Pareto front. However, Pareto optimal solutions may lead to failure of a decision, since they may not be acceptable socially (Madani 2010). Moreover, it is difficult to make a choice among Pareto front solutions due to the wide range of choices that it provides.

Game theory models, which provide a process of interactive decision-making, intend to find optimal solutions among conflicting interests of several players (Davila et al. 2005). Recently, various game theory models have been widely used to deal with the inter-basin water allocation conflicts (Sadegh et al. 2010; Wei et al. 2010; Jafarzadegan et al. 2014; Manshadi et al. 2015). However, less attention has been paid to the games with application of Nash equilibrium resulting from the negotiation. Lee (2012) proposed a methodology based on combination of multi-objective optimization and Nash equilibrium concepts for land use management, which results in easier decision-making.

Uncertainties of input data has been considered in many water allocation problems, since parameters of these models usually are not precisely known. Some studies focused on developing methods based on stochastic and fuzzy set concepts. In these studies, the probability density functions (PDFs) or fuzzy membership functions of uncertain data were assumed to be known. However, this is an unrealistic assumption for uncertain data. In this view, these methods may not address the risk of sub-optimality or infeasibility due to data uncertainty.

Robust optimization discovers solutions that remain reliable under uncertainty by providing a framework for controlling the effects of uncertainty. Although the application of robust optimization is considerable in water resource problems, the probabilistic and non-probabilistic robust optimization should be distinguished. During the past decades, application of probabilistic (scenario-based) robust optimization in water resource management has been extensive (Watkins and McKinney 1997; Escudero 2000; Pallottino et al. 2005; Jia and Culver 2006; Kang and Lansey 2012; Chen et al. 2013). However, its complexity cannot be ignored (Watkins and McKinney 1997). In this method, similar to stochastic approaches, PDFs of uncertain data are assumed to be unreasonably known (Housh et al. 2011).

In non-probabilistic robust optimization, known as robust counterpart, there is no need to scenarios, PDFs, or membership functions to present uncertainty (Ben-Tal and Nemirovski 1999). Among different robust counterpart models, Bertsimas and Sim (2004) have introduced a form which does not transform a linear programming model to a nonlinear one. Though there are numerous studies demonstrate applicability of their formulation for optimization problems, the literature is relatively poor in application of it to water allocation problems. Some studies can be mentioned as application of this model in water science, for instance, some attempt have been made to design a reliable water supply system (Chung et al. 2009) and to maximize the total gross margin of an irrigation network (Sabouni and Mardani 2013). Both studies confirm the applicability of such approach in tackling parameters uncertainties, without introducing additional complexity.

In view of the above discussion, this study presents a new approach for supporting decision-making process of water allocation problems in an uncertain environment. The proposed method is developed by combing multi-objective bargaining methodology and robust optimization. To this end, a deterministic multi-objective bargaining methodology (DMOBM) is extended to inter-basin water allocation problems for reflecting compromises between income and pollution. Then, the deterministic model is improved to a robust multi-objective bargaining methodology (RMOBM) formation in order to provide the capability of handling uncertainties and controlling risks of the model unreliability and infeasibility. The applicability of the model is explored by examining in the presence of the large-scale water transfer scheme of Karoon to Rafsanjan basin.

Material and methods

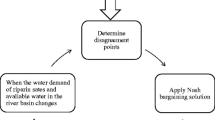
The diagram of the developed methodology is shown in Fig. 1. This figure illustrates how four main steps of the procedure were implemented. In step 1, the determination of major water users of studied basins, data collection, and selection of water quality indicator were carried out. To this regard, data of water demands, upstream flows, as well as quality and quantity of return flows were required. In the next step, the environmental and economic objective functions of the study were constructed. Also, in order to compute the variation range (negotiation interval) of each objective function, the maximum and minimum of objective functions were computed. The aim of the third step was to present the algorithm of DMOBM model. During this step, ɛ-constraint approach was used as a baseline for investigating the efficiency of the DMOBM model. In the last step, considering the main uncertain variables and application of robust formulation into the DMOBM model, the RMOBM was derived. The sensitivity of the RMOBM model to variations in uncertain parameters was also investigated.

Fig. 1

Flowchart of the developed model for inter-basin water resource allocation

It should be noted that the ɛ-constraint method, utilized to assess the DMOBM model, is one of the conventional and well-known approaches to solve multi-objective problems (Ehrgott and Gandibleux 2002). This technique is commonly used to produce Pareto front, which is a set of optimal solutions. Theoretically, in this method, one objective will be optimized, whereas remaining objectives are subjected to the upper and lower bound values (ɛ-vector). The Pareto optimal solutions are generated using different values of ɛ.

Study area

Location and the schematic view of the main water users of the study area is shown in Fig. 2. The Karoon river basin (donor basin) is located in the southwest part, whereas Rafsanjan basin (receiving basin) is located in central Iran. The receiving basin (RA) sector consists of Rafsanjan agricultural water user, and the donor basin sector involves three main water users of Khuzestan province, namely Khuzestan local agricultural (KLA), Khuzestan old agro-industrial (KOAI), and Khuzestan new agro-industrial (KNAI) water users.

Fig. 2

Location of case study and the schematic view of its main water users

The Karoon river basin with an area of 100,000 km² is the most important water basin in Iran, since it contains one-fifth of country’s surface water resources. It has two main rivers, namely Karoon and Dez. The major water pollution sources of this area are return flows of agricultural and agro-industrial activities, and domestic and industrial wastewaters. Sugar cane is the dominant crop of the KOAI and KNAI water users, while tomato, sugar cane, wheat, potato, date, corn, watermelon and other crops are cultivated in KLA water user.

The Rafsanjan basin with an area of about 20,000 km² is an arid region with hot summers and dry winters. Pistachio, which is an expensive and high-value horticultural product, is the main cultivated crop of this basin. Over 1300 deep wells are used to supply water to around 110,000 ha of pistachio orchards. The average annual precipitation and groundwater drawdown of Rafsanjan area is 170 mm and 80 cm, respectively. Significant groundwater overdraft leads to salinization of groundwater and 30 cm annual subsidence of earth as well.

The water transfer scheme has been designed to transfer 252 MCM/year from Solakan, one of the upstream branches of the Karoon river, to Rafsanjan basin. The main aim of the scheme is to produce pistachio and to control the groundwater level decline as well as its salinization. Among these issues, the possible environmental impacts of the scheme on the donor basin are also supposed to be taken into consideration. In other words, the scheme should be adjusted environmentally and economically.

The total water demand is significantly greater than Solakan water capacity. Thus, it is necessary to use an algorithm to allocate water optimally. Meanwhile, only monthly water allocation to agricultural demand is regarded as decision variable, since the environmental and municipal water demands are assumed to be satisfied completely. Table 1 presents the demands of water users that should be supplied from Solakan reservoir (MCM/month). Among different water quality monitoring variables, total dissolved solids (TDS) has the worst condition, and in some cases, it violated the standard level. Thus, it was selected as water quality indicator of this study. As a result of wastewater discharges, concentration of TDS increases along the river.

Table 1 Demands of water users from Solakan reservoir (MCM/month)

DMOBM formulation

In this following, a DMOBM formulation is presented. Equation 1 shows a multi-objective programming model.

$$ {\displaystyle \begin{array}{l}\mathit{\operatorname{Minimize}}\kern1em f(x)=\left[{f}_1(x),{f}_2(x),\dots, {f}_q(x)\right]\\ {} Subject\kern0.5em to:\\ {}{h}_r(x)\le 0\kern0.5em ,\kern0.5em r=1,2,\dots, l\\ {}{x}_p\ge 0\kern0.5em ,\kern0.5em p=1,2,\dots, v\end{array}} $$

(1)

where [f ₁(x), f ₂(x), …, f _q (x)] is a set of all q objective functions, x _p is the pth decision variable, and h _r (x) is the rth constraint function. In favor of applying the bargaining model to the multi-objective problem, two groups of stakeholders were considered as two players, environmental player (player 1) and economic player (player 2). The objective of players 1 and 2 was to minimize pollutant load discharged into the river and to maximize economic income of the scheme, respectively.

Primarily, the upper and lower values of each player should be determined. Negotiation interval, which is a payoff of the bargaining approach, is the difference between upper and lower levels of objective functions. These bounds can be found by maximizing and minimizing every individual single objective function. Consequently, computing procedure of the negotiation interval of each player is presented in Eq. 2:

$$ {\displaystyle \begin{array}{l}\mathrm{For}\kern0.5em \mathrm{player}\kern0.5em 1:{EP}_{\mathrm{min}}\le {f}_1(x)= EP\le {EP}_{\mathrm{max}}\\ {}\mathrm{For}\kern0.5em \mathrm{player}\kern0.5em 2:{EI}_{\mathrm{min}}\le {f}_2(x)= EI\le {EI}_{\mathrm{max}}\end{array}} $$

(2)

Since the aim is to maximize the economic income and minimize the environmental pollution as much as possible simultaneously, at the initial round of bargaining, EP_min and EI_max will be considered as goal values of each player i.e., EP_goal and EI_goal, respectively. As the strategies are shown for player 1 in Eq. (3) and for player 2 in Eq. (4), each player will be subjected by the goal value of the other player (Lee 2012).

The strategy for player 1:

$$ {\displaystyle \begin{array}{l}\mathit{\operatorname{Minimize}}\kern1em {f}_1(x)= EP\\ {} Subject\kern0.5em to:\\ {}{f}_2(x)\ge {EI}_{goal}\\ {}{h}_r(x)\le 0,\kern1.5em r=1,2,\dots, l\\ {}{x}_p\ge 0\kern0.5em ,\kern1em p=1,2,\dots, v\end{array}} $$

(3)

And the strategy for player 2:

$$ {\displaystyle \begin{array}{l}\mathit{\operatorname{Maximize}}\kern1em {f}_2(x)= EI\\ {} Subject to:\\ {}{f}_1(x)\le {EP}_{goal}\\ {}{h}_r(x)\le 0,\kern1.5em r=1,2,\dots, l\\ {}{x}_p\ge 0\kern0.5em ,\kern1em p=1,2,\dots, v\end{array}} $$

(4)

The players will begin a sequential bargaining round, since they will not be satisfied with the results from the other player’s goal. Thus, players 1 and 2 will reduce the environmental concerns and economic expectation, respectively. By increasing the bargaining rounds, the value of EI_goal and EP_goal will decrease and increase, respectively. Thus, the difference between the reset goal values and the results of DMOBM approach will become less and less. In order to compute the concession (Cn) of each player, the maximum and minimum values of the environmental pollution (EP) and economic income (EI) were divided into small same-size parts. The calculation of Cn value is as Eq. (5):

$$ {\displaystyle \begin{array}{l} Cn\kern0.5em 1=\frac{EP_{\mathrm{max}}-{EP}_{\mathrm{min}}}{f}\\ {} Cn\kern0.5em 2=\frac{EI_{\mathrm{max}}-{EI}_{\mathrm{min}}}{f}\end{array}} $$

(5)

where f is a coefficient which provides the most rational concession for not influencing the satisfaction values of both players, considerably (Üçler et al. 2015). Finally, the bargaining process for players will be stopped if final solutions of EP_final and EI_final are reached as follows:

$$ {\displaystyle \begin{array}{l}{EP}_{final}\le {EP}_{goal}\\ {}{EI}_{final}\ge {EI}_{goal}\end{array}} $$

(6)

The values of EP_final and EI_final are the Nash equilibrium of the problem (Gibbons 1997). A numerical example on this topic has been described in (Üçler et al. 2015).

Robust counterpart formulation

In mathematical programming, a small deviation of the input data may cause the final solution no longer be optimal or even feasible. Under this condition, application of robust optimization, which is a methodology for designing solution approaches that are immune to data uncertainty, can be quite useful (Bertsimas and Sim 2004).

As mentioned above, the robust counterpart approach is an alternative robust optimization method that has no need to specify the probability distribution function of uncertain parameters. Among different robust counterpart formulations, Bertsimas and Sim (2004) have presented a model with interval-polyhedral uncertainty set in which the robust counterpart form of a linear deterministic model still remains linear. It is possible to adjust conservatism degree of their model using budget parameter (Γ).The formulation of a linear model can be considered as Eq. (7):

$$ {\displaystyle \begin{array}{l}\mathit{\operatorname{Minimize}}\kern1.5em {c}^{\prime }x\\ {} Subject\kern0.5em to:\\ {}\sum \limits_j{a}_{ij}{x}_j\le {b}_i\kern1em \forall i\\ {}{x}_j\ge 0\kern1em \forall j\end{array}} $$

(7)

Consider the ith constraint of a _ij x _j  ≤ b _i and suppose J _i represents the set of uncertain coefficients (a _ij ) in the ith constraint (${\tilde{a}}_{ij}$, j ∈ J _i ). Assume that each uncertain parameter ${\tilde{a}}_{ij}$ can take values in the interval $\left[{a}_{ij}-{\widehat{a}}_{ij},{a}_{ij}+{\widehat{a}}_{ij}\right]$ where ${\widehat{a}}_{ij}$ is the perturbation in each uncertain parameter ${\tilde{a}}_{ij}$, and a _ij is regarded as the deterministic value of the uncertain parameter. By introducing parameter Γ _i for each i, which is called uncertainty budget and can vary in the interval of [0, |J _i |], it would be possible to adjust the conservatism level of the model and explore robustness of the system against failure.

When Γ _i  = 0, the influence of deviations will be ignored completely, while if Γ _i  = |J _i |, the constraint i is entirely hedged against uncertainty. Besides, when Γ _i  ∈ [0, |J _i |], a trade-off exists between the desired robustness and the optimality. Bertsimas and Sim (2004) illustrate that it is possible to rewrite Eq. (7) as following nonlinear formulation:

$$ {\displaystyle \begin{array}{l}\mathit{\operatorname{Minimize}}\kern1em {c}^{\prime }x\\ {} Subject\kern0.5em to:\\ {}\sum \limits_j{a}_{ij}{x}_j+\underset{\left\{{S}_i\cup \left\{{t}_i\right\}\left|{S}_i\subseteq {J}_i,\left|{S}_i\right|=\left[{\varGamma}_i\right]\right.,{t}_i\in {J}_i\backslash {S}_i\right\}}{\max}\left\{\sum \limits_{j\in {S}_i}{\widehat{a}}_{ij}{x}_j+\left({\varGamma}_i-\left[{\varGamma}_i\right]\right){\widehat{a}}_{it_i}{x}_j\right\}\le {b}_i\kern2em \forall i\\ {}{x}_j\ge 0\kern1em \forall j\end{array}} $$

(8)

Based on their procedure, by supposing x ^* as the optimal solution of Eq. (8), the function ${\beta}_i\left({x}^{\ast },{\varGamma}_i\right)={\max}_{\varOmega}\left\{{\sum}_{j\in {S}_i}{\widehat{a}}_{ij}{x}_j^{\ast }+\left({\varGamma}_i-\left[{\varGamma}_i\right]{\widehat{a}}_{it_i}{x}_j^{\ast}\right)\right\}$, which is known as protection function, can be represented as a linear optimization program. Thus, the robust solution can be solved using linear programming, without changing complexity of the optimization problem. Ultimately, the final robust counterpart model can be derived as following equation:

$$ {\displaystyle \begin{array}{l}\mathit{\operatorname{Minimize}}\kern1em {c}^{\prime }x\\ {} Subject\kern0.5em to:\\ {}\sum \limits_j{a}_{ij}{x}_j+{z}_i{\varGamma}_i+\sum \limits_{j\in J}{p}_{ij}\le {b}_i\kern2em \forall i\\ {}{z}_i+{p}_{ij}\ge {\widehat{a}}_{ij}{x}_j\kern2em ,\forall i,j\in J\\ {}{z}_i\ge 0\kern1em ,\forall i\\ {}{p}_{ij}\ge 0\kern1em ,\forall i,j\in J\\ {}{x}_j\ge 0\kern1em ,\forall j\end{array}} $$

(9)

where z _i and p _ij are required auxiliary variables related to robust counterpart formulation. It should be noted that while less than Γ _i uncertain parameters change from their deterministic values, the feasibility of robust solutions can be ensured. If more than Γ _i parameters vary, the solution still will be feasible with a high probability of:

$$ P\left(\sum \limits_j{\tilde{a}}_{ij}{x}_j^{\ast }>{b}_i\right)\le {B}_i\left(n,{\varGamma}_i\right) $$

(10)

The description of the Γ _i calculation can be found in Bertsimas and Sim (2004).

Models frameworks

Framework of DMOBM for water allocation

The introduced DMOBM approach was applied to an inter-basin water allocation problem in favor of balancing economic and environmental issues in such schemes. It contained environmental (player 1) and economic (player 2) objective functions. The aim of optimization model of player 1 is to minimize the total amount of waste load pollution that is discharged into the river by water users. It is written in Eq. 11:

$$ {\displaystyle \begin{array}{l}\mathit{\operatorname{Minimize}}\kern1em {f}_1(x)= EP=\sum \limits_u\sum \limits_m\sum \limits_c\left({Ca}_{um}\kern0.5em {b}_{um}\kern0.5em {x}_{um c}\right)\\ {} Subject\kern0.5em to:\\ {}\alpha \kern0.5em {d}_{um c}\le {x}_{um c}\le d{}_{um c}\kern1.50em \forall u,m,c\\ {}\beta \kern0.5em {Q}_m\le \sum \limits_u\sum \limits_c{x}_{um c}\le {Q}_m\kern1.5em \forall m\\ {}\sum \limits_u\sum \limits_c Pl{}_{um c}\le \sum \limits_uT{}_{um}\kern1em \forall m\\ {} EI\ge {EI}_{goal}\end{array}} $$

(11)

where EP is the environmental pollution; u, m, and c are the counter of water users, months, and cultivated crops, respectively; Ca _um is the average TDS concentration in return flows; b _um is the factor of return flow discharged into the river of user u in month m; x _umc is the allocated water to crop c of user u in month m; and d _umc is water demand of user u (MCM/month). Q _m is the available water during month m, Pl _umc is the pollution load discharged into the river of user u in month m and crop c, and T _um is the pollution discharge permit of user u in month m. EI is the economic income, and α and β are the non-negative coefficients for determining the lower level of water demands and the river flow, respectively.

The optimization model of player 2 which aims to maximize the total benefit of water users is as follows:

$$ {\displaystyle \begin{array}{l}\mathit{\operatorname{Maximize}}\kern1em {f}_2(x)= EI=\sum \limits_u\sum \limits_c{CPD}_{uc}\kern0.5em {NB}_{uc}\kern0.5em \sum \limits_m{x}_{um c}\kern0.24em \\ {} Subject to:\\ {}\alpha \kern0.5em {d}_{um c}\le {x}_{um c}\le d{}_{um c}\kern0.48em \forall u,m,c\\ {}\beta \kern0.5em {Q}_m\le \sum \limits_u\sum \limits_c{x}_{um c}\le {Q}_m\kern0.48em \forall m\\ {}\sum \limits_u\sum \limits_c Pl{}_{um c}\le \sum \limits_uT{}_{um}\kern0.48em \forall m\\ {} EP\le {EP}_{goal}\end{array}} $$

(12)

where CPD _uc is the average produced crop c per unit of supplied water (crop per drop) for water user u (kg/m³), and NB _uc is the total net benefit due to crop c of water user u (USD/kg), which is the difference between total benefits and total costs (USD/kg) of each water user.

Framework of RMOBM for water allocation

The procedure of Bertsimas and Sim (2004) is employed to the proposed DMOBM model for water allocation, to transform it into the robust counterpart model. Accordingly, uncertainties of demand and available water of the river was incorporated to construct a RMOBM. Thus, to address the uncertainty of water demand and river flow, their equations in the optimization model need to be rewritten in robust formulation. For EP (player 1), the DMOBM can be rewritten as follows:

$$ {\displaystyle \begin{array}{l}\mathit{\operatorname{Minimize}}\kern1em {f}_1(x)= EP=\sum \limits_u\sum \limits_m\sum \limits_c\left({Ca}_{um}\kern0.5em {b}_{um}\kern0.5em {x}_{um c}\right)\\ {} Subject to:\\ {}C1\kern1.5em \left\{\begin{array}{l}{x}_{um c}+{z}_1\kern0.5em {\varGamma}_1+{p}_{1 umc}\le d{}_{um c}\kern0.48em \forall u,m,c\\ {}{z}_1+{p}_{1\; umc}\ge {\varepsilon}_d\kern0.5em {d}_{um c}\kern0.96em \forall u,m,c\end{array}\right.\\ {}C2\kern1.5em \left\{\begin{array}{l}\alpha {d}_{um c}+{z}_2\kern0.5em {\varGamma}_2+{p}_{2\; umc}\le {x}_{um c}\kern0.48em \forall u,m,c\\ {}{z}_2+{p}_{2\; umc}\ge \alpha \kern0.5em {\varepsilon}_d\kern0.5em {d}_{um c}\kern0.96em \forall u,m,c\end{array}\right.\\ {}C3\kern1.5em \left\{\begin{array}{l}\sum \limits_u\sum \limits_c{x}_{um c}+{z}_3\kern0.5em {\varGamma}_3+{p}_{3\;i}\le {Q}_m\kern0.48em \forall m\;\\ {}{z}_3+{p}_{3\;m}\ge {\varepsilon}^Q\kern0.5em {Q}_m\kern0.6em \forall m\end{array}\right.\\ {}C4\kern1.5em \left\{\begin{array}{l}\beta {Q}_m+{z}_4{\varGamma}_4+{p}_{4\;m}\le \sum \limits_u\sum \limits_c{x}_{um c}\kern1.5em \forall m\;\\ {}{z}_4+{p}_{4\;m}\ge {\varepsilon}_Q\kern0.5em \beta \kern0.5em {Q}_m\kern0.6em \forall m\end{array}\right.\\ {}C5\kern1.5em \sum \limits_u\sum \limits_c Pl{}_{um c}\le \sum \limits_{\mathrm{u}}{T}_{um}\kern0.48em \forall m\\ {}C6\kern1em \sum \limits_j\sum \limits_c CPD{}_{jc}N{B}_{jc}\kern1.5em \sum \limits_i{x}_{ijc}\ge {EI}_{goal}\end{array}} $$

(13)

For the EI (player 2), the DMOBM model can be rewritten as follows:

$$ {\displaystyle \begin{array}{l}\mathit{\operatorname{Maximize}}\kern1em {f}_2(x)= EI=\sum \limits_u\sum \limits_c{CPD}_{uc}\kern0.5em {NB}_{uc}\kern0.5em \sum \limits_i{x}_{um c}\;\\ {} Subject to:\\ {}F1\kern1.5em \left\{\begin{array}{l}{x}_{um c}+{z}_5\kern0.5em {\varGamma}_5+{p}_{5\; umc}\le d{}_{um c}\kern0.48em \forall u,m,c\\ {}{z}_5+{p}_{5\; umc}\ge {\varepsilon}_d\kern0.5em {d}_{um c}\kern0.96em \forall u,m,c\end{array}\right.\\ {}F2\kern1.5em \left\{\begin{array}{l}\alpha \kern0.5em {d}_{um c}+{z}_6\kern0.5em {\varGamma}_6+{p}_{6\; umc}\le {x}_{um c}\kern0.48em \forall u,m,c\\ {}{z}_6+{p}_{6\; umc}\ge \alpha \kern0.5em {\varepsilon}_d\kern0.5em {d}_{um c}\kern0.96em \forall u,m,c\end{array}\right.\\ {}F3\kern1.5em \left\{\begin{array}{l}\sum \limits_u\sum \limits_c{x}_{um c}+{z}_7\kern0.5em {\varGamma}_7+{p}_{7\;m}\le {Q}_m\kern0.48em \forall m\;\\ {}{z}_7+{p}_{7\;m}\ge {\varepsilon}^Q{Q}_m\kern0.6em \forall m\end{array}\right.\\ {}F4\kern1.5em \left\{\begin{array}{l}\beta \kern0.5em {Q}_m+{z}_8{\varGamma}_8+{p}_{8m}\le \sum \limits_u\sum \limits_c{x}_{um c}\kern0.36em \forall m\\ {}{z}_8+{p}_{8\;m}\ge \beta \kern0.5em {\varepsilon}_Q\kern0.5em {Q}_m\kern0.6em \forall m\end{array}\right.\\ {}F5\kern1.5em \sum \limits_u\sum \limits_c Pl{}_{um c}\le \sum \limits_uT{}_{um}\kern0.48em \forall m\\ {}F6\kern1.5em \sum \limits_u\sum \limits_m\sum \limits_c\left({Ca}_{um}{c}_{um}{x}_{um c}\right)\le {EP}_{goal}\end{array}} $$

(14)

where ε _d and ε _Q are uncertainty levels of d (water demand) and Q (available water), respectively, C1-C6 and F1-F6 are constraints of the problem. Also, as presented, the variables z _i and p _i are additional variables for robust counterpart formulation, and the parameter Γ_i is used to control the level of conservatism. Note that the counterpart form is only applied in formulations which contain uncertain parameters.

In order to investigate the effects of robustness on the RMOBM model, it was optimized for different uncertainty levels (ɛ) and constraint violation probabilities (P). The violation probabilities (P) ranged from 0.01 (most conservative state) to 1.0 (deterministic condition), and uncertainty levels were equal to ε = 0.01, ε = 0.05, and ε = 0.1.

Results and discussion

Results of DMOBM

In order to determine the variation range of two objective functions, each player computes the minimum and maximum values by running single objective function. It should be noted that, since the objective function and constraints of the problem are linear, it is easy to find the exact solutions of the problem in the developed models. The computed range of EP (player 1) was between EP_min = 17,396 and EP_max = 115,971 ton pollution loads per year, while the range of EI (player 2) were between EI_min = 74,324 and EI_max = 477,706 thousand dollars per year. As earlier discussed, these ranges are negotiation interval of bargaining process. The most desirable value for player 1 (17,396) is much less than EP_max = 115,971 ton pollution loads per year, while the best value for player 2 (478,842) is much higher than EI_min = 74,324 thousand dollars per year. After rerunning the model for several times, the f coefficient of Eq. (5) was selected to be 46. Based on the variation range of each objective function and Eq. (5), the strategy of players in the bargaining process was set (Goal column of Table 2).

Table 2 The results of deterministic multi-objective bargaining methodology (DMOBM)

The results of DMOBM model are shown in Table 2. The state *0–1 stands for initial bargaining round (0) for player 1, and the state *0–2 stands for initial bargaining round (0) of player 2. In the state *0–1, the initial goal value of player 2 (EI_goal = 477,706 10³ USD/year) was constrained in objective function of player 1, and then, EP was computed as 44,703 ton per year. Similarly, in the state *0–2, the initial goal value of player 1 (EP_goal = 17,396 ton/year) was constrained in the objective function of player 2, and therefore, EI was computed as 391,473 10³ USD/year. Since the computed EI (391,473) is less than EI_goal = 477,706 and the computed EP (44,703) is more than EP_goal = 17,396, none of the players are satisfied with the initial rounds of DMOBM results. Therefore, the players were entered into the bargaining process.

During the bargaining rounds, the players lowered their expectations. Accordingly, the environmental player reduced the environmental goal by rising pollution load from 17,396 to 19,539 tons per year, and the economic player decreased the economic goal by reducing economic income from 477,706 to 468,937 thousand dollars per year (Table 2). Even though the goals of the players are adjusted in the first bargaining round, both players still were not satisfied with the results of the other player’s goal. Thus, consequent rounds of bargaining were continued by revising the goals of each player and running the model. In the fourth round, the computed EP and EI were 24,919 ton per year and 447,999 thousand dollars per year, respectively. Based on these values, both players are satisfied with the results of the other player’s goal. Consequently, Nash equilibrium was reached (eq. 6). Hence, at Nash equilibrium condition EP ranged from 24,919 to 25,968 tons per year and EI ranged from 442,630 to 447,999 thousand dollars per year.

Table 2 highlights that by increasing the bargaining rounds, the annual allocated water to users is gradually converged together. For instance, in the initial round of bargaining, the annual allocated water to KNAI water user for player 1 and player 2 were 22.1 and 6.6 MCM per year, while in the fourth round, the allocated water to this area was 15.7 and 17.1 MCM per year, respectively. This occurred for water users of both donor and receiving basins. Note that the monthly water allocation values were added together to gain the yearly values. During this process, the total allocated water of player 1 (EP) decreased, whereas for player 2 (EI), it increased. Additionally, the results showed that, the allocated water to KLA was highly influenced and changed by increasing the bargaining rounds, while the allocated water to RA did not vary considerably. This can be due to the higher crop per drop of pistachio.

In Fig. 3, the results of DMOBM were compared with the results of ɛ-constraint method (which is a conventional multi-objective method). The Pareto optimal solutions of ɛ-constraint method are shown in Fig. 3a, and the Nash equilibrium solutions of DMOBM are shown in Fig. 3b. Accordingly, the wide ranges of Pareto optimal solutions may make it difficult to select a final solution. However, Nash equilibrium results had significantly smaller range of solution, in comparison to the Pareto front. This rather narrow range, which was obtained to be between 24,919 and 25,968 tons per year for EP and between 442,630 and 447,999 thousand dollars per year for EI may result in easier decision-making.

Fig. 3

Results of multi-objective methods. a ɛ-constraint approach. b DMOBM approach

In the conventional multi-objective method, the problem is solved as a single decision-making problem, and it only expresses the problem from an optimization viewpoint considering the minimum of EP and the maximum of EI. Its solutions may be utilized merely once there is no prejudgment available about environment versus economy. Unlike the conventional multi-objective methods, DMOBM approach provides a framework to incorporate the behavior of different stakeholders, which leads to find socially acceptable results (Carraro et al. 2007). In other words, DMOBM approach would be more useful for policy-making, since it provides a better understanding of stakeholders’ behavior.

Monthly allocated water to users at the Nash equilibrium for two objective functions is presented in Table 3. These values are related to the state *4–1 and *4–2 of Table 2. As discussed, two objective functions (Min. EP and Max. EI) met the goals at the fourth round of bargaining. Decision makers will select which one to apply. The environmentalists are willing to choose the lower pollution load option (minimization of EP), while the economists prefer to select the higher economic income results (maximization of EI).

Table 3 Monthly allocated water to users at Nash equilibrium of DMOBM approach (MCM/month)

Results of RMOBM

The values of Gama parameter (Γ) as a function of constraint violation probability (P) are given in Table 4. Γ = 0is related to conditions with no uncertainty (P = 1). Also, at the constraint violation probability of 0.01, the solution will remain feasible at least 99% of the time.

Table 4 Selection of Gamma based on the probability of constraint violation

Table 5 provides the optimal values of EP and EI for deterministic and robust problems, by considering three levels of uncertainty (0.01, 0.05, and 0.1) when Γ = 1. It is observed from this table that when the level of uncertainty increases, the required rounds of reaching Nash equilibrium will increase. For instance, for an uncertainty level of ɛ = 0.1, the required round to achieve Nash equilibrium changed from four to seven.

Table 5 Optimal economic and environmental solutions for deterministic and robust problems

In addition, application of the robust counterpart approach leads to change in values of the objective functions. Comparing the results of uncertainty level of ε = 0.1 with deterministic condition indicates that EI decreased to the range of 416,322 to 419,216 thousand dollars per year and EP increased to the range of 30,538 to 32,397 tons per year. Although by incorporating the uncertainty of the input data into the deterministic model, the economic benefits of the scheme decreased; the risk of achieving such an income also decreased. In other words, the RMOBM model has led to reliable solution with lower risk. It should be noted that since there is a trade-off between the conservatism degree and amounts of two objective functions, the manager of the water transfer scheme is able to adjust the robustness of the plan by changing the level of uncertainty.

It can also be seen from Table 5 that for both environmental and economic players, at higher uncertainty levels, allocated water to users of the donor basin (KNAI, KOAI, and KLA) increased, whereas the allocated water to user of RA decreased. For instance, as a result of robustness, allocated water of RA water user decreased for player 1 (environmentalist) from 142.9 to 130.9 MCM per year and for player 2 from 145.3 to 131.1 MCM per year. Accordingly, RMOBM approach led to a more conservative solution in such a way that less water was transferred, while lower income with high stability was achieved.

Table 6 gives the monthly allocated water to the users at the Nash equilibrium of RMOBM approach when ɛ and Γ were selected to be 0.1 and 1, respectively. These values are related to the state *7–1 and *7–2 of the Table 5. Both objective functions satisfied the goals at seventh bargaining rounds so decision maker can choose which one to apply. Meanwhile, these values insure reliability, fairness, and optimality of the solutions. Comparison of Tables 3 and 6 shows how robustness influences monthly allocated water of users. Although in comparison to DMOBM model, the yearly allocated water for both players decreased under RMOBM model and comparison of Tables 3 and 6 shows that the reduction did not happen for all months. For instance, in the case of player 1, April and in the case of player 2, April and September were exceptions. Both solutions of Table 6 (Min EP and Max EI) can be utilized depending on the choice of decision maker. The environmental player prefers to select the lower pollution load choice (Min EP), while the economic player is willing to choose the higher economic income option (Max EI).

Table 6 Monthly allocated water to users at the Nash equilibrium of RMOBM approach when ε = 0.1 (MCM/month)

Sensitivity analysis

In order to show how objective function values change with respect to variations in uncertain parameters, a sensitivity analysis was performed. It can provide information for investigating the effects of robustness levels on the RMOBM model. The sensitivity analysis was performed using different constraint violation probabilities (conservatism degree) at given uncertainty levels (ɛ = 0.01, ɛ = 0.05, and ɛ = 0. 1).

The amount of deterioration in environmental and economic objective functions with different levels of conservatism and uncertainties is shown in Fig. 4. This figure shows that reducing conservatism level (violation probability is increased) results in decreasing the environmental objective function and increasing the economic objective function. The bigger the uncertainty level, the greater the impacts on objective function changes will be. Meanwhile, the optimal values of objective functions depend on both constraint violation probability (P) and uncertainty level (ɛ).

Fig. 4

Sensitivity of environmental pollution (EP) and economic income (EI) to different robustness levels

The results also demonstrate that up to violation probability of 0.5 (P = 0.5), the performances of three uncertainty levels are equal without any changes. In the case of violation probability more than P = 0.5, EP and EI values decreased and increased at different uncertainty levels, respectively. Higher levels of uncertainty lead to greater changes in values of both objective functions. The responses of two objective functions to changes in parameters were similar, but reverse. At uncertainty levels of 0.01, 0.05, and 0.1, the value of EP decreased by 3.5, 8.1, and 16.9%, and the value of EI increased by 1, 4.1, and 8.6%, respectively. In comparison to EP, EI values are less sensitive to changes in uncertain parameters.

Conclusions

In this study, a new methodology has been developed for planning water allocation issues of inter-basin water transfer schemes in the presence of uncertainty. This method has been applied to large-scale case study of transferring water from Karoon to Rafsanjan basin, to investigate its efficiency. The developed model (RMOBM) had following capabilities: (1) considering different stakeholders’ interests, (2) balancing economic and environmental concerns of the problem, and (3) remaining reliable in the face of data uncertainties.

The DMOBM presents a compromise between environmental protection and economic income in water resource allocation problems. In comparison to a conventional multi-objective method, it has provided slightly a narrow range of solutions, which makes the decision-making process easier. The RMOBM model can handle data uncertainties without adding extra complexity to the DMOBM model and specifying PDFs of uncertain parameters. The linearity of it has led to low run-time and made it easy to find global solutions.

The results showed that by considering the uncertainty of the input data into the DMOBM model using robust counterpart optimization, the economic income of the scheme decreased. Meanwhile, these solutions are more reliable as a result of hedging against uncertainties. The finding revealed that increasing the uncertainty level leads to increase in the required rounds to reach Nash equilibrium. Also, the robustness results in an increasing and decreasing of the value of the allocated water to users of the donor and receiving basins, respectively. Hence, the transferred water was reduced from the range of 142.9–145.3 MCM per year under deterministic condition to the range of 130.6–131.1 MCM per year under uncertainty level of 0.1. Sensitivity analysis illustrates that the optimal solutions of two objective functions depend upon both values of constraint violation probability and level of uncertainty. The bigger these values, the greater the impacts on objective function changes will be. However, economic income has been less sensitive to changes of uncertain parameters than environmental pollution.

The developed methodology could balance the scheme economically and environmentally. It has also considered both quantity and quality issues of water allocation problem and could immune the model against uncertainties. Therefore, it can be applied as a comprehensive decision-making approach to water allocation schemes and sustainable development.