Introduction

Municipal and industrial wastewaters from human activities are the major factors that contribute to the deterioration of water quality in urban areas. Water quality (WQ) can be used to assess the water properties in reference to human health and natural quality effects. The poor quality of surface water is a serious problem in the world which threatens human health, ecosystems, and plant/animal life. Consequently, water quality analysis has become a main concern in water resource and environmental systems (Espejo et al. 2012; Vanlandeghem et al. 2012; Zhang et al. 2013a, b; Wang et al. 2012). In terms of environmental and ecological problems, the number of water quality parameters is quite extensive. Hence, a robust mathematical technique is required to combine the physicochemical characterization of water into a single variable which describes the water quality. A water quality index (WQI) is a single number which uses a set of physicochemical water parameters to express the quality of water at a certain place and time.

In 1974, the Department of Environment of Malaysia (DoE) recommended the WQI parameter for categorizing and estimating water quality. Based on this parameter, the water quality was classified into five different classes according to the water’s suitability for various uses such as water supplies, irrigation, and fish culture. The conventional method suggested by DoE requires lengthy transformations to estimate subindices. In addition, the subindices required the inclusion of different equations, which need lengthy effort and time to calculate the final WQI. Therefore, estimation of such a WQI is cumbersome and can lead to occasional mistakes. However, the support vector machine (SVM) and artificial neural networks (ANNs) can be suggested as alternatives for estimation of WQI, as both employ the raw data instead of subindices.

The performance of free surface wetlands to enhance water quality and reduce a wide range of wastewater was reported in several studies (Zedler and Kercher 2005; Vymazal 2011; Zhang et al. 2012; Wang et al. 2012; Shih et al. 2013; Mohammadpour et al. 2014). Wetlands have high ability to absorb and reduce agriculture and municipal wastewater and can also highly decrease various nutrients (Mitsch and Gosselink 2007; Kadlec and Wallace 2008). To remove pollutants and nutrients associated with fine particulates, several processes occur in the constructed wetlands such as settling, filtration, absorption, and biological uptake (Guardo 1999). Generally, three parts can be recognized in the free surface wetlands such as inlet, macrophyte, and open water area (Zakaria et al. 2003). The macrophyte area (wetland plants) has a high effect on the wetland ecosystem and water quality (Brix 1997; Kadlec and Wallace 2008). Since the number of variables which affect water quality is too high, the SVM can be proposed as a robust technique for prediction of water quality in a free constructed wetland environment.

Recently, soft computing techniques such as SVM, genetic programming (GP), and ANNs have been successfully employed to solve the problems related to engineering (Mohammadpour et al. 2011; Tabari et al. 2012; Kakaei Lafdani et al. 2013; Mohammadpour et al. 2013b; Ghani and Azamathulla 2014; He et al. 2014). The SVM is proposed as a leading technique which can be used for regression and classification purposes (Noori et al. 2011; Singh et al. 2011a, b). The SVM has high ability for generalization and is less prone to overfitting. Furthermore, it simultaneously minimizes the estimation of error and model dimensions (Singh et al. 2011a, b; Li et al. 2013). Sivapragasam and Muttil (2005) applied the SVM for prediction of water level in rivers by extension of rating curves. Khan and Coulibaly (2006) recommended the SVM as the appropriate tool to forecast lake water levels and obtained quite acceptable results. Singh et al. (2011a, b) employed the SVM for classification and regression of water quality. The SVM was applied as a classification tool for some studies related to wetlands (Dronova et al. 2012; Betbeder et al. 2013; Zhang and Xie 2013). Sadeghi et al. (2012) predicted the distribution pattern of Azolla filiculoides (Lam.) in wetlands using the SVM.

The ANNs have been recommended as an effective tool for the prediction of water pollution and water quality in the wetlands (Schmid and Koskiaho 2006; Wang et al. 2012; Dong et al. 2012; Dadaser-Celik and Cengiz 2013; Li et al. 2013; Song et al. 2013). The ANNs were employed to model the constructed wetlands in different fields (Tomenko et al. 2007; Singh et al. 2011a, b; Zhang et al. 2013a, b). The ANNs are a useful technique that was used to speed up the calculation of water quality index in rivers (Khuan et al. 2002; Juahir et al. 2004; Gazzaz et al. 2012). Mohammadpour et al. (2013a) examined two kinds of ANNs, feed forward back propagation (FFBP) and radial basis function (RBF), for the prediction of time variation of local scour in rivers. Nourani et al. (2013) applied the FFBP network to determine the quality of treated water. Diamantopoulou et al. (2005) used the neural networks to predict water quality in a river in Greece. Khalil et al. (2011) estimated water quality characteristics at ungauged sites using ANN and ensemble ANN (EANN). The results showed that the EANN provides better prediction than the ANN.

In this research, both SVM and ANNs were used as robust techniques for rapid and direct prediction of the WQI in the constructed wetlands which can be used as another alternative for some long-lasting conventional methods. Seventeen points in the wetland were monitored twice a month over a period of 14 months and an extensive dataset was collected for 11 water quality variables. A sensitivity analysis was conducted to find more significant variables on WQI. Finally, the SVM result was compared with two models of neural networks, namely the FFBP and RBF.

Materials and methods

Study area

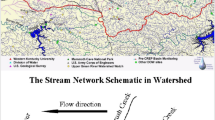
The free surface constructed wetland in the Universiti Sains Malaysia (USM) was chosen as a case study in this research. The wetland is covered by different kinds of plant species where the Hanguana malayana was the dominant species. The volume of wetland is 16,312 m3 with a water depth between 0.25 and 2.54 m from inlet to outlet of the wetland (Table 1). The wetland is located at latitude 5° 9′ 7.8294″ North and longitude 100° 29′ 53.1672″ East. It was designed based on the Stormwater Management Manual for Malaysia to improve water quality and provide better wildlife habitat (Zakaria et al. 2003; Shaharuddin et al. 2013). Seventeen sampling points with different plant species and water depths were chosen to monitor the water quality. As shown in Fig. 1, these points included the inlet, six stations in macrophyte area (W1 to W6), nine points in micropool (MA1 to MC3), and the outlet.

Table 1 Plant species and the water depth in the USM wetland
Full size table
Fig. 1
figure 1

Seventeen sample points in the constructed wetland of USM

Full size image

The data collection was carried out twice a month over a period of 14 months (from October 2010 to December 2011). Totally, 11 water quality variables (WQVs) were collected in the wetland, including temperature, pH, dissolved oxygen (DO), conductivity, suspended solid (SS), nitrite, nitrate, ammoniacal nitrogen (AN), biochemical oxygen demand (BOD), chemical oxygen demand (COD), and phosphate. The final dataset consisted of 442 samples and 11 WQVs. Table 2 indicates the statistical parameters of WQVs in the wetland.

Table 2 Descriptive statistics of wetland parameters (number of data = 442)
Full size table

The local water quality index

To determine the WQI, six physicochemical parameters were proposed by Department of Environment (DoE 2005), namely DO, BOD, COD, AN, SS, and pH. The WQI was recognized as a unitless variable with a value from 0 to 100, where a high value of WQI represents high water quality. As shown in Table 2, the mentioned WQVs should be converted into nondimensional variables using subindex functions (SI). Finally, the WQI can be estimated using the following equation (DoE 2005; Khuan et al. 2002):

$$ \mathrm{W}\mathrm{Q}\mathrm{I}=0.22\;{\mathrm{SI}}_{\mathrm{DO}}+0.19\;{\mathrm{SI}}_{\mathrm{BOD}}+0.16\;{\mathrm{SI}}_{\mathrm{COD}}+0.15\;{\mathrm{SI}}_{\mathrm{AN}}+0.16\;{\mathrm{SI}}_{\mathrm{SS}}+0.12\;{\mathrm{SI}}_{\mathrm{pH}} $$
(1)

The subindices equations were provided in Table 3, where X is the concentration parameter in terms of mg/l, except for pH and DO. For DO, the X refers to the percentage of saturation, and for pH, it refers to the pH value. According to the calculated WQI, the water can be classified into one of five classes. Table 4 shows the water quality classes suggested by the DoE.

Table 3 The subindex equation for WQI in Malaysia (DoE 2005)
Full size table
Table 4 Water quality classes, WQI, and water status (DoE 2005)
Full size table

Support vector machine technique

The SVM proposed by Vapnik (1995, 1998) was developed based on the statistical learning theory. The SVM is a novel classification technique which uses the principle of structural risk minimization (SRM) and transforms it into quadratic programming.

The SVM uses suitable kernel function to map the original data into a high-dimensional feature space where a maximal separating plane (SP) is constructed. To separate the data, two parallel hyperplanes can be developed on each side of the SP. The SVM simultaneously maximizes the geometric margin and minimizes the empirical classification error (Singh et al. 2011a, b). The SVM was extended to solve the regression problems with the introduction of ε-insensitive loss function (Pan et al. 2008). In this case, the SVM attempts to determine the optimal hyperplane which minimizes the distance of all data points (Qu and Zuo 2010; Lin et al. 2008).

A detailed expression of the SVM may be found elsewhere (Vapnik 1995; Smola and Scholkopf 2004). However, a brief discussion of this technique is mentioned here. For a set of training data {x i , y i }, the objective of SVM is to determine a function f(x) with high deviation (ε) from targets (y i ) and it should be flat as possible at the same time. If f(x) is introduced as a linear discriminant function, then the SVM can be presented as (Smola and Scholkopf 2004):

$$ f(x)=\left(w,x\right)+b $$
(2)

where w is the weight vector (w∈R n), and b is the bias. The f(x) function is flatted by minimizing the values of w. Using a convex optimization problem, minimization can be expressed as (Singh et al. 2011a, b):

$$ \left\{\begin{array}{l}\mathrm{Minimize}\frac{1}{2}{\left\Vert w\right\Vert}^2\\ {}\mathrm{subject}\;\mathrm{t}\mathrm{o}\left\{\begin{array}{l}{y}_i-\left(w,{x}_i\right)-b\le \varepsilon \\ {}\left(w,{x}_i\right)+b-{y}_i\le \varepsilon \end{array}\right.\end{array}\right. $$
(3)

The last equation in some cases with more errors can be introduced with slack variables ξ i , then minimization formula changes as follows: (Vapnik 1995):

$$ \left\{\begin{array}{l}\mathrm{Minimize}\frac{1}{2}{\left\Vert w\right\Vert}^2+C{\displaystyle \sum_{i=1}^m\left({\xi}_i+{\xi}_i^{*}\right)}\\ {}\mathrm{subject}\;\mathrm{t}\mathrm{o}\left\{\begin{array}{l}{y}_i-\left({w}_i,{x}_i\right)-b\le \varepsilon +{\xi}_i\\ {}\left(w,{x}_i\right)+b-{y}_i\le \varepsilon +{\xi}_i^{*}\\ {}{\xi}_i,{\xi}_i^{*}\ge 0\end{array}\right.\end{array}\right. $$
(4)

The C is a penalty parameter, and it should be defined by the user. This parameter determines the trade-off between the tolerable amount larger than ε and flatness of f(x). The Lagrangian form of minimization formula can be express as:

$$ \begin{array}{l}L=\frac{1}{2}{\left\Vert w\right\Vert}^2+C{\displaystyle \sum_{i=1}^m\left({\xi}_i+{\xi}_i^{*}\right)}-{\displaystyle \sum_{i=1}^m\left({\eta}_i{\xi}_i+{\eta}_i^{*}{\xi}_i^{*}\right)}-{\displaystyle \sum_{i=1}^m{\alpha}_i\left({\varepsilon}_i+{\xi}_i-{y}_i+\left(w,{x}_i\right)+b\right)}\\ {}-{\displaystyle \sum_{i=1}^m{\alpha}_i^{*}\left({\varepsilon}_i+{\xi}_i-{y}_i+\left(w,{x}_i\right)+b\right)};\\ {}\left\{\begin{array}{l}{\alpha}_i,{\eta}_i\ge 0\\ {}{\alpha}_i^{*},{\eta}_i^{*}\ge 0\end{array}\right.\end{array} $$
(5)

where are α i, η i , α i *, and η i * are Lagrangian parameters. The saddle points of Eq. (5) can be estimated as:

$$ \frac{\partial L}{\partial b}=0\kern1em \mathrm{then}\kern1em {\displaystyle \sum_{i=1}^m\left({\alpha}_i^{*}-{\alpha}_i\right)=0} $$
(6)
$$ \frac{\partial L}{\partial w}=0\kern1em \mathrm{then}\kern1em w-{\displaystyle \sum_{i=1}^m\left({\alpha}_i^{*}-{\alpha}_i\right){x}_i=0} $$
(7)
$$ \frac{\partial L}{\partial {\xi}_i^{*}}=0\kern1em \mathrm{then}\kern1em C-{\alpha}_i^{*}-{\eta}_i^{*}=0 $$
(8)

Dual maximization problem is determined by substituting Eqs. (6) to (8) into Eq. (5) as (Smola and Scholkopf 2004):

$$ \mathrm{Maximize}\left\{-,\frac{1}{2},{\displaystyle \sum_{i=1}^m\left({\alpha}_i^{*}-{\alpha}_i\right)\left({\alpha}_j-{\alpha}_j^{*}\right)\left({x}_i,{x}_j\right)},-,\varepsilon, {\displaystyle \sum_{i=1}^m\left({\alpha}_j+{\alpha}_j^{*}\right)+{\displaystyle \sum_{i=1}^m{y}_i\left({\alpha}_j-{\alpha}_j^{*}\right)}}\right.\mathrm{subject}\;\mathrm{t}\mathrm{o}{\displaystyle \sum_{i=1}^m\left({\alpha}_j-{\alpha}_j^{*}\right)=0\kern0.5em \mathrm{and}\kern0.5em {\alpha}_i,{\alpha}_i^{*}}\in \left[0,C\right] $$
(9)

Finally the SVM function can be expressed as:

$$ f(x)={\displaystyle \sum_{i=1}^m\left({\alpha}_i-{\alpha}_i^{*}\right)\left({x}_i,{x}_j\right)+b} $$
(10)

The kernel function was used to solve the nonlinear problem in the support vector regression. This function maps the data into higher dimension feature space (Vapnik 1995). The support vector regression problem in the feature space was expressed using K(x i , x j ) instead of (x i , x j ), then the SVM can be written as:

$$ f(x)={\displaystyle \sum_{i=1}^m\left({\alpha}_i-{\alpha}_i^{*}\right)K\left({x}_i,{x}_j\right)+b} $$
(11)

Four possible choices for the kernel function are suggested, namely linear, polynomial, sigmoid, and radial Gaussian. The most common kernel functions are polynomial and Gaussian or RBF which were expressed as:

$$ K\left({x}_i,{x}_j\right)={\left(1+{x}_i.{x}_j\right)}^p\;\mathrm{Polynomial}\;\mathrm{kernel}\;\mathrm{function} $$
(12)
$$ K\left({x}_i,{x}_j\right)= \exp \left(-\gamma {\left\Vert {x}_i.{x}_j\right\Vert}^2\right)\mathrm{Gaussian}\;\mathrm{kernel}\;\mathrm{function} $$
(13)

where p and γ are adjustable kernel parameters. The performance of SVM depends on the combination of several parameters, such as the type of kernel function and its adjustable parameters, penalty parameter, C, and ε-insensitive loss function. The selection of kernel function depends on the distribution of the data and generally can be selected through the trial and error approach (Widodo and Yang 2007). Since the RBF is employed in most of the applications (Xie et al. 2008), then in this study, the RBF (Gaussian kernel function) was chosen as kernel function for the prediction of WQI.

The γ is the most important parameter for the RBF kernel function. The amplitude of the kernel can be controlled by this parameter, and it can lead to overfitting and underfitting in prediction. The best value of γ can be found by trial and error (Noori et al. 2011). The C is a regularization parameter that controls the trade-off between maximizing the margin and minimizing the training error. For a low value of C, insufficient fitting will be placed on the training data, while the algorithm will overfit for too large of C (Wang et al. 2007). A well-performing and robust regression model is dependent on a proper choice of C in combination with ε (Ustun et al. 2005). A range of 0.001–20,000 was chosen for the C parameter to investigate the optimal value (Fig. 3). Furthermore, since the exact contribution of the noise in the training set is usually unknown, the ε was optimized in the range of 0.00001 and 0.1 (Ustun et al. 2005). To achieve a good combination of the two variables (C and ε), an internal cross-validation was performed during the construction of the SVM model. In this study, the SVM-base classification was performed using Library for Support Vector Machines (LIBSVM) in MATLAB (Chang and Lin 2011).

Artificial neural network methods

ANNs are a computational process which attempts to represent and compute a mapping from multivariate dataset as inputs to another as outputs. A neuron is the smallest part of the neural network; these artificial neurons are arranged in the structure like a network. In this study, two models of neural networks, FFBP and RBF, were presented and a brief description of these methods are given here.

Feed forward back propagation neural network

The network consists of a set of neurons in three, inputs, hidden, and output, layers to approximate a multivariant function f(x). The number of neurons in hidden layers can be detected by trial and error. The learning procedure includes the best weight vector to achieve the best approximation of f(x). Firstly, a set of input data (x 1,x 2,…x R) is fed to the input layer, and the output of each neuron can be determined from the following relation:

$$ n={{\displaystyle \sum {w}_{i\;j}{x}_i+b}}_i $$
(14)

where n is the neuron output, w ij is the weight of the connection between the jth neuron in the present layer and ith neuron in the previous layer, x i is the neuron value in the previous layer, and b i is the bias. The sigmoid function can be used as a transfer function to generate the output of each neuron (Bateni et al. 2007) given by:

$$ {y}_i=\frac{1}{1+{e}^{-{C}_1\left({\displaystyle \sum {w}_{i\;j}}{x}_i+{b}_i\right)}},{C}_1>0 $$
(15)

The network error calculation uses a comparison between the target value and the obtained results, while the back propagation algorithm corrects the weight between neurons. The back propagation (BP) method is a descent algorithm, which tries to minimize the error at each iteration. The network weights are set by the algorithm such that the network error decreases along a descent direction (gradient descent). Generally, two parameters, called momentum factor (MF) and learning rate (LR), are used to control the weight adjustment in the descent direction.

Radial basis function neural network

The RBF network is a general regression tool for approximate function that uses a radial basis function as activation function. In this study, the Softmax transfer function is used to estimate the ∅ value at each node.

$$ {\varphi}_j(x)=\frac{ \exp \left(-\frac{{\left\Vert x-{\mu}_j\right\Vert}^2}{2{\sigma}_j^2}\right)}{{\displaystyle \sum \exp \left(-\frac{{\left\Vert x-{\mu}_j\right\Vert}^2}{2{\sigma}_j^2}\right)}} $$
(16)

where x is the input dataset, μ j is the center of the radial basis function for the jth hidden node, σ j is a radius of the radial basis function for the jth hidden node, and ‖x − μ j ‖2 is the Euclidean norm. The linear interconnectedness between network outputs and hidden nodes can be explained by the following equation:

$$ {y}_k={\displaystyle \sum {w}_{k\;j}{\varphi}_j}(x) $$
(17)

where y k is the kth component of the output layer, and w kj is the weight between the jth hidden node and kth node of the output layer.

In this study, the collected dataset was normalized within the range of 0.1–0.9. Three common statistical measures, namely the coefficient of correlation (R 2), root mean square error (RMSE), and mean absolute error (MAE), were used to validate the provided results.

Results and discussion

Determining the main water quality variables

To determine the main WQVs in the prediction of the WQI, a sensitivity analysis was carried out using ANN. The sensitivity analysis was conducted using the FFBP network with one hidden layer. The number of neurons in the input layer was determined based on the number of WQVs as input to ANN. In the output, a layer with one neuron was chosen for WQI. The leave-one-out technique was employed to assess the effect of each variable on the WQI. By removing one variable in the input at each time, two indicators were determined, namely the ratio of ANN error and its rank (Ha and Stenstrom 2003). The ratio of ANN error was found by removing an individual variable to the error obtained using all variables. The high value for this ratio can be interpreted as high significance of individual variable and vice versa. The result of this analysis is shown in Table 5. Generally, in the environmental works, the simple equations with a few variables are more practical and useful in comparison with complex equations. Therefore, another sensitivity analysis was conducted to simplify the classification and reduce the number of variables on WQI. Table 6 compares the ANN models with one of the independent variables removed in each case. As shown in this table, pH, COD, DO, AN, and SS are significant variables, with a high performance of ANNs (R 2 = 0.9882, RMSE = 0.0179, and MAE = 0.0136). The performance of ANNs decreases with removal of one of these variables in the next rows. Therefore, these variables were chosen to develop the SVM, FFBP, and ANNs-RBF models. It was observed that removing more variables such as BOD, phosphate, nitrate, nitrite, and conductivity has no considerably effect on the performance of ANNs. In light of these findings, the pH with the highest rank in the sensitive analysis can be considered as a main parameter (Table 5), while it is ranked as the sixth variable in the conventional WQI equation (Eq. 1). This equation is recommended for estimation of WQI in the rivers, and the difference between ranking of pH in Eq. 1 and the present study can be due to the discharge at the point source and nonpoint pollution to rivers. However, the selected wetland is discharged just by nonpoint source pollution due to storm water. Same ranking results were observed by Gazzaz et al. (2012). This point may be considered for re-establishment of a new equation for WQI in the wetlands and other water resource with nonpoint pollution discharge.

Table 5 Sensitivity analysis using ANNs
Full size table
Table 6 Sensitivity analysis using different variables
Full size table

The SVM result

Based on the provided result by sensitivity analysis, all 11 water quality variables can be reduced to just six significant variables including pH, COD, DO, AN, SS, and BOD. In the present study, the selected dataset (442 samples × 6 variables) was randomly divided into training dataset (354 samples × 7 variables) and testing subsets dataset (88 samples × 7 variables). Thus, the training and validation (testing) dataset were comprised of 80 and 20 % of samples, respectively. Table 7 summarizes the range of training and testing dataset.

Table 7 Range of data used for training and testing
Full size table

The SVM models with different values of γ were developed to determine the best value for this parameter. The RMSE was chosen to assess the accuracy of SVM models. Figure 2 indicates that the minimum error was obtained for γ = 0.9, and this value was chosen to determine C and ε in the next steps. Furthermore, a tenfold cross-validation and grid search algorithm were employed to find the optimal values of C and ε (Hsu et al. 2003).

Fig. 2
figure 2

Variation of gamma values in terms of RMSE in the SVM model

Full size image

In tenfold cross-validation, the collected data were randomly divided into ten equal groups, where eight groups were used for training, and the rest of the groups were employed for validation. The grid search algorithm takes different samples from the space of the independent variables. In each step, the prediction of the model was compared with the best value provided from the previous iterations. If the newly found values were better than the previous one, the new values were used. The grid search algorithm is an unguided technique, and it was developed based on trial and error (Hsu et al. 2003; Noori et al. 2011). A two-step grid search with cross-validation was employed to solve this problem and determine the tune values of C and ε (Chen and Yu 2007). In the first step, a coarse grid search was applied to determine the best region of demanded parameters. In the next step, a finer grid search was employed to recognize the optimal combination of parameters. In Fig. 3, the accuracy of SVM was assessed regarding C and ε values. Through a coarse grid search (Fig. 3a), the optimum values of C and ε were determined over a space of 10–100 and 0.0001–0.01, respectively. Finally, the best value of C and ε was found equal to 57 and 0.007 through the fine grid search (Fig. 3b).

Fig. 3
figure 3

The accuracy of SVM model in terms of C and ε: a coarse grid, b fine grid

Full size image

The neural network results

The ANN model was developed using the same dataset employed for the SVM. Figure 4 indicates the architecture of FFBP with six neurons in the input layer for WQVs and one neuron in the output layer for WQI. Two types of ANNs, FFBP and RBF, were developed to investigate the best network for the reliable prediction of WQI. Based on trial and error, the FFBP network with 2000 epochs and the RBF network with the spread constant of 1.1 provided better results in comparison to the other networks.

Fig. 4
figure 4

Architecture of neural network for free constructed wetland

Full size image

Since the ANNs are sensitive to the number of neurons in the hidden layer and these neurons were unknown in the first step, then the ANNs were developed with different numbers of neurons in the hidden layer. The RMSE was employed to assess overfitting of network (low training error but high test error). As shown in Fig. 5, the RMSE decreased dramatically with increasing number of neurons in the hidden layer, especially in the FFBP method. An overfitting was observed in the FFBP networks when the number of neurons was more than 16. The performance of both FFBP and RBF with different neurons in the hidden layer is indicated in Table 8.

Fig. 5
figure 5

Variation of RMSE for testing data in terms of the number of neurons

Full size image
Table 8 List of statistical data for training and testing
Full size table

The testing data was assessed to find the optimum number of neurons. The best performance for FFBP and RBF was provided for networks with six and 40 neurons in the hidden layer. For testing data, the FFBP with R 2 = 0.9988, RMSE = 0.0056, and MAE = 0.0044 predicts the WQI with high accuracy. As shown in this table, the accuracy of RBF (R 2 = 0.9960, RMSE = 0.0103, and MAE = 0.0080) is a little lower than the FFBP method.

Comparison between SVM and ANNs

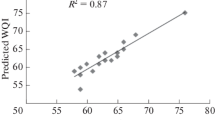
In Table 9, the performance of the SVM was compared with both the FFBP and RBF models. The SVM with R 2 = 0.9984, RMSE = 0.0066, and MAE = 0.0052 forecasts the WQI in the wetland better than the RBF (R 2 = 0.9960, RMSE = 0.0103, and MAE = 0.0080). Furthermore, statistical parameters and scatter plot (Fig. 6) show that the prediction of SVM is comparable with FFBP with R 2 = 0.9988, RMSE = 0.0056, and MAE = 0.0044.

Table 9 Comparison of three techniques to predict WQI in constructed wetland
Full size table
Fig. 6
figure 6

Comparison between predicted and observed WQI

Full size image

In light of this research, it can be concluded that to predict the WQI in free surface constructed wetland environment, both the SVM and FFBP propose some advantages over the conventional method. The method recommended by DoE (2005) employs six subindices parameters, which need more effort and a long time to convert the six raw data (DO, BOD, COD, AN, SS, and pH) into its subindices (Table 3). Furthermore, instead of using the original parameters, all calculations are based on the subindices (Eq. 1) which are obtained from rating curves. In contrast, both the SVM and FFBP approaches use the raw WQVs for training and testing rather than the subindices which led to a direct prediction of the WQI. Therefore, the SVM and FFBP methods are more direct, rapid, and convenient techniques than the conventional method.

Accordingly, this research highlights that the SVM and FFBP can be used as valuable methods for the prediction of water quality in the constructed wetland as they simplify the calculation of the WQI and reduce substantial efforts and time by optimizing the computations. These approaches can be commonly used for any aquatic system in the world. This research should encourage the managers and authorities to use the SVM and FFBP methods as more direct and highly reliable alternatives to predict water quality in wetlands and other water bodies.

Conclusions

In this study, the SVM and two methods of ANNs, namely FFBP and RBF, were employed to investigate the WQI in the free surface constructed wetland. Seventeen points of the wetland were monitored twice a month over a period of 14 months, and an extensive dataset was collected for 11 water quality variables. A sensitivity analysis was carried out using ANN and six significant variables that included pH, COD, DO, AN, SS, and BOD to develop the SVM, FFBP, and ANNs-RBF models. The results illustrate that the SVM technique was able to successfully predict the WQI with high accuracy. The high value of the coefficient of correlation (R 2 = 0.9984) and low error (MAE = 0.0052) indicated that the SVM model provides better prediction compared to the RBF network with R 2 = 0.9960 and MAE = 0.0080. Furthermore, the result provided by SVM was comparable with that of the FFBP network (R 2 = 0.9988 and MAE = 0.0044). This research highlights that the SVM and FFBP can be successfully used as valuable methods for the prediction of water quality in the wetlands. These methods simplify the calculation of the WQI and decrease the substantial efforts and time by optimizing the computations. The mentioned approaches can be commonly used as more direct and highly reliable techniques to predict water quality at any aquatic system worldwide.