Path-Integrated X-Ray Images for Multi-Surface Digital Image Correlation (PI-DIC)

Abstract

Background

X-ray imaging offers unique possibilities for Digital Image Correlation (DIC), opening the door for full-field deformation measurements of a test article in complex environments where optical DIC suffers severe biases or is impossible. While X-ray DIC has been performed in the past with standard DIC codes designed for optical images, the path-integrated nature of X-ray images places constraints on the experimental setup, predominantly that only a single surface of interest moves/deforms. These requirements are difficult to realize for many practical situations and limit the amount of information that can be garnered in a single test. Other X-ray based diagnostics such as Digital Volume Correlation (DVC) and Projection DVC (P-DVC) overcome these obstacles, but DVC is limited to quasi-static tests, and both DVC and P-DVC necessitate high-resolution computed tomography (CT) scan(s) and often require a potentially invasive pattern throughout the volume of the specimen.

Objective

This work presents a novel approach to measure time-resolved displacements and strains on multiple surfaces from a single series of 2D, path-integrated (PI) X-ray images, called PI-DIC.

Methods

The principle of optical flow or conservation of intensity—the foundation of DIC—was reframed for path-integrated images, for an exemplar setup comprised of two plates moving and deforming independently. Synthetic images were generated for rigid translations, rigid rotations, and uniform stretches, where each plate underwent a unique motion/deformation. Experimental specimens were fabricated (either an aluminum plate with tantalum features or a plastic plate with steel features) and the two specimens were independently translated.

Results

PI-DIC was successfully demonstrated with the synthetic images and validated with the experimental images. Prescribed displacements were recovered for each plate from the single set of path-integrated, deformed images. Errors were approximately 0.02 px for the synthetic images with 1.5% image noise, and 0.05 px for the experimental images.

Conclusions

These results provide the foundation for PI-DIC to measure motion and deformation of multiple, independent surfaces with subpixel accuracy from a single series of path-integrated X-ray images.

Introduction

Digital Image Correlation (DIC) is a powerful diagnostic technique providing full-field measurements of shape and deformation of solid parts. However, DIC traditionally requires optical access to the specimen, which can be impractical for some challenging and complex tests. For example, Fig. 1(a) shows a test specimen (aluminum-clad, fiber-reinforced epoxy composite cylinder) subjected to thermal loading in a custom thermal chamber [1]. Even if the chamber were modified to provide optical access, heat waves at temperatures greater than 600 °C and flames from combusting gasses from decomposing epoxy would severely degrade or completely disrupt optical DIC measurements. In general, optical DIC suffers from significant susceptibility to disturbances in the air between the surface of interest and the camera, like heat waves or shocks [2,3,4,5,6,7,8,9,10,11,12,13,14]. Moreover, optical DIC does not allow for internal measurements, where the surface of interest is not visible. 

Fig. 1

Example of an extreme test environment requiring X-ray DIC [1]. (a) Lack of optical access in custom thermal chamber, severe heat waves at temperatures greater than 600 °C, and flames from combusting gasses prevent use of optical DIC. (b) Change in radius of one sector of a cylindrical test specimen successfully measured with stereo X-ray DIC. (c) Asymmetry of test specimen deformation motivates multi-surface X-ray DIC

X-ray imaging has been employed for DIC to combat these shortcomings of optical DIC. The first demonstrations were for 2D-DIC, where a single plane was seeded with high-density, X-ray opaque particles to create a pattern. X-ray images were captured before, during (in some cases), and after deformation, and different types of cross-correlation or DIC algorithms were used to measure 2D displacements of the seeded plane [15,16,17,18,19]. As an alternative to seeding a plane, radiographs of heterogeneous samples have also been used for 2D-DIC, resulting in thickness-averaged displacement and strain results [20, 21].

To extend from 2D to 3D displacement measurements on a single surface, stereo X-ray DIC was developed [22], with this first demonstration requiring manual measurements with a ruler of the equipment geometry in order to calibrate the stereo imaging system. Stereo X-ray DIC was improved by developing X-ray specific calibration targets, allowing the X-ray images to be processed with commercial DIC software without modification to either calibration or correlation algorithms [23]. Past efforts at Sandia National Laboratories have benchmarked stereo X-ray DIC in several applications: (1) X-ray DIC captured the motion of a rigid translating plate comparably to optical DIC and proved far superior when heat waves were introduced [23]; (2) X-ray DIC eliminated errors from imaging through density gradients in a fluid flow in time-resolved (10 kHz) fluid structure interactions within a shock tube [24]; (3) X-ray DIC accurately measured mode shapes in structural dynamics testing at 4096 Hz [25]; and (4) X-ray DIC was demonstrated on a completely occluded aluminum-clad composite cylinder subjected to radiant heating and ultimately combustion (Fig. 1) [1].

This prior work on “single-surface” X-ray DIC employed standard, optical DIC algorithms to infer displacements from a single patterned surface in either two (2D-DIC) or three (stereo-DIC) directions. The direct substitution of X-ray images for optical images was made possible by realizing several constraints on the experimental setup: (1) only one surface of interest can be patterned for DIC measurements, and (2) all other objects between the source and the detector must be homogeneous, constant thickness along the X-ray path, and stationary. These constraints were necessary to enforce conservation of intensity or optical flow—the fundamental principle of optical DIC—which states that the grey-level value of an image is conserved as the object is deformed. In general, however, path-integrated X-ray images do not inherently obey conservation of intensity, since the intensity of the image is governed by X-ray attenuation from all components in the path between the X-ray source and the detector. If more than one surface/object moves during the test, conservation of intensity is violated, and standard DIC algorithms fail. The requirements placed on single-surface X-ray DIC to enforce conservation of intensity are challenging to meet in practical experiments, severely limit the usefulness of the technique, and restrict the information garnered from a test. For instance, post-mortem images of the aluminum-clad composite cylinder showed that the specimen deformed asymmetrically (Fig. 1(c)), but only the deformation of one sector of the cylinder was captured in situ during the test due to the necessity of patterning only a single surface (Fig. 1(b)).

A related technique employing X-ray imaging is Digital Volume Correlation (DVC), in which computed tomography (CT) reconstructions of a specimen before and after deformation are used to extract fully 3D or volumetric deformation measurements [26]. DVC typically requires hundreds to thousands of views of the sample that are captured as the sample is rotated, a time-intensive process that restricts DVC to quasi-static tests where loading is applied in isolated steps. Researchers have sought to relax the quasi-static constraint of CT through limited-view CT, where the volumetric reconstruction is performed with ca. five 2D views of the specimen from different angles captured simultaneously while the specimen is deformed. Several groups are developing high-speed X-ray CT using flash X-ray [27,28,29] and quasi-continuous X-ray sources [30]. Extending the limited-view CT systems to DVC is of interest and the topic of current work in the community. Another alternative is Projection Digital Volume Correlation (P-DVC), where a traditional X-ray CT scan of an undeformed specimen is combined with in situ, 2D X-ray images to extract time-resolved volumetric information [31,32,33,34].

The current work presents a complementary diagnostic to single-surface X-ray DIC, DVC, and P-DVC, addressing their respective challenges and limitations. This method is called “multi-surface, path-integrated (PI), X-ray DIC”, abbreviated as PI-DIC. In PI-DIC, conservation of intensity is reframed for path-integrated images based on an approximation of the Beer-Lambert law. Specifically, the matching or correlation criterion for DIC is reformulated to express the intensity of the path-integrated image as a function of X-ray attenuation through two DIC patterns. This fundamental alteration at the core of DIC allows motion/deformation of two independent surfaces to be measured from a single series of path-integrated images.

Compared to single-surface X-ray DIC, PI-DIC separates and measures deformation of multiple surfaces, thereby allowing more information to be garnered from a test. It also relaxes constraints on the experimental setup regarding the motion of other components in the X-ray path. Compared to DVC and P-DVC, no CT or volumetric reconstruction is required, and only one (for 2D-PI-DIC) or two (for stereo-PI-DIC) X-ray imaging systems are needed, reducing equipment and facilities requirements. Additionally, only the surfaces of interest need to be patterned, minimizing the intrusiveness of the X-ray DIC pattern for homogeneous specimens. As a trade-off, though, PI-DIC only provides displacements and strains on the patterned surfaces, whereas DVC and P-DVC provide fully volumetric measurements. Lastly, PI-DIC provides time-resolved measurements of dynamic events, similar to single-surface X-ray DIC and P-DVC, but in contrast to DVC. Thus, PI-DIC is a novel diagnostic and fills a niche that is not currently covered by other measurement methods.

This article is organized as follows. First, a theoretical background is presented, outlining standard conservation of intensity for optical images, contrasting it with an approximation of the Beer-Lambert law for path-integrated images, and developing the DIC algorithms and fundamental equations for PI-DIC. Next, synthetic images are generated for three test cases, where two plates are rigidly translating, rigidly rotating, or strained uniformly, and 2D (in-plane) PI-DIC results are presented. Lastly, PI-DIC is successfully demonstrated experimentally for the case of two plates rigidly translating.

In this work, the PI-DIC technique is demonstrated for 2D measurements of two, independent planar surfaces, but extending the algorithms to stereo-DIC to measure 3D displacements of multiple (potentially nonplanar) surfaces is the ultimate aim. The results presented here provide the foundation for PI-DIC to measure motion and deformation of independent surfaces with subpixel accuracy from a single series of X-ray images. All together, PI-DIC offers a unique contribution to the field of DIC and experimental mechanics, as it opens the door for full-field deformation measurements in complex and extreme environments by providing time-resolved displacements and strains on multiple surfaces from 2D, path-integrated X-ray images.

Theoretical Background

In this section, the theoretical background for 2D-DIC is presented, where the test piece is assumed to be planar and undergo only in-plane motion/deformation. A high-level overview of optical DIC is presented in the “Conservation of Intensity for Optical Images” section, and then the approach for multi-surface, path-integrated X-ray DIC is presented in the “Conservation of Intensity for Path-Integrated X-Ray Images” section for a simplified exemplar with two planar surfaces.

Conservation of Intensity for Optical Images

Conservation of intensity, or optical flow, is illustrated in Fig. 2 for an exemplar where an image is stretched horizontally. The image coordinate system has origin at the top-left pixel of the image and is defined by axes $\mathbb {X}$ and $\mathbb {Y}$. Optical flow dictates that the intensity of the undeformed image, F, at a reference location in the image coordinate system, $(X_F,Y_F)$, should equal the intensity of the deformed image, G, at its new position, $(X_G,Y_G)$ [35, Sec. 5.2]:

$$\begin{aligned} F\left( X_F,Y_F\right) = G\left( X_G,Y_G\right) \end{aligned}$$

(1)

Because of the so-called aperture problem, the displacement of a single pixel cannot typically be determined [35, Sec. 5.1]. Therefore, local DIC analysis tracks small regions around the pixels of interest, called subsets, with one representative undeformed subset illustrated by the green box in Fig. 2. The coordinates of the subset centers, $\left( X_F,Y_F\right)$, are typically user defined as a grid of points in the undeformed image coordinate system, illustrated by the green circles in Fig. 2. A subset coordinate system is also defined for each subset, with origin at the center of the subset and with axes $\mathbb {X}_{ss}$ and $\mathbb {Y}_{ss}$.

A subset shape function approximates the deformation or warping of the subset between the undeformed and deformed image [35, Sec. 5.3], illustrated by the elongated pink box in Fig. 2. An affine subset shape function is described mathematically as:

$$\begin{aligned} \begin{aligned} X_{SS,G}&= X_F + X_{SS} + U + P_{XX}X_{SS} + P_{XY}Y_{SS} \\ Y_{SS,G}&= Y_F + Y_{SS} + V + P_{YX}X_{SS} + P_{YY}Y_{SS} \end{aligned} \end{aligned}$$

(2)

where $\left( X_{SS,G},Y_{SS,G}\right)$ are the coordinates of pixels within the deformed subset in the image coordinate system, and $\left( X_{F},Y_{F}\right)$ are the coordinates of the undeformed subset center in the image coordinate system. $(X_{SS},Y_{SS})$ are the coordinates of pixels within the subset in the subset coordinate system, and are integer pixel values in the range of $\pm \frac{1}{2}(L_{SS}-1)$, where $L_{SS}$ is the odd-numbered subset size. The vector $\underline{P}$ collects the six affine shape function parameters as:

$$\begin{aligned} \underline{P} = [U,V,P_{XX},P_{XY},P_{YX},P_{YY}] \end{aligned}$$

(3)

where U and V describe the displacement of the subset center, $P_{XX}$ and $P_{YY}$ describe the normal strain of the subset, and $P_{XY}$ and $P_{YX}$ describe the shear strain of the subset.

Fig. 2

Schematic illustrating optical flow for an exemplar where an image is stretched horizontally

To compute the mismatch in intensity between the undeformed and deformed subsets, a matching criterion is formulated (also called a correlation criterion or a cost function), such as the Sum-of-Squared-Differences (SSD) [35], Sec. 5.4]:

$$\begin{aligned} \Psi ^2 = \sum _{\Omega }{\left\{ G\left( X_{SS,G},Y_{SS,G}\right) - F\left( X_{SS,F},Y_{SS,F}\right) \right\} ^2} \end{aligned}$$

(4)

where $\Psi$ is the value of the matching criterion, and $\left( X_{SS,F},Y_{SS,F}\right)$ are the coordinates of pixels in the undeformed subset in the image coordinate system. The sum is carried out over all the pixels in the subset, $\Omega$. An optimization algorithm (e.g. steepest descent, Newton-Raphson, Gauss-Newton, Levenberg-Marquardt [35, Appen. D]) is employed to identify the parameters $\underline{P}^*$ that minimize the value of the matching criterion $\Psi$:

$$\begin{aligned} \underline{P}^* = \mathop {\mathrm {arg\,min}}\limits _{\underline{P}} (\Psi ) \end{aligned}$$

(5)

The correlation process is performed with the reference image F and the series of deformed images, G. Equation (2) is evaluated with the identified parameters, $\underline{P}^*$ (specifically the two displacement parameters, $U^*$ and $V^*$) at the subset center, $(X_{SS},Y_{SS})=(0,0)$, to map the user-defined point in the reference image, $(X_F,Y_F)$, to the corresponding point in the deformed image, $(X_G^j,Y_G^j)$:

$$\begin{aligned} \begin{aligned} X_{G}^j&= X_F + U^{*,j} \\ Y_{G}^j&= Y_F + V^{*,j} \end{aligned} \end{aligned}$$

(6)

where the superscript j indicates the $j^{th}$ image in the deformed-image series. The displacements, U and V, of material points defined on the reference image F are then given by:

$$\begin{aligned} \begin{aligned} U^j&= X_{G}^j - X_{F} \\ V^j&= Y_{G}^j - Y_{F} \end{aligned} \end{aligned}$$

(7)

Conservation of Intensity for Path-Integrated X-Ray Images

Beer-Lambert law for X-ray image intensity

X-ray images are path-integrated since all objects/materials between the X-ray machine and the detector attenuate the X-rays to some extent and contribute to the final image intensity. The Beer-Lambert law for monochromatic X-rays specifies the intensity, $I_{PI}$, of the transmitted X-rays through the relationship:

$$\begin{aligned} I_{PI}=I_0 \exp \left\{ -\sum _{k\mathop{=}1}^{N_k} \left( \mu _k l_k \right) \right\} \end{aligned}$$

(8)

where $I_0$ is the unimpeded X-ray intensity, $\mu _k$ and $l_k$ are the material attenuation coefficient and path length, respectively, for a given material/object k, and the sum is carried out for $N_k$ materials/objects in the path.

Fig. 3

Schematic of an X-ray imaging setup with an X-ray machine, two plates each patterned for DIC, and a detector capturing the path-integrated image

PI-DIC is developed for the simplified exemplar setup shown in Fig. 3, where two weakly attenuating plates (e.g. plastic or aluminum) with strongly attenuating DIC pattern features (e.g. steel or tantalum) are placed between the X-ray machine and the detector. Assuming the attenuation of X-rays due to air is negligible compared to the plate and feature materials (i.e. $I=I_0$ for X-rays passing only through air), the summation in equation (8) can be separated into two summations, one for each sequential plate, as:

$$\begin{aligned} I_{PI}=I_0 \exp \left\{ - \left( \sum _{k_1\mathop{=}1}^{N_{k_1}} \left( \mu _{k_1} l_{k_1} \right) + \sum _{k_2\mathop{=}1}^{N_{k_2}} \left( \mu _{k_2} l_{k_2} \right) \right) \right\} \end{aligned}$$

(9)

where the subscripts 1 and 2 refer to each plate, respectively. Using identities of exponentials and multiplying by $I_0/I_0$, equation (9) can be further rewritten as:

$$\begin{aligned} I_{PI}=\frac{1}{I_0} \left[ I_0 \exp \left\{ -\sum _{k_1\mathop{=}1}^{N_{k_1}} \left( \mu _{k_1} l_{k_1} \right) \right\} \right]\; \left[ I_0 \exp \left\{ -\sum _{k_2\mathop{=}1}^{N_{k_2}} \left( \mu _{k_2} l_{k_2} \right) \right\} \right] \end{aligned}$$

(10)

Note that each term in square brackets in equation (10) represents the transmitted X-ray intensity if only a single plate were in the path between the X-ray machine and the detector. Thus, the transmitted intensity of X-rays passing through both plates sequentially, $I_{PI}$, can be written in terms of the intensity transmitted through each single plate individually as:

$$\begin{aligned} I_{PI} = \frac{1}{I_0} I_1 I_2 \end{aligned}$$

(11)

with

$$\begin{aligned} I_m = I_0 \exp \left\{ -\sum _{k_m\mathop{=}1}^{N_{k_m}} \left( \mu _{k_m} l_{k_m} \right) \right\} \end{aligned}$$

(12)

where $m \in [1,2]$ represents either Plate 1 or Plate 2.

When the transmitted X-rays impinge upon the digital detector, the signal is discretized into individual pixels located at position $\left( X_{F},Y_{F} \right)$ in the image coordinates. Assuming the image intensity, $F_{PI}$, is linearly proportional to the X-ray intensity, $I_{PI}$, equation (11) can be written in terms of image intensities as:

$$\begin{aligned} F^C_{PI} \left( X_{F_{PI}},Y_{F_{PI}} \right) = \frac{1}{I_0} \left[ F_1(X_{F_1},Y_{F_1})\right] \left[ F_2(X_{F_2},Y_{F_2})\right] \end{aligned}$$

(13)

where $F_1$ and $F_2$ represent reference images of each plate individually.

Remark

The composition of the path-integrated image, $F^C_{PI}$, from the two individual reference images, $F_1$ and $F_2$, is a pillar of the PI-DIC algorithm. However, several poignant remarks should be made:

• In the current work, the individual reference images, $F_1$ and $F_2$, were obtained by simply removing one of the plates from the experimental setup and imaging the other plate individually, as discussed in the “Experimental Setup” section. In real applications of PI-DIC, this process could be used when, for instance, the test article is an assembly that can be disassembled for these reference images. In other applications, such as the one shown in Fig. 1, where ideally both sides of the cylinder would have been patterned, imaging each pattern individually is not feasible. In this case, synthetic reference images can be generated based on the prescribed DIC patterns for each surface; then, the correlation of the experimental, path-integrated images could be performed against the synthetic reference images. This concept is similar to the “virtual DIC” approach recently proposed for optical DIC [36]. The use of synthetic reference images for PI-DIC is currently being investigated.

• With a conical X-ray beam, the path length varies as a function of emittance angle of the X-rays, leading to a radial decrease in transmitted intensity, even for a flat plate of uniform thickness. In the current experimental investigation, the change in path length is negligible, as discussed in the “Evaluation of the Beer-Lambert Approximation” section. However, in cases where this effect is significant and motions are large, a zero-normalized sum-of-squared differences (ZNSSD) matching criterion is proposed, similar to how the ZNSSD compensates for spatially non-uniform lighting conditions in optical DIC [35, Sec. 5.4].

• Several additional factors can lead to spatial variations of the X-ray and/or image intensity, even with no objects (besides air) in the X-ray path, including varying radiant intensity for conical X-ray beams, spatial non-uniformities of the detector, and nonlinear detector gain. The PI-DIC algorithm developed here assumes all of these factors are corrected during image pre-processing using a multi-point flat-field correction, as described in the “Experimental Setup” section.

• In summary, equation (13) is an approximation of the Beer-Lambert law and assumes the following: (1) a monochromatic X-ray source (rather than the common polychromatic lab sources) is used; (2) the image intensity is linearly proportional to the X-ray intensity; (3) air attenuation of X-rays is negligible compared to the plate and feature materials (e.g. aluminum and tantalum, respectively); (4) the change in image intensity due to the emittance angle of the X-rays is negligible; (5) spatial variations of the X-ray and/or image intensity are corrected during image pre-processing. A higher-fidelity model could be developed to allow the relaxation of these assumptions. However, a simple model is sought that does not require careful characterization of the experimental setup (e.g. the wavelength distribution of the X-ray source, wavelength-dependent attenuation coefficient for the materials of the test articles, detector linearity, etc.). The accuracy and efficacy of this simplified Beer-Lambert approximation is discussed in the “Demonstration Experimental Images” for real experimental images.

Shape functions for path-integrated images

In order to preserve the conservation of intensity for path-integrated images, the independent deformation / warping of each plate must be related to the deformed, path-integrated image, $G_{PI}$. The problem is formulated in a Lagrangian framework, first tracking material points on Plate 1 and then repeating the process to track material points on Plate 2. See section S1 in the supplementary information for comments on formulating the problem in an Eulerian framework. The core components of the PI-DIC process are illustrated in Fig. 4 and outlined as follows:

• 1. Similar to standard DIC, a grid of interrogation points is defined on the undeformed reference image for the first plate, $F_1$, based on the region-of-interest and a prescribed step size. These points, shown as green dots in Fig. 4, are located at the subset centers.

• 2. For each subset in $F_1$—consider the green starred subset, $S_{F_1}$—a corresponding subset exists in the deformed, path-integrated image, $G_{PI}$—labeled as the purple subset, $S_{G_{PI}}$.

• 3. The intensity of subset $S_{G_{PI}}$ is a function of X-ray attenuation through both plates. Therefore, the corresponding subset in the second plate image, $F_2$, must also be identified—labeled as the blue subset $S_{F_2}$.

Fig. 4

Schematic illustrating the correlation process for PI-DIC for an example where Plate 1 is stretched horizontally to the right and Plate 2 is compressed vertically upwards. The warped subset shapes for $S_{F_1}$ and $S_{F_2}$ are exaggerated for illustrative purposes

In this example, two independent deformations from Plate 1 and Plate 2 must be identified from three unique subsets ($S_{F_1}$, $S_{F_2}$ and $S_{G_{PI}}$). The coordinates of the center point of the subset $S_{F_1}$, $(X_{F_1}, Y_{F_1})$, are prescribed in Step 1 above when the grid of interrogation points are defined on the undeformed reference image for the first plate. Therefore, the center of subset $S_{F_1}$ is stationary and cannot translate within the image. However, the subset $S_{F_1}$ is allowed to warp because Plate 1 is deforming. This warping is shown qualitatively in Fig. 4 by the horizontally compressed subset $S_{F_1}$ (compared to the square subset $S_{G_{PI}}$), and is described mathematically as:

$$\begin{aligned} \begin{aligned} X_{SS, F_1}&= X_{F_1} + X_{SS} + P_{XX, F_1}X_{SS} + P_{XY, F_1}Y_{SS} \\ Y_{SS, F_1}&= Y_{F_1} + Y_{SS} + P_{YX, F_1}X_{SS} + P_{YY, F_1}Y_{SS} \end{aligned} \end{aligned}$$

(14)

where $(X_{SS, F_1}, Y_{SS, F_1})$ are the coordinates of the pixels within subset $S_{F_1}$ in the image coordinate system, $(X_{F_1}, Y_{F_1})$ are the user-defined coordinates of the center of the subset in the image coordinate system, $(X_{SS},Y_{SS})$ are the coordinates of the pixels within the subset in the subset coordinate system, and the parameters $[P_{XX, F_1}, P_{XY, F_1}, P_{YX, F_1}, P_{YY, F_1}]$ are the four warping parameters of the affine shape function.

The location of the corresponding subset $S_{F_2}$ can be anywhere in the image $F_2$, and the subset can warp as Plate 2 undergoes independent deformation. This behavior is shown qualitatively in Fig. 4 by the vertically elongated subset $S_{F_2}$ (compared to the square subset $S_{G_{PI}}$), and is described mathematically as:

$$\begin{aligned} \begin{aligned} X_{SS, F_2}&= X_{F_1} + X_{SS} + U_{F_2} + P_{XX, F_2}X_{SS} + P_{XY, F_2}Y_{SS} \\ Y_{SS, F_2}&= Y_{F_1} + Y_{SS} + V_{F_2} + P_{YX, F_2}X_{SS} + P_{YY, F_2}Y_{SS} \end{aligned} \end{aligned}$$

(15)

where $U_{F_2}$ and $V_{F_2}$ are the two translation parameters of the affine shape function, and all other terms are the same as described above, but now applied to subset $S_{F_2}$.

Finally, the location of the deformed, path-integrated subset, $S_{G_{PI}}$, can be anywhere in the image $G_{PI}$, but is not allowed to warp; thus, the subset $S_{G_{PI}}$ is shown as a square with the user-defined subset size in Fig. 4. This behavior is described mathematically as:

$$\begin{aligned} \begin{aligned} X_{SS, G_{PI}}&= X_{F_1} + X_{SS} + U_{G_{PI}} \\ Y_{SS, G_{PI}}&= Y_{F_1} + Y_{SS} + V_{G_{PI}} \end{aligned} \end{aligned}$$

(16)

where $U_{G_{PI}}$ and $V_{G_{PI}}$ are the two translation parameters of the affine shape function. In sum, there are 12 parameters that need to be identified to describe the affine deformation/warping of the two individual plates:

$$\begin{aligned} \underline{P}_{PI} =\ &[P_{XX, F_1}, P_{XY, F_1}, P_{YX, F_1}, P_{YY, F_1}, U_{F_2}, V_{F_2}, \\&P_{XX, F_2}, P_{XY, F_2}, P_{YX, F_2}, P_{YY, F_2},U_{G_{PI}}, V_{G_{PI}}] \end{aligned}$$

(17)

Remark

In this development of PI-DIC, the four warping parameters are applied to subsets in each of the reference images, while subset in the path-integrated, deformed image is kept square. Alternatively, the subset in the first reference image, $F_1$, could be kept square, and subsets in the second reference image, $F_2$, and the path-integrated, deformed image, $G_{PI}$, could be allowed to warp. However, this option has the potential to lead to severe subset shape change for the second reference image, $F_2$, which could negatively affect the correlation process. Rigorous evaluation of this option, though, is outside the scope of this work.

The matching criterion for the two-plate, path-integrated, X-ray DIC, $\Psi _{PI}$, is given by:

$$\begin{aligned} \Psi _{PI}^2 = \sum _{\Omega }{\left\{ G_{PI}\left( X_{SS,G_{PI}},Y_{SS,G_{PI}}\right) - F_{PI}^C\left( X_{SS,F_{PI}},Y_{SS,F_{PI}}\right) \right\} ^2} \end{aligned}$$

(18)

As with standard DIC, an optimization algorithm is employed to identify the parameters $\underline{P}^*_{PI}$ that minimize the value of the matching criterion:

$$\begin{aligned} \underline{P}^*_{PI} = \mathop {\mathrm {arg\,min}}\limits _{\underline{P}_{PI}} (\Psi _{PI}) \end{aligned}$$

(19)

The correlation process is performed with the two individual reference images, $F_1$ and $F_2$, and the series of path-integrated, deformed images, $G_{PI}$. Equation (16) is evaluated with the identified parameters at the subset center, $(X_{SS},Y_{SS}) = (0,0)$, to map the user-defined point in the reference image for Plate 1, $(X_{F_1},Y_{F_1})$, to the corresponding point in the path-integrated image, $(X^j_{G_{PI}},Y^j_{G_{PI}})$, where the superscript j indicates the $j^{th}$ image in the series:

$$\begin{aligned} \begin{aligned} X^j_{G_{PI}}&= X_{F_1} + U^j_{G_{PI}} \\ Y^j_{G_{PI}}&= Y_{F_1} + V^j_{G_{PI}} \end{aligned} \end{aligned}$$

(20)

The displacements of the material points on Plate 1 are then given by:

$$\begin{aligned} \begin{aligned} U^j_{F_1} (X_{F_1},Y_{F_1})&= X^j_{G_{PI}} - X^0_{G_{PI}} \\ V^j_{F_1} (X_{F_1},Y_{F_1})&= Y^j_{G_{PI}} - Y^0_{G_{PI}} \end{aligned} \end{aligned}$$

(21)

Comparison of optical DIC and PI-DIC algorithms

In summary, optical DIC and PI-DIC algorithms have an identical structure with the following substitutions:

• The deformed image G is replaced by the deformed, path-integrated image, $G_{PI}$.

• The single reference image F is replaced by the path-integrated reference image $F^C_{PI}$ composed from the two individual reference images, $F_1$ and $F_2$, according to equation (13).

• The subset warping and translation defined in equation (2) are replaced by equations (14)–(16).

• The six-parameter vector $\underline{P}$ defined in equation (3) is replaced by the twelve-parameter vector $\underline{P}_{PI}$ defined in equation (17).

• The matching criterion $\Psi$ defined in equation (4) is replaced by $\Psi _{PI}$ defined in equation (18).

• The displacements of the material points on the reference image, F, defined by equation (7) are replaced by displacements of the material points on the reference image for Plate 1, $F_1$, defined by equation (21).

As mentioned previously, the PI-DIC algorithms presented here are developed in a Lagrangian framework. In order to track material points on Plate 2, the entire process described in the “Shape Functions for Path-Integrated Images” section is repeated, switching the roles of Plate 1 and Plate 2, and images $F_1$ and $F_2$. See section S1 in the supplementary information for comments on formulating the problem in an Eulerian framework.

Multi-Surface, Path-Integrated, X-Ray DIC Algorithm Implementation

Multi-surface, path-integrated, X-ray DIC (PI-DIC) is implemented in MATLAB for the two-plate example described in the “Conservation of Intensity for Path-Integrated X-Ray Images” section. Inputs are the two reference images of the individual plates, $F_1$ and $F_2$, the series of path-integrated images of the deforming plates, $G_{PI}$, and the image intensity of the unimpeded light, $I_0$ (measured as the average pixel intensity of a light-field image captured with nothing but air in the X-ray path). Additional user-defined parameters include two grids of points of interest (one for each plate, defined in the respective reference images), subset size, and image prefiltering (using the function imgaussfilt with user-defined values for the standard deviation and filter size).

The gradient-based, nonlinear optimizer fminunc is used to minimize the matching criterion and identify the parameters $P_{PI}$, with the options¹ of: a forward finite-difference to estimate gradients, an optimality tolerance of $1 \cdot 10^{-6}$, a step tolerance of $1 \cdot 10^{-6}$, a limit on function evaluations of 1000, and a limit on iterations of 100.

The optimizer successfully converges if the displacements are 2 px or less; larger displacements require an initial guess. Initial guesses for the parameters are set to zero for the initial correlation of the undeformed, path-integrated image, $G_{PI}^0$, to the two reference images, $F_1$ and $F_2$. Afterward, initial guesses are seeded based on the correlation results from the previous image, using the mean for the current point and its eight surrounding neighbors. This approach requires that the displacements between consecutive images be less than 2 px. Improving this initial guess process is currently in progress.

Demonstration with Synthetic Images

In this section, the PI-DIC algorithm is demonstrated with synthetic images undergoing rigid translations, rigid rotations, and uniform stretches. The “Synthetic Image Generation” section describes the synthetic image generation process, the “DIC Processing for Synthetic Images” section presents the image processing parameters, and the “Synthetic Results and Discussion” section presents the recovered displacements and discusses their accuracies and precisions for all three test cases.

Synthetic Image Generation

The process of creating synthetic images to evaluate DIC algorithms is nuanced, and care must be taken to ensure no inadvertent biases are introduced. For this reason, community-wide efforts such as the DIC Challenge [37, 38] have created vetted sets of synthetic images for the DIC community to use to verify and validate DIC codes. However, the optical images from the DIC Challenge are not applicable for PI-DIC, necessitating the creation of synthetic path-integrated images here.

Reference image

Two synthetic reference images were generated to mimic pattern AT2 of the two experimental aluminum-tantalum plates (see the “Specimen Fabrication” section). First, a super-resolution image of size $25,000 \times 25,000$ px² was created with a background intensity of $I_{bg} = 35,786$ counts on a 16-bit scale, representing a single plate of aluminum. Then, circular features of diameter 500 px with intensity of $I_{f} = 21,846$ counts, representing the aluminum plate plus one tantalum feature, were placed at the same locations as the features on the two experimental plates. Finally, the images were binned by a factor of 100 to create a final, double-precision image of size $250 \times 250$ px². These binned images were taken as the reference images for Plate 1 and Plate 2 and are shown in the top row of Fig. 5.

Deformed images

Three types of deformation were explored: rigid translations, rigid rotations, and uniform stretches. To create the rigid translation images, the super-resolution reference image was translated in whole-pixel increments, and then binned down by a factor of 100. This super-resolution and binning process created rigid translations of subpixel increments in the final image resolution with no interpolant [39], similar to Sample Set 6 in the DIC Challenge [37].

To create the rigid rotation images, the binned reference image was rotated using the function imrotate in MATLAB with a bilinear interpolant. The super-resolution image had to be binned before applying the rotation; if the rotation were applied to the super-resolution image first and then the image were binned, the binned image would have a different and unknown applied rotation compared to the prescribed rotation in the super-resolution image.

To create the uniform stretch images, a bilinear intensity interpolant was created for the binned image using the MATLAB function griddedInterpolant. Then, the interpolant was evaluated at a new set of locations, $X_{eval}$, determined by the prescribed stretch, $\lambda$, as:

$$\begin{aligned} X_{eval} = X_{ref}/\lambda \end{aligned}$$

(22)

where $X_{ref}$ is the initial coordinate of the undeformed image. As with the rotation images, the super-resolution image had to be binned before applying the stretches; otherwise, the binning process altered the prescribed stretch.

Remark

When working with synthetic images for DIC, the interpolant used to create the images can interact with the interpolant used in the DIC algorithm, such that the DIC results are artificially improved [40]. This interaction can be avoided by deforming synthetic images in the Fourier domain [39] or based on transformation of an analytical pattern or texture function [40], among other methods.

Concurrent research by the authors investigated an alternative approach to PI-DIC where images were processed in the Fourier domain; a consistent synthetic image deformation method in the spatial domain was preferred to avoid potential conflicts between multiple Fourier transforms in that work. Additionally, the pattern used here replicated the physical pattern from the experimental sample, which prevented the use of an analytical pattern function.

For the rigid translation images, there was no issue with interpolant interaction since no interpolant was used to create the images. To avoid conflating the DIC results for the rotation and stretch images, a linear interpolant was used for image deformation, while a cubic spline was used for the DIC analysis (see the “DIC Processing for Synthetic Images” section).

For all three deformation types, two sets of images were created, one in which the deformations were in opposite directions but of the same magnitude (called “opposing” deformations), and one in which the deformations were in the same direction but with the second plate deforming 20% more at each time increment (called “paired” deformations). For brevity, only the “opposing” deformations are presented in the main article, with the “paired” deformations presented in section S3 in the supplementary information.

For the opposing translations, Plate 1 moved to the right and Plate 2 moved to the left. For the opposing rotations, Plate 1 moved counter-clockwise (CCW) and Plate 2 moved clockwise (CW). For the opposing stretches, Plate 1 was elongated to the right and Plate 2 was compressed upwards. See Fig. 5. Images were created for both small and large motions, to evaluate the PI-DIC algorithm in both the sub-pixel regime and the large deformation regime. Translation images were created in increments of 0.1 px from 0 to 1 px, and then in increments of 1 px from 2 to 10 px. Rotation images were created in increments of 0.2 deg. from 0 to 4 deg., and then in increments of 1 deg. from 5 to 10 deg. Stretch images were created in increments of 0.002 px/px from 1.00 to 1.04 px/px (Plate 1) or from 1.00 to 0.96 px/px (Plate 2), and then in increments of 0.01 px/px from 1.05 to 1.20 px/px (Plate 1) or from 0.95 to 0.80 px/px (Plate 2). These motion/deformation directions and increments are summarized in Table 1.

Table 1 Prescribed “opposing” motions/deformations for the synthetic images

Undeformed and deformed images of the two individual plates were created first, as shown in the first two columns of Fig. 5. In order to verify the image deformation processes, these individual image series were processed with commercial (optical) DIC software, and results are presented in section S2 in the supplementary information. Next, the path-integrated images were composed by combining the individual images according to the Beer-Lambert law approximation (“Beer-Lambert Law for X-Ray Image Intensity” section, specifically equation (13)). The resulting path-integrated images are shown in the third column of Fig. 5. All images were kept as floating-point matrices with no truncation to unsigned integers.

Fig. 5

Examples of the synthetic images for the “opposing” deformations at the final deformation step

Image noise

After the path-integrated images were created, homoscedastic, zero-mean image noise was added, with a normal distribution and standard deviations of either 0.5%, 1.5% or 3.0% of the 16-bit depth scale (328, 983, or 1966 counts). Representative subsets of the undeformed, path-integrated image with these noise values are shown in Fig. 6.

Remark

The actual experimental images have heteroscedastic noise with a standard deviation of approximately 51 counts or 0.08% of the 16-bit depth of the image (see section S5.1 in the supplementary information). This low value is due to temporal averaging and image binning, as described in the “Experimental Method” section. For more practical applications, the image noise of the deformed image series is anticipated to be higher; thus, larger image noise values were used in the synthetic images to stress the algorithms. However, no noise was added to the individual reference images, $F_1$ and $F_2$, because experimentally, it is assumed such noise-free reference images could be generated via temporal averaging. A homoscedastic noise profile (i.e. noise independent of pixel intensity) was used for simplicity.

Fig. 6

Representative subset ($31 \times 31$ px²) of the undeformed, path-integrated image for different image noise levels

DIC Processing for Synthetic Images

The synthetic, floating-point images were processed in the PI-DIC code using the user-defined parameters listed in Table 2. The effects of changing the image prefiltering and subset size are explored in section S4 in the supplementary information. Grid points of interest were defined from 50 to 200 px in increments of 10 px in both the horizontal and vertical directions, leading to 256 points analyzed for each plate. A threshold was set on the final value of the matching criterion, $\Psi _{PI}^2$ (equation (18)), evaluated with the final parameters, $P^*_{PI}$ (equation (19)), such that grid points with a final matching criterion value above this threshold were removed from the analysis. The rigid translations did not contain any poorly correlated or uncorrelated points, and thus no points were removed based on the matching criterion threshold. Values for the matching criterion threshold for the rigid rotation and uniform stretch images were selected based on manual inspection of spurious points.

Table 2 User-defined DIC parameters for the synthetic images

Synthetic Results and Discussion

This section presents the displacements recovered from PI-DIC for the synthetic images. Results are shown for the case of 1.5% image noise; the effect of image noise is presented in section S5 in the supplementary information. Additionally, metrics of the optimizer performance, including number of iterations to convergence and matching criterion residual, are discussed in section S6.1 in the supplementary information. The “Measurement Uncertainty” section first defines the metrological quantities used to evaluate the PI-DIC measurement uncertainty, and then the “Rigid Translation”, “Rigid Rotation” and “Uniform Stretch” sections present the recovered displacements and their uncertainties for the rigid translations, rigid rotations, and uniform stretches, respectively.

Measurement uncertainty

Following the International vocabulary of basic and general terms in metrology (VIM) [41], the following terms are used to characterize the measurement uncertainty of the recovered displacements. The true quantity value (Definition 2.11), $d^j_{true}$, was taken to be the known, prescribed displacement used to generate the synthetic images as described in the “Deformed Images” section and Table 1. The measurement bias (Definition 2.18), $d^j_b$, was computed according to equation (23a) for each image in the series as the mean displacement of all points in the region-of-interest, $\mu ^j$, minus the true value. The standard measurement uncertainty (Definition 2.30), $\sigma ^j$, was computed according to equation (23b) for each image in the series as the standard deviation of all points in the region-of-interest.

$$\begin{aligned} d^j_b = \mu ^j - d^j_{true} \end{aligned}$$

(23a)

$$\begin{aligned} \sigma ^j = \sqrt{\frac{1}{N_p-1} \sum _{i\mathop{=}1}^{N_p} |d^j_i-\mu ^j|^2} \end{aligned}$$

(23b)

$$\begin{aligned} \mu ^j = \frac{1}{N_p} \sum _{i\mathop{=}1}^{N_p} d^j_i \end{aligned}$$

(23c)

where d represents either in-plane displacement component, U (horizontal displacements) or V (vertical displacements), j represents the image number in the series of deformed images, i represents the points in the region-of-interest, and $N_p$ is the total number of points in the region-of-interest.

Rigid translation

Figure 7 shows representative results for the “opposing” rigid translations, where Plate 1 moved to the right and Plate 2 moved to the left. The top and bottom rows present the recovered displacements from the path-integrated images for the first and second plate, respectively. The left and center columns show the horizontal and vertical displacements, respectively, for the final translation step, where the prescribed displacement was 10 px to the right for Plate 1 and 10 px to the left (i.e. −10 px) for Plate 2, with 0 px displacement in the vertical direction for both plates. As seen in these full-field plots, the prescribed displacements are recovered well for both plates with no points removed due to poor correlation.

The bias and standard uncertainty were computed as described in the “Measurement Uncertainty” section. These errors are quantified for all prescribed translations in the right column. The bias (solid lines) is around 0.005–0.008 px for the whole-pixel displacements from 1–10 px. For the subpixel displacements from 0–1 px, the characteristic S-shaped interpolation bias [42] (corrupted some by the image noise) is observed with magnitude of approximately 0.02 px for the horizontal displacements in both plates. The standard uncertainty (dashed lines) is approximately 0.02 px for all steps for both plates. These results demonstrate the ability of the multi-surface, path-integrated algorithm to correctly separate the two independent plate motions from the series of path-integrated images with excellent accuracy and subpixel precision. Similar results are obtained for the translations in the same direction (“paired” motions), as shown in section S3.1.2 in the supplementary information.

Fig. 7

Representative results for rigid “opposing” translations. Full-field displacement results are shown for the final translation step, with the bias (solid lines) and standard uncertainty (dashed lines) quantified for all prescribed displacements

Rigid rotation

Figure 8 presents results for the “opposing” rigid rotations, where Plate 1 rotated counter clockwise and Plate 2 rotated clockwise. The displacement magnitude, D, for the final rotation step is shown in the left column, computed as $D_m = \sqrt{ U_{F_m}^2 + V_{F_m}^2}$, where $U_{F_m}$ and $V_{F_m}$ are the DIC displacements for Plate m in the horizontal and vertical direction, respectively. The recovered rotation angle, $\theta _m$, is shown in the center column, computed via the four-quadrant inverse tangent as:

$$\begin{aligned} \theta _m = \tan ^{-1} \left( \frac{Y_{F_m,\,def} -N_{y,\,m}/2 + n}{X_{F_m,\,def} -N_{x,\,m}/2 + n} \right) - \theta _{ref} \end{aligned}$$

(24)

where $\theta _{ref}$ is the initial angle of each grid point in the reference image, $X_{F_m,\,def}$ and $Y_{F_m,\,def}$ are the deformed coordinates of the grid points for Plate m, $N_{x,\,m}$ and $N_{y,\,m}$ are the number of pixels in the horizontal and vertical directions, respectively, of image $F_m$, and $n=-0.5$ px is a shift factor necessary to correctly compute the center of image rotation when using the MATLAB function imrotate.²

The displacement magnitudes for both plates are as expected, with zero displacement at the center of the image and larger displacements moving radially away from the center. The recovered rotations agree well with the prescribed rotations for points away from the center of the image, recovering 10 deg. and -10 deg. for Plate 1 and Plate 2, respectively. The rotations show some error near the center of the image, where small displacement errors are magnified due to the denominator in equation (24) being close to zero.

There are some poorly correlated or uncorrelated points that are removed based on the matching criterion threshold of $\Psi _{SSD,\,PI}^2 = 50,000$ px² (9.4% of points for Plate 1 and 10.9% for Plate 2, for the final rotation step). The current PI-DIC algorithm is formulated to consider two plates contributing to the path-integrated image intensity at each pixel. Large motions in opposite directions can result in the two plates no longer overlapping in portions of the region-of-interest (see Fig. 5). In this case, the PI-DIC algorithm should revert back to the standard “optical” DIC algorithm, and implementing this type of feature is a subject of on-going work.

Fig. 8

Representative results for rigid “opposing” rotations. Full-field results for displacement magnitude and rotation are shown for the final rotation step, with the bias (solid lines) and standard uncertainty (dashed lines) quantified for all prescribed rotations

Lastly, looking at the right column, the bias errors are less than 0.01 px for all data sets, and standard uncertainty is again approximately 0.02 px. Collectively, these results demonstrate the efficacy of the PI-DIC algorithm to successfully separate independent rigid rotations from two plates. Similar results are obtained for the rotations in the same direction, as shown in section S3.1.3 in the supplementary information.

Uniform stretch

Figure 9 presents results for the uniform stretches in opposite directions, where Plate 1 was stretched horizontally to the right and Plate 2 was compressed vertically upwards. The recovered displacements shown in the full-field plots clearly reflect these applied deformations, with the horizontal displacement for Plate 1 increasing from left-to-right, and the vertical displacement for Plate 2 increasing in magnitude from the top-to-bottom.

Some uncorrelated points are removed based on the threshold of $\Psi _{SSD,\,PI}^2 = 25,000$ px² (18.4% of points for Plate 1 and 5.9% for Plate 2, for the final deformation step). Compared to the rigid rotations, a lower threshold is required to remove points that are clearly incorrect based on manual inspection. In particular, points near the bottom of the image are lost, (around $Y=200$ px), where Plate 1 compressed up until it was no longer overlapping with Plate 2 (see Fig. 5). Here again, to recover these points correctly, the the matching criterion should switch from the PI-DIC criterion to the standard “optical” DIC criterion.

Fig. 9

Representative results for uniform stretches in “opposing” directions. Full-field displacement results are shown for the final deformation step, with the bias (solid lines) and standard uncertainty (dashed lines) quantified for all prescribed stretches

Finally, the bias is around 0.005–0.008 px, and the standard uncertainty is approximately 0.02 px. Thus, the ability of the PI-DIC algorithm to recover two independent uniform stretches is demonstrated. Similar results are obtained for the uniform stretches in the same direction, as shown in section S3.1.4 in the supplementary information.

Demonstration Experimental Images

Following the successful demonstration of PI-DIC with synthetic images, the algorithm was next validated experimentally, where two plates were patterned and rigidly translated. As the PI-DIC algorithms are currently developed for 2D measurements, the plates were perpendicular to the X-ray machine and parallel to the X-ray detector, and the in-plane displacement components were recovered. The “Experimental Method” section presents the experimental methods, including specimen fabrication, X-ray imaging configuration, calibration of the image scale, and image processing parameters. The “Experimental Results and Discussion” section presents the results and discussion, including an evaluation of the Beer-Lambert approximation and measurement uncertainty results for the recovered translations of each plate.

Experimental Method

Specimen fabrication

Two different fabrication methods were employed to create specimens for X-ray PI-DIC. The first method involved using either plasma spray (back plate) or cold spray (front plate) through a shadow mask to create tantalum features on an aluminum plate, as shown in Fig. 10. Four different sized features were generated, with diameters of 0.5 mm, 1 mm, 2 mm, and 3 mm, referred to as “AT1”, “AT2”, “AT3”, and “AT4”, respectively. The aluminum plates were $140 \times 140$ mm.² ($5.5 \times 5.5$ in.²) and 3.18 mm (1/8 in.) thick. The tantalum features were approximately 90 µm thick with local variations of about 10 µm. Details on the spray coating process are found in [23].

Fig. 10

Optical images of the pair of aluminum plates with (left) cold-sprayed or (right) plasma-sprayed tantalum patterns of varying size. The holes in the left plate were for fixturing the sample for the spray process and are outside of any regions of interest used in the DIC analysis

In addition to the Al-Ta samples, a pair of urethane dimethacrylate-based plates (Formlabs, “white resin”, product code FLGPWH04) were printed (Formlabs SLA printer). The plates were $76 \times 76$ mm² ($3 \times 3$ in.²) and 4.8 mm (3/16 in.) thick, and were printed with randomly-located holes of diameter 1.56 mm. Stainless steel ball bearings of 1.59 mm (1/16 in.) diameter were then seated in the holes and adhered using Loctite cyanoacrylate adhesive (“super glue”). These patterns are referred to as pattern “PS”, shown in Fig. 11.

Fig. 11

Optical images of the two plastic-steel bearing samples

Experimental setup

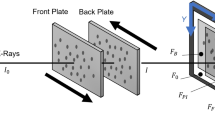
The experimental setup is shown in Fig. 12. The two plates were oriented with the DIC features (either tantalum for the Al-Ta plates, or steel bearings for the plastic-steel plates) facing each other. The specimens were translated on motorized stages (Newmark Systems, Inc., Model: NLS4-8-12-NC) horizontally between the X-ray source (front) and the X-ray detector (back). The same translation increments, in terms of pixels, were used as for the synthetic images (see Table 1 for the “opposing” motions and Table S2 in the supplementary information for the “paired” motions). Computing the physical translation increments in millimeters required to produce the desired image translation increments in pixels is discussed in the “Image Scale Calibration and Image Binning” section.

Fig. 12

Experimental set-up including the two plate specimens between the X-ray source (front), and the detector (back). The specimens were mounted to motorized translation stages. “Opposing” motions are illustrated by the purple arrows, with the front plate moving to the right and the back plate moving to the left. “Paired” motions are illustrated by the yellow arrows, with both plates moving to the right but at different rates

The detector was placed 1087 mm from the source. To minimize differences in geometric magnification, blur, X-ray intensity, etc. arising from a conical X-ray beam, the two plates were placed as close to each other as possible. Augmenting the PI-DIC algorithm to account for plates that have significantly different distances from the source and detector is on-going. For the Al-Ta specimens, the distance between the plates and the source was 710 mm for the front plate and 730 mm for the back plate. For the plastic-steel specimens, the distance between the plates and the source was 520 mm for the front plate and 541 mm for the back plate.

The X-rays were produced using an X-RAY WorX (Model: XWT-225 SE) source operating at 220 keV with 30 µA current. Images were acquired at 7 Hz by a Varex (formerly Varian) PaxScan2520DX detector (physical square pixel size of 127 µm; resolution of $1880 \times 1496$ px²) and averaged in groups of 10. A total of 10 of these averaged static images were captured at each displacement increment. Five of the ten images were analyzed with the PI-DIC code (“Rigid Translation” section); all 10 images were analyzed when characterizing the detector noise (see section S5.1 in the supplementary information). After averaging, a multi-point flat-field correction [43] was applied using North Star Imaging, efX-dr software (version 1.3.5.8), using 3 bright-field images with currents of 10 µA, 20 µA, and 30 µA. This correction accounts for spatial detector variations, nonlinear detector gain, and the radial reduction of the conical X-ray beam intensity. After the flat-field correction, the unimpeded X-ray intensity, i.e. the image intensity for pixels where the X-rays passed through only air, was $I_0=44,500$ counts.

Three sets of translations were performed: a set with both plates moving to capture the path-integrated images, and a set of each plate moving individually. The individual plate images served as a benchmark for standard, “optical” 2D-DIC, for comparison against the PI-DIC. Additionally, the reference images from the individual plate image series also served as the reference images for the PI-DIC algorithm as discussed in the “Conservation of Intensity for Path-Integrated X-Ray Images” section.

Image scale calibration and image binning

In order to convert experimental PI-DIC measurements from pixels to millimeters, the average image scales were determined as follows. A dot-grid calibration target was designed specifically for X-ray images, fabricated using printed circuit board methods to have copper dots or circles on an FR-4 substrate (a glass fiber reinforced epoxy laminate). The dot spacing was either $L=12$ mm for the Al-Ta plates or $L=7$ mm for the plastic-steel plates. The dot-grid calibration target was inserted in each of the sample holders for the front and back plates and imaged.

The centers of the dots were identified in the images using the function imfindcircles in MATLAB, and the distance between the center of each dot and its horizontal and vertical neighbors was calculated in pixels, $\beta$. The original image scale, $S_{org}$, was calculated as $S_{org} = \frac{L}{\beta }$ mm/px. A representative X-ray image of the calibration target, with identified dots outlined in red and the computed image scale ($S_{org}$) represented by the colored lines, is shown in Fig. 13. There was a small gradient in $S_{org}$ across the calibration target, but the variation was small and thus the average value was used.

Fig. 13

X-ray image of the dot-grid calibration target in the sample holder for the front Al-Ta plate. Identified dots are outlined in red and the original image scale, $S_{org}$, is represented by the colored lines spanning the distances between each of the dots

Given the geometry of the experimental setup described in the “Experimental Setup” section, the original image scales, $S_{org}$, for all four plates are shown in Table 3. After images were captured, they were binned to reduce the feature sizes, leading to the effective image scales, $S_{eff}$, also shown in Table 3. The physical feature sizes, original image feature sizes, and effective image feature sizes of the binned images are listed in Table 4. Finally, the physical translation increments in millimeters were computed by scaling the desired image translation steps in pixels (see Tables 1 and S2) by the effective image scales for each plate.

Table 3 Original and effective image scales for each of the plates given the experimental geometry configuration

Table 4 Physical feature sizes of the experimental patterns and corresponding approximate image feature sizes for both the original and binned images

DIC processing for experimental images

After images were averaged, flat-field corrected, and binned, the experimental floating-point images were processed in the PI-DIC code using the user-defined parameters listed in Table 5. Compared to the synthetic images, no image pre-filtering was used because it had a negative effect on the displacement standard uncertainty (see section S4.1 in the supplementary information). Similar to the rigid translations with the synthetic images, all points correlated well, so no points were removed based on the matching criterion threshold. Representative subsets are shown in Fig. 14, overlaid on the experimental, path-integrated reference image. The effect of subset size is briefly discussed in section S4.2 in the supplementary information.

Table 5 User-defined DIC parameters for the experimental images. Patterns “AT1–AT4” refer to the four quadrants of the Al-Ta plates, with feature sizes of 0.5 mm, 1 mm, 2 mm and 3 mm, respectively. Pattern “PS” refers to the plastic-steel bearing plates

Fig. 14

Experimental X-ray images for the Al-Ta plates (top) and plastic-steel plates (bottom), showing the front plate (left) and back plate (middle) individually, and the path-integrated image (right). Representative subsets (Table 5) are overlaid, with blue, red, yellow and purple subsets corresponding to the 0.5 mm, 1.0 mm, 2.0 mm, and 3.0 mm features of the Al-Ta plates, and green subset corresponding to the plastic-steel plates

Experimental Results and Discussion

Evaluation of the Beer-Lambert approximation

The accuracy of the Beer-Lambert approximation given in equation (13) is first evaluated by composing the path-integrated reference image, $F_{PI}^C$, from the two individual experimental reference images, and comparing it to the experimental path-integrated reference image, $F_{PI}^E$. Figure 15 presents these two images for a cropped region of pattern AT4 (3 mm feature size) of the Al-Ta plates.

Fig. 15

Evaluation of the Beer-Lambert approximation: Cropped regions of pattern AT4 (3 mm feature size) of the Al-Ta plates are shown for either the experimental path-integrated image (left) or the path-integrated image composed from the two individual reference images (right), along with the respective histograms (bottom). Intensity values at the locations marked by the symbols are quantified in Table 6

The histograms of intensity values in Fig. 15 show that the composed path-integrated image is overall slightly darker than the experimental path-integrated image. Two main peaks are apparent, which correspond approximately to the intensity of X-rays passing through the aluminum (light peak) and the aluminum plus one tantalum feature (dark peak). Table 6 quantifies these peaks, as well as the intensity of three individual pixels marked in Fig. 15. In general, the Beer-Lambert approximation is more accurate for lighter pixels where the X-rays are not attenuated as strongly. Overall, though, the error is less than 3%. While this error increases the matching criterion residual, the PI-DIC algorithm is still able to minimize the criterion to find the best match in intensity pattern between the composed, path-integrated reference image and the experimental path-integrated deformed images, as shown in the following sections.

Next, the effect of the radially varying path length due to a conical X-ray beam is evaluated. Given a maximum radius of the Al-Ta plate of $r_{max}=99$ mm from the center to the corners (see “Specimen Fabrication” section) and a minimum stand-off distance from the X-ray source to the plate of $h=710$ mm (see “Experimental Setup” section), the maximum angle of the conical X-ray beam that transmitted through the corners of the specimens is $\theta _{max}=\tan ^{-1}(r_{max}/h)=7.9$^o. Thus, considering only a single plate with no DIC features, the maximum path length of the plate at the corner is $l_{\theta _{max}} = \frac{l_{\theta _0}}{\cos (\theta _{max})}$, where $l_{\theta _0}$ is the path length at the center of the plate, equal to the plate thickness with an X-ray impinging perpendicularly to the plate.

Table 6 Evaluation of the Beer-Lambert approximation: Select intensity values of the experimental and composed path-integrated images. Symbols refer to locations marked in Fig. 15. Percent error is computed as the difference between the experimental and composed path-integrated images, normalized by the image bit depth ($2^{16}$)

The resulting transmitted X-ray intensity at the corners of the plate is then given by $I_{\theta _{max}}$:

$$\begin{aligned} \begin{aligned} I_{\theta _{max}}&= I_0 \exp \left\{ -\mu l_{\theta _{max}} \right\} \\&= I_0 \exp \left\{ -\mu l_{\theta _0} \frac{1}{\cos (\theta _{max})} \right\} \\&= I_0 \left[ \exp \left\{ -\mu l_{\theta _0} \right\} \right] ^{\frac{1}{\cos (\theta _{max})}} \\&= \left( \left[ I_0 \exp \left\{ -\mu l_{\theta _0} \right\} \right] ^{\frac{1}{\cos (\theta _{max})}} \right) I_0^{1-\frac{1}{\cos (\theta _{max})}} \\&= I_{\theta _0}^{\frac{1}{\cos (\theta _{max})}} I_0^{1-\frac{1}{\cos (\theta _{max})}} \end{aligned} \end{aligned}$$

(25)

with

$$\begin{aligned} I_{\theta _0} = I_0 \exp \left\{ -\mu l_{\theta _0} \right\} \end{aligned}$$

(26)

where $I_{\theta _0}$ is the transmitted intensity at the center of the plate where the path length is $l_{\theta _o}$.

Substituting representative values from the experimental images of $I_0 = 44,500$ counts and $I_{\theta _0} = 35,786$ counts, $I_{\theta _{max}} = 35,711$ counts. A difference of $|I_{\theta _{max}} - I_{\theta _0}| \approx 75$ counts on a 16-bit scale is within the experimental image noise (see section S5.1 in the supplementary information). Moreover, the experiments here involve small (10 px) displacements; thus, the mean path length of each individual subset remains nearly constant as the plate translates. Therefore, the effect of the radially varying path length due to a conical X-ray beam is negligible for these experiments.

Measurement uncertainty

Similar to the results from the synthetic images, bias and standard uncertainty errors were computed for the experimental results following terminology defined in the International vocabulary of basic and general terms in metrology (VIM) [41]. The true quantity value (Definition 2.11) was initially taken to be the prescribed displacement input to the translation stages. However, a slight misalignment between the translation stages and the detector caused a bias error to grow with the applied displacements. To prevent this misalignment from clouding the results, the series of individual plate images were correlated using standard, “optical” 2D-DIC, and this data was taken as the true displacement. For simplicity, the displacement magnitude, $D_i^j = \sqrt{ (U_i^j)^2 + (V_i^j)^2}$, was analyzed, rather than the individual displacement components, $U_i^j$ (horizontal displacement) and $V_i^j$ (vertical displacement). The displacement magnitude recovered from the individual plates, $D_{i,\,true}^j$, was subtracted from the displacement magnitude recovered from the path-integrated images, $D_i^j$, on a point-by-point basis to compute the displacement error, $\Delta D_i^j$, according to equation (27a). The measurement bias (Definition 2.18), $D^j_b$, of the displacement magnitude was computed for each image in the series according to equation (27b). The standard measurement uncertainty (Definition 2.30), $\sigma ^j$, was computed for each image in the series as the standard deviation of all points in the region-of-interest according to equation (27c).

$$\begin{aligned} \Delta D_i^j = D_i^j - D_{i,\,true}^j \end{aligned}$$

(27a)

$$\begin{aligned} D^j_b = \frac{1}{N_p} \sum _{i\mathop{=}1}^{N_p} \Delta D^j_i \end{aligned}$$

(27b)

$$\begin{aligned} \sigma ^j = \sqrt{\frac{1}{N_p-1} \sum _{i\mathop{=}1}^{N_p} |\Delta D^j_i|^2} \end{aligned}$$

(27c)

where j represents the image number in the series of deformed images, i represents the points in the region-of-interest, and $N_p$ is the total number of points in the region-of-interest.

Rigid translation

Figure 16 shows representative results for the rigid translations in opposite directions, for the experimental images. The full-field displacement magnitudes are shown for pattern AT2 (1.0 mm feature size) of the Al-Ta plates for two translation steps, where the prescribed displacement was either 0.7 px or 10 px, to the right for Plate 1 and to the left for Plate 2. These steps are chosen for display due to their relatively high subpixel bias (for the 0.7 px prescribed displacement case) and large standard uncertainty (for the 10 px prescribed displacement case). The top and bottom rows present the recovered displacement magnitude from the path-integrated images for the first and second plate, respectively. The bias and standard uncertainty for the displacement magnitude is quantified as described in the “Measurement Uncertainty” section for all prescribed translations and all 5 patterns in the right column of Fig. 16.

Fig. 16

Representative results for the rigid “opposing” translations of the experimental images. Full-field displacement magnitude results are shown for two translation steps, 0.7 px (left) and 10 px (right) for pattern AT2 of the Al-Ta plates. Bias (solid line) and standard uncertainty (dashed lines) are quantified for all prescribed displacements and all patterns$^{\dagger }$. Patterns “AT1–AT4” refer to the four quadrants of the Al-Ta plates, with feature sizes of 0.5 mm, 1 mm, 2 mm and 3 mm, respectively. Pattern “PS” refers to the plastic-steel plates.

$^{\dagger }$Due to a typographical error input to the Plate 1 translation stage during the experiment, the 9 px displacement step was incorrectly performed for pattern B1 and is thus omitted from the results

The experimental results have higher levels of bias and standard uncertainty than the synthetic results (see Fig. 7). The correlation was re-run using a zero-normalized sum-of-squared differences (ZNSSD) criterion to account for the overall darker intensity of the composed path-integrated image compared to the true experimental path-integrated images (see Fig. 15), but the results were nearly identical. Therefore, the increase in error is primarily attributed to the nonlinear error of the Beer-Lambert approximation (equation (13)), with darker pixels having more error than lighter pixels.

Despite the increase in error compared to the synthetic images, all experimental results have bias and standard uncertainties that remain below 0.05 px, with the exception of pattern PS, which has higher standard uncertainty. The “paired” experiment performs with even better accuracy and precision than the “opposing” translation, with bias and standard uncertainty errors less than 0.02 px for the Al-Ta plates, as shown section S3.2 in the supplementary information. As with the synthetic images, results of the optimizer performance are shown in section S6.2 in the supplementary information. In total, these experimental results show that multi-surface, path-integrated X-ray DIC can be employed with real experimental images to recover two independent rigid translations with fair subpixel accuracy and precision.

Conclusions

X-ray DIC offers unique advantages over optical DIC to provide full-field measurements of the deformation of a test article subjected to complex and/or occluded loading environments. However, conservation of intensity for path-integrated X-ray images is difficult to guarantee in practical experiments, and the restriction of patterning only a single surface limits the information garnered from a test. To address this challenge, multi-surface, path-integrated X-ray DIC (PI-DIC) was developed to extract displacements of multiple surfaces deforming independently from a single series of path-integrated X-ray images.

The theoretical background was first presented for an exemplar setup consisting of two individual plates patterned for X-ray DIC, each undergoing independent motions/deformations. An approximation of the Beer-Lambert law was formulated to describe the intensity of the path-integrated image as a function of the intensities of the two reference images of the individual plates. A unique presentation of 12 affine shape function parameters described the warpings/deformations of the two reference images. The PI-DIC algorithms were formulated in a Lagrangian framework, allowing material points on each plate to be tracked through the series of path-integrated, deformed images. The PI-DIC method was implemented in a custom code in MATLAB.

PI-DIC was then demonstrated with synthetic images, where each plate underwent either rigid translation, rigid rotation, or uniform stretch, in either “opposed” or “paired” motions. Results from all test cases showed the ability of PI-DIC to accurately and precisely recover the independent displacements from each plate, with bias and standard uncertainty errors both less than 0.02 px when images had 1.5% noise.

PI-DIC was next validated experimentally for the case of rigid translations predominately using an aluminum plate with tantalum features. The Beer-Lambert approximation was found to agree with the experimental, path-integrated images with 0.5–3.1% error for light and dark pixels, respectively. Results from the rigid translations again showed that the displacements of each plate were accurately recovered, with bias and standard uncertainty errors both less than 0.05 px for nearly all the test cases.

Finally, the supplementary information provided additional details on the performance of PI-DIC for both the synthetic and experimental images. Moderate image prefiltering was found to reduce subpixel interpolation bias in some cases, but increase standard uncertainty in other cases. Comparing PI-DIC to “optical” DIC, a larger subset size was required to obtain comparable displacement standard uncertainy, approximately twice as many iterations were required for optimizer convergence, and the matching criterion residual was either constant (for synthetic images) or higher (for experimental images). PI-DIC was found to be robust to relatively large levels of image noise (up to 3%).

These results provide the foundation for PI-DIC to measure motion and deformation of independent surfaces with subpixel accuracy and precision from a single series of path-integrated X-ray images. The PI-DIC algorithms presented here were developed for a specific setup involving two plates undergoing planar motions, and provided 2D displacements of each plate. Future work involves extending PI-DIC for more than two surfaces and for stereo measurements to provide 3D displacements of non-planar surfaces. Additionally, work is currently on-going to use synthetic reference images of the individual patterns, to expand the applicability of PI-DIC to configurations where each pattern cannot be experimentally imaged individually. As PI-DIC continues to be improved, it is anticipated to become an invaluable diagnostic for complex test environments where optical DIC suffers severe biases or is not possible, such as: thermo-mechanical tests with heat waves, flames, and/or soot; fluid-structure interaction tests with fluid density gradients; explosive tests with shock waves; and tests of assemblies with no optical access to internal components.