Introduction

During manufacture of metallic components, residual stresses are generated as a result of any inhomogeneous plastic deformation of thermal, chemical, mechanical or metallurgical origin. The mechanical and metallurgical properties of the component, such as fatigue life [1], resistance to stress corrosion cracking, crack initiation and propagation [2] and wear [3], are influenced by the residual stresses. Laser shock peening (LSP) surface treatment is increasingly used to induce beneficial compressive residual stress in the near-surface region of metallic components to improve the mechanical and metallurgical properties since fatigue cracks often initiate at free surfaces. LPS processing can, however, introduce defects into the material [4, 5] and so the parameters must be carefully selected and optimised. This requires that the LSP-induced residual stress distribution be accurately measured to aid the optimisation of process parameters for a particular application.

Many different non-destructive techniques and semi or fully destructive relaxation techniques exist to measure residual stresses, each with varying degrees of complexity, accuracy, and ease of implementation. Multiple residual stress measurement techniques are often used on a single specimen since each technique has its own strengths and weaknesses. The residual stress measurements obtained from different techniques can be used to supplement each other to more accurately describe the residual stress distribution. Incremental hole-drilling (IHD) and X-ray diffraction (XRD) are two of the most commonly used techniques to measure LSP-induced residual stresses due to their ease of use, low cost and general availability [6]. IHD involves incrementally drilling a small hole in a specimen while measuring the released strain around the hole on the surface of the specimen. The measured strains are related to the residual stresses extant in the material prior to drilling through the use of integral equations. An inverse solution of these equations is required to determine the residual stresses from the measured strain response. Calibration coefficients are necessary for this solution and can be determined for known stress distributions as a function of hole depth using finite element (FE) calculations for a particular strain gauge rosette geometry, hole position and hole diameter [7].

The unit pulse integral method is the most commonly used IHD computational method and is used in the standardised IHD test procedure, ASTM E837 [8]. Calibration coefficients are determined for unit pulses of uniform stress released at every incremental depth as the depth of the hole increases [9]. This results in a calibration matrix that is lower triangular [10] and the inverse solution of the integral method yields an exact fit to the measured strains [11]. The method is consequently sensitive to measurement errors [12, 13]. Second derivative Tikhonov regularisation [14] is normally utilised to reduce sensitivity to measurement errors by adding continuity in the stress solution to the objective function. This results in smoothing the calculated residual stresses through removal of strain noise artefacts by allowing a misfit between the measured strains and those corresponding to the regularized stress solution. Residual stress distributions that exhibit steep gradients near the surface, such as in LSP treated material, can be captured using Tikhonov regularization combined with small depth increments as in the works of Petan et al. [15] and Nobre et al. [16].

The IHD technique is prone to greater stress uncertainties in the first few measurements, irrespective of the computational method employed. This is primarily a consequence of errors in establishing the exact position of the specimen surface. Additionally, low magnitude strain measurements at small depth increments mean that any noise error is a high percentage of the actual measurement. This is exacerbated by the hole bottom fillet radius that has an appreciable effect on the first few depth increments in particular [17]. XRD measurements are, therefore, commonly used to complement IHD measurements near the surface.

XRD uses high energy X-rays to irradiate a specimen. These X-rays are diffracted by crystal lattice planes within the material according to Bragg’s Law. Detectors, situated at different angular positions around the specimen, record the intensity of the diffracted rays from which the strains in the crystal lattice can be determined [18]. The residual stresses can be calculated from the measured strains using associated X-ray elastic constants. The X-rays penetrate some depth into the specimen (20-30 µm for soft X-rays in aluminium alloys [19]) and so the measured strain and residual stress is averaged over this depth of a few microns beneath the surface. Different types of residual stresses exist that are characterised by the characteristic length scale over which they self-equilibrate [20]. While hole drilling is only able to measure macro residual stresses since micro residual stresses average out to zero over the comparatively large volume of material removal [6], XRD measures the combined residual stresses across all length scales, macro (type I) and micro (type II and III) residual stresses. As a result, XRD measurements are sensitive to small variations in the crystal lattice [18, 20] and to errors arising from determination of the diffraction peak [21], and can therefore exhibit relatively high uncertainty. It is difficult to perform robust uncertainty estimation for XRD measurements since many of the uncertainty sources are non-quantifiable [21]. Grain size can adversely affect the XRD measurement since large grain size reduces the number of grains within the irradiated volume that contribute to the diffraction peak. This results in lower peak intensities and reduced accuracy in location of the peaks [21]. The texture of the material is also important since it can cause large variation in diffraction peak intensity between \(\psi\) tilts. This effect can be mitigated somewhat by using appropriate \(\psi\) tilts and by oscillation in \(\psi\) by typically \(\pm 2^\circ\) such that grains over a larger area contribute to the measurement [21]. Inter-laboratory comparisons [22] have investigated XRD uncertainty sources and found that primary contributors to the measurement uncertainty are associated with the peak fitting software and the operator. XRD measurement uncertainty in the range of ±20 MPa is common [20, 23]. XRD has been widely used to measure LSP-induced residual stress distributions [24, 25]. In these studies, successive layer removal through electro-polishing was used to obtain stresses beneath the surface. This process is expensive, cumbersome and fully destructive, however.

To overcome these limitations of IHD and XRD, it was recently demonstrated how near-surface XRD measurements can be incorporated into the IHD solution using series expansion [26]. This alternative computational method to the regularized integral method makes use of stress distributions defined by power series [27, 28]. Since the calculated residual stress distribution is governed by mathematical functions, the imposition of magnitude and/or slope constraints to known data at any depth is facilitated. This readily allows incorporation of other residual stress measurements into the inverse solution. The regularized integral method is, however, the preferred computational method among IHD practitioners due to the ASTM standard. It is therefore necessary to extend application of this method to incorporate complementary residual stress measurements. This work presents such an approach. Near-surface XRD measurements are imposed as constraints on the regularized solution of the integral method. The XRD measurements can thereby be incorporated into the regularized IHD solution in explicit form. A residual stress distribution that is consistent with both measurement techniques is thus determined up to 1 mm depth. This distribution has reduced near-surface stress uncertainty, through the combination of XRD and IHD results. Implementation of the constrained integral approach is demonstrated on an LSP treated aluminium alloy 7075 plate of 10 mm thickness.

IHD Computational Methods

Regularized Integral Method

The integral method is well established and fully documented in the ASTM E837 Standard Test Procedure [8], therefore, it is only briefly described here. Residual stresses are related to the measured strains using calibration matrices, \(\bar{\mathbf {A}}\) and \(\bar{\mathbf {B}}\), according to equations (1)–(3). The ASTM E837-13a standard provides calibration coefficients for twenty uniform depth increments for a number of strain gauge rosette types, and includes the use of Tikhonov regularization which allows a misfit between the measured combination strains (\(\mathbf {p}\), \(\mathbf {q}\) and \(\mathbf {t}\)) and the regularized strains that correspond to the calculated stresses (\(\varvec{\sigma }_{p}\), \(\varvec{\sigma }_{q}\) and \(\varvec{\sigma }_{t}\)) in equations (1)–(3). The Cartesian stresses can be determined from \(\varvec{\sigma }_{p}\), \(\varvec{\sigma }_{q}\) and \(\varvec{\sigma }_{t}\) [8].

$$\begin{aligned} \left( \bar{\mathbf {A}}^T \bar{\mathbf {A}}+\alpha _p \ \mathbf {L}^T \mathbf {S}^T \mathbf {H} \mathbf {S} \mathbf {L}\right) \varvec{\sigma }_{p}&=\frac{E}{1+\nu }\ \bar{\mathbf {A}}^T \ \mathbf {p} \end{aligned}$$
(1)
$$\begin{aligned} \left( \bar{\mathbf {B}}^T \bar{\mathbf {B}}+\alpha _q \ \mathbf {L}^T \mathbf {S}^T \mathbf {H} \mathbf {S} \mathbf {L}\right) \varvec{\sigma }_{q}&=E\ \bar{\mathbf {B}}^T \ \mathbf {q} \end{aligned}$$
(2)
$$\begin{aligned} \left( \bar{\mathbf {B}}^T \bar{\mathbf {B}}+\alpha _t \ \mathbf {L}^T \mathbf {S}^T \mathbf {H} \mathbf {S} \mathbf {L}\right) \varvec{\sigma }_{t}&=E\ \bar{\mathbf {B}}^T \ \mathbf {t} \end{aligned}$$
(3)

where \(\alpha _p\), \(\alpha _q\) and \(\alpha _t\) are the regularization factors, \(\varvec{\sigma }_{p}\) is the isotropic (equi-biaxial) stress, \(\varvec{\sigma }_{q}\) is the 45° shear stress and \(\varvec{\sigma }_{t}\) is the x-y shear stress.

Tikhonov regularization is employed through the use of matrix \(\mathbf {L}\):

$$\mathbf {L} = \begin{bmatrix} 0 &{}0 &{} 0&{}0 &{}\cdots &{} 0 &{}0 &{} 0&{}0 \\ -1 &{}2 &{}-1 &{}0 &{}\cdots &{} 0 &{}0 &{} 0&{}0 \\ 0&{}-1 &{}2 &{}-1 &{}\cdots &{} 0 &{}0 &{} 0&{}0 \\ \vdots &{} \vdots &{}\vdots &{}\vdots &{}\ddots &{} \vdots &{}\vdots &{} \vdots &{}\vdots \\ 0 &{}0 &{} 0&{}0 &{}\cdots &{} 0&{}-1 &{}2 &{}-1 \\ 0&{} 0 &{}0 &{}0 &{}\cdots &{} 0 &{}0 &{} 0&{}0 \\ \end{bmatrix}$$
(4)

The \(\mathbf {H}\) and \(\mathbf {S}\) matrices have the following form [29]:

$$\begin{aligned} \mathbf {H}&= \begin{bmatrix} \frac {\left( z_1-z_0\right) }{w} &{} &{} &{} \\ &{}\frac {\left( z_2-z_1\right) }{w} &{} &{} \\ &{} &{} \frac {\left( z_3-z_2\right) }{w} &{} \\ &{} &{} &{} \frac {\left( z_4-z_3\right) }{w} \\ \end{bmatrix} \end{aligned}$$
(5)
$$\begin{aligned} \mathbf {S}&= \begin{bmatrix} s_1 &{} &{} &{} \\ &{}s_2 &{} &{} \\ &{} &{} s_3 &{} \\ &{} &{} &{}s_4 \\ \end{bmatrix} \end{aligned}$$
(6)

where n is the number of depth increments, w is the final hole depth, \(z_i\) is the hole depth at increment i, and \(s_i\) is the standard error in the strain measurement at increment i. This can be estimated from the strain measurement uncertainties.

The \(\mathbf {S}\) matrix adjusts the amount of regularization to fit the expected measurement error at each depth increment. The regularization factors \(\alpha _p\), \(\alpha _q\) and \(\alpha _t\) globally adjust the degree of regularization that is applied. Insufficient regularization leads to greater uncertainty in the calculated stress results due to noise artefacts remaining in the strain measurements. Excessive regularization distorts the stress results due to removal of some true strain variation along with the noise artefacts. An appropriate balance must be found between these two tendencies. The Morozov Discrepancy Principle [14] can be used to iteratively determine the optimal degree of regularization to apply. This principle specifies that an optimal degree of regularization is achieved when the chi-squared statistic, \(\chi ^2\), equals the number of depth increment as shown in equation (7) for the \(\mathbf {p}\) combination strains, but similarly for \(\mathbf {q}\) and \(\mathbf {t}\). The relationships between the measured strain data in the x, y and 45° directions at the relevant strain gauge locations and the combination strains, \(\mathbf {q}\) and \(\mathbf {t}\), are provided in the ASTM E837 standard.

$$\begin{aligned} \begin{aligned} \mathbf {p}&=\dfrac{\mathbf {\epsilon }_x+\mathbf {\epsilon }_y}{2}\\ \chi ^2&=\sum _{i=1}^{n}\left( \frac{p_i^{reg}-p_i^{meas}}{s_i^p}\right) ^2 \end{aligned} \end{aligned}$$
(7)

where \(\mathbf {p}^{meas}\) are the measured combination strains, \(\mathbf {p}^{reg}\) are the combination strains corresponding to the regularized \(\varvec{\sigma }_{p}\) stresses calculated using equation (1), and \(\mathbf {s}^p\) are the standard errors specified in equation (6).

Despite the use of the Morozov Discrepancy Principle, it may be necessary to adjust the amount of regularization applied if noise artefacts remain, or if distortion of the stress solution occurs [29]. The misfit between the regularized and measured strain data should be included in any uncertainty estimation.

Imposition of Constraints On the Regularized Integral Method

To enable concise discussion, the approach to impose constraints on the regularized solution is shown only for the isotropic (equi-biaxial) stress, \(\varvec{\sigma }_p\). The approach for the 45° shear stress, \(\varvec{\sigma }_q\), and the x-y shear stress, \(\varvec{\sigma }_t\), is the same. The standard regularized integral solution for \(\varvec{\sigma }_p\) is given by equation (1).

Multiple constraints can be imposed at any depths using this approach which allows data from laboratory XRD with successive layer removal, or synchrotron XRD, or neutron diffraction, or data from a combination of these techniques to be used at various depth increments. To impose constraints on the regularized integral solution at any number of depths the stress solution at these depths must be equal to the known stresses, \(\mathbf {m}\). Vector \(\mathbf {m}\) has the same dimensions as \(\varvec{\sigma }_{p}\) and contains the known stresses at the relevant depth increments and zeros at the unconstrained increments. For example, if constraints are imposed on the 1st, 3rd and 5th depth increments, the constraint equations are given by

$$\begin{aligned} \begin{aligned} \sigma _{p_1}&=m_{1}\\ \sigma _{p_3}&=m_{3}\\ \sigma _{p_5}&=m_{5} \end{aligned} \end{aligned}$$
(8)

which can be represented in vector-matrix form as

$$\begin{aligned} \begin{bmatrix} 1 &{} 0 &{} 0 &{} 0 &{} 0&{} \cdots &{} 0\\ 0 &{} 0 &{} 1 &{} 0 &{} 0&{} \cdots &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 1&{} \cdots &{} 0\\ \end{bmatrix} \begin{Bmatrix} \sigma _{p_1}\\ \sigma _{p_2}\\ \sigma _{p_3}\\ \sigma _{p_4}\\ \sigma _{p_5}\\ \vdots \\ \sigma _{p_n} \end{Bmatrix}&= \begin{bmatrix} 1 &{} 0 &{} 0 &{} 0 &{} 0&{} \cdots &{} 0\\ 0 &{} 0 &{} 1 &{} 0 &{} 0&{} \cdots &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 1&{} \cdots &{} 0\\ \end{bmatrix} \begin{Bmatrix} m_{1}\\ 0\\ m_{3}\\ 0\\ m_{5}\\ \vdots \\ 0 \end{Bmatrix} \end{aligned}$$
$$\mathbf {C} \ \varvec{\sigma }_{p}=\mathbf {C} \ \mathbf {m}$$
(9)

The standard regularized solution is re-formulated as a constrained optimisation problem:

$$\begin{aligned} \begin{aligned}&\text {minimize} \qquad f\left( \varvec{\sigma }_{p}\right) =\frac{1}{2}\left\| \mathbf {A}\varvec{\sigma }_{p} - \mathbf {y}\right\| ^2\\&\text {subject to} \qquad \mathbf {c}_i \ \varvec{\sigma }_{p}=\mathbf {c}_i \ \mathbf {m}, \qquad i=1,\ldots ,k \end{aligned} \end{aligned}$$
(10)

where \(\mathbf {c}_i\) is a vector containing the \(i^{th}\) row of the constraint matrix \(\mathbf {C}\), k is the number of imposed constraints and

$$\begin{aligned} \mathbf {A}&=\left( \bar{\mathbf {A}}^T \bar{\mathbf {A}}+\alpha _p \ \mathbf {L}^T \mathbf {S}^T \mathbf {H} \mathbf {S} \mathbf {L}\right) \end{aligned}$$
(11)
$$\begin{aligned} \mathbf {y}&=\frac{E}{1+\nu }\ \bar{\mathbf {A}}^T\mathbf {p} \end{aligned}$$
(12)

The constrained optimisation problem can be solved using the method of Lagrange multipliers [30]. A Lagrange function, \(\mathcal {L}\left( \varvec{\sigma }_{p},\varvec{\lambda }\right)\), with Lagrange multipliers, \(\lambda _1,\dots ,\lambda _k\), is formed:

$$\begin{aligned} \mathcal {L}\left( \varvec{\sigma }_{p},\varvec{\lambda }\right) =f\left( \varvec{\sigma }_{p}\right) +\lambda _1\left( \mathbf {c}_1 \ \varvec{\sigma }_{p}-\mathbf {c}_1 \ \mathbf {m}\right) +\dots +\lambda _k\left( \mathbf {c}_k \ \varvec{\sigma }_{p}-\mathbf {c}_k \ \mathbf {m}\right) \end{aligned}$$
(13)

The first-order conditions for a stationary point of this Lagrange function are sufficient for a global optimal solution since the optimisation problem in equation (10) consists of a convex objective function and only linear equality constraints [31]. A stationary point requires that the gradient of \(\mathcal {L}\left( \varvec{\sigma }_{p}^*,\varvec{\lambda }^*\right)\) be zero:

$$\begin{aligned} \begin{aligned} \frac{\partial \mathcal {L}}{\partial \varvec{\sigma }_{p}^*}\left( \varvec{\sigma }_{p}^*,\varvec{\lambda }^*\right)&=0 \\ \frac{\partial \mathcal {L}}{\partial \varvec{\sigma }_{p}^*}\left( \varvec{\sigma }_{p}^*,\varvec{\lambda }^*\right)&= \left( \mathbf {A}^T \ \mathbf {A}\right) \varvec{\sigma }_{p}^*-\left( \mathbf {A}^T \ \mathbf {y}\right) +\mathbf {C}^T \ \varvec{\lambda }^*=0 \\ \left( \mathbf {A}^T \ \mathbf {A}\right) \varvec{\sigma }_{p}^*+\mathbf {C}^T \ \varvec{\lambda }^*&=\left( \mathbf {A}^T \ \mathbf {y}\right) \end{aligned} \end{aligned}$$
(14)

and

$$\begin{aligned} \begin{aligned} \frac{\partial \mathcal {L}}{\partial \varvec{\lambda }^*}\left( \varvec{\sigma }_{p}^*,\varvec{\lambda }^*\right)&=0 \\ \frac{\partial \mathcal {L}}{\partial \varvec{\lambda }^*}\left( \varvec{\sigma }_{p}^*,\varvec{\lambda }^*\right)&= \mathbf {C} \ \varvec{\sigma }_{p}^*-\mathbf {C} \ \mathbf {m}=0\\ \mathbf {C} \ \varvec{\sigma }_{p}^*&=\mathbf {C} \ \mathbf {m} \end{aligned} \end{aligned}$$
(15)

where \(\varvec{\sigma }_{p}^*\) is the regularized optimal stress solution that satisfies the imposed constraints and \(\varvec{\lambda }^*\) is a vector containing the Lagrange multipliers required to enforce the constraints.

Equations (14) and (15) are linear and can be solved directly as shown in equation (16). The matrix in equation (16) is also known as the Karush-Kuhn-Tucker (KKT) matrix [31]. The KKT approach [32, 33] generalises the Lagrange multiplier method by also allowing inequality constraints to be included in the constrained optimisation problem and the solution verified for optimality through additional KKT conditions. Once stress measurements from other experimental techniques are obtained, they are used to impose constraints through \(\mathbf {C}\) and \(\mathbf {m}\) which are found from equation (9). Each of the remaining terms in equation (16) is readily found from equations (11) and (12). The \(\bar{\mathbf {A}}\) matrix is already required by the standard integral method and is provided in the ASTM standard. The constrained solution is therefore easily determined using information that is readily available.

$$\begin{aligned} \begin{bmatrix} \mathbf {A}^T \mathbf {A} &{} \mathbf {C}^T\\ \mathbf {C} &{} \mathbf {0} \end{bmatrix} \begin{Bmatrix} \varvec{\sigma }_{p}^* \\ \varvec{\lambda }^* \end{Bmatrix} = \begin{Bmatrix} \mathbf {A}^T \mathbf {y} \\ \mathbf {C} \ \mathbf {m} \end{Bmatrix} \end{aligned}$$
(16)

The simplest way to demonstrate this approach is to constrain the stress in the first depth increment to a known value such as might be obtained from a near-surface XRD measurement. In this case, the constraint matrix, \(\mathbf {C}\), simply becomes a row vector where all entries are zero except for the first entry of unity. All entries except for the first entry of the known stress vector, \(\mathbf {m}\), are also zero and the first entry is the XRD stress measurement. Equation (16) is then used to find the optimal stress distribution that satisfies Tikhonov regularization and the imposed constraints. The Morozov Discrepancy Principle is employed to determine the optimal degree of regularization to apply. The effective depth of the XRD measurement must be included in the calibration matrices, \(\bar{\mathbf {A}}\) and \(\bar{\mathbf {B}}\), with appropriate coefficients for this depth increment and stress application depth. A row for the depth increment and a column for the stress application depth corresponding to the XRD measurement must be added to the calibration matrices. The first depth increment of the uniform depth calibration matrices is split into two smaller depths to ensure that the mid-step depth of the first increment aligns with the effective depth of the XRD measurement. The coefficients corresponding to the two smaller depth increments and stress application depths can be obtained from the uniform depth cumulative calibration coefficients [9]. The depth of the XRD measurement must also be included in the combination strain vectors (\(\mathbf {p}\), \(\mathbf {q}\) and \(\mathbf {t}\)).

Obviously, the need for the constrained approach needs to be evaluated in each specific case to determine whether or not the imposition of constraints on the IHD solution is beneficial or not. There is no benefit to be obtained by constraining the IHD results to fit complementary measurements with larger uncertainty than that of IHD.

Experimental

Specimen and LSP

A rolled aluminium alloy 7075-T651 plate was reduced from 15 mm thickness to 10 mm by machining 1 mm from the top face of the plate and 4 mm from the bottom. Thereafter, individual specimens of 60 mm \(\times\) 60 mm were prepared from the 10 mm plate. The mechanical properties and chemical composition of aluminium alloy 7075-T651 are provided in Table 1. LSP treatment was applied to an area of 11.25 mm \(\times\) 11.25 mm on the upper face of the plate at the National Laser Centre (NLC) of the Council for Scientific and Industrial Research (CSIR) in Pretoria, South Africa, using a Quanta-Ray Pro Spectra Physics (QRPSP) Nd:YAG laser. An X-Y raster pattern was used as the spot sequence strategy, with equidistant spot placement in the horizontal and vertical directions. In this work, the LSP step and scan directions correspond to the x and y directions, respectively. The specifications of the laser and LSP parameters are provided in Table 2.

Table 1 Mechanical properties and chemical composition of aluminium alloy 7075-T651 [34]
Full size table
Table 2 Laser specifications and LSP parameters
Full size table

XRD

The specimen was analysed by laboratory XRD before conducting IHD. The \(\sin ^2 \psi\) method [35] was used to measure near-surface residual stresses in the specimen. Measurements were performed using a Proto iXRD (Proto Manufacturing Inc.,Taylor, Michigan USA) instrument at the CSIR. To obtain an illustrative XRD measurement for this work, lattice spacing of the {311} planes was measured for 7 \(\psi\) angles between −27\(^\circ\) and +27\(^\circ\) using Cr-K\(\alpha\) radiation with a wavelength of 2.291 Å at a 2\(\theta\) angle of approximately 139°. In general a minimum of 10 \(\psi\) angles between greater limits should be used to obtain accurate data [21]. Measurements were taken using a 2 mm round aperture in the x, y and 45° directions to obtain the in-plane stress-tensor. The sample was oscillated by ±3° in \(\psi\) to improve counting statistics and reduce the effect of large grain sizes and texture in the aluminium specimen. The residual stresses were calculated for plane stress conditions using X-ray elastic constants of \(\frac {1}{2}S_2\) = 19.54 \(\times\) 10−6 MPa−1 and \(S_1\) = −5.11 \(\times\) 10−6 MPa−1 for the {311} lattice plane. The XRD information depth was estimated to be 10.5 µm [36]. The near-surface XRD measurements were incorporated into those obtained through IHD by imposing these measurements as constraints on the integral solution. The common XRD uncertainty of ±20 MPa [20, 23] was used in this work to illustrate the method.

IHD

IHD was performed using a Sint Technology Restan MTS 3000 in the centre of the LSP area. A tungsten carbide inverted cone end mill with a 1.6 mm diameter was used to drill the hole that had a final diameter of 1.83 mm. An inverted cone end mill was used to create a hole-bottom that is as flat as possible and achieve the best match between the FE model used to obtain the calibration coefficients and the physical hole. Establishing the zero depth position is crucial for IHD measurements, especially when a steep stress gradient exists near the surface as is normally the case in a LSP-induced stress distribution. Incorrect zero depth determination can significantly affect the magnitude of the first few calculated stresses which, in turn, can also affect the remainder of the calculated stress distribution. Surface roughness from LSP precluded using the electrical contact technique to establish the zero depth. Instead, finely spaced depth increments of 5 µm were used for the first 0.2 mm of incremental drilling and coarser depth increments of 25 µm were used thereafter up to a depth of 1.2 mm. Drilling was started slightly above the surface to ensure that the incremental depth that penetrated the surface was captured. The experimental strain measurements were investigated after IHD to determine the most likely position of the surface where an appreciable strain response first occurs. This method is not advised for general use since it relies on an observable strain response when the surface is penetrated and therefore requires that some residual stress exists near the surface. It was conservatively assumed that strain measurements associated with two depth increments into the specimen could be missed due to measurement noise. Therefore, the zero depth uncertainty is considered as two depth increments, or 10 µm, in this case.

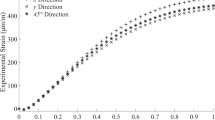
A 6-element HBM 1.5/350M RY61 strain gauge rosette, connected to a National Instruments data acquisition system, was used to record strain measurements throughout the IHD experiment. For temperature compensation, each strain gauge was connected in a quarter-bridge type II configuration to an identical gauge attached to the same material. The measured incremental strains in the x, y and 45° directions at the relevant strain gauge locations are presented at depth increments of 25 µm in Fig. 1. The strain measurements at the finer depth increments of 5 µm over the first 0.2 mm of the test are omitted to improve the clarity of the figure. Likewise, the error-bars representing measurement uncertainty are also omitted.

Fig. 1
figure 1

Measured strain relief variation in the x, y and 45° gauge directions

Full size image

Computational

Calibration coefficients provided in the ASTM E837-13a standard have several limitations regarding their use, such as those related to the thickness of the specimen and allowable hole diameter ranges for a specific rosette. Schajer [37] recently reduced the bulk calibration data for IHD residual stress measurement with the integral method to a two-variable polynomial formulation to extend the application of the integral method and further increase ease of implementation. The polynomial formulation comprises 15 numerical coefficients and provides calibration data with average accuracy within 1%, with occasional outliers reaching around 2%. The latest version of the ASTM standard, ASTM E837-20, has been updated to incorporate this polynomial formulation. However, the particular rosette and hole diameter used in this work falls outside the scope of the ASTM standard. Therefore, the necessary calibration coefficients were instead determined through FE calculations using MSC Nastran FE analysis. The coefficients of matrices \(\bar{\mathbf {A}}\) and \(\bar{\mathbf {B}}\) were obtained by applying equi-biaxial and pure shear stress, respectively, to the face of the hole using PLOAD4 cards for every loading increment at each incremental depth. A quarter model was used with symmetric and anti-symmetric boundary conditions depending on the applied loading.

The specimen was modelled using HEX8 type 3D elements; 24 elements of 50 µm height were used in the region from the surface up to 1.2 mm depth and 100 elements of linearly increasing height were used through the remaining thickness. Calibration coefficients were determined for twenty uniform depth increments of 50 µm up to a depth of 1 mm. The strain gauge grids were not directly included in the FE model, instead, nodal displacement data in and around the region of the grids was used to determine the longitudinal and transverse strains at each gauge for every loading condition and drilling increment using bi-harmonic spline interpolation. The longitudinal and transverse strains were used to correct the calibration coefficients for transverse sensitivity [38]. The position of the drilled hole relative to the centre of the strain gauge rosette is important since it can have an appreciable effect on the the measured strains and subsequently the calculated residual stresses [39, 40]. The measured location of the hole relative to the centre of the rosette was, therefore, included in the analysis during the bi-harmonic spline interpolation of the displacement data by adjusting the position of the strain gauge grids relative to the hole [41].

Every second 25 µm incremental strain measurement presented in Fig. 1 was used with the calculated \(\bar{\mathbf {A}}\) and \(\bar{\mathbf {B}}\) matrices having 50 µm depth increments from the FE model. In the case of the constrained integral method, the first 50 µm depth increment of the uniform depth calibration matrices is split into two smaller depth increments of 21 µm and 29 µm, respectively. This ensures that the mid-step depth of the first increment aligns with the XRD depth at 10.5 µm. The calibration coefficients for the depth increments from the surface to 21 µm and then from 21 µm to 50 µm were obtained from the cumulative calibration coefficients [9], which can be determined from the uniform depth matrices, \(\bar{\mathbf {A}}\) and \(\bar{\mathbf {B}}\). Spline interpolation was used to find the x, y and 45° strains at the XRD depth, from which the combination strains were calculated.

Propagation of Uncertainties

Monte Carlo simulation [42] was used to estimate the uncertainty in the calculated residual stress measurements. Only the dominant experimental and computational uncertainty sources were considered. These are provided in Table 3. Other uncertainty sources, such as uncertainty in hole diameter and hole location, can be easily incorporated into the analysis. However, it has been demonstrated [28, 41] that their contribution to the overall stress uncertainty is small compared to the uncertainties considered in Table 3.

Table 3 Uncertainty sources and their assigned probability density functions
Full size table

Within each Monte Carlo trial, the measured strains were all first adjusted for the uncertainty in indicated strain. Thereafter, each strain measurement was individually adjusted for uncertainty in incremental depth, and all measurements were adjusted for the uncertainty in zero depth position. Spline interpolation was then used to determine the strains corresponding to the uniform depth increments of 50 µm in the \(\bar{\mathbf {A}}\) and \(\bar{\mathbf {B}}\) matrices. Finally, uncertainty due to strain measurement noise and the misfit between the regularized and measured strain data was included. Uncertainty in the material properties was included within equations (1)–(3) and (12). FE calculations also have associated uncertainty since they are not able to fully represent all the deformations that are possible in reality. The calibration coefficients of the \(\bar{\mathbf {A}}\) and \(\bar{\mathbf {B}}\) matrices were all varied by the same random variable within each Monte Carlo trial since the matrices are considered to be fully correlated [43].

The combination strains were calculated from the x, y and 45° strain measurements of each Monte Carlo trial and used with calibration matrices, \(\bar{\mathbf {A}}\) and \(\bar{\mathbf {B}}\), in equations (1)–(3) in the case of the standard integral method. The combination strains and calibration matrices were similarly used with the XRD measurements of that trial in equations (11), (12) and (16) to calculate the stress distributions of the constrained integral method.

Following the Monte Carlo simulation, the stress uncertainty at each information depth for each method was obtained from the standard deviation in calculated stress at that depth across the ten thousand trials used in the simulation.

Results and Discussion

The regularized fits to the measured strain data in the x-direction are presented in Fig. 2 for the standard and constrained integral methods. The imposition of the near-surface constraint on the IHD solution using XRD data has minimal effect on the regularized curve fit. This is especially true at increasing depths from the near-surface constraint.

Fig. 2
figure 2

Regularized fits to the measured strain data in the x-direction

Full size image

The calculated stress distributions and associated uncertainties of the constrained and standard integral methods are shown in Figs. 3 and 4 for the x and y stress components, respectively. All uncertainty presented in the figures corresponds to two standard deviations. The shear stress distributions are omitted since the shear stresses are close to zero throughout the 1 mm depth. The magnitude and form of the residual stress distributions in the x and y directions, and the associated uncertainties, compare favourably. The combination of laser specification, LSP parameters, target material and specimen geometry did not result in the desired compressive stress at the surface. Localised yielding can occur around the drilled hole due to stress concentration which can introduce increasingly significant errors if the stress exceeds 60% of the yield strength when measuring highly non-uniform stress distributions [44]. The mean minimum principle stress was measured to be -299 MPa. Considering that this stress is slightly lower than the 60% threshold and that the surface layers are work hardened by the LSP treatment, plasticity effects were not present.

Fig. 3
figure 3

\(\sigma _x\) distributions and associated uncertainties of each method

Full size image
Fig. 4
figure 4

\(\sigma _y\) distributions and associated uncertainties of each method

Full size image

The standard integral method is able to represent the residual stress distribution well, but high stress uncertainty occurs near the surface. In contrast, when the constrained approach is used, the near-surface stress uncertainty at the XRD depth is significantly reduced. The measured stresses change from 34.2±34.4 MPa and 39.5±33.4 MPa in the x and y directions, respectively, for the standard integral method to those of the XRD measurements (79.9±20.0 MPa and 58.3±20.0 MPa) for the constrained approach. The reduction in near-surface uncertainty comes at the expense of greater uncertainty at other depths, however, particularly in the region between the XRD measurement and the maximum compressive stress. The constrained integral solution has nearly identical uncertainty compared to the standard method at greater depths since similar regularization factors were used while enforcing the constraint to the XRD data. Table 4 compares the RMS uncertainty in stress over the 1 mm depth for each stress component. The stress uncertainty for the constrained integral method compares well to the standard regularized integral method for all stress components but is somewhat higher. This increase arises because inclusion of the XRD measurements near the surface introduces an additional source of stress uncertainty.

Table 4 RMS uncertainty in stress (MPa)
Full size table

For illustrative purposes, the effect of varying levels of XRD uncertainty on the IHD solution is presented in Fig. 5 for the x-direction data. As is required, the near-surface stress uncertainty is directly dependent on the uncertainty in XRD results. The effect of this uncertainty, however, is localised to the region of the imposed constraint. The uncertainty in IHD data dominates at regions remote from the XRD datum and so the XRD uncertainty has a negligible effect on the stress uncertainty below the first few depth increments. Clearly there is no benefit to be gained in incorporating XRD measurements with higher uncertainty than those of the IHD results.

Fig. 5
figure 5

IHD residual stress uncertainty distributions for varying levels of XRD uncertainty

Full size image

Conclusions

The physical characteristics of the IHD technique result in large stress uncertainty in near-surface measurements when steep stress gradients exist, irrespective of the computational method employed. An approach has been developed to incorporate any number of residual stress data from complementary measurement techniques into the regularized integral method of IHD, thereby allowing these results to be properly consolidated. Implementation of the approach is demonstrated on an aluminium alloy 7075 plate of 10 mm thickness that underwent LSP treatment. Near-surface XRD measurements are incorporated into the IHD solution to fully define a rapidly varying LSP-induced residual stress distribution. The effect of incorporating surface XRD measurements into the IHD solution is localised to the near-surface measurements where the stress uncertainty is significantly reduced. At greater depths, however, there is no significant change in stress uncertainty.