Application of Moiré Interferometry to the Characterization of Orthotropic Materials in the Antisymmetric Configuration using the Virtual Fields Method

Abstract

Moiré interferometry is an effective full-field deformation measurement technique and has been utilized for mechanical behavior analysis of materials and structures. For isotropic materials, Moiré patterns can be obtained by performing standard tests, such as, tensile and bending tests, to calculate the displacement and strain. Then, the mechanical properties can be characterized. However, standard tests are not sufficient to characterize the mechanical parameters of anisotropic materials due to the complexity of their material properties. Thus, in this work, Moiré interferometry was combined with the Virtual Fields Method to obtain the four in-plane elastic constants (Q₁₁, Q₂₂, Q₁₂, and Q₆₆) of orthotropic materials in the form of a diametrically compressed disk. Firstly, according to finite element method simulation results, optimized parameters can be achieved when the principal direction of the material does not coincide with the loading direction, making the loading configuration antisymmetric. Therefore, Moiré interferometry experiment was simulated to demonstrate the feasibility of measurement in the antisymmetric configuration. Finally, the Q₁₁, Q₂₂, Q₁₂ and Q₆₆ values of a unidirectional carbon fiber composite were measured in a real Moiré interferometry experiment using the proposed method, yielding results that agreed closely with those obtained using the strain gauges.

Introduction

Moiré interferometry [1] is a widely used optical interference technique for full-field measurements. It is well known for its high accuracy (wavelength scale) and insensitivity to out-of-plane displacements, and has been successfully applied in many fields, such as, material characterization [2,3,4,5], fracture mechanics [6], residual stress [7] and so on [8]. In terms of material characterization, Moiré interferometry has the advantages of full field measurement and high accuracy, and efforts have been made in many fields, such as, welding [2], composites [3, 4], concrete materials [5] and so on.

To characterize the mechanical properties of anisotropic materials, traditional methods involving standard tests, such as, tensile and bending tests, are not suitable because of the complexity of the mechanical properties. Therefore, in this study, the virtual fields method (VFM) [9,10,11] was combined with Moiré interferometry to measure the four in-plane elastic constants (Q₁₁, Q₂₂, Q₁₂, and Q₆₆) of an orthotropic material. The VFM is able to inverse all of the in-plane elastic constants from the full-field strain simultaneously and requires less computational time than other methods of solving the inverse problem, such as, the finite element model updating technique [12], the constitutive equation gap method [13], and deformation-pattern-based digital speckle correlation [14].

Many efforts have been made to characterize the mechanical properties of orthotropic materials by combining the VFM and full-field measurement techniques [4, 15,16,17,18,19,20]. According to some research [17,18,19], the off-axis angle (the angle between the principal axis of the material and the coordinate axis) significantly influences the accuracy of the inversed constants. Therefore, a diametrically compressed disk can be used as the loading configuration together with the VFM to facilitate adjustment of the off-axis angle to obtain optimal values in the characterization.

Notably, when the principal direction of the material does not coincide with the loading direction, the deformation field will be antisymmetric. However, in Moiré interferometry, the fringe patterns generated by real deformations and rigid-body rotations are coupled when the displacement fields are antisymmetric. Consequently, further study is necessary to discuss the feasibility of Moiré interferometry application in such situations.

In this work, firstly, the strain field of the disk configuration obtained from the finite element method (FEM) simulation was used for the VFM program to inverse the four elastic constants (Q₁₁, Q₂₂, Q₁₂, and Q₆₆) with high accuracy. Then, a Moiré interferometry experiment was simulated to demonstrate the feasibility of combining VFM and Moiré interferometry. The results of the simulated experiments illustrate that Moiré interferometry can be employed to measure strain fields for the VFM with sufficient accuracy when the displacement field is antisymmetric. Finally, the values of Q₁₁, Q₂₂, Q₁₂ and Q₆₆ for a unidirectional carbon fiber composite were measured in a real experiment conducted using a Moiré interferometer, which yielded results very similar to those obtained using the strain gauges.

Theory

Moiré Interferometry

In Moiré interferometry, high-frequency cross-line gratings are fabricated on the surface of the specimen. Upon loading, the gratings deform with the specimen. Then, two laser beams are incident on the deformed gratings at symmetric angles to form virtual reference gratings. The specimen gratings subsequently interfere with the virtual reference gratings to generate Moiré fringe patterns, which can be recorded by a camera, as shown in Fig. 1. [1]

Fig. 1

Schematic diagram of Moiré interferometry

The relationships between the number of the fringes and the displacement are as follows [1]:

$$ \left\{\begin{array}{l}u\left(x,y\right)=\frac{N_x}{2f}\\ {}v\left(x,y\right)=\frac{N_y}{2f}\end{array}\right. $$

(1)

where u(x, y) and v(x, y) are the displacements along the x and y axes, respectively; N _x and N _y are the number of fringes along the x and y axes, respectively; and f is the initial frequency of the specimen gratings.

In this work, gratings with a frequency of 1200 lines/mm were used. Then one fringe indicates the displacement of 417 nm.

Constitutive Equation of Orthotropic Materials

A brief introduction and some notations used in the constitutive equation of orthotropic materials are given in this section. For orthotropic materials, there are five in-plane engineering constants: E₁, E₂, v₁₂, v₂₁, and G₁₂ [21]. Considering that v₁₂/ E₁ = v₂₁/ E₂, there are four independent elastic constants in total. Then, to describe the relation between stress and strain, four elastic constants denoted as Q₁₁, Q₂₂, Q₁₂, and Q₆₆ are commonly used and the constitutive equation is as follows:

$$ \left[\begin{array}{l}{\sigma}_1\\ {}{\sigma}_2\\ {}{\tau}_{12}\end{array}\right]=\left[\begin{array}{ccc}{Q}_{11}& {Q}_{12}& 0\\ {}{Q}_{12}& {Q}_{22}& 0\\ {}0& 0& {Q}_{66}\end{array}\right]\left[\begin{array}{l}{\varepsilon}_1\\ {}{\varepsilon}_2\\ {}{\gamma}_{12}\end{array}\right] $$

(2)

where (σ₁, σ₂, τ₁₂) is the stress tensor and (ε₁, ε₂, γ₁₂) is the engineering strain tensor. The subscript ‘12’ indicates the principal axis of the material.

The relationships between the four elastic constants and the engineering constants are then:

$$ \left\{\begin{array}{l}{Q}_{11}=\frac{E_1}{1-{v}_{12}{v}_{21}}\\ {}{Q}_{22}=\frac{E_1}{1-{v}_{12}{v}_{21}}\\ {}{Q}_{12}={v}_{12}{Q}_{22}={v}_{21}{Q}_{11}\\ {}{Q}_{66}={G}_{12}\end{array}\right. $$

(3)

Virtual Fields Method

The virtual fields method is based on the principle of virtual work (PVW). When static and in-plane problems are considered and the body force is ignored, the simplified PVW equation can be written as follows [22]:

$$ \underset{S}{\int}\boldsymbol{\upsigma} :{\boldsymbol{\upvarepsilon}}^{\ast}\mathrm{d}S=\underset{\partial S}{\int}\overline{\mathbf{T}}\cdot {\mathbf{u}}^{\ast}\mathrm{d}l,\forall {\mathbf{u}}^{\ast}\mathrm{KA} $$

(4)

where σ is the stress tensor, ε^∗ is the virtual strain tensor, S is the external surface, $\overline{\mathbf{T}}$ is the traction on the boundary, and u^∗ is the virtual displacement tensor. “KA” stands for “kinematically admissible”, which means that u^∗ must satisfy the boundary condition.

For the in-plane orthotropic elastic model, introducing equation (3) into equation (4) yields:

$$ {Q}_{11}\underset{S}{\int }{\varepsilon}_1{\varepsilon}_1^{\ast}\mathrm{d}S+{Q}_{22}\underset{S}{\int }{\varepsilon}_2{\varepsilon}_2^{\ast}\mathrm{d}S+{Q}_{12}\left(\underset{S}{\int }{\varepsilon}_1{\varepsilon}_2^{\ast}\mathrm{d}S+\underset{S}{\int }{\varepsilon}_2{\varepsilon}_1^{\ast}\mathrm{d}S\right)+{Q}_{66}\underset{S}{\int }{\tau}_{12}{\gamma}_{12}^{\ast}\mathrm{d}S=\underset{\partial S}{\int}\overline{\mathbf{T}}\cdot {\mathbf{u}}^{\ast}\mathrm{d}l $$

(5)

where $\left({\varepsilon}_1^{\ast },{\varepsilon}_2^{\ast },{\gamma}_{12}^{\ast}\right)$ is the virtual strain tensor.

In this work, polynomials were used to define the virtual strain field $\left({\varepsilon}_1^{\ast },{\varepsilon}_2^{\ast },{\gamma}_{12}^{\ast}\right)$ in equation (5) [22]. Since there are four unknown parameters to be calculated, four groups of the virtual fields are required. Then equation (4) becomes:

$$ \left[\underset{s}{\int }{\varepsilon}_1{\varepsilon}_1^{\ast }(1)\mathrm{d}s\underset{s}{\int }{\varepsilon}_2{\varepsilon}_2^{\ast }(1)\mathrm{d}s\underset{s}{\int }{\varepsilon}_1{\varepsilon}_2^{\ast }(1)+{\varepsilon}_2{\varepsilon}_1^{\ast }(1)\mathrm{d}s\underset{s}{\int }{\gamma}_{12}{\gamma}_{12}^{\ast }(1)\mathrm{d}s\underset{s}{\int }{\varepsilon}_1{\varepsilon}_1^{\ast }(2)\mathrm{d}s\underset{s}{\int }{\varepsilon}_2{\varepsilon}_2^{\ast }(2)\mathrm{d}s\underset{s}{\int }{\varepsilon}_1{\varepsilon}_2^{\ast }(2)+{\varepsilon}_2{\varepsilon}_1^{\ast }(2)\mathrm{d}s\underset{s}{\int }{\gamma}_{12}{\gamma}_{12}^{\ast }(2)\mathrm{d}s\underset{s}{\int }{\varepsilon}_1{\varepsilon}_1^{\ast }(3)\mathrm{d}s\underset{s}{\int }{\varepsilon}_2{\varepsilon}_2^{\ast }(3)\mathrm{d}s\underset{s}{\int }{\varepsilon}_1{\varepsilon}_2^{\ast }(3)+{\varepsilon}_2{\varepsilon}_1^{\ast }(3)\mathrm{d}s\underset{s}{\int }{\gamma}_{12}{\gamma}_{12}^{\ast }(3)\mathrm{d}s\underset{s}{\int }{\varepsilon}_1{\varepsilon}_1^{\ast }(4)\mathrm{d}s\underset{s}{\int }{\varepsilon}_2{\varepsilon}_2^{\ast }(4)\mathrm{d}s\underset{s}{\int }{\varepsilon}_1{\varepsilon}_2^{\ast }(4)+{\varepsilon}_2{\varepsilon}_1^{\ast }(4)\mathrm{d}s\underset{s}{\int }{\gamma}_{12}{\gamma}_{12}^{\ast }(4)\mathrm{d}s\right]\left[{Q}_{11}{Q}_{22}{Q}_{12}{Q}_{66}\right]=\left[\underset{\mathrm{\partial S}}{\int}\overline{\mathbf{T}}\cdot {\mathbf{u}}^{\ast }(1)\mathrm{d}l\underset{\mathrm{\partial S}}{\int}\overline{\mathbf{T}}\cdot {\mathbf{u}}^{\ast }(2)\mathrm{d}l\underset{\mathrm{\partial S}}{\int}\overline{\mathbf{T}}\cdot {\mathbf{u}}^{\ast }(3)\mathrm{d}l\underset{\mathrm{\partial S}}{\int}\overline{\mathbf{T}}\cdot {\mathbf{u}}^{\ast }(4)\mathrm{d}l\right] $$

(6)

and Q₁₁, Q₂₂, Q₁₂, and Q₆₆ can be obtained directly by inverting equation (6).

Numerical Simulation Analysis

To verify the feasibility of the proposed method, numerical simulations were conducted using ABAQUS to obtain the strain field. The calculations were performed for two different models to make the results more convincing. Notably, E₁ and E₂ (defined in Section 2.2) differ significantly from one another for the unidirectional carbon fiber composite. Therefore, E₁ was chosen to be larger than E₂ in both models. The applied parameters are summarized in Table 1. In the FEM simulation, the top of the disk was subjected to a concentrated force and the bottom was fixed. A static step was applied for loading. CPS3 elements were used, and their total number was 1906.

Table 1 ABAQUS model parameters

Since the angle between the principal axis of the material and the coordinate axis (called the off-axis angle) significantly influences the measurement accuracy [17,18,19], cases with 12 different off-axis angles (−75^°, −60^°, −45^°, −30^°, −15^°, 0^°, 15^°, 30^°, 45^°, 60^°, 75^°, and 90^°) were simulated. The relative errors of the inversed parameters in Models 1 and 2 with those off-axis angles are illustrated in Figs. 2 and 3, respectively.

Fig. 2

Relative errors of Q₁₁, Q₂₂, Q₁₂, and Q₆₆ in Model 1 with off-axis angles of a-75^°, −60^°, −45^°, −30^°, −15^°, 0^°, 15^°, 30^°, 45^°, 60^°, 75^°, and 90^° b -75^°, −60^°, −45^°, −30^°, −15^°, 15^°, 30^°, 45^°, 60^°, and 75^°

Fig. 3

Relative errors of Q₁₁, Q₂₂, Q₁₂, and Q₆₆ in Model 2 with off-axis angles of a-75^°, −60^°, −45^°, −30^°, −15^°, 0^°, 15^°, 30^°, 45^°, 60^°, 75^°, and 90^° b -75^°, −60^°, −45^°, −30^°, −15^°, 15^°, 30^°, 45^°, 60^°, and 75^°

Figures 2 and 3 show the accuracies of the four elastic constants corresponding to different off-axis angles calculated by employing the VFM using the strain field in FEM simulation of both Models 1 and 2. As mentioned, the simulations were performed using 12 angles from −75^° to 90^°, and the relative errors of Q₁₁, Q₂₂, Q₁₂, and Q₆₆ are presented. Obviously, the angles of 0^° and 90^° yielded highly inaccurate results. For clarity, curves without the 0^° and 90^° data are also provided.

The results indicate that the different parameters have different optimal off-axis angles, which is of great importance for measurement accuracy. Therefore, to find the corresponding off-axis angles, further analysis was conducted by comparing the accuracy of each parameter with different off-axis angles. Practically, since the off-axis angle measurement error can hardly be avoided, the influence of this error was also considered. The results are presented in Figs. 4 and 5 for Models 1 and 2, respectively. Notably, for off-axis angles with the same magnitude and opposite signs, the inversed parameters are almost the same. Thus, in the following part, only positive angles are discussed.

Fig. 4

Relative errors of a Q₁₁, b Q₂₂, c Q₁₂ and d Q₆₆ in Model 1 with off-axis angles of 15^°,30^°,45^°, 60^°, and 75^° including off-axis angles errors ranging from −5^° to 5^°

Fig. 5

Relative errors of a Q₁₁, b Q₂₂, c Q₁₂ and d Q₆₆ in Model 2 with off-axis angles of 15^°,30^°,45^°, 60^°, and 75^° including off-axis angles errors ranging from −5^° to 5^°

As shown in Figs. 4 and 5, for each parameter, the two models yielded similar optimal off-axis angles. For off-axis angles of 60^° and 75^°, the off-axis angle error has little influence on Q₁₁. The relative error of Q₁₁ remains below 5% when the off-axis angle error is its maximum of 5^°. Q₂₂ exhibits similar behavior but has optimal off-axis angles of 15^° and 30^°. It is clear that the accuracy of Q₆₆ is the highest, while that of Q₁₂ is the lowest. When the off-axis angle is 45^°, the relative error of Q₆₆ remains below 2%. However, for Q₁₂, the minimum relative error is about 20% when the off-axis angle error is 5^° and the off-axis angle itself is 30^°. Even so, the measurement accuracy is still acceptable since it is also very difficult to obtain accurate Q₁₂ value using traditional methods, such as, strain gauges according to the measured results presented in Section 5.

The analysis in this section demonstrates that the proposed approach using the VFM is feasible and has some advantages, such as, a simplified experimental process, low cost and reasonable accuracy. Furthermore, according to the FEM simulation results, it is obvious that the off-axis angle influenced the accuracies of Q₁₁, Q₂₂, Q₁₂, and Q₆₆ differently. For off-axis angles of 60^° and 75^°, highly accurate Q₁₁ results were obtained and for Q₂₂, the corresponding off-axis angles were 15^° and 30^°. For Q₁₂, 30^° was the most suitable off-axis angle. Finally, for Q₆₆, the off-axis angle of 45 ^° provided better results than the other angles, however, the accuracy of Q₆₆ was also acceptable for other off-axis angles, such as, 30 ^° and 60^°, since Q₆₆ was the least sensitive to errors as mentioned above.

Moiré Interferometry Experiment Simulation

For the VFM, full field measurement is the key to improving the precision of the mechanical characterization. In this work, Moiré interferometry was combined with the VFM to perform a diametrical compression test on a disk. To demonstrate the feasibility and effectiveness of the proposed method, the Moiré interferometry experiment was simulated, and the detailed process and error analysis are described in this section.

Simulated Experiments

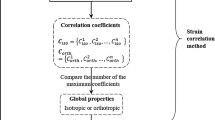
The flow chart of the experiments is provided in Fig. 6. Firstly, the disk was prepared with orthotropic gratings (1200 lines/mm) on it. The angle between the principal direction of the gratings and the fiber orientation of the lamina (denoted by θ) was changeable because the gratings could be fabricated on the specimen along any direction. Then, since the displacement field can be measured only in the principal direction of the gratings in Moiré interferometry, the load should be applied in the principal direction of the gratings. In this case, the off-axis angle was θ, as shown in Fig. 6c. After that, the specimen was rotated by 90^°, and the off-axis angle became -(90-θ)^°, as shown in Fig. 6d.

Fig. 6

Flow chart of Moiré interferometry experiment

According to the analysis in Section 3, 30 ^° was selected as θ so that the displacement field corresponding to the off-axis angle of 30^° and −60 ^° could be obtained. Highly accurate values of Q₁₁ and Q₂₂ were acquired using the off-axis angle of −60^° and 30^°, respectively. For Q₁₂, an off-axis angle of 30^° provided satisfying results, and for Q₆₆, both angles yielded little error.

To verify the feasibility of combining the VFM with Moiré interferometry, the above mentioned experiments were firstly conducted by performing numerical simulations.

Figure 7 provides a flow chart of the simulated experiments. For clarity, Model 2 (see Table 1) with an off-axis angle of 30^° is used as an example. The displacement field and the corresponding fringe pattern of in this case are depicted in Fig. 8. Figure 8a and b show the displacements in the horizontal and vertical directions, respectively, and the fringe patterns in Fig. 8c and d were generated from the displacement fields in Fig. 8a and b, respectively. Since the grating frequency in the real experiment was 1200 lines/mm, each fringe in Fig. 8 represents the displacement of 0.4167 μm, as explained in Section 2. In addition, phase shifting technology [23] was used to process the fringe patterns in this work. Therefore, four fringe patterns with different phase were generated. An example is provided in Fig. 9.

Fig. 7

Flow chart of the simulated Moiré interferometry experiment

Fig. 8

Displacement fields obtained from the FEM simulations: displacements along the a x axis and b y axis, and fringe patterns along the c x axis and d y axis generated from the displacement fields

Fig. 9

Four fringe patterns generated using phase shifting technology

Then, the strain field presented in Fig. 10a was acquired from the fringe patterns using software Moire [24]. The strain field obtained from the FEM simulation is also provided in Fig. 10b for comparison. The VFM program was then employed to calculate the four elastic constants. Both of the models described in Table 1 were used with off-axis angles of 30^° and −60^°. The results of the simulated experiments are presented in Table 2.

Fig. 10

Strain fields obtained from a-c the simulated experiment; d-f the FEM simulation

Table 2 Q₁₁, Q₂₂, Q₁₂, and Q₆₆ values obtained from the simulated experiments

From Table 2, it is evident that both of the models provided reasonably accurate results for Q₂₂ and Q₁₂ when the off-axis angle was 30^°. In contrast, more accurate values of Q₁₁ were achieved when the off-axis angle was −60^° than when it was 30^°. For Q₆₆, the error is very small in each case. It is obvious that the results of the simulated experiments are in accordance with the FEM simulation results presented in Section 3. Therefore, it is feasible to use the same configuration and calculation method in real experiments.

Error Analysis

In real experiments, many factors induce errors in the measured deformation fields. In Moiré interferometry, since the displacement fields are extracted from the fringes, high quality gratings and null fields are the key to the accuracy of the measured displacements [25]. The gratings used in the real experiment as well as the null fields will be shown in Section 5. However, in this study, it was necessary to consider some additional factors because of the load configuration, as will be discussed in the following subsections.

Influence of the strain concentration

In this work, the concentrated force was applied to the top and bottom of the disk specimen. Therefore, strain concentration around the loading points was inevitable, resulting in high fringe densities in these areas, as shown in Fig. 11. Two problems would result from the strain concentration. First, the deformation in these areas may be out of the range of elasticity. In addition, it is difficult to obtain accurate displacements from dense fringes in real experiments. To analyze how the strain concentration affects the inversed results, the data from the simulated experiments were used and the strain in the concentration areas was set to zero, as shown in Fig. 11. The results obtained using the data without strain concentration areas are presented in Table 3.

Fig. 11

Areas of strain concentration in the fringe patterns

Table 3 Q₁₁, Q₂₂, Q₁₂, and Q₆₆ values obtained using the data without the strain concentration areas

The results presented in Table 3 indicate that removing the data from the strain concentration areas did not significantly influence on the results in general. The errors of Q₁₁ in the −60^° case, Q₂₂ in the 30^° case, and Q₆₆ in both cases are less than 5%. However, as mentioned above, Q₁₂ is more sensitive to errors than the other parameters. Even so, the accuracy of Q₁₂ is still acceptable based on the comparison to the strain gauge results, which will be presented in Section 5.

Influence of rigid-body rotation

Moiré interferometry is usually applied to measure symmetric displacement field. For such fields, the rigid-body displacement can be removed by adjusting the specimen position to make the fringe pattern symmetric. However, in the present work, the deformation field was antisymmetric, because the material was orthotropic. Therefore, in this part, the influence of rigid-body rotation on the accuracy of the obtained parameters is discussed, and the results indicate that this influence can be ignored.

The process is explained in detail Fig. 12. Firstly, the parameters to be used in the simulated experiments, such as, the model dimension and the off-axis angle, were determined. Then, the displacement field was obtained using ABAQUS, as described in Section 3. After that, rigid-body rotation was added to the real displacement as shown in equation (7) and the fringe patterns were generated numerically. Finally, the VFM program was used to calculate the four elastic constants.

$$ \left\{\begin{array}{l}{u}^{\hbox{'}}=\left(\cos \theta -1\right)\cdot x+\cos \theta \cdot u-\sin \theta \cdot y-\sin \theta \cdot v\\ {}{v}^{\hbox{'}}=\left(\cos \theta -1\right)\cdot y+\sin \theta \cdot x+\sin \theta \cdot u+\cos \theta \cdot v\end{array}\right. $$

(7)

Here, u^′ and v^′ are the revised displacements with rigid-body rotation, u and v are the real displacements, and θ is the rotation angle.

Fig. 12

Flow chart of the simulated Moiré interferometry experiment with rigid-body rotation

To determine a suitable value of θ, fringe patterns with rigid-body rotation when θ=0.0025^°, 0.025^°, and 0.25^° were generated, as shown in Fig. 13. It is obvious that when θ=0.025^°, the difference between the fringe patterns with and without rigid-body rotation displacement is sufficiently large to be recognized in real experiments. Therefore, 0.025^° was chosen as the rotation angle for the analysis. Then, both of the models described in Table 1 with off-axis angles of 30^° and −60^° were applied to see how the rigid-body rotation affected the inversed values of the four elastic constants. The results are presented in Table 4.

Fig. 13

Fringe patterns a without rigid-body rotation and with; b 0.0025^°; c 0.025^°; d 0.25^° rigid-body rotation

Table 4 Q₁₁, Q₂₂, Q₁₂, and Q₆₆ values obtained using the displacement with 0.025^° rigid-body rotation

It is obvious that the elastic constants calculated using the displacements with rigid-body rotation are very close to those obtained using the real displacements. The results indicate that the strain fields measured using moiré interferometry are reasonably accurate for the VFM when the deformation field is antisymmetric, even though the rigid-body rotation cannot be eliminated.

Experimental Validation and Discussion

Experimental Validation

A real experiment was conducted using a unidirectional carbon fiber composite and Moiré interferometry to demonstrate the feasibility of the proposed method. Firstly, for comparison, strain gauges were used to measure the four elastic constants of the composite. Three types of specimens with off-axis angles of 0^°, 45^°, and 90^° were used, as shown in Fig. 14. From the normal strain of the 0^° specimen, E₁ and v₁₂ were obtained. Similarly, E₂ and v₂₁ were calculated using the 90^° specimen. Then, G₁₂ was obtained using the 45^° specimen. The results are presented in Table 5.

Fig. 14

Unidirectional composite specimens measured using strain gauges

Table 5 Elastic constants measured using strain gauges

Theoretically, E₁, v₁₂, E₂,and v₂₁ should satisfy the relationship E₁v₂₁ = E₂v₁₂. However, E₁v₂₁ and E₂v₁₂ were found to be 3.57 GPa and 2.66 GPa respectively, which indicates that the measurement error of Q₁₂ by strain gauges is large. Here, Q₁₂ = v₁₂Q₂₂ was used to calculate Q₁₂ as the reference value, and Q₁₁, Q₂₂, Q₁₂, and Q₆₆ were measured using the strain gauges to be 157.79 GPa, 8.80 GPa, 2.68 GPa, and 4.81GPa, respectively.

Then, the experiment was performed to determine Q₁₁, Q₂₂, Q₁₂, and Q₆₆ for the unidirectional carbon fiber composite using Moiré interferometry and the virtual fields method. The experimental setup and the specimen with 1200 lines/mm gratings are shown in Fig. 15. The wavelength of the laser was 532 nm (TEM00, 20 mW), and the diameter and thickness of the specimen were 15 mm and 2 mm, respectively. The experimental process was explained in Section 4 and depicted in Fig. 6. According to this process, two tests were conducted with off-axis angle of 30^° and −60^° and a load of 100 N. The null fields and fringe patterns of the two tests captured by a camera (DH-HVI302UM) are shown in Fig. 16. In addition, since the phase shifting technology [23] was applied, the four fringe patterns obtained by the phase shifting with an off-axis angle of 30^° are also provided in Fig. 17 as an example. The displacement and strain fields corresponding to the four fringe patterns are shown in Fig. 18.

Fig. 15

Experimental setup

Fig. 16

Null-field patterns along the a x and b y axes; fringe patterns with an off-axis angle of 30^° and a load of 100 N along the c x and d y axes, and fringe patterns with an off-axis angle of −60^° and a load of 100 N along the e x and f y axes

Fig. 17

Four fringe patterns obtained using phase shifting technology with an off-axis angle of 30^° and a load of 100 N along the a-d x and e-f y axes

Fig. 18

a-b Displacement and c-e strain fields obtained with an off-axis angle of 30^° and a load of 100 N

After the strain fields were obtained, the VFM was used to calculate the four elastic constants. The results of the two tests are presented in Table 6.

Table 6 Q₁₁, Q₂₂, Q₁₂, and Q₆₆ values obtained in the real experiments

Discussion

From Table 6, it is obvious that the experimental values of Q₂₂, Q₁₂, and Q₆₆ obtained in the 30^° test are close to those measured using strain gauges and that the Q₁₁ and Q₆₆ values obtained in the −60^° test exhibit better performance. These results are in accordance with the conclusions drawn based upon the simulated experiments described in Section 4.

To summarize, the main advantage of the VFM is that all of the elastic constants can be obtained from one test. In our work, to improve the measurement accuracy, two tests were conducted. However, only one specimen was used because the disk was selected as the configuration. In contrast, the strain gauge-based approach requires three specimens, and a standard tensile test is conducted on each of them to obtain all the four in-plane elastic constants. In addition, the measurement error of Q₁₂ in the strain-gauge based approach is large, as mentioned in Section 5.1. Therefore, according to the measurement results in Table 6, the accuracy of the proposed approach is acceptable in general.

Conclusion

In this work, Moiré interferometry was combined with the virtual fields method to characterize the four elastic constants of an orthotropic material. The loading configuration was a diametrically compressed disk. Moiré interferometry was successfully applied in this antisymmetric configuration. FEM simulations, simulated experiments as well as real experiments were conducted, and all of them demonstrated the feasibility of the proposed approach. According to the results of the simulations and experiments, the following conclusions can be drawn:

• (1) In the FEM simulation, cases with off-axis angles of −75^°, −60^°, −45^°, −30^°, −15^°, 0^°, 15^°, 30^°, 45^°, 60^°, 75^°, and 90^° were analyzed. The results show that when the off-axis angle was −30^° or 30^°, Q₂₂, Q₁₂, and Q₆₆ were less sensitive to errors than they were at the other angles and that when the off-axis angle was −60^° or 60^°, Q₁₁ and Q₆₆ exhibited better performance, which provided guidance for the experiment.

• (2) The errors of the four elastic constants obtained in the simulated Moiré interferometry experiment were less than 0.35 GPa. The influence of strain concentration was also analyzed, illustrating that the maximum error of the constants was around 3.9 GPa when the area with strain concentration was removed. In addition, to simulate the real condition of Moiré interferometry in antisymmetric measurements, rigid-body rotation was added to the displacement field. The results show that the influence of rigid-body rotation on the measurements was negligible.

• (3) The results obtained in the real experiment performing using unidirectional carbon fiber composite were compared with the values measured using strain gauges and were found to exhibit reasonable accuracy. Therefore, the strain measured using Moiré interferometry in the antisymmetric configuration is suitable for application in the VFM to characterize the mechanical properties of orthotropic materials.

Furthermore, in our former research [17], efforts were made to characterize fused deposition modeling-fabricated materials, whose principle axes were unknown in advance, using the virtual fields method and digital image correlation. However, the digital image correlation measurement accuracy was not sufficiently high for application to high-strength materials. Thus, the Moiré interferometry method used in the present work enables more accurate strain field determination. Therefore, in the future, unknown materials can be characterized using a combination of the methods employed in the present work and our former research.