Introduction

The instrumented indentation technique (IIT) is a versatile mechanical test that allows us to probe the mechanical behaviour of materials [1]. It is commonly used to extract an indentation elastic modulus by analysing the unloading part of the force-displacement curve [2]. This technique can also be employed to extract mechanical parameters from constitutive equations aimed at describing the inelastic behaviour of materials (plasticity, viscoplasticity…) [3]. IIT can be used at shallow depths of penetration (typically less than 100 nm) with the aid of modern and powerful sensing devices. This nano indentation technique offers the possibility to probe the mechanical behaviour at shallow depths in fibres, thin films or in bulk brittle materials with a low load to prevent the onset of cracking [1, 4]. In many studies modelling IIT data, it is assumed that the indenter (commonly diamond) will not deform during the test since the indenter stiffness is generally much higher than that of the material. This is the assumption made in most reverse analysis methods (see e.g. [5–8]). However, this classical assumption is questionable when the material is either very hard (Meyer’s hardness > 10 GPa) or very stiff (Young’s modulus > 100 GPa) or even both. This is the first issue examined here.

In some cases, IIT is used at very shallow depths of penetration, for example on hard materials or coatings. This raises an additional issue concerning the blunted tip of the indenter. This type of tip defect can be neglected for IIT data obtained at sufficient depths of penetration [9] but should be taken into account at shallower depths. This issue becomes even more important when the tip is used repeatedly so that the size of the defect [9] is increased. In any case, at these shallow depths, the material is indented by a blunt indenter rather than a sharp one. In such cases, there is no longer any geometrical similarity resulting in a parabolic behaviour for the loading part of the force-displacement curve. In other words, a length scale is introduced by the indenter. Various methods [10–13] have been developed to take into account of tip defects when estimating the material’s stiffness by analysing the unloading part of the indentation curve. However, these methods are not transposable for the determination of plastic parameters derived from constitutive equations. Moreover, some numerical studies [14] demonstrate the strong influence of the tip defect for shallow penetration depths.

In this study, we first illustrate the issues of indenter tip imperfection and deformability by using a carefully chosen stiff and hard material. We then propose a way to circumvent the problems arising from indenter deformability and show that this issue must be also taken account. The originality of this paper is that it addresses simultaneously both indenter imperfection and deformability and proposes a dedicated procedure for extracting plastic parameters by using IIT applied to a real material.

Experimental and Numerical Methods

Materials and Indentation Procedures

This study is based on an iron-based amorphous alloy (or bulk metallic glass) with a nominal composition of Fe41Co7Cr15Mo14 C 15 B 6 Y 2 (at. %). This material is chosen here for the purposes of this study since it exhibits suitable features: it is homogeneous, with an isotropic mechanical behaviour, and does not show any length scale for the indentation test or any cracking features. Moreover, it is hard, stiff [15] and can be modeled easily and accurately by classical plasticity models (assuming it behaves like Zr- or Pd-based metallic glasses as in [16]). The glass transition temperature is 838 K and the crystallisation temperature is 876 K [17]. The elastic properties of this material have been reported elsewhere [18]. The Young’s modulus and Poisson’s ratio are E = 226 ± 15 GPa and ν = 0.337 ± 0.023, respectively. Instrumented indentation tests were carried out with a nano-indenter testing device (TI950, Hysitron, USA) at ambient conditions (23 ∘C and 55 % relative humidity). The indenter tip is a modified Berkovich diamond pyramid. Based on AFM (Atomic Force Microscopy, Bruker, Nanoscope V, USA) imaging using a procedure described in [19], and a standard indenter tip calibration method on a fused quartz standard sample [10], we obtain an indenter tip radius value of ∼ 260 nm.

Nano-indentation tests were carried out on a dedicated sample, with a ’10-10-10’ loading sequence: 10 s to reach the maximum load P m , 10 s of holding time, and 10 s to unload the sample’s surface. The tests were load-controlled and the P m value was 10 mN. Due to the high reproducibility of the nano-indentation test on the glass surface, five indents were performed. All imprints were free of cracks, since the critical load for cracking is ∼ 5 N [18].

Numerical Procedures

Finite Element simulations of the indentation process were performed using a two-dimensional axisymmetric model with a sample and an indenter. The sample is divided into a core zone, underneath the indenter tip, where the mesh is fine, and a shell zone where the mesh is coarse. The core zone is itself divided into a square zone with 32 × 32 square elements and an outer zone with quadrangular elements (32 again along the axis z = 0). The shell zone is divided into a transition zone and an outer zone, both with quadrangular elements.

All elements are linear. The dimensions of the mesh are chosen to minimize the effect of the far-field boundary conditions. This is achieved by using a sufficient number of outer elements in the shell zone. The typical ratio of the maximum contact radius to sample size is about 2×103. The indenter is modelled as a perfect cone exhibiting an half-angle Ψ=70.29∘ to match the theoretical projected area function of the modified Berkovich indenter. Its mesh is the same as that of the sample with a geometrical transformation accounting for the geometry of the indenter. The indenter (in diamond) is assumed to be composed of an isotropic, linear elastic material (Poisson’s ratio of 0.07 and Young’s modulus of 1100 GPa). The contact between the indenter and the sample surface is ideal (in accordance with Signorini conditions) and taken as frictionless. The contact zone is situated along the core zone. The boundary conditions correspond to a nil displacement on the outer nodes of the sample, in addition to an axisymmetric condition along the vertical axis. The force on the indenter, P (taken as positive), is controlled and the displacement of the indenter, δ (counted positively), is recorded far from its tip. The boundary-value problem is solved using the commercial software ABAQUSTM (version 6.10). The pre- and post-processing tasks are performed with the Abapy toolbox [20]. Details and views of the meshes are given in the documentation associated with Ref. [20].

We assume that the constitutive behaviour of the studied iron-based amorphous alloy can be described in terms of linear isotropic elasticity (parameters E - Young’s modulus - and ν - Poisson’s ratio) followed by rate-independent (with a plastic multiplier \(\dot {\lambda }\) in equation (1)) perfectly plastic flow (no strain hardening) using a threshold defined by a Drucker-Prager yield criterion (f in equation (1)) in the stress space (\(\underset {\sim }{\sigma }\) is the Cauchy stress tensor). The plastic flow rule (\(\underset {\sim }{\dot \epsilon }^{p}\) in equation (1)) is assumed to be associated i.e. the dilatancy angle is equal to the friction angle φ [21], and \(\dot {\lambda }\) is the plastic multiplier :

$$ \left\{ \begin{array}{l} f\,\left( \underset{\sim}{\sigma};Y_{c},\varphi\right) = \sigma_{\text{eq}}^{\textsf{VM}} -p\,\tan\varphi - \left( 1-\frac{\tan\varphi}{3}\right)\,Y_{c} \leq 0 \\ \underset{\sim}{\dot\epsilon}^{p} = \dot{\lambda}\frac{\partial f}{\partial\underset{\sim}{\sigma}} = \dot{\lambda} \left( \frac{3}{2}\frac{\underset{\sim}{s}}{\sigma_{\text{eq}}^{\textsf{VM}}} + \frac{1}{3}\,\text{tr}\,(\underset{\sim}{\sigma})\,\underset{\sim}{i} \right) \end{array} \right. $$
(1)

where \(\underset {\sim }{s}\) is the deviatoric part of \(\underset {\sim }{\sigma }\), \(\sigma _{\text {eq}}^{\textsf {VM}}=\sqrt {\frac {3}{2}\text {tr}\left (\underset {\sim }{s}\cdot \underset {\sim }{s}\right )}\) the von Mises equivalent shear stress in tension, \(\underset {\sim }{i}\) is the second-order unit tensor, \(p=-\frac {1}{3}\text {tr}\,\left (\underset {\sim }{\sigma }\right )\) is the hydrostatic pressure, tr is the trace operator, and Y c the compression yield strength.

The use of such a constitutive model for metallic glasses has already been discussed in the literature for example in the case of Zr- or Pd-based metallic glass [22–25]. We do not aim to show that the Fe-base alloy follows the same behaviour but rather use a simple and robust constitutive equation able to model accurately the experimental results. Accordingly, the numerical values of the parameters are not be discussed in detail in terms of the material’s behaviour.

To obtain a match between experimental and numerical results (the force-displacement curves), we use an automated procedure for identifying material parameters based on a hybrid method (Levenberg-Marquardt, gradient and Newton-Raphson algorithms, SiDoLo software) [3]. Imposing the same loading conditions (force versus time) as the experiment, the square of the difference between the model (sim) and the experimental values (∗) is evaluated at the M q instants of observation t i on the displacement δ, by the residual \(\mathcal {L}\) for a given value of the set of material parameters A = (Y c , φ):

$$ \mathcal{L}(A) = \frac{1}{M_{q}}\sum\limits_{i=1}^{M_{q}}\,\left( \delta^{\textsf{sim}}(t_{i})-\delta^{*}(t_{i})\right)^{2} $$
(2)

The identification procedure consists of finding the minima in \(\mathcal {L}(A)\).

Another way to proceed would involve fitting both the loading and unloading stages, the former with a parabola (using one parameter, the loading prefactor C), the latter by a power-law fit including the maximum load P m , the final depth δ f and an exponent m (or using the ratio of reversible and irreversible works to the total work [26]). This alternative procedure was not adopted in the present study.

Results and discussion

Experimental Results

The mechanical response of the indentation test is represented on a plot showing the force P vs. the displacement δ (counted positively). Figure 1 presents the experimental results obtained on the Fe-based glass. The curves obtained are highly reproducible. A way to qualify the bluntness of the tip, without imaging it by AFM, an issue raised in “Materials and Indentation Procedures”, is to calculate a truncated length [11]. The truncated tip defect length, Δδ, is obtained straightforwardly by plotting \(\sqrt {P}\) vs. δ for the fused quartz reference sample or for the iron-based amorphous alloy, during the loading stage (increasing P). This curve should be linear with its origin at (0,0) for a perfect tip (similitude regime, self similarity of sharp indentation, see e.g. [4, 26, 27]). This is not the case for shallow depths of penetration below ∼ 50 nm, so Δδ was calculated by taking the intercept of a linear fit of this curve for high values of δ, as seen in Fig. 2. Δδ is found to be ∼ 15 nm. The loading prefactor C (the square of the slope at depths greater than 50 nm in Fig. 2) is found to be 274 ± 2 GPa.

Fig. 1
figure 1

Force-displacement curves for the Fe-based metallic glass under a nanoindentation test (five tests)

Full size image
Fig. 2
figure 2

Plot of the square root of the force versus the indentation depth during the loading stage of a 10 mN indentation test on the Fe-based glass. A linear fit for depths higher than 50 nm (for which we are in the similitude regime) is extrapolated down to the x-axis to give the tip defect in terms of a truncated length Δδ ∼ 15 nm

Full size image

Numerical Results

Estimation of initial material parameters

We use here the elastic parameters discussed above (E = 225 GPa, ν = 0.337). The compressive yield strength is estimated taking the quasi-universal compressive yield strain for iron-based alloys, which is 𝜖 y ∼ 2 % [28] (for a reduced temperature T(= 293 K)/T g = 0.35), so that Y c = 4500 MPa. The friction coefficient is estimated at ∼ 10 ∘, which is the value commonly found for metallic glasses [29].

Creating the material’s response for a perfectly sharp tip

To identify the material parameters of the constitutive equation, we will compare the numerical simulation results to the experimental data. The latter are shifted to greater penetration depths by Δδ. Such a method allows us to capture the material’s response to IIT assuming a perfectly sharp indenter. This comparison is nevertheless valid only for depths greater than ∼ 2-3 times the tip defect. To our knowledge, this method is not used for identifying plastic parameters derived from numerical simulations.

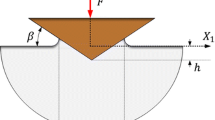
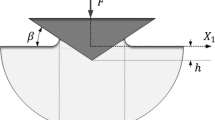
To assess this methodology, we present some numerical simulations (with controlled displacement), using a rigid indenter with a blunted tip modelled as spherical with a radius of 260 nm, in accordance with the experimental AFM measurements and tip calibration described in “Materials and Indentation Procedures”. Such a geometry is represented in Fig. 3. The spherical part (in red) and the conical part (in blue) are joined so that they have the same slope at point T. The tip defect length (td) is given by the radius of the spherical tip (R = 260 nm) and the angle between the horizontal axis and the conical part (β = 19.7 ∘). In our case td is 16 nm. The vertical distance between the horizontal axis and point T (z t ) is 15 nm.

Fig. 3
figure 3

Blunted indenter tip modelled as sphero-conical. The spherical part (in red) and the conical part (in blue) are joined so that they have the same slope at point T. The tip defect length (td) is given by the radius of the spherical tip (R) and the angle between the horizontal axis and the conical part (β). The vertical distance between the horizontal axis and point T is z t

Full size image

The material is elasto-plastic (J2 plasticity without strain hardening) with the parameters described above, apart from the friction coefficient φ, which is taken as nil, and the maximum penetration depth is 292 nm. The fit of the loading stage of the resulting force-displacement curve gives a truncated length Δδ of ∼ 15 nm in accordance with the tip defect length td = 16 nm, as well as the AFM measurements of this defect length (also 15 nm). Then, another simulation is run but with a perfectly sharp indenter with a maximum penetration depth increased by 15 nm i.e. 307 nm. Figure 4 reports the results of these two simulations, along with the curve from the first simulation shifted by 15 nm to the right. By comparing the sharp indentation with the shifted blunted simulation, it is clear that the two curves are the same for depths greater than 2-3 times the truncated length Δδ. This numerically validates the approach used to create the material’s response to perfectly sharp indentation.

Fig. 4
figure 4

Numerical simulations (force-displacement curves) with a rounded tip of 260 nm (in accordance with AFM measurements) at a given arbitrary penetration depth δ m = 292 nm and a perfectly sharp tip (at a penetration depth δ m +Δδ, where Δδ is the truncated length (found by fitting the loading stage of the rounded tip simulation, here 15 nm). When shifted by Δδ to greater penetration depths, the rounded tip simulation yields results overlapping with those obtained with a perfect tip. The inset indicates furthermore that this is only valid for δ greater than ∼ 40 nm that is ∼ 2-3 times Δδ

Full size image

Taking into account the indenter tip defect and its deformability

The experimental results (shifted by Δδ) are shown along with a numerical simulation with the identified parameters (reported in Table 1, (d)). On Fig. 5, we can see a very close match between the two reported curves. The very small value of the residual (0.6) is also indicative of the quality of the match. The identified parameters are in accordance with literature results.

Fig. 5
figure 5

Results of the identification procedure (d). When taking into account the indenter deformability, the force-displacement curve obtained from numerical simulations with the parameters found in Table 1 (d), matches the experimental curve (shifted by the truncated length Δδ = 15 nm). The results of a direct simulation with the same material parameters but with a rigid indenter highlight the dramatic influence of indenterb deformability for hard and stiff materials

Full size image
Table 1 Results of the four different identification procedures in terms of material parameters. Y c (compressive strength) and φ (friction angle) are the identified plastic parameters (see equation (1)); \({\epsilon _{y}^{c}}=Y_{c}/E\) is the compressive yield strain; \(\mathcal {L}\) is the residual of the identification procedure (see equation (2))
Full size table

Using the same material parameters, another simulation is presented considering this time with a rigid indenter. The force-displacement curve is plotted on the same Fig. 5 exhibiting a stiffer response as expected. The loading pre-factor, C, which is 274 GPa for the simulation with the deformable indenter now becomes 301 GPa, with the rigid one, that is 10 % higher.

We have then carried out three other identification procedures:

  • a first one, referred to as (a), without taking the tip defect into account (therefore without shifting the experimental data by the truncated length Δ δ) and with a rigid indenter,

  • a second one, referred to as (b), without taking the tip into account but with a deformable indenter,

  • a third one, referred to as (c), by taking the tip into account (therefore by shifting the experimental data by the truncated length Δ δ) and with a rigid indenter.

Table 1 and Fig. 6 show the results of these identifications in terms of material parameters and residuals. None of these three identification procedures is able to match the experiments. The discrepancies are mainly explained by the failure to take account of the tip defect (as in cases (a) and (b)). This situation would become even more exacerbated for IIT tests performed at shallower penetration depths. Moreover, case (c) shows that it is insufficient to take the tip defect into account while ignoring the indenter deformability.

Fig. 6
figure 6

Results of the four different identification procedures in terms of force-displacement curves (experiment versus numerical simulation). Case (a) is when taking into account neither the indenter tip defect nor its deformability. Case (b) is when taking into account only the indenter deformability. Case (c) is when taking into account only the tip defect. Case (d) is when taking into account both the indenter tip defect and its deformability

Full size image

We could explicitly take into account the tip defect for analysis of the whole force-displacement curve [9, 30]. Such an approach would involve imaging the real geometry of the indenter, exporting it to a computer-aided design software and/or meshing it before running a Finite-Element analysis. Although this procedure may appear straightforward, it is nevertheless somewhat tedious and time-consuming since it requires fine AFM imaging and a three- dimensional numerical simulation. By contrast, the method proposed here is much easier to apply and requires only a fit of the loading step of indentation. As regards indenter deformability, we need to use a deformable indenter in the numerical simulations. The identification results of case (c) show that this requirement is crucial.

Concluding Remarks

We performed instrumented nano-indentation tests on an amorphous alloy (or metallic glass) of the FeC family. This material is chosen since it is both very stiff (as steel) and very hard (as single-crystal quartz), with isotropic and homogeneous properties, exhibiting no length scale for the range of penetration depths studied. Moreover, its mechanical behaviour is known to be adequately described by simple constitutive equations involving a small number (two) of plastic properties. We present an identification procedure for extracting the plastic properties by minimising the discrepancy between the experimental force-displacement curve and the numerical simulation. The experimental curve is modified to take into account the truncation of the indenter tip by simply shifting the raw data to greater penetration depths by an amount referred to as the truncated length, which is readily determined by fitting the loading stage of the force-displacement curve. The simulation is obtained by performing Finite Element Analyses with a deformable indenter. The identification procedure allows us to obtain a perfect match with the experimental data, and the identified parameters are highly consistent with values expected from the literature data. Moreover, this approach is validated numerically. We also show that the identification procedure fails when it does not take into account the tip defect or the indenter deformability or both. The present results obtained on a stiff and hard material clearly show the crucial importance of considering the tip defect of the indenter as well as its deformability, when developing a constitutive model to describe the mechanical response of indentation tests. The results obtained with this particular material can be generalized. The higher the yield strain and the elastic stiffness, the more important it is to consider the indenter as deformable.