Introduction

Since the significant theoretical studies of Adkins and Rivlin in 1952 and the onset of industrial applications of rubber materials, numerous engineers have developed constitutive modeling, experimental efforts, and finite element analysis of these materials. Among the well-known experiments conducted for calibration of unknown properties of elastomers, there are three desirable elastomeric configurations: inflation of a rubber membrane by injecting gas or fluid, indentation of a thin rubber by a spherical, flat, cylindrical, or conical indenter, and indentation of an elastic half space. Treloar [1] carried out a comprehensive investigation on shapes and strain distributions at various degrees of inflation. Adkins and Rivlin [2] developed a comprehensive theoretical framework for these experimental observations. They used the strain energy function forms of the so-called neo-Hookean [3, 4] and Mooney-Rivlin [5] methods and employed a Taylor′s series approach to calculating the deformation arising from the inflation of an initially flat circular hyperelastic membrane. The deformed shapes of the inflated membranes were compared to Treloar′s data. Assuming a general form for the strain energy function, Green and Shield [6] examined the necessary pressure for inflation of a thick spherical shell made of incompressible isotopic rubbers. Schmidt and Carley [7] studied the comparison of numerical solutions and experimental data for the inflation of three different circular membranes. They implemented five polynomial forms of strain energy proposed by Rivlin [8] and used the Runge-Kutta method to numerically solve the system of equations. Pajura et al. [9] studied the effect of different strain energy functions on the inflation of a circular membrane and compared the results with those predicted, based on the Hookean constitutive relationship. They showed that the results employed different strain energy functions that have similarity with small deformations. The problem of axisymmetric indentation of a circular membrane through a spherical indenter was investigated by Bhatia and Nachbar [10]. They presented a solution for a nonlinear elastic membrane based on specific assumptions, including small strains and explicit treatment of the contact region during indentation. Bhatia and Nachbar also compared their solution with the experimental data of Jahsman et al. [11]. Yang and Hsu [12] treated the same problem using two distinct regions, including contact and noncontact regions by means of a numerical scheme based on the Mooney-Rivlin form of the strain energy function. Przybylo and Arruda [13] reported experimental profiles of inflated rubber and compared them with results of finite element calculations using various constitutive models. Hassager et al. [14] presented a finite element formulation for simulation of the inflation of axisymmetric viscoelastic membranes. Numerical results showed that the variation of wall thickness at the pole of inflated membrane and the prediction of instability occurrence were strongly dependent on the selection of constitutive equations.

The dependency of a simulated structure’s response to the constitutive model was more evident in Verron and Marckmann [15], in which they implemented and compared chain models and a neo-Hookean strain energy function for the numerical solution of the inflation of two initially spherical or circular hyperelastic membranes. The result of these works showed that both the inflation profile and thickness distribution were highly influenced by the nature of the material model. Reuge et al. [16] and Rachik et al. [17] compared the material parameters found using the direct identification method based on the uniaxial and equibiaxial extension test data, and those parameter values were obtained by employing an inverse method, based on the bubble inflation test data. They employed the Levenberg-Marquardt optimization procedure to calculate the cost parameters for various classical strain energy functions. Cloonan et al. [18], using the indentation test on a PDMS and two porcine tissues, discovered the associated material parameters. The Mooney-Rivlin model was used for the comparison of results obtained from test and computational modeling. Through the indentation force comparison between prostate tissue and two elastomers, silicone, and PVA hydrogel, Li et al. [19] found that those structures had the same mechanical properties. Although a number of researchers performed structural deformations or multiple homogeneous deformations to describe the parameters of tissue-mimicking phantoms, others preferred to perform uniaxial tensile or compression tests on such materials. For example, Doyle et al. [20] created several silicone rubbers having distinct material properties. They calibrated an Ogden model using uniaxial test data and used the obtained material parameters for comparison of numerical results with an experiment for an abdominal aortic aneurysm. Using uniaxial tensile data on a fiber-reinforced silicone rubber membranes, Bailly et al. [21] proved that this material was a very good candidate for new biomimetic membranes. Krone et al. [22], using just a uniaxial tensile test of bi-layer laminates, composed of one layer of a very soft isotropic hyperelastic hydrogel bonded to one layer of silicone rubber, to characterize the mechanical properties of the hydrogel. They used a polynomial form of strain energy for a fitting procedure. Payne et al. [23] used PDMS silicone to match the mechanical properties of skeletal muscle tissues. The material parameters of that silicone material were obtained by fitting several constitutive hyperelastic models to a uniaxial compression test. Selvadurai [24] performed the axisymmetric and asymmetric indentation of a natural rubber circular membrane under a spherical indenter, both experimentally and numerically. In this work, the numerical results were obtained using finite element FE software through implementing various constitutive models. These models were validated by conducting a uniaxial experiment on the natural rubber. Pearce et al. [25] examined different strain energy functions used for analyzing the features of elastomeric membranes’ indentation under a convex rigid indenter. The numerical results showed that the simulation of the indentation problem was dependent on choosing the correct form of the strain energy density function. Two new applications for the indentation of circular membranes by a spherical indenter can be also found in recent studies [26, 27].

Taking advantage of optical methods and digital image correlation (DIC) techniques, Meunier et al. [28] subjected an unfilled silicone rubber to four different tests: uniaxial tension, pure shear, compression, and the inflation of a circular membrane to define the equibiaxial data. In their study, various constitutive models were fitted to these experimental data. Similar experiments were performed by Österlöf et al. [29] on a filled elastomer, and the unloading stress-strain curves were used to fit various constitutive models. Selvadurai and Shi [30] used the results of only uniaxial experiments in FE modeling to numerically simulate the test of fluid pressure loading on a natural gum rubber membrane fixed along a circular boundary, and they compared the simulation results with those of experiments. In this work, several hyperelastic models were considered to describe the mechanical behavior of rubber within a large range of strain situations. In addition, Jones et al. [31] presented the time-dependent response of a carbon-black filled natural rubber under high temperatures using an inflated structure.

The hybrid experimental-numerical method, also called the inverse method, was introduced by Kavanagh and Clough [32], and it has been widely used to determine the material parameters of both elastomeric and biological membranes. In this method, the material parameters are found through considering the deformed membranous configurations, usually inflated or indented structures, rather than standard experiments, such as uniaxial, equibiaxial, and pure shear. Iding et al. [33] implemented this hybrid method to characterize the constitutive equation of an isotropic hyperelastic material, where a Newton-Raphson method was used to iteratively solve the equations. Wineman et al. [34] showed how the shapes of measured profiles and stretch ratio distributions in an inflated hyperelastic circular membrane can be considered part of an inverse identification method, to determine the material parameters in the strain energy function. Elkut et al. [35] designed a different experiment: indentation of a circular hyperelastic membrane using a spherical indenter, to predict the material parameters of the Mooney-Rivlin model over a low-strain range. They discussed the importance of the choice of material models on the accuracy and robustness of the inverse FE modeling results. Further references related to the application of the inverse method for characterizing hyperelastic materials can be found in several recent studies [36–39].

In the next section, we present a brief review of several hyperelastic constitutive models. The work presented here makes two new contributions to the study of hyperelastic materials. First, we performed a multitude of tests on silicone rubber to provide researchers with a better understanding of rubber’s responses to various mechanical loads. The collected experimental observations included experimental tests for uniaxial extension, equibiaxial tension, inflation, and indentation using a spherical indenter. Correlations with uniaxial and equibiaxial test data were used to characterize the constitutive response of the rubber material in terms of the hyperelastic models described by Mooney-Rivlin, Mansouri-Darijani, and Ogden, and using neo-Hookean forms. Second, we introduced optimal ranges for efficiency of various strain energy functions responsible for nonlinear material behaviors, based on the correlation of FE results with the experimental results for two structures.

A Brief Review of Hyperelastic Constitutive Models

The general motion of a continuum is described by x = χ (X, t), where X and x denote the position vectors of material particles in their reference configurations, and the current configuration at time t, respectively. The deformation gradient is shown by F = ∂x/∂X. Since det(F) > 0, and the polar decomposition theorem states that F is uniquely decomposed as

$$ F=RU=VR $$
(1)

where U and V are the right and left stretch tensors, respectively. U and V are positive definite symmetric tensors, and R is a proper orthogonal rotation tensor, which represents the rotation of the eigenvectors of U, N i , to the eigenvectors of V, n that can be written as

$$ {n}_i=R{N}_i $$
(2)

Let λ i  (i = 1, 2, 3) be the eigenvalues of the stretch tensors. Indeed, the multiple λ i are the principal stretches of the deformation. The invariants of the right Cauchy − Green strain tensor are

$$ {I}_1={\lambda}_1^2+{\lambda}_2^2+{\lambda}_3^2,{I}_2={\lambda}_1^2{\lambda}_2^2+{\lambda}_1^2{\lambda}_3^2+{\lambda}_2^2{\lambda}_3^2,{I}_3={\lambda}_1^2{\lambda}_2^2{\lambda}_3^2 $$
(3)

The constitutive equation of an isothermal elastic body, which supports no residual stress, relates the Cauchy stress tensor σ = σ (x, t) at each place x = χ (X, t) to the deformation gradient F [40] as

$$ \sigma =\varSigma (F) $$
(4)

For a strain energy density function of the form W (I 1 , I 2 ) in terms of strain invariants, the constitutive equation for the Cauchy stress of an incompressible, isotropic, nonlinear elastic material, whose response function Σ has a physical expression, can be found by

$$ \sigma =\varSigma (F)=- pI+2\frac{\partial W}{\partial {I}_1}B-2\frac{\partial W}{\partial {I}_2}{B}^{-1} $$
(5)

where p is the indeterminate scalar arising from the constraint of incompressibility, and B denotes the left Cauchy–Green strain tensor and is shown by B = FF T. In this case, the strain invariants become \( {I}_1={\lambda}_1^2+{\lambda}_2^2+{\lambda}_3^2 \), \( {I}_2={\lambda}_1^{-2}+{\lambda}_2^{-2}+{\lambda}_3^{-2} \) and I 3 = 1.

In this section, the capability of the neo–Hookean model, the Mooney–Rivlin strain energy density function, the Ogden [41] model, and a recent constitutive model proposed by Mansouri and Darijani [42] are examined for a rubber material with medical applications, experiencing different states of finite deformation.

Treloar [3, 4] proposed a so–called neo–Hookean material model in terms of I 1with only one material parameter. This model is the simplest phenomenological form of a strain energy function and is widely used in modeling the mechanical response of elastomers. It has the following simple form

$$ W=\frac{\mu_o}{2}\left({I}_1-3\right) $$
(6)

where 2μ 0 is the initial shear modulus.

Undoubtedly, the Mooney–Rivlin model stands as the most-cited strain energy function in the literature. Mooney published an invariant-based phenomenological model demonstrating the principal invariants of the right Cauchy–Green strain tensors, I 1 and I 2 . Due to its simplicity and suitability in describing the mechanical behavior of elastomers that undergo moderately large deformations, this model is of interest. This model can be seen in the form

$$ W={C}_1\left({I}_1-3\right)+{C}_2\left({I}_2-3\right) $$
(7)

where C 1 and C 2 are material parameters. The initial shear modulus, μ 0 , can be found through the relation μ 0 = 2(C 1 + C 2).

Another stretch-based strain energy function is the Ogden model. It delivers good agreement with Treloar’s experimental data for the extension of unfilled natural rubber. With a sufficient number of parameters, it can also be fitted to a broad range of deformation states. The versatility of this model has resulted in its appearance in many studies. Recently, Ehret [43] found a relation between the Ogden model and molecular statistical theory. The Ogden model takes the form

$$ W={\displaystyle \sum_{i=1}^N\frac{2{\mu}_i}{\alpha_i^2}}\left({\lambda}_1^{\alpha_i}+{\lambda}_2^{\alpha_i}+{\lambda}_3^{\alpha_i}-3\right) $$
(8)

where μ i  ′ s and α i are material parameters. The initial shear modulus, μ 0 , can be calculated through the consistency condition \( \sum_{i=1}^N{\mu}_i={\mu}_0 \). In this work, the two-term Ogden model, N = 2, is examined.

The last evaluated hyperelastic elastomers’ model, proposed by Mansouri and Darijani [42], was developed based on the first and second strain invariants. The model appears in an exponential framework and is based on research collected by Darijani and Naghdabadi [44] that examines all combinations of the power law, and polynomial, logarithmic, and exponential functions. As a result of this investigation, they concluded that a strain energy function in terms of exponential forms, in comparison with others, achieves superior agreement with the homogeneous experimental data. The proposed model benefits from these pivotal characteristics: the presence of a second strain invariant, simplicity, stability of the parameters through implementation of restrictions on the strain energy density, and superior accuracy, based on the best phenomenological combination of functions. The introduced model is in the form

$$ W={A}_1\left[ \exp \left({m}_1\left({I}_1-3\right)\right)-1\right]+{B}_1\left[ \exp \left({n}_1\left({I}_2-3\right)\right)-1\right] $$
(9)

where A 1 and B 1 are material parameters and m 1 and n 1 are non-dimensional values. The initial shear modulus, μ 0 , is computed through the relation μ 0 = 2(A 1 m 1 + B 1 n 1).

There exist several comprehensive comparisons and excellent reviews of the development of phenomenological and statistical mechanics treatment of rubber elasticity in recent publications [42, 45–48].

Experimental Observations

To create a desired silicone membrane, the principles described by Nijhof and Cubera [49] were used here for the curing process. The uncured silicone was cast into a ferrous mold, and the designed mold system was placed inside a rubber sheet curing press machine. Using this machine, the system was put simultaneously under the pressure of 100 tons and a curing temperature of 180 ° C for 15 min. Finally, the silicone rubber membrane was placed inside an oven at 80 ° C for 180 min to complete the crosslink-forming procedure.

Uniaxial Extension

The uniaxial testing of the silicone rubber was carried out using a TCS-2000 servo control system universal testing machine equipped with an extensometer for accurate acquisition of strain data and a load cell with a capacity of 20 kN (Fig. 1). The tensile tests were performed using three dumbbell-shaped samples with a thickness h 0 = 1.50 – 1.75 mm and a width of 6.04–6.09 mm, which were cut from the same sheet. The average stress-stretch curve for loading of the three samples will be shown in Fig. 5. This experiment was performed at the rate of 30 mm/min. The controlled conditions were a temperature of 23 οC and humidity of 53 %. To be able to describe the material behavior in the conventional theory of finite elasticity, the Mullins effect should be examined. More information on this effect can be found elsewhere [50–53]. As Meunier et al. [28] showed with unfilled silicone rubber, the Mullins effects, hysteresis, and strain rate sensitivity can be considered negligible.

Fig. 1
figure 1

Uniaxial testing machine and elastomeric dumbbell

Full size image

Equibiaxial Inflation Test

The inflation test of a rubber membrane is largely used to experimentally evaluate both the equibiaxial stress-strain curves and the deformation shape of membranous elastomers. A number of techniques are used to measure the full-field displacements. In the case of large deformations, the pioneering works of Septanika et al. [54], Laraba-Abbes et al. [55], and Chevalier et al. [56] can be highlighted. In this study, a test bed for equibiaxial extension on the rubber material was designed and developed. We facilitated integrated 3-D analysis of the structure without using the complicated 3-D DIC method. The strain measurements were performed by a system made of a high resolution camera mounted on a movable arm in order to keep a fixed distance between the camera and top of the inflated membrane at each time increment. The entire procedure is described in the following paragraphs.

A rotating handle at the end of a ball screw permitted the camera to move perpendicularly to the plane of the test bed. As the apex height of the inflated membrane increased, a needle coupled to the camera and tangent to the apex controlled the camera’s motion using a digital depth caliper. The depth caliper was fixed to the immovable part of the test tower, and its movable tip was connected to a moving part of the tower system. This arrangement enabled the system to not only measure the apex height directly but also to maintain an unchanged camera perspective, keeping a constant distance between the camera and the apex of the inflated membrane. This technique made 3-D measurement procedures free from both 3-D calibration of the camera and reconstruction of the picture through overlapping pictures taken by two cameras, which are essential for performing 3-D stereo-correlation. The perspectives and details of the designed system for the inflation test are shown in Fig. 2.

Fig. 2
figure 2

The inflation test apparatus. The section on the top left corner shows deposition of speckles on the specimen for the purpose of full-field measurements. The arrows show the target points for full-field measurements in the DIC procedure

Full size image

The rubber membrane used in the inflation test has a diameter of 240 mm and a thickness of 1.83 mm. The internal diameter of the flange was large enough to let the specimen expand, while avoiding any border effect [57]. To enhance the fixity condition at the clamped boundary, an additional layer of a hard silicone was attached to the rubber. In this study, the membrane was pressurized until a maximum displacement at the apex, δ max  = 120 mm, was reached. The pressure-apex displacement diagram is shown in Fig. 3, left. The deflected profiles at different pressures were measured by an optical technique that is depicted in Fig. 3, right. The deflected shapes corresponding to the applied pressures were numbered from point 1, P = 3.4 kPa and δ = 41.6 mm, to point 5, P = 10.6 kPa and δ = 103.2 mm. The images were colored to make the changes more visible. The image processing method was carried out entirely through considering image pixels rather than an actual physical distance for both acquisition of strain and deflected shapes. In the case of the deflected shapes, the image pixels were calibrated against a known physical distance, which in this case was the apex height measured by a digital-depth caliper. The measured results for the equibiaxial stress-strain curves are reported in the next subsection.

Fig. 3
figure 3

Deformed profiles illustrating the inflation test at different pressures for membrane thickness h0 = 1.83 mm, right, and its corresponding pressure − apex displacement response, left. A second camera placed in front of the inflated membrane acquired the profiles of inflated membrane

Full size image

Prior to this research, some studies discussed the importance of equibiaxial data in constitutive modeling of hyperelastic materials [58, 59], and other studies attempted to describe that uniaxial and equibiaxial deformations are the most different in terms of possible deformation states when considering the relative variation of the first and second strain invariants, I 1 and I 2 [60, 61]. However, this research highlighted the importance of including equibiaxial deformation data for modeling of hyperelastic structures, and it’s prominent role in FE simulation for the first time. In addition, we examined whether or not the accuracy of the correlation of one constitutive model with homogeneous experiments signified similar accuracy for prediction of inhomogeneous structures. These contributions are presented in the next sections.

For a circular, inflated, or indented elastic membranes, clamped along the edge at r = a, the local deformations are a complex function of radius, from the equibiaxial state at the apex to the pure shear at the outer radius [1, 62]. When the initially flat membrane was deformed into a curved state, the principal stretches λ 1 and λ 2 become inhomogeneous. Figure 4 illustrates the cross-sections for both axisymmetric structures. As shown in Fig. 4, a material point originally located at (r = ρ,  z = 0) was then displaced to the point [r = r (ρ),  z = z (ρ)]. Let ξ denote the arc length of the cross-section curve of the deformed membrane. The two principal stretches are

$$ {\lambda}_1=\frac{d\xi }{dr},{\lambda}_2=\frac{\rho }{r} $$
(10)
Fig. 4
figure 4

Cross-section view of the axisymmetric deformation of a silicone membrane clamped between two flanges: the left figure shows the inflation test, while the right figure demonstrates the indentation of a circular membrane by a spherical indenter

Full size image

Note that λ 1 is the longitudinal stretch, running along the cross-section curve in the r–z plane, and λ 2 is the latitudinal stretch, running along the direction normal to the r–z plane. In the apex neighborhood, both stretches are homogeneous in the membrane λ 1 = λ 2 = λ. Note that the material is assumed to be incompressible; thus, the extension ratio in the thickness direction is equal to \( {\lambda}_1^{-1}{\lambda}_2^{-1} \). With these assumptions, the equibiaxial stress-strain data can be easily calculated through inflation test measurements. To achieve this goal, knowing the radius of curvature, tangential stretches at the apex, and pressure recorded during the test are required. Once the thickness dimension was much smaller than the other two planar dimensions, the stress was also assumed to be negligible along the thickness. In the inflation test, the deformed membrane can be viewed as a section of a sphere with a constant radius of curvature. Therefore, for the stress components, we may write

$$ {\sigma}_1={\sigma}_2=\sigma =\frac{PR\lambda }{2{h}_o},{\sigma}_3=0,R=\frac{a^2+{\delta}^2}{2\delta } $$
(11)

where σ i (i = 1, 2, 3) are principal engineering stresses; R is the radius of curvature; h 0 is the initial thickness of the membrane, and δ is the apex displacement. The stress-strain curves for both uniaxial extension and equibiaxial tension are plotted in Fig. 5.

Fig. 5
figure 5

Stress-stretch response of silicone rubber subjected to multiple experiments, uniaxial extension and equibiaxial tension, as well as relating errors. The proposed results are the average of three experiments conducted on three specimens, for each deformation-state dependent response of silicone undergoing finite deformation

Full size image

Indentation Test

The designed apparatus and testing facilities, shown in Fig. 6, were applied to the indentation of an initially circular hyperelastic membrane with a thickness of h 0  = 1.75 mm. All other dimensions and clamping conditions were similar to those adopted in the inflation test. The radius of the spherical indenter was R 0 = 26.94 mm, and it was attached by a rigid lever to a TCS-2000 servo control system universal testing machine. The membrane was deformed up to a maximum apex displacement of δ max  = 110 mm, with the corresponding force of F max  = 202.4 N. The test was carried out at a constant loading rate of 40 mm/min, followed by unloading at the same strain rate. The left side of Fig. 6 depicts the force-displacement curves, showing a perfect nonlinear and reversible behavior with no hysteresis effect. The axisymmetric deformed shapes are also acquired by means of the methods explained for the inflation test.

Fig. 6
figure 6

The designed structure and facilities required for the indentation of rubber with membrane thickness h 0 = 1.75 mm : showing the force – apex displacement response of the structure under loading, followed by unloading on the left, while using a spherical indenter, right

Full size image

Material Parameters

In this work, the material parameters were determined based on the correlation between values of the strain energy density rebuilt from the test data and the applicable theory. This approach was introduced by Darijani and Naghdabadi [44] and is preferred over the conventional method of stress correlation discussed by Drozdov [63], Ogden et al. [64], Hartmann [65], and Gendy and Saleeb [66]. In this paper, the strain energy density function, including the unknown material parameters, were fitted to the values of the strain energy density cast from the test data. In this fitting procedure, the discrepancy between the model results and the experimental data, commonly referred to as residual sum of squares (RSS), is defined as

$$ RSS={\displaystyle \sum_{i=1}^n\parallel {W}_{data}}-{W}_{\mod el}{\parallel}^2 $$
(12)

A Perfect Fit would Yield a Residual Sum of Squares of 0.0.

The material parameters, which are fitted simultaneously to the uniaxial and biaxial data, initial shear modulus, and residual sum of squares are listed in Table 1, for the four investigated models. The Mansouri-Darijani model had minimum values of RSS, while the maximum value was achieved using the neo-Hookean strain energy function. The Mansouri–Darijani material model and the Mooney– Rivlin model produced the lowest and highest values of shear modulus, respectively. Shear modulus is a quantity for measuring the stiffness of materials, which in these results showed a small difference of about 0.013 MPa. This discrepancy increases to 0.292 MPa when the latter constitutive models are fitted to just uniaxial extension data. Accordingly, adopting equibiaxial data and uniaxial experimental data provided a more localized response pattern in the form of the various constitutive models.

Table 1 Material parameter values from fitting various strain energy functions to the results of multiple experiments shown in Fig. 5, including their relevant residual sum of squares (RSSs) and initial shear moduli.
Full size table

Comparison of Experiments with FEM Simulation

Treatment of large elastic deformations of hyperelastic membrane configurations yielded a system of nonlinear coupled differential equations with singularities in pole that can be solved given the system parameters and boundary conditions. The construction of a solution in this manner, however, becomes extremely unwieldy for all but the simplest forms of the strain energy function. As mentioned in the introduction, applications of the numerical integration approaches to the solution of problems in hyperelasticity are many and varied. Nevertheless, because of the convenience and versatility of modern nonlinear FE codes, they are capable of handling difficulties with complex boundary conditions. These contributions become more noticeable when Coulomb friction and non-stationary contact are accompanied by the nonlinear process associated with hyperelasticity. To date, the reliability of the FE simulation of nonlinear hyperelastic materials were concerned strictly with two main subjects: the selection of an appropriate strain energy function, and inserting true material coefficients into the FE codes. In this research, a comprehensive study was conducted to demonstrate that within the range of applied loads used here, which was common to real-world scenarios, how reliability reflected the implementation of true material coefficients and how to select an appropriate strain energy function. To achieve this, the accuracy of the correlation of FEM with the experimental observations was adequately verified through simulation of two deformation configurations: the first one was the inflation of an initially flat circular hyperelastic membrane subjected to a uniform pressure, and the second one was the indentation of a clamped circular membrane by a spherical indenter.

For the simulation, we used the commercially available, implicit finite element software Abaqus/CAE Version 6.13 (Abaqus, 2013). To simulate the rubber’s behavior, we implemented the constitutive models described former, and we adopted the framework UHYPER to create user-defined isotropic hyperelastic material, as a user subroutine to utilize Mansouri and Darijani’s model within the FE software. We discretized the rubber membrane with 3422 S4R bi-linear quadrilateral finite strain shell elements with discrete Kirchhoff thin-shell kinematics. A finer mesh did not make any significant difference in displacement measures for the applied loads. Sensitivity tests were also performed to assess the influence of mesh size, element types (shell and solid elements), and element shapes (triangular and quadrilateral) to ensure the FE simulation was accurate with an optimum requirement on the computational resources.

Computational Modeling of the Inflation Test

The results of FE simulation for the inflation structure were compared to those of the previously conducted experiments. The effect of various values of pressure for various prescribed constitutive models is illustrated in Fig. 7. The material parameters are tabulated in Table 1, which were computed from the simultaneous fitting procedures of the four constitutive models to the uniaxial and biaxial data, and they were used for the purpose of FE simulation of the inflation structure. Table 2 displays how accurately each constitutive model predicted the apex displacements during the inflation test by reporting related errors.

Fig. 7
figure 7

Comparison of deflected shapes of the inflation experiment with the computational results of the same problem at different pressures, shown along the left side, for the four constitutive models

Full size image
Table 2 The values of apex displacements for various constitutive models in finite element simulation of inflation test and related errors
Full size table

Computational Modeling of the Indentation Test

All conditions used to conduct the simulation of the inflation structure were similarly carried out for FE modeling of the indentation test. In the indentation of a rubber membrane using an indenter, the main concern was related to friction from the surface-to-surface contact. Nasto et al. [67] measured the friction coefficients between the indenter and a silicone rubber to be about 1.46. In this paper, we virtually considered this result. For the FE simulation of contact behavior in the normal direction, the hard pressure-overclosure option was selected, and the separation after the contact was allowed. Figure 8 illustrates comparisons between the computational predictions and the experiments’ results using typical deflected shapes of the membrane during the indentation at the indentation load levels of 37.9 N, 87.9 N, 144.8 N, and 202.4 N. All models predicted the experiments’ results very closely. When the constitutive models were fitted to just the uniaxial data, the divergence between the computational and the experiments’ results were increased, remarkably. For example, the Mooney–Rivlin and Mansouri–Darijani models predicted the experimental results as 9 % higher and 10 % lower, respectively, at the load level of 202.4 N.

Fig. 8
figure 8

Comparison of the deflected shapes for the indentation experiments using the computational results of the same problem at different loads for the four constitutive models: (a) Mooney-Rivlin, (b) Mansouri-Darijani (c) Ogden, and (d) neo-Hookean

Full size image

Results

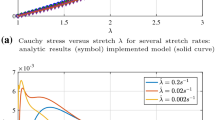
Presenting more than one category of experiments involving two specific boundary value problems—inflation and indentation of an edge-supported circular membrane—enhanced the model development procedure. As Figs. 7 and 8 illustrate, through comparison of experimental results with their computational predictions, when constitutive models were fitted to multiple experiments, the degree of correlation was not generally restricted by the selection of the constitutive model, and all models functioned nearly the same. The exception concerned the Ogden model during the inflation test, which fared poorly in matching large deformations. Instead, the correlations of a constitutive model with experimental results strongly depended on the range of applied strains. These accuracies were attributed to the inclusion of both equibiaxial and uniaxial data within the fitting procedures of different strain energy functions. The similar abilities of strain energy functions were violated when only data from the uniaxial or equibiaxial test data was used for the fitting procedure. The computational results of FE simulations shown in Fig. 9(a) were established by means of only uniaxial or equibiaxial test data. In the case of fitting constitutive models to only uniaxial data, the selection of a particular form of a strain energy function for computational treatment of a problem should be given special attention. As shown in Fig. 9(b), the selection of a particular model was not a matter of concern when the material parameters were obtained from fitting with multiple experiments (both uniaxial and equibiaxial data). The results of fitting various constitutive models to equibiaxial data alone is shown in Fig. 9(a). All models predicted the experimental results similarly, and at a low strain, equibiaxial data alone fit the simulation results accurately. As Fig. 9(a) depicts, whenever the nonlinearity level of a particular constitutive model increased, the inaccuracies also increased when constitutive models were fitted to only the uniaxial data. For instance, as can be seen in Fig. 9(a), the neo-Hookean model seemed to fit the experimental data better by simply using uniaxial data while the Mansourip-Darijani model fitted the experiments inaccurately. Therefore, the use of strain energy functions that are inherently more linear in behavior derived more reliable results for FE simulation. In addition, the deformations presented here induced large deformations, but the strains encountered in the structures were still within the moderate range.

Fig. 9
figure 9

The results of pressure-apex displacement during the inflation experiment compared with computational responses to the same problem under various strain energy functions, when (a) fitted to only uniaxial or equibiaxial test data (all models functioned very similarly when fitted to just equibiaxial data), and when (b) fitted to uniaxial and equibiaxial data simultaneously

Full size image

Results and Discussion

This work was motivated by the need for integrated experiments on deformation-state dependent responses of elastomers to investigate the accurate constitutive responses of these materials. The standard experiments included uniaxial extension and equibiaxial tension, upon which various constitutive models were fitted. The inhomogeneous experiments were inflation and indentation of a clamped circular membrane using pressure and a spherical indenter, respectively. The FE simulations of these structures were established using material constants obtained from the correlation of the constitutive models to standard experiments. The FE simulation showed that all the forms of strain energy functions predicted similar results and had a good agreement with the deformation profiles of the two above-mentioned structures under various levels of pressures and loads. These accuracies were attributed to using multiple experiments rather than using only uniaxial or equibiaxial data in the fitting procedure for determination of the material constants. Instead, the correlations of one constitutive model with the experiments strongly depended on the range of applied strains. For situations in which multiple experiments are not possible, at least for the presented ranges of deformation shown in this study, the use of strain energy functions that are inherently less nonlinear in behavior can bring more reliable results for FE simulation, when fitted to only uniaxial data.

The hybrid experimental-numerical method, or the inverse method, is widely used to characterize material parameters of both rubber-like materials and biological membranes. In this method, the material parameters were obtained using the deformation of membranous configurations, usually inflated or indented structures. Figures 7 and 8 depict that under small deformations the FE modeling was not able to predict the experiment well, while at moderate to large deformations, the correlations matched the experimental data. Therefore, adopting the use of deformation profiles at large deformations, as a part of an inverse identification method, can produce true material parameters in the inverse FE modeling procedure. In other words, the inverse FE procedure should not be restricted to the choice of the constitutive models when the strains are moderate. Instead, more attention should be given to the choice of the range of deformation. However, high loads could lead to puncturing and blur the test results; therefore, a secure experimental area, as preserved here, should be considered.