Indentation of Metal Foam Core Sandwich Beams: Experimental and Theoretical Investigations

Abstract

Indentation behavior of metal foam core sandwich beams is investigated experimentally and theoretically. The deformation mechanisms of indentation are explored. The interaction of plastic bending and stretching in the local deformation regions of the top face sheet is considered. An analytical model is developed to predict large deflections of indentation of the sandwich beams transversely loaded at any location of the span. The analytical predictions are in good agreement with experiment results. Effects of the punch shape, the face sheet thickness and loading location on the indentation are discussed. It is shown that the loading location drives various deformation mechanisms of indentation for a given sandwich beam. The membrane force plays an important role in the large deflection of indentation of sandwich beams when the loading point exceeds the face sheet thickness.

Introduction

Lightweight sandwich structures are being widely used in a number of critical engineering, such as aircraft, spacecraft, vehicle and ship, etc. Metal foam core sandwich structures are typical sandwich structures with a number of advantages, e.g., high specific strength and stiffness, high resistances to impact and blast loadings. In engineering application, the intense local loads on sandwich structures are unavoidable, and may arise accidentally, such as a consequence of collisions or dropped objects. Local indentation may cause a serious reduction in load-carrying capacity of sandwich structure [1, 2]. Thus, investigations on indentation of sandwich structures with metal foam cores have been paid much attention.

In earlier investigations on indentation of sandwich beams, Frostig et al. [3, 4] modeled the face sheets and the foam core as elastic beams and an elastic foundation. Triantafillow and Gibson [5, 6] neglected the effect of the strength of face sheets and the indentation load is indicated by plastic strength of foam core. Apparently, this underestimates the indentation load. Soden [7] and Shuaeib and Soden [8] developed analytical models for indentation of the sandwich beam, in which an elastic beam was resting on a rigid-perfectly plastic foundation and an elastic-perfectly plastic foundation, respectively. Using a simple upper bound calculation, Ashby et al. [2] analytically studied the indentation of metal foam core sandwich beams without considering the effect of shear strength of the foam core. Subsequently, Koissin et al. [9] obtained an analytical solution for the quasi-static indentation of sandwich structure. They assumed that the face sheets deflect elastically and the foam core is idealized as elastic-perfectly-plastic foundation without strain rate, shear effects and overall bending. Rubino et al. [10] proposed an analytical model for the indentation of the metal sandwich beams, in which effect of the shear strength of the core on the indentation and compression of the core and bending of the face sheet are considered. Wang et al. [11] analytically and experimentally investigated indentation responses of foam sandwich beams and plates reinforced by fiber columns. Based on the superposition principle and the principle of minimum energy, analytical models were derived for sandwich beams and plates, respectively, and analytical solutions are well compared with the experimental results. However, all the aforementioned studies are based on the assumption of the small deflection.

Recently, Rubino et al. [12] modified the previous analytical model [10] to consider the contribution of the stretching of the face sheet by neglecting interactions between plastic bending and stretching in deformation regions. Qin and Wang [13] developed an analytical model for the local indentation of metal foam core sandwich beams transversely loaded by a flat punch considering interactions between plastic bending and stretching in deformation regions, while the deformation region length is fixed. Wierzbicki and Hoo Fatt [14] proposed a large deformation model for a plastic string resting on a plastic foundation subjected to a concentrated loading neglecting the effect of plastic bending of the face sheet. Later on this model has been applied to predict the local indentation of the metal foam core sandwich beam considering the size effects of indenters [15] whilst neglecting the contribution of the shear strength of the core.

The experimental investigations were devoted to analyzing the quasi-static indentation of sandwich beams and panels with various foam cores. Zenkert et al. [16] experimentally studied static indentation tests of composite sandwich beams with GFRP face sheets and two different foam cores. The load–displacement response, the size of a crushed core zone and the depth of a residual dent were measured in the tests. The experimental results are in good agreement with the numerical data. Recently, Flores-Johnson and Li [17] experimentally studied the quasi-static indentation of sandwich panels with the carbon fibre-reinforced polymer face and polymeric foam core. It was found that both the nose shape and foam core density have large influence on the indentation response, and the difference in indentation resistance between the sandwich panel and core material depends on the core density. Pitarresi and Amorim [18] experimentally studied the indentation curves of thermoplastic sandwich beams with PMI, PA and XPS foam cores under local loading. Besides the investigations on indentation experiments of the sandwich beams with cores, Rizov et al. [19] and Rizov [20] experimentally investigated the nonlinear behaviors of foam core composite sandwich panels subjected to local indentation. Both the experiment and the finite element model described the loading and unloading behaviors and a good correlation between the experimental data and the numerical simulations was achieved. Li et al. [21] carried out quasi-static indentation tests to study the deformation, failure behaviors and the energy absorption of sandwich panels with aluminum foam cores and composite face sheets subjected to three kinds of indenters.

As mentioned above, most theoretical investigations focused on the indentation response of sandwich beams with an infinite length, in which the effects of boundary condition and loading location were neglected. To the authors’ knowledge, very few theoretical and experimental investigations were reported regarding the effects of boundary condition and loading location on the indentation of the metal sandwich beams. The objective of this work is to study the large deflection of indentation of metal foam core sandwich beams transversely loaded at any location of the span. The paper is organized as follows. The indentation experiments performed are discussed in Section 2. An analytical model for the large deflection of indentation of the metal foam core sandwich beam is developed in Section 3. Analytical solutions for the post-yield deformation modes are obtained in Section 4. Analytical predications and experimental results are compared in Section 5 and concluding remarks are presented in Section 6.

Experimental Setup

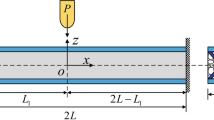
A schematic of metal foam core sandwich beam with the width b supported at a rigid foundation transversely loaded by a flat punch P with the length 2a is shown in Fig. 1. Two identical face sheets with thickness h are bonded to the core with thickness c. The beam length is 2L and the distance is L ₁ from the punch to the end of the beam.

Fig. 1

A 3-D schematic of metal sandwich beam transversely loaded by a flat punch

Specimens

Three-dimensional metal foam core sandwich beams have been tested in the experiments. Two identical face sheets are bonded to the metal foam core. The face sheets were made of 5052H32 aluminum alloy with thicknesses of 0.4, 0.5 and 1.0 mm, respectively. The relative density of closed-cell aluminum alloy foams provided by Foamtech Co., Ltd., Korea is about 0.14 and the average cell size is approximately 2.5 mm.

All sandwich beams have the width b = 40 mm and foam core height c = 30 mm. The beam length 2L = 240 mm for the cases loaded at midspan and 2L = 150 mm for the cases loaded at the location L ₁ = 20 or 30 mm of the spans. The geometries and dimensions of the specimens are listed in Table 1 for more details.

Table 1 Dimensions of the specimens for the indentation experiments

Tensile and Compressive Tests

The mechanical properties of the foam core and the face sheets with thicknesses of 0.5 and 1.0 mm have already been reported [22], and the tensile mechanical properties of the face sheet with the thickness of 0.4 mm are measured herein. To measure the axial strain accurately, the electronic extensometer is oriented in the axial direction of tensile specimens with dog-bone shape, which are cut from the aluminum alloy face sheets. The compressive specimens of metal foams are cuboid shape geometries with dimensions of 35 × 35 × 55 mm. The compressive tests of metal foams are performed by measuring the displacement between two parallel platens.

From the measured tensile stress–strain curves, the 0.2 % offset yield strengths of the aluminum alloy face sheets are 185, 177, and 173 MPa for thicknesses of 0.4, 0.5 and 1.0 mm, respectively, and the average value is 180 MPa. The compressive yield strength σ _c of the aluminium alloy foam is 2.23 MPa.

Experimental Set-Up for Indentation

Indentation tests were performed by using the Hualong testing machine with crosshead speed of 0.5 mm/min, as shown in Fig. 2. Two loading heads are considered, i.e., a steel circular cylindrical punch with a diameter of 10 mm and a steel flat punch with the length of 20 mm. The punch is placed at the center of the specimen in the width direction, and the length of the specimen in the width direction is fully loaded by the punch, as shown in Fig. 1. Two ends of the specimen are fixed by C-clamps to constrain the degrees of freedom of the face sheets and foam core. No evident movements of end of the specimen were observed in the present experiments.

Fig. 2

Indentation experimental test of sandwich beam loaded at midspan

Analytical Model

In this section, an analytical model is developed to predict the large deflection of indentation of the metal foam core sandwich beam. It is assumed that the face sheets obey rigid-perfectly plastic (r-p-p) law with yield stress σ _f . The foam core is modeled as a rigid-perfectly-plastic-locking (r-p-p-l) material with plateau-stress σ _c , critical densification strain ε _D and shear stress τ _c . The r-p-p and r-p-p-l models are useful to approximately describe the post-yield behavior of sandwich structures, respectively, although elastic deformation and hardening behavior are neglected in analysis.

Herein, the top face sheet is idealized as a homogenous r-p-p beam, while the foam core is idealized as a perfectly plastic foundation [23].

• (1) When the local deformation region λ has evolved towards the end of the beam, i.e., λ ≥ L ₁, the assumed deformation mode for indentation of the metal sandwich beam is sketched in Fig. 3(a). Similar to the indentation of the sandwich beam loaded at midspan [12], we assume the following deformation field

  $$ u\left({x}_1,\kern0.5em {x}_3\right)=0 $$

  (1)

  and

  $$ v\left({x}_1,{x}_3\right)=\left\{\begin{array}{l}\frac{{\overset{.}{\theta}}_2}{c}\left(\lambda +a-{x}_1\right){x}_3,\kern3em a\le {x}_1\le a+\lambda \hfill \\ {}\frac{{\overset{.}{\theta}}_2}{c}\lambda \kern0.1em {x}_3,\kern7.5em -a\le {x}_1\le a\hfill \\ {}\frac{{\overset{.}{\theta}}_1}{c}\left({L}_1+a+{x}_1\right){x}_3,\kern1em -a-{L}_1\le {x}_1\le -a\hfill \end{array}\right. $$

  (2)

  where u and v are material point velocities in the x ₁ and x ₃ directions, respectively, ${\overset{.}{\theta}}_1$ and $\overset{.}{\theta }$ are rotation rates of plastic hinges at the left and right sides of the punch. Then the displacement rate of the punch is ${\overset{.}{w}}_0=\lambda {\overset{.}{\theta}}_2={L}_1{\overset{.}{\theta}}_1$ at loading point, as shown in Fig. 3(a).

  Fig. 3

  

  The assumed deformation mode for the indentation of the metal foam core sandwich beam (a) as the local deformation region has evolved towards the end of the beam, and (b) as the local deformation region has not evolved towards the end of the beam

  According to the principle of virtual work and take w ₀ as the transverse deflection at loading location, the rate of dissipation of plastic work is given by

  $$ P\lambda \kern0.1em {\overset{.}{\theta}}_2=2M\left({\overset{.}{\theta}}_1+{\overset{.}{\theta}}_2\right)+N\kern0.1em {\overset{.}{e}}_1+N\kern0.1em {\overset{.}{e}}_2+{\displaystyle {\int}_A{\sigma}_c\kern0.1em {\overset{.}{\varepsilon}}_{33}\operatorname{d}\operatorname{A}}+{\displaystyle {\int}_A{\tau}_c\kern0.20em {\overset{.}{\gamma}}_{13}\operatorname{d}\operatorname{A}} $$

  (3)

  where M and N are the plastic bending moment and axial force, respectively, and ${\overset{.}{e}}_1$ and ${\overset{.}{e}}_2$ are the extension rates of the deformation region of the top face sheet at the left and right sides of the punch,

  $$ {\overset{.}{e}}_1=\frac{1}{L_1}{w}_0{\overset{.}{w}}_0 $$

  (4)

  and

  $$ {\overset{.}{e}}_2=\frac{1}{\lambda }{w}_0{\overset{.}{w}}_0. $$

  (5)

  From equations (1) and (2), we have the compressive strain rate of the foam core and the shear strain rate of the foam core,

  $$ {\overset{.}{\varepsilon}}_{33}\left({x}_1,{x}_3\right)=\frac{\partial v}{\partial {x}_3}=\left\{\begin{array}{l}-\frac{{\overset{.}{\theta}}_2}{c}\left({x}_1-\lambda -a\right),\kern2.6em a\le {x}_1\le a+\lambda \hfill \\ {}\frac{{\overset{.}{\theta}}_2}{c}\lambda, \kern8em -a\le {x}_1\le a\hfill \\ {}\frac{{\overset{.}{\theta}}_1}{c}\left({x}_1+{L}_1+a\right),\kern1.12em -a-{L}_1\le {x}_1\le -a\hfill \end{array}\right. $$

  (6)

  and

  $$ {\overset{.}{\gamma}}_{13}\left({x}_1,{x}_3\right)=\frac{\partial v}{\partial {x}_1}+\frac{\partial u}{\partial {x}_3}=\left\{\begin{array}{l}-\frac{{\overset{.}{\theta}}_2}{c}{x}_3,\kern2.1em a\le {x}_1\le a+\lambda \hfill \\ {}0,\kern5em -a\le {x}_1\le a\hfill \\ {}\frac{{\overset{.}{\theta}}_1}{c}{x}_3,\kern1.5em -a-{L}_1\le {x}_1\le -a\hfill \end{array}\right. $$

  (7)

• (2) When the local deformation region λ has not evolved towards the end of the beam, i.e., λ < L ₁, the assumed deformation mode for indentation of the metal sandwich beam is sketched in Fig. 3(b). The assumed deformation field for the indentation of the sandwich beam loaded at any location of the span is same as that for that loaded at midspan [12],

  $$ u\left({x}_1,\kern0.5em {x}_3\right)=0 $$

  (8)

  and

  $$ v\left({x}_1,{x}_3\right)=\left\{\begin{array}{c}\hfill \frac{\overset{.}{\theta }}{c}\left(\lambda +a-{x}_1\right){x}_3,\kern3.22em a\le {x}_1\le a+\lambda \hfill \\ {}\hfill \frac{\overset{.}{\theta }}{c}\lambda \kern0.1em {x}_3,\kern8em -a\le {x}_1\le a\hfill \\ {}\hfill \frac{\overset{.}{\theta }}{c}\left(\lambda +a+{x}_1\right){x}_3,\kern2em -a-\lambda \le {x}_1\le -a\hfill \end{array}\right. $$

  (9)

  where $\overset{.}{\theta }$ is rotation rate of plastic hinges at the left and right sides of the punch, and a displacement rate of the punch is ${\overset{.}{w}}_0=\lambda \overset{.}{\theta }$ at loading point.

  To determine the load-deflection relationship after collapse, principle of virtual work is applied during the plastic deformation. The rate of dissipation of plastic work is

  $$ P\lambda \kern0.1em \overset{.}{\theta }=4M\overset{.}{\theta }+2N\kern0.1em \overset{.}{e}+{\displaystyle {\int}_A{\sigma}_c\kern0.1em {\overset{.}{\varepsilon}}_{33}\operatorname{d}\operatorname{A}}+{\displaystyle {\int}_A{\tau}_c\kern0.20em {\overset{.}{\gamma}}_{13}\operatorname{d}\operatorname{A}} $$

  (10)

  where $\overset{.}{e}$ is the extension rate of the deformation region of the top face sheet at the left and right sides of the punch,

  $$ \overset{.}{e}=\frac{1}{\lambda }{w}_0{\overset{.}{w}}_0. $$

  (11)

  From equations (8) and (9), the compressive strain rate is

  $$ {\overset{.}{\varepsilon}}_{33}\left({x}_1,{x}_3\right)=\frac{\partial v}{\partial {x}_3}=\left\{\begin{array}{c}\hfill -\frac{\overset{.}{\theta }}{c}\left({x}_1-\lambda -a\right),\kern2.1em a\le {x}_1\le a+\lambda \hfill \\ {}\hfill \frac{\overset{.}{\theta }}{c}\lambda, \kern8em -a\le {x}_1\le a\hfill \\ {}\hfill \frac{\overset{.}{\theta }}{c}\left({x}_1+\lambda +a\right),\kern1.62em -a-\lambda \le {x}_1\le -a\hfill \end{array}\right., $$

  (12)

  and the shear strain rate is

  $$ {\overset{.}{\gamma}}_{13}\left({x}_1,{x}_3\right)=\frac{\partial v}{\partial {x}_1}+\frac{\partial u}{\partial {x}_3}=\left\{\begin{array}{l}-\frac{\overset{.}{\theta }}{c}{x}_3,\kern2.6em a\le {x}_1\le a+\lambda \hfill \\ {}0,\kern5em -a\le {x}_1\le a\hfill \\ {}\frac{\overset{.}{\theta }}{c}{x}_3,\kern1.5em -a-\lambda \le {x}_1\le -a\hfill \end{array}\right.. $$

  (13)

  Due to the characteristics of beam-on-foundation model, the axial (membrane) force would be induced by the finite deflection of top face sheet. Moreover, the axial (membrane) force would dissipates energy and stiffens the deformation portion of the top face sheet. The plastic redecoration of the top face sheet mainly comes from plastic bending and longitudinal stretching. Onat and Prager [24] gave a yield criterion for the top face sheet,

  $$ \left|m\right|+{n}^2=1 $$

  (14)

  where m = M/M ₀ and n = N/N ₀. Meanwhile, the fully plastic bending moment and axial force in the top face sheet are respectively given by

  $$ {M}_0=\frac{1}{4}{\sigma}_fb{h}^2 $$

  (15)

  and

  $$ {N}_0={\sigma}_fbh=\frac{4{M}_0}{h} $$

  (16)

  According to the associated flow rule for yield criterion equation (14), we have

  $$ \frac{dm}{dn}=-2n=-\frac{2\overset{.}{e}}{h\kern0.1em \overset{.}{\theta }}=-\frac{2{\overset{.}{e}}_1}{h{\overset{.}{\theta}}_1}=-\frac{2{\overset{.}{e}}_2}{h{\overset{.}{\theta}}_2} $$

  (17)

  When the local deformation region λ has evolved towards the end of the beam,

  $$ {\overset{.}{e}}_1={\overset{.}{\theta}}_1h\kern0.1em n=\frac{{\overset{.}{w}}_0}{L_1}\cdot h\kern0.1em n $$

  (18)

  and

  $$ {\overset{.}{e}}_2={\overset{.}{\theta}}_2h\kern0.1em n=\frac{{\overset{.}{w}}_0}{\lambda}\cdot h\kern0.1em n $$

  (19)

  When the local deformation region λ has not evolved towards the end of the beam,

  $$ \overset{.}{e}=\overset{.}{\theta }h\kern0.1em n=\frac{{\overset{.}{w}}_0}{\lambda}\cdot h\kern0.1em n $$

  (20)

  Substituting equation (18) into equation (4), equation (19) into equation (5), and equation (20) into equation (11), we obtain

  $$ n=\frac{w_0}{h} $$

  (21)

  for w ₀ ≤ h. Combination of equations (14) and (21) results in

  $$ \left|m\right|=1-{\left(\frac{w_0}{h}\right)}^2 $$

  (22)

  When w ₀ ≥ h, we obtain

  $$ n=1\kern0.5em \mathrm{and}\kern0.5em m=0 $$

  (23)

  In what follows, we derive the analytical solutions for the aforementioned post-yield deformation modes of the metal sandwich beams relative to the loading locations.

Analytical Solutions

Before analysis, the initial wavelength λ ₀ of local denting deformation of the sandwich beam is given [2]

$$ {\lambda}_0=h\sqrt{\frac{\sigma_f}{\sigma_c}} $$

(24)

The post-yield behavior of indention of the metal foam core sandwich beams can be obtained as follows.

The Case of L ₁ ≤ λ ₀

The case of L ₁ ≤ λ ₀ means that the local deformation region has evolved towards the end of the sandwich beam when w ₀ = 0 for the rigid plastic model.

• (1) When w ₀ ≤ h, combining equations (3) to (7), (14) to (19), (21) and (22) yields

  $$ P=\frac{\sigma_fb{h}^2}{2}\left[1+{\left(\frac{w_0}{h}\right)}^2\right]\left(\frac{1}{L_1}+\frac{1}{\lambda}\right)+\frac{\sigma_cb}{2}\left(\lambda +{L}_1\right)+2{\sigma}_c ab+{\tau}_cbc $$

  (25)

  The local deformation region λ can be obtained by minimizing P in equation (25) with respect to the free parameter λ, i.e., ∂P/∂λ = 0. That is

  $$ \lambda =h\sqrt{\frac{\sigma_f}{\sigma_c}\left[1+{\left(\frac{w_0}{h}\right)}^2\right]} $$

  (26)

  Substitution of equation (26) into equation (25) yields the following load-deflection relationship of local denting deformation,

  $$ P=\frac{\sigma_fb{h}^2}{2{L}_1}\left[1+{\left(\frac{w_0}{h}\right)}^2\right]+hb\sqrt{\sigma_f{\sigma}_c\left[1+{\left(\frac{w_0}{h}\right)}^2\right]}+\frac{\sigma_cb}{2}\left(4a+{L}_1\right)+{\tau}_cbc $$

  (27)

  When w ₀ = 0, the initial load P _i of local denting deformation of the sandwich beam is

  $$ {P}_i=\frac{\sigma_fb{h}^2}{2{L}_1}+hb\sqrt{\sigma_f{\sigma}_c}+\frac{\sigma_cb}{2}\left(4a+{L}_1\right)+{\tau}_cbc $$

  (28)

  When w ₀ = h, equation (26) can reduce to

  $$ {\lambda}_1=h\sqrt{\frac{2{\sigma}_f}{\sigma_c}} $$

  (29)

• (2) When w ₀ ≥ h, the deformation portion of top face sheet is in membrane state. We obtain the load-deflection relationship of local denting deformation from equations (3) to (7) and (23), such that

  $$ P={\sigma}_fb{h}^2\cdot \frac{w_0}{h}\left(\frac{1}{L_1}+\frac{1}{\lambda}\right)+\frac{\sigma_cb}{2}\left(\lambda +{L}_1\right)+2{\sigma}_c ab+{\tau}_cbc $$

  (30)

  Minimization of the loading P in equation (30) with respect to the free parameter λ, i.e., ∂P/∂λ = 0, gives a wavelength expression,

  $$ \lambda =h\sqrt{\frac{2{\sigma}_f}{\sigma_c}\cdot \frac{w_0}{h}} $$

  (31)

  Substitution of equation (31) into equation (30) yields the load-deflection relationship of local denting deformation,

  $$ P=\frac{\sigma_fb{h}^2}{L_1}\cdot \frac{w_0}{h}+hb\sqrt{2{\sigma}_f{\sigma}_c\cdot \frac{w_0}{h}}+\frac{\sigma_cb}{2}\left(4a+{L}_1\right)+{\tau}_cb\kern0.1em c $$

  (32)

  If effect of the shear strength of the foam core is very small and can be neglected, the corresponding reduced equation can be obtained from equations (27) and (32) by letting τ _c  → 0. Also, if the sandwich beam is loaded at midspan, i.e., L ₁ = L − a, then the corresponding reduced equation can be obtained from equations (27) and (32). Moreover, it is concluded from equations (26) and (31) that the local denting deformation region increases monotonically with increasing deflection. From equations (27) and (32), we obtain the plastic energy absorption U _i induced by the local denting deformation,

  $$ {U}_i={\displaystyle \underset{0}{\overset{w_0}{\int }}P\left({w}_0\right)\kern0.5em }d{w}_0 $$

  (33)

  Or

  $$ {U}_i=\left\{\begin{array}{ll}\frac{\sigma_fb{h}^2}{2{L}_1}\left[{w}_0+\frac{h}{3}{\left(\frac{w_0}{h}\right)}^2\right]+\left[\frac{\sigma_c}{2}\left(4a+{L}_1\right)+{\tau}_cc\right]bh\cdot \frac{w_0}{h}+\frac{b{h}^2}{2}\sqrt{\sigma_f{\sigma}_c}\left[\frac{w_0}{h}\sqrt{1+{\left(\frac{w_0}{h}\right)}^2}+ \ln \left(\frac{w_0}{h}+\sqrt{1+{\left(\frac{w_0}{h}\right)}^2}\right)\right],\hfill & {w}_0\le h\hfill \\ {}\frac{\sigma_fbh}{2{L}_1}{w}_0^2+\frac{2}{3}\sqrt{2{\sigma}_f{\sigma}_ch}\cdot {w}_0^{{\scriptscriptstyle \frac{3}{2}}}b+\left[\frac{\sigma_c}{2}\left(4a+{L}_1\right)+{\tau}_cc\right]b{w}_0+{K}_1,\hfill & {w}_0\ge h\hfill \end{array}\right. $$

  (34)

  where

  $$ {K}_1=\frac{\sigma_fb{h}^3}{6{L}_1}+\frac{1}{2}\left[ \ln \left(1+\sqrt{2}\right)-\frac{1}{3}\sqrt{2}\right]\sqrt{\sigma_f{\sigma}_c}{h}^2b. $$

The Case of λ ₀ ≤ L ₁ ≤ λ ₁

Similarly, the case of λ ₀ ≤ L ₁ ≤ λ ₁, i.e., $h\sqrt{\sigma_f/{\sigma}_c}\le {L}_1\le h\sqrt{2{\sigma}_f/{\sigma}_c}$, means that the local deformation region has not evolved towards the end of the sandwich beam as w ₀ = 0, and has evolved towards the end of the one before w ₀ = h. Then, we can obtain the following solutions.

• (1) If w ₀ ≤ h, combining equations (10) to (17), and (20) to (22), we obtain the load-deflection relation of local denting deformation

  $$ P=2hb\sqrt{\sigma_f{\sigma}_c\left[1+{\left(\frac{w_0}{h}\right)}^2\right]}+2{\sigma}_c ab+{\tau}_cbc, $$

  (35)

  and the local deformation region

  $$ \lambda =h\sqrt{\frac{\sigma_f}{\sigma_c}\left[1+{\left(\frac{w_0}{h}\right)}^2\right]} $$

  (36)

  If w ₀ = 0, the initial load P _i of local denting deformation of the sandwich beam is

  $$ {P}_i=2hb\sqrt{\sigma_f{\sigma}_c}+2{\sigma}_c ab+{\tau}_cbc $$

  (37)

• (2) If w ₀ ≤ h, the local deformation region λ has evolved towards the left end of the sandwich beam. From equations (3) to (7), (14) to (19), (21) and (22), we obtain the load-deflection relationships,

  $$ P=\frac{\sigma_f{h}^2b}{2{L}_1}\left[1+{\left(\frac{w_0}{h}\right)}^2\right]+hb\sqrt{\sigma_f{\sigma}_c\left[1+{\left(\frac{w_0}{h}\right)}^2\right]}+\frac{\sigma_cb}{2}\left(4a+{L}_1\right)+{\tau}_cbc, $$

  (38)

  and the local deformation region at the right side of the punch

  $$ \lambda =h\sqrt{\frac{\sigma_f}{\sigma_c}\left[1+{\left(\frac{w_0}{h}\right)}^2\right]} $$

  (39)

• (3) If w ₀ ≥ h, the deformation portion of the top face sheet is in membrane state. From equations (3) to (7) and (23), we obtain the load-deflection relationship of local denting deformation,

  $$ P=\frac{\sigma_fb{h}^2}{L_1}\cdot \frac{w_0}{h}+hb\sqrt{2{\sigma}_f{\sigma}_c\cdot \frac{w_0}{h}}+\frac{\sigma_cb}{2}\left(4a+{L}_1\right)+{\tau}_cbc, $$

  (40)

  and the local deformation region at the right side of the punch

  $$ \lambda =h\sqrt{\frac{2{\sigma}_f}{\sigma_c}\cdot \frac{w_0}{h}} $$

  (41)

  From equations (33), (35), (38) and (40), the energy-deflection relationship of local denting deformation can be obtained. If the effect of shear strength of the foam core is very small and can be neglected, the reduced equations can be obtained from equations (35), (38) and (40) by letting τ _c  → 0. Also, if the sandwich beam is loaded at midspan, i.e., L ₁ = L − a, then the reduced equations can be obtained from equations (35), (38) and (40).

The Case of L ₁ ≥ λ ₁

The case of L ₁ ≥ λ ₁, i.e., ${L}_1\ge h\sqrt{2{\sigma}_f/{\sigma}_c}$, means that the local deformation region has not evolved towards the end of the sandwich beam when w ₀ = h. Then, we can obtain the solutions as follows.

• (1) If w ₀ ≤ h, combining equations (10) to (17), (20) to (22), we obtain the load-deflection relationship of the local denting deformation,

  $$ P=2hb\sqrt{\sigma_f{\sigma}_c\left[1+{\left(\frac{w_0}{h}\right)}^2\right]}+2{\sigma}_c ab+{\tau}_cbc, $$

  (42)

  and the local deformation region

  $$ \lambda =h\sqrt{\frac{\sigma_f}{\sigma_c}\left[1+{\left(\frac{w_0}{h}\right)}^2\right]} $$

  (43)

  If w ₀ = 0, we obtain the initial load P _i for local denting of the sandwich beam,

  $$ {P}_i=2hb\sqrt{\sigma_f{\sigma}_c}+2{\sigma}_c ab+{\tau}_cbc $$

  (44)

• (2) If w ₀ ≥ h, combining equations (10) to (13) and (23), the deformation portion of the top face sheet is in a membrane state. The load-deflection relationship is

  $$ P=2hb\sqrt{2{\sigma}_f{\sigma}_c\cdot \frac{w_0}{h}}+2{\sigma}_ca\kern0.1em b+{\tau}_cbc, $$

  (45)

  and the local deformation region is

  $$ \lambda =h\sqrt{\frac{2{\sigma}_f}{\sigma_c}\cdot \frac{w_0}{h}} $$

  (46)

• (3) If w ₀ ≥ h, the local deformation region λ has evolved towards the end of beam. From equations (3) to (7) and (23), we obtain the load-deflection relationship,

  $$ P=\frac{\sigma_f{h}^2b}{L_1}\cdot \frac{w_0}{h}+hb\sqrt{2{\sigma}_f{\sigma}_c\cdot \frac{w_0}{h}}+\frac{\sigma_cb}{2}\left(4a+{L}_1\right)+{\tau}_cbc, $$

  (47)

  and the local deformation region at the right side of the punch

  $$ \lambda =h\sqrt{\frac{2{\sigma}_f}{\sigma_c}\cdot \frac{w_0}{h}} $$

  (48)

  From equations (33), (42), (45) and (47), the energy-deflection relationship can be obtained. If the shear strength of the foam core is neglectable in analysis, then equations (42), (45) and (47) reduce to

  $$ P=\left\{\begin{array}{ll}2h\kern0.1em b\sqrt{\sigma_f{\sigma}_c\left[1+{\left(\frac{w_0}{h}\right)}^2\right]}+2{\sigma}_ca\kern0.1em b,\hfill & {w}_0\le h,\kern0.5em \lambda <{L}_1\hfill \\ {}2h\kern0.1em b\sqrt{2{\sigma}_f{\sigma}_c\cdot \frac{w_0}{h}}+2{\sigma}_ca\kern0.1em b,\hfill & {w}_0\ge h,\kern0.5em \lambda <{L}_1\hfill \\ {}\frac{\sigma_f{h}^2b}{L_1}\cdot \frac{w_0}{h}+hb\sqrt{2{\sigma}_f{\sigma}_c\cdot \frac{w_0}{h}}+\frac{\sigma_cb}{2}\left(4a+{L}_1\right),\hfill & {w}_0\ge h,\kern0.5em \lambda ={L}_1\hfill \end{array}\right. $$

  (49)

  For the case of the sandwich beam loaded at midspan, i.e., L ₁ = L − a, equations (42), (45) and (47) reduce to

  $$ P=\left\{\begin{array}{ll}2hb\sqrt{\sigma_f{\sigma}_c\left[1+{\left(\frac{w_0}{h}\right)}^2\right]}+2{\sigma}_ca\kern0.1em b+{\tau}_cbc,\hfill & {w}_0\le h,\kern0.5em \lambda <L-a\hfill \\ {}2hb\sqrt{2{\sigma}_f{\sigma}_c\cdot \frac{w_0}{h}}+2{\sigma}_ca\kern0.1em b+{\tau}_cbc,\hfill & {w}_0\ge h,\kern0.5em \lambda <L-a\hfill \\ {}\frac{\sigma_f{h}^2b}{L-a}\cdot \frac{w_0}{h}+hb\sqrt{2{\sigma}_f{\sigma}_c\cdot \frac{w_0}{h}}+\frac{\sigma_cb}{2}\left(3a+L\right)+{\tau}_cbc,\hfill & {w}_0\ge h,\kern0.5em \lambda =L-a\hfill \end{array}\right. $$

  (50)

  If the sandwich beam is loaded at midspan by a concentrated loading, i.e., L ₁ → L, equations (42), (43), (45) to (47) reduce to the following solutions [25]

  $$ P=\left\{\begin{array}{ll}2hb\sqrt{\sigma_f{\sigma}_c\left[1+{\left(\frac{w_0}{h}\right)}^2\right]}+{\tau}_cbc,\hfill & {w}_0\le h,\kern0.5em \lambda <L\hfill \\ {}2hb\sqrt{2{\sigma}_f{\sigma}_c\cdot \frac{w_0}{h}}+{\tau}_cbc,\hfill & {w}_0\ge h,\kern0.5em \lambda <L\hfill \\ {}\frac{\sigma_f{h}^2b}{L}\cdot \frac{w_0}{h}+hb\sqrt{2{\sigma}_f{\sigma}_c\cdot \frac{w_0}{h}}+\frac{\sigma_cbL}{2}+{\tau}_cbc,\hfill & {w}_0\ge h,\kern0.5em \lambda =L\hfill \end{array}\right. $$

  (51)

  and

  $$ \lambda =\left\{\begin{array}{ll}h\sqrt{\frac{\sigma_f}{\sigma_c}\left[1+{\left(\frac{w_0}{h}\right)}^2\right]},\hfill & {w}_0\le h,\kern0.5em \lambda <L\hfill \\ {}h\sqrt{\frac{2{\sigma}_f}{\sigma_c}\cdot \frac{w_0}{h}},\hfill & {w}_0\ge h,\kern0.5em \lambda \le L\hfill \end{array}\right. $$

  (52)

  If core strain ε ₃₃ = ε _D , the foam core beneath the punch attains densification. From equations (27), (32), (35), (38), (40), (42), (45) and (47), we obtain the maximum indentation loads by letting w ₀ = c ⋅ ε _D .

Results and Discussion

In this section, the analytical predictions and experimental (EXP) results of the local indentation of the metal foam core sandwich beams under transverse loading by a punch are compared and deformation mechanisms are discussed in detail.

Loaded at Midspan by a Circular Cylindrical Punch

The analytical and experimental load-deflection curves of the indentation response for sandwich beam specimens A-1 and A-2 with the two different face sheet thicknesses are shown in Fig. 4(a) and (c), respectively, loaded at midspan by a circular cylindrical punch. The linear elastic behavior is limited to relatively low values of the indentation. Following the initial linear elastic phase, the slopes of the load-deflection curves decrease gradually in Fig. 4(a) and (c). In the post-yield stage, the load-deflection curves increases nearly linearly. The shear effect of the foam is not evident in experimental observations, and then the contribution of the shear strength of the foam core with low shear strength may be neglected in analysis. One can see analytical predictions based on equation (51) slightly overestimate experimental results in the post-yield stage for specimens A-1 and A-2. The reasons for this discrepancy may be that the effects of bonding layer between the top face sheet and core, and local yield and crush in the foam core beneath the punch were not considered in the analytical solutions, whereas the experiments reveal a local yield and crush in the foam core beneath the punch. Figure 4(b) and (d) show the local deformation regions of indentation for the specimen A-1 and A-2, respectively. The local deformation regions were measured using camera images. We define δ = Δ/w _0 max to valuate the local deformation region, where w _0 max is the maximum deflection of the punch, and Δ is vertical distance from the tangent line between two ends of sandwich beams to the top face sheet occurring the local deformation, as shown in Fig. 5. The measured values are defined as the end/edge of the local deformation region λ when δ ≤ 1 %. As can be seen in Fig. 4(b) and (d), the local deformation regions increase with increasing the indentation. The analytical predications based on equation (52) are in good agreement with observed results for the specimen A-2 with h = 1.0 mm, and a little lower than the observed results for the specimen A-1 with h = 0.5 mm.

Fig. 4

Local indentation of the metal foam core sandwich beam specimens loaded at midspan by a circular cylindrical punch. (a) Load versus deflection for specimen A-1, (b) local deformation region versus deflection for specimen A-1, (c) load versus deflection for specimen A-2, and (d) local deformation region versus deflection for specimen A-2

Fig. 5

Definition of the local deformation region λ

The deformation process images of the typical sandwich specimen A-2 are shown in Fig. 6(a)–(d). No visible damage in the face sheet and face/core interface was observed. The indentation process is characterized with formation of a densified zone which propagates gradually down the core when the deflection increases, as shown in Fig. 6(a)–(d). It is clear that the indentation effects are localized in the vicinity of the punch. There is no obvious deformation of the foam core in the region far away from the punch in Fig. 6(a)–(d).

Fig. 6

Evolution process of the circular cylindrical punch of indentation of the metal sandwich beam specimen A-2 with the face sheet thickness h = 1.0 mm. (a) w ₀ = 2.0 mm, (b) w ₀ = 4.0 mm, (c) w ₀ = 6.0 mm and (d) w ₀ = 8.0 mm

Figure 7 shows the effect of face sheet thickness on the indentation of the sandwich beams. The face sheet thicknesses of sandwich specimens A-1 and A-2 are 0.5 and 1.0 mm, respectively. The other geometric parameters are almost same. As expected, the load increases with increasing the face sheet thickness for a given displacement. However, the increment is nearly constant when the deflection exceeds the face sheet thickness.

Fig. 7

The effect of the face sheet thickness on load versus deflection for indentation of the metal foam core sandwich beam specimens A-1 and A-2 loaded at midspan by a circular cylindrical punch

Loaded at Midspan by a Flat Punch

The load-deflection curve of the experimental results and analytical predictions of the indentation response of sandwich beam specimen B-1 loaded at midspan by a flat punch is shown in Fig. 8(a). The analytical model based on equation (50) captures the experimental results reasonably accurately in the post-yield stage. When the displacement of the punch is about 6.0 mm, the top face sheet fractures due to the local stretching of the face sheet.

Fig. 8

(a) Load versus deflection for indentation of the metal foam core sandwich beam specimen B-1 loaded at midspan by a flat punch, and (b) the effect of the punch shape on load versus deflection for indentation of the metal foam core sandwich beam specimens A-1 and B-1 loaded at midspan

Figure 8(b) illustrates the influences of punch shapes on the indentation behavior of the sandwich beams. The geometric parameters of the sandwich specimens A-1 and B-1 loaded by the flat punch and circular cylindrical punch are almost identical. It is clear that the load of the sandwich beam specimen B-1 loaded by the flat punch is higher than specimen A-1 loaded by the circular cylindrical punch in the post-yield stage for a given displacement. This can be explained by the fact that the flat punch results in formation of a larger contact area between the punch and the top face sheet. However, the increment is nearly constant when the deflection exceeds the thickness of the face sheet. It is possible that the effect of the punch shape on the indentation of sandwich beams is not obvious when the deflection exceeds the thickness of the face sheet.

Loaded at Non-midspan by a Punch

The analytical and experimental results of load-deflection curves of the indentation of specimen C-1 loaded at L ₁ = 20 mm by a circular cylindrical punch are shown in Fig. 9(a), and specimen C-2 loaded at L ₁ = 30 mm by a circular cylindrical punch are shown in Fig. 9(c). It is readily seen that the analytical predications for load-deflection curves agree well with the experimental results in Fig. 9(a) and (c). Figure 9(b) and (d) show the local deformation regions for local indentation of metal foam core sandwich beam specimens C-1 and C-2 loaded at the non-midspan by a circular cylindrical punch, respectively. The analytical predications based on equations (42), (45) and (47) are in good agreement with the observed results. Figure 10(a)–(d) show the deformation images for the indentation of the metal foam core sandwich beam specimen C-2 loaded at the non-midspan by a circular cylindrical punch. When the top face sheet has small deflection, the local deformation zone is firstly developed near the punch and grows with increasing the deflection until travelling to the left end of the beam.

Fig. 9

Indentation of the metal foam core sandwich beam specimen loaded at non-midspan by a circular cylindrical punch. (a) Load versus deflection for specimen C-1, (b) local deformation region versus deflection for specimen C-1, (c) load versus deflection for specimen C-2, and (d) local deformation region versus deflection for specimen C-2

Fig. 10

Evolution process of the circular cylindrical punch of indentation of metal sandwich beam specimen C-2 with h = 1.0 mm. (a) w ₀ = 2.0 mm, (b) w ₀ = 4.0 mm, (c) w ₀ = 6.0 mm and (d) w ₀ = 8.0 mm

Analytical predications for load-deflection curves of specimens D-1 and E-1 are shown in Fig. 11(a) to study the effect of punch shapes on the indentation of sandwich beams loaded at non-midspan. The geometric parameters of specimens D-1 and E-1 loaded by the flat punch and circular cylindrical punch are identical, as listed in Table 2. It is seen that the load of specimen D-1 loaded by the flat punch is bigger than that of specimen E-1 loaded by the circular cylindrical punch, and the increment of load between specimens D-1 and E-1 is same for a given displacement. The effect of punch shape on the indentation of sandwich beam loaded at non-midspan is similar to that loaded at midspan.

Fig. 11

(a) Effect of the punch shape on load versus deflection for indentation of specimens D-1 and E-1 loaded at non-midspan, (b) effect of the face sheet thickness on load versus deflection for indentation of specimens E-1 and E-2 loaded at non-midspan by a circular cylindrical punch, and (c) effect of the loading location on load versus deflection for indentation of specimens A-1, E-1, E-3 and E-4 loaded at non-midspan by a circular cylindrical punch

Table 2 Specimen dimensions of the indentation of sandwich beams loaded at non-midspan

Analytical solutions for the effect of face sheet thickness on the indentation behavior of the sandwich beam loaded at non-midspan by the circular cylindrical punch is shown in Fig. 11(b). The face sheet thicknesses of specimens E-1 and E-2 are 0.5 and 1.0 mm, and the other geometric parameters are same, as listed in Table 2. It is clear that the load increases with increasing the face sheet thickness for a given displacement, and the increment becomes big with increasing the displacement of punch.

Figure 11(c) shows analytical predications for the effect of loading location on the indentation of the sandwich beams loaded at non-midspan by the circular cylindrical punch. The geometric parameters of specimens A-1, E-1, E-3 and E-4 are almost same and listed in Table 2. It is seen that the load increases with decreasing of L ₁ for a given displacement in large deflections. It means that sandwich beams can bear more loads when the loading location is closer to the end of the sandwich beams for a given displacement of the punch. In the smaller deflection, the load of sandwich beams is almost same for four cases. Also, the load–displacement curve of specimen A-1 loaded at midspan is almost same as that of specimen E-1 loaded at L ₁ = 20 mm.

Concluding Remarks

Indentation of metal foam core sandwich beams is investigated experimentally and analytically. Indentation tests are conducted and the effects of the punch shape, face sheet thickness and loading location on the indentation are studied experimentally. According to the local deformation region and loading location, the analytical solutions are obtained for the large deflection of indentation of the sandwich beam loaded by a punch at any location of the span. The solutions can reduce to solutions for those loaded at midspan. The interaction of plastic bending moment and axial force in the local deformation regions of the face sheet is considered.

The results show that the effect of the loading location is to drive the deformation mechanism of the indentation. It is necessary to consider the interaction of plastic bending and stretching in the local deformation regions, and the membrane force plays an important role in large deflection of indentation of the sandwich beams when the punch deflection exceeds the face sheet thickness. The load of the sandwich beam loaded by a flat punch is higher than that loaded by a circular cylindrical punch, while the increment is nearly constant when the deflection exceeds the thickness of the face sheet. Sandwich beams can bear more loads when the loading location is closer to the left end of the sandwich beams for a given displacement of the punch.