Introduction

Residual stress can play a role in many failure mechanisms. Fatigue [1, 2] and stress corrosion cracking [3–6] are particularly sensitive to the presence of tensile residual stresses. Residual stresses can be difficult to predict because they are often the result of complex manufacturing processes, which makes their measurement important for both understanding failure [7, 8] and for validation of computational models of stress inducing processes [9–14].

Many methods exist for measuring residual stress, and all provide a limited portion of the stress tensor and have different limitations. For example, large samples or samples with difficult microstructure (e.g., texture, large grains, etc.) are difficult to measure with diffraction techniques [15]. Conversely, some mechanical stress release methods can have difficulty measuring large magnitude residual stresses [16] especially when the stresses become large when a part is being sectioned [17, 18]. One mechanical stress release method, the contour method, has been found to be especially useful since it inherently measures a map of residual stress over a cross-section. The contour method measures the change in stress when cutting a part in half (at the cut plane). Since the cut has created a free surface, the stress normal to the cut plane must be zero after the cut, so that the contour method completely determines the out-of-plane stress component that existed at the cut plane, prior to cutting. Pagliaro, Prime, et al. [19] further showed that the contour method also determines the change in stress for the in-plane normal components of residual stress at the cut plane. Therefore, additional measurements of in-plane stresses on the cut surface can be used to determine the original in-plane stresses. The first measurement of this type was reported in [19] and used x-ray diffraction to measure the remaining in-plane stress at the contour cut plane (after the contour measurement). Our recent work has extended this methodology to use only mechanical stress release methods [20, 21], but that extension lacks validation.

This paper describes an approach for mechanical biaxial residual stress mapping and verifies the fundamental mechanics with a numerical experiment. The approach is then carried out on a quenched bar, and the residual stresses determined are validated with complementary measurements.

Methods

Measurement Approach

The new measurement approach comprises multiple mechanical stress release measurements, in conjunction with superposition, to determine multiple stress components in the part at a single plane of interest. Each mechanical stress release measurement will change the part configuration (i.e., change the geometry of the part) and each configuration will be denoted with a capital letter (e.g., A, B, C). The residual stress tensor in each configuration, at the plane of interest, is indicated with a superscripted σ (e.g., σA). The biaxial stress mapping approach determines the out-of-plane stress, σzz, and one component of the in-plane stress, either σxx or σyy, at the plane of interest.

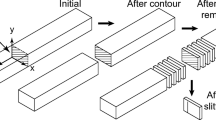
The configuration changes comprising the new approach are shown in Fig. 1(a) and include cutting the part in half at the plane of interest (configuration A to B) and removing a thin slice (configuration B to C) adjacent to the plane of interest. Assumed coordinates are also shown in Fig. 1, with x and y lying in the plane of interest, and z along the length. Using superposition, the stress in configuration A can be found with

Fig. 1
figure 1

Stress decomposition diagrams. (a) The original stresses (σA, all stress components, at the plane of interest) are equal to the stress release from cutting the part in half (σi), the stress released when removing a thin slice (σii), and the stress remaining in the slice (σC). (b) The original stress (σA) is equal to the stress remaining in a thin slice (σC) plus the effect of total longitudinal stress on the thin slice (σA(z))

Full size image
$$ {\sigma}^{\mathrm{A}}\left(x,\;y,\;0\right)={\sigma}^i\left(x,\;y,\;0\right)+{\sigma}^{\mathrm{B}}\left(x,\;y,\;0\right)={\sigma}^i\left(x,\;y,\;0\right)+{\sigma}^{ii}\left(x,\;y,\;0\right)+{\sigma}^C\left(x,\;y,\;0\right) $$
(1)

where σ with a superscripted Roman numeral denotes the stress released by a change of configuration, defined as the stress in the current configuration subtracted from the stress in the prior configuration (e.g., σi  = σA – σB). Although equation (1) applies at all spatial locations, our concern is only the plane of interest at z = 0. The contour method is used to determine σi, and this measurement completely determines the out of plane component (σzz) of σA, since the plane of interest is a free surface in configuration B. The slitting method is used to determine one in-plane component of σC.

As shown in Fig. 1(b), σA can be decomposed so that

$$ {\sigma}^{\mathrm{A}}\left(x,\;y,\;0\right)={\sigma}^{\mathrm{A}(z)}\left(x,\;y,\;0\right)+{\sigma}^C\left(x,\;y,\;0\right) $$
(2)

where σA(z) is the effect of the out-of-plane stress on the thin slice of configuration C, which can be determined using σzz found by the contour method. Furthermore, σA(z) is a theoretical construct that gives the change in stress that would occur in a thin slice, if the out-of-plane stress were removed; and it is the sum of σi and σii. Using equation (1) and (2), only σi and σC need to be measured to find σA, thus there is no need to directly measure σii. A locally smooth stress field is requited so that σC(x, y, 0) can be assumed equal to an average of σC(x, y, z) through the slice thickness, as would be measured with slitting.

Numerical Verification

As a first step, it is useful to verify the biaxial mapping approach using a numerical simulation. The goal of the simulation is to show that the original stress state, σA, is equal to the stress remaining in a thin slice, σC, and the effect of the out-of-plane stress on the slice, σA(z).

The verification simulations comprise finite element analysis of three geometries, one for each configuration A, B, and C. The finite element computations used commercial finite element software [22]. A block was used for configuration A, with a cross-section of 50.8 mm × 76.2 mm and a length of 144.4 mm, with rounded corners of 5 mm radius. The model was 72.2 mm long, using a symmetry boundary condition at the mid-length. The model assumed an elastic modulus of 71.7 GPa and a Poisson’s ratio of 0.33, which are typical of aluminum alloy. The mesh was highly refined with in-plane node spacing of 0.5 mm and a biased node spacing along the length, varying from 0.5 mm at the symmetry plane to 4 mm at the free end of the block. The total number of eight-node brick elements used was around 800,000. The stress state in each configuration results from a bivariate uniaxial thermal strain field

$$ \begin{array}{c}\hfill {\varepsilon}_{zz}^{th}\left(x,\;y,\;z\right)=-0.0075f(x)\;g(y)\hfill \\ {}\hfill f(x)=\frac{1}{2} \cos \left(\frac{\pi }{3}\left(\frac{8x}{W}-1\right)\right),x\in \left[W/8,\;7W/8\right]\hfill \\ {}\hfill g(y)=\frac{1}{2} \cos \left(\frac{\pi }{3}\left(\frac{8y}{H}-1\right)\right),y\in \left[H/8,\;7H/8\right]\hfill \end{array} $$
(3)

with all other components of the thermal strain zero. Here the coordinate origin is at the lower left corner of the cross-section, with W the maximum dimension along x (76.2 mm), and H the maximum dimension along y (50.8 mm). The field is chosen to have a complex shape including discontinuities near the surface to rigorously test the measurement approach.

To determine stress in configuration B, the symmetry boundary condition was removed from the configuration A model. To determine stress in configuration C, all elements farther than 5 mm from the symmetry plane were removed, leaving a 5 mm slice. Stress from these three models provides known values of σA, σB, and σC.

To find σA(z), a similar model was used, having a length 2.5 mm, and a symmetry boundary condition at the mid-length. The in-plane mesh was the same as for configuration A, and there were five elements through the thickness, resulting in roughly 77,000 eight-node linear brick elements. The original longitudinal stress in the block, along the mid-length, was applied as a traction boundary condition to the slice model to find σA(z). To verify the mapping approach, σA will be compared to (σC + σA(z)), to verify equation (2).

Validation

Biaxial mapping

The experimental validation requires two sets of measurements; the first is the biaxial measurement itself and the second additional measurements to confirm those results. Measurements were done on an aluminum bar that was cut from 51.2 mm (2.02 in. thick, rolled 7050 aluminum plate to form a bar with a cross section 51.2 mm (2.02 in. thick by 77.8 mm (3.06 in. wide, and a length of 304.8 mm (12 in), as shown in Fig. 2. The original plate was in the T7451 condition, being over-aged and stress relieved by stretching. The bar had an additional heat treatment performed to introduce a higher stress, that was representative of that used for the T74 temper [23]. The heat treatment consisted of solution heat treatment at 477 °C for 3 h, immersion quenching in room temperature water with 16 % polyalkylene glycol (Aqua-Quench 260), and a dual artificial age at 121 °C for 8 h then 177 °C for 8 h.

Fig. 2
figure 2

Dimensioned diagram of the measurement article with the location of measurement planes (W = 77.8 mm, H = 51.2 mm, and L = 304.8 mm). The biaxial measurement plane is at z = 0 mm and the three confirmation measurements (V1, V2A and V2B) are at x = 38.9 mm, 19.45 mm, and 58.35 mm. Three slices were removed adjacent to the plane of interest by cutting at z = −5 mm (S1), −10 mm (S2), and −15 mm (S3). Each slice has a slitting measurement at the mid-width of the slice and at ±10 mm (S1), ±15 mm (S2), and ±20 mm (S3) from the mid-width

Full size image

The biaxial mapping approach consists of a measurement of σzz with the contour method [24], removing three thin slices, each 5 mm thick, adjacent to the contour measurement cutting plane, and measuring the remaining σxx in the slices with the slitting method [25].

The theoretical underpinning of the contour method has been established earlier by Prime [26] and detailed experimental steps have been established by DeWald and Hill [27]; a brief summary of the experimental procedure is given here, which followed the practical advice in [24]. The specimen is cut in two using a wire electric discharge machine (EDM) along the plane of interest, at the mid-length of the bar (Fig. 2). Cutting is performed with the specimen rigidly clamped to the EDM frame. Following cutting, the profile of each of the two opposing cut faces is measured with a laser scanning profilometer to determine the surface height normal to the cut plane as a function of in-plane position. The surface height data are taken on a grid of points with spacing of 200 μm × 200 μm, so that there are roughly 96,000 data points for each surface. The two surface profiles are then averaged on a common grid, and the average is fit to a smooth bivariate Fourier series [28], where the number of coefficients in the surface is determined by the choice of the maximum fitting parameters (m, n) for the (x, y) spatial dimensions. A level of smoothing is determined by choosing the fitting parameters (m, n) during data reduction.

The residual stress on the contour plane is found with a linear elastic finite element analysis that applies the negative of the smoothed surface profile as a displacement boundary condition on the cut plane. The finite element mesh used eight-node, linear displacement brick elements with node spacing of 1 mm on the cut face, and node spacing normal to the cut face that increased with distance away from the cut, being 1 mm at the cut face and 5 mm at the end of the bar. The mesh was sufficiently refined such that when the node spacing is halved there is negligible change of stress. The model used an elastic modulus of 71.0 GPa and a Poisson’s ratio of 0.33.

To find the remaining transverse stress in the three removed slices, slitting (also known as the crack compliance technique) was used. The theoretical underpinning of the slitting measurements has been given by Prime [29] and best experimental practices have been given by Hill [25]. Slitting measurements consisted of incrementally cutting through the sample (along y) using a wire EDM while measuring strain at the back face of the cut plane for each cut increment. The stress normal to the cut plane is then determined from measured strain vs. cut depth data using an elastic inverse, with smoothing of the stress profile provided by Tikhonov regularization [30]. The elastic inverse uses a compliance matrix that provides the strain that would occur at a specified set of cut depths for stress given by an assumed set of basis functions. Details of the compliance matrix development are given in [31]. The compliance matrix development uses a finite element model of the part geometry with 2D bilinear plane strain elements and a stiffness correction scheme developed by Aydiner and Prime [32] to accurately reflect the finite thickness of the slice.

Since the goal of this work is to determine a map of the stress, multiple slitting measurements are needed, and were made in a set of three slices. The three slices, each 5 mm thick, were removed adjacent to the contour measurement plane by cutting with wire EDM at z = −5 mm, −10 mm, and −15 mm. The slitting measurements provided σxx(y) and were made at x locations symmetric about the midwidth, x m  = 38.9 mm. Measurement locations in the first slice were at x m and at x m  ± 10 mm; measurement locations in the second slice were at x m and at x m  ± 15 mm; and, measurement locations in the third slice were at x m and at x m  ± 20 mm.

We assume that the stress near the plane of interest is invariant of z, so that the stresses determined in different slices can be collapsed onto a single measurement plane. Since we are performing multiple slitting measurements on each slice, the effect of previous slitting measurements on the current measurement is needed and is found with a supplemental stress analysis. A detailed description of the supplemental stress analysis is given in [33] and consists of applying the measured stress from a previous slitting measurement as a traction boundary condition at the prior measurement plane, in a finite element model of the part, and extracting the resulting stress at the current measurement site. The total stress, at a given plane is a superposition of the stress measured from slitting and the effect of any prior measurement, determined with a supplemental stress analysis.

To find σA(z), the longitudinal stress field found with the contour method is applied as a traction boundary condition to both in-plane (x-y) faces of a finite element model of the thin slice used in the slitting measurements. The finite element mesh used eight-node, linear displacement brick (C3D8) elements with node spacing of 1 mm on the cut face, and five elements through the thickness. The material behavior was elastic, using the properties stated earlier.

Biaxial Mapping Uncertainty

An uncertainty estimate for each step of the biaxial measurement provides an assessment of the robustness of the measurement approach, to check that the cumulative uncertainty doesn’t become unreasonably large. The uncertainty for the contour method is found using the approach described in [34], which accounts for two uncertainty sources that are present in every contour measurement, the uncertainty associated with noise in the displacement profiles, called the displacement error, and the uncertainty associated with selecting an analytical form to smooth the displacement profile, called the model error. The model error definition takes the standard deviation of the stresses determined from five different levels smoothing

$$ {U}_{model,\left(m,n\right)}\left(x,y\right)=std\left({\sigma}_{\left(m,n\right)}\left(x,y\right),{\sigma}_{\left(m+1,n\right)}\left(x,y\right),{\sigma}_{\left(m,n+1\right)}\left(x,y\right),{\sigma}_{\left(m-1,n\right)}\left(x,y\right),{\sigma}_{\left(m,n-1\right)}\left(x,y\right)\right) $$
(4)

where U model.(m,n)(x, y) is the model error as function of in-plane position and σ(m,n)(x, y) is the contour stress, both for a choice of fitting parameters, and std is the standard deviation operator.

The displacement error is found using a Monte Carlo approach. Uncertainty in the displacement field is estimated to be 3 μm, which is superposed as normally distributed noise with the measured displacement field. After noise is added to the data, standard contour data processing is performed. The standard deviation of five contour measurements with “noisy” data is taken as the displacement error for a chosen set of fitting parameters (m, n). Additional “noisy” simulations were performed to confirm the displacement error converged with five simulations. The two error sources are combined using

$$ {U}_{contour,\left(m,n\right)}\left(x,y\right)=\sqrt{{U^2}_{model,\left(m,n\right)}\left(x,y\right)+{U}_{disp,\left(m,n\right)}^2\left(x,y\right)} $$
(5)

where U contour,(m,n)(x, y) is the total uncertainty of the contour measurement and U disp,(m,n)(x, y) is the displacement error, each for a given set of smoothing parameters (m, n) and as functions of in-plane spatial position (x, y). Since the contour measurement is the only contributor to the out of plane stress, the uncertainty in σzz for the original configuration is given by the contour uncertainty (i.e., U zz (x, y) = U contour,(m,n)(x, y)).

The uncertainty analysis for slitting measurements followed the procedure given in [35]. Since regularized unit pulses were used as the basis functions, only the random uncertainty term described in [35] was used, and was taken as the maximum of either the misfit between measured strain and fitted strain, or 2 με. The uncertainty in the corrections for prior slitting measurements was estimated using a Monte Carlo approach. The prior stresses were assumed to have normally distributed noise, corresponding to their uncertainty. The error was then taken as the standard deviation of the results of five such Monte Carlo simulations. The total uncertainty was found using

$$ {U}_C\left(x,y\right)=\sqrt{{U^2}_{slitting}\left(x,y\right)+{U^2}_{correction}\left(x,y\right)} $$
(6)

where U C (x, y) is the uncertainty in σC, U slitting (x, y) is the uncertainty from the slitting measurements, and U correction (x, y) is the uncertainty in the corrections that accounted for the prior slitting measurement.

The uncertainty in σA(z), U A(z) (x, y), was also found using Monte Carlo. The uncertainty was estimated by taking the standard deviation of the results of σA(z) when the underlying longitudinal stress had normally distributed noise with a standard deviation corresponding to the uncertainty in σzz.

The two uncertainty sources for the transverse stress (those relating to σC and σA(z)) are combined using

$$ {U}_{xx}\left(x,y\right)=\sqrt{U_C^2\left(x,y\right)+{U}_{A(z)}^2\left(x,y\right)} $$
(7)

where U xx (x, y) is the total uncertainty in σxx as a function of in-plane spatial position (x, y).

Confirmation Measurements

Confirmation measurements are required to validate the biaxial mapping approach. To do so, σxx is measured at specific planes using the contour method on configuration B, the half-length bar. Three contour measurements are made at planes V1, V2A, and V2B shown in Fig. 2. The first validation measurement, at plane V1, is made at x = 38.9 mm and the second and third measurements are made at x = 19.45 mm (plane V2A) and 58.35 mm (plane V2B). The first validation measurement aligns with measurements from the biaxial map, but the second and third measurements are not exactly aligned with the measurement locations from the biaxial map (i.e., slitting measurements were offset in x by 0.55 mm). The transverse stress from the biaxial mapping result will be interpolated from nearby data to evaluate stresses at the same positions. Since the stress in the bar was induced with quenching, it is expected that the stress should be constant along the length of the bar, except near the ends.

The confirmation measurements and uncertainty estimation followed the methods for contour measurement described above. The effect of the measurement at plane V1 on stress at planes V2A and V2B was accounted for using superposition. The confirmation contour measurements are cut along the z direction, and determine σ xx (y, z) at a set of points with approximately 1 mm in-plane spacing. Since the stress is due to quenching, it is expected to be invariant with z, except near the ends of the half-length bar (at z = -152 mm and 0 mm) where σ xx would be affected by the free surface condition. To compare the results of the confirmation contour measurements with results from the biaxial mapping, we report σ xx (y) as an average of results at the set of z-positions farther than one thickness from the free end of the half-length bar (i.e., for −100 ≤ z ≤ -52), rather than reporting results for an arbitrarily chosen value of z. At a given value of y, the uncertainty of the confirmation measurement is taken to be the standard deviation of the values from which the average was determined; at nearly all locations, this uncertainty exceeded the underlying contour method uncertainty.

Results

Numerical Verification

The numerical verification results are shown in Fig. 3. The results confirm that σA is the sum of σC and σA(z). Line plots of the results along the horizontal direction at the mid-vertical dimension can be seen in Fig. 4. As the results show, the sum of σC and σA(z) equals σA, but interestingly σC and σA(z) have significantly different magnitudes for σxx and σyy. The contribution of σC to σzz is nearly zero as expected, since the slice is thin, except in a small region where the stress field is discontinuous. For σxx and σyy, σC and σA(z) are both major contributors to the total.

Fig. 3
figure 3

Contour plots of the initial stress (σA) (top row), the effect of the longitudinal stress in the slice (σA(z)) (second row), the stress remaining in the slice (σC) (third row), and the sum of σA(z) and σC (bottom row) for each stress component

Full size image
Fig. 4
figure 4

Line plots comparing the contribution of the stresses remaining in the slice (σC), the effect of the longitudinal stress on the slice (σA(z)), and their sum, to the original stress (σA) for (a) longitudinal stress, (b) short transverse stress, and (c) long transverse stress

Full size image

Validation

Biaxial mapping

The raw surface profiles from the contour measurement can be seen in Fig. 5. The surface profiles from each side of the cut show similar distributions, which indicate good clamping during cutting. The fitting parameters for the contour measurement selected during data processing are (m, n) = (1, 1). The average and fit surface profiles have shapes similar to the measured surface profiles. Line plots of the surface profile data (Fig. 6) show that the fit surface appropriately represents the underlying data.

Fig. 5
figure 5

Measured surface displacement from the contour method measurement. (a) Surface “1”, (b) surface “2”, (c) averaged surface, and (d) fitted surface

Full size image
Fig. 6
figure 6

Measured surface displacements along the (a) horizontal direction at mid-vertical dimension and (b) vertical direction at mid-horizontal dimension. Note: the data from surface 1 is offset by 30 μm and the data from surface 2 is offset by −30 μm, so that the average and fit are also visible on the same plot

Full size image

The longitudinal stress and uncertainty can be seen in Fig. 7. The stress has a paraboloid distribution with compressive stresses along the exterior (minimum of −153 MPa) and tensile stresses toward the center (maximum of 157 MPa), as would be expected in a quenched bar [36]. The uncertainty is low away from the cross section boundaries (mostly below 8 MPa) with a maximum uncertainty at the top and bottom edges of 21 MPa at a 68 % confidence interval.

Fig. 7
figure 7

Measured longitudinal (a) stress and (b) uncertainty (68 % confidence interval)

Full size image

The measured strain for the slitting measurement at x = 18.9 mm is shown in Fig. 8(a), and the calculated stress is shown in Fig. 8(b). The stress profile is roughly parabolic, as would be expected from a rapid quench. The strain data and stress results at other planes resemble those at x = 18.9 mm.

Fig. 8
figure 8

(a) Measured strain and (b) calculated stress for the slitting measurement at x = 18.9 mm

Full size image

The transverse stress and uncertainty from the biaxial map can be seen in Fig. 9. The stresses remaining in the slice, σC, have compressive stresses along the exterior (minimum of −90 MPa) and tensile stresses toward the center (maximum of 55 MPa). The uncertainty is low, with most points below 4 MPa and a maximum of 8 MPa. The effect of the longitudinal stress, σA(z), has a paraboloid distribution, with compressive stresses along the exterior (minimum of −70 MPa) and tensile stresses toward the center (maximum of 33 MPa). The uncertainty is also very low, with most points below 1 MPa and a maximum near the top and bottom edges at 6 MPa. The total transverse stress also has a paraboloid distribution, with compressive stresses along the exterior (minimum of −160 MPa) and tensile stresses toward the center (maximum of 90 MPa), which is expected for quenched samples. Line plots of the two contributions to the total transverse stress at a horizontal position of 18.9 mm can be seen in Fig. 10 (same spatial position as the plot shown in Fig. 8). The plot shows that both contributions are significant parts of the total.

Fig. 9
figure 9

Long transverse stress: (a) remaining in slice, (b) effect of longitudinal stress on the thin slice, and (c) total, with (d) through (f) showing corresponding uncertainty, at a 68 % confidence interval

Full size image
Fig. 10
figure 10

Stress and uncertainty of the two contributions to the transverse stress measurement and the total (σA), at a horizontal position of 18.9 mm. Uncertainty is shown as dotted lines

Full size image

Confirmation Measurements

The results of the three confirmation measurements and their uncertainties can be seen in Fig. 11. The fitting parameters for the contour measurement at x = 38.9 mm, 19.45 mm, and 58.35 have (m, n) = (2, 1), (3, 1), and (3, 1), respectively. The results for the first confirmation measurement at x = 38.9 mm shows a roughly parabolic distribution through thickness (away from the edges), with compressive stresses along the exterior (minimum of −160 MPa) and tensile stresses toward the center (maximum of 75 MPa). The uncertainty for this measurement has a roughly similar distribution as that found in the contour measurement used for the biaxial map. The uncertainty is largest at the edges (25 MPa), but is fairly low over most of the interior (below 10 MPa). The stress for the two secondary confirmation measurements at horizontal positions of 19.45 mm and 58.35 mm have essentially the same measured stress as each other and both have very similar distributions to the measurement at x = 38.9 mm, but with lower magnitudes (minimum of −100 MPa and maximum of 55 MPa). The uncertainty of both measurements is also very similar to each other, with very low uncertainty in the interior (under 2 MPa), and maximums at the top and bottom edges of 9 MPa.

Fig. 11
figure 11

Measured transverse stress and uncertainty (68 % confidence interval) at x = 38.9 mm ((a) and (b)); x = 18.9 mm ((c) and (d)); and x = 58.9 mm ((e) and (f))

Full size image

The comparison of the transverse stress from the biaxial map and from the confirmation measurements can be seen in Fig. 12. The results show that the confirmation measurements agree well with the biaxial mapping at all three intersecting planes. The comparison at x = 38.9 mm has the largest disagreement of the three, with a maximum difference of 25 MPa near y = 50 mm. However, at most points, the error bars from the two different measurement techniques are close to one another, so differences in technique are not statistically significant. Overall, there is excellent agreement between the two methods, validating the biaxial mapping approach.

Fig. 12
figure 12

Line plots comparing the biaxial measurement of the transverse stress and the confirmation measurement at x = (a) 38.9 mm, (b) 19.9 mm, and (c) 58.9 mm

Full size image

Discussion

One point of concern in developing the biaxial mapping approach is that the superposition of multiple measurements could result in poor precision. However, we have found that not to be the case. The uncertainty in the transverse stress (of the biaxial map) is low, under 10 MPa, in large part because slitting has excellent precision [35, 37]. To contrast, the longitudinal stress, which consisted of a single contour measurement, had somewhat larger uncertainties, up to 20 MPa. The 20 MPa uncertainty found in the contour measurement will affect the uncertainty in σxx A(z), but to smaller degree because the effect of the longitudinal stress on the axial stress in the thin slice is always smaller than the longitudinal stress itself. The uncertainty found here compares favorably with uncertainties typical of other residual stress measurement techniques [38].

The new biaxial mapping method has some advantages over other established residual stress measurement techniques. For example, biaxial mapping measurements in welded components have been shown to be especially useful [20, 39, 40]. In welds, the primary advantage derives from the use of mechanical stress release, which is largely unaffected by the microstructural issues commonly present in welds that very often complicate diffraction based measurements. Furthermore, the use of slitting brings the excellent precision offered by that technique, as compared to somewhat poorer precision of other methods that could be used for mapping stress in the thin slice [41].

Another issue that is relevant for biaxial mapping is the optimal selection of slitting measurement locations. If measurements in the slice are too close to one another, the precision of the measurement decreases. A recent study has addressed this topic [33] and found the minimum distance between slitting planes for good measurement precision is 0.2 times the part thickness.

Summary

A biaxial residual stress mapping approach using mechanical stress release methods was described. The measurement consists of decomposing the initial residual stress into the stress remaining in a thin slice and the effect of the longitudinal stress on that slice. The longitudinal stress is found using the contour method. The effect of the longitudinal stress on a thin slice is found using a finite element computation. The transverse stress remaining in the slice is found using several slitting measurements. Numerical simulations were performed to verify the measurement concept.

Physical experiments were performed to find a biaxial map of longitudinal and transverse stress in a quenched aluminum bar. Both the longitudinal and transverse stresses were found to have a paraboloid distribution, with tensile stress in the center of the cross-section and compressive stress along the edges, which agrees with the residual stress field typical of quenching. The minimum and maximum of the longitudinal stresses are −153 and 157 MPa and of the transverse stress are −160 and 90 MPa. The uncertainty in the longitudinal stress was found to be low over most of the interior, under 8 MPa, with higher uncertainty toward the edges, with a maximum of 21 MPa. The uncertainty for the transverse stress had several contributing error sources, but is very low, with maximum uncertainty of 6 MPa.

The results of the biaxial mapping measurement were compared to confirmation measurements of the transverse stress at three planes. The good agreement with the confirmation measurements validates the biaxial mapping approach.