Response Mixture Modeling: Accounting for Heterogeneity in Item Characteristics across Response Times

Abstract

In item response theory modeling of responses and response times, it is commonly assumed that the item responses have the same characteristics across the response times. However, heterogeneity might arise in the data if subjects resort to different response processes when solving the test items. These differences may be within-subject effects, that is, a subject might use a certain process on some of the items and a different process with different item characteristics on the other items. If the probability of using one process over the other process depends on the subject’s response time, within-subject heterogeneity of the item characteristics across the response times arises. In this paper, the method of response mixture modeling is presented to account for such heterogeneity. Contrary to traditional mixture modeling where the full response vectors are classified, response mixture modeling involves classification of the individual elements in the response vector. In a simulation study, the response mixture model is shown to be viable in terms of parameter recovery. In addition, the response mixture model is applied to a real dataset to illustrate its use in investigating within-subject heterogeneity in the item characteristics across response times.

1 Introduction

Many of the current approaches to the analysis of responses and response times assume local independence of the data conditional upon the latent variables in the model (e.g., Ferrando & Lorenzo-Seva, 2007a, b; Molenaar, Tuerlinckx, & Van der Maas, 2015; Ranger, & Ortner, 2011; Thissen, 1983; Van der Linden, 2007; Tuerlinckx & De Boeck, 2005; Van der Maas, Molenaar, Maris, Kievit, & Borsboom, 2011). Specifically, three types of local independence can be distinguished in these models (Bolsinova & Maris, 2016; Bolsinova & Tijmstra, 2016; Ranger & Ortner, 2012; Van der Linden, 2009; Van der Linden & Glas, 2010). That is: (1) local independence between the responses; (2) local independence between the response times; and (3) local independence between the responses and the response times.

Violations of assumptions (1) and (2) are relatively well understood as they are similar to the local independence assumption commonly posed in generalized linear latent variable models (Bartholomew, Knott, & Moustaki, 2011; Mellenbergh, 1994). That is, a residual dependence between two items may indicate that an additional skill is involved in solving these two items but which is not involved in the other items of the same latent variable. For example, it is a well-established finding that the ‘block design’ and ‘object assembly’ subtests of the Wechsler Adult Intelligence Scale (WAIS-III) have a residual dependence while they both involve the latent variable ‘perceptual organization’ (see, e.g., Dolan et al., 2006). This result can be explained by the motoric component involved in both tasks but not in the others (matrices, picture arrangement, and picture completion). For the response time model, similar explanations for the violation of local independence are possible. For instance, if two items of an arithmetic test both require a large text to be read in order to answer the items, a residual dependency may arise between the response times of these items because of individual differences in reading speed.

In the present paper, we focus on assumption (3), that is, the assumption of local independence between the responses and responses times. In applications to large-scale computerized assessments, Van der Linden and Glas (2010) found this type of local independence to be violated in 56 of the 96 items and Bolsinova and Maris (2016) found this type of local independence to be violated in 25 of the 30 items. Although these dependencies may be small, question arises how such a systematic departure from local independence may occur.

A conditional association between the responses and response times of a given item arises if the item difficulties of the item responses are heterogeneous with respect to the response times (Bolsinova, Tijmstra, Molenaar, & De Boeck, 2017). Similarly, the item discriminations may not be invariant across the response time variable. Thus, the characteristics of the items may not be the same for responses that differ in their response time. Heterogeneity might arise in the item responses if subjects resort to different response processes when solving the test items. These differences may be within-subject effects, that is, a subject might use a certain process on some of the items and a different process with different item characteristics on the other items. If the probability of using one process over the other process depends on the subject’s response time, within-subject heterogeneity of the item characteristics across the response times arises. Note that this is a within-subject effect: If the effect is between-subjects, that is, subjects differ in the process that is used during the test, these individual differences are captured in the latent ability and latent speed variable. Within-subject differences in the use of response processes may occur in, for instance, an arithmetic test where subjects solve some of the items by retrieving the answer from memory and other items are solved by actually performing the requested operation, see Grabner et al. 2009. In addition, Carpenter, Just, and Shell (1990) used eye tracking and verbal protocols to show that subject use different response processes in the different items of the Raven progressive matrices test. Other phenomena that indicate within-subject differences in response processes during the test include guessing (Schnipke, & Scrams, 1997), item preknowledge (McLeod, Lewis, & Thissen, 2003), and post-error slowing (Rabbitt, 1979). In all of these examples, heterogeneity in the data will arise across the response times.

A suitable procedure to account for the heterogeneity of the item responses with respect to the response times is the IRT tree model (De Boeck & Partchev, 2012; Jeon & De Boeck, 2016). In this procedure, prior to modeling, the response times are dichotomized into fast responses and slow responses by an item median split or a person median split (Partchev & De Boeck, 2012; DiTrapani, Jeon, De Boeck, & Partchev, 2016). Subsequently, to these data, a model with three latent variables is fit: a latent speed variable, a latent fast ability variable, and a latent slow ability variable. Item characteristics of the fast and slow responses can then be compared across the fast and slow ability variables.

Although valuable, the IRT tree approach requires the continuous response time data to be dichotomized. This has two important implications. First, it makes the approach deterministic. As a result, it is not straightforward to test statistical hypothesis about the exact cut-off point to use to split the response times into two categories. Main problem is that using a different cut-off point will result in a different dataset which invalidates model comparison using likelihood based fit indices like AIC or BIC. In addition, the ad hoc approach of trying out different cut-offs to infer the most optimal cut-off is from our perspective a statistically suboptimal procedure as the same data are used repeatedly. Second, dichotomization of the response times implies that the amount of information concerning individual differences in the response times is reduced (see, e.g., Cohen, 1983; MacCallum, Zhang, Preacher, & Rucker, 2002) while one of the motivations to add the response times is to increase measurement precision (Van der Linden, Entink, & Fox, 2010).

Therefore, in this paper, we propose an explicit statistical model to account for the heterogeneity of the item characteristics with respect to the response times. The model is referred to as a response mixture model as—contrary to the traditional mixture models where each item response vector is classified into one of the classes—each element of the response vector is classified into one of the classes. The idea of response classification instead of response vector classification has previously been adopted to account for rapid guessing (Schnipke, & Scrams, 1997; Wang & Xu, 2015; Wang, Xu, & Shang, 2016) and to account for zero-inflated responses in repeated measures count data (e.g., Hall, 2000; Min & Agresti, 2005). In addition, the three-parameter model (Birnbaum, 1968) can be seen as a model that classifies responses. That is, in the three-parameter model, the probability of a correct response is modeled using a two-parameter model in one class and a uniform guessing probability in the other class.

We account for possible sources of heterogeneity in the item characteristics with respect to the response times by imposing two item-specific latent classes to underlie the responses of each item. First, the classes are allowed to differ in their item characteristics (discrimination and difficulty). Next, class membership is regressed on the response times to test whether the responses with a relatively large response time are more likely to belong to one class (a ‘slower class’) and the responses with a relatively small response time are more likely to belong to the other class (a ‘faster class’). Doing so avoids the dichotomization of the response times in the IRT tree approach above, and the response classification is inferred from the data instead of by a deterministic ad hoc cut-off.

The aim of the present paper is to derive, test, and illustrate the response mixture modeling approach. We use the response mixture approach mainly in an ‘indirect application’ (e.g., Yung, 1997). That is, similarly to the indirect application of traditional mixture models, the two classes are not necessarily substantively meaningful. They are rather used as a statistical tool to detect the heterogeneity in the responses with respect to the response times. That is, there may be more classes in the data, or the difference in the item characteristics across response times might be continuous (see Bolsinova, Tijmstra, & De Boeck, in press). However, the two classes imposed in the response mixture model are used to statistically capture the most significant part of the heterogeneity in the data. Such an application might be valuable to test the assumption of homogeneity as imposed in the modeling approach discussed above or to detect aberrant responses (e.g., Van der Linden, & Guo, 2008).

The outline of this paper is as follows: First, a general item response theory approach to response time analysis is outlined which characterizes many of the current approaches. Next, the response mixture model for responses and response times is derived using this general model. Then, the viability of the response mixture model is studied in a simulation study. Next, the model is applied to a real dataset pertaining to arithmetic ability to test for heterogeneity in the item characteristic across response times. We end with a discussion of the possibilities and limitations of the present approach.

2 A Response Mixture Model for Responses and Response Times

Many of the existing item response theory models for responses and response times can be characterized by a separate measurement model for the responses and a separate measurement model for the response times which are connected in a certain way. For instance, Thissen (1983) used a two-parameter item response theory model for the responses and a linear factor model for the log-transformed response times, and connected the models by allowing linear cross-loadings from the response times on the latent ability variable. Ferrando & Lorenzo-Seva (2007a; 2007b) proposed a comparable model but with nonlinear cross-loadings. In addition, Van der Linden (2007) used a three-parameter model and a linear factor model, but connected both measurement models by correlating the random subject and random item effects across the models. Also, mathematically more complex process models like the diffusion-based item response theory model (Tuerlinckx & De Boeck, 2005; Van der Maas et al., 2011) can be seen as consisting of a separate model for the responses (which is, under some assumptions, equivalent to a two-parameter item response theory model) and a separate model for the response times.

To formulate the response mixture model, we also use the idea of separate measurement models for the responses and response times. For the response times, we follow Van der Linden (2007) and use a normal linear homoscedastic factor model, that is,

$$\begin{aligned} \hbox {ln}\left( {T_{pi}} \right) =\lambda _i -\tau _p +\varepsilon _{pi} \end{aligned}$$

(1)

Because the raw response times $\hbox {T}_{\mathrm{pi}}$ for subject $p = 1, {\ldots }, N$, on item $i = 1, {\ldots }, n$, are bounded by zero and skewed (Luce, 1986), a log-transformation is used to make the assumption of linearity and homoscedasticity in Eq. 1 more plausible. Other possible transformations include the square root transformation and the reciprocal transformation (see Rummel, 1970 for more options). In Eq. 1 $\lambda _{i}$ is the main effect of the item on the log-response time distribution (time intensity parameter), $\tau _{p}$ is the main effect of the subject on the log-response time distribution (subject speed parameter) that accounts for some subjects being on average faster than others. Finally, $\varepsilon _{pi}$ is the error with VAR($\varepsilon _{pi}) = \sigma _{\varepsilon i}^{2}$.

For the responses, we adopt the idea by Partchev and De Boeck (2012) who specified a separate measurement model for the faster responses and a separate measurement model for the slower responses. Partchev and De Boeck separated faster responses from slower responses by a median split of the item response times. Next, the faster and slower measurement models were fit as a multidimensional item response theory model to the responses and the categorized response time data. In the present paper, we avoid the necessity of dichotomization of the response time data by formulating a general measurement model for the responses which consists of a mixture of two measurement models, that is

$$\begin{aligned} P\left( {X_{pi} =1|\theta _p ,\alpha _{0i} ,\alpha _{1i} ,\beta _{0i} ,\beta _{1i}} \right)= & {} {\pi }_{pi} P\left( {X_{pi} =1|\theta _p ,\alpha _{0i} ,\beta _{0i}} \right) \nonumber \\&+\left( {1-_{pi}} \right) P\left( {X_{pi} =1|\theta _p ,\alpha _{1i} ,\beta _{1i}} \right) . \end{aligned}$$

(2)

where $\pi _{pi}$ is the mixing proportion which denotes the probability that the response by subject p to item i follows the measurement model in class 0, $\pi _{pi}$ = P($\hbox {C}_{pi} = 0$) where $\hbox {C}_{pi} = 0$, 1, is the latent class variable underlying item i. The measurement models for classes $\hbox {C}_{pi} = 0$ and $\hbox {C}_{pi} = 1$ in Eq. 2 are given by, respectively,

$$\begin{aligned} \textit{logit}\left[ {P\left( {X_{pi} =1|\theta _p ,\alpha _{0i} ,\beta _{0i}} \right) } \right] =\alpha _{0i} \theta _p -\beta _{0i} \end{aligned}$$

(3)

and

$$\begin{aligned} \textit{logit}\left[ {P\left( {X_{pi} =1|\theta _p ,\alpha _{1i} ,\beta _{1i}} \right) } \right] =\alpha _{1i} \theta _p -\beta _{1i} \end{aligned}$$

(4)

where $\upalpha _{0\mathrm{i}}$ and $\upbeta _{0\mathrm{i}}$ are, respectively, the discrimination and difficulty parameters for $\hbox {C}_{\mathrm{pi}} = 0$, and $\upalpha _{1\mathrm{i}}$ and $\upbeta _{1\mathrm{i}}$ are, respectively, the discrimination and difficulty parameters for $\hbox {C}_{\mathrm{pi}} = 1$.

To identify the two classes in terms of the response times, class membership is regressed on the subject and item-corrected log-response times. That is,

$$\begin{aligned} \textit{logit}\left[ {P(C_{pi} =0|T_{pi} ,\lambda _i ,\tau _p ,\sigma _{\varepsilon i} ,\zeta _1 ,\zeta _0} \right) ]=\zeta _1 \left( {\frac{\hbox {ln}\left( {T_{pi}} \right) -\left( {\lambda _i -_p} \right) }{\sigma _{\varepsilon i}} -\zeta _0} \right) . \end{aligned}$$

(5)

where $\uplambda _{\mathrm{i}},\uptau _{\mathrm{p}}$ and $\upsigma _{\upvarepsilon \mathrm{i}}$ are the free parameters that also appear in Eq. 1. We explicitly take the main effects of the subjects (i.e., $\uptau _{\mathrm{p}})$ and the main effects of the items (i.e., $\uplambda _{\mathrm{i}})$ on the log-response times into account in Eq. 5. Neglecting these main effects would confound the within-subject effects by the between-subject differences in basic speed (which are now separated by parameter $\uptau _{\mathrm{p}})$ and the between-item differences in time intensity (which are now separated by parameter $\uplambda _{\mathrm{i}})$. Note that the detection of speediness (Van Der Linden, Breithaupt, Chuah, & Zhang, 2007) and aberrant responses (Van der Linden & van Krimpen-Stoop, 2003) has also been based on a similar procedure.

In Eq. 5, parameter $\zeta _1 \in [ {0,\infty } )$ is constrained to be nonnegative to avoid label switching (i.e., switching of the statistical properties of the two classes during parameter estimation). As a result, class 1 with parameters $\upalpha _{1i}$ and $\upbeta _{1i}$ correspond to the item characteristics of the faster responses. Parameter $\upzeta _{0}$ is an intercept parameter for which smaller values denote a larger class size of the slower class 0. In the present parameterization, $\upzeta _{0}$ can be interpreted as the ‘difficulty’ to respond according to the slower class. Note that the item median split procedure used by Partchev and De Boeck to operationalize faster and slower responses does not estimate the class size from the data but assumes the slower class to contain 50% of the responses. The present approach is a statistical variant of this deterministic procedure which additionally retains the continuous information in the response times to operationalize faster and slower responses.

In our approach above, the response times enter the response mixture model in Eq. 2 as a covariate (i.e., via Eq. 5). That is, the response times are a predictor for the latent class variable, $\hbox {C}_\mathrm{pi}$. Using predictor variables to identify latent classes is common practice in mixture modeling (e.g., Lubke & Muthen, 2005). Note that this does not imply a mixture distribution for the covariate. That is, the present response mixture model is a mixture model for the responses but not for the response times. The present approach therefore differs from the mixture approaches by Molenaar, Oberski, Vermunt, and De Boeck (2016), Schnipke and Scrams (1997), Wang and Xu (2015), and Wang et al., (2016) in which it is assumed that the latent class variable affects both the responses and the response time distribution.

Using the mixing proportion $\uppi _\mathrm{pi}$, inferences can be made about the marginal class size for class 0, $\hbox {C}_\mathrm{pi}$ = 0, for the items (${\tilde{\uppi }}_{\mathrm{i}} =\frac{1}{\hbox {N}}\mathop \sum \nolimits _{p=1}^N \pi _{pi} )$, for the subjects (${\tilde{\uppi }}_{\mathrm{p}} =\frac{1}{\mathrm{n}}\mathop \sum \nolimits _{i=1}^n \pi _{pi} )$, or overall ($\tilde{\uppi } =\frac{1}{\mathrm{N}\times \mathrm{n}}\mathop \sum \nolimits _{p=1}^N \mathop \sum \nolimits _{i=1}^n \pi _{pi} )$. In the population, $\uppi _\mathrm{pi}$ is equal across items and subjects as the mixing parameters $\upzeta _{0}$ and $\upzeta _{1}$ are not subject specific or item specific. This assumption of equal class sizes across items in the population is referred to as the assumption of time homogeneity in the longitudinal modeling literature (e.g, Bacci, Pandolfi, & Pennoni, 2014) and can be relaxed in principle. We do not consider such extensions in the present study. We return to this point in the discussion section. Note that $\tilde{\uppi } _{\mathrm{i}}$ and $\tilde{\uppi }_{\mathrm{p}}$ are implicitly assumed to be equal to 0.50 in, respectively, the item median split and the person median split procedure by Partchev and De Boeck (2012).

2.1 Estimation

Let $\varvec{\upeta }_\mathrm{i}$ denote the vector of item parameters for item i,

$\varvec{\upeta }_\mathrm{i}$ = [ln($\upalpha _\mathrm{0i})$, ln($\upalpha _\mathrm{1i}), \upbeta _\mathrm{0i},\upbeta _\mathrm{1i},\uplambda _\mathrm{i}$, ln($\upsigma _{\upvarepsilon \mathrm{i}}^{2})$] for $I = 1, {\ldots }$, n, let $\varvec{\upomega }_\mathrm{p}$ denote a vector containing the parameters for subject $p, \varvec{\upomega }_{\mathrm{p}} = [\uptheta _{\mathrm{p}},\uptau _{\mathrm{p}}$] for p = 1, ..., N, and let $\varvec{\upzeta }$ denote a vector with the mixing parameters $\varvec{\upzeta } = [\upzeta _{0}$, ln($\upzeta _{1})$]. Note that we use logarithmic transformations for the parameters that are strictly positive. The likelihood of the data for subject p on item i given the model is then equal to

$$\begin{aligned} L\left( {X_{pi} ,\hbox {ln}\left( {T_{pi}} \right) ;{\varvec{\eta }} _i ,{\varvec{\omega }} _p ,{\varvec{\zeta }}} \right)= & {} f\left( {X_{pi} \hbox {|ln}\left( {T_{pi}} \right) ,\alpha _{0i} ,\alpha _{1i} ,\beta _{0i} ,\beta _{1i} ,\zeta _0 ,\zeta _1 ,\theta _p} \right) \nonumber \\&g\left( {\hbox {ln}(T_{pi}} \right) |\lambda _i ,\sigma _{\varepsilon i}^2 ,\tau _p ) \end{aligned}$$

(6)

where $f\left( . \right)$ is a mixture Bernoulli probability function with the success parameter given by Eq. 2 and the mixing proportion given by Eq. 5. In addition, $g\left( . \right)$ is a normal density function.

The model can be fit to data by assuming the item parameters $\varvec{\upeta }_{\mathrm{i}}$ and $\varvec{\upzeta }$ to be fixed parameters and numerically integrating over the random parameters, $\uptheta _{\mathrm{p}}$ and $\uptau _{\mathrm{p}}$, in the likelihood function by assuming a prior distribution for these parameters. Next, this marginal likelihood is maximized for the unknown fixed parameters in ${\varvec{\eta }}_i$ and $\varvec{\upzeta }$ (Bock & Aitkin, 1981). Another possibility, which is adopted here, is to assume prior distributions for all parameters in ${\varvec{\eta }}_i ,{\varvec{\omega }}_p$, and $\varvec{\upzeta }$ and use a Markov Chain Monte Carlo approach to draw samples from the joint posterior parameter distribution (MCMC; see, e.g., Gilks, Richardson, & Spiegelhalter, 1996).

2.2 Prior Distributions

In choosing our priors, we generally follow Fox, Klein Entink, and Van der Linden (2007) and Van der Linden (2007) who discuss prior and hyperprior specification in a general hierarchical modeling framework for responses and response times. First, we parameterized a bivariate normal distribution for the vector $\varvec{\upomega }_\mathrm{p}$ using

$$\begin{aligned}&{\uptheta }_{\mathrm{p}} \sim \hbox {Normal}\left( {0,1} \right) \end{aligned}$$

(7)

$$\begin{aligned}&{\uptau } _{\mathrm{p}} \sim \hbox {Normal}\left( {{\upsigma } _{{\uptheta \tau } } {\uptheta } _{\mathrm{p}} ;{\upsigma } _{\uptau } ^{2}-{\upsigma } _{{\uptheta \tau } } ^{2}} \right) \end{aligned}$$

(8)

which can be derived by considering the distribution of $\uptheta _{\mathrm{p}}$ conditional on $\uptau _{\mathrm{p}}$ in a bivariate normal distribution (see, e.g., Fox et al., 2007). Note that the above ensures that VAR($\uptheta _{\mathrm{p}})$ = 1 and that the covariance matrix of $\upomega _{\mathrm{p}}$ (denoted $\Sigma _{\mathrm{P}})$ is positive definite, which identifies the model. No additional identification constraints are needed as the scale of $\uptau _{\mathrm{p}}$ is identified by the unit of the log-response times. Note that due to the parametrization above, besides $\upsigma _{\uptheta \uptau }$, we estimate the hyperparameter $\upsigma _{\uptau }^{\prime 2}=\upsigma _{\uptau } ^{2}-\upsigma _{\uptheta \uptau } ^{2}$ instead of $\upsigma _{\uptau }^{2}$.

For the item parameters in $\varvec{\upeta }_{\mathrm{i}}$, we use

$$\begin{aligned} \varvec{\upeta } _{\mathrm{i}} \sim \hbox { Multivariate}-\hbox {Normal}\left( {\varvec{\upmu } _{\upeta } ;\varvec{\Sigma } _{\upeta } } \right) \end{aligned}$$

(9)

in which all hyperparameters in the mean vector $\varvec{\upmu }_{\upeta }$ and covariance matrix $\varvec{\Sigma }_{\upeta }$ are estimated (see Van der Linden, 2007). Finally, for $\upzeta _{0}$ and ln($\upzeta _{1})$, we use

$$\begin{aligned}&{\upzeta } _0 \sim \hbox { Normal}({\upmu } _{{{\upzeta }}_0} ,{\upsigma } _{{\upzeta }_0} ^{2}) \end{aligned}$$

(10)

$$\begin{aligned}&\ln ({\upzeta }_{1}) \sim \hbox {Normal}(\upmu _{{\upzeta }_1}, {\upsigma }_{{\upzeta }_1}^{2}). \end{aligned}$$

(11)

2.3 Hyperpriors

For the hyperparameters above, we specified the following hyperpriors

$$\begin{aligned}&{\upsigma } _{{\uptheta \uptau } } \sim \hbox {Normal}\left( {{\upmu } _{\uprho } ,{ \upsigma } _{\uprho } ^{2}} \right) \end{aligned}$$

(12)

$$\begin{aligned}&{\upsigma } _{\uptau } {\prime }^{2}\sim \hbox { Inverse}-\hbox {Gamma}\left( {\hbox {v}_1 ,\hbox {v}_2} \right) \end{aligned}$$

(13)

In addition, for $\varvec{\upmu }_{\upeta }$ we follow Van der Linden et al (2007) and Fox et al. (2007) and specify

$$\begin{aligned} \varvec{\upmu } _{\upeta } \sim \hbox { Multivariate}-\hbox {Normal}\left( {\varvec{\upmu } _0 ,\varvec{\Sigma }_{\upeta } } \right) \end{aligned}$$

(14)

with

$$\begin{aligned} \varvec{\Sigma } _{\upeta } \sim \hbox { Inverse}-\hbox {Wishart}\left( {\hbox {v}_{\mathrm{I}} ,\mathbf{V}_\mathbf{I}} \right) . \end{aligned}$$

(15)

The model can be implemented in the freely available software packages JAGS (Plummer, 2003), STAN (Stan Development Team, 2015), and BUGS (Spiegelhalter, Thomas, Best, & Gilks, 1995). Here we implemented the model in OpenBUGS (Thomas, Hara, Ligges, & Sturtz, 2006). The syntax file is given in “Appendix.”

2.4 Model Fit Diagnosis

To assess the goodness-of-fit of the response mixture model, we want to compare the model to a baseline model. First, a reasonable baseline model can be derived by assuming that the responses in the two classes have the same item characteristics, that is $\upalpha _{i}=\upalpha _{0i}=\upalpha _{1i}$ and $\upbeta _{i}=\upbeta _{0i}=\upbeta _{1i}$. As a result, in Eq. 2 it will hold that $P({X_{pi} =1|\theta _p ,\alpha _{0i} ,\beta _{0i}})=P({X_{pi} =1|\theta _p ,\alpha _{1i} ,\beta _{1i}})$. Therefore, the model for the responses will reduce to a standard two-parameter item response theory model, that is,

$$\begin{aligned} \textit{logit}\left[ {P\left( {X_{pi} =1|\theta _p ,\alpha _i ,\beta _i} \right) } \right] =\alpha _i \theta _p -\beta _i, \end{aligned}$$

(16)

and consequently $\upzeta _{0}$ and $\upzeta _{1}$ from Eq. 5 cancel out of the likelihood function. The baseline model that results (i.e., Eqs. 1 and 16) is equivalent to the hierarchical model of Van der Linden (2007).

A common model fit index is the Deviance Information Criterion (DIC; Spiegelhalter, Best, Carlin, & van der Linde, 2002). Although valuable in a variety of model selection situations in practice, it has been noted that the DIC may perform suboptimally in mixture models (e.g., Celeux, Forbes, Robert, & Titterington, 2006). The main problem is that the estimate of the number of parameters, which is needed to evaluate the DIC, may be wrong in mixture models or highly nonlinear models. In preliminary simulations (not presented), we established that the DIC and an alternative fit index, the Watanabe-Aike Information Criterion (WAIC, Watanabe, 2010), are both indeed unsuitable for the present model fit comparison.

As common model fit indices can thus not be used, we focus on the key objective for which we apply the response mixture model: accounting for heterogeneity in the item characteristic across the response times. Thus, to decide if the response mixture model is of use in a given data application, the central question is whether there is heterogeneity in the item characteristic across response times. Therefore, as a diagnostic tool to investigate parameter heterogeneity, we consider the posterior parameter distributions of $\Delta \upalpha _{\mathrm{i}}=\upalpha _{\mathrm{0i}} -\upalpha _{\mathrm{1i}}$ and $\Delta \upbeta _{\mathrm{i}}=\upbeta _{\mathrm{0i}} -\upbeta _{\mathrm{1i}}$ and we consider the posterior probabilities that $\upalpha _{\mathrm{0i}} > \upalpha _{\mathrm{1i}}$, and $\upbeta _{\mathrm{0i}} > \upbeta _{\mathrm{1i}}$. If the data do not contain any heterogeneity in the item characteristics with respect to the response times, the baseline model will hold for the data and the posterior parameter distributions of $\Delta \upalpha _{\mathrm{i}}$, and $\Delta \upbeta _{\mathrm{i}}$ will all have their posterior probability mass concentrated around 0. In addition, the posterior probabilities of $\upalpha _{\mathrm{0i}} > \upalpha _{\mathrm{1i}}$ and $\upbeta _{\mathrm{0i}} > \upbeta _{\mathrm{1i}}$ will tend to 0.5. As a consequence, the mixing parameters $\upzeta _{0}$ and $\upzeta _{1}$ will be poorly identified reflected by estimates near the parameter boundary and a large variance of the sampling distribution. Such signals of poor identification are characteristic for mixture models in general (i.e., also for more basic mixture models), that is, if the data truly consist of a single component, any two component mixture model will be poorly identified in these data. However, this problem is easily diagnosed from the sampling distributions of the mixture model parameters as we will show below.

3 Simulation Study

3.1 Data

We conducted a simulation study to investigate the parameter recovery of the response mixture model in the case that the data truly follow a response mixture model and in the case that the data actually follow a baseline model without mixtures. To this end, we simulated data according to the response mixture model (Eqs. 1, 2, and 5) and according to the baseline model (Eqs. 1 and 16). In the case of the response mixture model, we drew the vector of true item parameters for item $i, \varvec{\upeta }_{\mathrm{i}} = [\ln (\upalpha _{0\mathrm{i}})$, ln($\upalpha _{\mathrm{1i}}),\upbeta _{0\mathrm{i}}, \upbeta _{\mathrm{1i}}, \uplambda _{\mathrm{i}}$, ln($\upsigma _{\upvarepsilon \mathrm{i}}^{2})$], from a multivariate normal distribution with mean vector [ln(1), ln(1.5), − 1, 1, 2, ln(.3)] and a covariance matrix with diagonal elements equal to 0.2, 0.2, 0.7, 0.7, 0.02, and 0.02, and with COR($\upalpha _{0\mathrm{i}},\upalpha _{\mathrm{1i}})$ = 0.8, COR($\upbeta _{\mathrm{0i}}, \upbeta _{\mathrm{1i}})$ = 0.8, COR($\upbeta _{0\mathrm{i}}, \uplambda _{\mathrm{i}})=0.4$, and COR($\upbeta _{\mathrm{0i}},\uplambda _{\mathrm{i}}) = 0.4$. All other parameter correlations were equal to 0. We used the same true item parameters in all replications to study the recovery of the item parameters. In each replication, we drew the vector of person parameters for person $p, \varvec{\upomega }_{\mathrm{p}} = [\uptheta _{\mathrm{p}},\uptau _{\mathrm{p}}]$, from a bivariate normal distribution with mean vector [0,0] and a covariance matrix with $\upsigma _{\uptheta }^{2}=1, \upsigma _{\tau } ^{2} = 0.16$, and $\upsigma _{\uptheta \uptau } = 0.16$ which implies COR($\uptheta _{\mathrm{p}}, \uptau _{\mathrm{p}})$ = 0.4. The mixing parameters were chosen to equal $\upzeta _{1} = 1$ and $\upzeta _{0} =0.5$ which imply a marginal probability of a slow response of 0.40. The parameter values above result in untransformed response times between roughly 1 and 60 s with the mean around 9 s. In the case of the baseline model, we used $\upalpha _{\mathrm{i}}=\upalpha _{0\mathrm{i}}$ and $\upbeta _{\mathrm{i}}=\upbeta _{0\mathrm{i}}$, all other values (i.e., the values for $\uplambda _{\mathrm{i}},\upsigma _{\upvarepsilon \mathrm{i}}^{2},\upsigma _{\uptau } ^{2}$, and $\upsigma _{\uptheta \uptau } )$ were equal to those above. We simulated data for N = 2000 subjects and n = 20 items. We conducted 80 replications.

Fig. 1

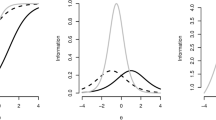
Plots of the average posterior means across replications for $\alpha _{0i},\alpha _{1i},\beta _{0i}, \beta _{1i},\lambda _{i}$, and $\sigma _{\varepsilon i}^{2}$ (y-axis) and the true parameters values (x-axis). The vertical lines denote the range between the $1{\mathrm{th}}$ and $99{\mathrm{th}}$ percentile of the posterior parameter means across replications. The striped gray line denotes a one-to-one correspondence.

Fig. 2

Plots of the posterior means of $\Delta \alpha _{i}=\alpha _{0i}$ – $\alpha _{1i}$ and $\Delta \beta _{i}=\beta _{0i}$ – $\beta _{1i}$ across the replications in which the data follow the baseline model. The vertical lines denote the range between the $1{\mathrm{th}}$ and $99{\mathrm{th}}$ percentile of the posterior parameter means across replications.

3.2 Estimation

In our OpenBUGS implementation of the model, the hyper parameters are set as follows: We set $\upmu _{\upzeta 0},\upmu _{\upzeta 1}$, and $\upmu _{\uprho }$ to be equal to 0, and $\upsigma _{\upzeta 0}^{2}, \upsigma _{\upzeta 1}^{2}$, and $\upsigma _{\uprho }^{2}$ were all set equal to 10. In addition, $\hbox {v}_{\mathrm{I}}$ was set to 6 and $\mathbf{V}_{\mathrm{I}}$ was equal to a diagonal matrix with elements equal to 0.01. Finally, $\hbox {v}_{1}$ and $\hbox {v}_{2}$ were set to 0.01, and $\varvec{\upmu }_{\upeta }$ was equal to [0,0,0,0,0]. Note that these choices reflect vague information about $\varvec{\upzeta }, \upsigma _{\uptheta \uptau } ,\upsigma _{\uptau } ^{\prime 2}, \varvec{\upomega }_{\mathrm{p}}$, and $\varvec{\upeta }_{\mathrm{i}}$. We drew 8,000 samples from the posterior parameter distribution of which we discarded the first 4,000 samples as burn-in. Preliminary data simulations showed that this is sufficient to ensure convergence of the chain to its stationary distribution.

3.3 Results

3.3.1 Data Follow the Response Mixture Model

Plots of the posterior parameter means with the range between their $1\mathrm{th}$ and $99\mathrm{th}$ percentile across the replications are depicted for $\upalpha _{0\mathrm{i}}, \upalpha _{\mathrm{1i}},\upbeta _{\mathrm{0i}}, \upbeta _{\mathrm{1i}},\uplambda _{\mathrm{i}}$, and $\upsigma _{\upvarepsilon \mathrm{i}}^{2}$ in Fig. 1. As can be seen, the parameter recovery is generally acceptable as the posterior means fluctuate around their true value suggesting that they are not biased. For $\upbeta _{\mathrm{1i}}$ and $\upalpha _{1\mathrm{i}}$, parameter variability is somewhat larger as compared to $\upbeta _{0\mathrm{i}}$ and $\upalpha _{0\mathrm{i}}$ due to the faster class being proportionally larger in the data (due to the true value of $\upzeta _{0}$ being 0.5).

The other parameters are recovered acceptably as well: For the mixing parameters, $\upzeta _{0}$ we found an average posterior mean across replications equal to 0.49 ($1{\mathrm{th}}$ and $99{\mathrm{th}}$ percentile: 0.24; 0.82) where the true value equaled 0.5. For the mixing parameter $\upzeta _{1}$, we found an average posterior mean across replications equal to 1.03 ($1{\mathrm{th}}$ and $99{\mathrm{th}}$ percentile: 0.86, 1.31) where the true value equaled 1.0. The average posterior mean across replications for $\upsigma _{\uptheta \uptau }$ equaled 0.16 ($1{\mathrm{th}}$ and $99\mathrm{th}$ percentile: 0.14, 0.18) and 0.14 ($1\mathrm{th}$ and $99\mathrm{th}$ percentile: 0.12, 0.14) for $\upsigma _{\uptau } ^{\prime 2}$ where the true values equaled, respectively, 0.16 and 0.14.

3.3.2 Data Follow the Baseline Model

Here we study whether we can diagnose model misfit of the full response mixture model if the data follow the baseline model without classes. In Fig. 2, plots of the posterior parameter means with the range between their $1\mathrm{th}$ and $99\mathrm{th}$ percentile across the replications are depicted for $\Delta \upalpha _{\mathrm{i}}$ and $\Delta \upbeta _{\mathrm{i}}$. As can be seen from the figure, the posterior parameter means fluctuate around 0 indicating that $\upalpha _{0\mathrm{i}}=\upalpha _{1\mathrm{i}}$ and $\upbeta _{0\mathrm{i}}=\upbeta _{\mathrm{1i}}$. In addition, the posterior probabilities of $\upalpha _{\mathrm{0i}} > \upalpha _{\mathrm{1i}}$ and $\upbeta _{\mathrm{0i}} > \upbeta _{\mathrm{1i}}$ averaged over replications and items are, respectively, equal to 0.53 and 0.50 indicating that these inequalities do not hold and that the discrimination and difficulty parameters are equal over classes. In addition, the overall class probability $\tilde{\uppi }$ is close to 0 or 1 in, respectively, 22 (27.5%) and 46 (57.5%) of the replications. For 11 replications (13.75%), $\tilde{\uppi }$ was estimated to be close to 0.5 due to $\zeta _{1}$ approaching 0. Only in 1 replication (1.25%), there was no indication of model misfit in $\tilde{\uppi }$ as the estimate equaled 0.64 in this replication.¹ Thus, in conclusions, it seems that the model diagnostics above can indeed be used to study model misfit of the full response mixture model.

3.4 Application

3.4.1 Data

The data comprise a computerized arithmetic test which was a part of the secondary school exams in the Netherlands in 2013. These data have previously been analyzed by Bolsinova and Maris (2016) who tested the responses and response times on the assumption of conditional independence. The total dataset contains the responses and response times of 10,369 subjects to 60 items. Here, we randomly selected 2000 subjects and 20 items to match the setting in the simulation study above. See Table 1 for the item discrimination, item difficulty, time intensity, and error variance of the responses and response times in the baseline model (Eqs. 1 and 16, based on 8000 iterations with 4000 as burn-in).

Table 1 Posterior Means with 99% HPD regions of the response and response time parameters in the baseline model.

3.5 Response Mixture Model

To investigate whether item characteristics are heterogeneous across response times, we resorted to response mixture modeling. All prior specifications are the same as in the simulation study. We run 20,000 iterations with 10,000 as burn-in. The Gelman and Rubin statistic indicated (based on 5 chains with randomly drawn starting values) that this number of iterations was sufficient to ensure that the MCMC sampling scheme converged to its stationary distribution (Gelman & Rubin, 1992). In addition, from the trace plots all chains seemed to vary randomly around a stable average.

3.5.1 Results

The posterior mean of $\upzeta _{0}$ equals − 0.70 with 99% HPD bounds of − 0.79 and − 0.62. The posterior mean of $\upzeta _{1}$ equals 5.785 with 99% HPD bounds of 4.25 and 7.73. Using these parameters, the posterior class probabilities, $\tilde{\uppi } ,\tilde{\uppi } _{\mathrm{p}}$ and $\tilde{\uppi } _{\mathrm{i}}$ are obtained. The overall class probability (the overall size of the slow class, $\hbox {C}_{\mathrm{pi}}= 0$) equals 0.79. The item- and person-specific class probabilities are depicted in Fig. 3. Table 2 contains the posterior parameter means for the item parameters in the two classes according to the full model. The posterior means of the estimates of $\upalpha _{0i},\upalpha _{1i},\upbeta _{0i}$, and $\upbeta _{1i}$ are plotted in Fig. 4 for the items as ordered according to their general difficulty (i.e., the difficulty as estimated using the baseline model, see Table 1). As can be seen from the figure, the slower responses are associated with uniformly smaller discrimination parameters. In addition, there appears to be an interaction effect between the overall difficulty of the items and the difference between the fast and slow difficulty. That is, for the overall more difficult items, the slower responses have a smaller difficulty (larger probability of a correct response), while for the overall less difficult items, the faster responses have a smaller difficulty (larger probability of a correct response).

Fig. 3

Histograms of the item ($\widetilde{{\uppi } _{\mathrm{i}}})$ and subject ($\tilde{\uppi } _{\mathrm{p}} )$ specific marginal class probabilities.

Table 2 Posterior Means and 99% HPD regions of the response parameters in the response mixture model.

To investigate how well the above observations concerning the differences between the fast and slow response characteristics are supported by the data, we depicted the posterior parameter distributions of $\Delta \upalpha _{\mathrm{i}}=\upalpha _{\mathrm{0i}} -\upalpha _{\mathrm{1i}}$ and $\Delta \upbeta _{\mathrm{i}}=\upbeta _{\mathrm{0i}} -\upbeta _{\mathrm{1i}}$ in Fig. 5 for the items as ordered according to their general difficulty. As can be seen, for most items, the conclusion that the slower responses (class 0) are associated with smaller discrimination parameters is supported by the 99% HPD regions of $\Delta \upalpha _{\mathrm{i}}$. In addition, for eleven items the difficulty parameters differ between the classes according to their 99% HPD regions. As already observed above, the difference is not in the same direction for all these items. That is, for the overall easier items, the responses in the faster class are associated with smaller item difficulty parameters as compared to the difficulty parameters of the responses in the slower class ($\Delta \upbeta _{\mathrm{i}}>0$), while for the overall more difficult items, this difference is in the opposite direction ($\Delta \upbeta _{\mathrm{i}} <0$). This provides some evidence for the interaction between the overall difficulty of the items and the difference between the fast and slow difficulty as already noticed in Fig. 4. Furthermore, we depicted the posterior probabilities of $\upalpha _{\mathrm{0i}} > \upalpha _{\mathrm{1i}}$ and $\upbeta _{\mathrm{0i}} > \beta _{\mathrm{1i}}$ in Table 3. As can be seen, the conclusion are the same as those from Fig. 5.

Fig. 4

Plots of the posterior means of the $\alpha _{0i}, \alpha _{1i},\beta _{0i}$, and $\beta _{1i}$ parameters (y-axis) across item as ordered on their difficulty according to the baseline model (x-axis).

Fig. 5

Plots of the posterior means of $\Delta \alpha _{i}=\alpha _{0i}$ – $\alpha _{1i}$ and $\Delta \beta _{i}=\beta _{0i}$ – $\beta _{1i}$ for each item in the application. The vertical lines denote the range of the 99% HPD regions.

3.6 Discussion

In the real data application, it is concluded that the faster responses are associated with larger discrimination parameters as compared to the slower responses. This finding is not line with the ‘worst performance rule’ from experimental psychology (Larson, & Alderton, 1990) which predicts that slower responses contain more information about individual differences in ability than faster responses. This contrasting result might suggest that the worst performance rule, which is typically established using experimental tasks with extremely fast responses (500–1000 ms), does not hold for cognitive ability tasks with responses between 5–120 s.

Table 3 Posterior probabilities of $\alpha _{0i} > \alpha _{1i}$ and $\beta _{0i} > \beta _{1i}$.

A second finding in the application is that there is an interaction between the overall item difficulty and the probability of a correct response in the faster and slower classes. Specifically, we found that the faster responses are more successful for the easier items while the slower responses are being more successful for the more difficult items. This finding is in line with Bolsinova et al. (in press), De Boeck, Chen, & Davison (2017), Goldhammer et al. (2014), and Partchev and De Boeck (2012) who found a similar effect. These findings suggest that for easier items, successful responses are given by more or less automated processes while if these automated processes fail, other controlled processes are being used which are more error prone. On the contrary, for the more difficult items, it holds that the responses for which subjects take more time are generally more successful than the faster responses.

4 General Discussion

In this paper, we outlined the method of response mixture modeling to account for heterogeneity in the item characteristics across response times. As compared to the hierarchical model of Van der Linden (2007), the model put forward in this paper contains two additional parameters per item (an additional discrimination and an additional difficulty) and two additional mixing parameters. The model is thus reasonably complex reflected by relatively large posterior standard deviations of the parameter estimates for the class-specific discrimination parameters (see, e.g., Fig. 1 from the simulation study). We therefore did not consider more general cases of the present model. However, various extensions can be thought of. That is, two separate latent variables can be assumed to underlie the responses in the faster and slower classes. In doing so, the correlation between the ability in the faster and slower classes can be investigated, as well as the correlation of the faster and slower ability with the latent speed variable. Another extension might be to relax the assumption of time homogeneity (Bacci, Pandolfi, & Pennoni, 2014) by making the mixing parameters item specific. From our perspective, this is feasible, but will require large datasets.

A key assumption in our model is that there are two latent classes underlying the responses to a given test. As discussed above, we focused mainly on the indirect application (Yung, 1997) in which we do not necessarily interpret these classes substantively. That is, we treat the classes as statistical tools to capture the heterogeneity of the item characteristics across the response times. If our model is applied to data that contain more than two classes, the present approach will likely still capture the most important patterns in the data. That is, the model will capture the possible systematic differences in the discrimination and difficulty of the items for larger and smaller response times. However, if some subjects in the data do not display heterogeneity in their response characteristics, e.g., because they only use a single response process, the model does not hold for that subject (person misfit). As a result, the model will produce invalid posterior class assignments for this subject. Such person misfit can be diagnosed by consulting the posterior means of the class probabilities. If only a single class holds for a given subject, the class probabilities will tend to 0.5 indicating chance assignment.

In this paper, we did not so much focus on direct applications of the mixture model in which the two classes are indeed substantively interpreted (e.g., Titterington, Smith, & Makov, 1985; Dolan & Van der Maas, 1998). However, in the presence of a strong theory or strong empirical justification, such applications of the response mixture model are certainly possible. For instance, Jansen and Van der Maas (2001) studied two strategies to solve the balance scale task. These strategies can be derived from Piaget’s theory on conservation (see Siegler, 1976). Another example of a theoretical framework where two classes are assumed to underlie response behavior is the dual processing framework (Shiffrin & Schneider, 1977; Goldhammer et al., 2014). In this framework, faster responses are assumed to reflect automated processes that are proceduralized, parallel, and do not require active control, while slower responses are assumed to reflect controlled processes that are serial and require attentional control. In addition, in cognitive psychology it has been shown that decision making may involve a slower selective search strategy or a faster pattern recognition strategy in medical decisions (Ericsson & Staszewski 1989) and in solving chess puzzles (Van Harreveld, Wagenmakers, and Van der Maas, 2007). Finally, as discussed above, in arithmetic tests it can be expected that subjects use both memory retrieval and actual calculation to solve the arithmetic problems of a test (Gabner et al., 2009).

Appendix: OpenBUS Syntax to Fit the Full Response Mixture Model