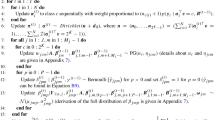A Nonparametric Multidimensional Latent Class IRT Model in a Bayesian Framework

Abstract

We propose a nonparametric item response theory model for dichotomously-scored items in a Bayesian framework. The model is based on a latent class (LC) formulation, and it is multidimensional, with dimensions corresponding to a partition of the items in homogenous groups that are specified on the basis of inequality constraints among the conditional success probabilities given the latent class. Moreover, an innovative system of prior distributions is proposed following the encompassing approach, in which the largest model is the unconstrained LC model. A reversible-jump type algorithm is described for sampling from the joint posterior distribution of the model parameters of the encompassing model. By suitably post-processing its output, we then make inference on the number of dimensions (i.e., number of groups of items measuring the same latent trait) and we cluster items according to the dimensions when unidimensionality is violated. The approach is illustrated by two examples on simulated data and two applications based on educational and quality-of-life data.

1 Introduction

A crucial aspect in the analysis of item responses is that of dimensionality, corresponding to the number of latent traits measured by the test items. Typically, item response theory (IRT) models (Hambleton & Swaminathan, 1985; Bartolucci et al., 2015) assume unidimensionality, that is, the test items measure a single dimension that in education corresponds to the ability in a certain domain. Obviously, this assumption may lead to misleading results when it is not realistic. This is particularly true for the Rasch model (Rasch, 1961), the main IRT model for dichotomous items, under which the raw score is a sufficient statistic for the ability level of an examinee. In fact, if unidimensionality does not hold, summarizing his/her performance by this simple statistic is not correct.

The problem of testing unidimensionality has attracted a great interest in the psychometric literature. One of the main contributions in this literature is due to Martin-Löf (1973), who proposed a test of unidimensionality against bidimensionality under the assumptions of the Rasch model. The main advantage of the test is its simple use, as it is based on conditional maximum likelihood estimates of the item parameters (under the unidimensional and bidimensional hypotheses), which may be easily obtained by using different softwares. Furthermore, this approach does not require to formulate assumptions on the distribution of the latent traits. On the other hand, the assumptions that are formulated on the conditional distribution of the item responses given the latent traits may be restrictive. Mainly, it is required that all items have the same discriminating power, leading the test to over-rejecting unidimensionality when this assumption does not hold. Moreover, it does not allow us to measure the correlation between the two latent traits assumed to exist under the most general model. See Verhelst (2001) for further comments about the Martin-Löf (1973)’s test and an analysis of its performance.

More recently, two interesting approaches were proposed by Christensen et al. (2002) and Bartolucci (2007). The first may be seen as an extension of the approach of Martin-Löf (1973) to the case of polytomous items. In their proposal, Christensen et al. (2002) also considered marginal maximum likelihood (MML) estimation based on the assumption of normality of the latent traits. In particular, under the bidimensional model, a bivariate normal distribution with arbitrary correlation is assumed, which may be estimated on the basis of the data. On the other hand, the approach of Bartolucci (2007), extended to the case of polytomous items by Bacci et al. (2014), is based on MML estimation under the assumption that the latent traits have a discrete distribution that defines a certain number of latent classes of subjects (Lazarsfeld & Henry, 1968; Goodman, 1974). Then, the approach may be seen as semiparametric, in the sense of Lindsay et al. (1991). Moreover, in Bartolucci (2007) a two-parameter logistic (2PL) parametrization (Birnbaum, 1968) is adopted and an algorithm for discovering the number of dimensions, and clustering the items in separate groups corresponding to these dimensions, is provided. See also von Davier (2008) for a related class of IRT models with a high degree of flexibility that may be used to analyze multidimensional item responses.

The 2PL parametrization, on which the approach of Bartolucci (2007) relies, is more flexible than the Rasch parametrization of the item response distribution given the underlying latent trait; in fact, it allows for different discrimination levels among items. However, the assumption that a group of items measures the same latent trait may be defined in a nonparametric fashion through inequality constraints under the assumption that the latent distribution is discrete (Bartolucci & Forcina, 2005), which amounts to assume a latent class (LC) model. In this article, and for the case of dichotomously-scored items, we develop this result to define an IRT model that allows us to discover the number of dimensions measured by the questionnaire, without making any parametric assumption on either the distribution of the latent traits or the conditional distribution of the item responses given such traits.

In order to estimate the proposed model, we rely on a Bayesian inference framework that we consider convenient given the uncertainty on both the number of latent classes and model dimensionality. Therefore, we specify a new system of priors and develop suitable algorithms for parameter estimation. In particular, for the prior distributions on the model parameters we rely on the encompassing approach of Klugkist et al. (2005). Accordingly, we formulate priors on the parameters of the most general model, which is an unconstrained LC model with a certain number of classes. Then, priors are “automatically” defined for any nested model formulated by suitable inequalities on the conditional success probabilities in order to specify the number of dimensions. Regarding estimation, we rely on an algorithm of reversible-jump Markov chain Monte Carlo (RJ-MCMC) type (Green, 1995; Green & Richardson, 2001) applied to the LC model and followed by a suitable post-processing procedure to cluster items. As a result, the proposed approach allows us to select the number of latent classes and the number of dimensions, and also provides a clustering of the items into disjoint groups measuring different latent traits.

Overall, the framework here proposed is related to the Bayesian inference approach of Hojtink and Molenaar (1997) that may be used to test different assumptions about IRT models. Their approach is based on a suitably constrained LC model to express the hypothesis of multidimensionality in a way similar to that we follow in the present paper, whereas the IRT assumptions are tested on the basis of suitably formulated statistics. The approach of Hojtink and Molenaar (1997), as well as Bayesian inference for the constrained LC models at issue, has been developed in several directions; see, among others, Béguin and Glas (2001), Van Onna (2002), and Bolt and Lall (2003), and the recent work by Kuo and Sheng (2015). With respect to these Bayesian approaches, our approach is based on a innovative and flexible set of priors on the model parameters of the unrestricted LC model, which permits to arbitrarily specify the prior probability of the hypothesis of unidimensionality. Moreover, we present an innovative approach of model selection, in terms of number of latent classes and number of dimensions, which is directly connected with the encompassing approach of Klugkist et al. (2005). On the other hand, as already mentioned above, the proposed approach is also innovative with respect to parametric or semiparametric multidimensional IRT approaches typically based on maximum likelihood inference, as those described in Christensen et al. (2002) and Bartolucci (2007), and related papers. This is because we reduce the number of assumptions and avoid the specification of a parametric item response function. In this regard, it is also worth considering the approaches described in Junker and Sijtsma (2001), Vermunt (2001), and Karabatsos (2001).

The article is organized as follows. In the next section we formulate the nonparametric IRT model, corresponding to a constrained LC model, which is used to evaluate the dimensionality of a set of items. Then, we illustrate Bayesian inference for this model based on the RJ-MCMC algorithm, paying particular attention to the formulation of the prior distributions of the model parameters. This approach to assess dimensionality is illustrated through empirical examples based on both simulated and real data. The final section contains main conclusions.

We implemented the proposed approach in a series of Matlab functions that we make available to the reader upon request.

2 Model Formulation

Let $Y_{ij}$, $i=1,\ldots ,n$, $j=1,\ldots ,r$, denote the random variable corresponding to the binary response provided by the i-th subject to the j-th item. In the following, we briefly review the LC model for the distribution of these variables and then we introduce constrained versions of this model, which are formulated through suitable inequality constraints and may be seen as nonparametric IRT models. Furthermore, we compare this approach with that proposed by Bartolucci (2007), showing that the present one is more general.

2.1 Unconstrained Latent Class Model

The LC model assumes that the sample of respondents is drawn from a population divided into k latent classes, with individuals in the same class sharing the same distribution of the response variables (Lazarsfeld & Henry, 1968). Thus, for each subject i, the latent traits of interest, which in the educational setting correspond to certain types of ability, are represented by a discrete latent variable $C_i$ having k support points denoted, without loss of generality, by $1,\ldots ,k$. The model also assumes local independence (LI), that is, the response variables $Y_{i1},\ldots ,Y_{ir}$ are conditionally independent given $C_i$. Consequently, the model parameters are the class weights $\pi _1,\ldots ,\pi _k$, with $\pi _c=p(C_i=c)$, and $\lambda _{jc}=p(Y_{ij}=1|C_i=c)$ corresponding to the probability of success for the j-th item given class c, with $c=1,\ldots ,k$ and $j=1,\ldots ,r$. These parameters are common to all individuals, and then the previous definitions are independent of the specific i.

Before introducing constrained formulations of the LC model defined above, we recall the observed and complete data log-likelihood functions of this unconstrained model, which are required for inference. With reference to an observed matrix of data ${\varvec{Y}}$, with elements $y_{ij}$, $i=1,\ldots ,n$, $j=1,\ldots ,r$, corresponding to realizations of the random variables $Y_{ij}$, the observed log-likelihood is defined as

$$\begin{aligned} \ell ({\varvec{Y}}|\varvec{\Lambda },\varvec{\pi }) = \sum _{i=1}^n\log \left[ \sum _{c=1}^k \pi _c \prod _{j=1}^r\lambda _{jc}^{y_{ij}}(1-\lambda _{jc})^{1-y_{ij}} \right] , \end{aligned}$$

(1)

where $\varvec{\Lambda }$ is the $r\times k$ dimensional matrix of the conditional probabilities $\lambda _{jc}$ and $\varvec{\pi }$ is the k-dimensional vector of the class weights $\pi _c$. Note that, due to the LI assumption, $\prod _{j=1}^r\lambda _{jc}^{y_{ij}}(1-\lambda _{jc})^{1-y_{ij}}$ in (1) corresponds to the conditional probability of the responses provided by subject i given that he/she belongs to latent class c; these responses are collected in the vector ${\varvec{y}}_i$.

In order to define the complete data log-likelihood, we introduce the latent class indicators $z_{ic}$, $i=1,\ldots ,n$, $c=1,\ldots ,k$, where $z_{ic}=1$ if the i-th subject belongs to latent class c and $z_{ic}=0$ otherwise; see for instance Diebolt and Robert (1994). Then, augmenting the data with these indicator variables, we write the complete log-likelihood as

$$\begin{aligned} \ell _C({\varvec{Y}}, {\varvec{Z}}|\varvec{\Lambda },\varvec{\pi }) = \ell ({\varvec{Y}}|{\varvec{Z}},\varvec{\Lambda })+\ell ({\varvec{Z}}|\varvec{\pi }). \end{aligned}$$

The first addend at the right hand side is equal to

$$\begin{aligned} \sum _{c=1}^k\sum _{i=1}^n\sum _{j=1}^r z_{ic} [y_{ij}\log \lambda _{jc}+(1-y_{ij})\log (1-\lambda _{jc})], \end{aligned}$$

as only the Bernoulli log-likelihoods corresponding to $z_{ic}=1$ must be considered. The second addend corresponds to the usual log-likelihood of multinomial distributions. Hence the complete, or augmented, log-likelihood can be written as

$$\begin{aligned} \ell _\mathrm{C}({\varvec{Y}}, {\varvec{Z}}|\varvec{\Lambda },\varvec{\pi }) = \sum _{c=1}^k\sum _{i=1}^n\sum _{j=1}^r z_{ic} [y_{ij}\log \lambda _{jc}+(1-y_{ij})\log (1-\lambda _{jc})]+\sum _{c=1}^k z_{ic}\log \pi _c. \end{aligned}$$

(2)

In the following, an LC model based on k classes is denoted by $\mathrm{LC}(k)$ when its parameters $\lambda _{jc}$ are unconstrained.

2.2 Constrained Latent Class Model

In the proposed nonparametric IRT setting and using the previous notation, two items, $j_1$ and $j_2$, are said to measure the same dimension if there exists a permutation of the indices $1,\ldots ,k$, denoted by ${\varvec{c}}=(c_1,\ldots ,c_k)$, such that

$$\begin{aligned} \lambda _{jc_1}< \cdots < \lambda _{jc_k}, \quad j=j_1,j_2. \end{aligned}$$

(3)

In other words, the success probabilities of the two items are ordered in the same way. This property may be referred to a set of items with size larger than two and may be easily understood considering the case of $k=2$ latent classes. In this case, items $j_1$ and $j_2$ measure the same latent trait if the classes are ordered in the same way in terms of probability of success with respect to both items, that is, if

$$\begin{aligned} \lambda _{j_11}<\lambda _{j_12}\quad \hbox {and}\quad \lambda _{j_21}<\lambda _{j_22} \end{aligned}$$

or

$$\begin{aligned} \lambda _{j_11}>\lambda _{j_12}\quad \hbox {and}\quad \lambda _{j_21}>\lambda _{j_22}. \end{aligned}$$

On the basis of the above arguments, we define an s-dimensional nonparametric IRT model as an LC model for which a partition $\mathcal{P}=\{\mathcal{J}_1,\ldots ,\mathcal{J}_s\}$ of the full set of items exists such that:

• A1. condition (3) holds for every pair of items $(j_1,j_2)\in \mathcal{J}_d$, $d=1,\ldots ,s$, based on a unique permutation ${\varvec{c}}^{(d)}=(c_1^{(d)},\ldots ,c_k^{(d)})$;

• A2. ${\varvec{c}}^{(d_1)}\ne {\varvec{c}}^{(d_2)}$, for all $d_1,d_2=1,\ldots ,s$, with $d_1\ne d_2$.

In practice, any pair of items $(j_1,j_2)$ is assumed to measure the same dimension, so that the latent classes are ordered in the same way according to the conditional success probabilities $\lambda _{j_1c}$ and $\lambda _{j_2c}$, if the items are in the same subset $\mathcal{J}_d$. On the other hand, these conditional success probabilities are ordered in a different way when the items belong to two different subsets $\mathcal{J}_{d_1}$ and $\mathcal{J}_{d_2}$, and then they measure two different latent traits (or dimensions). An obvious consequence is that, under the unidimensional model, the latent classes are ordered in the same way according to all items. Moreover, there is a relation between the number of latent classes k and the model dimension s. In particular, it may be simply proved that $s\le \min (k!,r)$, where $k!=k(k-1)\cdots 1$ is the number of possible permutations of k elements.

Under assumptions A1 and A2, the observed log-likelihood for the constrained LC model has the same expression as in (1) and the corresponding complete log-likelihood is as in (2). Moreover, it is clear that any nonparametric IRT model defined above depends on k and a specific partition of items $\mathcal{P}$ made of s subsets $\mathcal{J}_1,\ldots ,\mathcal{J}_s$. This model is then denoted by $\mathrm{LC}(k,\mathcal{P})$ and we also use the symbol $|\mathcal{P}|$ for the number of subsets in partition $\mathcal{P}$. In this regard it is worth noting that our definition, based on condition (3), rules out the case of equality between two probability parameters $\lambda _{jc_1}$ and $\lambda _{jc_2}$ for $c_1,c_2=1,\ldots ,k$, with $c_1\ne c_2$. This constraint is necessary to avoid a possible ambiguity due to the lack of uniqueness of ${\varvec{c}}^{(d)}$ considered in assumption A1 for some dimension d. However, such a constraint has no practical relevance in our Bayesian inferential framework as the probability that $\lambda _{jc_1}=\lambda _{jc_2}$ is equal to 0 for any j and any pair $(c_1,c_2)$.

2.3 Comparison with the Semiparametric Approach

The previous characterization of a model measuring s dimensions is completely nonparametric, in contrast with the one in Bartolucci (2007) that is based on a parametric formulation for the success probabilities $\lambda _{jc}$ of 2PL type. The latter amounts to assume that

$$\begin{aligned} \mathrm{logit}\,(\lambda _{jc}) = \gamma _j \left( \sum _{d=1}^s \delta _{jd} \theta _{cd} - \phi _j\right) ,\quad c=1,\ldots ,k,\,j=1,\ldots ,r, \end{aligned}$$

(4)

where $\delta _{jd}$ is an indicator of item grouping, which is equal to 1 if item j measures dimension d ($j\in \mathcal{J}_d$) and to 0 otherwise. Moreover, $\theta _{cd}$ corresponds to the ability of the subjects in class c in answering correctly to the items measuring dimension d, while $\gamma _j$ and $\phi _j$ may be interpreted as the discriminating power and the difficulty of the j-th item, respectively.

In order to prove that, being based on parametric assumption (4), the formulation in Bartolucci (2007) is less general than ours, suppose that $\delta _{j_1d}=\delta _{j_2d}=1$, that is, items $j_1$ and $j_2$ belong to the same group $\mathcal{J}_d$, and for both of them such an assumption is satisfied. Suppose, without loss of generality, that $k=2$ and that $\theta _{1d}<\theta _{2d}$. A simple consequence is that

$$\begin{aligned} \gamma _j \left( \theta _{1d}-\phi _j\right) < \gamma _j \left( \theta _{2d}-\phi _j\right) ,\quad j=j_1,j_2, \end{aligned}$$

implying that

$$\begin{aligned} \mathrm{logit}\,(\lambda _{j1})< \mathrm{logit}\,(\lambda _{j2})\quad \iff \quad \lambda _{j1} < \lambda _{j2},\quad j=j_1,j_2; \end{aligned}$$

that is, the items belong to the same group also according to our characterization based on (3). On the other hand, it is obvious that even if for two items this inequality holds, this does not imply that the corresponding conditional success probabilities satisfy (4).

Note that the same reasoning applies, for instance, to the approaches of Martin-Löf (1973) and Christensen et al. (2002), which are even more constrained, being based on a Rasch parametrization of the conditional success probabilities, which is a particular case of (4) with all parameters $\gamma _j$ equal to 1.

3 Bayesian Inference

In this section, we introduce a flexible class of prior distributions for the parameters of the LC models defined in the previous section, with particular attention to the conditional success probabilities given the latent class, $\lambda _{jc}$. Consequently, we illustrate the RJ-MCMC algorithm that is adopted to simulate the joint posterior distribution of the model parameters and that is used for Bayesian estimation and testing, after a suitable post-processing of its output.

3.1 Prior Distributions

It is clear that any constrained LC model (or equivalently nonparametric IRT model) of type $\mathrm{LC}(k,\mathcal{P})$ is nested in the model $\mathrm{LC}(k)$ having the same number of classes and in which the probabilities $\lambda _{jc}$ are left unconstrained. Then, once the priors have been specified for the latter model, we can “automatically” specify those of any nested model through the encompassing approach (Klugkist et al., 2005): prior distributions for nested models are derived by truncating the parameter space according to the constraints of interest; see also Bartolucci et al. (2012). In practice, let $p(\varvec{\Lambda }, \varvec{\pi }|\mathrm{LC}(k))$ represent the encompassing prior, that is the prior specified for the encompassing $\mathrm{LC}(k)$ model. The prior distribution of any nested model $\mathrm{LC}(k,\mathcal{P})$ follows directly as

$$\begin{aligned} p(\varvec{\Lambda }, \varvec{\pi }|\mathrm{LC}(k,\mathcal{P})) = \frac{p(\varvec{\Lambda }, \varvec{\pi }|\mathrm{LC}(k))I\{\varvec{\Lambda }, \varvec{\pi }|\mathrm{LC}(k,\mathcal{P})\}}{\int \int p(\varvec{\Lambda }, \varvec{\pi }|\mathrm{LC}(k))I\{\varvec{\Lambda }, \varvec{\pi }|\mathrm{LC}(k,\mathcal{P})\}\hbox {d}\varvec{\Lambda }\,\hbox {d} \varvec{\pi }}, \end{aligned}$$

(5)

where the indicator function $I\{\varvec{\Lambda }, \varvec{\pi }|\mathrm{LC}(k,\mathcal{P})\}$ has value 1 if its argument is true (i.e., the parameter values are in accordance with the constraints imposed by model $\mathrm{LC}(k,\mathcal{P})$) and 0 otherwise. In other words, the prior of a certain constrained model is obtained by imposing a zero value to the prior of the encompassing model for all parameter values that do not respect the constraints of interest. This prior is then normalized to integrate to 1 over the restricted parameter space.

For the encompassing model, Bayes–Laplace priors are a natural choice for the success probabilities and class weights (Tuyl et al., 2009). This choice reduces to a uniform prior between 0 and 1 for $\lambda _{jc}$, $j=1,\ldots ,r$, $c=1,\ldots ,k$, while for the class weights $\pi _c$ it corresponds to a Dirichlet distribution with vector of hyper-parameters having all elements equal to 1. Finally, a discrete uniform prior can be used for the number of classes k in the discrete set $1,\ldots ,k_{\tiny \text {max}}$, where ${k_{\tiny \text {max}}}$ is the maximum value of k that is allowed. With small samples, large values of k could be penalized by using a Poisson prior with a small hyper-parameter value. Note however that, while we retain the standard choice for the priors of parameters k and $\pi _c$, we adopt a different system of priors for the success probabilities $\lambda _{jc}$, as illustrated in detail in the following.

3.2 A Flexible Class of Priors for the Success Probabilities

It is worth noting that, according to the encompassing approach, the prior on the success probabilities $\lambda _{jc}$ “automatically” determines the prior probability of any specific partition $\mathcal{P}$, as well as the prior distribution of the number of groups s. In fact, the prior probability $p(\mathcal{P}|k)$ of a specific partition $\mathcal{P}$ is simply the double integral at the denominator of (5), while p(s|k) can be obtained by summing up the probabilities $p(\mathcal{P}|k)$ over all those partitions for which $|\mathcal{P}|=s$. Notice that under a uniform prior for $\lambda _{jc}$, $p(\mathcal{P}|k)$ and p(s|k) can be easily calculated; see “Appendix” for details.

The above point implies that the choice of the prior on the $\lambda _{jc}$ parameters deserves some more reasoning, since it might favor a certain partition or a certain number of groups. Despite the simplicity of a uniform prior on these parameters and the consequent simplifications for the RJ-MCMC algorithm, such a choice might be not completely meaningful. This is particularly true if the main purpose of the analysis is testing the hypothesis of unidimensionality, as a uniform prior on the $\lambda _{jc}$ determines a prior on s which often assigns a small probability to the null hypothesis. To clarify this point, Table 1 shows the prior distribution for s, as determined by a uniform prior on the $\lambda _{jc}$, both conditionally on k and marginally, with reference to a hypothetic set of $r=12$ items (the same number of items as one of the datasets considered in our applications) and setting $k_{\tiny \text {max}}=10$. The values in the table have been calculated as explained in “Appendix.”

An unconditional prior probability of 0.1 is given to the hypothesis of unidimensionality under a uniform prior on the $\lambda _{jc}$ parameters. To make the point even clearer, consider that for $r=3$ and $k=2$, we would have $p(s=1|k=2)=0.25$, meaning that, even with just three items and two latent classes, the probability that all items belong to the same dimension would be quite small.

Table 1 Conditional and unconditional prior distribution of the number of partitions, as determined by a uniform prior on the success probabilities, when $r=12$ and $k_{\tiny \text {max}}=10.$

For the reasons above, we propose a flexible class of priors for the success probabilities $\lambda _{jc}$, which is defined as

$$\begin{aligned} \lambda _{jc}\sim \hbox {Beta}(\alpha _c,\beta _c),\quad c=1,\ldots ,k,\, j=1,\ldots ,r, \end{aligned}$$

(6)

where the parameters $\alpha _c$ and $\beta _c$ are given by

$$\begin{aligned} \alpha _c = v_{\alpha }c+1,\quad \beta _c=v_{\beta }(k+1-c)+1, \quad c=1,\ldots ,k, \end{aligned}$$

(7)

with $v_{\alpha }$ and $v_{\beta }$ being hyper-parameters with values to be appropriately chosen. With such a prior, the expected value of $\lambda _{jc}$ increases with c, while its variance is approximately the same for all c and rapidly decreases as k increases. In order to choose $v_{\alpha }$ and $v_{\beta }$, it should be noted that

$$\begin{aligned} \mathrm{E}[\lambda _{jc}]= & {} (v_{\alpha }c+1)/[v_{\alpha }c+2+v_{\beta }(k+1-c)], \end{aligned}$$

(8)

$$\begin{aligned} \mathrm{Var}[\lambda _{jc}]= & {} \alpha _c\beta _c/[(\alpha _c+\beta _c)^2(\alpha _c+\beta _c+1)]. \end{aligned}$$

(9)

Hence, it is natural to calibrate these hyper-parameters so that the expected values of the success probabilities are reasonably centered and well separated, and these parameters have a reasonable variability a priori. Note that one might choose an expected value and variance for one fixed c (e.g., $c=1$) and then obtain $v_{\alpha }$ and $v_{\beta }$ by inverting functions (8) and (9).

The choice of the prior parameters obviously involves an arbitrary decision regarding p(s). A possible solution to overcome this problem would be to assign hyper-priors to $v_{\alpha }$ and $v_{\beta }$, assuming for instance that they are Gamma distributed. This would allow extra flexibility to the model and cope with uncertainty about these parameters. In this way, in fact, the shrinkage parameters would be chosen by the data. In the present context, however, we consider the free choice of the shrinkage parameters as an advantage of the model rather than a problem to be solved. By varying the shrinkage parameters, in fact, we can assign a measure to the strength of our personal belief in the unidimensionality of the data generating model.

The prior distribution defined in (6) is particularly flexible, since with adequate choices it might both deliver an approximately uniform prior on s (Table 2), which is advisable for explorative purposes, or a prior which assigns a reasonable probability to $s=1$ (Table 3), which can be adopted in testing the hypothesis of unidimensionality. The prior in (6) includes the uniform prior as a special case (for $v_{\alpha }=v_{\beta }=0$). The results in Tables 2 and 3 have been obtained by running the RJ-MCMC algorithm, described in the following section, always sampling from the prior (i.e., without data). Our post-processing algorithm has then been used to evaluate the conditional and unconditional distribution of s.

As a final remark, notice that the prior in (6) is not invariant with respect to the relabeling of the classes, unless $v_\alpha =v_\beta =0$. This determines, in turn, a joint posterior which is not invariant to relabeling and should prevent from label switching in the RJ-MCMC algorithm that simulates the posterior distribution of the model parameters.

Table 2 Simulated conditional and unconditional prior distribution of the number of partitions, as determined by a Beta prior with $v_{\alpha }=v_{\beta }=3$ on the success probabilities, when $r=12$ and $k_{\tiny \text {max}}=10$.

Table 3 Simulated conditional and unconditional prior distribution of the number of partitions, as determined by a Beta prior with $v_{\alpha }=v_{\beta }=14$ on the success probabilities, when $r=12$ and $k_{\tiny \text {max}}=10$.

In conclusion, it is worth recalling that Klugkist et al. (2005) deeply discussed the sensitivity of inferential results to the specification of the encompassing prior. In particular, they stated that a vague encompassing prior, conceived not to favor any particular parameter ordering, determines a virtually objective model selection. In our setting, such a prior would be a uniform prior between 0 and 1 for $\lambda _{jc}$, $j=1,\ldots ,r$, $c=1,\ldots ,k$, which assigns the same probability to any ordering of the $\lambda _{jc}$, conditionally on k (see “Appendix”). However, the main purpose of this paper is to make inference on the number of dimensions s, rather than on a particular ordering of the parameters such as in Klugkist et al. (2005). Thus, as already discussed, a uniform prior on the success probabilities is not advisable, since it would assign a very small prior probability to models of interest (for example the unidimensional model). Obviously, also the prior specified in (6) is expected to affect inferential results, since the choice of $v_{\alpha }$ and $v_{\beta }$ may determine very different values of p(s). For this reason, a sensitivity analysis to evaluate the effect on the results of different choices of $v_\alpha$ and $v_\beta$ is highly recommended. Notice, however, that due to the type of inequality constraints considered in (3), model selection should not be as strongly affected by the encompassing prior, as it would be in the case of approximate equality constraints. For this kind of constraints, the evidence in favor of the constrained model is known to increase with the amount of vagueness of the encompassing prior, a phenomenon known as Bartlett’s or Lindley’s paradox (Lindley, 1957).

3.3 Reversible Jump Implementation

The complexity of the model presented above makes the joint posterior of all parameters, including k, analytically intractable, due to the high-dimensional integrals needed to evaluate its normalizing constant. Therefore, we resort to an RJ-MCMC method to approximate this posterior distribution (Green, 1995; Green & Richardson, 2001). In general, MCMC methods allow us to sample from a probability distribution, known up to its normalizing constant. They are based on the construction of an irreducible and aperiodic Markov chain that has the desired distribution as its equilibrium distribution. Details of these computational methods can be found in Tierney (1994). In particular, the RJ-MCMC is an extension of a standard MCMC algorithm that may be used to draw values from a probability distribution defined on parameter spaces of varying dimension. Thus, in our framework, it permits to simulate the posterior distribution even when the number of latent classes, k, is unknown.

The RJ-MCMC sampler performs T sweeps and, at each sweep t, all the parameters, including k, are updated in turn. This is performed by drawing the new values of certain parameters conditionally on the data and all the other parameters. The algorithm uses different fixed-dimension moves to update the model parameters, conditionally on a fixed k, further to two different variable dimension moves to update the number of latent classes k. In particular, updating the value of k implies a change of dimensionality for the success probabilities, the class weights, and the allocation variables. We accomplish this by introducing two different types of RJ move. The first one consists of a random choice between splitting an existing class in two and merging two existing classes into one. The second one consists of a random choice between the birth of an empty class or the death of an empty class. The probabilities of the split/merge alternatives are $b_k$ and $d_k = 1 - b_k$, respectively, and depend only on the current value of k. Of course, $d_1 = 0$ and $b_{k_{\tiny \text {max}}} = 0$; otherwise we choose $b_k = d_k = 0.5$, for $k = 2,\ldots , k_{\tiny \text {max}}- 1$. The same probabilities $b_k$ and $d_k$ are used for the birth/death alternatives, while a probability of 0.5 is used for choosing between a split/combine or a death/birth move.

A schematic description of the algorithm is provided below, where $q(\cdot |\cdot )$ is used to denote an appropriate proposal distribution used in the Metropolis-Hastings steps for a certain parameter vector, while $p(\cdot |\cdots )$ is the full conditional distribution in the Gibbs sampling steps, with “$\cdots$” standing for “all other parameters and data”; moreover, t is the sweep counter and T is the overall number of sweeps. A more detailed illustration of the algorithm, in which all quantities used below are precisely defined, is given in “Appendix.”

The algorithm presented above is quite standard. See, for example, Pan and Huang (2014) for an implementation of the RJ-MCMC algorithm to an LC model for polytomous response variables. On the other hand, the post-processing algorithm, applied to the RJ-MCMC output to assess dimensionality and illustrated in the next section, is completely innovative.

3.4 Post-processing for Assessing Model Dimension

In practice, the RJ-MCMC sampling algorithm outlined in the previous section is used to approximate the joint posterior distribution of the model parameters. It is important to underline that the algorithm also updates the success probabilities without imposing any constraint on them; therefore, the simulated joint posterior distribution we obtain is that of the unconstrained (encompassing) $\mathrm{LC}(k)$ model, for $k=1,\ldots ,k_{\tiny \text {max}}$. In order to obtain the posterior probability of any constrained model $\mathrm{LC}(k,\mathcal{P})$ and to assess dimensionality, we then need to post-process the simulated posterior distribution. In practice, for each sweep of the RJ-MCMC algorithm, we need to verify the particular partition $\mathcal{P}$ with which the success probabilities $\lambda _{jc}$ are in accordance, following the definition given in the previous section and based on assumptions A1 and A2. This also indicates the dimension of the model visited at each sweep. The proposed post-processing method is described below.

Let $k^{(t)}$ be the number of classes of the model visited at sweep t of the RJ-MCMC algorithm and let $\varvec{\Lambda }^{(t)}$ and $\varvec{\pi }^{(t)}$ be the simulated parameters of this model, with $t=1,\ldots ,T$. Then, we examine every matrix $\varvec{\Lambda }^{(t)}$ and we obtain the corresponding partition $\mathcal{P}^{(t)}$ made of the subsets of items $\mathcal{J}_1^{(t)},\ldots ,\mathcal{J}_{s^{(t)}}^{(t)}$ such that A1 and A2 hold; thus, the model measures $s^{(t)}=|\mathcal{P}^{(t)}|$ different dimensions. To avoid a sort of label-switching problem, the groups are ordered so that $\mathcal{J}_1^{(t)}$ includes the first item, $\mathcal{J}_2^{(t)}$ includes the item with the smallest index among those excluded from $\mathcal{J}_1^{(t)}$, and so on.

More in detail, at each sweep t, let ${\varvec{P}}^{(t)}$ be a matrix of zeros, having a number of rows equal to $\min (k^{(t)}!,r)$, which corresponds to the maximum possible model dimensions given k and r, and a number of columns equal to $k^{(t)}$. Let ${\varvec{p}}_d^{(t)}$ indicate the d-th row vector of ${\varvec{P}}^{(t)}$. Initialize the post-processing algorithm by considering the first item and finding the permutation ${\varvec{c}}^{(1)}=(c_1^{(1)},\ldots ,c_k^{(1)})$ such that $\lambda _{1c_1}^{(t)}< \cdots < \lambda _{1c_k}^{(t)}$. Set ${\varvec{p}}^{(t)}_1= {\varvec{c}}^{(1)}$, $s^{(t)}=1$, $j=1$ and allocate the first item to $\mathcal{J}_1^{(t)}$. Then the proposed post-processing algorithm proceeds as follows:

Finally, the posterior probability of model LC$(k,\mathcal{P})$ with a certain number of classes k and a certain partition of items $\mathcal{P}=\{\mathcal{J}_1,\ldots ,\mathcal{J}_s\}$ is estimated as:

$$\begin{aligned} p(k,\mathcal{P}|{\varvec{Y}})= & {} \frac{1}{T} \sum _{t=1}^TI\left\{ k^{(t)}=k,\mathcal{P}^{(t)}=\mathcal{P}\right\} \\= & {} \frac{1}{T} \sum _{t:s^{(t)}=s}I\left\{ k^{(t)}=k,\mathcal{J}_1^{(t)}=\mathcal{J}_1,\ldots , \mathcal{J}_{s^{(t)}}^{(t)}=\mathcal{J}_s\right\} , \end{aligned}$$

where the sum is over all sweeps for which $s^{(t)}=s$.

3.5 Testing Unidimensionality

The above RJ-MCMC output post-processing can also be used to obtain posterior probabilities or Bayes factors (BFs; Kass & Raftery, 1995), which may be used to test the unidimensionality hypothesis. The conditional posterior probability of the number of dimensions can be readily obtained as

$$\begin{aligned} p(s|k,{\varvec{Y}}) = \frac{\sum _{t=1}^TI\left\{ k^{(t)}=k,s^{(t)}=s\right\} }{\sum _{t=1}^TI\left\{ k^{(t)}=k\right\} }. \end{aligned}$$

(10)

Otherwise, using model averaging principles, we can estimate the marginal posterior distribution of s as

$$\begin{aligned} p(s|{\varvec{Y}}) = \frac{1}{T}\sum _{t=1}^TI\left\{ s^{(t)}=s\right\} . \end{aligned}$$

(11)

From (10) and (11) we obtain, respectively, $p(s=1|k,{\varvec{Y}})$ and $p(s=1|{\varvec{Y}})$, that is, the conditional and marginal posterior probability of the unidimensional model. In order to get the corresponding BFs, we need p(s|k) and p(s), which can both be obtained by simulation, as already explained. Given that we use the encompassing prior approach, the BFs are in fact obtained as the ratio of posterior and prior probabilities of the restricted model.

3.6 Other Elaborations of the Simulated Posterior Distribution

The proposed approach, and in particular the simulated posterior distribution obtained from the algorithm described above, can also be used for certain elaborations that are typical of IRT applications.

First of all, for a given k and s, it is possible to characterize the latent classes in terms of probability of success and weight. For this aim, we rely on the Bayesian estimates of the parameters $\lambda _{jc}$, that is,

$$\begin{aligned} \hat{\lambda }_{jc}(k,s)=\frac{\sum _{t=1}^T\lambda _{jc}^{(t)}I\{k^{(t)}=k,s^{(t)}=s\}}{\sum _{t=1}^T I\{k^{(t)}=k,s^{(t)}=s\}}, \quad j=1,\ldots ,r,\,c=1,\ldots ,k, \end{aligned}$$

(12)

and the parameters $\pi _c$, that is,

$$\begin{aligned} \hat{\pi }_c(k,s)=\frac{\sum _{t=1}^T\pi _c^{(t)}I\{k^{(t)}=k,s^{(t)}=s\}}{\sum _{t=1}^T I\{k^{(t)}=k,s^{(t)}=s\}}, \quad c=1,\ldots ,k. \end{aligned}$$

(13)

This characterization is particularly useful, for instance, in educational assessment, where the probability of success is a measure of the ability of individuals in a certain class. On the other hand, the weight corresponds to the proportion of individuals in the class, and then of examinees with a certain ability level. For this aim, we can also use the unconditional (with respect to the model dimension) posterior estimates, so as to evaluate the impact of imposing a certain number of dimensions on the latent class identification. This amounts to use the following expressions

$$\begin{aligned} \hat{\lambda }_{jc}(k)= & {} \frac{\sum _{t=1}^T\lambda _{jc}^{(t)}I\{k^{(t)}=k\}}{\sum _{t=1}^T I\{k^{(t)}=k\}},\\ \hat{\pi }_c(k)= & {} \frac{\sum _{t=1}^T\pi _c^{(t)}I\{k^{(t)}=k\}}{\sum _{t=1}^TI\{k^{(t)}=k\}}, \end{aligned}$$

instead of (12) and (13). Alternatively, it is possible to compute these estimates given a certain partition of items $\mathcal{P}$ and not just conditionally on the number of dimensions.

Another relevant elaboration leads to clustering individuals on the basis of the response configuration they provide, so as to produce an estimate of their ability level. More precisely, for a certain value of k and s, it is possible to estimate the conditional probability that individual i belongs to latent class c given the response configuration ${\varvec{y}}_i$ he/she provided, with $i=1,\ldots ,n$ and $c=1,\ldots ,k$. This estimate is obtained as

$$\begin{aligned} \hat{\pi }_c(k,s,{\varvec{y}}_i) = \frac{\sum _{t=1}^T I\{z_{ic}^{(t)}=1,k^{(t)}=k,s^{(t)}=s\}}{\sum _{t=1}^T I\{k^{(t)}=k,s^{(t)}=s\}}, \end{aligned}$$

(14)

where $z_{ic}^{(t)}$ is the value of the indicator variable $z_{ic}$ at the t-th sweep of the RJ-MCMC algorithm. In practice $z_{ic}^{(t)}=1$ if, for this sweep, individual i has been assigned to latent class c and $z_{ic}^{(t)}=0$ otherwise. Then, this individual is assigned to the class corresponding the highest value of $\hat{\pi }_c(k,s,{\varvec{y}}_i)$ or, equivalently, to the class with the largest number of visits. In a simple way, we can also use different conditioning arguments and, for instance, obtain the estimate of the conditional probability of belonging to class c given ${\varvec{y}}_i$ and k only, namely $\hat{\pi }_c(k,{\varvec{y}}_i)$. Moreover, if more individuals have the same response configuration, we can average $\hat{\pi }_c(k,s,{\varvec{y}}_i)$ or $\hat{\pi }_c(k,{\varvec{y}}_i)$ over the subsample of these individuals to obtain more stable results.

Finally, if the dataset includes individual covariates, corresponding for instance to gender or describing the family background, it may be of interest to relate the probabilities of belonging to a certain class to these covariates to understand, for instance, the effect of these covariates on the ability in an educational application. This may be based on computing the previous estimates for separate covariate configurations and then making suitable comparisons. However, this comparison is outside the scope of the present paper, whose main focus is on the assessment of dimensionality of a certain questionnaire from an IRT perspective.

4 Applications

To illustrate the proposed approach we consider four examples. The first two are based on different datasets simulated from a unidimensional model and from a multidimensional model. In this way, we assess the capability of the proposed algorithm in recovering these two situations and the correct partition of items in the multidimensional case. The third application is based on educational data for assessment in Mathematics, while the fourth considers hospital anxiety and depression data.

4.1 Simulated Data: Unidimensional Case

For the first example, we set $n=500$, $r=10$, $k=4$, $v_\alpha =4$, and $v_\beta =4$, and we generated an $r\times k$ matrix $\varvec{\Lambda }$ according to (6), ordering all conditional probabilities $\lambda _{jc}$ in the same way, so that unidimensionality is attained. Then, we drew $\varvec{\pi }$ from its prior and allocated each subject i to latent class c with probability $\pi _c$, $c=1,\ldots ,k$; this amounts to suitably define the indicator variables $z_{ic}$, $i=1,\ldots ,n$, $c=1,\ldots ,k$. Finally, we simulated the data ${\varvec{Y}}$ by letting, for $i=1,\ldots ,n$ and $j=1,\ldots ,r$, $y_{ij}=1$ with probability $\lambda _{jc}$, where c is the class to which subject i is allocated ($z_{ic}=1$).

Based on the simulated data, we ran 150,000 sweeps of the proposed RJ-MCMC algorithm after a burn-in of 50,000 sweeps and considered models with a number of latent classes up to $k_{\tiny \text {max}}= 10$. Table 4 shows the simulated posterior distribution $p(k|{\varvec{Y}})$. Considering that the prior for k is a discrete uniform distribution between 1 and $k_{\tiny \text {max}}$, the data provide evidence in favor of the model with $k=4$ latent classes.

Table 4 Estimated posterior probabilities of the number of latent classes.

Regarding dimensionality, Table 5 provides the (conditional) prior and posterior probabilities of s, as well as the BFs. We note that the unidimensional model is visited around 64% of times and is the one with the highest posterior probability, confirming that, at least in this case, the proposed strategy works properly.

Table 5 Prior and posterior probabilities of s, and BFs.

In order to check the convergence of the posterior distributions $p(k|{\varvec{Y}})$ and $p(s|k,{\varvec{Y}})$ to the real values of k and s, as the sample size increases, we considered a small Monte Carlo study. Under the same settings and the same parameters $\varvec{\Lambda }$ and $\varvec{\pi }$ as above, we considered increasing sample sizes: $n= 500, \; 750, \; 1000$. For each sample size, we generated ten different datasets. Each dataset was obtained by drawing the allocation variables $z_{ic}$, $i=1,\ldots ,n$, $c=1,\ldots ,k$, and the data ${\varvec{Y}}$ as described above. For each dataset we then ran the RJ-MCMC algorithm and for every parameter we calculated the root-mean-squared error (RMSE); the RMSE for s, $\varvec{\pi }$, and $\varvec{\Lambda }$ were calculated conditionally on $k=4$. Table 6 shows these RMSEs, averaged over the 10 replications, for increasing values of n. As expected, for all parameters the RMSEs tend to decrease as n increases. In particular, the posterior distribution of the number of dimensions becomes more and more concentrated on its true value $s=1$, corresponding to the unidimensionality hypothesis. Also notice that, out of the 10 replications and for $n=500, 750, 1000$, the number of latent classes was correctly recovered 8, 10, and 10 times, respectively, and the number of dimensions was correctly recovered 7, 9, and 9 times, respectively.

Table 6 RMSE for each parameter, averaged over 10 replications, for increasing values of n.

4.2 Simulated Data: Multidimensional Case

For the multidimensional case, we set $r=10$, $k=4$, $v_\alpha =1.5$, and $v_\beta =1.5$, and we generated a unique $r\times k$ matrix $\varvec{\Lambda }$ according to (6). Post-processing of this matrix revealed the following partition of the items into $s=4$ groups: $\{(1, 6),(2,8),(4,5),(3,7,9,10)\}$. Then we drew class weights, allocation variables, and data as in the previous example. Finally, for the simulated data we ran 150 000 sweeps of the proposed algorithm after a burn-in of 50 000 sweeps, and let $k_{\tiny \text {max}} = 10$.

Table 7 Estimated posterior probabilities of the number of latent classes.

Table 7 shows the posterior distribution $p(k|{\varvec{Y}})$, from which the model with $k=4$ latent classes seems to be favored. Table 8 provides the prior and posterior probabilities of s, and the BFs. The unidimensional model is rarely visited, and the model with the highest posterior probability is the one with $s=4$ groups, corresponding to the true number of dimensions. The partitions into four groups receiving the highest BF (1.74) were those having three groups of two items each and a group of four items. Among these a priori equally probable partitions, the most visited one (15% of times) is the correct one, that is, $\{(1, 6),(2,8),(4,5),(3,7,9,10)\}$. The second most visited partition is $\{(1, 6),(7,8),(4,5),(2,3,9,10)\}$, which only differs from the correct one for the switching between items 2 and 7, and has a simulated posterior probability (conditional on k, s, and type of partition) of 0.11.

Table 8 Prior and posterior probabilities of s, and BFs.

Also for the multidimensional case, we checked the convergence of the posterior distributions to the real values of the parameters, as the sample size increases. Under the same settings and the same $\varvec{\Lambda }$ and $\varvec{\pi }$ as above, we considered increasing sample sizes and for each of them, we generated ten different datasets. Table 9 shows the RMSE for each parameter, averaged over the 10 replications, for increasing values of n. As for the unidimensional case, the RMSEs tend to decrease as n increases and the posterior distribution of the number of dimensions becomes more and more concentrated on its true value $s=4$. Out of the 10 replications for $n=500, 750, 1000$, respectively, the number of latent classes was correctly recovered 9, 10, and 10 times, the number of dimensions was correctly recovered 8, 8, and 9 times, while the correct partition was correctly recovered 5, 5, and 6 times.

Table 9 RMSE for each parameter, averaged over 10 replications, for increasing values of n.

4.3 An Application in Educational Assessment

The proposed approach is applied to the analysis of a dataset concerning a sample of $n = 1510$ examinees who responded to a set of $r = 12$ items on Mathematics, the same dataset analyzed in Bartolucci (2007).

The 12 items concern the following subjects:

• 1. Round to thousand place;

• 2. Write fraction that represents shaded region;

• 3. Multiply two negative integers;

• 4. Reason about sample space (number correct);

• 5. Find amount of restaurant tip;

• 6. Identify representative sample;

• 7. Read dials on a meter;

• 8. Find (x; y) solution of linear equation;

• 9. Translate words to symbols;

• 10. Find number of diagonals in polygon from a vertex;

• 11. Find perimeter (quadrilateral);

• 12. Reason about betweenness.

This dataset, available in the R package MultiLCIRT (Bartolucci et al., 2016), is part of a larger dataset collected in 1996 by the Educational Testing Service within the NAEP project; see Bartolucci and Forcina (2005) for a more detailed description.

We considered models with a number of latent classes up to $k_{\tiny \text {max}} = 10$ under assumption (6), with $\alpha _c$ and $\beta _c$, $c=1,\ldots ,k$, fixed according to the rule in (7). In this regard we recall that it is necessary to fix $v_{\alpha }$ and $v_{\beta }$ and we calibrated them for a specific, most likely k. In particular, we considered $k=4$ latent classes as found in Bartolucci (2007) and we looked for prior parameters such that the four latent classes are reasonably separated, and variances are relatively small, with $v_{\alpha }$ and $v_{\beta }$ taken from a grid of possible values. Our final choice is $v_\alpha =2.5$ and $v_\beta =1$ and leads to an expected value of the vector of the $\lambda _{jc}$ parameters equal to $(0.2000, \; 0.5385,\; 0.7500, \; 0.8947)$, computed according to (8), and corresponding variances equal to $(0.0267, \; 0.0331,\; 0.0208, \; 0.0090)$, computed according to (9).

We then proceeded, as for the previous examples, with 150 000 sweeps of the RJ-MCMC algorithm after a burn-in of 50 000 sweeps. Overall, $s=1$ occurred around 42% of times. In this regard note that, using the encompassing approach, we have a prior probability of about 0.14 and then the resulting BF is 3.0. We, therefore, actually have evidence in favor of unidimensionality.

Table 10 Estimated posterior probabilities of the number of latent classes for the NAEP data.

Table 10 shows the posterior distribution $p(k|{\varvec{Y}})$. Considering the uniform prior on k, the model with $k=4$ latent classes seems to be favored. Table 11 shows the estimated prior and posterior probabilities for s, as well as BFs conditionally on $k=4$. According to the encompassing prior approach, also conditioning on k, the case $s=1$ is receiving the largest BF, corresponding to 177.7.

Table 11 Estimated prior and posterior probabilities of the number of dimensions and corresponding BFs for the NAEP data.

We also performed a sensitivity analysis to evaluate the effect on the results of different choices of $v_\alpha$ and $v_\beta$. We found that, for the data at hand, the value of the BF is only slightly affected by reasonable changes in the value of these hyper-parameters, so that the evidence in favor of unidimensionality is left unaltered. We, therefore, conclude that for these data there is founded evidence in favor of unidimensionality, and that, likely, there are four groups of students of increasing mathematical ability. In this regard, it is important to recall that for these data Bartolucci (2007) concluded in favor of a model measuring $s=3$ dimensions corresponding to the following partition: $\{(1, 2, 9, 10),(3, 5, 8, 11),(4, 6, 7, 12)\}$. This difference in the main conclusion (unidimensionality vs. multidimensionality) is likely due to the less stringent assumptions of the present approach with respect to that in Bartolucci (2007), which is based on a 2PL model, as discussed at the beginning of the present paper.

Finally, as an illustration of the practical use of the model for student’ assessment, we report in Table 12 the Bayesian estimates of the $\lambda _{jc}$ parameters conditional on the selected model, with $k=4$ and $s=1$, and only conditional on $k=4$, together with the proportion of exact responses for each item, denoted by $\bar{y}_{\cdot j}$, for $j=1,\ldots ,r$. The corresponding estimates of the $\pi _c$ parameters are also given in Table 12. These estimates are obtained on the basis of expressions (12) and (13), when conditional on k and s, and the similar expressions reported in the same section when conditional on k only.

Table 12 Estimates of the $\lambda _{jc}$ and $\pi _c$ parameters, together with proportion of correct response, for NAEP data.

It is evident from the results in Table 12 that the latent classes are increasingly ordered in terms of probability of success and thus of ability. This is exactly true for the unidimensional model ($s=1$) and true, with only one exception for the second item, when there is no restriction on the model dimensionality. In any case, there is a strong agreement between the estimates of the $\lambda _{jc}$ parameters under the two scenarios (conditional on $s=1$ and unconditional on s) confirming that the data provide evidence in favor of unidimensionality. Obviously, there is also agreement between these estimates and the proportions $\bar{y}_{\cdot j}$, confirming the validity of the proposed Bayesian estimation algorithm.

Regarding the class description, we also observe on the basis of the results in Table 12 that the classes of intermediate ability, which are the second and the third, have the largest size, whereas the class of the examinees with the highest ability level is the smallest. Note that, also for the Bayesian estimates of parameters $\pi _c$, conditioning or not on s does not make any relevant difference.

The proposed model can also be used to cluster individuals on the basis of the posterior probability of belonging to the latent classes. To illustrate this process, in Table 13 we consider five respondents’ configurations ${\varvec{y}}_i$, increasingly ordered according to the proportion of correct responses, $\bar{y}_{i\cdot }$ For each of these configurations, the table shows the number of individuals in the dataset and the posterior estimates $\hat{\pi }_c({\varvec{y}}_i,k,s)$, computed according to (14), and $\hat{\pi }_c({\varvec{y}}_i,k)$.

Table 13 Estimated posterior probabilities of $\pi _c({\varvec{y}}_i)$ parameters for NAEP data.

We observe that the individuals in Table 13 with all wrong responses must be clearly assigned to the first class and, in general, the probabilities $\hat{\pi }_c({\varvec{y}}_i,k,s)$ and $\hat{\pi }_c({\varvec{y}}_i,k)$ increase for the last latent class, corresponding to the highest ability level, as the number of correct responses increases. This is in agreement with the characterization of the latent classes provided above. Also note that such estimated probabilities reflect the level of uncertainty involved in the clustering process and then, for instance, there is uncertainty in assigning individuals with all correct responses to the third or the fourth latent class.

As already noted, for the NAEP data our approach provides evidence of unidimensionality and this result is in contrast with that provided by alternative approaches and, in particular, with that of Bartolucci (2007) that finds evidence of multidimensionality. This is a crucial difference that, as already conjectured in the previous sections, we can expect considering that our approach is nonparametric, while alternative approaches formulate the conditional distribution of the response variables given the latent variables in a parametric way. In order to clarify and better justify this conjecture, we performed the following experiment. We considered the estimated conditional response probabilities $\hat{\lambda }_{jc}(4,1)$ and class weights $\hat{\pi }_c(4,1)$ given in Table 12. We used the class weights to draw the indicator variables $z_{ic}$, for $i=1,\ldots ,n$ and $c=1,\ldots ,k$, with $n=1510$. Then, we simulated the data ${\varvec{Y}}$ as explained before. In this way, we obtained a dataset comparable to the one for which our nonparametric approach and the semiparametric approach in Bartolucci (2007) produced contrasting results. However, for this simulated dataset unidimensionality holds. We then fitted our model and the 2PL model to the simulated data, to test dimensionality. While our approach determined a BF for the unidimensional model equal to 187.3 (the BF for $s=2$ being equal to 18.8), the 2PL model concluded in favor of two dimensions, with a strong evidence against unidimensionality (p-value equal to 0.002).

For comparison we also report some results based on alternative IRT models. We considered both classical Rasch models and a full information item factor analysis (as in Bock & Muraki, 1988; see also Reckase, 2009), which is different from that of Bartolucci (2007) and related approach because each item response is allowed to depend on more latent variables or factors (within-item multidimensionality), under the assumption that these variables have a normal distribution; see also Bacci and Bartolucci (2016) for further comments. In particular we considered the multi-factor exploratory IRT models, as implemented in the R package mirt (Chalmers et al., 2017). We initially fitted a 2PL specification of this model with 1, 2, and 3 factors, obtaining values of Akaike Information Criterion (AIC; Akaike, 1973) equal to 20273.59, 20262.61, and 20267.35, respectively. The corresponding values of the Bayesian Information Criterion (BIC; Schwarz, 1978) are 20401.27, 20448.81, and 20506.67, respectively. Therefore, according to BIC there is evidence of unidimensionality as according to our approach, but according to AIC there is evidence of bidimensionality; the latter conclusion is also reached according to the corrected Akaike Information Criterion (cAIC; Hurvich & Tsai, 1989), which leads to selecting the two-dimensional factor model. It is worth noting that under the three-parameter logistic (3PL) model, AIC, cAIC, and BIC lead to the same conclusions: the data generating model is unidimensional according to AIC and cAIC, whereas it is bidimensional according to BIC. Therefore, the conclusion does not depend on the specific parametrization of the conditional distribution of the responses given the latent variables but more crucially on the model selection criteria that is adopted. This point must be considered also regarding the comparison between the results of the proposed approach based on the BF and that of Bartolucci (2007), which is based on likelihood ratio testing.

To conclude this comparison, in Table 14 we report the results of a classical Rasch model, a 2-PL and 3-PL model (where guessing parameters for the 3-PL model are reported in Table 15) and the factor loadings corresponding to a two-dimensional item factor analysis. We do not report a two-dimensional item factor analysis after rotation, as the final factor correlations are very high (0.67 after oblimin rotation). For the Rasch model, 37 out of 704 response patterns have person-fit p-value smaller than 5%. With 2-PL and 3-PL models this figure does not improve, as with 2-PL we have 39 outlying person-fits and with 3-PL we have once again 37. For the unrotated two-factors item response analysis, it is difficult to interpret the second factor as loadings that are not close to zero are all negative and correspond to clearly nonzero loadings also for the first factor.

Table 14 Unidimensional and two-dimensional classical item response analysis of NAEP data.

Table 15 Guessing parameters for the 3-PL model for NAEP data.

4.4 An Application to Anxiety and Depression

The Italian version of the Hospital Anxiety and Depression Scale (HADS, Zigmond & Snaith, 1983) consists of 14 polytomous items equally divided between the two dimensions: anxiety and depression. Hence, by definition, $s=2$ in this example. The items of the questionnaire, which are an Italian validated translation (Costantini et al., 1999) of the original HADS questionnaire, are the following:

• 1. I can laugh and see the funny side of things;

• 2. I get a sort of frightened feeling like butterflies in the stomach;

• 3. I have lost interest in my appearance;

• 4. I feel as if I am slowed down;

• 5. I look forward with enjoyment to things;

• 6. I get sudden feelings of panic;

• 7. I get a sort of frightened feeling as if something bad is about to happen;

• 8. Worrying thoughts go through my mind;

• 9. I feel cheerful;

• 10. I can sit at ease and feel relaxed;

• 11. I feel restless and have to be on the move;

• 12. I feel tense or wound up;

• 13. I still enjoy the things I used to enjoy;

• 14. I can enjoy a good book or radio or TV program.

Items 2, 6, 7, 8, 10, 11, 12 are classified as measuring anxiety, and the remaining ones as measuring depression. The data available to us pertain to $n=201$ oncological Italian patients; for a detailed description see Bartolucci et al. (2015), Section 1.8. The responses have been dichotomized so that the observed binary variables correspond to the presence of a certain symptom, when equal to 1, or to its absence, when equal to 0.

We set $v_\alpha =4$ and $v_\beta =1$. For a model with $k=4$ (found to be a reasonable number of latent classes in previous analyses of these data) these settings determine an expected value of the vector of the success probabilities of the four classes equal to $(0.2000,\; 0.6250,\; 0.8182,\; 0.9286)$, whose elements are reasonably centered and separated, with corresponding variance values of $(0.0267,\; 0.0260,\; 0.0124,\; 0.0044)$. Also, the unconditional prior probability for the number of dimensions is adequately spread over its support.

As usual, we run our algorithm for $T={150 000}$ sweeps, after discarding 50 000 iterations as burn-in; regardless of k, $s=1$ never occurred providing definitive evidence against unidimensionality. Table 16 shows the posterior distribution $p(k|{\varvec{Y}})$. The values of k being all a priori equally probable, the model with $k=4$ latent classes seems to be favored.

Table 16 Estimated posterior probabilities of the number of latent classes for the HADS data.

Table 17 Estimated prior and posterior probabilities of the number of dimensions and corresponding BFs for the HADS data.

In Table 17, we show the estimated prior and posterior probabilities for s, as well as BFs conditionally on $k=4$. According to the encompassing prior approach the case $s=2$ is receiving the largest BF, corresponding to 2.99. The most visited partitions were those with the same number of items split in two groups (posterior probability of 49%). These partitions were also those receiving the highest BF (257.82). Among them, the most visited partition was $\{(1, 2, 3, 4, 6, 7, 10),(5, 8, 9, 11, 12, 13, 14)\}$ (posterior probability of 78%). Since partitions consisting of two groups of seven items each are equally probable a priori, the most visited one is also the one with the highest BF and, thus, the one which is favored by the data.

We can compare our result with that obtained through the MultiLCIRT package, where the likelihood-based method of Bartolucci (2007) is implemented. In this case, assuming $k=4$ latent classes and a Rasch parameterization, $s=4$ groups of items seem to be detected on the basis of the likelihood ratio test: $\{(1, 2), (3, 4, 6, 7, 10),(5, 9, 12, 14),(8, 11, 13)\}$. The last step of the clustering algorithm produced exactly the same partition obtained through our method. However, it shall be noted again that these results are based on parametric assumptions that might not hold in general.

Finally, we remark that the algorithm we propose is quite fast. The whole analysis (sampling from the prior, sampling from the posterior, and post-processing both outputs) took around 47 minutes on an Intel Core i7 4810MQ CPU with a clock rate of 2.8 GHz, a time which is well comparable with the one required using the MultiLCIRT package (34 minutes).

5 Conclusions

We propose an approach to assess the number of dimensions measured by a set of dichotomously-scored items. The approach is based on nonparametric item response theory (IRT) models, which are constrained versions of the latent class (LC) model of Lazarsfeld and Henry (1968) formulated through a set of inequality constraints. This model is less restrictive than alternative models used to assess dimensionality, such as those adopted in Martin-Löf (1973), Christensen et al. (2002), and Bartolucci (2007), in which the distribution of the response variables given the latent trait is parametrized as in the Rasch or in the two-parameter logistic model (Rasch, 1961; Birnbaum, 1968).

Also considering the complexity of maximum likelihood estimation for the proposed nonparametric IRT models, we adopt a Bayesian framework based on the encompassing prior approach (Klugkist et al., 2005) to estimate such models. This amounts to assuming a system of priors for the parameters of the unconstrained LC model with a certain number of classes; then, the priors for the parameters of any constrained nonparametric IRT model with the same number of classes are “automatically” defined. These models are estimated by a reversible-jump Markov chain Monte Carlo sampler (Green, 1995; Green & Richardson, 2001), and a suitable post-processing algorithm is then used to specifically assess the model dimensionality.

Overall, an advantage of the proposed approach is that, given a certain dataset, it allows us to jointly determine the number of latent classes and the number of dimensions measured by the items, without requiring any parametric assumption on the distribution of the response variables given the latent class. This may lead to more reasonable results with respect to parametric/semiparametric approaches; see in particular the application in education here developed. Also note that the adoption of a latent class approach avoids the formulation of any parametric assumption on the distribution of the latent trait of interest in the population from which the observed sample is drawn and, at the same time, allows for a clustering of the subjects in terms of latent characteristics. Obviously, in applying the proposed approach, attention must be paid to the choice of the priors on the unconstrained LC model. In this regard, we propose a sensible system of priors, but a sensitivity analysis with respect to the parameters of these priors is mandatory in applications, as we show on the basis of the educational dataset.

Finally, the approach may be extended to the case of polytomously scored items in which every response variable may have more than two categories. However, this requires a proper definition of dimensionality that, when the response categories are ordered, is a natural extension of that given in the present article for dichotomous items. In any case, the system of priors and the inferential approach are essentially equivalent to those here proposed.

Appendix

1.1 Prior Probabilities of $\mathcal{P}$ and s

In this section, we show how to calculate the prior probability of any partition $\mathcal{P}$ and the prior probability of the number s of groups, conditionally on k, under independent uniform priors on the success probabilities $\lambda _{jc}$. Under more general priors of type (6), analytical derivation of the priors for $\mathcal{P}$ and s becomes prohibitive and resorting to simulations is unavoidable.

We start by calculating the conditional prior probability of a single partition $\mathcal{P}$. For this aim, it is convenient to associate to each item j the ranking vector ${\varvec{q}}_j=(q_{j1},\ldots ,q_{jk})$, in which $q_{jc}$ represents the rank of $\lambda _{jc}$ after ordering $\lambda _{j1},\ldots ,\lambda _{jk}$ in increasing order. Let ${\varvec{Q}}=({\varvec{q}}{'}_{1},\ldots ,{\varvec{q}}{'}_{r})$ be the $k\times r$ matrix of the vectors ${\varvec{q}}_j$, arranged by columns. Each vector ${\varvec{q}}_{j_1}$ can have one out of k! possible configurations, independently from any other ${\varvec{q}}_{j_2}$, for $j_1\ne j_2$. Thus, there are $(k!)^r$ possible configurations of the matrix ${\varvec{Q}}$, all having the same probability under a uniform prior on the success probabilities $\lambda _{jc}$. Notice that ${\varvec{Q}}$ is a function of $\varvec{\Lambda }$.

The number of matrices ${\varvec{Q}}$ determining the same partition $\mathcal{P}$ is

$$\begin{aligned} k!(k!-1)\cdots (k!-s+1), \end{aligned}$$

where $s=|\mathcal{P}|$. This is easily proved considering that the ranking vector of the first item in the first group can have any of the k! possible configurations, which consequently determines the configuration for the ranking vectors of the other items in the same group; the ranking vector of the first item in the second group can have any possible configuration but that of the items in the first group, that is, $k!-1$ possible configurations. By iterating this process, we conclude that the ranking vector of the first item in the s-th group can have any possible configuration but those of the items in the previous groups, that is, $k!-s+1$ possible configurations. Therefore, the probability of any partition $\mathcal{P}$, conditionally on k is given by

$$\begin{aligned} p(\mathcal{P}|k)=\frac{k!(k!-1)\cdots (k!-s+1)}{(k!)^r}, \end{aligned}$$

(15)

where the denominator corresponds to the number of possible configurations of ${\varvec{Q}}$.

We now consider the prior conditional probability of the number s of groups, that is, p(s|k). Since any partition into s groups has the same probability, given in (15), to obtain p(s|k) we simply have to count how many partitions into s groups can be obtained and multiply this number by the probability of the single partition. The number of ways in which a set of r items can be partitioned into s nonempty groups is known as the Stirling number of the second kind (Graham et al., 1988), which is equal to

with

Thus, the conditional probability of s can be obtained as

where $p(\mathcal{P}|k)$ is the probability of a partition $\mathcal{P}$ such that $|\mathcal{P}|=s$, which is given in (15).

1.2 The RJ-MCMC Algorithm

In this section we provide a detailed description of the RJ-MCMC algorithm implemented in this paper. We first illustrate the fixed-dimension moves and then present the changing dimension moves for updating the number of latent classes.

1.2.1 Fixed-Dimension Moves

Model parameters are updated according to the following steps:

• Update class weights. The full conditional distribution of $\varvec{\pi }$ is a Dirichlet distribution with parameters $(1+n_{1},\ldots ,1+ n_{k})$, where $n_c = \#\{i:z_{ic}=1\}$. The vector $\varvec{\pi }$ is then updated by means of Gibbs sampling, drawing a new vector from such a distribution.

• Update latent class variables. The latent class allocation variables $z_{ic}$, $i=1,\ldots ,n$, $c=1,\ldots ,k$, can be updated by means of Gibbs sampling, drawing them independently from their full conditional

  $$\begin{aligned} p(z_{ic}=1|\cdots ) = \frac{\pi _c \prod _{j=1}^r (1-\lambda _{jc})^{1-y_{ij}}\lambda _{jc}^{y_{ij}}}{\sum _{c=1}^k \pi _c \prod _{j=1}^r (1-\lambda _{jc})^{1-y_{ij}}\lambda _{jc}^{y_{ij}}}, \end{aligned}$$

  where “$\cdots$” denotes “all other parameters and data.”

• Update the success probabilities. In order to update the success probabilities, we build a proposal based on independent zero-centered normal increments of $\mathrm{logit}\,(\lambda _{jc})$, separately for each $j=1,\ldots ,r$ and $c=1,\ldots ,k$. The candidate $\lambda _{jc}^{\star }$ is accepted with probability equal to $\min (1,p_{\lambda _{jc}^\star })$, where

  $$\begin{aligned} p_{\lambda _{jc}^\star }=\prod _{i=1}^n&\{ (\lambda _{jc}^\star /\lambda _{jc})^{y_{ij}}[(1-\lambda _{jc}^\star )/(1-\lambda _{jc})]^{(1-y_{ij})}\}^{z_{ic}}\nonumber \\&\times (\lambda _{jc}^\star /\lambda _{jc})^{(\alpha _c-1)}[(1-\lambda _{jc}^\star )/(1-\lambda _{jc})]^{(\beta _c-1)}\nonumber \\&\times (\lambda _{jc}^\star )(1-\lambda _{jc}^\star )/[(\lambda _{jc})(1-\lambda _{jc})]. \end{aligned}$$

  (16)

  The first line on the right side is the likelihood ratio, while the second line corresponds to the ratio between the prior densities. The ratio between the proposal densities cancels out, apart from the Jacobian of the logit transformation, given in the third line of (16).

1.2.2 Changing Dimension Moves for Updating k

• Split/merge move. For the combine proposal, we pick a class at random among $2,\ldots ,k$, with probability $1/(k-1)$, and denote it with $c_2$. Then, we draw another class at random among $1,\ldots ,c_2-1$, with probability $1/(c_2-1)$, and denote it with $c_1$. Classes $c_1$ and $c_2$ are then merged into a new class $c^\prime$, decreasing k by 1, with the merged class $c^\prime$ occupying the place $c_2-1$, once the place $c_1$ has been deleted. We then create new values for $\pi _{c^\prime }$ and $\lambda _{jc^\prime }$, for $j=1,\ldots ,r$, and we reallocate all those observations for which $z_{ic_1}=1$ or $z_{ic_2}=1$ to the merged class $c^\prime$. A new vector of weights is created by letting

  $$\begin{aligned} \pi _{c^\prime }=\pi _{c_1}+\pi _{c_2}. \end{aligned}$$

  The new parameters $\lambda _{jc^\prime }$ are created in such a way that $\lambda _{jc^\prime }=\lambda _{jc_2}$, while the $\lambda _{jc_1}$ are simply deleted for all j. The split proposal begins by choosing a class at random among $1,\ldots ,k$, say $c^\prime$, with probability 1 / k and splitting it into two new classes, labeled $c_1$ and $c_2$, augmenting k by 1. Let $c_2$ take the place $c^\prime +1$ and $c_1$ be inserted in a place preceding $c_2$ and chosen at random with probability $1/c^\prime$. We then need to create new values for $\pi _{c_1},\pi _{c_2}$ and for $\lambda _{jc_1},\lambda _{jc_2}$, $j=1,\ldots ,r$, and reallocate all those observations for which $z_{ic^\prime }=1$, while the hyper-parameters $\alpha _c$ and $\beta _c$ are simply recalculated as $\alpha _c^\star = vc+1$ and $\beta _c^\star =v(k^\star +1-c)+1$, for $c=1,\ldots ,k^\star$, with $k^\star =k+1$. Let us start by splitting the weight $\pi _{c^\prime }$ into $\pi _{c_1}$ and $\pi _{c_2}$ in such a way that $\pi _{c_1}+\pi _{c_2}=\pi _{c^\prime }$. We accomplish this by generating a random value $u\sim \hbox {Beta}\left( u_1,u_2\right)$, where $u_1$ and $u_2$ are the parameters of the Beta density, and setting

  $$\begin{aligned} \pi _{c_1}=\pi _{c^\prime }u \quad \hbox {and}\quad \pi _{c_2}=\pi _{c^\prime }(1-u). \end{aligned}$$

  The new vector of weights is denoted by $\varvec{\pi }^\star$. We then split the parameters $\lambda _{jc^\prime }$ into $\lambda _{jc_1}$ and $\lambda _{jc_2}$ for all j. We accomplish this by sampling a vector ${\varvec{w}}=(w_1,\ldots ,w_r)$ from the prior distribution of $\lambda _{jc_1}$, that is, $w_j\sim \hbox {Beta}(\alpha ^\star _{c_1},\beta _{c_1}^\star )$, for $j=1,\ldots ,r$, and thus setting

  $$\begin{aligned} \lambda _{jc_1}=w_j \quad \hbox {and}\quad \lambda _{jc_2}=\lambda _{jc^\prime }, \quad j=1,\ldots ,r. \end{aligned}$$

  The new matrix of success probabilities is denoted by $\varvec{\Lambda }^\star$. Finally, we reallocate all those observations for which $z_{ic^\prime }=1$ between $c_1$ and $c_2$ in a way analogous to the standard Gibbs allocation move and we let ${\varvec{Z}}^\star$ denote the new allocation matrix. According to the RJ framework, the acceptance probability for the split move is min$(1,p_k)$, where

  $$\begin{aligned} p_k= & {} \prod _{i=1}^n\prod _{j=1}^r \frac{[ (\lambda _{jc_1}^\star )^{y_{ij}} (1-\lambda _{jc_1}^\star )^{(1-y_{ij})}]^{z_{ic_1}^\star } [ (\lambda _{jc_2}^\star )^{y_{ij}} (1-\lambda _{jc_2}^\star )^{(1-y_{ij})}]^{z_{ic_2}^\star }}{[ (\lambda _{jc^\prime })^{y_{ij}} (1-\lambda _{jc^\prime })^{(1-y_{ij})}]^{z_{ic^\prime }}}\nonumber \\&\times \frac{p(k^\star )}{p(k)}\times \frac{\mathcal {D}(\pi _1^\star ,\ldots ,\pi _{k^\star }^\star )}{\mathcal {D}(\pi _1,\ldots ,\pi _{k})}\times \frac{(\pi _{c_1}^\star )^{\sum _{i=1}^n z_{ic_1}^\star }(\pi _{c_2}^\star )^{\sum _{i=1}^n z_{ic_2}^\star }}{(\pi _{c^\prime })^{\sum _{i=1}^n z_{ic^\prime }}} \nonumber \\&\times \frac{\prod _{j=1}^r \prod _{c=1}^{k^\star }\mathcal {B}_{\alpha _c^\star ,\beta _c^\star }(\lambda _{jc}^\star )}{\prod _{j=1}^r \prod _{c=1}^{k} \mathcal {B}_{\alpha _c,\beta _c}(\lambda _{jc})}\times \frac{d_{k^\star }}{b_k p_{\hbox {alloc}}\mathcal {B}_{u_1,u_2}(u)\prod _{j=1}^r \mathcal {B}_{\alpha _{c_1}^\star ,\beta _{c_1}^\star }(w_j)}\times \pi _{c^\prime }.\qquad \end{aligned}$$

  (17)

  The first two lines in (17) represent, respectively, the likelihood and the priors ratio, with $\mathcal {D}$ being the Dirichlet density with parameters all equal to 1, and $\mathcal {B}$ being the Beta density with parameters specified in the subscript. In the third line, the first term represents the proposal ratio, with $p_{\hbox {alloc}}$ being the probability of the particular allocation made in the split move, and the second term is the Jacobian of the transformation from $(\pi _{c^\prime }, \lambda _{1 c^\prime },\ldots , \lambda _{r c^\prime }, u,w_{1}, \ldots , w_{r})$ to $(\pi _{c_1}^\star , \lambda _{1 c_2}^\star ,\ldots , \lambda _{r c_2}^\star , \pi _{c_2}^\star , \lambda _{1 c_1}^\star ,\ldots , \lambda _{r c_1}^\star )$. The combine move is accepted with probability $\min (1,p_k^{-1})$, with some obvious substitutions in the expression for $p_k$.

• Birth/death move. We first make a random choice between birth and death, using the same probabilities $b_k$ and $d_k$ as above. For a birth, we pick a position at random among $1,\ldots ,k^\star$, with probability $1/k^\star$ for the place to be occupied by the new class $c^\prime$. Then, a weight and a vector of success probabilities for the new class are drawn using

  $$\begin{aligned} \pi _{c^\prime }\sim \hbox {Beta}(1,k), \quad \lambda _{jc^\prime }\sim \hbox {Beta}(\alpha ^\star _{c^\prime },\beta _{c^\prime }^\star ), \quad j=1,\ldots ,r, \end{aligned}$$

  where the hyper-parameters $\varvec{\alpha }$ and $\varvec{\beta }$ are recalculated as in the split move, leading to $\varvec{\alpha }^\star$ and $\varvec{\beta }^\star$, respectively. To “make space” for the new class, the existing weights are rescaled, so that all weights sum to 1, using $\pi _c^\star = \pi _c(1 - \pi _{c^\prime })$. The weights and the success probabilities proposed under the birth move are denoted by $\varvec{\pi }^\star$ and $\varvec{\Lambda }^\star$, respectively. The allocation variables remain unchanged, and no subjects are allocated to the new component, that is, $z_{ic^\prime }=0$, $i=1,\ldots ,n$. The increased allocation matrix is indicated as ${\varvec{Z}}^\star$. For a death, a random choice is made between any existing empty components; the chosen component is deleted and the remaining weights are rescaled to sum to 1. No other changes are proposed to the variables and, in particular, the allocations are unaltered. The acceptance probabilities for birth and death are $\min (1, p_k)$ and $\min (1, p_k^{-1})$, respectively, where

  $$\begin{aligned} p_k= & {} \frac{p(k^\star )}{p(k)}\times \frac{\mathcal {D}(\pi _1^\star ,\ldots ,\pi _{k^\star }^\star )}{\mathcal {D}(\pi _1,\ldots ,\pi _{k})}\times \frac{\prod _{c=1}^{k^\star }(\pi _c^\star )^{\sum _{i=1}^n z_{ic}^\star }}{\prod _{c=1}^k \pi _c^{\sum _{i=1}^n z_{ic}}} \times \frac{\prod _{j=1}^r\prod _{c=1}^{k^\star }\mathcal {B}_{\alpha _c^\star ,\beta _c^\star }(\lambda _{jc}^\star )}{\prod _{j=1}^r \prod _{c=1}^{k} \mathcal {B}_{\alpha _c,\beta _c}(\lambda _{jc})}\nonumber \\&\times \frac{d_{k^\star }k^\star }{b_k (k_0+1) \mathcal {B}_{1,k}(\pi _{c^\prime }^\star )\prod _{j=1}^r \mathcal {B}_{\alpha _{c_1}^\star ,\beta _{c_1}^\star }(\lambda _{jc^\prime }^\star )}\times (1-\pi _{c^\prime }^\star ), \end{aligned}$$

  (18)

  with $k_0$ being the number of empty classes, before the birth. In equation (18), the first line is the prior ratio, and the second line contains the proposal ratio and the Jacobian; the likelihood ratio is equal to 1.