Learning-based symbolic assume-guarantee reasoning for Markov decision process by using interval Markov process

Abstract

Many real-life critical systems are described with large models and exhibit both probabilistic and non-deterministic behaviour. Verification of such systems requires techniques to avoid the state space explosion problem. Symbolic model checking and compositional verification such as assume-guarantee reasoning are two promising techniques to overcome this barrier. In this paper, we propose a probabilistic symbolic compositional verification approach (PSCV) to verify probabilistic systems where each component is a Markov decision process (MDP). PSCV starts by encoding implicitly the system components using compact data structures. To establish the symbolic compositional verification process, we propose a sound and complete symbolic assume-guarantee reasoning rule. To attain completeness of the symbolic assume-guarantee reasoning rule, we propose to model assumptions using interval MDP. In addition, we give a symbolic MTBDD-learning algorithm to generate automatically the symbolic assumptions. Moreover, we propose to use causality to generate small counterexamples in order to refine the conjecture assumptions. Experimental results suggest promising outlooks for our probabilistic symbolic compositional approach.

1 Introduction

1.1 Context and motivation

With the increase in complexity of modern computing systems, the chances of introducing errors have increased significantly. Detecting and fixing every error is a very important task, especially for safety-critical applications. The main approach to verify such systems is model checking [14, 15], which consists to verify systems by exhaustively searching the complete state space.

Many safety-critical systems exhibit non-deterministic stochastic behaviour [44], for example, probabilistic protocol [20], randomized distributed algorithms [28], fault tolerant systems [43], composition of inter-organizational workflow [7]. Probabilistic verification is a set of techniques for formal modelling and analysis of such systems. Probabilistic model checking [1, 4, 5] involves the construction of a finite-state model augmented with probabilistic information, such as Markov chains or probabilistic automaton [24, 34]. This is then checked against properties specified in probabilistic extensions of temporal logic, such as probabilistic computation tree logic (PCTL) [23]. As with any formal verification technique, one of the main challenges for probabilistic model checking is the state space explosion problem: the number of system states grows exponentially in the number of concurrent components. Indeed, even for small models, the size of the state space may be massive; and this can cause the failure of the verification process.

To cope with the state space explosion problem, several approaches have been proposed such as (1) compositional verification [21, 22, 25, 36] and (2) symbolic model checking [9, 26, 38, 39]. Compositional verification suggests a “divide and conquer” strategy to reduce the verification task into simpler subtasks. A popular approach is the assume-guarantee paradigm [11, 13, 41], in which individual system components are verified under assumptions about their environment. Once it has been verified that the other system components do indeed satisfy these assumptions, proof rules can be used to combine individual verification results, establishing correctness properties of the overall system. The success of assume-guarantee reasoning approach depends on discovering appropriate assumptions. The process of generating automatically useful assumptions can be solved by using an active model learning [13], such as $L^{*}$ learning algorithm [3].

Symbolic model checking is also a useful technique to cope with the state explosion problem. In symbolic model checking, system states are implicitly represented by predicates, as well as the initial states and transition relation of the system. Using advanced data structures such as binary decision diagrams (BDD) or multi-terminal BDD (MTBDD) [19], a large number of states could efficiently be stored and explored simultaneously.

The enormous success of assume-guarantee reasoning and symbolic model checking techniques to cope with the state space explosion problem motivated us to propose a new approach based on the combination of assume-guarantee reasoning and symbolic model checking techniques. For that, we propose a new approach named probabilistic symbolic compositional verification (PSCV) to take advantages of both approaches. The PSCV is based on a symbolic assume-guarantee reasoning rule. The main characteristics of our symbolic assume-guarantee reasoning rule are soundness and completeness. The completeness is guaranteed by the use of interval MDP to represent assumption. In addition, to reduce the size of the state space, PSCV encodes both system components and assumptions implicitly using compact data structures, such as BDD and MTBDD. We also adapt the $L^{*}$ learning algorithm to generate series of conjecture symbolic assumptions.

1.2 Contributions

Probabilistic symbolic compositional verification aims to avoid the state space explosion problem for probabilistic systems composed of MDP components. Different from the monolithic verification, in PSCV each system component is verified in isolation under an assumption about its contextual environment. To illustrate the PSCV, we consider a system S (Fig. 1) composed of two MDP components $M_{0}$ and $M_{1}$. In order to guarantee that S satisfies a probabilistic safety property, we first encode the components ($M_{0}$ and $M_{1}$) using symbolic data structures (symbolic MDP); many works such as [9, 19, 38, 39] show that the symbolic representation is often more efficient than the explicit representation. The second step aims to generate a symbolic assumption $S_{I_{i}}$, where $M_{0}$ is embedded in $S_{I_{i}}$. The notion of embedded, denoted by $M_{0} \preceq I$, means that the symbolic assumption $S_{I_{i}}$ should be expressive enough to capture the abstract behaviour of $M_{0}$ and amenable to automatic generation via algorithmic learning. If the size of the symbolic assumption $S_{I_{i}}$ is much smaller than the size of the corresponding component $M_{0}$, then we can expect significant gains of the verification performance. In addition, we propose a sound and complete symbolic assume-guarantee reasoning proof rule to define and establish the verification process of $S_{I_{i}}\parallel M_{1}$. Moreover, we propose a symbolic MTBDD-learning algorithm to generate automatically the symbolic assumptions $S_{I_{i}}$. We developed a prototype tool PSCV4MDP (probabilistic symbolic compositional verification for MDP), which implements the symbolic MTBDD-learning algorithm. We evaluate our approach on a several case studies derived from the PRISM benchmarks, and we have compared the results of our approach with the symbolic monolithic probabilistic verification [33]. Experimental results suggest promising outlooks.

Fig. 1

An overview of our approach, step 1 aims to encode MDP using symbolic MDP and step 2 aims to learn a symbolic assumption $S_{I_{i}}$, then the verification process will be established using a symbolic assume-guarantee reasoning proof rule

The remainder of this paper is organized as follows: In Sect. 2 we provide some background knowledge about MDP, interval MDP, the parallel composition $\hbox {MDP} \parallel \hbox {IMDP}$ and the symbolic data structures used to encode MDP and interval MDP. In Sect. 3, we present the PSCV approach, where we detail our symbolic assume-guarantee reasoning proof rule, the encoding process of MDP and interval MDP and the symbolic MTBDD-learning algorithm. Section 4 reports the experimental results of several case studies. Section 5 describes the most relevant works to ours, and Sect. 6 concludes the paper and talks about future works.

2 Preliminaries

In this section, we give some background knowledge about MDP, interval MDP, the parallel composition and the symbolic data structures used to encode implicitly MDP and interval MDP.

MDP are often used to describe and study systems exhibit non-deterministic and stochastic behaviour.

Definition 1

Markov decision process (MDP) is a tuple $M=(S_{M},s_{0}^{M},\varSigma _{M},\delta _{M})$ where $S_{M}$ is a finite set of states, $s_{0}^{M} \in S$ is an initial state, $\varSigma _{M}$ is a finite set of alphabets and $\delta _{M} \subseteq S \times (\varSigma _{M} \cup \{\tau \}) \times Dist(S)$ is a probabilistic transition relation.

In a state s of MDP M, one or more transitions, denoted $(s,a) \rightarrow \mu$, are available, where $a \in \varSigma _{M}$ is an action label, $\mu$ is a probability distribution over states and $(s, a, \mu ) \in \delta _{M}$. A path through MDP is a (finite or infinite) sequence $(s_{0},a_{0},\mu _{0}) \rightarrow (s_{1},a_{1},\mu _{1}) \rightarrow \cdots$ we denote by ${ FPath}$ a finite path through MDP M. To reason about MDP, we use the notion of adversaries, which resolve the non-deterministic choices in MDP, based on its execution history. We denote by $\sigma _{M}$ an adversary of MDP M. Formally, an adversary $\sigma _{M}$ maps any finite path $\textit{FPath}$ to a distribution over the available transitions in the last state on the part, i.e. mapping every ${ FPath}$ to an element $\sigma _{M} ({ FPath})$ of $\delta _{M}$. Indeed, we distinguish several classes of adversaries: (1) memoryless adversary, where it always pick the same choice in a state, i.e. the choice depends only on the current state, (2) finite-memory adversary, it stores information about the history in a finite-state automaton, (3) deterministic adversary, an adversary is deterministic if it always selects a single transition, or (3) randomized adversary, where it maps finite paths ${ FPath}$ in MDP to a probability distribution over element of $\delta _{M}$. In our case, the class of deterministic adversaries are sufficient for our problem.

An example of two MDP $M_{0}$ and $M_{1}$ is shown in Fig. 2.

Fig. 2

Example of two MDP, $M_{0}$ (above) and $M_{1}$ (below)

Interval Markov chains (IMDP) generalize ordinary MDP by using interval-valued transition probabilities rather than just probability value. In this paper, we use interval MDP to represent the assumptions used on the PSCV verification process.

Definition 2

Interval Markov Chain (IMDP) is a tuple $I=(S_{I},s_{0}^{I},\varSigma _{I},P^{l},P^{u})$ where $S_{I},s_{0}^{I}$ and $\varSigma _{I}$ are defined as for MDP. $P^{l},P^{u}: S \times \varSigma _{I} \times S \mapsto [0,1]$ are matrices representing the lower/upper bounds of transition probabilities such that: $P^{l}(s,a)(s') \le P^{u}(s,a)(s')$ for all states $s,s' \in S$ and $a \in \varSigma _{I}$.

An example of interval MDP I is shown in Fig. 3.

Fig. 3

Example of interval MDP I

In Definition 3, we describe how MDP and interval MDP are composed together. This is done by using the asynchronous parallel operator ($\parallel$) defined by [42], where MDP and interval MDP synchronize over shared actions and interleave otherwise.

Definition 3

Parallel composition $\hbox {MDP} \parallel \hbox {IMDP}$

Let M and I be MDP and interval MDP, respectively. Their parallel composition, denoted by $M \parallel I$, is an interval MDP MI, where $MI= M \parallel I$.

$MI= \{ S_{M} \times S_{I}, (s_{0}^{M},s_{0}^{I}), \varSigma _{M} \cup \varSigma _{I}, P^{l},P^{u} \},$ where $P^{l},P^{u}$ are defined such that:

$(s_{i}, s_{j}) \xrightarrow []{a} [P^{l}(s_{i}, a)(s_{j}) \times \mu _{i}, P^{u}(s_{i}, a)(s_{j}) \times \mu _{i}]$ if and only if one of the following conditions holds: let $s_{i}, s'_{i} \in S_{M}$ and $s_{j}, s'_{j} \in S_{I}$.

• $s_{i} \xrightarrow []{a,\mu _{i}} s'_{i}, s_{j} \xrightarrow []{P^{l}(s_{j}, a)(s'_{j}), P^{u}(s_{j}, a)(s'_{j})} s'_{j}$, where $a \in \varSigma _{M} \cap \varSigma _{I}$,

• $s_{i} \xrightarrow []{a,\mu _{i}} s'_{i}$, where $a \in \varSigma _{M} {\setminus } \varSigma _{I}$,

• $s_{j} \xrightarrow []{P^{l}(s_{j}, a)(s'_{j}), P^{u}(s_{j}, a)(s'_{j})} s'_{j}$, where $a \in \varSigma _{M} {\setminus } \varSigma _{I}$.

Example 1

To illustrate the parallel composition, we consider the example of MDP $M_{0}$ and interval MDP I shown in Figs. 2 and 3, respectively. The product $MI= M_{0} \parallel I$ obtained from their parallel composition is shown in Fig. 4. $M_{0}$ and I synchronize over their shared actions $\varSigma _{M_{0}} \cap \varSigma _{I} =\{detect, warn, send, restart, fail\}$.

Fig. 4

Interval MDP MI result of the parallel composition $M_{0} \parallel I$

MDP and interval MDP can be implicitly encoded using compact data structures such as BDD and MTBDD. Let B denote the Boolean domain $\{0,1\}$. Fix a finite ordered set of Boolean variables $X=\langle x_{1}, x_{2},\ldots , x_{n} \rangle$. A valuation $v=\langle v_{1}, v_{2},\ldots , v_{n} \rangle$ of X assigns the Boolean value $v_{i}$ to the Boolean variable $x_{i}$.

Definition 4

A binary decision diagram (BDD) is a rooted, directed acyclic graph with its vertex set partitioned into non-terminal and terminal vertices (also called nodes). A non-terminal node d is labelled by a variable $var(d) \in X$. Each non-terminal node has exactly two children nodes, denoted then(d) and else(d). A terminal node d is labelled by a Boolean value val(d) and has no children. The Boolean variable ordering < is imposed onto the graph by requiring that a child $d'$ of a non-terminal node d is either terminal, or is non-terminal and satisfies $var(d) < var(d')$.

Definition 5

A multi-terminal binary decision diagram (MTBDD) is a BDD where the terminal nodes are labelled by a real number.

In this work, we consider the verification of probabilistic safety properties specified using PCTL in the form of $P_{\le \rho }[\psi ]$ with $\rho \in [0,1]$ and

$$\begin{aligned}&\phi :{:}= true | a | \phi \wedge \phi | \lnot \phi \\&\psi :{:}= \phi \, U\, \phi \end{aligned}$$

where a is an atomic proposition, $\phi$ is a state formula, $\psi$ is a path formula and U is the Until temporal operator.

We use also the operator $\lozenge$ (diamond) operator to specify probabilistic safety property. Intuitively, a property of the form $\lozenge \phi$ means that $\phi$ is eventually satisfied. This operator can be expressed in terms of the PCTL until as follows:

$\lozenge \phi \equiv true U \phi$.

3 Probabilistic symbolic compositional verification

In this paper, we propose a probabilistic symbolic compositional verification approach (PSCV) to verify whether a system S composed of MDP components satisfies or not a probabilistic safety property $P_{\le \rho }[\psi ]$. The PSCV process is based on our proposed symbolic assume-guarantee reasoning proof rule, where assumptions are represented using interval MDP.

Definition 6

Let $M=(S_{M},s_{0}^{M},\varSigma _{M},\delta _{M})$ and $I=(S_{I},s_{0}^{I},\varSigma _{I},P^{l},P^{u})$ be MDP and interval MDP, respectively. We say M is embedded in I, written $M \preceq I$, if and only if: (1) $S_{M} = S_{I}$, (2) $s_{0}^{M} = s_{0}^{I}$, (3) $\varSigma _{M} = \varSigma _{I}$, and (4) $P^{l}(s,a)(s') \le \mu (s,a)(s') \le P^{u}(s,a)(s')$ for every $s,s' \in S_{M}$ and $a \in \varSigma _{M}$.

Example 2

Consider the MDP $M_{0}$ shown in Fig. 2 and interval MDP I shown in Fig. 3. They have the same state space, identical initial state $(s_{0}, i_{0})$ and the same set of actions $\{detect, warn, send, restart, fail\}$. In addition, the transition probability between any two states in $M_{0}$ lies within the corresponding transition probability interval in I by taking the same action. For example, the transition probability between $s_{0}$ and $s_{1}$ is $s_{0} \xrightarrow []{detect,0.8} s_{1}$, which falls into the interval [0, 1] labelled the transition $i_{0} \xrightarrow []{detect,[0,1]} i_{1}$ in I, formally $P^{l}(i_{0},detect)(i_{1}) \le \mu (s_{0},detect)(s_{1}) \le P^{u}(i_{0},detect)(i'_{0})$. Thus, we have $M_{0} \preceq I$.

Theorem 1

Let $M_{0}, M_{1}$ be MDP and $P_{\le \rho }[\psi ]$ a probabilistic safety property, then the following proof rule is sound and complete:

$M_{0} \preceq I$	(1)
$I \parallel M_{1} \models P_{\le \rho }[\psi ]$	(2)
$M_{0} \parallel M_{1} \models P_{\le \rho }[\psi ]$	(3)

This proof rule means if we have a system S composed of two components $M_{0}$ and $M_{1}$, where $S = M_{0} \parallel M_{1}$, then we can check the correctness of a probabilistic safety property $P_{\le \rho }[\psi ]$ over S without constructing and verifying the full state space. Instead, we first generate an appropriate assumption I, where I is an interval MDP, then we check if this assumption could be used to verify S by checking the two promises:

• (1) Check if $M_{0}$ is embedded in I, $M_{0} \preceq I$,

• (2) Check if $I \parallel M_{1}$ satisfies the probabilistic safety property $P_{\le \rho }[\psi ], I \parallel M_{1} \models P_{\le \rho }[\psi ]$.

If the two promises are satisfied, then we can conclude that $M_{0} \parallel M_{1}$ satisfies $P_{\le \rho }[\psi ]$.

Fig. 5

An overview of our approach probabilistic symbolic compositional verification approach (PSCV)

Proof

Let $M_{0}$ and $M_{1}$ be MDP, where $M_{0}=(S_{M_{0}}, s_{0}^{M_{0}}, \varSigma _{M_{0}}, \delta _{M_{0}}), M_{1}=(S_{M_{1}},s_{0}^{M_{1}},\varSigma _{M_{1}},\delta _{M_{1}})$, and interval MDP I, $I=(S_{I},s_{0}^{I},\varSigma _{I},P^{l},P^{u})$. If $M_{0} \preceq I$ and based on Definition 6 we have $S_{M} = S_{I}, s_{0}^{M} = s_{0}^{I}, \varSigma _{M} = \varSigma _{I}$, and $P^{l}(s,a)(s') \le \mu (s,a)(s') \le P^{u}(s,a)(s')$ for every $s,s' \in S_{M_{0}}$ and $a \in \varSigma _{M_{0}}$. Based on Definitions 3 and 6, $M_{0} \parallel M_{1}$ and $I \parallel M_{1}$ have the same state space, initial state and actions. Since $P^{l}(s,a)(s') \le \mu (s,a)(s') \le P^{u}(s,a)(s')$, and we suppose the transition probability of $M_{0} \parallel M_{1}$ as: $\mu _{M_{0}\parallel M_{1}}((s_{i},s_{j}),a)(s'_{i},s'_{j}) = \mu _{M_{0}}((s_{i}),a)(s'_{i})\times \mu _{M_{1}}((s_{j}),a)(s'_{j})$ for any state $s_{i},s'_{i} \in S_{M_{0}}$ and $s_{j},s'_{j} \in S_{M_{1}}$. Thus, $P^{l}((s_{i},s_{j}),a)(s'_{i},s'_{j}) \le \mu _{M_{0}\parallel M_{1}}((s_{i},s_{j}),a) (s'_{i},s'_{j}) \le P^{u}((s_{i},s_{j}),a)(s'_{i},s'_{j})$ for the probability between two states $(s_{i},s'_{i})$ and $(s_{j},s'_{j})$. In $I \parallel M_{1}$ the probability interval between any two states $(s_{i},s_{j})$ and $(s'_{i},s'_{j})$ is restricted by the interval $[P^{l}((s_{i},a)(s'_{i}) \times \mu _{M_{1}}(s_{j}),a)(s'_{j}), P^{u}((s_{i},a)(s'_{i}) \times \mu _{M_{1}}(s_{j}) ,a)(s'_{j})]$, this implies, if $M_{0} \preceq I$ and $I \parallel M_{1} \models P_{\le \rho }[\psi ]$ then $M_{0} \parallel M_{1} \models P_{\le \rho }[\psi ]$ is guaranteed. $\square$

The main characteristic of our PSCV approach is completeness:

• If $M_{0} \parallel M_{1} \models P_{\le \rho }[\psi ]$, then PSCV returns ${ true}$ and an assumption I, where $I \parallel M_{1} \models P_{\le \rho }[\psi ]$,

• If $M_{0} \parallel M_{1} \nvDash P_{\le \rho }[\psi ]$, then PSCV returns ${ false}$, assumption I and a counterexample showing the reason why $P_{\le \rho }[\psi ]$ is violated.

Proof

In our approach PSCV, the symbolic learning algorithm targets the component $M_{0}$, and it will infer an assumption I eventually. If $M_{0} \parallel M_{1} \models P_{\le \rho }[\psi ]$, the MTBDD-learning algorithm always infers I, where $M_{0} \preceq I$. In the worst case, the upper probability value of the final assumption I will be equal to transition probability value of $M_{0}$. Otherwise, if $M_{0} \parallel M_{1} \nvDash P_{\le \rho }[\psi ]$, the MTBDD-learning algorithm will start by generating an initial assumption $I_{0}$, if $I_{0}$ is too strong (the upper probability value is too big), the MTBDD-learning algorithm will refine I based on a counterexample. The refinement process will lead to generate a real counterexample showing the reason why $P_{\le \rho }[\psi ]$ is violated. In the worst case, the refinement process will set the upper probability value of the final assumption I as for transition probability value in $M_{0}$. $\square$

Figure 5 presents an overview of the PSCV approach. PSCV is based on the symbolic assume-guarantee reasoning proof rule. In our approach, assumptions are represented using interval MDP instead of DFA, and the state space is encoded using compact data structures. In addition, the $L^{*}$ learning algorithm is adapted to accept the implicit representation of the state space. Furthermore, our approach always terminate. The choice of using interval MDP to represent assumptions is motivated by: (1) MDP can be embedded in an interval MDP (Definition 6), this how make our assume-guarantee reasoning rule sound, where interval MDP captures the abstract behaviour of the original MDP; (2) it is amenable to generate assumption represented by interval MDP using the $L^{*}$ learning algorithm; (3) the implicit representation of interval MDP can be more efficient in size than the corresponding MDP; (4) completeness, it is always possible to find an interval MDP, where MDP is embedded on it; and (5) by using interval MDP, we can easily extend the PSCV to verify properties of the form $P_{\ge \rho }[\psi ]$.

The first step of PSCV aims to encode components ($M_{0}$ and $M_{1}$) by means of SMDP. Instead of representing the state space of MDP explicitly (using explicit representation), we encode the state space, transitions and actions using symbolic MDP (SMDP).

In Definition 7, we introduce SMDP and we provide the different data structures used to encode implicitly MDP.

Definition 7

Symbolic MDP (SMDP) is a tuple $S_{M}=(X, Init_{M}, Y,f_{S_{M}} (yxx'z),Z)$ where X, Y and Z are finite ordered set of Boolean variables with $X\cap Y\cap Z = \emptyset$. Init(X) is an initial predicate over X and $f_{S_{M}}(yxx'z)$ is a transition predicate over $Y\cup X\cup X' \cup Z$ where $y,x,x',z$ are valuations of receptively, $Y,X,X'$ and Z. The set X encodes the states of S, $X'$ next states, Y encodes alphabets, and Z encodes the non-deterministic choice.

More concretely, let $M = (S_{M},s_{0},\varSigma _{M},\delta _{M})$ be MDP, $n = |S_{M}|$, $m=|\varSigma _{M}|$ and $k = \lceil log_{2}(n) \rceil$. We can see $\delta _{M}$ as a function of the form $S_{M} \times \varSigma _{M} \times \{1,2,\ldots ,r\}\times S_{M} \rightarrow [0,1]$, where r is the number of non-deterministic choice of a transition. We use a function $enc: S_{M} \rightarrow \{0,1\}^{k}$ over $X=\langle x_{1}, x_{2}, \ldots ,x_{k} \rangle$ to encode states in $S_{M}$ and $X'=\langle x'_{1},x'_{2},\ldots ,x'_{k}\rangle$ to encode next states. We use also $Y=\langle y_{1}, y_{2}, \ldots ,y_{m} \rangle$ to encode actions and we represent the non-deterministic choice using $Z= \langle z_{1}, z_{2}, \ldots ,z_{r} \rangle$. Let $x,x',y,z$ be valuations of $X,X',Y$ and Z, respectively. A valuation x of X or $X'$ encodes a state s by $enc(s),s \in S_{M}$. A valid (true) valuation y encodes an action a by $enc(a),a\in \varSigma _{M}$.

Example 3

We consider the MDP $M_{0}$ (Fig. 2). $M_{0}$ contains the set of states $S_{M_{0}}=\{s_{0}, s_{1}, s_{2}, s_{3}, s_{4}, s_{5}\}$ and the set of actions $\varSigma _{M_{0}} = \{detect, warn, send, restart, fail\}$. We use $X=\langle x_{0},x_{1},x_{2}\rangle$ to encode the set of states in $S_{M_{0}}$: $enc(s_{0}) =(000), enc(s_{1}) =(001), enc(s_{2})=(010), enc(s_{3})=(011), enc(s_{4})=(100), enc(s_{5})=(101)$; and we use the set $Y=\langle d, w, s, r, f\rangle$ to encode the actions $\{detect, warn, send, restart, fail\}$, respectively. Table 1 summarizes the process of encoding the transition function $\delta _{M_{0}}$, and its corresponding MTBDD is shown in Fig. 6. In this figure, the terminal node labelled by the value 0 and its incoming edges are removed, solid (doted) edges are labelled by the value 1 (0), respectively.

Table 1 Encoding the set of states and the transition function of MDP $M_{0}$ (Fig. 2)

Fig. 6

MTBDD encoding the transition function $\delta _{M_{0}}$ ($M_{0}$ in Fig. 2)

Following the same process to encode MDP implicitly as SMDP, we can encode interval MDP as SIMDP.

Definition 8

Symbolic interval MDP (SIMDP) is a tuple $S_{I}=(X, Init_{I}, Y,f^{l}_{S_{I}} (yxx'z), f^{u}_{S_{I}} (yxx'z),Z)$ where X, Y and Z, $Init_{I}$ are defined as for interval MDP. $f^{l}_{S_{I}}(yxx'z)$ and $f^{u}_{S_{I}}(yxx'z)$ are a transition predicates over $Y \cup X \cup X' \cup Z$ where $y,x,x',z$ are valuations of receptively, $Y,X,X'$ and Z. In practice, $f^{l}_{S_{I}}(yxx'z)$ and $f^{u}_{S_{I}}(yxx'z)$ are MTBDD encoding the interval MDP, respectively, with lower and upper probability values.

As described in proof of Theorem 1, $M_{0} \parallel M_{1}$ and $I \parallel M_{1}$ have the same state space, initial state and actions. The implicit representation is introduced to reduce the size of the state space. Indeed, the implicit representation of $M_{0} \parallel M_{1}$ and $I \parallel M_{1}$ may be different. This is due to the probability values. Assumption I uses interval-valued transition probabilities rather than probability value in the original component $M_{0}$, and if the upper/lower bound is better uniformed than the probabilities in $M_{0}$, then we can expect a gain in the size of the state space. This is achieved because the final nodes in MTBDD encoding I are less than MTBDD encoding $M_{0}$, for that many non-terminal nodes will be merged together. In practice, and to improve the performance of our approach, in term of the size of the state space, our approach generates the first assumption with transitions, where the interval probability value is equal to [0, 1], between all states of the model, this will lead to merge many non-terminal nodes.

The second step in our approach, PSCV, aims to generate series of conjecture symbolic assumption $S_{I_{i}}$. Since we use symbolic data structures to encode MDP, in the aim of reducing the size of the state space, the symbolic assume-guarantee reasoning rule could be rephrased as follows.

Let $S_{M_{0}}, S_{M_{1}}$ be SMDP and $P_{\le \rho }[\psi ]$ a probabilistic safety property; the following proof rule is sound and complete:

$S_{M_{0}} \preceq S_{I_{i}}$	(1)
$S_{I_{i}} \parallel S_{M_{1}} \models P_{\le \rho }[\psi ]$	(2)
$S_{M_{0}} \parallel S_{M_{1}} \models P_{\le \rho }[\psi ]$	(3)

The proof of the rephrased symbolic assume-guarantee reasoning rule follows the same proof of the initial assume-reasoning rule.

3.1 Symbolic MTBDD-learning framework

According to the symbolic assume-guarantee rule for MDP, given an appropriate symbolic assumption $S_{I_{i}}$, we can check the correctness of a probabilistic safety property $P_{\le \rho }[\psi ]$ on $S_{M_{0}} \parallel S_{M_{1}}$, without constructing and analysing the full model. This rule is sound and complete. However, the main challenge consists of the automatic generation of an appropriate symbolic assumption. The aim of the second step, which is the symbolic MTBDD-learning framework is to learn such assumption. Our framework takes the symbolic representation of $M_{0}$ and $M_{1}$ result of the first step as input and uses the symbolic MTBDD-learning algorithm to generate a series of conjecture symbolic assumptions $S_{I_{i}}$. In Sect. 3.1.1, we detail the process of generating $S_{I_{i}}$.

3.1.1 The symbolic MTBDD-learning algorithm

The $L^{*}$ learning algorithm [3] is a formal method to learn a deterministic finite automata (DFA) with the minimal number of states that accepts an unknown language L over an alphabet $\varSigma$ (target language). During the learning process, the $L^{*}$ algorithm interacts with a Teacher to make two types of queries: (i) membership queries and (ii) equivalence queries. A membership queries are used to check whether some words w are in the target language or not. Equivalence queries are used to check whether a conjectured DFA A accepts the target language. If the conjectured DFA is not correct, the teacher would return a counterexample to $L^{*}$ to refine the automaton being learnt.

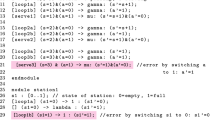
The $L^{*}$ learning algorithm has been widely used in compositional verification of non-probabilistic systems. However, for probabilistic systems such as MDP, it was demonstrated that it is undecidable to infer MDP under a version of $L^{*}$ learning algorithm, and a learning algorithm for general probabilistic systems may not exist after all [31]. In our work, we propose to use interval MDP to model assumptions instead of MDP or DFA. Moreover, we adapted the $L^{*}$ learning algorithm to accept the symbolic representation of MDP (SMDP) and learns a symbolic assumption $S_{I_{i}}$ encoded using SIMDP. Our proposed symbolic MTBDD-learning algorithm is shown in Algorithm 1.

The symbolic MTBDD-learning algorithm starts by generating an initial assumption $S_{I_{0}}$. Since we use symbolic data structures to represent the system components as well as assumptions, the function $Generate\_S_{I_{0}}$ accepts MDP $M_{0}$ and SMDP $S_{M}$ as inputs, and returns SIMDP $S_{I_{0}}$. The process of generating $S_{I_{0}}$ is described in Algorithm 2. According to the symbolic assume-guarantee reasoning proof rule, $S_{I_{0}}$ has the same state space as $M_{0}$, i.e. the same initial state, set of states and actions. Thus, the function $Generate \_S_{I_{0}}$ initializes the same data structures to $X^{I}$, $Init_{I}$ and $Y^{I}$ as for $S_{M_{0}}$. Since the initial assumption have the same state space as $S_{M_{0}}$, and to optimize the implicit representation of the transition function of $S_{I_{0}}$, $Generate \_S_{I_{0}}$ creates a new interval MDP $I_{0}$ equivalent to $M_{0}$, with transition equal to [0, 1] between all states, where the set of actions are hold in each transition, then it converts the transition function of $I_{0}$ to MTBDD $f^{u}_{S_{I}}$. The aim behind the generation of $S_{I_{0}}$ with transition equal to [0, 1] between all states is to reduce the size of the implicit representation of the state space. Indeed, for large probabilistic system, when we use uniform probabilities, 0 and 1 in our case, this will reduce the number of terminal nodes as well as non-terminal nodes. Adding transition between all states, will keep our assume-guarantee verified for the initial assumption, since $M_{0}$ is embedded in $I_{0}$, in addition, this process will help to reduce the size of the implicit representation of $I_{0}$ and this by combining any isomorphic sub-tree into a single tree, and eliminating any nodes whose left and right children are isomorphic. To illustrate the size gain of using this process, we consider the example of randomized dining philosophers [18, 35]. (This example is described in Sect. 4.) The results are reported in Table 2. In this table we compare the size of MTBDD encoding the transition function of $M_{0}$ and $I_{0}$ for randomized dining philosophers model, where T4MC describes the time for model construction and M. Nodes illustrates the number of model nodes.

Table 2 Comparison between the size of MTBDD encoding the transition function of $M_{0}$ and $I_{0}$ for randomized dining philosophers

Example 4

To illustrate the PSCV approach, we propose the verification of the system $S = M_{0} \parallel M_{1}$ (Fig. 2) against the probabilistic safety property: $\varphi = P_{\le 0.1}[\lozenge "fail"]$, where "fail" stands for the state $\langle s_{3} , t_{3} \rangle$. The property $\varphi$ means that the maximum probability that the system S should never fails, over all possible adversaries, is less than 0.1. Initially, PSCV starts by encoding the system components $M_{0}$ and $M_{1}$ using SMDP. Then, it calls the symbolic MTBDD-learning algorithm to generate an appropriate symbolic assumption $S_{I_{i}}$. The symbolic MTBDD-learning algorithm generates an initial conjecture symbolic assumption $S_{I_{0}}$.

An equivalence query is made in line 5 (Algorithm 1) to check whether the initial conjectured symbolic assumption $S_{I_{0}}$ could be used in the compositional verification. Like the $L^{*}$ learning algorithm, our symbolic MTBDD-learning algorithm interacts with a teacher to answer two types of queries: equivalence queries and membership queries. However, in our case, the interpretation of these latter is different.

3.1.2 Equivalence queries

In our approach, equivalence queries are used to check whenever a symbolic conjecture assumption $S_{I_{i}}$ can be used to establish the two promises of the symbolic assume-guarantee rule. The first step is to check if $S_{M_{0}} \preceq S_{I_{i}}$, this is done by checking if: (1) $S_{M} = S_{I_{i}}$, (2) $s_{0}^{M} = s_{0}^{I}$, (3) $\varSigma _{M} = \varSigma _{I}$, and (4) $P^{l}(s,a)(s') \le \mu (s,a)(s') \le P^{u}(s,a)(s')$ for every $s,s' \in S_{M}$ and $a \in \varSigma _{M}$ (see Definition 6). Since we use symbolic data structures to encode MDP and interval MDP, the checking process can be rephrased as follows:

Let $S_{M}=(X^{M},Init_{M},Y^{M},f_{S_{M}}(yxx'z),Z^{M})$ and $S_{I_{i}} =(X^{I},Init_{I},Y^{I},f^{l}_{S_{I}}(yxx'z) , f^{u}_{S_{I}}(yxx'z),Z^{I})$ be SMDP and SIMDP, respectively. We say that $S_{M_{0}} \preceq S_{I_{i}}$ if and only if: (1) $X^{M} = X^{I}$, (2) $Init_{M} = Init_{I}$, (3) $Y^{M} = Y^{I}$, and (4) $MQuery(S_{T},f^{u}_{S_{I}}) \le MQuery(S_{T},f_{S_{M}}) \le MQuery(S_{T},f^{l}_{S_{I}})$ for every $s \in S_{M}$, where $S_{T}$ is a BDD encoding a transition $s_{i} \xrightarrow []{a} s_{j}$ ($s_{i},s_{j} \in S_{M}$). EQuery calls the function Threshold if:

$Prob_{S_{M}} < Prob_{SI^{l}}$ or $Prob_{S_{M}} > Prob_{SI^{u}}$. Threshold changes the final nodes in $f^{l}_{S_{SI}}$ (or $f^{u}_{S_{SI}}$) to $Prob_{S_{M}}$ following the BDD $S_{T}$. Otherwise, if the first promise is valid, then the function EQuery would check the second promise of the symbolic assume-guarantee rule, i.e. Does $S_{I_{i}} \parallel S_{M_{2}}$ satisfy $P_{\le \rho }[\psi ]$?

The second step is done by applying a symbolic probabilistic model checking. In practice, to check whether $S_{I_{i}} \parallel S_{M_{2}} \models P_{\le \rho }[\psi ]$, the model checker needs first to compute the parallel composition $S_{I_{i}} \parallel S_{M_{2}}$, which results an SIMDP. The symbolic model checking algorithm SPMC used in the function EQuery (line 12) is described in Sect. 3.1.4. The function EQuery is illustrated in Algorithm 3.

3.1.3 Membership queries

Membership queries can be seen as a function $MQuery (BDD S_{T}, MTBDD f_{S_{M}}){:}Double$. MQuery tacks a BDD $S_{T}$ and MTBDD $f_{S_{M}}$ as inputs, where the BDD $S_{T}$ encodes a transition $s_{i} \xrightarrow []{a} s_{j}$ over $Y\cup X\cup X'$, and returns the probability value between $s_{i} \xrightarrow []{a} s_{j}$ in $f_{S_{M}}$ by applying the function $Apply(*,S_{T},f_{S_{M}})$, where apply returns an MTBDD representing the function $S_{T} * f_{S_{M}}$. Multiplying the BDD $S_{T}$ with the MTBDD $f_{S_{M}}$ removes all transitions from $f_{S_{M}}$ which do not connect states of $S_{T}$, i.e. the result MTBDD encodes only $s_{i} \xrightarrow []{a} s_{j}$ with the original probability value in $f_{S_{M}}$.

Example 5

It is clear that the initial assumption $S_{M_{0}}$ is embedded in $S_{I_{0}}$. Indeed, the main step in the equivalence query is the verification if $S_{I_{i}} \parallel S_{M_{1}}$ satisfies the property $\varphi$ or not. To model checking the system $S_{I_{0}} \parallel S_{M_{1}} \models ^{?} P_{\le \rho }[\psi ]$, the function EQuery calls the symbolic probabilistic model checking SPMC. In our example, EQuery calls the function SPMC the first time with $S_{I_{0}}$, the MTBDD $f_{S_{M_{1}}}$ and the property $\varphi$. After model checking the system $S_{I_{0}} \parallel S_{M_{1}} \models ^{?} P_{\le \rho }[\psi ]$, SPMC returns false, this means that the system $S_{I_{0}} \parallel S_{M_{1}}$ does not satisfy the property $\varphi$.

The function SPMC used in this paper is described in the next section (Sect. 3.1.4).

3.1.4 Symbolic probabilistic model checking

Model checking algorithm for interval MDP was considered in [6, 10], where it was demonstrated that the verification of interval MDP is often more consume, in time as well as in space, than the verification of MDP. In this work, our ultimate goal is reducing the size of the state space. Therefore, the verification of interval MDP needs to be avoided. Thus, we propose rather than verifying interval MDP $S_{I_{i}} \parallel S_{M_{1}}$, we verify only a restricted SIMDP RI, which is an MTBDD contains the upper probability value of the probability interval associate in each transition of $S_{I_{i}}$. This can be done by taking the MTBDD $f^{u}_{S_{I_{i}}}$ of $S_{I_{i}}$. Then, the verification of $RI \parallel S_{M_{1}}$ can be done using the standard probabilistic model checking proposed in [25]. The symbolic probabilistic model checking used in this work was proposed in [39].

When EQuery returns false, this means either the symbolic assumption is too strong (the upper probability value is big) or the system S does not satisfy the property $\varphi$. The symbolic MTBDD-learning algorithm calls the functions GenerateCex and AnalyseCex to generate and analyse the counterexamples.

3.1.5 Generate probabilistic counterexamples

The probabilistic counterexamples are generated when a probabilistic property $\varphi$ is not satisfied. They provide a valuable feed back about the reason why $\varphi$ is violated.

Definition 9

The probabilistic property $\varphi = P_{\le \rho }[\psi ]$ is refuted when the probability mass of the path satisfying $\varphi$ exceeds the bound $\rho$. Therefore, the counterexample can be formed as a set of paths satisfying $\varphi$, whose combined measure is greater than or equal to $\rho$.

As denoted in Definition 9, the probabilistic counterexample is a set of finite paths, for example, the verification of the property “a fail state is reached with probability at most 0.01” is refused by a set of paths whose total probability exceeds 0.01. The main techniques used for the generation of counterexamples are described in [29]. The probabilistic counterexamples are a crucial ingredient in our approach, since they are used to analyse and refine the conjecture symbolic assumptions. Thus, our need consist to find the most indicative counterexample. A most indicative counterexample is the minimal counterexample (which has the least number of paths). A recent work [16] proposed to use causality in order to generate small counterexamples. In this paper, we used the tool DiPro¹ to generate counterexamples. DiPro employs many algorithms to generate counterexamples, among these algorithms we use the $K^{*}$ algorithm [2]. In addition, we apply the algorithms in [17] to generate the most indicative counterexample, denoted by Cex.

3.1.6 Analysis probabilistic counterexamples

The function AnalyseCex aims to check whether the probabilistic counterexample Cex is real or not. Cex is a real counterexample of the system S if and only if $SM_{0}^{Cex} \parallel S_{M_{1}} \models P_{\le \rho }[\psi ]$ does not hold. In practice, the function AnalyseCex creates a fragment of the MDP $M_{0}$ based on the probabilistic counterexample Cex, where the MDP fragment $M_{0}^{Cex}$ contains only transitions present in Cex. Thus, the fragment $M_{0}^{Cex}$ is obtained by removing from $M_{0}$ all states and transitions not appearing in any path of the set Cex.

Since we use symbolic data structures to encode the state space, we encode the MDP fragment using SMDP $SM_{0}^{Cex}$ (following the same process to encode MDP). AnalyseCex returns true if and only if the symbolic probabilistic model cheeking of $SM_{0}^{Cex} \parallel S_{M_{1}} \models P_{\le \rho }[\psi ]$ returns false, or false otherwise. The computing of the product $SM_{0}^{Cex} \parallel S_{M_{1}}$ follows the same process as the parallel composition of $MDP \parallel IMPD$. The function AnalyseCex is described in Algorithm 5.

Example 6

The equivalence query for the initial assumption $S_{I_{0}}$ returns false. The PSCV calls the function GenerateCex to generate the most indicative probabilistic counterexample. For our example, since the system $S_{I_{0}} \parallel S_{M_{1}}$ does not satisfy the property $\varphi$.

GenerateCex returns the set Cex, where $Cex=\{ (s_{0},t_{0}) \xrightarrow []{detect,0.2} (s_{2},t_{2}) \xrightarrow []{send,0.7} (s_{3},t_{3}) \}$. To check whether the probabilistic counterexample Cex is real or not, the function AnalyseCex generates an MDP fragment $M_{0}^{Cex}$ (see Fig. 7), and calls the SPMC to model checking the system $SM_{0}^{Cex} \parallel S_{M_{1}} \models P_{\le 0.1}[\psi ]$. SPMC returns false, this means that Cex is a real counterexample, and the property $\varphi$ does not satisfy the system S.

Fig. 7

MDP fragment $M_{0}^{Cex}$

3.1.7 Refinement process of the conjecture symbolic assumption $S_{I_{i}}$

If the probabilistic counterexample is not real, the symbolic MTBDD-learning algorithm calls the function $Refine\_S_{I_{i}}$ to refine $S_{I_{i}}$. $Refine\_S_{I_{i}}$ takes the conjecture symbolic assumption $S_{I_{i}}$ and the probabilistic counterexample Cex as input. First, $Refine\_S_{I_{i}}$ searches the maximum probability value $Max_{p}$ in all paths of Cex. Then, it sets the upper probability value for all probability intervals of $S_{I_{i}}$ presenting in Cex to $Max_{p}$. The choice of using $Max_{p}$ to refine $S_{I_{i}}$ is to keep the upper bounds of the interval probability value more uniform, i.e. to reduce the number of terminal nodes of the MTBDD encoding $S_{I_{i}}$. As described in Algorithm 6, the refinement process of $S_{I_{i}}$ is based on the set of paths present in Cex. This process could bring the $S_{I_{i}}$ closer to the original competent $M_{0}$. In practice, the use of $Max_{p}$ could lead to generate a spurious counterexample. To resolve this, and to guarantee the completeness of our approach, we store the last set of counterexample $Last\_Cex$ and the current set Cex, and if a state s is present in the two sets of counterexample, Cex and $Last\_Cex$, then we set all the upper bounds of the outgoing transitions to the corresponding probability value in $\delta _{M_{0}}$. These states are stored to not change their outgoing transitions in the next refinement iterations.

Table 3 Experimental results for case studies randomized mutual exclusion and client–server

Our approach PSCV as well as our algorithm, symbolic MTBDD-learning algorithm, is characterized by:

• Soundness, this means if our symbolic MTBDD-learning algorithm generates a symbolic assumption $S_{I_{i}}$, where $S_{M_{0}} \preceq S_{I_{i}}$ and $S_{I_{i}} \parallel S_{M_{1}} \models P_{\le \rho }[\psi ]$, then we are sure that $S_{M_{0}} \parallel S_{M_{1}} \models P_{\le \rho }[\psi ]$, the soundness of our approach is based on Theorem 1, this proof rule has been precisely proven in Sect. 3.

• Completeness, this means that our symbolic MTBDD-learning algorithm will generate eventually a symbolic assumption $S_{I_{i}}$. Our symbolic MTBDD-learning algorithm always generates a new assumption either by learning an initial assumption $S_{I_{0}}$ or by refine $S_{I_{i}}$.

• Termination, this means that our algorithm will always terminate. Our symbolic MTBDD-learning algorithm targets a SIMDP $S_{I_{i}}$, where $S_{M_{0}} \preceq S_{I_{i}}$. Based on Theorem 1, we can always generate assumptions such $S_{M_{0}} \preceq S_{I_{i}}$; thus, the learning algorithm will always terminate, either by true if $S_{M_{0}} \parallel S_{M_{1}} \models P_{\le \rho }[\psi ]$ or false otherwise. In the worst case, our algorithm will generate $S_{M_{0}}$ as a symbolic assumption.

• Complexity, another important point is the complexity of our symbolic MTBDD-learning algorithm. Indeed, if we want to apply our algorithm to verify real-life systems then it needs to check these systems within a polynomial number of queries, thus, in a polynomial time. Our algorithm infers the symbolic assumption with at most n equivalence queries, where $n = |\delta _{M_{0}}|$.

As described before, the main goal of our work is to cope with the state space explosion problem. In the next section (Sect. 4), we apply our PSCV approach in a several case studies and we compare its performance against the symbolic monolithic probabilistic verification.

Table 4 Experimental results for the case studies randomized dining philosophers, randomized self-stabilizing algorithm and dice

4 Implementation and experimental results

We have implemented a prototype tool named PSCV4MDP (probabilistic symbolic compositional verification for MDP). Our tool accepts MDP specified using PRISM code and a probabilistic safety property as input and returns either true if the MDP satisfies the probabilistic safety property, or false and counterexample otherwise. In this section, we give the results obtained for the application of our approach in a several case studies derived from the PRISM benchmark.² For each case study, we check the model against a probabilistic safety property using: (1) symbolic monolithic probabilistic model checking and (2) symbolic probabilistic compositional verification. In addition, we compare, for each technique, the time for model construction T4MC, and the size of the state space, i.e. the number of nodes. We have summarized and compared the results in Tables 3 and 4. In Table 3 we report the results of the case studies randomized mutual exclusion and Client–Server; for these two case studies, it was necessary to generate counterexamples to refine the initial assumption, contrary to Table 4, where the initial assumption was sufficient for the verification process. For both tables, the column (No.) shows the number of components and the column [Red (%)] shows the reduction of model size of our PSCV to the symbolic monolithic verification. The tests were carried on a personal computer with Linux as operating system, 2.30 GHz CPU and 4GB RAM.

In addition, for each case study, we report the size of $S_{M_{0}} \parallel S_{M_{1}}$ for the symbolic monolithic verification or $S_{I_{f}} \parallel S_{M_{1}}$ for the symbolic compositional verification, where $S_{I_{f}}$ is the final symbolic assumption. We also report in Table 3 the T4MC and the size of $SM_{0}^{Cex} \parallel S_{M_{2}}$ and $S_{M_{2}}$. We observe that the PSCV successfully infers symbolic assumptions and $S_{I_{f}} \parallel S_{M_{1}}$ are much more compact than $S_{M_{0}} \parallel S_{M_{1}}$ in all cases. For example, in the first case study (mutual $N = 11$), $S_{I_{f}} \parallel S_{M_{1}}$ has 26,779 nodes while $S_{M_{0}} \parallel S_{M_{1}}$ has 34,034 nodes; in R. S. stab. ($N = 17$), $|S_{M_{0}} \parallel S_{M_{1}}| = 969$ while $|S_{I_{f}} \parallel S_{M_{1}}| = 53$. The column TT illustrates the total time for PSCV to check if the case study satisfies the property or not, i.e. $TT = T4MC$ (for PSCV) $+$ Time to generate $S_{I_{f}}$.

4.1 Randomized mutual exclusion

Our first case study, randomized mutual exclusion (Mutual), is based on Pnueli and Zuck’s [40] probabilistic symmetric solution to the n-process mutual exclusion problem. The model is represented as an MDP. We let No. denotes the number of processes. We check the system against the property: $\varphi _{1} =\,$The probability that two or more processes are simultaneously in their remainder phases is at most 0.999. The results for this case study are reported in Fig. 8. The results show that PSCV performs better then the symbolic monolithic verification and reduces the model size by 31% on average. For time to model checking this case study, the symbolic monolithic verification performs better than PSCV, and this is due to time to generate counterexample and refine assumptions.

Fig. 8

Case study results from the application of symbolic monolithic verification and PSCV: Mutual

4.2 Client–server

This case study is a variant of the Client–Server model from [41]. It models a server and N clients. The server can grant or deny a client’s request for using a common resource, once a client receives permission to access the resource, it can either use it or cancel the reservation. Failures might occur with certain probability in one or multiple clients, causing the violation of the mutual exclusion property (i.e. conflict in using resources between clients). In this case study, we consider the property: $\varphi _{5} =$ the probability a failure state is reached is at most 0.98. For this case study, PSCV reduces the size by 15.33% on average (Fig. 9).

Fig. 9

Case study results from the application of symbolic monolithic verification and PSCV: client–server

4.3 Randomized dining philosophers

The third case study is the randomized dining philosophers (R.D. Philos). This case study models a randomized solution to the dining philosophers problem, proposed by [18, 35]. R.D. Philos concerns the problem of resources allocation between processes. Several philosophers sit around a circular table. There is a fork between each pair of neighbouring philosophers. A philosopher can eat if and only if he obtains the resources from both sides. In this case study, No. denotes the number of philosophers. We analyse the solution proposed in [18, 35] by using the property: $\varphi _{2} =$ the probability that philosophers do not obtain their shared resource simultaneously is at most 0.980, formally: $P_{\le 0.980} [ \lozenge "err"]$, where label “err” sands for every states satisfy: $[(s_{N} \ge 8) \& (s_{N} \le 9)]$, and N is the component number. Results are reported in Fig. 10. In this case study, PSCV reduces the model size by 47.66% on average and improves the verification time as well.

Fig. 10

Case study results from the application of symbolic monolithic verification and PSCV: randomized dining philosophers

4.4 Randomized self-stabilizing algorithm

In the fourth case study we consider a number of randomized self-stabilizing algorithms (R.S. Stab.). A randomized self-stabilizing protocol for a network of processes is a protocol which, when started from some possibly illegal start configuration, returns to a legal/stable configuration without any outside intervention within some finite number of steps. In this paper, we consider the solution of Israeli and Jalfon [28] and we analyse the protocol through the following property: $\varphi _{3} =$ the probability to reach a stable configuration for all algorithms is at most 0.999. Experimental results are reported in Fig. 11. For this case study, the verification time is improved and the model size is reduced by 91.60% on average.

Fig. 11

Case study results from the application of symbolic monolithic verification and PSCV: randomized self-stabilizing algorithm

4.5 Dice

This case study considers probabilistic programs, due to Knuth and Yao [30], which model fair dice using only fair coins. At the implementation, we have used a reimplementation of the work done by [27]. The probabilistic programs are modelled using discrete time Markov chain (DTMC), which constitute a subclass of MDP. We consider the analysis of the property: $\varphi _{4} =$ the probability of reaching a state with $s = 7 \, \& \,d = k$ is at most 0.01, where $k \in [1 \ldots 6]$. Performing the verification of this case study, the PSCV reduces the size by 17.83% on average (Fig. 12).

Fig. 12

Case study results from the application of symbolic monolithic verification and PSCV: dice

4.6 Discussion

Table 3 reports the results for case studies Mutual and Client–Server. The average size reduction for these case studies is 22.54%. For Mutual model, the reduction size decreases by the number of components. As described in our paper, the size reduction depends on the number of terminal nodes and the combining process of isomorphic sub-tree. For this case study, the initial assumption $S_{I_{0}}$ was too string for PSCV to check if $M_{0} \parallel M_{1} \models P_{\le \rho }[\psi ]$; thus, PSCV refined $S_{I_{0}}$. At each refinement iteration, assumptions converge to the original component $M_{0}$, and this could lead to add other terminal nodes and many non-terminal nodes. Contrary to the first case study, the size reduction for Client–Server model is stable. For the model checking time, the symbolic monolithic verification performs better than PSCV, and this is due essentially to the time needed to analyse and refine the assumptions. The refinement process and counterexample generation consume more time than the monolithic verification. In Table 4, we report the results for case studies R.D. Philos, R.S. Stab. and Dice. For these case studies, $S_{I_{0}}$ was sufficient for the PSCV verification process. The average size reduction for these examples is 50.11. The reduction size for R.S. Stab model is stable, contrary to R.D. Philos and Dice, where the size reduction decrease by the number of components. Indeed, in these examples the size reduction depends on the number of terminal nodes and the combining process of isomorphic sub-tree.

The overall results show that PSCV is more effective than the symbolic monolithic verification. The PSCV successfully generates a symbolic assumption that establish the verification process. Moreover, the model size is reduced by 39.25% on average for the 28 cases (reported in Tables 3 and 4). The success of our approach, comparing with the symbolic monolithic verification, comes from the fact that PSCV avoids the construction of the whole model.

5 Related works

In this section, we review some research works related to the symbolic probabilistic model checking, compositional verification and assume-guarantee reasoning. Verification of probabilistic systems has been addressed by Vardi and Wolper [44,45,46], then by Pnueli and Zuck [40] and by Baier and Kwiatkowska [5]. The symbolic probabilistic model checking algorithms have been proposed by [12, 39]. These algorithms have been implemented in a symbolic probabilistic model checker PRISM [33]. Model checking algorithm for interval MDP was considered in [6, 10]. An important step in our approach is the generation of small counterexample. The main techniques used to generate counterexamples were detailed in [29]. A recent work [16] proposed to use causality in order to generate small counterexamples; the authors of this work propose to use the tool DiPro to generate counterexamples; then they applied an aided-diagnostic method to generate the most indicative counterexample [17]. For the compositional verification of non-probabilistic systems, several frameworks have been developed using the assume-guarantee reasoning approach [11, 13, 41]. The compositional verification of probabilistic systems has been a significant progress in these last years [8, 21, 22, 25, 32]. Our approach is inspired by the work of [21, 22]. In this work, assumptions are represented as deterministic finite automata (DFA) and the classical $L^{*}$ learning algorithm has been applied to infer assumptions. However, this work used a non-complete assume-guarantee reasoning rule, and the generation of an assumption to establish the compositional verification is not guaranteed. Another work relevant to ours is [25]. This work proposed the first sound and complete learning-based composition verification technique for probabilistic safety properties, where they used an adapted $L^{*}$ learning algorithm to learn weighted automata as assumptions, then they transformed them into MTBDD. In [37] authors proposed an algorithm for automatically learning a deterministic labelled Markov decision process model from the observed behaviour of a reactive system. The proposed learning algorithm adopt a passive learning model, which was adapted from algorithms for learning deterministic probabilistic finite automata, and extended to include both probabilistic and non-deterministic transitions.

6 Conclusion

In this paper, we proposed a fully automated probabilistic symbolic compositional verification approach (PSCV) to verify probabilistic systems, where each component is an MDP. The PSCV is based on our proposed symbolic assume-guarantee reasoning rule, which describes the symbolic compositional verification process. The main characteristics of our symbolic assume-guarantee reasoning rule are completeness and soundness. The completeness comes from the use of IMDP to represent the assumptions. Since we aim to overcome the state space explosion problem when verifying probabilistic safety properties, the system components and assumptions are represented by a compact symbolic data structures, i.e. SMDP and SIMDP. In addition, we proposed a symbolic MTBDD-learning algorithm to construct automatically these assumptions, where it used causality to generate small counterexamples in order to refine the conjecture symbolic assumptions. The experimental results are encouraging and demonstrated that our approach can reduce the state space by learning symbolic assumptions.

Our actual approach can be applied to sequential probabilistic systems. We plan to propose other assume-guarantee reasoning rule such as asymmetric rule or circular rule to verify n-components. Since we use interval MDP to represent assumptions, our approach can be easily extended to verify properties of the form $\varphi = P_{\ge P}[\psi ]$. Moreover, we plan to extend the PSCV to verify other probabilistic properties such as liveness.