1 Introduction

Driven by economic and environmental issues, the design of energy-efficient high-bandwidth wireless communication technology has become critical [1]. In this paper, the joint development of the millimeter-wave (mmWave) spectrum, which can provide high bandwidth, and Reconfigurable Intelligent Surfaces (RIS), which can reduce energy usage, has the potential to achieve this goal. The low-power, low-throughput nature of routinely deployed IoT devices has led to neglecting such high-frequency bands with rather severe propagation characteristics when building IoT environments. However, the emergence of large-scale IoT applications has spawned a large number of devices, putting pressure on low-bandwidth technologies below 6 GHz, and mmWave has emerged as a candidate solution for quasi-scenarios such as smart grids, smart cities, and intelligent industries [2]. The main challenge in this situation is that mmWave transceivers typically employ digital or hybrid beamforming, with multiple RF chains and numerous antenna arrays that can focus electromagnetic energy to specific angles to counter the high attenuation characteristic of the mmWave. However, it becomes infeasible when this approach is used for power-constrained IoT devices because multiple active devices consume energy [3]. For such problems and challenges, RIS can be a solution by exploiting the vast bandwidth resources of mmWave while allowing advanced large-scale IoT scenarios with an extremely low probability of service interruption [4]. RIS utilizes controllable transformations to incoming radio waves without power amplifiers, creating many possible solutions for optimizing low-cost, low-energy wireless systems [5]. RIS has acquired much attention [6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21] due to its ability to transform the random nature of the wireless environment into a programmable channel that has an active role in how the signal propagates. RIS has been proposed for various applications, including secure communications [15, 16], non-orthogonal multiple access [17], wireless computing [18], or energy-efficient cellular networks [19, 20]. RIS is a continuous meta-surface modeled as a grid of discrete unit cells separated by subwavelength distances that can programmatically change its electromagnetic response (such as phase, amplitude, polarization, and frequency). For example, they can be adjusted so that the signals bouncing off the RIS are combined constructively to improve the signal quality at the intended receiver end or destructively to avoid signal leakage to undesired receivers. Conceptually, RIS may raise some of the challenges behind traditional amplify-and-forward (AF) relay methods [22] and beamforming methods used in (massive) MIMO [23]. There are significant differences between conventional AF relays and RIS [24, 25]. The former relies on active low-noise power amplifiers and other active electronic components such as DAC or ADC converters, mixers, and filters. In contrast, RIS has a shallow hardware footprint and consists of one or a few layers of planar structures that can be built using photolithographic or nanoimprinting methods. Therefore, RIS is particularly attractive for seamless integration into walls, ceilings, object boxes, architectural glass, and clothing [26].

On the other hand, (massive) MIMO uses many antennas to obtain significant beamforming gains. In fact, under similar conditions, massive MIMO and RIS techniques can produce equal signal-to-noise ratio (SNR) profits. However, RIS passively achieves this beamforming gain. In this paper, active beamforming through the transmitter antenna array and passive beamforming through the RIS in the channel can compensate for each other and provide more significant gain when both are optimized together, which is precisely the goal of this paper. Although massive MIMO technology can significantly improve the efficiency of wireless information transfer (WIT) and wireless power transfer (WPT) in emerging IoT networks by exploiting the gain of large arrays, this usually comes at a high cost [27,28,29]. As a remedy, radio frequency (RF) chains can be used in so-called hybrid implementations than transmit/receive antennas. This can also result in high hardware costs, high signal processing overhead, and high energy consumption, hindering implementation. As a cost-effective alternative to massive MIMO technology, RIS enables unprecedented spectral and energy efficiency, especially in complex propagation scenarios with severe signal blocking. However, because RIS is a reconfigurable metal surface with many passive reflective elements, it cannot perform as complex signal processing as large arrays and active MIMO repeaters. It is usually served with lower hardware costs and low power consumption. By adjusting the phase shift and amplitude attenuation of each RIS reflective element, an excellent wireless propagation environment can be actively constructed for WIT and WPT [30, 31]. Because of the above advantages, research on RIS-assisted communication for various wireless systems such as MISO systems [32, 33], point-to-point MIMO systems [34], multicell multiuser MIMO systems [35], and MIMO-OFDM systems [36, 37] attracted attention. These studies usually assume perfect channel state information (CSI). Traditional training-based channel estimation schemes cannot be directly applied due to the lack of fundamental frequency processing capability of RIS operating without RF chains and the need to estimate many RIS-related channels. As an alternative, under the assumption of uplink-downlink channel reciprocity for flat frequency channels and frequency selective channels, various channel estimation schemes using RIS grouping strategies have been proposed previously [36,37,38,39,40,41].

Nonetheless, there are new challenges to integrating RF energy harvesting and advanced WIT technologies for sustainable green IoT networks. To this end, Simultaneous Wireless Information and Power Transfer (SWIPT) has been evaluated as an attractive, innovative technology [42]. Recently, there has been increasing interest in RIS-based SWIPT systems [9, 43,44,45]. For example, [43] studied weighted harvested energy maximization in a RIS-assisted MISO SWIPT system and demonstrated that dedicated energy beamforming is practically optional. As a further development, the maximization of the minimum harvested energy among all energy receivers (ERs) in this system is studied from a fairness perspective [44]. By deploying multiple RIS, [45] investigated total transmit power minimization subject to separate QoS constraints at the Information Decoder (ID) and ER. Pan et al. [35] considered a more general RIS-assisted MIMO SWIPT system and studied the weighted sum rate maximization of all IDs while guaranteeing a particular minimum total harvested energy across all ERs. Various advanced communication technologies in IoT networks, such as NOMA [46, 47], Physical Layer Security [48, 49], and Mobile Edge Computing (MEC), have also been integrated with this technology. RIS achieves better system performance, so in this paper, we consider a RIS-assisted MIMO SWIPT system consisting of a multi-antenna base station (BS), a RIS to assist communication, and multiple SWIPT-enabled systems. It consists of several IoT devices, and RIS is deployed to assist SWIPT from the BS to these IoT devices. From a fairness perspective, we further investigate the maximization of the minimum SINR among all IDs by jointly optimizing the active BS transmit beamforming vector and the passive RIS reflection coefficient, premised on the minimum total harvested energy required for all ERs.

2 System Model and Problem Formulation

This section introduces the system model and problem description. We first present the entire system’s architecture and then describe our goals and the problems.

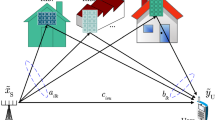
As shown in Fig. 1, we consider a RIS-assisted wireless communication system in which the RIS is deployed to assist the multi-antenna APs in the SWIPT system. It is transmitted from the AP of M antennas to two parts, including the information user (IU) and energy user (EU); the number of IU is \({K}_{I}\), and the number of EU is \({K}_{\varepsilon }\). For simplicity, we consider linear transmit precoding at the AP and assume that each IU/EU is assigned a separate information/energy beam without loss of generality. Therefore, the transmission signal from the AP can be expressed as

$$x=\sum_{i\in {K}_{I}}{w}_{i}{s}_{i}^{I}+\sum_{{\text{j}}\in {K}_{\varepsilon }}{v}_{j}{s}_{j}^{E},$$
(1)

where \({w}_{i}\in {C}^{M\times 1}\) is the precoding vector of IU, \({v}_{j}\in {C}^{M\times 1}\) is the precoding vector of EU, \({s}_{i}^{I}\) represents the message-bearing signal, and \({s}_{j}^{E}\) represents the energy signal. \({s}_{i}^{I}\) are assumed to be independent and identically distributed signals with zero mean and variance one, while \({s}_{j}^{E}\) carry no information; they can be any random signals. Therefore, the total transmit power required by the AP is expressed as follows.

Fig. 1
figure 1

System model

Full size image
$$E\left({x}^{H}x\right)=\sum_{i\in {K}_{I}}{\Vert {w}_{i}\Vert }^{2}+\sum_{{\text{j}}\in {K}_{\varepsilon }}{\Vert {v}_{j}\Vert }^{2},$$
(2)

Next is the part of the signal received by the IU, \({h}_{{\text{d}},k}^{H}\in {C}^{1\times M}\) is the channel directly transmitted by the AP to the IU, \({h}_{{\text{g}},k}^{H}\in {C}^{1\times L}\) is the channel that the RIS transmits to the IU, \({e}_{{\text{d}},k}^{H}\) is the channel that the AP transmits directly to the EU, \({e}_{{\text{g}},k}^{H}\) is the channel that the RIS sends to the EU, \({W}_{g}\left(l\right)\) indicates the channel transmitted from the AP to the RIS and \({\Phi }_{g}^{H}\left(l\right)\) represents the reflective element channel in the RIS. Since implementing independent control of reflection amplitude and phase is expensive, it is advantageous to design each element to maximize signal reflections for simplicity. Therefore, we express the signal received by the IU from AP to IU and AP to RIS and then to IU as the following equation:

$$ y_{k}^{I} = \left( {\sum\limits_{{l = 1}}^{L} {h_{{g,k}}^{H} } \left( l \right)\Phi _{g}^{H} \left( l \right)W_{g} \left( l \right) + h_{{d,k}}^{H} } \right)x + \sigma _{k} , $$
(3)

where \({\sigma }_{k}\sim CN\left(0,{\sigma }_{k}^{2}\right)\) is an independent and identically distributed Gaussian noise, and we simplify Eq. (3) and rewrite it as (4):

$${y}_{k}^{I}=\left({h}_{g,k}^{H}{\Phi }_{g}^{H}{W}_{g}+{h}_{d,k}^{H}\right)x+{\sigma }_{k},$$
(4)

where \({h}_{g,k}^{H}={\left[{h}_{g,k}^{H}\left(1\right),\dots ,{h}_{g,k}^{H}\left(L\right)\right]}^{T}\in {C}^{N\times N}\), \({W}_{g}={\left[{W}_{g}\left(1\right),\dots ,{W}_{g}\left(L\right)\right]}^{T}\in {C}^{N\times M}\), and \({\Phi }_{g}^{H}={\text{Diag}}\left({\Phi }_{g}^{H}\left(1\right), \dots ,{\Phi }_{g}^{H}\left(L\right)\right)\in {C}^{N\times N}\).

Since the energy beam carries no information but a pseudo-random signal, its waveform can be assumed to be known at the AP and each IU before data transmission. We hypothesize that the interference they cause can be canceled at each IU, which contributes to the fundamental performance limitations of our SWIPT system and the study of the impact of RIS on energy beamforming. Therefore, we express SINR as Eq. (5):

$${SINR}_{k}={\gamma }_{k}=\frac{{\left|\sum_{g=1}^{G}{h}_{g,k}^{H}{\Phi }_{g}^{H}{W}_{g}{w}_{i}\right|}^{2}}{{\sum_{k=1,k\ne i}^{K}{\left|\sum_{g=1}^{G}{h}_{g,k}^{H}{\Phi }_{g}^{H}{W}_{g}{w}_{k}\right|}^{2}}^{2}+{\sigma }_{i}^{2}}.$$
(5)

On the other hand, it is part of the energy received by the EU. We express the energy received by the EU with Eq. (6):

$${Q}_{j}=\sum_{i\epsilon {K}_{i}}{\left|{(e}_{g,j}^{H}{\Phi }_{g}^{H}{W}_{g}+{e}_{d,j}^{H}){w}_{i}\right|}^{2}+\sum_{i\epsilon {K}_{\varepsilon }}{\left|{(e}_{g,j}^{H}{\Phi }_{g}^{H}{W}_{g}+{e}_{d,j}^{H}){v}_{m}\right|}^{2}.$$
(6)

Then comes the problem description part; our goal is to maximize the transmission rate of the entire system through optimization subject to the constraints of the transmission power and the energy harvesting at the EU. We formulate the problem description as Eq. (7):

$$ \begin{gathered} \mathop {Maximize}\limits_{{P,\Phi_{g} }} f_{1} \left( {P,\Phi_{g} } \right) = \sum\limits_{k = 1}^{K} {z_{k} } log_{2} \left( {1 + \gamma_{k} } \right),{\text{Subject}}\;{\text{to}} \hfill \\ \sum\nolimits_{{i \in K_{I} }} {\left\| {w_{i} } \right\|^{2} } + \sum\nolimits_{{{\text{j}} \in K_{\varepsilon } }} {\left\| {v_{j} } \right\|^{2} } \le P, \hfill \\ \sum\nolimits_{{i \in K_{i} }} {\left| {\left( {e_{g,j}^{H} \Phi_{g}^{H} W_{g} + e_{{{\text{d}},j}}^{H} } \right)w_{i} } \right|^{2} } + \sum\nolimits_{{i \in K_{\varepsilon } }} {\left| {\left( {e_{g,j}^{H} \Phi_{g}^{H} W_{g} + e_{{{\text{d}},j}}^{H} } \right)v_{m} } \right|^{2} } \ge E_{j} , \hfill \\ 0 < \theta_{n} \le 2\pi ,\forall n \in N. \hfill \\ \end{gathered} $$
(7)

where \({z}_{k}\) is the data weight assigned to the kth IU, P represents the maximum transmission power, \({E}_{j}>0\) is the least energy received by each energy user, and \({\theta }_{n}\) represents the phase of the RIS.

3 The Proposed Method and Algorithm

First, we change the formula of power limit into the form of rank, such as Eq. (8):

$$ \begin{gathered} \mathop {maximize}\limits_{{P,\Phi_{g} }} f_{1} \left( {P,\Phi_{g} } \right) = \mathop \sum \limits_{k = 1}^{K} z_{k} log_{2} \left( {1 + \gamma_{k} } \right),{\text{Subject}}\;{\text{to}} \hfill \\ \sum\nolimits_{k \in K} {Tr\left( {W_{k} } \right) + Tr\left( {V_{l} } \right) \le P} , \hfill \\ \mathop \sum \limits_{{i \in K_{i} }} \left| {\left( {e_{g,j}^{H} \Phi_{g}^{H} W_{g} + e_{{{\text{d}},j}}^{H} } \right)w_{i} } \right|^{2} + \mathop \sum \limits_{{i \in K_{\varepsilon } }} \left| {\left( {e_{g,j}^{H} \Phi_{g}^{H} W_{g} + e_{{{\text{d}},j}}^{H} } \right)v_{m} } \right|^{2} \ge E_{j} , \hfill \\ 0 < \theta_{n} \le 2\pi ,\forall n \in N. \hfill \\ \end{gathered} $$
(8)

Next, we use the Lagrangian dual transformation (LDT) [29] that the term \(\sum_{k=1}^{K}{z}_{k}{\mathit{log}}_{2}\left(1+{\gamma }_{k}\right)\) can be converted into \(\sum_{k=1}^{K}{z}_{k}\mathit{ln}\left(1+{\alpha }_{k}\right)-{z}_{k}{\alpha }_{k}+\frac{{z}_{k}\left(1+{\alpha }_{k}\right){\gamma }_{k}}{1+{\gamma }_{k}}\). Therefore, we transform \({f}_{1}\) into problem \({f}_{2}\), which is represented by Eq. (9):

$$ \begin{gathered} \mathop {Maximize}\limits_{{P,\Phi_{g} ,\alpha }} f_{2} \left( {P,\Phi_{g} ,\alpha } \right) = \mathop \sum \limits_{k = 1}^{K} z_{k} ln\left( {1 + \alpha_{k} } \right) - z_{k} \alpha_{k} + \frac{{z_{k} \left( {1 + \alpha_{k} } \right)\gamma_{k} }}{{1 + \gamma_{k} }},{\text{Subject}}\;{\text{to}} \hfill \\ tr\left( {PP^{H} } \right) \le P, \sum\nolimits_{{i \in K_{i} }} {\left| {e_{j}^{H} w_{i} } \right|^{2} } + \sum\nolimits_{{i \in K_{\varepsilon } }} {\left| {e_{j}^{H} v_{m} } \right|^{2} } \ge E_{j} ,{\text{and}}\;\theta_{g,m} \in F_{c} ,\forall g,\forall m, \hfill \\ \end{gathered} $$
(9)

where α \(={\left[{\alpha }_{1},\cdots ,{\alpha }_{k}\right]}^{T}\) is the additional vector generated after conversion. Note that \({f}_{1}\) and \({f}_{2}\) are equivalent, so solving \({f}_{1}\) is equivalent to solving \({f}_{2}\). In addition, the formula of the transmission power is simplified again, and the mathematical symbol \({e}_{j}^{H}\) is used to represent \({e}_{j}^{H}\)= \({e}_{g,j}^{H}{\Phi }_{g}^{H}{W}_{g}+{e}_{{\text{d}},j}^{H}\). After the conversion, we give \({\alpha }_{k}\), optimize P and \({\Phi }_{g}\), and rewrite the problem \({f}_{2}\) into the problem \({f}_{3}\) as follows,

$$ \begin{gathered} \mathop {maximize}\limits_{{P,\Phi_{g} }} f_{3} \left( {P,\Phi_{g} } \right) = \mathop \sum \limits_{k = 1}^{K} \frac{{z_{k} \left( {1 + \alpha_{k} } \right)\gamma_{k} }}{{1 + \gamma_{k} }}tr\left( {PP^{H} } \right) \le P,\;{\text{Subject}}\;{\text{to}} \hfill \\ tr\left( {PP^{H} } \right) \le P,\sum\nolimits_{{i \in K_{i} }} {\left| {e_{j}^{H} w_{i} } \right|^{2} } + \sum\nolimits_{{i \in K_{\varepsilon } }} {\left| {e_{j}^{H} v_{m} } \right|^{2} } \ge E_{j} ,\;{\text{and}}\;\theta_{g,m} \in F_{c} ,\forall g,\forall m. \hfill \\ \end{gathered} $$
(10)

Given the set \(\left\{{\Phi }_{1},\cdots ,{\Phi }_{g}\right\}\) for convenience, we use the mathematical notation \({\widetilde{h}}_{k}^{H}\) to represent in Eq. (11):

$${\widetilde{h}}_{k}^{H}=\sum_{g=1}^{G}{h}_{g,k}^{H}{\Phi }_{g}^{H}{W}_{g}.$$
(11)

Substitute Eq. (11) into Eq. (5), and rearrange \({f}_{3}\) to generate \({f}_{4}\), Eq. (12) is given as:

$$\underset{P}{\mathit{Maximize}}{f}_{4}\left(P\right)=\sum_{k=1}^{K}\frac{{\overline{\alpha }}_{k}{\left|{\widetilde{h}}_{k}^{H}{p}_{k}\right|}^{2}}{\sum_{j=1}^{K}{\left|{\widetilde{h}}_{k}^{H}{p}_{j}\right|}^{2}+{\sigma }_{u}^{2}},\mathrm{ Subject to }\mathit{tr}\left(P{P}^{H}\right)\le P,$$
(12)

where the symbol \({\overline{\alpha }}_{k}={z}_{k}\left(1+{\alpha }_{k}\right)\), and we can see that \({f}_{4}\) is a multi-score programming problem, so we can use Quadratic Transform (QT) [29, 30] to convert \({f}_{4}\) to \({f}_{5}\), Eq. (13) is given as:

$$\underset{P,\beta }{\mathit{maximize}}{f}_{5}\left(P,\beta \right)=\sum_{k=1}^{K}2\sqrt{{\overline{\alpha }}_{k}}\mathfrak{R}\left\{{\beta }_{k}^{*}{\widetilde{h}}_{k}^{H}{p}_{k}\right\}-{\left|{\beta }_{k}\right|}^{2}\left(\sum_{j=1}^{K}{\left|{\widetilde{h}}_{k}^{H}{p}_{j}\right|}^{2}+{\sigma }_{u}^{2}\right).$$
(13)

Note that \(\beta ={\left[{\beta }_{1},\cdots ,{\beta }_{k}\right]}^{T}\) is the additional vector generated after the QT conversion in (13). To find the optimal solution of \({\beta }_{k}\), we need to calculate the partial derivative concerning \({\beta }_{k}\) for (13) as follows:

$$\frac{\partial {f}_{5}}{\partial {\beta }_{k}}=2\sqrt{{\overline{\alpha }}_{k}}{\widetilde{h}}_{k}^{H}{p}_{k}-2{\beta }_{k}\left(\sum_{j=1}^{K}{\left|{\widetilde{h}}_{k}^{H}{p}_{j}\right|}^{2}+{\sigma }_{u}^{2}\right)=0.$$
(14)
$${\beta }_{k}\left(\sum_{j=1}^{K}{\left|{\widetilde{h}}_{k}^{H}{p}_{j}\right|}^{2}+{\sigma }_{u}^{2}\right)=\sqrt{{\overline{\alpha }}_{k}}{\widetilde{h}}_{k}^{H}{p}_{k}.$$
(15)
$${\widehat{\beta }}_{k}=\frac{\sqrt{{\overline{\alpha }}_{k}}{\widetilde{h}}_{k}^{H}{p}_{k}}{\sum_{j=1}^{K}{\left|{\widetilde{h}}_{k}^{H}{p}_{j}\right|}^{2}+{\sigma }_{u}^{2}}.$$
(16)

Since the problem \({f}_{5}\) is a convex problem about \({p}_{{\text{k}}}\), using the Lagrange multiplier method, given β, the optimal solution of \({p}_{k}\) can be described as Eq. (17):

$${\widehat{p}}_{k}=\sqrt{{\overline{\alpha }}_{k}}{\beta }_{k}{\left(\mu {I}_{N}+\sum_{i=1}^{k}{\left|{\beta }_{i}\right|}^{2}{\widetilde{h}}_{i}{\widetilde{h}}_{i}^{H}\right)}^{-1}{\widetilde{h}}_{k}$$
(17)

Next, we simplify the mathematical formula to facilitate the operation and derivation, \({\widetilde{h}}_{k}^{H}{p}_{j}\) can be expressed as Eq. (18):

$${\widetilde{h}}_{k}^{H}{p}_{j}=\sum_{g=1}^{G}{\theta }_{g}^{H}diag\left({h}_{g,k}^{H}\right){W}_{g}{p}_{j},$$
(18)

where \({{\varvec{\theta}}}_{g}\) is defined as \({{\varvec{\theta}}}_{g}={\left[{\theta }_{g,1},\cdots ,{\theta }_{g,M}\right]}^{T}\) and \({v}_{g,k,j}\) is defined as \({v}_{g,k,j}={\text{diag}}\left({h}_{g,k}^{H}\right){W}_{g}{p}_{j}\). Given α and P, we rewrite the problem \({f}_{4}\) into the problem \({f}_{6}\), as shown in Eq. (19):

$$ \begin{gathered} \mathop {maximize}\limits_{{\theta_{g} }} f_{6} \left( {\theta_{g} } \right) = \mathop \sum \limits_{k = 1}^{K} \frac{{\overline{\alpha }_{k} \left| {\mathop \sum \nolimits_{g = 1}^{G} \theta_{g}^{H} v_{g,k,k} } \right|^{2} }}{{\mathop \sum \nolimits_{j = 1}^{K} \left| {\mathop \sum \nolimits_{g = 1}^{G} \theta_{g}^{H} v_{g,k,j} } \right|^{{2^{2} }} + \sigma_{u}^{2} }},\;subject\;to \hfill \\ \left| {\theta_{g,m} } \right|^{2} = 1,\forall g,\forall m \hfill \\ \end{gathered} $$
(19)

To facilitate the subsequent derivation, we first construct several symbols to represent the following equations, as shown in Eqs. (20) and (21):

$$\Theta =\left[{\theta }_{1},{\theta }_{2},\cdots ,{\theta }_{G}\right].$$
(20)
$${V}_{k,j}=\left[{v}_{1,k,j},{v}_{2,k,j},\cdots ,{v}_{G,k,j}\right].$$
(21)

After the construction is completed, we can rewrite the problem \({f}_{6}\) into the problem \({f}_{7}\), as shown in Eq. (22):

$$ \begin{aligned} \mathop {maximize}\limits_{{\tilde{\theta }}} f_{7} \left( {\tilde{\theta }} \right) = & \sum\limits_{{k = 1}}^{K} {\frac{{\bar{\alpha }_{k} \left| {tr\left( {\Theta ^{H} V_{{k,k}} } \right)} \right|^{2} }}{{\sum\nolimits_{{j = 1}}^{K} {\left| {tr\left( {\Theta ^{H} V_{{k,j}} } \right)} \right|^{{2^{2} }} } + \sigma _{u}^{2} }}} \\ = & \sum\limits_{{k = 1}}^{K} {\frac{{\bar{\alpha }_{k} \left| {\tilde{\theta }^{H} \tilde{v}_{{k,k}} } \right|^{2} }}{{\sum\nolimits_{{j = 1}}^{K} {\left| {\tilde{\theta }^{H} \tilde{v}_{{k,j}} } \right|^{{2^{2} }} } + \sigma _{u}^{2} }}} \left| {\theta _{{g,m}} } \right|^{2} \\ = & 1,\forall g,\forall m. \\ \end{aligned} $$
(22)

Where \(\tilde{\theta } = {\text{vec}}\left( {\Theta } \right)\), and \({\widetilde{v}}_{k,j}={\text{vec}}\left({V}_{k,j}\right)\). Next, we transform the problem \({f}_{7}\) into problem \({f}_{8}\) using quadratic transformation (QT) [29], as shown in Eq. (23):

$$ \begin{gathered} \mathop {maximize}\limits_{{\widetilde{\theta },\rho }} f_{8} \left( {\tilde{\theta },\rho } \right) = \mathop \sum \limits_{k = 1}^{K} 2\sqrt {\overline{\alpha }_{k} } {\mathbf{\Re }}\left\{ {\rho_{k}^{*} \tilde{\theta }^{H} \tilde{v}_{k,k} } \right\} - \left| {\rho_{k} } \right|^{2} \left( {\mathop \sum \limits_{j = 1}^{K} \left| {\tilde{\theta }^{H} \tilde{v}_{k,j} } \right|^{2} + \sigma_{u}^{2} } \right) \hfill \\ subject\;to\left| {\theta_{g,m} } \right|^{2} = 1,\forall g,\forall m. \hfill \\ \end{gathered} $$
(23)

After conversion, \(\rho ={\left[{\rho }_{1},\cdots ,{\rho }_{k}\right]}^{T}\) does the secondary conversion generate the additional vector. Using the Lagrange multiplier method [29], the optimal solution of \({\rho }_{k}\) is shown in formula (26):

$$2\sqrt{{\overline{\alpha }}_{k}}{\widetilde{\theta }}^{H}{\widetilde{v}}_{k,k}-2{\rho }_{k}\left(\sum_{j=1}^{K}{\left|{\widetilde{\theta }}^{H}{\widetilde{v}}_{k,j}\right|}^{2}+{\sigma }_{u}^{2}\right)=0.$$
(24)
$${\rho }_{k}\left(\sum_{j=1}^{K}{\left|{\widetilde{\theta }}^{H}{\widetilde{v}}_{k,j}\right|}^{2}+{\sigma }_{u}^{2}\right)=\sqrt{{\overline{\alpha }}_{k}}{\widetilde{\theta }}^{H}{\widetilde{v}}_{k,k}.$$
(25)
$${\widehat{\rho }}_{k}=\frac{\sqrt{{\overline{\alpha }}_{k}}{\widetilde{\theta }}^{H}{\widetilde{v}}_{k,k}}{\sum_{j=1}^{K}{\left|{\widetilde{\theta }}^{H}{\widetilde{v}}_{k,j}\right|}^{2}+{\sigma }_{u}^{2}}.$$
(26)

Finally, regarding the complete algorithm, the steps are as follows:

  1. 1.

    Set the initial value variables P and \({\Phi }_{g}\).

  2. 2.

    Use Eqs. (16) and (21) to find \({\beta }_{k}\) and \({p}_{k}\), respectively.

  3. 3.

    Using Eqs. (20) and (21) to construct Θ and \({V}_{k,j}\).

  4. 4.

    Use Eq. (26) to find \({\rho }_{k}\).

  5. 5.

    Output \(P {\text{and}} {\Phi }_{g}.\)

  6. 6.

    Based on the parameters we deduced earlier, we can use pushback to find \({w}_{k}\) and \({v}_{k}\) as follows:

    $$ w_{k} = \frac{1}{\sqrt 2 }\sqrt {\overline{\alpha }_{k} } \beta_{k} \left( {\underbrace {{\mu I_{N} + \mathop \sum \limits_{i = 1}^{k} \left| {\beta_{i} } \right|^{2} \tilde{h}_{i} \tilde{h}_{i}^{H} }}_{{A_{1} }}} \right)^{ - 1} \tilde{h}_{k} = \frac{1}{\sqrt 2 }\sqrt {\overline{\alpha }_{k} } \beta_{k} A_{1}^{ - 1} \tilde{h}_{k} . $$
    (27)
    $$ \begin{aligned} v_{k} = & \frac{1}{{\sqrt 2 }}\sqrt {\bar{\alpha }_{k} } \beta _{k} \left( {\underbrace {{\mu I_{N} + \sum\limits_{{i = 1}}^{k} {\left| {\beta _{i} } \right|^{2} } \tilde{h}_{i} \tilde{h}_{i}^{H} + \sum\limits_{{i = 1}}^{k} {\left| {\beta _{i} } \right|^{2} } \tilde{e}_{i} \tilde{e}_{i}^{H} }}_{{A_{2} }}} \right)^{{ - 1}} \left( {\tilde{h}_{k} + \tilde{e}_{k} } \right) \\ = & \frac{1}{{\sqrt 2 }}\sqrt {\bar{\alpha }_{k} } A_{2}^{{ - 1}} \beta _{k} \left( {\tilde{h}_{k} + \tilde{e}_{k} } \right). \\ \end{aligned} $$
    (28)

4 Simulation Results

This section presents the results of the Monte Carlo simulation to validate the effectiveness of the proposed method for the RIS-aided MIMO SWIPT system under different scenarios. The simulation parameters include the number of users (K), the number of antennas (N), the number of reflective elements (M), and the transmission power (P). For the channel part, we use the Rayleigh channel. Figure 2 is a schematic diagram of the simulation environment. Please refer to Case I and II conditions in Table 1 for the simulation parameters setting.

Fig. 2
figure 2

Simulation Schematic

Full size image
Table 1 Simulation parameters
Full size table

Figure 3 compares the sum-rate obtained by the proposed approach with or without employing RISs corresponding to the Case I condition: two users (information receiving end and energy receiving end), sixteen antennas, and twenty reflective elements, i.e., K = 2, N = 16., and M = 20. It can be observed from Fig. 3 that with or without employing RISs, the sum-rate increases as the transmit power at the AP increases. The curve of the proposed method with a 10% error is approximately the same as the proposed method. The sum-rate performance of the proposed method is higher than the system without employing RISs. The sum-rate improvement is approximately 2 (bps/Hz) and 4 (bps/Hz), corresponding to the transmit power at AP are 10 (dBm) and 70 (dBm), respectively.

Fig. 3
figure 3

The sum-rate against transmit power at the AP comparison in Case I condition with scenario: K = 2, N = 16, and M = 20

Full size image

Figure 4 compares the sum-rate obtained by the proposed approach with or without employing RISs corresponding to the Case I condition: three users (information receiving end and energy receiving end), sixteen antennas, and twenty reflective elements, i.e., K = 3, N = 16., and M = 20. It can be observed from Fig. 4 that with or without employing RISs, the sum-rate increases as the transmit power at the AP increases. The curve of the proposed method with a 10% error is approximately the same as the proposed method. The sum-rate performance of the proposed method is higher than the system without employing RISs. The sum-rate improvement is approximately 2 (bps/Hz) and 4 (bps/Hz), corresponding to the transmit power at AP are 10 (dBm) and 70 (dBm), respectively. Compared with Fig. 3, the sum-rate also increased by approximately 0.5 (bps/Hs) as the number of users increased.

Fig. 4
figure 4

The sum-rate against transmit power at the AP comparison in Case I condition with scenario: K = 3, N = 16, and M = 20

Full size image

Figure 5 compares the sum-rate obtained by the proposed approach with or without employing RISs corresponding to the Case I condition: five users (information receiving end and energy receiving end), sixteen antennas, and twenty reflective elements, i.e., K = 5, N = 16., and M = 20. It can be observed from Fig. 5 that with or without employing RISs, the sum-rate increases as the transmit power at the AP increases. The curve of the proposed method with 10% error is approximately the same as the proposed method. The sum-rate performance of the proposed method is higher than the system without employing RISs. The sum-rate improvement is approximately 2 (bps/Hz) and 4 (bps/Hz), corresponding to the transmit power at AP are 10 (dBm), and 70 (dBm), respectively. Compared with Fig. 4, the sum-rate also increased by approximately 0.5 (bps/Hs) as the number of users increased.

Fig. 5
figure 5

The sum-rate against transmit power at the AP comparison in Case I condition with scenario: K = 5, N = 16, and M = 20

Full size image

Figure 6 compares the sum-rate obtained by the proposed approach with or without employing RISs corresponding to the Case I condition: two users (information receiving end and energy receiving end), thirty-two antennas, and twenty reflective elements, i.e., K = 2, N = 32, and M = 20. It can be observed from Fig. 6 that with or without employing RISs, the sum-rate increases as the transmit power at the AP increases. The curve of the proposed method with 10% error is approximately the same as the proposed method. The sum-rate performance of the proposed method is higher than the system without employing RISs. The sum-rate improvement is approximately 2 (bps/Hz) and 4 (bps/Hz), corresponding to the transmit power at AP are 10 (dBm) and 70 (dBm), respectively. Compared with Fig. 3, the sum-rate also increased by approximately 0.5 (bps/Hs) as the number of antennae increased.

Fig. 6
figure 6

The sum-rate against transmit power at the AP comparison in Case I condition with scenario: K = 2, N = 32, and M = 20

Full size image

Figure 7 compares the sum-rate obtained by the proposed approach with or without employing RISs corresponding to the Case I condition: two users (information receiving end and energy receiving end), sixty-four antennas, and twenty reflective elements, i.e., K = 2, N = 64., and M = 20. It can be observed from Fig. 7 that with or without employing RISs, the sum-rate increases as the transmit power at the AP increases. The curve of the proposed method with 10% error is approximately the same as the proposed method. The sum-rate performance of the proposed method is higher than the system without employing RISs. The sum-rate improvement is approximately 2 (bps/Hz) and 4 (bps/Hz), corresponding to the transmit power at AP are 10 (dBm) and 70 (dBm), respectively. Compared with Fig. 6, the sum-rate also increased by approximately 1 (bps/Hs) as the number of antennae increased. It can be seen that the influence of the number of antennas on the transmission rate.

Fig. 7
figure 7

The sum-rate against transmit power at the AP comparison in Case I condition with scenario: K = 2, N = 64, and M = 20

Full size image

Figure 8 compares the sum-rate obtained by the proposed approach with or without employing RISs corresponding to the Case I condition: five users (information receiving end and energy receiving end), sixty-four antennas, and twenty reflective elements, i.e., K = 5, N = 64, and M = 20. It can be observed from Fig. 8 that with or without employing RISs, the sum-rate increases as the transmit power at the AP increases. The curve of the proposed method with a 10% error is approximately the same as the proposed method. The sum-rate performance of the proposed method is higher than the system without employing RISs. The sum-rate improvement is approximately 4 (bps/Hz) and 6 (bps/Hz), corresponding to the transmit power at AP are 10 (dBm) and 70 (dBm), respectively. Compared with Fig. 5, the sum-rate also increased by approximately 5 (bps/Hs) as the number of antennae increased. It can be seen that the influence of the number of antennas on the transmission rate.

Fig. 8
figure 8

The sum-rate against transmit power at the AP comparison in Case I condition with scenario: K = 5, N = 64, and M = 20

Full size image

Figure 9 compares the sum-rate obtained by the proposed approach with or without employing RISs corresponding to the Case I condition: two users (information receiving end and energy receiving end), sixteen antennas, and transmitting power is thirty dBm, i.e., K = 2, N = 16, and P = 30 (dBm). It can be observed from Fig. 9 that when employing RISs, the sum-rate increases as the number of reflecting elements increases. The curve of the proposed method with a 10% error is approximately close to the proposed method. However, the curve of the system without employing RISs remains constant because there are no reflecting elements to aid transmission; hence, the sum-rate will not be enhanced. The sum-rate improvement is approximately 2 (bps/Hz) and 6 (bps/Hz), corresponding to the number of reflecting elements as 5 and 35, respectively.

Fig. 9
figure 9

The sum-rate against the number of reflecting elements comparison in Case I condition with the scenario: K = 2, N = 16, and P = 30 (dBm)

Full size image

Figure 10 compares the sum-rate obtained by the proposed approach with or without employing RISs corresponding to the Case I condition: three users (information receiving end and energy receiving end), sixteen antennas, and transmitting power is thirty dBm, i.e., K = 3, N = 16, and P = 30 (dBm). It can be observed from Fig. 10 that when employing RISs, the sum-rate increases as the number of reflecting elements increases. The curve of the proposed method with a 10% error is approximately close to the proposed method. However, the curve of the system without employing RISs remains constant because there are no reflecting elements to aid transmission; hence, the sum-rate will not be enhanced. The sum-rate improvement is approximately 3 (bps/Hz) and 10 (bps/Hz), corresponding to the number of reflecting elements as 5 and 35, respectively. Compared with Fig. 9, the sum-rate also increased by approximately 2 (bps/Hs) as the number of reflecting elements is 35.

Fig. 10
figure 10

The sum-rate against the number of reflecting elements comparison in Case I condition with the scenario: K = 3, N = 16, and P = 30 (dBm)

Full size image

Figure 11 compares the sum-rate obtained by the proposed approach with or without employing RISs corresponding to the Case I condition: two users (information receiving end and energy receiving end), thirty-two antennas, and transmitting power is thirty dBm, i.e., K = 2, N = 32, and P = 30 (dBm). It can be observed from Fig. 11 that when employing RISs, the sum-rate increases as the number of reflecting elements increases. The curve of the proposed method with a 10% error is approximately close to the proposed method. However, the curve of the system without employing RISs remains constant because there are no reflecting elements to aid transmission; hence, the sum-rate will not be enhanced. The sum-rate improvement is approximately 4 (bps/Hz) and 10 (bps/Hz), corresponding to the number of reflecting elements as 5 and 35, respectively. Compared with Fig. 9, the sum-rate also increased by approximately 4 (bps/Hs) as the number of reflecting elements is 35.

Fig. 11
figure 11

The sum-rate against the number of reflecting elements comparison in Case I condition with the scenario: K = 2, N = 32, and P = 30 (dBm)

Full size image

Figure 12 compares the sum-rate obtained by the proposed approach with or without employing RISs corresponding to the Case I condition: three users (information receiving end and energy receiving end), thirty-two antennas, and transmitting power is thirty dBm, i.e., K = 3, N = 64, and P = 30 (dBm). It can be observed from Fig. 12 that when employing RISs, the sum-rate increases as the number of reflecting elements increases. The curve of the proposed method with a 10% error is approximately close to the proposed method. However, the curve of the system without employing RISs remains constant because there are no reflecting elements to aid transmission; hence, the sum-rate will not be enhanced. The sum-rate improvement is approximately 10 (bps/Hz) and 23 (bps/Hz), corresponding to the number of reflecting elements as 5 and 35, respectively. Compared with Fig. 10, the sum-rate also increased by approximately 10 (bps/Hs) as the number of reflecting elements is 35.

Fig. 12
figure 12

The sum-rate against the number of reflecting elements comparison in Case I condition with the scenario: K = 3, N = 64, and P = 30 (dBm)

Full size image

Figure 13 compares the sum-rate obtained by the proposed approach with or without employing RISs corresponding to the Case I condition: two users (information receiving end and energy receiving end), thirty-two antennas, and transmitting power is thirty dBm, i.e., K = 2, N = 16, and P = 30 (dBm). It can be observed from Fig. 13 that with or without employing RISs, the sum-rate decreases as the distance increases. Compare the sum-rate at distances 30 (m) and 50 (m), and it drops over 1 (bps/Hz). It can be seen that the influence of the distance on the transmission rate.

Fig. 13
figure 13

The sum-rate against the distance comparison in Case I condition with the scenario: K = 2, N = 16, and P = 30 (dBm)

Full size image

Following simulation, the \({x}_{IU}\) and \({x}_{EU}\) are set as 30 (m) and 100 (m), respectively. Other parameters remain unchanged. Please refer to Case II in Table 1 for the simulation parameters setting.

Figure 14 compares the sum-rate obtained by the proposed approach with or without employing RISs corresponding to the Case II condition: two users (information receiving end and energy receiving end), sixteen antennas, and twenty reflective elements, i.e., K = 2, N = 16., and M = 20. It can be observed from Fig. 14 that with or without employing RISs, the sum-rate increases as the transmit power at the AP increases. The curve of the proposed method with a 10% error is approximately the same as the proposed method. The sum-rate performance of the proposed method is higher than the system without employing RISs. The sum-rate improvement is approximately 2 (bps/Hz) and 4 (bps/Hz), corresponding to the transmit power at AP are 10 (dBm) and 70 (dBm), respectively. Compared with Fig. 3, the sum-rate curves are similar.

Fig. 14
figure 14

The sum-rate against transmit power at the AP comparison in Case II condition with scenario: K = 2, N = 16, and M = 20

Full size image

Figure 15 compares the sum-rate obtained by the proposed approach with or without employing RISs corresponding to the Case II condition: three users (information receiving end and energy receiving end), sixteen antennas, and twenty reflective elements, i.e., K = 3, N = 16., and M = 20. It can be observed from Fig. 15 that with or without employing RISs, the sum-rate increases as the transmit power at the AP increases. The curve of the proposed method with a 10% error is approximately the same as the proposed method. The sum-rate performance of the proposed method is higher than the system without employing RISs. The sum-rate improvement is approximately 2 (bps/Hz) and 4 (bps/Hz), corresponding to the transmit power at AP are 10 (dBm) and 70 (dBm), respectively. Compared with Fig. 4, the sum-rate curves are similar. Compared with Fig. 14, the sum-rate also increased as the number of users increased.

Fig. 15
figure 15

The sum-rate against transmit power at the AP comparison in Case II condition with scenario: K = 3, N = 16, and M = 20

Full size image

Figure 16 compares the sum-rate obtained by the proposed approach with or without employing RISs corresponding to the Case II condition: five users (information receiving end and energy receiving end), sixteen antennas, and twenty reflective elements, i.e., K = 5, N = 16., and M = 20. It can be observed from Fig. 16 that with or without employing RISs, the sum-rate increases as the transmit power at the AP increases. The curve of the proposed method with a 10% error is approximately the same as the proposed method. The sum-rate performance of the proposed method is higher than the system without employing RISs. The sum-rate improvement is approximately 2 (bps/Hz) and 4 (bps/Hz), corresponding to the transmit power at AP are 10 (dBm) and 70 (dBm), respectively. Compared with Fig. 5, the sum-rate curves are similar. Compared with Fig. 15, the sum-rate also increased as the number of users increased.

Fig. 16
figure 16

The sum-rate against transmit power at the AP comparison in Case II condition with scenario: K = 5, N = 16, and M = 20

Full size image

Figure 17 compares the sum-rate obtained by the proposed approach with or without employing RISs corresponding to the Case I condition: two users (information receiving end and energy receiving end), thirty-two antennas, and transmitting power is thirty dBm, i.e., K = 2, N = 32, and P = 30 (dBm). It can be observed from Fig. 17 that when employing RISs, the sum-rate increases as the number of reflecting elements increases. The curve of the proposed method with a 10% error is approximately close to the proposed method. However, the curve of the system without employing RISs remains constant because there are no reflecting elements to aid transmission; hence, the sum-rate will not be enhanced. Compared with Fig. 11, the sum-rate curves are similar.

Fig. 17
figure 17

The sum-rate against the number of reflecting elements comparison in Case II condition with the scenario: K = 2, N = 32, and P = 30 (dBm)

Full size image

Table 2 is the simulation summary.

Table 2 Simulation summary
Full size table

5 Conclusion

In this paper, we have studied a new method to improve the performance of a SWIPT communication system by taking advantage of the deployment of RISs. We have formulated the sum-rate maximization problem for the communication system by optimizing subject to the restrictions of the transmission power and the energy harvesting to make the best use of the sum-rate. The simulation outcomes verified the efficiency and effectiveness of the proposed approach.