1 Introduction

Millimeter wave communications (mmwave) have been suggested for future 6G networks to enhance the throughput of wireless communications and reach data rates of multiple Gb/s [1,2,3]. Millimeter-wave operates on a large bandwidth going from 30 to 300 Ghz [5,6,7]. Relay nodes can be deployed to improve the throughput of millimeter-wave communications to benefit from cooperative diversity and improve the throughput [7,8,9,10]. However, relaying techniques are complex to implement and require orthogonal channels to avoid interference between relayed signals [7,8,9,10]. Using orthogonal channels will reduce the throughput and spectral efficiency. Another solution is to use relay selection techniques for millimeter-wave communications. Relay selection techniques are complex to implement and require a central node to select the best relay. Relay selection techniques require extra-signalization to activate the relay and to send their SNRs to a central node. Besides, the number of relays is limited and cannot be around a hundred relays. Relaying consumes power at relay nodes and requires extra-processing.

To avoid these drawbacks, we suggest extending the coverage of millimeter-wave communications using RIS implemented as a reflector or a transmitter [11,12,13,14,15]. The link between source and relay node uses millimeter wave communications. The signals received at the relay node are affected by P interferers. The relay decodes the received packet and forwards it to the destination. RIS is placed between the relay node and destination. RIS contains a large number of reflectors \(N=16,32,64,128\) with phase shifts optimized so that all N reflections have the same phase at the destination. The phase of kth reflector compensates the phase shift of channel gains between relay/kth RIS reflector and kth RIS reflector/destination [16,17,18,19,20]. The receiver output at the destination is similar to that of a Maximum Ratio Combiner (MRC) with a number of branches equal to the number of reflectors N [20,21,22,23,24]. We propose a second implementation of RIS as a transmitter in which RIS is illuminated with the antenna of relay R. When RIS is implemented as a transmitter,the phase shift of kth RIS reflector depends on the phase of channel gain between relay node and destination. Some experimental results of RIS are discussed in [24].

Millimeter wave communications for NOMA systems using multiple antennas was suggested in [25, 26]. User assisted cooperative relaying for millimeter wave communications using NOMA was proposed in [27]. The coverage probability of millimeter wave communication using NOMA was derived in [28]. Hybrid precoding/combining techniques for millimeter wave communications was suggested in [29]. Deep learning assisted calibrated beam training was used in [30] for millimeter wave communications. A high gain resonant cavity antenna was proposed in [31] to improve the performance of millimeter wave communications.

The contributions of the paper are:

  • We suggest enhancing the throughput of millimeter wave communications using RIS. RIS is implemented as a reflector or a transmitter. We show that RIS allows up 19, 25, 31, 37 dB gain with respect to conventional millimeter wave communication without RIS for a number of reflectors \(N=16,32,64,128\).

  • The use of RIS to extend the coverage of millimeter wave communications has not been yet proposed in [1,2,3,4,5,6,7,8,9,10]. Previous papers implemented multiple relay nodes for millimeter wave communications [1,2,3,4,5,6,7,8,9,10].

  • We derive the throughput of millimeter wave communications using RIS as a reflector or a transmitter for Nakagami channels. We compare the obtained theoretical results to computer simulations.

  • We study the performance of wireless communications using RIS in the presence of interferers. In previous papers, there is no interference on RIS link [11,12,13,14,15,16,17,18,19,20,21,22,23,24].

  • The derived results evaluate the throughput at the packet level and are valid for any number of interferers at relay node and destination. Besides, the results are valid for any position of the source, relay node and RIS.

  • We propose the use of RIS for mmwave communications using NOMA. The proposed NOMA system using RIS offers 10, 13, 16, 20, 24, 27 and 30 dB gain with respect to conventional NOMA using millimeter wave communications without RIS [25,26,27,28] for a number of reflector per user \(N=N_1=N_2=8,16,32,64,128,256,512\).

The paper contains five sections. The next section studies the millimeter wave and RIS links when there is a single destination. RIS has been implemented as a reflector or a transmitter to enhance the throughput at the destination. Section 3 extends the system model to NOMA systems. Section 4 provides some theoretical and computer simulation results. Conclusions and perspectives are provided in last section.

2 Performance analysis of millimeter wave communications using RIS

2.1 Single destination

2.1.1 Millimeter wave link

Fig. 1
figure 1

RIS deployed as a reflector

Full size image

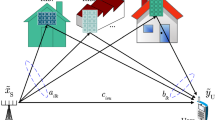
The system model depicted in Fig. 1 is composed of a source S, a relay node R, and a destination D. We assume that the received signal at R is affected by P interferers. In interference-limited millimeter-wave communications, the SINR at R is equal to [1,2,3,4,5]

$$\begin{aligned} \Gamma _{SR,mmwave}=\frac{E_{S}|f|^2}{I} \end{aligned}$$
(1)

in which \(E_{S}\) is the symbol energy S, f is the channel coefficient between S and R, I is the interference term at R composed of P interferers:

$$\begin{aligned} I=\sum _{q=1}^{P} E_q |i_q|^2 \end{aligned}$$
(2)

in which \(E_q\) is the transmitted energy per symbol of qth interferer, \(i_q\) is the channel gain between qth interferer and R.

For Nakagami fading channels, \(X=E_S |f|^2\) follows a Gamma distribution \(Gamma(M,\beta )\) defined as

$$\begin{aligned} \mathrm {f_{X}}(x)=\frac{x^{M}e^{-\frac{x}{\beta }}}{\Gamma (M)\beta ^{M}} \end{aligned}$$
(3)

\(M>0.5\) is the m-fading figure of Nakagami channel,

$$\begin{aligned} \beta =\frac{E_SE(|f|^2)}{M} \end{aligned}$$
(4)

E(.) is the expectation operator.

The interference I at the relay node is expressed as

$$\begin{aligned} I=\sum _{q=1}^{P} I_q \end{aligned}$$
(5)

in which \(I_q=E_q |i_q|^2\)

We assume that I is the sum of independent and identically distributed (i.i.d) Gamma random variables (r.v) \(I_q\) that follows a \(Gamma(M,\alpha )\)

$$\begin{aligned} \alpha =\frac{E(I_q)}{M} \end{aligned}$$
(6)

The sum of P i.i.d Gamma r.v. \(I_{q}\) is a Gamma r.v. \(G(PM,\alpha )\). We deduce that \(\Gamma _{SR,m}\) is the quotient of two Gamma r.v. that has a general prime distribution and Probability Density Function (PDF) [32]:

$$\begin{aligned} \mathrm {f}_{{\Gamma }_\mathrm {{SR,m}}}(x) =\frac{\Gamma (M+PM)\alpha ^Mx^{M-1}\left( 1+\frac{x\alpha }{\beta }\right) ^{-PM-M}}{\beta ^M\Gamma (M)\Gamma (PM)} \end{aligned}$$
(7)

in which subscript m refers to mmwave. The proof is provided in “Appendix 1”.

We have [33]

$$\begin{aligned}&{}_{{2}F_1(A,B;C;z)}=\frac{\Gamma (C)}{\Gamma (B)\Gamma (C-B)}\nonumber \\&\quad \times \int _0^1 x^{B-1}(1-x)^{C-B-1}(1-zx)^{-A}dx \end{aligned}$$
(8)

in which \(B>0\), \(C>0\), \(_{2}F_1(A,B;C;Z)\) is the hypergeometric function. We use (8) to write the Cumulative Distribution Function (CDF) of SINR as

$$\begin{aligned} \mathrm {F}_{{\Gamma _{\mathrm{SR,m}}}}(x)= & {} _{2}F_1\left( PM+M,M;M+1,\frac{-x\alpha }{\beta }\right) \nonumber \\&\quad \times \frac{\Gamma (M+PM)(x\alpha )^{M}}{\Gamma (M)\Gamma (PM)\beta ^{M}} \end{aligned}$$
(9)
Fig. 2
figure 2

RIS deployed as a transmitter

Full size image
Fig. 3
figure 3

Millimeter wave communications using RIS and NOMA

Full size image

2.1.2 RIS link

2.1.2.1 RIS implemented as a reflector

To extend the coverage of millimeter-wave communications, a RIS is placed between relay node R and destination D. We define \(h_k\) as the channel coefficient between R and kth RIS reflector with average power \(E(|h_k|^2)=\frac{1}{d_1^{PLE}}\) in which E(.) is the expectation operator, PLE is the path loss exponent and \(d_1\) is the distance between R and RIS. We define \(g_k\) as the channel coefficient between kth reflector of RIS and destination D with average power \(E(|g_k|^2)=\frac{1}{d_2^{PLE}}\) in which \(d_2\) is the distance between RIS and D. RIS are nearly-passive devices with very low complexity [11] made of electromagnetic material that can be deployed on several structures including but not limited to building facades, walls... Therefore, the use of RIS does not increase too much the overall computational complexity of the proposed system [11].

Let \(a_k\) and \(b_k\) be the absolute value and phase of \(h_k=a_ke^{-jb_k}\). For Nakagami channels, \(a_k\) has a Gamma distribution with \(E(a_k)=\frac{\Gamma (M+0.5)}{\Gamma (M)}\sqrt{\frac{1}{Md_1^{PLE}}}\) and \(E(a_k^2)=E(|h_k|^2)=\frac{1}{d_1^{PLE}}\) [34]. Let \(c_k\) and \(d_k\) be the absolute and phase of \(g_k=c_ke^{-jd_k}\). We have \(E(c_k)=\frac{\Gamma (M+0.5)}{\Gamma (M)}\sqrt{\frac{1}{Md_2^{PLE}}}\) and \(E(c_k^2)=E(|g_k|^2)=\frac{1}{d_2^{PLE}}\) [34].

RIS optimizes the phase \(\phi _k\) of kth reflector as follows

$$\begin{aligned} \phi _k=b_k+d_k. \end{aligned}$$
(10)

During pth symbol period, the received signal at D is equal to

$$\begin{aligned} r_p=s_p\sqrt{E_R}\sum _{q=1}^Nh_qg_qe^{j\phi _q}+n_p \end{aligned}$$
(11)

in which N is the number of RIS reflectors, \(s_p\) is the pth transmitted symbol, \(n_p\) is zero-mean Gaussian r.v. with variance \(N_0\) and \(E_R\) is the symbol energy of R.

Using (9–10), we obtain

$$\begin{aligned} r_p=\sqrt{E_R} s_p A +n_p, \end{aligned}$$
(12)

in which

$$\begin{aligned} A=\sum _{q=1}^Na_qc_q. \end{aligned}$$
(13)

where \(a_q=|h_q|\) and \(c_q=|g_q|\).

The Signal to Noise Ratio (SNR) at D is expressed as

$$\begin{aligned} \Gamma _{RD,r}=\frac{E_RA^2}{N_0}. \end{aligned}$$
(14)

in which subscript r refers to RIS.

Fig. 4
figure 4

RIS deployed as a reflector in the presence of Q interferers at D

Full size image
Fig. 5
figure 5

RIS deployed as a transmitter in the presence of Q interferers at D

Full size image
Fig. 6
figure 6

Millimeter wave communications using RIS in the presence of \(P_i\) interferers at user \(U_i\)

Full size image
Fig. 7
figure 7

Throughput of mmWave using RIS as a reflector: QPSK modulation

Full size image
Fig. 8
figure 8

Throughput of mmWave using RIS as a reflector: 16QAM modulation, weak turbulence

Full size image
Fig. 9
figure 9

Throughput of mmWave using RIS as a reflector: 64QAM modulation

Full size image
Fig. 10
figure 10

Throughput of mmWave using RIS as a reflector: 256QAM modulation

Full size image
Fig. 11
figure 11

Throughput of mmWave using RIS as a transmitter: 8PSK modulation

Full size image
Fig. 12
figure 12

Throughput of mmWave using RIS as a transmitter: 16PSK

Full size image
Fig. 13
figure 13

Exact and asymptotic PEP using RIS as a reflector: QPSK

Full size image
Fig. 14
figure 14

PEP using RIS or antenna selection at the destination: QPSK

Full size image
Fig. 15
figure 15

Total throughput for 16QAM modulation : : 2 users

Full size image
Fig. 16
figure 16

Total throughput for 16QAM modulation: :\(N=64,128,256,512\)

Full size image

\(a_q\) and \(a_{q'}\) are assumed to be independent for \(q\ne q'\) as they correspond to channel coefficient between R and qth, \(q'\)th RIS reflector. \(c_q\) and \(c_{q'}\) are assumed to be independent for \(q \ne q'\) as they correspond to channel coefficient between qth, \(q'\)th RIS reflector and destination. \(a_q\) and \(c_{q'}\) are assumed to be independent \(\forall q \forall q'\) as they correspond to channel coefficient of different links (relay to RIS and RIS to destination. Therefore, \(a_qc_q\) and \(a_{q'}c_{q'}\) are independent \(q \ne q'\). Using the Central Limit Theorem (CLT), A can be approximated by a Gaussian r.v. with mean \(m_A=\frac{N \Gamma (M+0.5)^2}{M\Gamma (M)^2d_1^{PLE/2}d_2^{PLE/2}}\) and variance \(\sigma _A^2=\frac{N}{d_2^{PLE}d_1^{PLE}}[1-\frac{ \Gamma (M+0.5)^4}{M^2\Gamma (M)^4}]\).

To obtain the values of \(m_A\) and \(\sigma _A^2\), we used the following results for Nakagami channels with fading figure M [34]: \(E(a_k^2)=\frac{1}{d_1^{PLE}}=\Omega _1\) and \(E(a_k^n)=\frac{\Gamma (M+0.5n)}{\Gamma (M)}(\frac{\Omega _1}{M})^{0.5n} \forall n \ge 1\). We deduce \(E(a_k)=\frac{\Gamma (M+0.5)}{\sqrt{M}\Gamma (M)d_1^{PLE/2}}\). Similarly, we have \(E(c_k^2)=\frac{1}{d_2^{PLE}}\) and \(E(c_k)=\frac{\Gamma (M+0.5)}{\sqrt{M}\Gamma (M)d_2^{PLE/2}}\). As \(a_q\) and \(c_q\) are independent, we deduce \(m_A=\sum _{q=1}^NE(a_qc_q)=NE(a_q)E(c_q)=N\frac{\Gamma (M+0.5)^2}{M\Gamma (M)^2d_1^{PLE/2}d_2^{PLE/2}}\).

Since \(a_qc_q\) and \(a_{q'}c_{q'}\) are independent \(q \ne q'\), \(Var(A)=\sigma _A^2=\sum _{q=1}^N Var(a_qc_q)=NVar(a_qc_q)=N[E(a_q^2c_q^2)-E(a_qc_q)^2.]\) Since \(a_q\) and \(c_q\) are independent, we obtain \(Var(A)=N[E(a_q^2)E(c_q^2)-E(a_q)^2E(c_q)^2]= N[\frac{1}{d_1^{PLE}d_2^{PLE}}-\frac{\Gamma (M+0.5)^4}{M^2\Gamma (M)^4d_1^{PLE}d_2^{PLE}}.]\)

The CDF of SNR at D is written as

$$\begin{aligned}&\mathrm {F}_{{\Gamma _\mathrm{RD,r}}}(x)=P\left( \frac{E_RA^2}{N_0}\le x\right) =P\left( -\sqrt{\frac{xN_0}{E_R}}\right. \\&\quad \left. \le A\le \sqrt{\frac{xN_0}{E_R}}\right) \end{aligned}$$
$$\begin{aligned} \simeq 0.5erfc\left( \frac{-\sqrt{\frac{xN_0}{E_R}}-m_A}{\sqrt{2}\sigma _A}\right) -0.5erfc\left( \frac{\sqrt{\frac{xN_0}{E_R}}-m_A}{\sqrt{2}\sigma _A}\right) \nonumber \\ \end{aligned}$$
(15)

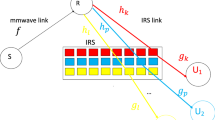
2.1.2.2 RIS implemented as a transmitter

In Fig. 2, a RIS is placed at relay R. As explained in section V of [11], RIS can be deployed as a transmitter at relay node R. It is used as a transmitter and illuminated with an antenna of R. We define \(q_k\) as the channel gain between RIS and destination D. Let \(e_k\) and \(\zeta _k\) be the absolute value and phase of \(q_k=e_ke^{-j\zeta _k}\). For Nakagami channels, \(e_k\) is Gamma distributed with mean \(E(e_k)=\frac{\Gamma (M+0.5)}{\Gamma (M)}\sqrt{\frac{1}{Md_3^{PLE}}}\) [34] and average power \(E(e_k^2)=E(|q_k|^2)=\frac{1}{d_3^{PLE}}\) in which \(d_3\) is the distance between relay R and D. RIS can be implemented using Q Phase Shift Keying (PSK) modulation. Let \(\mu _k\) be the phase of kth reflector of RIS:

$$\begin{aligned} \mu _k=\zeta _k+z_m, \end{aligned}$$
(16)

in which \(z_m=\frac{2\pi (n-1)}{M}\) is the phase of PSK symbol.

The received signal at D is written as

$$\begin{aligned} r_p=\sqrt{E_R}\sum _{l=1}^Nq_le^{j\mu _l}+n_k=\sqrt{E_R}e^{jz_m}\sum _{l=1}^Ne_l+n_p, \end{aligned}$$
(17)

The SNR at D is expressed as

$$\begin{aligned} \Gamma _{RD,r}=\frac{E_RB^2}{N_0}, \end{aligned}$$
(18)

in which subscript r refers to RIS and

$$\begin{aligned} B=\sum _{l=1}^Ne_l. \end{aligned}$$
(19)

\(e_l\) and \(e_{l'}\) are independent \(\forall l \ne l'\) as they correspond to absolute value of channel coefficient between lth, \(l'\)th RIS reflector and destination. Using the CLT, B is approximated by a Gaussian r.v. with mean \(m_B=N\frac{\Gamma (M+0.5)}{\Gamma (M)\sqrt{Md_3^{PLE}}}\) and variance \(\sigma _B^2=\frac{N(1-\frac{\Gamma (M+0.5)^2}{\Gamma (M)^2M})}{d_3^{PLE}}\), \(d_3\) is the distance between R equipped with RIS and D.

We use [34] \(E(e_l)=\frac{\Gamma (M+0.5)}{\sqrt{M}\Gamma (M)d_3^{PLE/2}}\) to compute \(m_B=\sum _{l=1}^NE(e_l)=N\frac{\Gamma (M+0.5)}{\sqrt{M}\Gamma (M)d_3^{PLE/2}}\). Since \(e_l\) and \(e_{l'}\) are independent \(\forall l \ne l'\), we deduce \(\sigma _B^2=\sum _{l=1}^NVar(e_l)=NVar(e_l)=N[E(e_l^2)-E(e_l)^2]=N[\frac{1}{d_3^{PLE}}-\frac{\Gamma (M+0.5)^2}{M\Gamma (M)^2d_3^{PLE}}]\).

The CDF of SNR is given by

$$\begin{aligned} \mathrm {F}_{{{\Gamma _\mathrm{RD,r}}\mathrm{(x)}}}=P(\frac{E_RB^2}{N_0}\le x)=P(-\sqrt{\frac{xN_0}{E_R}}\le B\le \sqrt{\frac{xN_0}{E_R}}) \nonumber \\ \simeq 0.5erfc\left( \frac{-\sqrt{\frac{xN_0}{E_R}}-m_B}{\sqrt{2}\sigma _B}\right) -0.5erfc\left( \frac{\sqrt{\frac{xN_0}{E_R}}-m_B}{\sqrt{2}\sigma _B}\right) \nonumber \\ \end{aligned}$$
(20)

2.2 RIS for mmwave communications using NOMA

2.2.1 Millimeter wave link

The system model of Fig. 3 shows a source S, a relay R and K NOMA users \(U_i\), \(i=1, \ldots K\). \(U_i\) is the ith strong user. The source transmits a combination of K symbols \(s_i\), \(i=1,2, \ldots K\) dedicated to K users:

$$\begin{aligned} s=\sqrt{E_S}\sum _{i=1}^K\sqrt{H_i}s_i \end{aligned}$$
(21)

in which \(0<H_i<1\) is the fraction of power allocated to user \(U_i\). More power is allocated to the weak user: \(0<H_1<H_2<\cdots <H_K\). We have

$$\begin{aligned} \sum _{i=1}^KH_i=1. \end{aligned}$$
(22)

It is assumed that the received signal at relay node R is affected by P interferers: [1,2,3,4,5]

$$\begin{aligned} r=fs+I=f\left[ \sqrt{E_S}\sum _{i=1}^K\sqrt{H_i}s_i\right] +I. \end{aligned}$$
(23)

in which f is the channel coefficient between S and R, I is the interference term at R:

$$\begin{aligned} I=\sum _{q=1}^{P} E_q |i_q|^2 \end{aligned}$$
(24)

\(E_q\) is the TES of qth interferer, \(i_q\) is the channel coefficient between qth interferer and R.

Relay node detects the symbol of user \(U_K\) since \(H_K>H_i\). The SINR is given by

$$\begin{aligned} \Gamma _{R,K}=\frac{H_KE_S|f|^2}{I+E_S|f|^2\sum _{i=1}^{K-1}H_i} \end{aligned}$$
(25)

Then, relay R removes the contribution of \(s_{K}\) and detects \(s_{K-1}\) with SINR

$$\begin{aligned} \Gamma _{R,K-1}=\frac{H_{K-1}E_S|f|^2}{I+E_S|f|^2\sum _{i=1}^{K-2}H_i} \end{aligned}$$
(26)

R will detect \(s_p\) \(p=K,K-1,\ldots ,1\) with SINR

$$\begin{aligned} \Gamma _{R,p}=\frac{H_{p}E_S|f|^2}{I+E_S|f|^2\sum _{i=1}^{p-1}H_i} \end{aligned}$$
(27)

The Cumulative Distribution Function (CDF) of \(\Gamma _{R,p}\) is given by

$$\begin{aligned} \mathrm {F}_{{\Gamma _\mathrm{R,p}}\mathrm{(x)}}= & {} P \left( \frac{H_{p}E_S|f|^2}{I+E_S|f|^2\sum _{i=1}^{p-1}H_i} \le x \right) \\&\quad =P \left( \frac{H_pU}{1+U\sum _{i=1}^{p-1}H_i} \le x \right) \end{aligned}$$
$$\begin{aligned} \qquad =\mathrm {F}_{{\Gamma _\mathrm{SR,m}}}(\frac{x}{H_p-x\sum _{i=1}^{p-1}H_i}) \end{aligned}$$
(28)

in which \(\mathrm {F}_{{\Gamma _\mathrm{SR,m}}}(x)\) is the CDF of \(\Gamma _{SR,m}\) (9).

There is no outage at R when SINR \(\Gamma _{R,1}\), \(\Gamma _{R,2}\), ...,\(\Gamma _{R,K}\) are higher than x:

$$\begin{aligned}&\mathrm {P}_{\mathrm{outage,R}}(x)=1-P(\Gamma _{R,1}>x, \ldots ,\Gamma _{R,K}>x)\nonumber \\&\quad =F_{\Gamma _{SR,m}}\left( \underset{1\le p\le K}{max}\left( \frac{x}{H_p-x\sum _{i=1}^{p-1}H_i}\right) \right) \end{aligned}$$
(29)

2.2.2 RIS link

RIS is located between relay node R and users \(U_1\), \(U_2\),...,\(U_K\). In Fig. 5, the red (respectively blue and yellow) reflectors are dedicated to user \(U_1\) (respectively \(U_2\) and \(U_K\)). A set \(O_i\) of reflectors are dedicated to user \(U_i\). We define \(h_k\) as the channel coefficient between R and kth RIS reflector such that \(E(|h_k|^2)=\frac{1}{D^{PLE}}\) and D is the distance between R and RIS. We define \(g_k \in O_i\) as the channel coefficient between kth reflector of RIS and user \(U_i\) such that \(E(|g_k|^2)=\frac{1}{D_i^{PLE}}\), \(D_i\) is the distance between RIS and \(U_i\). \(O_i\) is the set of RIS reflectors dedicated to user \(U_i\).

Let \(a_k\) and \(b_k\) be the absolute value and phase of \(h_k=a_ke^{-jb_k}\). For Nakagami channels, \(a_k\) has a Gamma distribution with \(E(a_k)=\frac{\Gamma (M+0.5)}{\Gamma (M)}\sqrt{\frac{1}{MD^{PLE}}}\) and \(E(a_k^2)=E(|h_k|^2)=\frac{1}{D^{PLE}}\) [34]. Let \(c_k\) and \(d_k\) be the absolute and phase of \(g_k=c_ke^{-jd_k}\). We have \(E(c_k)=\frac{\Gamma (M+0.5)}{\Gamma (M)}\sqrt{\frac{1}{MD_i^{PLE}}}\) and \(E(c_k^2)=E(|g_k|^2)=\frac{1}{D_i^{PLE}}\) [34].

RIS uses the following phase \(\phi _k\) of kth reflector

$$\begin{aligned} \phi _k=b_k+d_k. \end{aligned}$$
(30)

The received signal at \(U_i\) is written as

$$\begin{aligned} r=S\sqrt{E_R}\sum _{q\in O_i}h_qg_qe^{j\phi _q}+n \end{aligned}$$
(31)

in which \(O_i\) is the set of reflectors dedicated to \(U_i\), S is the transmitted NOMA symbol by relay node R, n is zero-mean Gaussian r.v. with variance \(N_0\) and \(E_R\) is the TES of R.

Let \(\widehat{s_i}\) the ith detected symbol at relay node R. When the detection is successful at the relay \(\widehat{s_i}=s_i\). The transmitted NOMA symbol S by relay R is written as

$$\begin{aligned} S=\sum _{l=1}^K\sqrt{G_l}\widehat{s_l} \end{aligned}$$
(32)

\(G_l\) is the fraction of power dedicated at \(U_l\) at relay R. More power is dedicated to weak user: \(0<G_1<G_2< \cdots <G_K\). We have \(\sum _{l=1}^KG_l=1\).

Using (31–32), we have

$$\begin{aligned} r=\sqrt{E_R}\left[ \sum _{l=1}^K\sqrt{G_l}\widehat{s_l}\right] \sum _{q\in O_i}h_qg_qe^{j\phi _q}+n \end{aligned}$$
(33)

Using (30), we obtain

$$\begin{aligned} r=\sqrt{E_R}A_i \left[ \sum _{l=1}^K\sqrt{G_l}\widehat{s_l}\right] +n, \end{aligned}$$
(34)

in which

$$\begin{aligned} A_i=\sum _{q\in O_i}a_qc_q. \end{aligned}$$
(35)

Using the Central Limit Theorem (CLT), \(A_i\) can be approximated by a Gaussian r.v. with mean \(m_{A_i}=\frac{N_i \Gamma (M+0.5)^2}{M\Gamma (M)^2d^{PLE/2}d_i^{PLE/2}}\) and variance \(\sigma _{A_i}^2=\frac{N_i}{d_i^{PLE}d^{PLE}}[1-\frac{ \Gamma (M+0.5)^4}{M^2\Gamma (M)^4}]\), \(N_i=|O_i|\) is the number of RIS reflectors dedicated to \(U_i\),.

The CDF of \(A_i^2\) is written as

$$\begin{aligned} \mathrm {F_{A_i^2}}(x)=P(A_i^2\le x)=P(-\sqrt{x}\le A_i\le \sqrt{x}) \end{aligned}$$
$$\begin{aligned} \simeq 0.5\mathrm {erfc}\left( \frac{-\sqrt{x}-m_{A_i}}{\sqrt{2}\sigma _{A_i}}\right) -0.5\mathrm {erfc}\left( \frac{\sqrt{x}-m_{A_i}}{\sqrt{2}\sigma _{A_i}}\right) \end{aligned}$$
(36)

User \(U_i\) detects first the symbol of user \(U_K\) as \(G_K>G_i\) \(\forall i\ne K\) with SINR

$$\begin{aligned} \Gamma _{U_i,K}=\frac{E_RA_i^2G_K}{N_0+E_RA_i^2\sum _{l=1}^{K-1}G_l} \end{aligned}$$
(37)

User \(U_i\) removes the signal of \(U_K\) using SIC and detect the symbol of \(U_{K-1}\) with SINR

$$\begin{aligned} \Gamma _{U_i,K-1}=\frac{E_RA_i^2G_{K-1}}{N_0+E_RA_i^2\sum _{l=1}^{K-2}G_l} \end{aligned}$$
(38)

User \(U_i\) detects the symbols of users \(U_p\) \(p=K,K-1, \ldots ,i\) with SINR

$$\begin{aligned} \Gamma _{U_i,p}=\frac{E_RA_i^2G_p}{N_0+E_RA_i^2\sum _{l=1}^{p-1}G_l} \end{aligned}$$
(39)

There is no outage at \(U_i\) when all SINR are larger than x:

$$\begin{aligned}&\mathrm {P}_{\mathrm{outage,U_i}}(x)=1-P(\Gamma _{U_i,K}>x,\Gamma _{U_i,K-1}>x, \ldots ,\nonumber \\&\quad \Gamma _{U_i,i}>x)=F_{A_i^2}\left( \underset{i\le p\le K}{max}\left( \frac{N_0x}{E_RG_p-xE_R\sum _{l=1}^{p-1}G_l}\right) \right) \end{aligned}$$
(40)

3 Throughput analysis in the presence of interferers

3.1 RIS link analysis in the presence of interferers and a single destination

Figures 4 and 5 depict the system model in the presence of Q interferers at the destination. The SINR at D is expressed as

$$\begin{aligned} \Gamma _{RD,r}=\frac{E_RC^2}{N_0+J} \end{aligned}$$
(41)

in which \(C=A\) (13) when RIS is implemented as a reflector, \(C=B\) (19) when RIS is implemented as a transmitter and J is the interference at D expressed as

$$\begin{aligned} J=\sum _{q=1}^Q J_q \end{aligned}$$
(42)

\(J_q=E_q'|j_q|^2\), \(E'_q\) is the transmitted energy per symbol of qth interferer and \(j_q\) is the channel coefficient between qth interferer and D. \(J_q\) are assumed to be i.i.d so that the J follows a Gamma distribution \(Gamma(QM,\zeta )\) written as

$$\begin{aligned} \mathrm {f}_{\mathrm{J(y)}}=\frac{y^{QM-1}e^{-\frac{y}{\zeta }}}{\Gamma (MQ)\zeta ^{MQ}} \end{aligned}$$
(43)

in which \(\zeta =\frac{E(J_q)}{M}\).

In the presence of Q interferers at D, the CDF of SNR is computed numerically as follows

$$\begin{aligned} \mathrm {F}_{\Gamma _{\mathrm{RD,r}}\mathrm{(x)}}=\int _0^{+\infty }P(E_RC^2\le (N_0+y)x)f_J(y)dy \end{aligned}$$
(44)

in which \(P(E_RC^2\le (N_0+y))\) is written as (15) and (20) by replacing x by \((N_0+y)x\) and \(N_0\) by 1:

$$\begin{aligned} P(E_RC^2\le (N_0+y)x)\simeq & {} 0.5erfc\left( \frac{-\sqrt{\frac{(N_0+y)x}{E_R}}-m_C}{\sqrt{2}\sigma _C}\right) \nonumber \\&\quad -0.5erfc\left( \frac{\sqrt{\frac{(N_0+y)x}{E_R}}-m_C}{\sqrt{2}\sigma _C}\right) \end{aligned}$$
(45)

\(m_C=m_A\), \(\sigma _C=\sigma _A\) when RIS is implemented as a reflector and \(m_C=m_B\), \(\sigma _C=\sigma _B\) when RIS is implemented as a transmitter.

3.2 Throughput analysis in the presence of a single destination

To avoid an outage at D, we should not have an outage on millimeter wave and RIS links. Therefore, the outage probability at D is written as

$$\begin{aligned} \mathrm {P}_{\mathrm{outage, m,r}\mathrm{(x)}}=1-[1-\mathrm {F}_{{{\Gamma }_{\mathrm{SR,m}}}\hbox {(x)}}][1-\mathrm {F}_{{{\Gamma }_{{\mathrm{RD,r}}}}\mathrm{(x)}}] \end{aligned}$$
(46)

in which subscript m, r refers to a system where the first hop uses conventional mmwave communications while the second one uses RIS.

When RIS is used as a reflector and at a high average SNR of RIS link, the asymptotic CDF is given by

$$\begin{aligned} F_{\Gamma _{SR,m}}(x)\approx \sqrt{\frac{N_02x}{\pi E_R}}\frac{e^{-\frac{m_A^2}{2\sigma _A^2}}}{\sigma _A} \end{aligned}$$
(47)

When RIS is used as a transmitter and at a high average SNR of RIS link, the asymptotic CDF is given by

$$\begin{aligned} F_{\Gamma _{SR,m}}(x)\approx \sqrt{\frac{N_02x}{\pi E_R}}\frac{e^{-\frac{m_B^2}{2\sigma _B^2}}}{\sigma _B} \end{aligned}$$
(48)

The asymptotic CDF is proportional to \(\sqrt{\frac{N_0}{E_R}}\). It decays exponentially in N and can be minimized by increasing the number of reflectors N. Using (46-48), we can deduce the asymptotic outage probability.

The Packet Error Probability (PEP) at D is upper bounded by the outage probability taken at waterfall threshold \(W_{TH}\) [35]

$$\begin{aligned} PEP_D<\mathrm {P_{outage, m,r}}(W_{TH}) \end{aligned}$$
(49)

in which \(W_{TH}\) is a waterfall threshold defined as [35]

$$\begin{aligned} W_{TH}=\int _0^{+\infty }\mathrm {PEP(y)}dy, \end{aligned}$$
(50)

For Quadrature Amplitude Modulation of size Q, PEP(y) is defined as

$$\begin{aligned} \mathrm {PEP(y)}=1-[1-2\left( 1-\frac{1}{\sqrt{Q}}\right) erfc(\sqrt{\frac{3y}{Q-1}})]^{L} \end{aligned}$$
(51)

For PSK modulation of size Q, \(\mathrm {PEP(y)}\) is defined as

$$\begin{aligned} \mathrm {pep(y)}=1-[1-\mathrm {erfc}(\sqrt{ysin^2}(\frac{\pi }{Q}))]^L \end{aligned}$$
(52)

in which L is packet length in symbols.

To compute the PEP in (51), we used equation (7) of [28] where the left term is the PEP and the right term is the outage probability at \(W_{TH}\).

Using (49 and 50), we can deduce the asymptotic PEP.

The throughput at D is evaluated as

$$\begin{aligned} \mathrm {Thr_D=0.5log_2(Q)[1-PEP_D]} \end{aligned}$$
(53)

3.3 RIS link analysis in the presence of \(P_i\) interferers at NOMA user \(U_i\)

Figure 6 depicts the system model in the presence of \(P_i\) interferers user \(U_i\). User \(U_i\) detects the symbols of users \(U_p\) \(p=K,K-1,\ldots ,i\) with SINR

$$\begin{aligned} \Gamma _{U_i,p}=\frac{E_RA_i^2G_p}{N_0+J_i+E_RA_i^2\sum _{l=1}^{p-1}G_l} \end{aligned}$$
(54)

in which \(J_i\) is the interference at \(U_i\) expressed as

$$\begin{aligned} J_i=\sum _{q=1}^{P_i} J_{i,q} \end{aligned}$$
(55)

\(J_q=E_q'|j_q|^2\), \(E'_q\) is the TES of qth interferer and \(j_q\) is the channel coefficient between qth interferer and D. \(J_q\) are assumed to be i.i.d so that the \(J_i\) follows a Gamma distribution \(Gamma(P_iM,\zeta _i)\) written as

$$\begin{aligned} \mathrm {f_{J_i}}(y)=\frac{y^{P_iM-1}e^{-\frac{y}{\zeta _i}}}{\Gamma (MP_i)\zeta _i^{MP_i}} \end{aligned}$$
(56)

in which \(\zeta _i=\frac{E(J_{i,q})}{M}\).

In the presence of \(P_i\) interferers at \(U_i\), the outage probability at \(U_i\) is computed numerically as follows

$$\begin{aligned}&\mathrm {P_{outage,U_i}}(x)=\int _{0}^{+\infty }F_{A_i^2}\left( \underset{i\le p\le K}{max}\left( \frac{(N_0+y)x}{E_RG_p-xE_R\sum _{l=1}^{p-1}G_l}\right) \right) \nonumber \\&\quad f_{J_i}(y)dy, \end{aligned}$$
(57)

in which \(f_{J_i}(y)\) is the PDF of interference at \(U_i\) (56) and \(F_{A_i^2}(x)\) is provided in (36).

3.4 Throughput optimization in the presence of K NOMA users

The end-to-end (e2e) outage probability at user \(U_i\) is given by

$$\begin{aligned} \mathrm {P_{outage,e2e,U_i}}(x)=1-[1-\mathrm {P_{outage,U_i}}(x)][1-\mathrm {P_{outage,R}}(x)].\nonumber \\ \end{aligned}$$
(58)

An upper bound of PEP is expressed as [35]

$$\begin{aligned}&\mathrm {PEP_i}(G_1,G_2, \ldots ,G_K,H_1,H_2, \ldots ,H_K)\nonumber \\&\quad <\mathrm {P_{outage,e2e,U_i}}(W_{TH}) \end{aligned}$$
(59)

in which \(W_{TH}\) is defined in (50).

We deduce the throughput at user \(U_i\):

$$\begin{aligned}&\mathrm {Thr_i}(G_1,G_2, \ldots ,G_K,H_1,H_2,\ldots ,H_K)=0.5 log_2(Q)\nonumber \\&\quad [1-\mathrm {PEP_i}(G_1,G_2,\ldots ,G_K,H_1,H_2,\ldots ,H_K)] \end{aligned}$$
(60)

The total throughput is given by

$$\begin{aligned}&\mathrm {Thr}(G_1,G_2,\ldots ,G_K,H_1,H_2,\ldots ,H_K)\nonumber \\&\quad =\sum _{i=1}^K\mathrm {Thr_i}(G_1,G_2,\ldots ,G_K,H_1,H_2,\ldots ,H_K) \end{aligned}$$
(61)

We optimize the fraction of powers allocated to users at the source (\(H_i\)) and relay (\(G_i\)) to enhance the total throughput

$$\begin{aligned} Thr^{max}= & {} \underset{0<G_1<G_2<\cdots<G_K<1,0<H_1<H_2<\cdots<H_K<1}{max}\mathrm {Thr}\nonumber \\&(G_1,G_2,\ldots ,G_K,H_1,H_2,\ldots ,H_K) \end{aligned}$$
(62)

under constraints \(\sum _{i=1}^KH_i=1\) and \(\sum _{i=1}^KG_i=1\).

The alternating maximization algorithm [36] was used to maximize the throughput in (62).

4 Theoretical and simulation results

4.1 Single destination

Figures 7, 8, 9 and 10 depict the throughput when RIS is deployed as a reflector to extend the millimeter wave link. These results correspond to fading figure \(M=2\), QPSK, 16QAM, 64 QAM, and 256QAM modulations. Packet length is \(L=400\) symbols. The distance between S and R is \(d_4=2\). The distance between R and RIS is \(d_1=1\). The distance between RIS and D is \(d_2=1\). The path loss exponent is \(PLE=3\). The number of interferers at R is \(P=4\), the number of interferers at D is \(Q=2\) and the average SINR at R is 20 dB. The transmitted energy per symbol of interferers are \(E_q=E'_q=0.01\). Figure 5 shows that RIS allows 19, 25, 31, 37 dB gain with respect to conventional millimeter wave communication without RIS for a number of reflectors \(N=16,32,64,128\). Significant throughput enhancement is observed in Figs. 6, 7 and 8 when RIS is used as a reflector for 16,64 and 256 QAM modulations. Theoretical curves are close to computer simulation results obtained with MATLAB software.

Figures 11 and 12 depict the throughput when RIS is deployed as a transmitter for 8PSK and 16 PSK modulation. The distance between relay and destination is \(d_3=2.5\) and the other parameter are those of Fig. 7. Figure 11 shows that RIS allows 13, 19, 25, 31 dB gain with respect to conventional millimeter wave communication without RIS for a number of reflectors \(N=16,32,64,128\).

For the same parameters as Fig. 7, Fig. 13 depicts the exact and asymptotic PEP when RIS is used as a reflector for QPSK modulation. To plot the asymptotic PEP, we used equations (26 and 27) and (29–31). At high average SNR, we observe that the asymptotic PEP is close to the exact PEP for a number of reflectors \(N=8,16,32\).

The throughput of millimeter wave communications can be improved using antenna selection at the destination [37]. For the same parameters as Fig. 13, Fig. 14 compares the PEP at the destination using RIS to antenna selection. When RIS uses \(N=32,16,8\) reflectors, we obtained 26.6, 19.6 and 12.3 dB gain with respect to antenna selection for \(n_r=2\) antennas [37]. When RIS uses \(N=32,16,8\) reflectors, we obtained 23.2 16.2 and 8.9 dB gain with respect to antenna selection for \(n_r=3\) antennas [37].

4.2 Results for NOMA systems

We did some simulations using Matlab when there are two NOMA users. The distance between S and R is 1.5 and the distance between R and RIS is 2. The distance between RIS and users are \(D_1=1\), \(D_2=1.5\). The number of interferers at R is \(P=3\). The number of interferers at users is \(P_1=2\), \(P_2=3\) . The m-fading figure is \(M=2\).

Figure 15 shows the total throughput for 16QAM modulation, \(H_1=0.4=1-H_2\) and \(G_1=0.4=1-G_2\). NOMA system using RIS offers 10,13,16 dB gain with respect to conventional NOMA using millimeter wave communications without RIS [25,26,27,28] for a number of reflectors per user \(N=N_1=N_2=8,16,32\). For an Optimal Power Allocation (OPA), the proposed NOMA using RIS offers 19 dB gain with respect to the absence of RIS [25,26,27,28] for a number of reflectors per user \(N=N_1=N_2=32\).

Figure 16 depicts the total throughput when there are two NOMA users for 16QAM modulation and \(N=N_1=N_2=64,128,256,512\) reflectors per user. The proposed NOMA system using RIS offers 20, 24, 27 and 30 dB gain with respect to conventional NOMA using millimeter wave communications without RIS [25,26,27,28] for \(N=N_1=N_2=64,128,256,512\).

5 Conclusions and perspectives

In this paper, we suggested extending the coverage of millimeter-wave communications using Reconfigurable Intelligent Surfaces (RIS). The first link between the source and relay node uses millimeter wave communications. In the second link, a RIS is placed between relay node and destination. We suggested implementing RIS as a reflector or a transmitter. The throughput at the destination was derived. Theoretical and simulation results have shown significant throughput enhancement when RIS is implemented as a transmitter or reflector. For QPSK modulation, RIS allows 19, 25, 31, 37 dB gain with respect to conventional millimeter wave communication without RIS for a number of reflectors \(N=16,32,64,128\). We also implemented RIS in mmwave communications using Non Orthogonal Multiple Access (NOMA). Different sets of RIS reflectors are dedicated to the served NOMA users. The proposed NOMA system using RIS offers 10, 13, 16, 20, 24, 27 and 30 dB gain with respect to conventional NOMA using millimeter wave communications without RIS for a number of reflector per user \(N=N_1=N_2=8,16,32,64,128,256,512\). One of the limitations of the paper is that the source and relay must have a battery that should be recharged or changed. As a perspective, we can study mmwave using RIS where the source and relay harvest energy using radio frequency signals, solar energy or wind.