Automated Medical Diagnosis System Based on Multi-modality Image Fusion and Deep Learning

Abstract

Multi-modality medical image fusion aims at integrating information from medical images with different modalities to aid in the diagnosis process. Most research work in this area ends with the fusion stage only. This paper, on the contrary, tries to present a complete diagnosis system based on multi-modality image fusion. This system works on MR and CT images. It begins with the registration step using Scale-Invariant Feature Transform registration algorithm. After that, histogram matching is performed to allow accurate fusion of the medical images. Two methods of the fusion are utilized and compared, wavelet and curvelet fusion. An interpolation stage is included to enhance the resolution of the obtained image after fusion. Finally, a deep learning approach is adopted for classification of images as normal or abnormal. Simulation results reveal good success of the proposed automated diagnosis system based on the fusion and interpolation results.

1 Introduction

Medical imaging has become a very powerful and efficient tool that can be used in the diagnosis of several diseases. There are several technologies to extract medical images such as X-ray imaging, mammography, Computed Tomography (CT), Computerized Axial Tomography (CAT), Magnetic Resonance Imaging (MRI), ultrasonic imaging, Positron Emission Tomography (PET), and confocal microscopy imaging. These imaging technologies have different principles for generating images, and hence different artifacts and limitations [1, 2]. In some scenarios, there is a need to integrate information from different medical images obtained with different modalities for the same object to help in a better diagnosis. The most popular example of this is the fusion of MR and CT images. To achieve a successful fusion process, there is a need first to understand the nature of both modalities of images.

CT imaging is based on X-rays by collecting several angular-projection X-ray images. Cross section slices can be generated from these images using different reconstruction algorithms. Some artifacts such as ringing, high attenuation around edges, ghosting, and stitching may appear in CT images. These artifacts need to be removed with efficient image processing algorithms [1, 2]. On the other hand, the idea of MRI differs from that of X-ray imaging. Here, no radiation is used. This technique just depends on a strong magnetic field, which causes hydrogen atoms to emit radio-wave pulses that can be used for imaging. Concentration of hydrogen atoms is reflected in the obtained MRI images, and hence tissues can be discriminated based on the amount of water in each of them. Several artifacts may appear in MRI images such as zebra stripes, inhomogeneity, shading, and aliasing [1, 2].

Multi-modality image fusion is used to merge information from multiple images obtained with different imaging techniques. The most common types of images that are incorporated in the fusion process include MR and CT images. These images need first to be registered for accurate fusion results. Different approaches have been presented for this objective. Ali et al. presented an approach for MR and CT image fusion based on both wavelet transform and curvelet transform [3, 4]. Unfortunately, this approach did not consider the histogram matching issue, and hence quality of the obtained fusion images is not good. Moreover, Ali et al. developed their work for resolution enhancement of medical images by incorporating inverse interpolation techniques such as maximum entropy interpolation, LMMSE interpolation, and regularized interpolation [5]. This work presented images of better resolution, but unfortunately did not consider the histogram matching issue. The main shortcoming of this work is that it was not extended to the diagnosis process. It stopped at the fusion and interpolation stages only. To be more feasible, there is a need to go to the further classification stage.

Some other attempts have been presented in the literature to combine the process of multi-modality image fusion with optimization to enhance the quality of the obtained fusion results subject to certain constraints [6, 7]. These attempts considered optimization techniques like the modified central force optimization in maximizing the visual quality of the obtained results. The attempts in [6, 7] considered the histogram matching issue and gave good fusion results. Unfortunately, these techniques did not consider the resolution enhancement scenario. They did not also consider the automated diagnosis process needed after obtaining the fusion results.

The work in this paper differs from the work presented by Ali et al. in that it considers the histogram matching as a very major stage to match the intensity levels of the CT image to those of the MR image for better fusion results. Moreover, the proposed work in this paper presents a full diagnosis system by introducing a classification stage for the fusion results based on a suggested deep learning model. Simulation results presented in the paper prove the feasibility and success of the proposed automated medical diagnosis system to differentiate between fusion results with tumors and fusion results without tumors.

2 Proposed Automated Diagnosis System

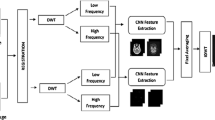
The proposed automated diagnosis system consists of five stages as shown in Fig. 1. These stages are registration, histogram matching, image fusion, image interpolation, and deep learning for classification. The first stage is the registration stage. This stage is performed to calibrate the coordinates of both MR and CT images to allow an accurate fusion process. The registration process can be performed using SIFT algorithm [8,9,10,11]. The SIFT algorithm is used to extract feature points across scales and represent these feature points with feature vectors containing angle histogram bins. The registration is performed by rotating one of the images with fixed step sizes and comparing the feature vectors between the reference image and each rotated image [8,9,10,11].

Fig. 1

The proposed approach

3 Registration of MR and CT Images

To extract the feature vector from an image, the first step is to convolve the image at hand with multiple Gaussian kernels with different scales [8,9,10,11]:

$$L\left( {x,y,\sigma } \right) = G\left( {x,y,\sigma } \right)*I\left( {x,y} \right)$$

(1)

where $\sigma$, and $G\left( {x,y,\sigma } \right)$ are the scale and the Gaussian kernel with scale $\sigma$, and $I\left( {x,y} \right)$ is the original image. The Gaussian kernel is defined as follows [8,9,10,11]:

$$G\left( {x,y,\sigma } \right) = \frac{1}{{2\pi \sigma^{2} }}e^{{ - \left( {x^{2} + y^{2} } \right)/2\sigma^{2} }}$$

(2)

Laplacian operator is applied to the different scales. In a simplified manner, the Difference of Gaussina (DoG) is used as an alternative strategy as illustrated in Fig. 2 for the determination of the keypoints. A comparison process is performed between pixels at similar coordinates to select the feature points across scales. The extrema points across scales are selected for further feature extraction processes. The DoG is a good alternative to the LoG as the Laplacian is eliminated for simplification [8,9,10,11].

Fig. 2

Implementation of the DoG

After keypoint selection, both magnitude and phase of the gradiant at this keypoint are estimated as follows [8,9,10,11]:

$$m\left( {x,y} \right) = \sqrt {\left( {L\left( {x + 1,y} \right) - L\left( {x - 1,y} \right)} \right)^{2} + \left( {L\left( {x,y + 1} \right) - L\left( {x,y - 1} \right)} \right)^{2} }$$

(3)

$$\theta \left( {x,y} \right) = \tan^{ - 1} \left( {\frac{{L\left( {x,y + 1} \right) - L\left( {x,y - 1} \right)}}{{L\left( {x + 1,y} \right) - L\left( {x - 1,y} \right)}}} \right)$$

(4)

where $L\left( {x,y} \right)$ is the gradient at $\left( {x,y} \right)$. A 16 × 16 window around each keypoint is selected and divided into four sub-windows as shown in Fig. 3. An angle histogram of gradients is estimated in each sub-window with four bins, and each bin represents 45°. This leads to a feature vector of 128 points representing each feature point.

Fig. 3

Keypoint description

The registration process is performed by taking the MR image as a reference image and extracting the feature points and feature vectors from that image. The feature points and feature vectors are also extracted from the CT image and matched to those of the MR image. The matching is based on the minimum distance criterion. To accommodate for rotation effects, a group of rotations of the CT image with step angles are performed and followed by a matching process after each rotation. The feature comparison is performed for each rotation angle and the decision of registration is taken based on the minimum distance criterion.

4 Histogram Matching

Histogram matching is a process that aims to adapt the histogram of an image to that of another one for the objective of enhancement of a poor-visual-quality image as in the case of infrared image enhancement [12, 13], or the objective of image fusion. It has become a must in mutlti-modality image fusion, because the intensity levels of the multi-modality images differ so much. In the scenario at hand of fusion of MR and CT images, the CT image is taken as the reference image f(k,l) as it has a larger dynamic range, and the MR image intensities $g\left( {m,n} \right)$ are adjusted based on this reference image. The steps of the histogram matching algorithm adopted in this paper is similar to that adopted by Ashiba et al. for infrared image enhancement and its steps are summarized below [12].

• 1. Estimate the mean of the MR image.

  $$\hat{g} = \left( {\frac{1}{\it{MN}}} \right)\mathop \sum \limits_{m = 1}^{\it M} \mathop \sum \limits_{n = 1}^{N} g\left( {m,n} \right)$$

  (5)

  where M and N are the dimensions of the MR image.

• 2. Estimate the mean of the CT image.

  $$\hat{f} = \left( {\frac{1}{KL}} \right)\mathop \sum \limits_{k = 1}^{K} \mathop \sum \limits_{l = 1}^{L} f\left( {k,l} \right)$$

  (6)

  where K and L are the dimensions of the CT image.

• 3. Estimate the standard deviation of the MR image.

  $$\sigma_{1} = \sqrt {\frac{1}{MN}\mathop \sum \limits_{m = 1}^{M} \mathop \sum \limits_{n = 1}^{N} \left( {g\left( {m,n} \right) - \hat{g}} \right)^{2} }$$

  (7)

• 4. Estimate the standard deviation of the CT image.

  $$\sigma_{2} = \sqrt {\frac{1}{KL}\mathop \sum \limits_{k = 1}^{K} \mathop \sum \limits_{l = 1}^{L} \left( {f\left( {k,l} \right) - \hat{f}} \right)^{2} }$$

  (8)

• 5. Estimate the correction factor.

  $$C = \frac{{\sigma_{2} }}{{\sigma_{1} }}$$

  (9)

• 6. Estimate the corrected mean of the MR image.

  $$f_{c } = \hat{f} - C. \hat{g}$$

  (10)

• 7. Estimate the histogram matched MR image.

  $$g_{h} \left( {m,n} \right) = f_{c} +C. g\left( {m,n} \right)$$

  (11)

An example of the adjustment of an MR image histogram to that of a CT image histogram is shown in Fig. 4. It is clear that after histogram matching, the intensities of the MR image become brighter to accommodate for the intensities of the CT image.

Fig. 4

The results of histogram matching of an MR image to a CT image

5 Fusion of MR and CT Images 

Fusion of MR and CT images is performed in this paper with either wavelet or curvelet fusion. They are implemented and compared.

5.1 Wavelet Fusion of MR and CT Images

Wavelet transform is utilized as a tool for the fusion of the MR and CT images after the histogram matching step as shown in Fig. 5. The wavelet transform is applied on both images and the fusion rule is applied on the wavelet coefficients as follows [3,4,5]:

$$I_{f} \left( {x,y} \right) = {\text{IDWT}} \left[ {\emptyset \left\{ {{\text{DWT}}\left( {I_{1} \left( {n_{1},n_{2}} \right)} \right) \cdot {\text{DWT}}\left( {I_{2} \left( {n_{1},n_{2}} \right)} \right)} \right\}} \right]$$

(12)

where DWT refers to the wavelet transform in two dimensions, IDWT refers to the inverse wavelet transform, and $\emptyset$ is the fusion rule.

Fig. 5

Wavelet fusion of MR and CT images

The fusion rule adopted in this paper is the maximum fusion rule, because with this rule, it is guaranteed that any sort of blurring in any of the images to be fused is eliminated. The wavelet transform is reported to give good fusion results, but it has a problem with the fusion of curved edges. So, the curvelet transform is a good candidate for this task.

5.2 Curvelet Fusion of MR and CT Images

The curvelet fusion of MR and CT images is based on the curvelet transform of both images. The curvelet transform is implemented on overlapping tiles of the images to approximate curved lines as short straight lines after applying the Additive Wavelet Transform (AWT) as shown in Fig. 6. Rigdelet transform is applied on each tile, and then maximum fusion rule is implemented in the fusion process [3,4,5].

Fig. 6

Cuvelet transform of an image

First of all, the additive wavelet transform is applied on both MR and CT images. The steps of the AWT are shown in Fig. 7. It is implemented through cascaded filtering stages and difference operations to get the detail planes and finally an approximation plane.

Fig. 7

Steps of the AWT of an image

Given an image P, it is possible to construct the sequence of approximations as follows [3,4,5]:

$$f_{1} \left( P \right) = P_{1} , f_{2 } \left( {P_{1} } \right) = P_{2 } , f_{3 } \left( {P_{2} } \right) = P_{3} , \ldots , f_{n } \left( {P_{n - 1} } \right) = P_{n} ,$$

(13)

where n is an integer. In constructing the above sequence, successive convolutions with the kernel H are performed,

$$H = \frac{1}{256}\left( {\begin{array}{*{20}c} 1 &\quad 4 &\quad 6 &\quad 4 &\quad 1 \\ 4 &\quad {16} &\quad {24} &\quad {16} &\quad 4 \\ 6 &\quad {24} &\quad {36} &\quad {24} &\quad 6 \\ 4 &\quad {16} &\quad {24} &\quad {16} &\quad 4 \\ 1 &\quad 4 &\quad 6 &\quad 4 &\quad 1 \\ \end{array} } \right)$$

(14)

The wavelet planes are calculated as the differences between two consecutive approximations P_l−1 and P_l, i.e. [3,4,5].

$$\Delta_{l} = P_{l - 1} - P_{l}$$

(15)

Therefore, the curvelet reconstruction formula is given by [3,4,5]:

$$P = \mathop \sum \limits_{l = 1}^{n - 1} \Delta_{l} + P_{n}$$

(16)

This step is performed after the fusion of the corresponding detail components of the MR and CT tiles, while keeping the approximation of the MR image as it is rich in details.

The ridgelet transform is applied to the tiles of the images prior to the fusion process. Assume a tile $f\left( {x_{1} ,x_{2} } \right)$, the ridgelet transform of that tile is given by [3,4,5]:

$$R_{f} \left( {p,q,\theta } \right) = \mathop \int \limits_{ - \infty }^{\infty } \mathop \int \limits_{ - \infty }^{\infty } \varphi_{p,q,\theta } \left( {x_{1} ,x_{2} } \right)f\left( {x_{1} ,x_{2} } \right) dx_{1} dx_{2}$$

(17)

where $\varphi_{p,q,\theta } \left( {x_{1} ,x_{2} } \right) = a^{{ - \frac{1}{2}}} \varphi \left( {\frac{{x_{1} \cos \theta + x_{2 } \sin \theta - b}}{a}} \right)$ is the ridgelet basis function, a > 0 and $\theta$∈ [0, 2π] [3,4,5].

The ridgelet transform is closely related to the Radon transform defined as,

$$R_{f} \left( {\theta ,t} \right) = \mathop \int \limits_{ - \infty }^{\infty } \mathop \int \limits_{ - \infty }^{\infty } f( {x_{1} ,x_{2} )\delta \left( {x_{1} \cos \theta + x_{2} \sin \theta - t} \right)dx_{1} dx_{2} } $$

(18)

This relation is given by [3,4,5]:

$$R_{f} \left( {p,q,\theta } \right) = \mathop \smallint \limits_{ - \infty }^{\infty } R_{f} \left( {\theta ,t} \right)a^{{ - \frac{1}{2}}} \left( {\frac{t - b}{a}} \right)dt$$

(19)

The main advantage of this relation is that the projection slice theorem of radon transform is combined with ridgelet transform to transform line singularities to point singularities.

6 Image Interpolation

After obtaining the fused image, it is required to increase the resolution of this image for better diagnosis. To achieve this objective, several interpolation techniques can be investigated. Prior to going to the interpolation problem, there is a need to understand the relation between the available fusion result and the required high-resolution image. This relation can be defined as follows [14,15,16]:

$${\mathbf{g}} = {\mathbf{Df}} + {\mathbf{v}}$$

(20)

where g, f, D, and v are the obtained fusion result in lexicographic format, the required high-resolution image in lexicographic format, the decimation matrix, and the noise vector, respectively.

The matrix D is defined as:

$${\mathbf{D}} = {\mathbf{D}}_{1} \otimes {\mathbf{D}}_{1}$$

(21)

where $\otimes$ represents the Kronecker product, and the M × N matrix ${\mathbf{D}}_{1}$ represents the 1-D filtering and down-sampling by a factor R. For N = 2M, ${\mathbf{D}}_{1}$ is given by [14,15,16]:

$${\mathbf{D}}_{1} = \frac{1}{2}\left[ {\begin{array}{*{20}c} 1 & \quad 1 & \quad 0 & \quad 0 & \ldots & \quad 0 & \quad 0 \\ 0 & \quad 0 & \quad 1 & \quad 1 & \quad \ldots & \quad 0 & \quad 0 \\ \vdots & \quad \vdots & \quad \vdots & \quad \vdots & \quad \ddots & \quad \vdots & \quad \vdots \\ 0 & \quad 0 & \quad 0 & \quad 0 & \quad \ldots & \quad 1 & \quad 1 \\ \end{array} } \right]$$

(22)

The model of filtering and down-sampling is illustrated in Fig. 8. The objective of the image interpolation process is the estimation of the vector ${\mathbf{f}}$ given the vector ${\mathbf{g}}$. Several algorithms can be used to achieve this objective.

Fig. 8

Down-sampling process from the N×N HR image to the (N/2) × N/2) LR image

6.1 Cubic Spline Image Interpolation

The signal synthesis approach to solve the interpolation problem is to use the following equation based on Fig. 9 [14,15,16]:

Fig. 9

1-D signal interpolation. The pixel at position x is estimated using its neighborhood pixels and the distance s

$$\hat{f}(x) = \sum\limits_{k = - \infty }^{\infty } {c(x_{k} )\beta (x - x_{k} )}$$

(23)

A good approximation to solve the interpolation equation is to use a spline of order n as follows [14,15,16]:

$$\hat{f}(x) = \sum\limits_{k \in Z}^{{}} {c(x_{k} )\beta^{n} (x - x_{k} )}$$

(24)

where Z is a finite neighborhood around x.

The B-spline function $\beta^{n} (x)$ is obtained by (n + 1) fold convolutions of $\beta^{0}$ given by [14,15,16]:

$$\beta^{0} (x) = \left\{ {\begin{array}{*{20}l} 1 \hfill & \quad { - \frac{1}{2} < x < \frac{1}{2}} \hfill \\ {\frac{1}{2}} \hfill & \quad {\left| x \right| = \frac{1}{2}} \hfill \\ 0 \hfill & \quad {\text{Otherwise}} \hfill \\ \end{array} } \right.$$

(25)

The most popular spline interpolation basis function is the cubic basis function defined as [14,15,16]:

$$\beta^{3} (x) = \left\{ {\begin{array}{*{20}l} {\frac{2}{3} - \left| x \right|^{2} + \frac{{\left| x \right|^{3} }}{2}} \hfill & {0 \le \left| x \right| < 1} \hfill \\ {\frac{{\left( {2 - \left| x \right|} \right)^{3} }}{6}} \hfill & {1 \le \left| x \right| < 2} \hfill \\ 0 \hfill & {2 \le \left| x \right|} \hfill \\ \end{array} } \right.$$

(26)

Solving Eq. (20) with the aid of Fig. 10, we get the following closed-form expression for the cubic spline interpolation formula.

Fig. 10

Estimation of the cubic spline interpolation coefficients

$$\begin{aligned} \hat{f}(x) & = c(x_{k - 1} )\left[ {(3 + s)^{3} - 4(2 + s)^{3} + 6(1 + s)^{3} - 4s^{3} } \right]/6 \\ & \quad + c(x_{k} )\left[ {(2 + s)^{3} - 4(1 + s)^{3} + 6s^{3} } \right]/6 + c(x_{k + 1} )\left[ {(1 + s)^{3} - 4s^{3} } \right]/6 + c(x_{k + 2} )s^{3} /6 \\ \end{aligned}$$

(27)

The cubic spline basis function is non-interpolating, and thus the coefficients in Eq. (27) need to be estimated prior to the interpolation process. The estimation process can be implemented using a digital filtering approach [17,18,19].

To begin the digital filtering algorithm required for the determination of the spline coefficients as shown in Fig. 11, we define the B-spline kernel $b_{m}^{n}$, which is obtained by sampling the B-spline basis function of degree n expanded by a factor m [17,18,19].

Fig. 11

Block diagram of B-spline image interpolation

$$b_{m}^{n} (x_{k} ) = \left. {\beta^{n} (x/m)} \right|_{{x = x_{k} }}$$

(28)

The z-transform of the B-spline kernel is given by:

$$B_{m}^{n} (z) = \sum\limits_{{x_{k} \in Z}} {b_{m}^{n} (x_{k} )z^{ - k} }$$

(29)

The main objective is to estimate the coefficients $c(x_{k} )$ to achieve a perfect fit at the integers, which means that [17,18,19]:

$$\sum\limits_{{x_{l} \in Z}} {c(x_{l} )\left. {\beta^{n} (x - x_{l} )} \right|}_{{x = x_{k} }} = f(x_{k} )$$

(30)

Using convolution notation [17,18,19]:

$$f(x_{k} ) = \left( {b_{1}^{n} *c} \right)(x_{k} )$$

(31)

Hence, the coefficients are given by [17,18,19]:

$$c(x_{k} ) = \left( {b_{1}^{n} } \right)^{ - 1} *f(x_{k} )$$

(32)

Since $b_{1}^{n}$ is a symmetric FIR filter, the direct B-Spline filter $\left( {b_{1}^{n} } \right)^{ - 1}$ is an all-pole filter that can be implemented using a cascade of first order causal and non-causal recursive filters [17,18,19].

For the case of cubic spline interpolation, we have [17,18,19]:

$$B_{1}^{3} (z) = \frac{{z + 4 + z^{ - 1} }}{6}$$

(33)

This gives:

$$\left[ {B_{1}^{3} \left( z \right)} \right]^{ - 1} = 6\left[ {\frac{1}{{1 - z_{1} z^{ - 1} }}} \right]\left[ {\frac{{ - z_{1} }}{{1 - z_{1} z}}} \right]$$

(34)

where $z_{1} = - 2 + \sqrt 3$.

The above equation can be implemented with two cascaded stages as illustrated in Fig. 10.

$$c^{ + } (x_{k} ) = f(x_{k} ) + z_{1} c^{ + } (x_{k - 1} )\quad (k = 1, \ldots , N - 1)$$

(35)

$$c(x_{k} ) = z_{1} \left( {c(x_{k + 1} ) - c^{ + } (x_{k} )} \right),\quad (k = N - 2, \ldots ,0)$$

(36)

N is the length of the data sequence used.

The initial conditions for the two stages can be calculated as follows [17,18,19]:

$$c_{{}}^{ + } (0) = \sum\limits_{k = 0}^{N - 1} {f(x_{k} )z_{1}^{k} }$$

(37)

$$c(x_{N - 1} ) = \frac{{z_{1} }}{{\left( {1 - z_{1}^{2} } \right)}}\left( {c^{ + } (x_{N - 1} ) + z_{1} c^{ + } (x_{N - 2} )} \right)$$

(38)

The block diagram of the image interpolation by an up-sampling factor m is illustrated in Fig. 11 in an all-digital implementation. We denote the interpolated image as $f_{m}^{n} (x_{k} )$, which can be obtained using the following equation [17,18,19]:

$$f_{m}^{n} (x_{k} ) = \sum\limits_{l = - \infty }^{\infty } {c\left( {x_{l} } \right)b_{m}^{n} (x_{k} - mx_{l} )}$$

(39)

The digital filter $B_{m}^{n} (z)$ is a symmetric FIR filter. The expression for $B_{m}^{n} (z)$ is given as follows [17,18,19]:

$$B_{m}^{n} (z) = \frac{{z^{\alpha } }}{{m^{n} }}\left( {\frac{{1 - z^{ - m} }}{{1 - z^{ - 1} }}} \right)^{n + 1} B_{1}^{n} (z)$$

(40)

where $\alpha = (m - 1)(n + 1)/2$.

6.2 Inverse Interpolation

The treatment of the interpolation as an inverse problem depends on the inversion of Eq. (20). Several models can be used for this objective such as the Linear Minimum Men Square Error (LMMSE), the maximum entropy, and the regularized models. In order to set the LMMSE solution, we need to solve [14,15,16]:

$$\mathop {\hbox{min} }\limits_{{\hat{\bf f}}} {\it{E}}\left[ {{\mathbf{e}}^{{\it{t}}} {\mathbf{e}}} \right] = {\text{E}}\left[ {Tr({\mathbf{ee}}^{t} )} \right]$$

(41)

with

$${\mathbf{e}} = {\mathbf{f}} - {\hat{\mathbf{f}}}$$

(42)

where ${\hat{\mathbf{f}}}$ is the estimate of the required HR image.

If we assume that:

$${\hat{\mathbf{f}}} = {\mathbf{Tg}}$$

(43)

The operator ${\mathbf{T}}$ is derived subject to minimizing Eq. (41) to give [14,15,16]:

$$\begin{aligned} \mathop {\hbox{min} }\limits_{{{\hat{\mathbf{f}}}}} {\it{E}}\left[ {Tr({\mathbf{ee}}^{t} )} \right] & = {\it{E}}\left[ {Tr\left\{ {{\mathbf{(f}} - {\mathbf{Tg)(f}} - {\mathbf{Tg)}}^{{\it{t}}} } \right\}} \right] \\ & = {\it{E}}\left[ {Tr\left\{ {{\mathbf{ff}}^{{\it{t}}} - {\mathbf{T(Dff}}^{{\it{t}}} + {\mathbf{vf}}^{{\it{t}}} {\mathbf{)}} - {\mathbf{(ff}}^{{\it{t}}} {\mathbf{D}}^{{\it{t}}} + {\mathbf{fv}}^{{\it{t}}} {\mathbf{)T}}^{{\it{t}}} + {\mathbf{T(Dff}}^{{\it{t}}} {\mathbf{D}}^{{\it{t}}} + {\mathbf{vf}}^{{\it{t}}} {\mathbf{D}}^{{\it{t}}} + {\mathbf{Dfv}}^{{\it{t}}} + {\mathbf{vv}}^{{\it{t}}} {\mathbf{)T}}^{{\it{t}}} } \right\}} \right] \, \\ \end{aligned}$$

(44)

We have $Tr({\mathbf{B}}) = Tr({\mathbf{B}}^{{\it{t}}} )$. Since the trace is linear, it can be interchanged with the expectation operator.

Equation (44) can be simplified with the assumptions:

$${\it{E}}\left[ {{\mathbf{fv}}^{{\it{t}}} } \right] = {\it{E}}\left[ {{\mathbf{v}}^{{\it{t}}} {\mathbf{f}}} \right] = \left[ {\mathbf{0}} \right]$$

(45)

The autocorrelation matrices for the image and noise can be defined as:

$${\it{E}}\left[ {{\mathbf{ff}}^{{\it{t}}} } \right] = {\mathbf{R}}_{{\mathbf{f}}}$$

(46)

and

$${\it{E}}\left[ {{\mathbf{vv}}^{{\it{t}}} } \right] = {\mathbf{R}}_{{\mathbf{v}}}$$

(47)

The matrix ${\mathbf{R}}_{{\mathbf{v}}}$ is a diagonal matrix whose main diagonal elements are equal to the noise variance in the noisy LR image.

This leads to the minimization problem:

$$\mathop {\hbox{min} }\limits_{{{\hat{\mathbf{f}}}}} {\it{E}}\left[ {Tr({\mathbf{ee}}^{t} )} \right] = Tr\left\{ {{\mathbf{R}}_{{\mathbf{f}}} - {\mathbf{2TDR}}_{{\mathbf{f}}} + {\mathbf{TDR}}_{{\mathbf{f}}} {\mathbf{D}}^{{\it{t}}} {\mathbf{T}}^{{\it{t}}} + {\mathbf{TR}}_{{\mathbf{v}}} {\mathbf{T}}^{{\it{t}}} } \right\}$$

(48)

Differentiating Eq. (48) with respect to ${\mathbf{T}}$ and setting the result equal to zero, the operator T is given by:

$${\mathbf{T}} = {\mathbf{R}}_{{\mathbf{f}}} {\mathbf{D}}^{{\it{t}}} {\mathbf{(DR}}_{{\mathbf{f}}} {\mathbf{D}}^{{\it{t}}} + {\mathbf{R}}_{{\mathbf{v}}} {\mathbf{)}}^{{ - {\mathbf{1}}}}$$

(49)

Thus, the LMMSE estimate of the HR image will be given by [14,15,16]:

$${\hat{\mathbf{f}}} = {\mathbf{R}}_{{\mathbf{f}}} {\mathbf{D}}^{{\it{t}}} {\mathbf{(DR}}_{{\mathbf{f}}} {\mathbf{D}}^{{\it{t}}} + {\mathbf{R}}_{{\mathbf{v}}} {\mathbf{)}}^{{ - {\mathbf{1}}}} {\mathbf{ g}}$$

(50)

To solve the problem of estimating the autocorrelation of the HR image, the matrix ${\mathbf{R}}_{{\mathbf{f}}}$ in Eq. (50) can be written in the form [14,15,16]:

$${\mathbf{R}}_{{\mathbf{f}}} = \left[ {\begin{array}{*{20}c} {{\mathbf{R}}_{{{{0}},{{0}}}} } & {{\mathbf{R}}_{{{{0}},{{1}}}} } & \cdots & {{\mathbf{R}}_{{{{0}},{\it{N}} - {{1}}}} } \\ {{\mathbf{R}}_{{{{1}},{{0}}}} } & {{\mathbf{R}}_{{{{1}},{{1}}}} } & \cdots & \vdots \\ \vdots & \ddots & \ddots & \vdots \\ {{\mathbf{R}}_{{{\it{N}} - {{1}},{{0}}}} } & \cdots & \cdots & {{\mathbf{R}}_{{{\it{N}} - {{1}},{\it{N}} - {{1}}}} } \\ \end{array} } \right]$$

(51)

where

$${\mathbf{R}}_{{{\it{i}},{\it{j}}}} = {\text{E}}\left[ {{\mathbf{f}}_{{\it{i}}} {\mathbf{f}}_{{\it{j}}}^{{\it{t}}} } \right]$$

(52)

${\mathbf{f}}_{{\it{i}}}$ and ${\mathbf{f}}_{{\it{j}}}^{{}}$ are the ith and jth column partitions of the lexicographically-ordered vector ${\mathbf{f}}$. Usually, pixels in an image have no predictable correlation beyond a correlation distance d. If we assume that d = 0, then the matrix ${\mathbf{R}}_{{\mathbf{f}}}$ can be dealt with as a diagonal matrix in the form [14,15,16]:

$${\mathbf{R}}_{{\mathbf{f}}} = \left[ {\begin{array}{*{20}c} {{\mathbf{R}}_{{{{0}},{{0}}}} } & {\mathbf{0}} & \cdots & {\mathbf{0}} \\ {\mathbf{0}} & {{\mathbf{R}}_{{{{1}},{{1}}}} } & \ddots & \vdots \\ \vdots & \ddots & \ddots & {\mathbf{0}} \\ {\mathbf{0}} & \cdots & {\mathbf{0}} & {{\mathbf{R}}_{{{\it{N}} - {{1}},{\it{N}} - {{1}}}} } \\ \end{array} } \right]$$

(53)

If the pixels of each column are uncorrelated except for each pixel with itself, each matrix ${\mathbf{R}}_{{{\it{i, i}}}}$ can be dealt with as a diagonal matrix for i = 0,1,…, N−1 as follows [14,15,16]:

$${\mathbf{R}}_{{{\it{i,i}}}} = \left[ {\begin{array}{*{20}c} {R_{f} (i,0)} & 0 & \cdots & 0 \\ 0 & {R_{f} (i,1)} & \ddots & \vdots \\ \vdots & \ddots & \ddots & 0 \\ 0 & \cdots & 0 & {R_{f} (i,N - 1)} \\ \end{array} } \right]$$

(54)

The diagonal elements of the matrix ${\mathbf{R}}_{{{\it{i, i}}}}$ can be estimated from a polynomial-based interpolated version of the available LR image.

For an image f’(n₁,n₂), the autocorrelation at the spatial location (n₁,n₂) can be estimated from the following relation [14,15,16]:

$$R_{f} (n_{1} ,n_{2} ) \cong \frac{1}{{w^{2} }}\sum\limits_{k = 1}^{w} {\sum\limits_{l = 1}^{w} {f'(k,l)f'(n_{1} + k,n_{2} + l)} }$$

(55)

where $R_{f} (n_{1} ,n_{2} )$ is the autocorrelation at spatial position $(n_{1} ,n_{2} )$ and $w$ is an arbitrary window length for the auto-correlation estimation.

The image $f'(n_{1} ,n_{2} )$ may be taken as the cubic spline interpolated image. Thus, the matrix ${\mathbf{R}}_{{\mathbf{f}}}$ can be approximated by a diagonal sparse matrix.

Another inverse solution is to adopt the maximum entropy concept to obtain the HR image. The required HR image is assumed to be treated as light quanta associated with each pixel value. Thus, the entropy of the required HR image is defined as follows [14,15,16]:

$$H_{e} = - \sum\limits_{i = 1}^{{N^{2} }} {f_{i} \log_{2} (f_{i} )}$$

(56)

where H_e is the entropy and f_i is the sampled signal.

This equation can be written in the vector form as follows [14,15,16]:

$$H_{e} = - {\mathbf{f}}^{t} \log_{2} ({\mathbf{f}})$$

(57)

For image interpolation, to maximize the entropy subject to the constraint that $\left\| {{\mathbf{g}} - {\mathbf{Df}}} \right\|^{2} = \left\| {\mathbf{v}} \right\|^{2}$, the following cost function must be minimized [14,15,16]:

$$\varPsi ({\mathbf{f}}) = {\mathbf{f}}^{t} \log_{2} ({\mathbf{f}}) - \lambda \left[ {\left\| {{\mathbf{g}} - {\mathbf{Df}}} \right\|^{2} - \left\| {\mathbf{v}} \right\|^{2} } \right]$$

(58)

where $\lambda$ is a Lagrangian multiplier.

Differentiating both sides of the above equation with respect to f and equating the result to zero:

$$\frac{{\partial \varPsi ({\mathbf{f}})}}{{\partial {\mathbf{f}}}} = 0 = \frac{1}{\ln (2)}\left\{ {{\mathbf{1}} + \ln ({\hat{\mathbf{f}}})} \right\} + \lambda \left[ {2{\mathbf{D}}^{t} \left( {{\mathbf{g}} - {\mathbf{D\hat{f}}}} \right)} \right]$$

(59)

Solving for the estimated HR image:

$$\ln ({\hat{\mathbf{f}}}) = - {\mathbf{1}} - \lambda \ln (2)\left[ {2{\mathbf{D}}^{t} \left( {{\mathbf{g}} - {\mathbf{D\hat{f}}}} \right)} \right]$$

(60)

Thus:

$${\hat{\mathbf{f}}} = \exp \left[ { - {\mathbf{1}} - \lambda \ln (2)\left[ {2{\mathbf{D}}^{t} \left( {{\mathbf{g}} - {\mathbf{D\hat{f}}}} \right)} \right]} \right]$$

(61)

Expanding the above equation using Taylor expansion and neglecting all but the first two terms, and since ${\mathbf{g}} - {\mathbf{D\hat{f}}}$ must be a small quantity, the following form is obtained:

$${\hat{\mathbf{f}}} \cong - \lambda \ln (2)\left[ {2{\mathbf{D}}^{t} \left( {{\mathbf{g}} - {\mathbf{D\hat{f}}}} \right)} \right]$$

(62)

Solving for ${\hat{\mathbf{f}}}$ leads to [14,15,16]:

$${\hat{\mathbf{f}}} \cong \left( {{\mathbf{D}}^{t} {\mathbf{D}} + \eta {\mathbf{I}}} \right)^{ - 1} {\mathbf{D}}^{t} {\mathbf{g}}$$

(63)

where $\eta = - 1/(2\lambda \ln (2))$.

The operation ${\mathbf{D}}^{t} {\mathbf{D}}$ stands for decimation followed by interpolation. Thus, if ${\mathbf{D}}$ decimates by a factor r, applying ${\mathbf{D}}^{t} {\mathbf{D}}$ causes all positions (1+ n₁r,1+ n₂r) for integer (n₁, n₂) to stay unchanged, whereas the remaining pixels are replaced by zeros. Thus, ${\mathbf{D}}^{t} {\mathbf{D}}$ stands for a masking operation, which is represented by a diagonal matrix. The effect of the term $\eta {\mathbf{I}}$ is to remove the ill-posedness nature of the inverse problem. The problem now is reduced to an inversion of a diagonal matrix.

Another solution is based on the regularization theory by modifying the cost function to be [14,15,16]:

$$\varPsi ({\hat{\mathbf{f}}}) = \left\| {{\mathbf{g}} - {\mathbf{D\hat{f}}}} \right\|^{2} + \lambda \left\| {{\mathbf{Q\hat{f}}}} \right\|^{2}$$

(64)

where ${\mathbf{Q}}$ is the 2-D regularization operator and $\lambda$ is the regularization parameter.

This minimization is performed by taking the derivative of the cost function yielding:

$$\frac{{\partial \varPsi ({\hat{\mathbf{f}}})}}{{\partial {\hat{\mathbf{f}}}}} = {\mathbf{0}} = 2{\mathbf{D}}^{t} ({\mathbf{g}} - {\mathbf{D\hat{f}}}) - 2\lambda {\mathbf{Q}}^{{\mathbf{t}}} {\mathbf{Q\hat{f}}}$$

(65)

Solving for ${\hat{\mathbf{f}}}$ that provides the minimum of the cost function yields [14,15,16]:

$${\hat{\mathbf{f}}} = ({\mathbf{D}}^{t} {\mathbf{D}} + \lambda {\mathbf{Q}}^{{\mathbf{t}}} {\mathbf{Q}})^{ - 1} {\mathbf{D}}^{t} {\mathbf{g}}$$

(66)

The regularization term in Eq. (66) allows matrix inversion even in the presence of singularities. This equation can be implemented on a block-by-block basis using overlapping blocks. The operator Q can be represented with the Laplacian illustrated in Fig. 12.

Fig. 12

The 2-D Laplacian operator

7 Deep Learning Classification

The deep learning classification is the last task in the proposed automated diagnosis system for tumor detection. Deep learning is a type for machine learning in which a model learns to perform classification tasks directly from images. Features are learnt automatically from the obtained HR fusion results by a convolutional neural network (CNN) and presented to a classifier. The CNN is a neural network for image recognition. It includes the feature extractor in the training process [20,21,22,23]. It consists of convolutional layers followed by activation functions, pooling layers, dropout layers and fully-connected layers. The inclusion of a dropout layer adds a regularization technique for reducing over fitting [20,21,22,23].

7.1 Convolutional Layer (CNV)

The convolutional layer contains filters that are used to perform a two-dimensional (2D) convolution on the input image. The resulting features of the convolutional layer vary depending on which convolution filter is used. This concept is very well suited to the HR fusion results as it is able to capture any slight change in the image local activity levels. Figure 13 shows a block diagram of the convolutional layer.

Fig. 13

Convolutional layer

7.2 Pooling Layer (PL)

The pooling layer is another type of feature extraction neural networks. The pooling layer decreases the size of the obtained HR image. It combines neighboring pixels of a certain area of the HR image into a single representative value. The used value is the maximum or mean value of the pixels. The max-pooling layer is used in the proposed technique. Figure 14 shows an example of the maximum pooling layer.

Fig. 14

Maximum pooling layer

7.3 Rectified Linear Unit (ReLU)

It allows faster and more effective training by mapping negative values to zero and maintaining positive values. The ReLU layer applies a linear activation function to the neuron output as shown in Eq. (67).

$$f\left( x \right) = \mathop {\hbox{max} }\limits_{{}} \left( {0,x} \right).$$

(67)

7.4 Fully-Connected (FC) Layer

This layer reduces the size of input data to the size of classes that the CNN is trained for by combining the outputs of the CNV layer with different weights. Each neuron at the output of the CNV layer will be connected to all other neurons after being weighted properly. Similar to the CNV layer, weights of the taps in the FC layer are found though the backpropagation algorithm.

7.5 Classification Layer

This is the final layer of the CNN that converts the output of the FC layer to a probability of each object being in a certain class. Typically, soft-max type of algorithms is used in this layer to provide the classification output as shown in Eq. (68).

$$P\left( {y = j|\bf x} \right) = \frac{{e^{{\bf x^{\it t} w_{\it j} }} }}{{\mathop \sum \nolimits_{k = 1}^{K} e^{{\bf x^{\it t} w_{\it k} }} }}$$

(68)

The proposed model consists of 3 CNV layers followed by 3 max pooling layers. Finally, a global average pooling is used. Figure 16 shows an exemplary architecture of the convolutional neural network. Images are input with size 224 × 224. Layers have numbers of filters of 16, 32 and 64 for layers 1, 2 and 3, respectively. Finally, a dense layer with size of 2 is used for the classification decision as shown in Figs. 15 and 16.

Fig. 15

Block diagram of the proposed classification approach

Fig. 16

Layers of the proposed deep learning classification model

8 Performance Metrics

In this proposed approach, accuracy is used to estimate the strength of the CNN model. Accuracy is calculated as follows:

$${\text{Accuracy}} = \frac{{{\text{No}} .\;{\text{of}}\;{\text{predicted}}\;{\text{images}}\;{\text{with}}\;{\text{tumors}}}}{{{\text{Total}}\;{\text{No}} .\;{\text{of}}\;{\text{HR}}\;{\text{images}}}} \times 100.$$

(69)

9 Simulation Results

Simulation experiments are performed on a dataset of MR and CT images using python 3.5 [24], Tensorflow [25] and Keras [26]. This simulation is carried out on about 370 images. These images are the results of image fusion and interpolation techniques. Figure 17 shows the CT and MR images on which the image fusion and interpolation techniques are performed. Figures 18, 19, 20 and 21 show the images after fusion and interpolation processes for both normal and tumor states.

Fig. 17

CT and MR images of normal and tumor states

Fig. 18

Images after applying wavelet transform for image fusion with interpolation techniques (normal images)

Fig. 19

Images after applying curvelet transform for image fusion with interpolation techniques (normal images)

Fig. 20

Images after applying wavelet transform for image fusion with interpolation techniques (images with tumor)

Fig. 21

Images after applying curvelet transform for image fusion with interpolation techniques (images with tumor)

Figures 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32 and 33 show observations of accuracy and loss along the training epochs. Ten epochs and a batch size of ten have been set to train the deep learning model. Table 1 shows the deep learning model accuracy of all scenarios. These results show that image fusion based on wavelet transform combined with spline interpolation has the optimum accuracy of 90.9%. Table 1 gives a summary of accuracy levels in all scenarios.

Fig. 22

Accuracy of Scenario #1

Fig. 23

Loss of Scenario #1

Fig. 24

Accuracy of Scenario #2

Fig. 25

Loss of Scenario #2

Fig. 26

Accuracy of Scenario #3

Fig. 27

Loss of Scenario #3

Fig. 28

Accuracy of Scenario #4

Fig. 29

Loss of Scenario #4

Fig. 30

Accuracy of Scenario #5

Fig. 31

Loss of Scenario #5

Fig. 32

Accuracy of Scenario #6

Fig. 33

Loss of Scenario #6

Table 1 Summary of accuracy levels of all scenarios

The scenarios considered are:

• Scenario #1: Wavelet fusion with cubic spline interpolation.

• Scenario #2: Wavelet fusion with maximum entropy interpolation.

• Scenario #3: Wavelet fusion with LMMSE interpolation.

• Scenario #4: Curvelet fusion with cubic spline interpolation.

• Scenario #5: Curvelet fusion with maximum entropy interpolation.

• Scenario #6: Curvelet fusion with LMMSE interpolation.

10 Conclusion

Automated medical image diagnosis is the main objective of medical imaging that has not yet been achieved. This objective is considered in this paper with a framework comprising multi-modality image fusion, image interpolation, and deep learning classification. The issue of multi-modality image fusion has been considered with two different fusion algorithms: wavelet fusion and curvelet fusion. Different interpolation schemes have also presented and studied. Finally, the new trend of deep learning have been implemented for tumor detection. Accuracy levels of detection and automated classification up to 90% have been obtained. These results are promising in the field of automated medical diagnosis and can open the door towards more accurate classification results and efficient utilization of automated diagnosis in other medical applications.