On the Ergodic Capacity of Distributed MIMO Antenna Systems

Abstract

We consider distributed multiple-input–multiple-output (MIMO) antenna systems, along with their certain generalizations. We show that distributed MIMO configuration can be mapped to a semicorrelated (one side correlated) Wishart model. For a given set of large-scale fading parameters, associated with the path loss and shadow fading, we derive exact and closed-form results for the marginal density of eigenvalues of $\mathbf{H}^\dag \mathbf{H}$ (or $\mathbf{H} \mathbf{H} ^\dag$), where $\mathbf{H}$ is the channel matrix. We also obtain exact and closed-form expressions for the ergodic channel capacity with the aid of Meijer G-function. The ergodic capacity of semicorrelated Rayleigh fading channel follows as a special case. All analytical results are validated by comparison with Monte-Carlo simulations.

1 Introduction

Achieving high capacity telecommunication is always desirable in cellular systems. However, various unavoidable effects associated with fading, path-loss and interference makes it extremely difficult to achieve such a goal. Multiple-input multiple-output (MIMO) antenna systems have been found to offer huge advantage over single-antenna systems, both with regard to capacity and error performance [1, 2]. Moreover, in recent years the idea of deployment of spatially distributed multiple antennas, instead of being centrally located, has caught much attention. Such distributed antenna systems (DAS), in general, lead to increased spectral efficiency and expanded coverage, and therefore has emerged as a promising technique towards satisfying growing demands for future wireless communication networks [3].

The concept of distributed antennas goes back to Salah et al. [4] who implemented this scheme to cover the dead spots in indoor wireless systems. Clark et al. [5], in their study of antenna array processing, showed that distributed arrays promise significant power and capacity gains over conventional centralized arrays. Roh and Paulraj [6] extended this idea and introduced the concept of a generalized distributed antenna system. They demonstrated that the distributed systems with multiple antennas per port yield more capacity than multiple co-located antennas, especially in the outage region [6, 7]. Several notable works [8–26] have examined various aspects of the distributed antenna systems and have concluded their superiority over the traditional centralized antenna systems.

Ergodic channel capacity serves as an important metric in characterizing the system performance in communication networks [2]. It provides information about the theoretical transmission limit, and therefore acts as a crucial guiding factor in the design of a given communication system. Channel capacity of DAS has been investigated by several authors by considering various scenarios [8–20]. The available analytical results are usually for some approximation, for some particular cases or in the asymptotic limit of large number of antennas. Therefore, a complete analytical understanding is still lacking.

In the present work we demonstrate that, remarkably, the MIMO DAS model can be mapped to a semicorrelated Wishart scenario for which several results are already available concerning the eigenvalue statistics [27–33]. The term semicorrelated refers to the case when correlations are present at only one of the ends of the communication channel, and thus the matrix elements of the channel matrix are correlated either row-wise or columnwise [34, 35]. Hence, often is it also referred to as one side correlated Wishart model. We use this connection with the semicorrelated Wishart model to tackle the MIMO DAS problem. We consider the distributed antenna system with a given set of large-scale fading parameters which take care of the path loss and shadow fading [12–16]. Such an assumption can be justified by the observation that typically the large-scale fading varies very slowly compared to the short-scale fading and therefore may be estimated. We derive exact and closed-form result for the marginal density of the eigenvalues of $\mathbf{H} ^\dag \mathbf{H}$ (or $\mathbf{HH} ^\dag$), where H is the full channel matrix. We also obtain exact and closed-form expression for the ergodic channel capacity with the aid of Meijer G-function. The result for the ergodic channel capacity of semicorrelated Rayleigh fading MIMO channel follows as a special case. We also consider certain generalizations of the MIMO DAS model and provide the corresponding marginal eigenvalue density as well as the channel capacity expressions.

The presentation scheme in this paper is as follows. In Sect. 2 we describe the channel model for DAS. In Sect. 3 we present exact result for the marginal density of eigenvalues of $\mathbf{H} ^\dag \mathbf{H}$ (or $\mathbf{H }\mathbf{H}^\dag$). We also give exact result for the the ergodic channel capacity. Section 4 deals with some of the possible generalizations of the setup. Finally, we conclude with a brief summary and general discussion in Sect. 5. The proofs have been outlined in the appendices.

2 Channel Model

We consider the distributed antenna system consisting of N ports at one end of the communication, with L antennas per port. While, on the other end (e.g., mobile) there are M antennas. We will refer to this scenario as the (M, N, L) DAS; see Fig. 1. The standard uncorrelated Rayleigh fading setup corresponds to (M, 1, L). The channel model for (M, N, L) DAS can be written as [7]

$$\mathbf{y} =\mathbf{H} \,\mathbf{x} +\mathbf{n} .$$

(1)

For uplink, x is the M-dimensional transmit signal vector, while y is the NL-dimensional received signal. Also, n is a complex Gaussian noise vector with zero mean and unit variance for each of its elements. We should remark at this point that in a very recent work [36] the uplink ergodic sum-rate capacity of a multi-user MIMO system has been analyzed and a tight lower bound has been obtained. Therein the authors consider a centralized and correlated multiple-antenna deployment scheme in a base station platform and several users, each equipped with single antenna devices. This problem can be related to the model considered here with a downlink scenario, and hence exact results can be obtained.

The full $NL\times M$ dimensional channel H matrix, in terms of the subchannel matrices, is

$$\begin{aligned} \mathbf{H} =\left[ \begin{array}{c} \mathbf{H} _1 \\ \vdots \\ \mathbf{H} _N \end{array}\right] . \end{aligned}$$

(2)

Here the subchannel matrix H _k is an $L\times M$ channel matrix from the mobile to the kth port. The matrix elements of H _k are taken as,

$$\begin{aligned} (\mathbf{H} _k)_{a,b}=\sqrt{v_k}\,h_{a,b};\quad a=1,2,\ldots ,L; \quad b=1,\ldots ,M. \end{aligned}$$

(3)

Here $h_{a,b}$ are independent and identically distributed (i.i.d.) complex Gaussians with mean zero and variance 1/2 for both real and imaginary parts. These represent the small-scale fast fading of the channel. Clearly, with such a choice the envelope of $h_{a,b}$ is Rayleigh distributed, viz.,

$$\begin{aligned} p_{|h|}(|h|)=2|h|\exp (-|h|^2). \end{aligned}$$

(4)

The parameters $v_k$ take care of the large-scale fading (including path loss and shadow fading) of the channel at different ports and are usually modeled as

$$\begin{aligned} v_k=\left( d_k\right) ^{-\gamma } s_k. \end{aligned}$$

(5)

Here $d_k$ represents the distance (normalized) between the mobile and the kth port, $\gamma$ is the path loss exponent, and the $s_k$ are i.i.d. random variables with lognormal probability distribution,

$$\begin{aligned} p_s(s)=\frac{1}{\sqrt{2\pi }\alpha \sigma s}\exp \left( -\frac{(\ln s)^2}{2\alpha ^2\sigma ^2}\right) ,\quad s>0, \end{aligned}$$

(6)

$\sigma$ being the shadowing standard deviation and $\alpha =(\ln 10)/10$. From the above discussion it is clear that a given subchannel matrix $\mathbf{H} _k$ follows the distribution

$$\begin{aligned} \mathcal{P}_k(\mathbf{H} _k)=(\pi v_k)^{-M L} \,\exp [-{\text{tr}}(v_k^{-1}\mathbf{H} _k^\dag \mathbf{H} _k)], \end{aligned}$$

(7)

where ‘tr’ represents the trace. We note that individually $\mathbf{H} _k$ carry i.i.d. complex Gaussians with mean zero and variance $v_k/2$ for both real and imaginary parts. However, the different subchannel matrices are independent but not identical because of the unequal parameters $v_k$. In what follows, we carry out the analysis for a fixed set of large-scale fading parameters $v_k$ [12–16].

Fig. 1

The (M, N, L) distributed antenna system. It consists of N ports on the one end, each consisting of L antennas. On the other end (e.g. a mobile) there are M antennas

As we will see below, the ergodic channel capacity can be obtained using the eigenvalue statistics of the Wishart matrices $\mathbf{H} ^\dag \mathbf{H}$ or $\mathbf{HH} ^\dag$ [2]. Let us define, for convenience,

$$\begin{aligned} \nu ={\text{min}}(M,NL). \end{aligned}$$

(8)

The matrices $\mathbf{H} ^\dag \mathbf{H}$ and $\mathbf{HH} ^\dag$ share the same nonzero $\nu$-eigenvalues ($\lambda _1,\ldots ,\lambda _\nu$), which are the square of the singular values (nonzero) of the channel matrix H. With the assumption of absence of channel state information at the transmitter¹ and equal power allocation scheme, the ergodic channel capacity is given by [1, 2]

$$\begin{aligned} C&=\mathbb{E}\left[ \log _2 \det \left( \mathbbm{1}_{M}+\frac{\rho }{M}\mathbf{H} ^\dag \mathbf{H} \right) \right] =\mathbb{E}\left[ \log _2 \det \left( \mathbbm{1}_{NL}+\frac{\rho }{M}\mathbf{HH} ^\dag \right) \right] \nonumber \\&=\mathbb{E}\left[{\text{tr}}\log _2 \left( \mathbbm{1}_{M}+\frac{\rho }{M}\mathbf{H} ^\dag \mathbf{H} \right) \right] =\mathbb{E}\left[{\text{tr}}\log _2 \left( \mathbbm{1}_{NL}+\frac{\rho }{M} \mathbf{HH} ^\dag \right) \right] , \end{aligned}$$

(9)

where ‘det’ represents the determinant and ‘tr’, as mentioned earlier, stands for the trace. Moreover, $\rho$ is the signal to noise ratio (SNR), and in view of unit variance for the Gaussian-noise vector elements, equals the total transmit-power magnitude. $\mathbb {E}[\cdot ]$ represents the averaging with respect to the ensemble of H matrices.

We should note that in the first line of (9), since determinant is invariant under unitary conjugation, we obtain $\log _2 \det \left( \mathbbm{1}_{M}+\frac{\rho }{M}\mathbf{H} ^\dag \mathbf{H} \right) =\log _2 \det \left[ \mathbf{U} ^\dag \left( \mathbbm{1}_{M}+\frac{\rho }{M}\mathbf{H} ^\dag \mathbf{H} \right) \mathbf{U} \right] =\log _2 \det \left( \mathbbm{1}_{M}+\frac{\rho }{M}\varvec{\Lambda }\right)$. We have used here U to denote the unitary matrix which diagonalizes $\mathbf{H} ^\dag \mathbf{H}$ and hence $\mathbbm{1}_{NL}+\frac{\rho }{M} \mathbf{H} ^\dag \mathbf{H}$ as well. Also, ${\varvec{\Lambda }}$ is the diagonal matrix containing nonzero eigenvalues $\lambda 's$ of the matrix $\mathbf{H} ^\dag \mathbf{H}$, and may be additional zeros (if $M>NL$). In a similar manner, the second line in (9) follows because ${\text{tr}}\log _2 \left( \mathbbm{1}_{M}+\frac{\rho }{M} \mathbf{HH} ^\dag \right) ={\text{tr}}\left[ \mathbf{U} ^\dag \log _2 \left( \mathbbm{1}_{M}+\frac{\rho }{M}{\varvec{\Lambda }} \right) \mathbf{U} \right] = {\text{tr}}\left[ \log _2 \left( \mathbbm{1}_{M}+\frac{\rho }{M} {\varvec{\Lambda }} \right) \right]$. Here, to go from the first expression to the second we used the standard procedure of implementing eigenvalue decomposition to calculate function of a matrix. In the next step we used the cyclic invariance of trace, and $\mathbf{U }\mathbf{U }^\dag =\mathbbm{1}_M$. Therefore, in both cases the expressions can be reduced in terms of eigenvalues as $\log _2\left[ \prod _{j=1}^\nu (1+\frac{\rho }{M}\lambda _j)\right] =\sum _{j=1}^\nu \log _2(1+\frac{\rho }{M}\lambda _j)$. Similar arguments apply when we consider $\mathbf{HH} ^\dag$ instead of $\mathbf{H} ^\dag \mathbf{H}$.

As discussed above, because of the unitarily-invariant nature of the expression within E in (9), the ergodic capacity can be expressed in terms the nonzero-eigenvalue of ${\mathbf{H}} ^\dag {\mathbf{H}}$ or ${\mathbf{H}} {\mathbf{H}} ^\dag$, viz.,

$$\begin{aligned} C=\int _0^\infty d\lambda _1\cdots \int _0^\infty d\lambda _{\nu }\, P_\varLambda (\lambda _1,\ldots ,\lambda _{\nu })\sum _{j=1}^{\nu }\log _2 \left( 1+\frac{\rho }{M}\lambda _j \right) , \end{aligned}$$

(10)

where $P_\varLambda (\lambda _1,\ldots ,\lambda _{\nu })$ is the joint probability density of eigenvalues. In view of the symmetry of the eigenvalues in the unordered joint density, this expression can be determined using the marginal density

$$\begin{aligned} p_\lambda (\lambda )=\int _0^\infty d\lambda _2\cdots \int _0^\infty d\lambda _{\nu } P_\varLambda (\lambda ,\lambda _2,\ldots ,\lambda _\nu ), \end{aligned}$$

(11)

which is normalized to unity:

$$\begin{aligned} \int _0^\infty d\lambda \, p_\lambda (\lambda )=1. \end{aligned}$$

(12)

We obtain

$$\begin{aligned} C=\nu \int _0^\infty d\lambda \, p_\lambda (\lambda )\, \log _2 \left( 1+\frac{\rho }{M}\lambda \right) . \end{aligned}$$

(13)

Therefore, to obtain the ergodic capacity we need the explicit expression for the marginal density of nonzero eigenvalues of the matrix ${\mathbf{H}} ^\dag {\mathbf{H}}$ or ${\mathbf{H}} {\mathbf{H}} ^\dag$.

3 Marginal Density and Ergodic Capacity for (M, N, L) DAS: Exact Results

In this section we present exact result for the marginal density of the nonzero eigenvalues of the matrix ${\mathbf{H}} ^\dag {\mathbf{H}}$ or ${\mathbf{H}} {\mathbf{H}} ^\dag$. We also give the exact closed-form expression for the ergodic channel capacity. Proofs are outlined in the appendices.

In view of (7), we can write down the density of matrices H as

$$\begin{aligned} P_{\mathbf{H}} ({\mathbf{H}} )=\pi ^{-MNL} \det \!\,^{-ML}{\mathbf{V}} \,\exp [-{\text{tr}}({\mathbf{H}} ^\dag {\mathbf{V}} ^{-1} {\mathbf{H}} )], \end{aligned}$$

(14)

where ${\mathbf{V}} ={\text{diag}}[v_1,\ldots ,v_N]\otimes \mathbbm{1}_L$. Therefore, we are looking essentially at a semicorrelated Wishart case, with the diagonal-covariance matrix having some equal-value entries (degeneracy/multiplicity). This correspondence of DAS with a semicorrelated Wishart case leads to exact solution of the former because of available exact results for the latter.

It should be noted that among other things the distribution of the matrices ${\mathbf{H}} ^\dag {\mathbf{H}}$ or ${\mathbf{H}} {\mathbf{H}} ^\dag$ where H as in (14), has been studied in, for example, [37–44] for real case, complex case, or both. Out interest here is in the complex case. Depending on the rank of these matrices, one obtains either the regular- or the singular-Wishart distribution.

The marginal density for (M, N, L) DAS is obtained as

$$\begin{aligned} p_\lambda (\lambda )=c\det \,\left[ \begin{array}{cccc} 0 &{} \left[ f_{k_1}(v_1,\lambda )\right] _{k_1=1,\ldots ,L} &{} \cdots &{} \left[ f_{k_N}(v_N,\lambda )\right] _{k_N=1,\ldots ,L}\\ \left[ g_j(\lambda )\right] _{j=1,\ldots ,NL}&{} \mathop {{\left[ h_{j_1,k_1}(v_1)\right] }_{{j_1=1,\ldots ,NL}}}\limits _{{\qquad \qquad k_1=1,\ldots ,L}} &{} \cdots &{} \mathop {{\left[ h_{j_N,k_N}(v_N)\right] }_{{j_N=1,\ldots ,NL}}}\limits _{{\qquad \qquad \, k_N=1,\ldots ,L}} \end{array}\right] . \end{aligned}$$

(15)

The entries within the determinant in the above equation are given by

$$\begin{aligned}&f_k(v,\lambda )=\varGamma (k)\,v^{k-M-1}\,\exp (-\lambda /v)\,\mathcal{L}_{k-1}^{(M-k+1)}(\lambda /v), \end{aligned}$$

(16)

$$\begin{aligned}&g_j(\lambda )=\lambda ^{M-j}/\varGamma (M-j+1), \end{aligned}$$

(17)

$$\begin{aligned}&h_{j,k}(v)=\frac{\varGamma (j)}{\varGamma (j-k+1)}\,v^{k-j}. \end{aligned}$$

(18)

The notation $\mathcal{L}_n^{(m)}(x)$ in the expression for $f_k(v,\lambda )$ represents the associated Laguerre polynomials.² The normalization c in (15) is given by

$$\begin{aligned} c^{-1}=-\nu \det \left[ \mathop {{\left[ h_{j_1,k_1}(v_1)\right] }_{{j_1=1, \ldots ,NL}}}\limits _{{\qquad \qquad k_1=1,\ldots ,L}}\quad \cdots \quad \mathop {{\left[ h_{j_N,k_N}(v_N)\right] }_{{j_N=1, \ldots ,NL}}}\limits _{{\qquad \qquad k_N=1,\ldots ,L}}\right] . \end{aligned}$$

(19)

In Fig. 2 we show the comparison between the analytical predictions and numerical simulation for the marginal density of eigenvalues. The parameters used are indicated in the caption. The Monte-Carlo simulation nicely corroborate the analytical result.

Fig. 2

Marginal density of eigenvalues: Comparison between analytical (solid line) and simulation (histogram) results for a (2, 3, 2) DAS with $(v_1,v_2,v_3)=(3/2,2/3,1/5)$, and b (4, 5, 3) DAS with $(v_1,v_2,v_3,v_4,v_5)=(7/10,2/5,1/11,2,6/5)$

The ergodic channel capacity can be expressed in a closed form with the aid of Meijer G-function. We have

$$\begin{aligned} C=-\nu \, c\, \sum _{\mu =1}^{\nu }\det \left[ \begin{array}{ccc} \mathop {{[\psi _{j_1,k_1}^{(\mu )}(v_1)]}_{{j_1=1, \ldots ,N L}}}\limits _{{\qquad \qquad k_1=1,\ldots ,L}}&\cdots&\mathop {{[\psi _{j_N,k_N}^{(\mu )}(v_N)]}_{{j_N=1, \ldots ,N L}}}\limits _{{\qquad \qquad k_N=1,\ldots ,L}} \end{array}\right] . \end{aligned}$$

(20)

Here

$$\begin{aligned} \psi _{j,k}^{(\mu )}(v)= {\left\{ \begin{array}{ll} \mathcal{G}_{j,k}(v), &{} j=\mu , \\ h_{j,k}(v), &{} j\ne \mu , \end{array}\right. } \end{aligned}$$

(21)

with

$$\begin{aligned} \mathcal{G}_{j,k}(v)=\dfrac{v^{k-1}}{(\ln 2)\,\varGamma (M-j+1)}\left( \dfrac{\rho }{M}\right) ^{j-1} G^{3,2}_{3,4} \left( \begin{array}{c} 0,\, j-1,\, j \\ j-1,\, j-1,\, M,\, k-1 \end{array}\Bigg |\, \dfrac{M}{\rho \,v } \right) , \end{aligned}$$

(22)

and $h_{j,k}(v)$ as in (18). The results for the uncorrelated Rayleigh fading follow trivially by setting $N=1$.

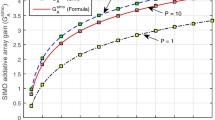
Figure 3 shows the comparison of ergodic channel capacity for various cases, as indicated in the labels and the caption. In all cases, an excellent agreement is found between the analytical prediction and the numerical simulation outcome.

Fig. 3

Ergodic capacity for various (M, N, L) DAS, as indicated beside the curves. Parameter values are $(v_1,v_2)=(3/2,2/3)$ for (2, 2, 3) DAS; $(v_1,v_2,v_3,v_4)=(3/2,2/3,7/10,2)$ for (2, 4, 3) DAS; $(v_1,v_2)=(3/2,2/3)$ for (4, 2, 4) DAS; and $(v_1,v_2,v_3,v_4,v_5)=(3/2,2/3,7/10,2,1/11)$ for (4, 5, 3) DAS

4 Generalizations

In this section we consider certain generalizations of the case dealt in the preceding section. We, again, present the explicit results for the marginal density and the ergodic capacity, and defer the proofs to the appendices.

4.1 Different Antenna Numbers at Different Ports

One can relax the condition of equal number of antennas, L, at different ports and allow $L_k$ antennas at the kth port; $k=1,\ldots ,N$. This results in something like $(M,N,\{L_1,\ldots ,L_N\})$ DAS. Therefore, the subchannel matrix ${\mathbf{H}} _k$ becomes $L_k\times M$ dimensional. Moreover, the covariance matrix is now ${\mathbf{V}} ={\text{diag}}[v_1\mathbbm{1}_{L_1},\ldots ,v_N \mathbbm{1}_{L_N}]$, and the parameter $\nu$ has to be modified to

$$\begin{aligned} \nu ={\text{min}}(M,\mathsf{L});\quad \mathsf{L}=L_1+\cdots +L_N. \end{aligned}$$

(23)

The marginal density in the above setting is given by

$$\begin{aligned} p_\lambda (\lambda )=c\det \,\left[ \begin{array}{cccc} 0 &{} \left[ f_{k_1}(v_1,\lambda )\right] _{k_1=1,\ldots ,L_1} &{} \cdots &{} \left[ f_{k_N}(v_N,\lambda )\right] _{k_N=1,\ldots ,L_N}\\ \left[ g_j(\lambda )\right] _{j=1,\ldots ,\mathsf{L}}&{} \mathop {{\left[ h_{j_1,k_1}(v_1)\right] }_{{j_1=1, \ldots ,\mathsf{L}}}}\limits _{{\qquad \qquad k_1=1,\ldots ,L_1}} &{} \cdots &{} \mathop {{\left[ h_{j_N,k_N}(v_N) \right] }_{{j_N=1,\ldots ,\mathsf{L}}}}\limits _{{\qquad \qquad k_N=1,\ldots ,L_N}} \end{array}\right] \end{aligned}$$

(24)

The entries $f_k(v,\lambda ), g_j(\lambda ), h_{j,k}(v)$ inside the determinant in the above expression are still given by (16), (17) and (18), respectively. The normalization c in (24) is given by

$$\begin{aligned} c^{-1}=-\nu \det \left[ \mathop {{\left[ h_{j_1,k_1}(v_1)\right] }_{{j_1=1,\ldots ,\mathsf{L}}}}\limits _{{\qquad \qquad k_1=1,\ldots ,L_1}}\quad \cdots \quad \mathop {{\left[ h_{j_N,k_N}(v_N)\right] }_{{j_N=1,\ldots ,\mathsf{L}}}}\limits _{{\qquad \qquad k_N=1,\ldots ,L_N}}\right] . \end{aligned}$$

(25)

The ergodic channel capacity turns out to be

$$\begin{aligned} C=-\nu \, c\, \sum _{\mu =1}^{\nu }\det \left[ \begin{array}{ccc} \mathop {{[\psi _{j_1,k_1}^{(\mu )}(v_1)]}_{{j_1=1,\ldots ,\mathsf{L}}}}\limits _{{\qquad \qquad k_1=1,\ldots ,L_1}}&\cdots&\mathop {{[\psi _{j_N,k_N}^{(\mu )}(v_N)]}_{{j_N=1,\ldots ,\mathsf{L}}}}\limits _{{\qquad \qquad k_N=1,\ldots ,L_N}} \end{array}\right] , \end{aligned}$$

(26)

where $\psi _{j,k}^{(\mu )}(v)$ is same as in (21). Equations (15) and (20) follow from these more general expressions when the $L_k$’s are equal.

In Fig. 4 we show the marginal density obtained using the analytical expression as well as using Monte-Carlo simulation. The parameters used are mentioned in the caption. Figure 5 shows the comparison of ergodic channel capacity for several parameter values, as indicated in the labels and the caption. We find excellent agreement in all cases.

Fig. 4

Analytical (solid line) and simulation (histogram) results for $(2,4,\{2,4,1,3\})$ DAS marginal density. Parameter values are $(v_1,v_2,v_3,v_4)=(1,3/4,2,3/2)$

Fig. 5

Ergodic channel capacity. Parameter values are $(v_1,v_2)=(1/4,5/4)$ for $(2,2,\{2,3\})$ DAS; $(v_1,v_2,v_3)=(5/3,1/2,2)$ for $(2,3,\{2,3,4\})$ DAS; $(v_1,v_2,v_3)=(9/7,3/4,4/3)$ for $(4,3,\{3,4,1\})$ DAS; and $(v_1,v_2,v_3,v_4)=(7/5,3/2,7/10,3)$ for $(4,4,\{4,2,3,2\})$ DAS

4.2 Unequal Large-Scale Fading Parameters

For the sake of completeness, and also because all above cases follow from this one, we consider the situation when all the large-scale fading parameters $v_k$ are different. Such a scenario can arise when the antennas connected to each port are themselves spatially distributed to constitute a cell, and then all such cells are utilized simultaneously for communication [11, 14, 21]. In this case ${\mathbf{V}} ={\text{diag}}[v_{1,1},\ldots ,v_{1,L_1};\ldots ;v_{N,1}, \ldots ,v_{N,L_N}]\equiv {\text{diag}}[\hat{v}_1,\hat{v}_2,\ldots , \hat{v}_{L_1+\cdots +L_N}]$, while parameter $\nu$ is still given by (23). It is obvious that this case actually maps to a semicorrelated Rayleigh fading with different correlations at the receiver end.

As discussed in Appendix 6, the marginal density in this case is given as

$$\begin{aligned} p_\lambda (\lambda )=c \det \left[ \begin{array}{ccc} 0 &{} \left[ f_k(\hat{v},\lambda )\right] _{k=1,\ldots ,\mathsf{L}} \\ \left[ g_j(\lambda )\right] _{j=1,\ldots ,\mathsf{L}} &{} \left[ h_{j,k}(\hat{v})\right] _{j,k=1,\ldots ,\mathsf{L}} \end{array}\right] ; \end{aligned}$$

(27)

where now

$$\begin{aligned}&f_k(\hat{v},\lambda )=\hat{v}_k^{-M} \exp (-\lambda /\hat{v}_k), \end{aligned}$$

(28)

$$\begin{aligned}&h_{j,k}(\hat{v})=\hat{v}_k^{-j+1}, \end{aligned}$$

(29)

and $g_j(\lambda )$ continues to be same as that in (17). The normalization is determined using

$$\begin{aligned} c^{-1}=-\nu \det [h_{j,k}(\hat{v})]_{j,k=1,\ldots ,{\mathsf{L}}}. \end{aligned}$$

(30)

The ergodic channel capacity is given by

$$\begin{aligned} C=-\nu \, c\, \sum _{\mu =1}^{\nu }\det \left[ \psi _{j,k}^{(\mu )}(\hat{v})\right] _{j,k=1,\ldots ,\mathsf{L}}. \end{aligned}$$

(31)

Here

$$\begin{aligned} \psi _{j,k}^{(\mu )}(\hat{v})= {\left\{ \begin{array}{ll} \mathcal{G}_{j,k}(\hat{v}), &{} j=\mu \\ h_{j,k}(\hat{v}), &{} j\ne \mu . \end{array}\right. } \end{aligned}$$

(32)

with

$$\begin{aligned} \mathcal{G}_{j,k}(\hat{v})=\dfrac{1}{(\ln 2)\,\varGamma (M-j+1)}\left( \dfrac{\rho }{M}\right) ^{j-1}\, G^{3,1}_{2,3} \left( \begin{array}{c} j-1,\, j \\ j-1,\, j-1,\, M \end{array}\Bigg |\, \dfrac{M}{\rho \,\hat{v}_k} \right) . \end{aligned}$$

(33)

We note that $\mathcal{G}_{j,k}(\hat{v})$ has a simple representation in terms of exponential integral (Ei) as well:

$$\begin{aligned} \mathcal{G}_{j,k}(\hat{v})=\frac{e^{M/(\rho \,\hat{v}_k)}}{(\ln 2)\,\hat{v}_k^{j-1}}\sum _{i=1}^{M-j+1}{\text{Ei}}\left( \dfrac{M}{\rho \,\hat{v}_k}\right) . \end{aligned}$$

(34)

The expressions in preceding sections follow from (27) and (31) by considering appropriate limits; see Appendix 7. Furthermore, it should be noted that using $L=1$ with arbitrary N in (15) and (20) produces the same results as in this section.

We validate the analytical result for the marginal density using Monte-Carlo simulation in Fig. 6. The parameters values used are indicated in the caption. Similarly, Fig. 7 shows the comparison of ergodic channel capacity in several cases, as specified in the labels and the caption.

Fig. 6

Analytical (solid line) and simulation (histogram) results for $(3,2,\{3,2\})$ DAS marginal density. Parameter values are$(v_{1,1},v_{1,2},v_{1,3};v_{2,1},v_{2,2})=(4/3,5/6,5/2;4/7,2/3)$

Fig. 7

Ergodic channel capacity. Parameter values are $(v_{1,1};v_{2,1},v_{2,2})=(4/5;3/4,1/2)$ for $(2,2,\{1,2\})$ DAS; $(v_{1,1},v_{1,2};v_{2,1},v_{2,2},v_{2,3},v_{2,4})=(1/4,3/4;1/3,2/3,4/3,2)$ for $(2,2,\{2,4\})$ DAS; $(v_{1,1},v_{1,2};v_{2,1},v_{2,2},v_{2,3};v_{3,1},v_{3,2})=(1/9,2/5;2/3,4/9,3/7;1/4,7/5)$ for $(3,3,\{2,3,2\})$ DAS; and $(v_{1,1},v_{1,2};v_{2,1};v_{3,1};v_{41},v_{4,2})=(4/7,5/3;1;2;1/2,9/4)$ for $(4,4,\{2,1,1,2\})$ DAS

5 Summary and Conclusion

We demonstrated that the MIMO DAS configuration is mathematically equivalent to a semicorrelated Wishart model with a diagonal covariance (scale) matrix with multiplicities in its entries. With this information at our disposal we considered the distributed MIMO antenna system with a given set of large-scale fading parameters. We provided exact result for the marginal density of eigenvalues of ${\mathbf{H}} ^\dag {\mathbf{H}}$ (or ${\mathbf{H}} {\mathbf{H}} ^\dag$), where H is the channel matrix. These were further used to obtain exact and closed form result for the ergodic channel capacity with the aid of Meijer G-function. The expressions possess a determinantal structure and can be readily implemented in computation software packages such as Mathematica [45], that incorporates Meijer-G as an inbuilt function with option for high precision evaluation.

It is highly desirable to relax the fixed-valued conditions for the large-scale fading parameters and to be able to perform the averaging over them using the corresponding probability distributions, see for example (5) and (6). Interestingly, the individual large-scale fading parameters appear in distinct columns of the determinants in the final results. Unfortunately, in addition, the expressions involve ratios of two such determinants, thereby making the desired averaging nontrivial. It, therefore, remains an outstanding problem to derive exact expressions for the general scenario when both the short-scale and the large-scale fadings are stochastic in nature.

Finally we would like to remark that the problem involving the weighted sum of Wishart matrices, with covariance matrices as identity matrix, can also be mapped to a semicorrelated Wishart model [46]. Weighted sum of Wishart matrices appears in the calculation of sum rate capacity in MIMO multiuser communication. Therefore we find a remarkable mathematical relationship between the MIMO DAS-, sum of Wishart-, and semicorrelated Wishart-models.

Appendices

Proofs for Eqs. (27) and (31)

As pointed out in Sect. 5, the MIMO DAS model and weighted sum of Wishart matrices, both can be mapped to a semicorrelated Wishart scenario. The eigenvalue statistics for weighted sum of Wishart matrices has already been worked out in [46]. As a consequence the proofs in the present case run parallel to those in [46]. However, for the sake of completeness, we reproduce the derivations here as well.

Exact result for the marginal density of eigenvalues for semicorrelated Wishart matrices is available from the notable works of several authors [27–33]. We employ here the determinantal expression obtained in [32, 33].

Consider $n\times m$ dimensional complex matrices W taken from the distribution

$$\begin{aligned} P_\mathbf{W }({\mathbf{W}} )=\pi ^{-mn} \det \!\,^{-m}\hat{\mathbf{V }}\,\exp [-{\text{tr}}({\mathbf{W}} ^\dag \hat{\mathbf{V }}^{-1}{\mathbf{W}} )], \end{aligned}$$

(35)

where the $n\times n$ dimensional covariance matrix is $\hat{\mathbf{V }}={\text{diag}}(\hat{v}_1,\ldots ,\hat{v}_n)$. We assumed here that there are no multiplicities in the entries of $\hat{\mathbf{V }}$, i.e., $\hat{v}_1,\ldots ,\hat{v}_n$ are distinct. In such a scenario the marginal density of nonzero-eigenvalues of ${\mathbf{W}} {\mathbf{W}} ^\dag$ or ${\mathbf{W}} ^\dag {\mathbf{W}}$ is given by

$$\begin{aligned} p_\lambda (\lambda )=\frac{1}{\nu \Delta _m(\{\hat{v}^{-1}\}) } \det \left[ \begin{array}{ccc} 0 &{} \left[ \frac{\exp (-\lambda /\hat{v}_k)}{\hat{v}_k^m}\right] _{k=1,\ldots ,n} \\ \left[ \frac{\lambda ^{m-j}}{\varGamma (m-j+1)}\right] _{j=1,\ldots ,n} &{} \left[ \hat{v}_k^{-j+1}\right] _{j,k=1,\ldots ,n} \end{array}\right] . \end{aligned}$$

(36)

Here $\nu =\min (m,n)$, and $\Delta _m(\{\hat{v}^{-1}\})=\prod _{j>k}(\hat{v}_j^{-1}-\hat{v}_k^{-1})$ is the Vandermonde determinant. Equation (27) follows from (36) by setting $m=M$ and $n=\mathsf{L}$ and using the well known result $\Delta (\{r\})=\det [r_j^{k-1}]$.

We now proceed to derive the ergodic channel capacity using the relation (13). To this end we expand (27) using the first column and obtain

$$\begin{aligned} p_\lambda (\lambda )=c\, \sum _{\mu =1}^{\mathsf{L}}(-1)^{\mu }g_\mu (\lambda )\det \,\left[ \begin{array}{ccc} \left[ f_k(\hat{v},\lambda )\right] _{k=1,\ldots ,L_1+\cdots +L_N} \\ \mathop {{\left[ h_{j,k}(\hat{v})\right] }_{{j,k=1, \ldots ,\mathsf{L}}}}\limits _{{\qquad (j\ne \mu )}}\end{array}\right] . \end{aligned}$$

(37)

We note at this point that $g_j(\lambda )=\lambda ^{M-j}/\varGamma (M-j+1)=0$ if $j> M$ because of the diverging gamma function in the denominator. If $\mathsf{L}\le M$ this situation is not encountered. However, if $\mathsf{L}> M$ then $g_j(\lambda )$ is nonzero only for $1\le j\le M$. Thus in both cases we see that the nonzero terms in the summation in (37) involve $j=1,\ldots ,\nu$, with $\nu =\min (M,\mathsf{L})$. We incorporate this observation by changing the upper limit of the summation. We now bring in the $g_\mu (\lambda )$ occurring before the determinants to the respective first rows, i.e., with $f_k(\hat{v},\lambda )$, and obtain

$$\begin{aligned} p_\lambda (\lambda )=c\, \sum _{\mu =1}^{\nu }(-1)^{\mu }\det \,\left[ \begin{array}{ccc} \left[ g_\mu (\lambda )f_k(\hat{v},\lambda )\right] _{k=1,\ldots ,\mathsf{L}} \\ \mathop {{\left[ h_{j,k}(\hat{v})\right] }_{{j,k=1,\ldots ,\mathsf{L}}}}\limits _ {{\qquad (j\ne \mu )}}\end{array}\right] . \end{aligned}$$

(38)

This equation serves as yet another expression for the marginal density. We now use (13) and obtain the following expression for the ergodic capacity by interchanging the $\lambda$-integral and the summation:

$$\begin{aligned} C=\nu \,c \sum _{\mu =1}^{\nu }(-1)^{\mu } \int _0^\infty d\lambda \, \left( \det \,\left[ \begin{array}{ccc} \left[ g_\mu (\lambda )f_k(\hat{v},\lambda )\right] _{k=1,\ldots ,\mathsf{L}} \\ \mathop {{\left[ h_{j,k}(\hat{v})\right] }_{{j,k=1,\ldots ,\mathsf{L}}}}\limits _ {{\qquad (j\ne \mu )}}\end{array}\right] \right) \, \log _2 \left( 1+\frac{\rho }{M}\lambda \right) . \end{aligned}$$

(39)

The $\lambda$-integral can be introduced in the first row of the determinant, along with the term $\log _2 \left( 1+\frac{\rho }{M}\lambda \right)$ to yield

$$\begin{aligned} C=\nu \,c \sum _{\mu =1}^{\nu }(-1)^{\mu } \det \,\left[ \begin{array}{ccc} \left[ \mathcal{G}_{\mu ,k}(\hat{v})\right] _{k=1,\ldots ,\mathsf{L}} \\ \mathop {{\left[ h_{j,k}(\hat{v})\right] }_{{j,k=1,\ldots ,\mathsf{L}}}}\limits _ {{\qquad (j\ne \mu )}}\end{array}\right] , \end{aligned}$$

(40)

where

$$\begin{aligned} \mathcal{G}_{\mu ,k}(\hat{v})=\int _0^\infty d\lambda \, g_\mu (\lambda )f_k(\hat{v},\lambda )\log _2 \left( 1+\frac{\rho }{M}\lambda \right) . \end{aligned}$$

(41)

This integral can be expressed in a closed form in terms of Meijer G-function or exponential-integral-functions as in (33) and (34), respectively. To obtain (33) we identify the following special cases of Meijer G-functions [47]:

$$\begin{aligned}&G^{1,0}_{0,1} \left( \begin{array}{c} \_ \\ \beta \end{array}\bigg |\, z \right) = z^{\beta }e^{-z}, \end{aligned}$$

(42)

$$\begin{aligned}&\quad G^{1,2}_{2,2} \left( \begin{array}{c} 1,\, 1 \\ 1,\, 0 \end{array}\bigg |\, z \right) = \ln (1+z), \end{aligned}$$

(43)

We also employ the convolution integral for Meijer G-function:

$$\begin{aligned}&\int _0^\infty dz\,G^{m,n}_{p,q} \left( \begin{array}{c} a_1,\,\ldots \, a_p \\ b_1,\,\ldots \, b_q \end{array}\bigg |\, \eta z \right) \, G^{\mu ,\nu }_{\sigma ,\tau } \left( \begin{array}{c} c_1,\,\ldots \, c_\sigma \\ d_1,\,\ldots \, d_\tau \end{array}\bigg |\, \omega z \right) \nonumber \\&\quad =\frac{1}{\eta }\,G^{n+\mu ,m+\nu }_{q+\sigma ,p+\tau } \left( \begin{array}{c} -b_1,\ldots ,-b_m,\,c_1,\,\ldots \, c_\sigma ,\,-b_{m+1},\ldots ,\,-b_q \\ -a_1,\ldots ,-a_n,\,d_1,\,\ldots \, d_\tau ,\,-a_{n+1},\ldots ,\,-a_p \end{array}\Bigg |\, \frac{\omega }{\eta } \right) \nonumber \\&\quad =\frac{1}{\omega }\,G^{m+\nu ,n+\mu }_{p+\tau ,q+\sigma } \left( \begin{array}{c} a_1,\ldots ,a_n,\,-d_1,\,\ldots \, -d_\tau ,\,a_{n+1},\ldots ,\,a_p \\ b_1,\ldots ,b_m,\,-c_1,\,\ldots \, -c_\sigma ,\,b_{m+1},\ldots ,\,b_q \end{array}\Bigg |\,\frac{\eta }{\omega } \right) . \end{aligned}$$

(44)

The restrictions on the indices for this integration formula can be found in [47]. Next we perform row interchanges in the determinants to bring $\mathcal{G}_{\mu ,k}$ in the respective $\mu$th row. Consequently, we have the expression for ergodic channel capacity as provided in (31).

Proofs for Eqs. (15), (20), (24), and (26)

To arrive at Eqs. (24) and (26) we need to set $\hat{v_1}=\cdots =\hat{v}_{L_1}=v_1; \hat{v}_{L_1+1}=\cdots =\hat{v}_{L_2}=v_2\,;\ldots ; \hat{v}_{L_{(N-1)}+1}=\cdots =\hat{v}_{L_N}=v_N$ in (27) and (31). However, direct substitution of these values makes the determinant in the numerator, as well as the determinant in the denominator (contained in the normalization) to become zero. Therefore, we must invoke a limiting procedure to obtain the proper results, as described below.

Let us focus on the columns involving up to $L_1$ in (27). The ratio of the determinants appears as

$$\begin{aligned} \frac{\det \left[ \begin{array}{cccccc} 0 &{} (\hat{v}_1^{-1})^M e^{\hat{v}_1^{-1}\lambda } &{} (\hat{v}_2^{-1})^M e^{\hat{v}_2^{-1}\lambda } &{} \ldots &{} (\hat{v}_{L_1}^{-1})^M e^{\hat{v}_{L_1}^{-1}\lambda } &{} \ldots \\ g_j (\lambda ) &{} (\hat{v}_1^{-1})^{j-1} &{} (\hat{v}_2^{-1})^{j-1} &{} \ldots &{} (\hat{v}_{L_1}^{-1})^{j-1} &{} \ldots \end{array}\right] }{\det \left[ \begin{array}{ccccc} (\hat{v}_1^{-1})^{j-1}&(\hat{v}_2^{-1})^{j-1}&\ldots&(\hat{v}_{L_1}^{-1})^{j-1}&\ldots \end{array}\right] } \end{aligned}$$

(45)

We take $\hat{v}_k^{-1}=\hat{v}_1^{-1}+\epsilon _k$ with small $\epsilon _k$ for $k=2,3,\ldots$, and Taylor-expand up to the term $\epsilon _k^{k-1}$:

$$\begin{aligned} (\hat{v}_k^{-1})^M e^{\hat{v}_k^{-1}\lambda }\approx & {} \sum _{r=0}^{k-1}\frac{\epsilon _k^r}{r!}\frac{\partial ^r}{\partial (\hat{v}_1^{-1})^r} (\hat{v}_1^{-1})^M e^{\hat{v}_1^{-1}\lambda };\\ (\hat{v}_k^{-1})^{j-1}\approx & {} \sum _{r=0}^{k-1}\frac{\epsilon _k^r}{r!}\frac{\partial ^r}{\partial (\hat{v}_1^{-1})^r} (\hat{v}_1^{-1})^{j-1}. \end{aligned}$$

Now, employing adequate column operations, we obtain

$$\begin{aligned} \frac{\det \,\left[ \begin{array}{cccccc} 0 &{} (\hat{v}_1^{-1})^M e^{\hat{v}_1^{-1}\lambda } &{} \frac{\epsilon _k}{1!}\frac{\partial }{\partial (\hat{v}_1^{-1})} (\hat{v}_1^{-1})^M e^{\hat{v}_1^{-1}\lambda } &{} \ldots &{} \frac{\epsilon _k^{k-1}}{(k-1)!}\frac{\partial ^{k-1}}{\partial (\hat{v}_1^{-1})^{k-1}} (\hat{v}_1^{-1})^M e^{\hat{v}_1^{-1}\lambda } &{} \ldots \\ g_j (\lambda ) &{} (\hat{v}_1^{-1})^{j-1} &{}\frac{\epsilon _k}{1!}\frac{\partial }{\partial (\hat{v}_1^{-1})} (\hat{v}_1^{-1})^{j-1} &{} \ldots &{} \frac{\epsilon _k^{k-1}}{(k-1)!}\frac{\partial ^{k-1}}{\partial (\hat{v}_1^{-1})^{k-1}}(\hat{v}_1^{-1})^{j-1} &{} \ldots \end{array}\right] }{\det \,\left[ \begin{array}{ccccc} (\hat{v}_1^{-1})^{j-1}&\frac{\epsilon _k}{1!}\frac{\partial }{\partial (\hat{v}_1^{-1})} (\hat{v}_1^{-1})^{j-1}&\ldots&\frac{\epsilon _k^{k-1}}{(k-1)!}\frac{\partial ^{k-1}}{\partial (\hat{v}_1^{-1})^{k-1}}(\hat{v}_1^{-1})^{j-1}&\ldots \end{array}\right] } \end{aligned}$$

(46)

The factors containing $\epsilon _k$ and factorial can be taken out of the columns, both from numerator and denominator, and cancelled out. This leaves us with

$$\begin{aligned} \frac{\det \,\left[ \begin{array}{cccccc} 0 &{} (\hat{v}_1^{-1})^M e^{\hat{v}_1^{-1}\lambda } &{} \frac{\partial }{\partial (\hat{v}_1^{-1})} (\hat{v}_k^{-1})^M e^{\hat{v}_1^{-1}\lambda } &{} \ldots &{} \frac{\partial ^{k-1}}{\partial (\hat{v}_1^{-1})^{k-1}} (\hat{v}_k^{-1})^M e^{\hat{v}_1^{-1}\lambda } &{} \ldots \\ g_j (\lambda ) &{} (\hat{v}_1^{-1})^{j-1} &{}\frac{\partial }{\partial (\hat{v}_1^{-1})} (\hat{v}_1^{-1})^{j-1} &{} \ldots &{} \frac{\partial ^{k-1}}{\partial (\hat{v}_1^{-1})^{k-1}}(\hat{v}_1^{-1})^{j-1} &{} \ldots \end{array}\right] }{\det \,\left[ \begin{array}{ccccc} (\hat{v}_1^{-1})^{j-1}&\frac{\partial }{\partial (\hat{v}_1^{-1})} (\hat{v}_1^{-1})^{j-1}&\ldots&\frac{\partial ^{k-1}}{\partial (\hat{v}_1^{-1})^{k-1}}(\hat{v}_1^{-1})^{j-1}&\ldots \end{array}\right] } \end{aligned}$$

(47)

To evaluate the derivatives of $(\hat{v}_k^{-1})^M e^{\hat{v}_1^{-1}\lambda }$ we use Rodrigues’ formula for the associated Laguerre polynomials,

$$\begin{aligned} \mathcal{L}_k^{(\beta )}(z)=\frac{z^{-\beta } e^z }{k!}\frac{\partial ^k}{\partial z^k}\left( z^{k+\beta } e^{-z} \right) , \end{aligned}$$

(48)

with adequate scaling of the variables. Similar steps are followed for rest of the columns and consequently we arrive at (24).

We employ a similar procedure in (31) to arrive at (26). To evaluate the derivative of Meijer G-function we use the result

$$\begin{aligned} z^r \frac{\partial ^r}{\partial z^r} G^{3,1}_{2,3} \left( \begin{array}{c} a_1,\, a_2 \\ b_1,\, b_2,\, b_3 \end{array}\Bigg |\, z \right) = G^{3,2}_{3,4} \left( \begin{array}{c} 0,\, a_1,\, a_2 \\ b_1,\, b_2,\, b_3,\, r \end{array}\Bigg |\, z \right) , \end{aligned}$$

(49)

which follows from the following more general expression [47]:

$$\begin{aligned} z^r \frac{\partial ^r}{\partial z^r}G^{m,n}_{p,q} \left( \begin{array}{c} a_1,\, \ldots ,\, a_p \\ b_1,\,\ldots ,\, b_q \end{array}\bigg |\, z \right) = G^{m,n+1}_{p+1,q+1}\left( \begin{array}{c} 0,\,a_1,\, \ldots ,\, a_p \\ b_1,\,\ldots ,\, b_q,\,r \end{array}\bigg |\, z \right) . \end{aligned}$$

(50)

Finally, (15) and (20) follow trivially from, respectively, (24) and (26) by setting identical number of antennas at each port, i.e., $L_1=\cdots =L_N=L$.