1 Introduction

Traditional one-way relaying which consists of a source, relay and destination, has attracted considerable interest recently as it can improve coverage and spatial diversity [1, 2]. However, as the transmission in half-duplex channels is working in one-way fashion, relayed transmission with two source nodes suffers from spectral efficiency. To overcome this efficiency loss, two-way relaying is proposed in the literature [3, 4]. In two way relay networks (TWRNs), two terminals concurrently transmit their messages to relay in the first time slot, then relay broadcasts the combined signals to both sources in the second time slot. Hence, both terminals can get the desired message after removing the self interference terms. Motivated from the advantages of bidirectional relaying, TWRNs with single antennas are investigated considerably in [5–7] and the references therein. In [5] and [6], symbol error rate and system OPs are derived for Rayleigh fading channels respectively whereas [7] investigates both outage and symbol error rate performance over Nakagami-m fading channels.

In an attempt to enhance the communication reliability in TWRNs, multiple antennas and relays have been studied to explore the improved performance [8–18]. In [8, 9] and [10], system outage performance of an AF opportunistic TWRN is analyzed for Rayleigh, Nakagami-m and Rician fading channels respectively. Moreover, in [11], both relay selection and all-relays participating networks are considered where OP and SER are derived. In [12, 13], power optimization is studied in opportunistic TWRNs, where [12] obtains system outage for Nakagami-m fading channels and [13] derives both OP and SER for Rayleigh fading channels. Similar to multi-relay transmission scenarios, using multiple antennas at the sources employing maximal ratio transmission (MRT) become popular in TWRNs. User OP of an amplify-and-forward (AF) multi-input multi-output (MIMO) TWRN is investigated over Nakagami-m fading channels in [15] whereas in [16], joint optimization of power allocation and relay location are examined over Nakagami-m fading channels. In addition, a comparison of antenna selection and MRT is considered in [17], where SSER expression is obtained for Nakagami-m fading channels. In [18], an AF MIMO TWRN is analyzed where MRT-receive antenna selection is compared with joint transmit-receive antenna selection and system OP is derived for Nakagami-m fading channels.

In the wide body of literature, there is no previous work which investigates the performance of MRT with relay selection in TWRNs even for Rayleigh fading channels. In this paper, we examine the performance of an AF MIMO TWRN where multiple-antenna sources employing MRT and the information is exchanged through the best relay having single antenna. For this network, we derive user, system outage probabilities and sum symbol error rate over flat Nakagami-m fading channels. The main contributions of this paper can be listed as follows:

  • User, system outage probabilities and sum symbol error rate over flat Nakagami-m fading channels are derived.

  • Asymptotic sum symbol error rate and system outage expressions are derived and also diversity and array gains are obtained.

  • The impact of imperfect channel estimations and limited feedback are investigated on the proposed structure.

  • To improve overall system performance, the problem of relay location optimization is presented.

  • To verify the correctness of analytical results, numerical examples are presented and compared with theoretical results.

The remainder of the paper is organized as follows. Channel model is presented in Sect. 2. In Sect. 3, probability density function, cumulative distribution function and moment generating function of the end-to-end (e2e) SNR are derived. In Sect. 4, user, system outages and sum symbol error rate expressions are derived. Then, to obtain diversity and array gains, asymptotic system OP and sum symbol error rate are obtained. In addition, impact of imperfect channel estimations and limited feedback is presented. In Sect. 5, optimum relay location to minimize system OP is obtained and numerical examples are given in Sect. 6. Finally conclusions are drawn in Sect. 7.

Notations: Bold letters denote vectors where italic symbols specify scalar variables. The following symbols \((\cdot )^T, (\cdot )^\dagger\) and \(\Vert \cdot \Vert\) are used for transpose, conjugate-transpose and Frobenius norm respectively. Furthermore, \(\Pr [\cdot ], {{\mathbb{E}}[\cdot ]}\) stand for probability and expectation operations respectively and \({\mathcal {Q}}(\cdot )\) specifies the Q-function.

2 System Model

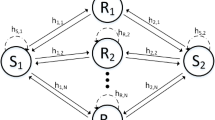
This paper focuses on an AF MIMO TWRN consisting of two source terminals (\(S_1\) and \(S_2\)) having \(N_1\) and \(N_2\) antennas respectively, communicates via R-relays each having single antenna as depicted in Fig. 1. The direct link between two source terminals is assumed to be not available due to large path loss effect, distance or heavy shadowing. Therefore, the transmission between \(S_1\) and \(S_2\) can be done with the help of selected relay r, {\(1\le r \le R\)}. All channel coefficients between \(S_1 \rightarrow r\) and \(S_2 \rightarrow r\) hops are modeled as independent and identically distributed (i.i.d) flat Nakagami-m fading with \(m_1\) and \(m_2\) severity parameters respectively, whereas both hops are assumed to be independent but not identically distributed (i.n.i.d) Nakagami-m fading channel i.e., \(m_1\ne m_2\), and \(N_1 \ne N_2\). The communication between two source terminals is divided into two time slots. In the first time slot, \(S_1\) and \(S_2\) simultaneously transmit their signals \(x_1\) and \(x_2\) respectively by using MRT technique [19]. As we assume equal power at all nodes, the received signal at the r-th relay can be written as follows

$$\begin{aligned} y_r = \sqrt{Pd_{1,r}^{-\alpha }}{\mathbf{h}}_{1,r}{\mathbf{w}}_{1,r}x_1 + \sqrt{Pd_{2,r}^{-\alpha }}{\mathbf{h}}_{2,r}{\mathbf{w}}_{2,r}x_2 + n_r. \end{aligned}$$
(1)

In the second time slot, relay amplifies the received signal with a scaling factor \(G_r\) and forwards to \(S_1\) and \(S_2\) by using maximum ratio combining (MRC). The received signal at both source nodes can be expressed as

$$\begin{aligned} y_{s_1} & = {\mathbf{w}}_{1,r}^{T}\left( \sqrt{Pd_{1,r}^{-\alpha }}G_r{\mathbf{h}}^T_{1,r}y_r +{\mathbf{n}}_1\right) \nonumber \\ y_{s_2}&= {\mathbf{w}}_{2,r}^{T}\left( \sqrt{Pd_{2,r}^{-\alpha }}G_r{\mathbf{h}}^T_{2,r}y_r +{\mathbf{n}}_2\right) , \end{aligned}$$
(2)

where \(d_{1,r}\) and \(d_{2,r}\) are distances between \(S_1 \rightarrow r\) and \(S_2 \rightarrow r\) respectively, \(\alpha\) is the path loss component, \({\mathbf{h}}_{1,r}\) and \({\mathbf{h}}_{2,r}\) are \(N_1\times 1\) and \(N_2\times 1\) channel vectors between \(S_1 \rightarrow r\) and \(S_2 \rightarrow r\) respectively. MRT based weight vectors \({\mathbf{w}}_{1,r}\) and \({\mathbf{w}}_{2,r}\) are specified as \({\mathbf{w}}_{1,r}= ({\mathbf{h}}_{1,r}^{\dagger }/\Vert {\mathbf{h}}_{1,r}\Vert )\) and \({\mathbf{w}}_{2,r}= ({\mathbf{h}}_{2,r}^{\dagger }/\Vert {\mathbf{h}}_{2,r}\Vert )\). Noise sample \(n_r\) and vectors \({\mathbf{n}}_1, {\mathbf{n}}_2\) are modeled as complex additive white Gaussian noise (AWGN) with zero mean and \(N_0\) noise power. Scaling factor \(G_r\) is given as

$$\begin{aligned} G_r = \frac{1}{\sqrt{Pd_{1,r}^{-\alpha }\Vert {\mathbf{h}}_{1,r}\Vert ^2+Pd_{2,r}^{-\alpha }\Vert {\mathbf{h}}_{2,r}}\Vert ^2}. \end{aligned}$$
(3)

Substituting (1) in (2) with the help of (3) and after the self interference term drops due to perfect channel reciprocity, the following e2e SNRs can be obtained as below

$$\begin{aligned} \gamma _{S_1 \rightarrow r \rightarrow S_2 }= & {} \frac{\frac{P}{N_0}d_{1,r}^{-\alpha } \Vert {\mathbf{h}}_{1,r}\Vert ^2\frac{P}{N_0}d_{2,r}^{-\alpha } \Vert {\mathbf{h}}_{2,r}\Vert ^2}{2\frac{P}{N_0}d_{1,r}^{-\alpha } \Vert {\mathbf{h}}_{1,r}\Vert ^2 + \frac{P}{N_0}d_{2,r}^{-\alpha }\Vert {\mathbf{h}}_{2,r}\Vert ^2} = \frac{\gamma _{S_1}\gamma _{S_2}}{2\gamma _{S_1}+\gamma _{S_2}} \nonumber \\ \gamma _{S_2 \rightarrow r \rightarrow S_1}= & {} \frac{\frac{P}{N_0}d_{1,r}^{-\alpha } \Vert {\mathbf{h}}_{1,r}\Vert ^2\frac{P}{N_0}d_{2,r}^{-\alpha } \Vert {\mathbf{h}}_{2,r}\Vert ^2}{\frac{P}{N_0}d_{1,r}^{-\alpha } \Vert {\mathbf{h}}_{1,r}\Vert ^2 + 2\frac{P}{N_0}d_{2,r}^{-\alpha }\Vert {\mathbf{h}}_{2,r}\Vert ^2} = \frac{\gamma _{S_1}\gamma _{S_2}}{\gamma _{S_1}+2\gamma _{S_2}}, \end{aligned}$$
(4)

where \(\gamma _{S_1}=\frac{P}{N_0}d_{1,r}^{-\alpha } \Vert {\mathbf{h}}_{1,r}\Vert ^2\) and \(\gamma _{S_2}=\frac{P}{N_0}d_{2,r}^{-\alpha } \Vert {\mathbf{h}}_{2,r}\Vert ^2\) are the instantaneous SNRs at \(S_1 \rightarrow r\) and \(S_2 \rightarrow r\) hops. As the exact system OP and SSER becomes quite complicated in MIMO TWRNs, we resort computing tight lower bounds on these performance indicators by simplifying the e2e SNRs given in (4) as

$$\begin{aligned} \gamma _{S_i \rightarrow r \rightarrow S_j}\leqslant \gamma _{S_i \rightarrow r \rightarrow S_j }^{up}=\min (\gamma _{S_i},\gamma _{S_j}/2), \end{aligned}$$
(5)

where \(i,j\in \{1,2\}\) and \(i\ne j\). Since user outage is defined as the probability of e2e SNR being lower than a certain threshold \(\gamma _{th}\), optimal relay selection (for user 1 or 2) can be shown as follows

$$\begin{aligned} R_*^{us}=\arg \max _{1\leqslant r \leqslant R}\min (\gamma _{S_i},\gamma _{S_j}/2). \end{aligned}$$
(6)

System outage on the other hand can be defined as if at least one of the source nodes is in outage and relay selection can be expressed as [20, Eq. 11]

$$\begin{aligned} R_*^{sys}=\arg \max _{1\leqslant r \leqslant R}\min (\gamma _{S_1 \rightarrow r \rightarrow S_2},\gamma _{S_2 \rightarrow r \rightarrow S_1}). \end{aligned}$$
(7)

Equations (6) and (7) show the selection policy of the best relay for each user or overall system respectively.

Fig. 1
figure 1

Block diagram of MIMO TWRN with maximal ratio transmission and relay selection

Full size image

3 SNR Statistics

In this section, we derive probability density function (PDF), cumulative distribution function (CDF) and moment generating function (MGF) of the SNR for any user \(i,j=\{1,2\}, i\ne j\). With the help of (5), CDF of \(S_i \rightarrow r \rightarrow S_j\) can be expressed as

$$\begin{aligned} {\mathcal {F}}_{\gamma _{S_i \rightarrow r \rightarrow S_j}^{up}}(\gamma )= & {} \Pr \left[ \min (\gamma _{S_i},\gamma _{S_j}/2)\leqslant \gamma \right] \nonumber \\= & {} 1-\Pr [\gamma _{S_i}>\gamma ]\Pr [\gamma _{S_j}> 2\gamma ], \end{aligned}$$
(8)

and the PDFs of \(\gamma _{S_i}\) and \(\gamma _{S_j}\) can be written as

$$\begin{aligned} f_{\gamma _{S_i}}(\gamma ) = \frac{m_i^{m_iN_i}\gamma ^{m_iN_i-1}e^{-m_i\gamma /{\varOmega }_i}}{{\varOmega }_i^{m_iN_i}{\varGamma }(m_iN_i)}, \end{aligned}$$
(9)

and \(f_{\gamma _{S_j}}(\gamma )\) is the same as in (9) after replacing the subscript i with j. Therefore, integrating (9) w.r.t \(\gamma\), with the help of [27, Eq. (8.350.2)] and then substituting in (8), \({\mathcal {F}}_{\gamma _{S_i \rightarrow r \rightarrow S_j}^{up}}(\gamma )\) can be obtained as

$$\begin{aligned} {\mathcal {F}}_{\gamma _{S_i \rightarrow r \rightarrow S_j}^{up}}(\gamma )=\left( 1-\frac{{\varGamma }\left( m_iN_i,m_i\frac{\gamma }{{\varOmega }_i}\right) }{{\varGamma }(m_iN_i)}\times \frac{{\varGamma }\left( m_jN_j,2m_j\frac{\gamma }{{\varOmega }_j}\right) }{{\varGamma }(m_jN_j)}\right) , \end{aligned}$$
(10)

where \({\varGamma }(\cdot ,\cdot )\) specifies upper incomplete Gamma function and \({\varGamma }(\cdot )\) stands for Gamma function [27, Eq. (8.339.1)]. We denote \({\varOmega }_i=d_{i,r}^{-\alpha }\bar{\gamma }, {\varOmega }_j=d_{j,r}^{-\alpha }\bar{\gamma }\) as average SNRs and \(\bar{\gamma }=P/N_0\). With the help of [27, Eq. (8.352.7)], (10) can be expressed as

$$\begin{aligned} {\mathcal {F}}_{\gamma _{S_i \rightarrow r \rightarrow S_j}^{up}}(\gamma )= & {} \left( 1-e^{-m_i\frac{\gamma }{{\varOmega }_i}}\sum _{z=0}^{m_iN_i-1}\left( m_i\frac{\gamma }{{\varOmega }_i}\right) ^z\frac{1}{z!} \right. \nonumber \\&\left. \times e^{-2m_j\frac{\gamma }{{\varOmega }_j}}\sum _{v=0}^{m_jN_j-1}\left( 2m_j\frac{\gamma }{{\varOmega }_j}\right) ^v\frac{1}{v!}\right) . \end{aligned}$$
(11)

With the help of high order statistics [26] and Eq. (6), \({\mathcal {F}}_{\gamma _{S_i \rightarrow R_*^{us}\rightarrow S_j}^{up}}(\gamma ) =\left\{ {\mathcal {F}}_{\gamma _{S_i \rightarrow r \rightarrow S_j}^{up}}(\gamma )\right\} ^R\). By applying binomial [27, Eq. (1.111.1)] and multinomial expansions [27, Eq. (0.314)] respectively, \({\mathcal {F}}_{\gamma _{S_i \rightarrow R_*^{us} \rightarrow S_j}^{up}}(\gamma )\) can be obtained as

$$\begin{aligned} {\mathcal {F}}_{\gamma _{S_i \rightarrow R_*^{us} \rightarrow S_j}^{up}}(\gamma )= & {} \sum _{r=0}^{R}\sum _{z=0}^{r(m_iN_i-1)}\sum _{v=0}^{r(m_jN_j-1)}\left( {\begin{array}{c}R\\ r\end{array}}\right) (-1)^re^{-\gamma \left( \frac{rm_i{\varOmega }_j+2rm_j{\varOmega }_i}{{\varOmega }_i{\varOmega }_j}\right) } \nonumber \\&\times {\mathcal {X}}_z(r){\mathcal {X}}_v(r)\gamma ^{v+z}, \end{aligned}$$
(12)

where combination operation denotes binomial coefficients and \({\mathcal {X}}_t(r)\) shows multinomial coefficients which can be found as

$$\begin{aligned} {\mathcal {X}}_t(r)=\frac{1}{tk_0}\sum _{\rho =1}^{t}(r\rho -t+\rho )k_\rho {\mathcal {X}}_{t-\rho }(r), t\geqslant 1. \end{aligned}$$
(13)

Multinomial coefficients can be obtained by using [27, Eq. (0.314)]; \(k_\rho =(Am_l\frac{1}{{\varOmega }_l})^{\rho }\times \frac{1}{\rho !}, {\mathcal {X}}_0(r)=k_0^r=1, t\in \{v,z\}, A=\{1,2\}\) and \(l\in \{i,j\}\). As we obtain \({\mathcal {F}}_{\gamma _{S_i \rightarrow R_*^{us} \rightarrow S_j}^{up}}(\gamma )\), the PDF of \(\gamma _{S_i \rightarrow R_*^{us} \rightarrow S_j}^{up}\) can be found by taking the derivative of (12) w.r.t. \(\gamma\) as

$$\begin{aligned} f_{\gamma _{S_i \rightarrow R_*^{us} \rightarrow S_j}^{up}}(\gamma )= & {} \sum _{r=0}^{R}\sum _{z=0}^{r(m_iN_i-1)}\sum _{v=0}^{r(m_jN_j-1)}\left( {\begin{array}{c}R\\ r\end{array}}\right) (-1)^r{\mathcal {X}}_z(r){\mathcal {X}}_v(r) \nonumber \\&\times \,e^{-\gamma \left( \frac{rm_i}{{\varOmega }_i}+\frac{2rm_j}{{\varOmega }_j}\right) }\gamma ^{v+z}\left( \gamma (v+z)-\frac{rm_i}{{\varOmega }_i}-\frac{2rm_j}{{\varOmega }_j}\right) , \end{aligned}$$
(14)

and the MGF of \({\gamma _{S_i \rightarrow R_*^{us} \rightarrow S_j}^{up}}\) can be obtained as

$$\begin{aligned} {\mathcal {M}}_{\gamma _{S_i \rightarrow R_*^{us} \rightarrow S_j}^{up}}(s)=s\int _{0}^{\infty }e^{-s\gamma }{\mathcal {F}}_{\gamma _{S_i \rightarrow R_*^{us} \rightarrow S_j}^{up}}(\gamma )d\gamma , \end{aligned}$$
(15)

which can be obtained by substituting (12) in (15) and with the help of [27, Eq. 3.351.3], as

$$\begin{aligned} {\mathcal {M}}_{\gamma _{S_i \rightarrow R_*^{us} \rightarrow S_j}^{up}}(s)= & {} \sum _{r=0}^{R}\sum _{z=0}^{r(m_iN_i-1)}\sum _{v=0}^{r(m_jN_j-1)}\left( {\begin{array}{c}R\\ r\end{array}}\right) (-1)^rs{\mathcal {X}}_z(r){\mathcal {X}}_v(r){\varGamma }(v+z-1) \nonumber \\&\times \left( s+\frac{rm_i}{{\varOmega }_i}+\frac{2rm_j}{{\varOmega }_j}\right) ^{-v-z-1}. \end{aligned}$$
(16)

MGF of SNR (16) or CDF of SNR (12) can be used to obtain SSER and outage probabilities.

4 Performance Analysis

In this section, we first derive outage probabilities and sum symbol error rate for flat Nakagami-m fading channels. Then, by deriving asymptotic expressions of SSER and system OP, we find diversity and array gains. Finally, the impact of practical transmission impairments such as limited feedback (of channel coefficients) and channel estimation errors are investigated.

4.1 User and System Outage Probabilities

User OP is defined as the probability of e2e SNR (\(\gamma _{S_i \rightarrow r \rightarrow S_j }^{up}\)) falling below a certain threshold \(\gamma _{th}\) and it can be computed as \(P_{out}^{us}={\mathcal {F}}_{\gamma _{S_i \rightarrow R_*^{us} \rightarrow S_j}^{up}}(\gamma _{th})\). System OP on the other hand means if \(S_1 \rightarrow r \rightarrow S_2\) or \(S_2 \rightarrow r \rightarrow S_1\) path is in outage. With the help of (7), system OP can be expressed as

$$\begin{aligned} P_{out}^{sys}= & {} {\mathcal {F}}_{\gamma }(\gamma _{th}), \nonumber \\ {\mathcal {F}}_{\gamma }(\gamma _{th})= & {} \prod _{r=1}^{R}\Pr \left( \min \left( \gamma _{{S_1 \rightarrow r \rightarrow S_2}},\gamma _{{S_2 \rightarrow r \rightarrow S_1}}\right) \leqslant \gamma _{th}\right) , \nonumber \\= & {} \prod _{r=1}^{R}\left( 1-\Pr \left[ \gamma _{{S_1 \rightarrow r \rightarrow S_2}}>\gamma _{th}\right] \times \Pr \left[ \gamma _{{S_2 \rightarrow r \rightarrow S_1}}>\gamma _{th}\right] \right) . \end{aligned}$$
(17)

Substituting (5) in (17) gives

$$\begin{aligned} {\mathcal {F}}_{\gamma }(\gamma _{th})= & {} \prod _{r=1}^{R}\left( 1-\Pr \left[ \min \left( \gamma _{S_1},\frac{\gamma _{S_2}}{2}\right) >\gamma _{th}\right] \right. \nonumber \\&\left. \times \,\Pr \left[ \min \left( \frac{\gamma _{S_1}}{2},\gamma _{S_2}\right) >\gamma _{th}\right] \right) . \end{aligned}$$
(18)

As (18) is highly complicated, simple lower bounds on system OP is investigated. For this, the following Lemma is used [21].

Lemma

E2e SNRs can be upper bounded by dividing (4) to \(\gamma _{S_1}=\frac{P}{N_0}d_{1,r}^{-\alpha } \Vert {\mathbf{h}}_{1,r}\Vert ^2\) and \(\gamma _{S_2}=\frac{P}{N_0}d_{2,r}^{-\alpha } \Vert {\mathbf{h}}_{2,r}\Vert ^2\), which is

$$\begin{aligned} \gamma _{S_1 \rightarrow r \rightarrow S_2 }=\frac{\frac{P}{N_0}d_{2,r}^{-\alpha } \Vert {\mathbf{h}}_{2,r}\Vert ^2}{2 + \frac{d_{2,r}^{-\alpha }\Vert {\mathbf{h}}_{2,r}\Vert ^2}{d_{1,r}^{-\alpha }\Vert {\mathbf{h}}_{1,r}\Vert ^2}}\leqslant \frac{P}{2N_0}d_{2,r}^{-\alpha }\Vert {\mathbf{h}}_{2,r}\Vert ^2=\frac{1}{2}\gamma _{S_2}, \end{aligned}$$
(19)

and similarly \(\gamma _{S_2 \rightarrow r \rightarrow S_1} \leqslant \frac{1}{2}\gamma _{S_1}\). As \(\frac{P}{N_0}d_{1,r}^{-\alpha } \Vert {\mathbf{h}}_{1,r}\Vert ^2 > 0\) and \(\frac{P}{N_0}d_{2,r}^{-\alpha } \Vert {\mathbf{h}}_{2,r}\Vert ^2 > 0\), these approximate results are valid. Therefore, (18) can be simplified as

$$\begin{aligned} P_{out}^{sys}= & {} {\mathcal {F}}_{\gamma }^{up}(\gamma _{th}), \nonumber \\ {\mathcal {F}}_{\gamma }^{up}(\gamma _{th})= & {} \prod _{r=1}^{R}\Pr \left[ \min \left( \gamma _{S_1}/2,\gamma _{S_2}/2\right) \leqslant \gamma _{th}\right] . \end{aligned}$$
(20)

By using similar theoretical steps as given in (8–12), a tight upper bound on system OP can be obtained as follows

$$\begin{aligned} P_{out}^{sys}= & {} \sum _{r=0}^{R}\sum _{z=0}^{r(m_1N_1-1)}\sum _{v=0}^{r(m_2N_2-1)}\left( {\begin{array}{c}R\\ r\end{array}}\right) (-1)^re^{-\gamma _{th} \left( \frac{2rm_1{\varOmega }_2+2rm_2{\varOmega }_1}{{\varOmega }_1{\varOmega }_2}\right) }\nonumber \\&\times {\mathcal {X}}_z(r){\mathcal {X}}_v(r)\gamma _{th}^{v+z}, \end{aligned}$$
(21)

where multinomial coefficients are as given in (13), only difference is \(k_\rho =(2m_l\frac{1}{{\varOmega }_l})^{\rho }\frac{1}{\rho !}, l=\{1,2\}\).

4.2 Sum Symbol Error Rate

SSER which can be defined as the summation of SER at \(S_1\) and \(S_2\) nodes, is one of the most important performance criterion in TWRNs. Mathematically, it can be expressed as

$$\begin{aligned} P_s(e)=P_{s_1}(e)+P_{s_2}(e). \end{aligned}$$
(22)

For M-PSK modulation, by using the MGF of SNR (16), we can write SSER as follows [26]

$$\begin{aligned} P_{s,PSK}(e)=\frac{1}{ \pi }\int _{0}^{\phi }\left[ {\mathcal {M}}_{\gamma _{S_1\rightarrow R_*^{us} \rightarrow S_2}}^{up}\left( \frac{g_{PSK}}{\sin ^2(\theta )}\right) +{\mathcal {M}}_{\gamma _{S_2\rightarrow R_*^{us} \rightarrow S_1}}^{up}\left( \frac{g_{PSK}}{\sin ^2(\theta )}\right) \right] d\theta , \end{aligned}$$
(23)

where \(g_{PSK}=\sin ^2(\pi /M)\) and \(\phi = (M-1)\pi /M\). For M-QAM modulation, SSER can be written as [26]

$$\begin{aligned} P_{s,QAM}(e)= & {} \frac{4}{\pi }B\left[ \int _{0}^{\pi /2}{{\mathcal {M}}}_{\gamma _{S_1\rightarrow R_*^{us} \rightarrow S_2}}^{up}\left( \frac{g_{QAM}}{\sin ^2(\theta )}\right) +{{\mathcal {M}}}_{\gamma _{S_2\rightarrow R_*^{us} \rightarrow S_1}}^{up}\left( \frac{g_{QAM}}{\sin ^2(\theta )}\right) d\theta \right] \nonumber \\&-\frac{4}{\pi }B^2\left[ \int _{0}^{\pi /4}{{\mathcal {M}}}_{\gamma _{S_1\rightarrow R_*^{us} \rightarrow S_2}}^{up}\left( \frac{g_{QAM}}{\sin ^2(\theta )}\right) +{{\mathcal {M}}}_{\gamma _{S_2\rightarrow R_*^{us} \rightarrow S_1}}^{up}\left( \frac{g_{QAM}}{\sin ^2(\theta )}\right) d\theta \right] , \end{aligned}$$
(24)

where \(B = (1-1/\sqrt{M})\). By substituting (16) in (23) and (24), SSER can be obtained for M-ary modulations. In addition, for the systems whose conditional error probability is in the form of \(a{\mathbb {E}}[Q(\sqrt{2b\gamma })]\), SSER can also be obtained by using the CDF of SNR as follows

$$\begin{aligned} P_s(e)=\frac{a\sqrt{b}}{2\sqrt{\pi }}\int _{0}^{\infty }\gamma ^{-1/2}e^{-b\gamma }\left( {\mathcal {F}}_{\gamma _{S_1 \rightarrow R_*^{us} \rightarrow S_2}^{up}}(\gamma ) +{\mathcal {F}}_{\gamma _{S_2 \rightarrow R_*^{us} \rightarrow S_1}^{up}}(\gamma )\right) d\gamma , \end{aligned}$$
(25)

where a and b denotes modulation coefficients, i.e., \(\{a = 1, b = 0.5\}\) for BFSK modulation, \(\{a = 1, b = 1\}\) for BPSK and \(\{a=2(M-1)/M, b=3/(M^2-1)\}\) for M-ary PAM. Furthermore, we can obtain approximate results for M-ary modulation types [26]. Substituting (12) into (25), with the help of [27, Eq. 3.351.3], \(P_s(e)\) can be obtained as follows

$$\begin{aligned} P_s(e)= & {} \frac{a\sqrt{b}}{2\sqrt{\pi }}\sum _{r=0}^{R}\left( {\begin{array}{c}R\\ r\end{array}}\right) (-1)^r \nonumber \\&\times \left[ \sum _{z=0}^{r(m_1N_1-1)}\sum _{v=0}^{r(m_2N_2-1)}{\mathcal {X}}_z(r){\mathcal {X}}_v(r){\varGamma }({\mathcal {V}}) \left( b+\frac{rm_1}{{\varOmega }_1}+\frac{2rm_2}{{\varOmega }_2}\right) ^{{\mathcal {N}}}\right. \nonumber \\&\left. +\sum _{z=0}^{r(m_2N_2-1)}\sum _{v=0}^{r(m_1N_1-1)}{\mathcal {X}}_z(r){\mathcal {X}}_v(r){\varGamma }({\mathcal {V}}) \left( b+\frac{rm_2}{{\varOmega }_2}+\frac{2rm_1}{{\varOmega }_1}\right) ^{{\mathcal {N}}}\right] , \end{aligned}$$
(26)

where \({\mathcal {N}}=-v-z-1/2\) and \({\mathcal {V}}=v+z-3/2\).

4.3 Asymptotic Analysis

In this section, we investigate asymptotic system OP and SSER expressions to obtain diversity (\({\mathcal {G}}_d\)) and array gains (\({\mathcal {G}}_a\)) [29]. At high SNR, by using [22, Eq. 6], (20) can be expressed as

$$\begin{aligned} P_{out}^{sys}= & {} \prod _{r=1}^{R}\left( {\mathcal {F}}_{\gamma _{S_1}}(2\gamma _{th})+{\mathcal {F}}_{\gamma _{S_2}}(2\gamma _{th})\right) \nonumber \\= & {} \prod _{r=1}^{R}\left( \frac{{\varUpsilon }\left( m_1N_1,2m_1\frac{\gamma _{th}}{{\varOmega }_1}\right) }{{\varGamma }(m_1N_1)}+\frac{{\varUpsilon }\left( m_2N_2,2m_2\frac{\gamma _{th}}{{\varOmega }_2}\right) }{{\varGamma }(m_2N_2)}\right) . \end{aligned}$$
(27)

By using the asymptotic behavior of lower incomplete gamma function \({\varUpsilon }(\cdot ,\cdot )\) given in [28, Eq. (45.9.1)], i.e., \({\varUpsilon }(k,v \rightarrow 0)\rightarrow v^k/k\), (27) can be expressed as

$$P_{out}^{sys,\infty } =\prod _{r=1}^{R}\left( \frac{(2m_1\gamma _{th})^{m_1N_1}}{{\varGamma }(m_1N_1+1){\varOmega }_1^{m_1N_1}} + \frac{(2m_2\gamma _{th})^{m_2N_2}}{{\varGamma }(m_2N_2+1){\varOmega }_2^{m_2N_2}}\right) .$$
(28)

For large enough \(\bar{\gamma }\) and with the help of [29], asymptotic system OP can be obtained as

$$\begin{aligned} P_{out}^{sys,\infty }\approx {\mathcal {J}}\times \left( \bar{\gamma }\right) ^{-\sum _{r=1}^{R}\min (m_1N_1,m_2N_2)}+\,{\text{H.O.T.}}, \end{aligned}$$
(29)

where H.O.T denotes high order terms and \({\mathcal {J}}\) is given as

$$\begin{aligned} {\mathcal {J}}= {\left\{ \begin{array}{ll} \prod _{r=1}^{R}\left( \frac{(2m_1\gamma _{th})^{m_1N_1}}{{\varGamma }(m_1N_1+1)d_1^{-\alpha m_1N_1}} \right) ,&{} m_1N_1 < m_2N_2\\ \prod _{r=1}^{R}\left( \frac{(2m_1\gamma _{th})^{m_1N_1}}{{\varGamma }(m_1N_1+1)d_1^{-\alpha m_1N_1}}+\frac{(2m_2\gamma _{th})^{m_2N_2}}{{\varGamma }(m_2N_2+1)d_2^{-\alpha m_2N_2}}\right) , &{} m_1N_1 = m_2N_2\\ \prod _{r=1}^{R}\left( \frac{(2m_2\gamma _{th})^{m_2N_2}}{{\varGamma }(m_2N_2+1)d_2^{-\alpha m_1N_1}}\right) , &{} m_1N_1 > m_2N_2. \end{array}\right. } \end{aligned}$$
(30)

As described in [29], \(P_{out}^{sys,\infty }\approx ({\mathcal {G}}_a\bar{\gamma })^{-{\mathcal {G}}_d}\), so diversity and array gains become

$$\begin{aligned} {\mathcal {G}}_d= & {} \sum _{r=1}^{R}\min (m_1N_1,m_2N_2) \nonumber \\ {\mathcal {G}}_a= & {} {\mathcal {J}}^{-1/\sum _{r=1}^{R}\min (m_1N_1,m_2N_2)}. \end{aligned}$$
(31)

From (31), we can understand that, the number of relays have a direct impact on the diversity order. On the other hand, minimum number of severity parameters and antennas at both sources are more important. To obtain asymptotic SSER, we use the asymptotic property of lower incomplete Gamma function as described above. Similar to (28), \({\mathcal {F}}_{\gamma _{S_i} \rightarrow R_*^{us} \rightarrow {S_j}}^{up,\infty }\) can be expressed as

$$\begin{aligned} {\mathcal {F}}_{\gamma _{S_i} \rightarrow R_*^{us} \rightarrow {S_j}}^{up,\infty }(\gamma )=\prod _{r=1}^{R}\left( \frac{(2m_i\gamma )^{m_iN_i}}{{\varGamma }(m_iN_i+1){\varOmega }_i^{m_iN_i}} + \frac{(m_j\gamma )^{m_jN_j}}{{\varGamma }(m_jN_j+1){\varOmega }_j^{m_jN_j}}\right) . \end{aligned}$$
(32)

To simplify the theoretical complexity, we assume \(S_1 \rightarrow r\) and \(S_2 \rightarrow r\) hops are balanced i.e., \(m_i=m_j=m, N_i=N_j=N\) and \({\varOmega }_i={\varOmega }_j={\varOmega }\), then (32) can be expressed in a simple form

$$\begin{aligned} {\mathcal {F}}_{\gamma _{S_i} \rightarrow R_*^{us} \rightarrow {S_j}}^{up,\infty }(\gamma )={\mathcal {A}}\left( \frac{\gamma }{{\varOmega }}\right) ^{{\mathcal {B}}}, \end{aligned}$$
(33)

where \({\mathcal {A}}=\left[ (2^{mN}+1)(m)^{mN}/{\varGamma }(mN+1)\right] ^R\) and \({\mathcal {B}}=mNR\). For balanced hops, (25) becomes

$$\begin{aligned} P_s(e)=\frac{a\sqrt{b}}{\sqrt{\pi }}\int _{0}^{\infty }\gamma ^{-1/2}e^{-b\gamma }{\mathcal {F}}_{\gamma _{S_i \rightarrow R_*^{us} \rightarrow S_j}^{up,\infty }}(\gamma )d\gamma . \end{aligned}$$
(34)

By substituting (33) in (34), with the help of [29, Prop.1], asymptotic SSER can be expressed as

$$\begin{aligned} P_s^{\infty }(e)= \frac{{{\mathcal {A}}}a{\varGamma }({\mathcal {B}}+1/2)}{\sqrt{\pi }(b{\varOmega })^{{\mathcal {B}}}} +\text {H.O.T.}, \end{aligned}$$
(35)

where a, b are modulation coefficients as described above and \({\mathcal {G}}_d={{\mathcal {B}}}=mNR\). Therefore, the diversity order of the asymptotic system OP derived in (31) verifies the diversity order obtained from (35) when the hops are balanced.

4.4 Impact of Practical Transmission Impairments

To maximize the effects of MRT, we mainly assume a full-rate perfect feedback of channel coefficients at the relay node. However, if a wireless network suffers from power or bandwidth constraints, the feedback rate becomes insufficient which causes huge loses on the MRT performance. As shown in [23], the effects of limited feedback on the PDF of SNR can be expressed as

$$\begin{aligned} f_{\gamma _{S_i}}(\gamma ) = \frac{m_i^{m_iN_i}\gamma ^{m_iN_i-1}e^{-m_i\gamma /{\varOmega }_i(1-\xi )}}{({\varOmega }_i(1-\xi ))^{m_iN_i}{\varGamma }(m_iN_i)}, \end{aligned}$$
(36)

where \(f_{\gamma _{S_j}}(\gamma )\) can be obtained similarly. In (36), \(\xi\) denotes the rate of feedback, i.e., \(\xi =0\) shows full-rate feedback. Substituting (36) in (9) and applying same theoretical steps as shown above, system OP and SSER in the presence of limited feedback can be obtained.

In addition, to examine the impact of imperfect channel estimations, we derive effective e2e SNRs and obtain CDF of SNR. For this, we assume both hops are erroneously estimated and show the relationship between channel vectors and estimation errors as [20–24]

$$\begin{aligned} {\mathbf{h}}_{1,r}= & {} \bar{\mathbf {h}}_{1,r}+{\mathbf{e}}_{1,r} \nonumber \\ {\mathbf{h}}_{2,r}= & {} \bar{\mathbf{h}}_{2,r}+{\mathbf{e}}_{2,r}, \end{aligned}$$
(37)

where \(\bar{\mathbf {h}}_{1,r}\) and \(\bar{\mathbf {h}}_{2,r}\) are channel estimates and \({\mathbf{e}}_{1,r}, {\mathbf{e}}_{2,r}\) are estimation error vectors. Note that MRT based weight vectors become \({\mathbf{w}}_{1,r}=(\mathbf{\bar{h}}_{1,r}^{\dagger }/\Vert {\mathbf{h}}_{1,r}\Vert )\) and \({\mathbf{w}}_{2,r}= (\mathbf {\bar{h}}_{2,r}^{\dagger }/\Vert {\mathbf{h}}_{2,r}\Vert )\). Substituting (37) into (1), (2) and substituting \(\bar{\mathbf{h}}_{1,r}, \bar{\mathbf{h}}_{2,r}\) into (3) and after removing the self-interference term, e2e SNRs can be written as follows

$$\begin{aligned} \gamma _{S_i \rightarrow r \rightarrow S_j}=\frac{\gamma _{S_i}\gamma _{S_j}}{\varphi \gamma _{S_i}+\beta \gamma _{S_j}+\lambda }, \end{aligned}$$
(38)

where, \(\varphi =2 + 4\frac{P}{N_0}\sigma _{e_{i,r}}^2 +\frac{P}{N_0}\sigma _{e_{j,r}}^2, \beta = 1 + \frac{P}{N_0}\sigma _{e_{i,r}}^2, \lambda = \frac{P^2}{N_0^2}\sigma _{e_{i,r}}^2\sigma _{e_{j}}^2 + \frac{P}{N_0}\sigma _{e_{i,r}}^2 + \frac{P^2}{N_0^2}\sigma _{e_{i,r}}^2\sigma _{e_{j,r}}^2\) and \(i,j=\{1,2\}, i\ne j\). Note that \(\sigma _{e_{i,r}}^2\) and \(\sigma _{e_{j,r}}^2\) show the variances of the estimation errors. The upper bound given in (5) becomes \(\gamma _{S_i \rightarrow r \rightarrow S_j}\leqslant \min \left( \frac{\gamma _{S_i}}{\beta },\frac{\gamma _{S_j}}{\varphi }\right)\) and for Rayleigh fading channel i.e., \(m_1=m_2=1\), (8) can be written as

$$\begin{aligned} {\mathcal {F}}_{\gamma _{S_i \rightarrow r \rightarrow S_j}^{up}}(\gamma )= & {} \left( 1-\Pr [\gamma _{S_i}>\beta \gamma ]\Pr [\gamma _{S_j}> \varphi \gamma ]\right) \nonumber \\= & {} 1-\frac{{\varGamma }\left( N_i,\beta \frac{\gamma }{{\varOmega }_i}\right) }{{\varGamma }(N_i)}\times \frac{{\varGamma }\left( N_j,\varphi \frac{\gamma }{{\varOmega }_j}\right) }{{\varGamma }(N_j)}. \end{aligned}$$
(39)

From (39), it can be observed that the CDF of SNR deteriorates from the negative effects of imperfect channel estimations e.g., \(\varphi\) and \(\beta\). Applying same theoretical steps to (39), SSER and system OP in the presence of channel estimation errors can be easily derived.

5 Relay Location Optimization

Relay location optimization is an important design problem in relay networks to improve overall system performance and to combat the effects of co-channel interference. We assume normalized distance between \(S_1\) and \(S_2\) i.e., \(d_1 + d_2=1, d_1=d, d_2=1-d\) and \(R=1\). Under these assumptions, we optimize relay location to minimize asymptotic system OP as shown below

$$\begin{aligned} \mathop{{\min}}\limits_{d} P_{out}^{sys,\infty } \text { subject to: } 0< \text{d} < 1. \end{aligned}$$
(40)

We first take the second derivative of \(P_{out}^{sys,\infty }\), which is

$$\begin{aligned} \frac{\partial ^2P_{out}^{sys,\infty }}{\partial d^2}= & {} {\mathcal {Z}}_1m_1N_1\alpha (m_1N_1\alpha -1)d^{m_1N_1\alpha -2} \nonumber \\&+{\mathcal {Z}}_2m_2N_2\alpha (m_2N_2\alpha -1)(1-d)^{m_2N_2\alpha -2}, \end{aligned}$$
(41)

where \({\mathcal {Z}}_1=\frac{(2m_1\gamma _{th})^{m_1N_1}}{{\varGamma }(m_1N_1+1)\bar{\gamma }^{m_1N_1}}\) and \({\mathcal {Z}}_2=\frac{(2m_2\gamma _{th})^{m_2N_2}}{{\varGamma }(m_2N_2+1)\bar{\gamma }^{m_2N_2}}\). Since \(m_1N_1\alpha >1\) and \(m_2N_2\alpha >1\), we understand that the proposed problem is convex i.e., \(\frac{\partial ^2P_{out}^{sys,\infty }}{\partial d^2}>0\). Hence, if we take the first derivative of \(P_{out}^{sys,\infty }\) w.r.t d and equalize to zero, optimum relay location can be found

$$\begin{aligned} \frac{\partial P_{out}^{sys,\infty }}{\partial d}={\mathcal {Z}}_1m_1N_1\alpha d^{m_1N_1\alpha -1} -{\mathcal {Z}}_2m_2N_2\alpha (1-d)^{m_2N_2\alpha -1}=0. \end{aligned}$$
(42)

After some manipulations

$$\begin{aligned} d^{m_1N_1\alpha -1} =\frac{{\mathcal {Z}}_2m_2N_2}{{\mathcal {Z}}_1m_1N_1} (1-d)^{m_2N_2\alpha -1}. \end{aligned}$$
(43)

To obtain optimum relay distance, root finding algorithms can be applied. For different channel conditions and number of antennas, Table 1 shows optimum relay distances when \(\bar{\gamma }=10\) dB, \(\alpha =2\) and \(\gamma _{th}=3\) dB. We infer from the table that when \(m_1N_1>m_2N_2\), optimum relay location must be close to \(S_2\) and when \(m_2N_2>m_1N_1\), optimum position of relay must be near \(S_1\) to minimize system OP. Besides, when \(m_1=N_1=m_2=N_2\), optimum relay location is in the middle of both sources, i.e., \(d=1/2\).

Table 1 Optimum relay distance for \(\alpha =2, \gamma _{th}=3\) dB and \({\bar{\gamma }}=10\) dB
Full size table

6 Numerical Examples

In this section, we present various numerical examples for different number of antennas, relays and fading severity to verify the analytical results and demonstrate the usefulness of the proposed system. SSER and system OP curves are obtained via Monte-Carlo simulations where BPSK signalling is used. In the simulations, path-loss component is chosen as \(\alpha =1.6\) to represent factory or office environment [30] and distances are given as \(d_1=d_2=d=0.5\) unless otherwise stated.

Figure 2 depicts the SSER versus \({\varOmega }\) performance of the proposed network for balanced hops \(m_1 = m_2 = 1, N_1 = N_2 = 2\) and different number of relays. It is observed from the figure that using more relays both yield a much better performance and enhanced diversity orders (slope of the curves), i.e., 16 dB SNR gain can be obtained and the diversity order becomes 2 to 4 if \(R=1\) is compared with \(R=2\). Besides, the theoretical results precisely match with the simulation at all cases and the slopes of the curves verify the diversity gains obtained e.g., 2, 4 and 6. In addition, from the system design perspective, we observe that using 2 relays and 2 antennas at both sources can achieve \(10^{-8}\) SSER at 19 dB SNR which is quite appealing.

Fig. 2
figure 2

Sum SER performance of MIMO AF TWRN for \(m_1=m_2=1\) i.e., Rayleigh fading channel and \(R=1, 2, 3\)

Full size image

Figure 3 illustrates the system OP for unbalanced links and different number of relays when \(\gamma _{th}=8.5\) dB. As can be seen, the proposed lower bound for system OP is in an excellent agreement with the simulation results in all cases especially at medium to high SNRs. In addition, the asymptotic curves of the system OP verifies the diversity order derived in (31) i.e., \({\mathcal {G}}_d=\sum _{r=1}^{R}\min (m_1N_1,m_2N_2)\). As we observed in the previous figure, increasing the total number of relays have a direct impact both on system performance and diversity orders.

Fig. 3
figure 3

System OP performance for different number of relays and fading severity

Full size image

In Figs. 4 and 5, the impact of limited feedback and imperfect channel estimations on SSER and system OP are demonstrated respectively. From Fig. 4, we can clearly observe that, although the limited feedback deteriorates the SSER performance, there is no change on the diversity gains. Note that in Fig. 5, we remove subscript r as we are considering a single-relay case and the estimation error variances are shown as \(\sigma _{e_{1}}^2\) and \(\sigma _{e_{2}}^2\). As can be seen in Fig. 5, imperfect channel estimations not only have an adverse effect on the performance of system OP but also error floors result in huge performance loses as no diversity can be obtained. Besides, as seen in the previous figures, asymptotic SSER matches quite good with simulation in Fig. 4 and the proposed lower bound for system OP provides an excellent match with the simulations in Fig. 5. We also observe that in two-way relaying, erroneously estimated channel vectors have more adverse effect on the system OP performance as both \(S_1 \rightarrow R \rightarrow S_2\) and \(S_2 \rightarrow R \rightarrow S_1\) paths are being affected. However, in one-way relaying, the impact of imperfect channel estimations are less affective then the two-way relaying as there is only a single path. The difference can be better understood by comparing Eq. (38) in the manuscript and [25].

Fig. 4
figure 4

Impact of limited feedback on the SSER performance

Full size image
Fig. 5
figure 5

Impact of imperfect channel estimations on the system OP

Full size image

Figure 6 plots optimum relay locations for different number of antennas and fading severity when \(P/N_0=10\) dB and \(R=1\). As can be seen, this figure can be easily used to obtain optimum relay locations. For example, when \(m_2N_2>m_1N_1, d_2>d_1\). In contrast, \(d_1>d_2\), when \(m_1N_1>m_2N_2\). Likewise, when \(m_1N_1=m_2N_2\) optimum distance becomes \(d_1=d_2=1/2\). All these results can be justified by using Eq. (43). In addition, Fig. 7 presents the effect of optimum relay location on the system OP for different number of antennas, relays and fading severity. Especially in this figure, we use the optimum values obtained in Table 1 and investigate the effect of optimum relay location on the system OP. As can be seen from both cases that optimum relay position can bring up to 6 dB performance gain and can enhance the diversity orders from \({\mathcal {G}}_d=\sum _{r=1}^{R}\min (m_1N_1,m_2N_2)\) to \({\mathcal {G}}_d=\sum _{r=1}^{R}\max (m_1N_1,m_2N_2)\).

Fig. 6
figure 6

System OP versus \(d_1\) for different number of antennas and severity parameters

Full size image
Fig. 7
figure 7

System OP performance for different number of antennas, relays and severity parameter for optimum and suboptimum (\(d_1=d_2=1/2\)) relay location

Full size image

7 Conclusions

In this work, the performance of maximal ratio transmission with relay selection is analyzed in AF MIMO TWRNs. For the proposed structure, we derive approximate and asymptotic user, system outage probabilities and sum symbol error rate for flat i.n.i.d Nakagami-m fading channels and obtain diversity and array gains. In addition, important performance indicators such as limited feedback and imperfect channel estimations are investigated which are critical on the performance of MRT. Finally, relay location optimization which can both improve system performance and diversity gains are obtained. Note that, the proposed network can be a promising option in slow-fading wireless sensor or mesh networks with massive number of relays and antennas which prohibits the use of channel coding techniques to obtain high reliability in practice.