1 Introduction

User cooperation has emerged as a spatial diversity technique to provide robustness against channel fluctuations by utilizing the broadcast nature of the wireless transmission [1, 2]. Cooperative diversity [3, 4] is an important technique for achieving spatial diversity and provides performance improvements through the use of available resources in distributed wireless networks. The basic idea of cooperative networks is that multiple relays assist the source transmit a message to the destination, thereby the destination can receive multiple independent copies of the same signal and achieve diversity.

Although some literatures about cooperative relaying focus on simultaneous transmissions from multiple relays [5], it is showed that carefully selected single-relay transmission incurs little performance loss compared to multiple-relay transmissions [6,7,8,9,10]. Bletsas, Lippman and Reed proposes the concept of opportunistic relaying (OR) and analyzes the performance of OR scheme in [6,7,8,9]. Simple OR scheme was present in [6], which select the best relay based on local measurements of the instantaneous channel conditions. [7] showed that OR scheme achieves the same diversity-multiplexing tradeoff as distributed space–time coding by information theoretic analysis. The optimal selection of a single relay to minimize the outage probability in Amplify-and-Forward (AF) strategy was given in [8]. In [9], the outage probability was analyzed under an aggregate power constraint in AF and Decode-and-Forward (DF) strategies. The performance of OR schemes in three different types of channel state information (CSI) scenarios was studied in [10]. Prior works on relay selection focus on the case that all relays have single antenna. However, in many practical situations, it is feasible that multiple antennas are deployed at one or more relays.

The impact of multiple antennas on relays in cooperative networks is considered in [11,12,13,14]. The performance of maximum ratio combining (MRC) on receive and transmit beamforming (TB) methods at multiple relays with multiple antennas was analyzed in [11] in terms of diversity-multiplexing tradeoff. Furthermore, [12] studied the outage performance of the distributed MRC-TB scheme and prove that distributed MRC-TB scheme could offer significant power gain over distributed space–time coding techniques. In [13], the end-to-end error performance of threshold maximal ratio combining (T-MRC) and threshold selection combining (T-SC) in multi-antenna multi-relay cooperative networks was present over Nakagami-m fading channels. Based on [13, 14] studied the outage probability of T-MRC and T-SC of multi-antenna multi-relay with beamforming in DF networks under total sum power constraint (TSPC) of all relays and maximum per-relay power constraint (PRPC). In these papers, all decoded relays select one antenna and transmit simultaneously, which induces large synchronization signaling overheads among relays. However, there are few investigations on the performance of choosing one relay with multiple antennas.

Motivated by this, we propose two different centralized multi-antenna relay selection schemes (Opportunistic Multi-antenna Relay Selection; Average Best Relay Selection) and derive the outage probability and error performance for binary phase shift keying (BPSK) modulation of OMRS and ABRS over independent, non-identical Nakagami-m fading channels with Decode-and-Forward (DF) relaying in multi-antenna multi-relay cooperative networks. The optimal relay is chosen based on instantaneous Signal-to-Noise Ratio (SNR) in OMRS, while ABRS selects relay based on average SNR. In our proposed scheme, different from OR scheme [5], the selected relay with multiple antennas decodes the received signal from the source with MRC and retransmits the decoded signal to the destination with beamforming. By comparing the outage probability and error performance of our proposed schemes with other scheme, we show that opportunistic relay with multiple antennas can achieve significant performance improvement.

The remainder of this paper is structured as follows: In Sect. 2, we introduce our system model. The performance of proposed schemes are analyzed and presented in Sect. 3. In Sect. 4, some simulation results are given. Finally, we draw some conclusion in Sect. 5.

2 System Model

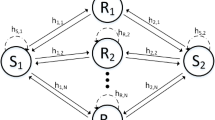
As illustrated in Fig. 1, we consider a two hop network model, where a source (S) communicates with a destination (D), via a direct path as well as N relays using DF relaying. Supposed that relay i is deployed with n i antennas, while S and D have only one antenna. The channels are assumed to be mutually-independent and reciprocal. This condition is fulfilled in time division duplexing systems where the round-trip duplex time is much shorter than the coherence time of the channel, or in frequency division duplexing systems where the frequency duplex separation is smaller than the coherence bandwidth [15]. We also assume that all additive white Gaussian noise (AWGN) terms have zero mean and equal variance N 0.

Fig. 1
figure 1

Multi-antenna multi-relay networks

Full size image

The date transmission is over two time slots using two hops. In the first hop, the source broadcasts the signal to D and all the relays. The received signal at relay i in the first hop can be written as

$$\begin{aligned} {\mathbf{y}}_{s,i} &= \left[ {\begin{array}{*{20}c} {h_{i1} } & {h_{i2} } & \cdots & {h_{{in_{i} }} } \\ \end{array} } \right]^{T} s + \left[ {\begin{array}{*{20}c} {n_{i1} } & {n_{i2} } & \cdots & {n_{{in_{i} }} } \\ \end{array} } \right]^{T}\\&= {\mathbf{h}}_{i} s + {\mathbf{n}}_{i}\end{aligned}$$
(1)

where \( {\mathbf{y}}_{s,i}\) is the m i  × 1 receive signal vector, and s is the transmitted symbol. The vector \( {\mathbf{h}}_{i}\) is the n i  × 1 channel transfer vector from source to the relay i, and h ij is the channel coefficient from S to the jth antenna of relay i, which follows Nakagami-m distribution with the shape fading parameter m si and average power fading parameter \( \varOmega_{si}\). The vector n i is the m i  × 1 complex circular additive white Gaussian noise (AWGN) vector at relay i and n ij follows \( \mathcal{\mathcal{C}\mathcal{N}} ( 0 , 1 )\).

The received signal at D in the first hop can be expressed as

$$ y_{s,d} = h_{sd} s + n_{sd}$$
(2)

where \( y_{s,d}\) is the receive signal, h sd is the channel coefficient from S to D following Nakagami-m distribution with the shape fading parameter m sd and average power fading parameter \( \varOmega_{sd}\).

Since each relay combines its received signal with MRC technique, the instantaneous SNR at relay i and D in the first hop can be obtained as following, respectively

$$ \gamma_{s,i} = \rho_{1} \left\| {{\mathbf{h}}_{i} } \right\|^{2} = \rho_{1} \sum\limits_{j = 1}^{{n_{i} }} {\left| {h_{ij} } \right|^{2} }$$
(3)
$$ \gamma_{s,d} = \rho_{1} \left| {h_{sd} } \right|^{2}$$
(4)

where \( \gamma_{s,i}\) is the instantaneous SNR at relay i, \( \gamma_{s,d}\) is the instantaneous SNR at D. \( \rho_{1} = {{P_{s} } \mathord{\left/ {\vphantom {{P_{s} } {N_{0} }}} \right. \kern-0pt} {N_{0} }}\) is the transmit SNR on the source, since n ij follows \( \mathcal{\mathcal{C}\mathcal{N}} ( 0 , 1 )\), then \( \rho_{1} = P_{s}\), and \( P_{s}\) is the source transmission power.

In the second hop, the relay i, which successfully decodes the received signal, is using its corresponding beamforming weight, w i , to forward the signal. For the relay is assumed to have perfect CSI, we can obtain its beamforming weight as \( {\mathbf{w}}_{i} = {{{\mathbf{g}}_{i} } \mathord{\left/ {\vphantom {{{\mathbf{g}}_{i} } {\left\| {{\mathbf{g}}_{i} } \right\|}}} \right. \kern-0pt} {\left\| {{\mathbf{g}}_{i} } \right\|}}\). The received signal at D from relay i in the second hop is

$$ y_{i,d} = \left[ {\begin{array}{*{20}c} {g_{i1} } & {g_{i2} } & \cdots & {g_{{in_{i} }} } \\ \end{array} } \right]^{T} \left[ {\begin{array}{*{20}c} {w_{i1} } & {w_{i2} } & \cdots & {w_{{in_{i} }} } \\ \end{array} } \right]r + n_{id}$$
$$ = {\mathbf{g}}_{i} {\mathbf{w}}_{i}^{H} r + n_{id}$$
(5)

where g i represents the 1 × m i channel transfer vector from relay i to the destination, and \( g_{ij}\) is the channel coefficient from the jth antenna at relay i to D, which follows Nakagami-m distributed with the shape fading parameter m id and average power fading parameter \( \varOmega_{id}\). r is the decoded signal at the relay. \( n_{id}\) is the AWGN at D which follows \( \mathcal{\mathcal{C}\mathcal{N}} ( 0 , 1 )\).

Then the instantaneous SNR at D in the second hop can be obtained as

$$ \gamma_{i,d} = \rho_{2} \left\| {{\mathbf{g}}_{i} } \right\|^{2} = \rho_{2} \sum\limits_{j = 1}^{{n_{i} }} {\left| {g_{ij} } \right|^{2} }$$
(6)

where \( \rho_{2} = {{P_{r} } \mathord{\left/ {\vphantom {{P_{r} } {N_{0} }}} \right. \kern-0pt} {N_{0} }}\) is the transmit SNR on relay, since the \( n_{id}\) follows \( \mathcal{\mathcal{C}\mathcal{N}} ( 0 , 1 )\), then \( \rho_{2} = P_{r}\), and \( P_{r}\) is the relay transmission power.

We further consider the total end-to-end transmission power \( P_{total}\) constraint, then \( P_{s} = \zeta P_{total}\), \( P_{r} = \left( {1 - \zeta } \right)P_{total}\). Note that ζ∈(0,1] and (1-ζ)denote the fractions of the total end-to-end power allocated to the source transmission and overall relay transmission, respectively.

3 Performance Analysis

The set of the available relays is defined as R relay  = {R 1, R 2,…, R N }. \( \mathcal{\mathcal{C}}\) denotes the decoding set which constitutes all subset of R relay . For simplicity, we assume that the elements of \( \mathcal{\mathcal{C}}\) is \( \Theta_{1}\), \( \Theta_{2}\),…, \( \Theta_{L}\), defined as\( \Theta_{n} \mathop = \limits^{\Delta } \left\{ {R_{{r_{j} }} \in \mathcal{\ominus }R_{relay} :\frac{1}{2}\log_{2} (1 + \gamma_{{s,R_{{r_{j} }} }} ) \ge R,\sum\limits_{j = 1}^{l} {2^{{r_{j} - 1}} } = n - 1,r_{1} \ne r_{2} \ne \cdots \ne r_{l} } \right\}\) where \( n = 1,2, \cdots ,L\), \( L = 2^{N}\) represents the size of \( \mathcal{\mathcal{C}}\) and l represents the total relay number in \( \Theta _{n}\). Relay \( R_{{r_{j} }}\) is defined to successfully decode the transmitted signal from S if \( \frac{1}{2}\log_{2} (1 + \gamma_{{s,R_{{r_{j} }} }} ) \ge R\), i.e., no outage event happens during the first hop. R is the end-to-end spectral efficiency. Then we note γ th  = 22R-1 as the threshold SNR.

We now use the moment generating function (MGF) as \( M_{X} \left( s \right) = {\text{E}}\left( {e^{ - sX} } \right)\) (where E is the statistical average operator) to find the distribution of \( \gamma_{s,i}\) in (3). Since each |h ij | is Nakagami-m random variable (RV), then the probability density function (PDF) of |h ij | can be written as [16]

$$ f_{{\left| {h_{ij} } \right|}} \left( r \right) = \frac{2}{{\varGamma \left( {m_{si} } \right)}}\left( {\frac{{m_{si} }}{{\varOmega_{si} }}} \right)^{{m_{si} }} r^{{2m_{si} - 1}} e^{{ - m_{si} r^{2} /\varOmega_{si} }}$$
(7)

According to (7), we can derive the PDF of \( \left| {h_{ij} } \right|^{2}\) as following

$$ f_{{\left| {h_{ij} } \right|^{2} }} \left( r \right) = \frac{1}{{\varGamma \left( {m_{si} } \right)}}\left( {\frac{{m_{si} }}{{\varOmega_{si} }}} \right)^{{m_{si} }} r^{{m_{si} - 1}} e^{{ - m_{si} r/\varOmega_{si} }}$$
$$ = \varGamma \left( {\begin{array}{*{20}c} {\frac{{m_{si} }}{{\varOmega_{si} }},} & {m_{si} } \\ \end{array} } \right)$$
(8)

We notice that \( \left| {h_{ij} } \right|^{2}\) is gamma distributed RV with parameters \( {{m_{si} } \mathord{\left/ {\vphantom {{m_{si} } {\varOmega_{si} }}} \right. \kern-0pt} {\varOmega_{si} }}\) and \( m_{si}\), its MGF can be obtained as

$$ M_{{\left| {h_{ij} } \right|^{2} }} \left( s \right) = \left( {1 + {{\varOmega_{si} } \mathord{\left/ {\vphantom {{\varOmega_{si} } {m_{si} }}} \right. \kern-0pt} {m_{si} }}s} \right)^{{ - m_{si} }}$$
(9)

Because of the independence of \( \left| {h_{ij} } \right|^{2}\), j = 1,2,…,n i , the MGF of \( \gamma_{s,i}\) can be obtained as

$$ M_{{\gamma_{s,i} }} \left( s \right) = \prod\limits_{j = 1}^{{n_{i} }} {M_{{\left| {h_{ij} } \right|^{2} }} \left( {\rho_{1} s} \right)} = \left( {1 + \rho_{1} {{\varOmega_{si} } \mathord{\left/ {\vphantom {{\varOmega_{si} } {m_{si} }}} \right. \kern-0pt} {m_{si} }}s} \right)^{{ - n_{i} m_{si} }}$$
(10)

Taking into account that the fading parameter m si is considered to be integer, we can get the cumulative distribution function (CDF) of \( \gamma_{s,i}\) as

$$ F_{{\gamma_{s,i} }} \left( \gamma \right) = \mathcal{\mathcal{L}}^{ - 1} \left( {s^{ - 1} M_{{\gamma_{s,i} }} \left( s \right)} \right)\left| {_{\gamma } } \right. = \mathcal{\mathcal{L}}^{ - 1} \left( {s^{ - 1} \left( {1 + \rho_{1} \frac{{\varOmega_{si} }}{{m_{si} }}s} \right)^{{ - n_{i} m_{si} }} } \right)\left| {_{\gamma } } \right.$$
$$ = 1 - \sum\limits_{k = 0}^{{n_{i} m_{si} - 1}} {\left( {\frac{{m_{si} }}{{\varOmega_{si} \rho_{1} }}} \right)^{k} \frac{{\gamma^{k} }}{k!}e^{{ - \frac{{m_{si} }}{{\varOmega_{si} \rho_{1} }}\gamma }} }$$
(11)

where \( \mathcal{\mathcal{L}}^{ - 1} \left( \cdot \right)\) denotes the inverse Laplace Transform.

Then, the probability of Θ n can be written as

$$ \begin{aligned} \Pr \left\{ {\Theta_{n} } \right\} = \left( {\prod\limits_{{i \in \Theta_{n} }} {\left( {1 - F_{{\gamma_{s,i} }} \left( {\gamma_{th} } \right)} \right)} } \right)\left( {\prod\limits_{{j \in \bar{\Theta }_{n} }} {F_{{\gamma_{s,j} }} \left( {\gamma_{th} } \right)} } \right) \hfill \\ = \left( {\prod\limits_{{i \in \Theta_{n} }} {\left( {\sum\limits_{k = 0}^{{n_{i} m_{si} - 1}} {\left( {\frac{{m_{si} }}{{\varOmega_{si} \rho_{1} }}} \right)^{k} \frac{{\gamma_{th}^{k} }}{k!}e^{{ - \frac{{m_{si} }}{{\varOmega_{si} \rho_{1} }}\gamma_{th} }} } } \right)} } \right) \hfill \\ \times \left( {\prod\limits_{{j \in \bar{\Theta }_{n} }} {\left( {1 - \sum\limits_{k = 0}^{{n_{j} m_{sj} - 1}} {\left( {\frac{{m_{sj} }}{{\varOmega_{sj} \rho_{1} }}} \right)^{k} \frac{{\gamma_{th}^{k} }}{k!}e^{{ - \frac{{m_{sj} }}{{\varOmega_{sj} \rho_{1} }}\gamma_{th} }} } } \right)} } \right) \hfill \\ \end{aligned}$$
(12)

where \( \Theta_{n}\) and \( \bar{\Theta }_{n}\) denote the sets composed of correctly decoded relay and incorrectly decoded relay respectively. i and j represent the index of relays in set \( \Theta_{n}\) and \( \bar{\Theta }_{n}\).

In this paper, according to which type of SNR can be exploited for relay selection, two opportunistic relay schemes are proposed: OMRS and ABRS. We now describe the steps for the transmission of both OMRS and ABRS schemes in detail.

  1. 1.

    OMRS scheme

Step 1 the source broadcasts the signal and all relays listen.

Step 2 the relays, which decode the signal from the source successfully, send training sequence to the destination in Time-Division-Duplex (TDD) mode or Frequency-Division- Duplex (FDD) mode. This enables the destination to estimate the instantaneous SNR and CSI from the relays to the destination. Notice that the acquisition of the instantaneous SNR with training sequence requires additional signaling overhead, thus inducing time inefficiency in TDD mode or reducing the spectral efficiency in FDD mode. Therefore, the training sequence should be carefully designed to minimize the signaling overhead.

Step 3 based on the instantaneous SNR, destination selects a “best” relay with the best instantaneous SNR to the destination. Then the destination broadcasts the selected relay’s identity (ID) to all relays and feeds back the required CSI to the selected relay.

Step 4 the selected relay sends the decoded signal to the destination by beamforming.

  1. 2.

    ABRS scheme

Step 1 the source broadcasts signal to all relays.

Step 2 the successfully decoding relays send flag message to the destination in TDD mode or FDD mode so that the destination knows the decoding relay subset \( \Theta_{n}\). Note that the signaling overhead of flag message in ABRS scheme is obviously lower than that of training sequence in OMRS scheme.

Step 3 the destination, which is assumed to obtain the average SNR from all relays to the destination by using statistical CSI achieved previously, selects a “best” relay with the best average SNR. Then the destination broadcasts the selected relay’s ID to all relays and sends training sequence to the selected relay. Since all channels are assumed to be reciprocal, the selected relay can obtain the required CSI by training sequence.

Step 4 Finally, the selected relay beamforming the decoded signal to the destination.

We assume that the transmission strategies described above can be implemented correctly, so the outage probabilities of OMRS and ABRS schemes are derived as follows.

3.1 Performance Analysis of OMRS Scheme

  1. 1.

    Outage Probability of OMRS scheme

In OMRS scheme with DF protocol, the “best” relay i sel in the decoding subset Θ n is chosen to maximize the instantaneous SNR at D for all i∈Θ n :

$$ i_{sel} = \mathop {\arg \hbox{max} }\limits_{{i \in \Theta_{n} }} \left\{ {\gamma_{i,d} } \right\}$$
(13)

The MGF and CDF of \( \gamma_{i,d}\) can be obtained as

$$ M_{{\gamma_{i,d} }} \left( s \right) = \left( {1 + \rho_{2} \frac{{\varOmega_{id} }}{{m_{id} }}s} \right)^{{ - n_{i} m_{id} }}$$
(14)
$$ F_{{\gamma_{i,d} }} \left( \gamma \right) = 1 - \sum\limits_{k = 0}^{{n_{i} m_{id} - 1}} {\left( {\frac{{m_{id} }}{{\rho_{2} \varOmega_{id} }}} \right)^{k} \frac{{\gamma^{k} }}{k!}e^{{ - \frac{{m_{id} }}{{\rho_{2} \varOmega_{id} }}\gamma }} }$$
(15)

Given Θ n , the conditional probability of \( \gamma_{{i_{sel} ,d}} = \hbox{max} \left\{ {\gamma_{i,d} } \right\}\) can be achieved as

$$ \Pr \left\{ {\gamma_{{i_{sel} ,d}} < \gamma |\Theta_{n} } \right\} = \prod\limits_{{i \in \Theta_{n} }} {F_{{\gamma_{i,d} }} \left( \gamma \right)} = \prod\limits_{{i \in \Theta_{n} }} {\left( {1 - \sum\limits_{k = 0}^{{n_{i} m_{id} - 1}} {\left( {\frac{{m_{id} }}{{\rho_{2} \varOmega_{id} }}} \right)^{k} \frac{{\gamma^{k} }}{k!}e^{{ - \frac{{m_{id} }}{{\rho_{2} \varOmega_{id} }}\gamma }} } } \right)}$$
(16)

The MGF of \( \gamma_{{i_{sel} ,d}}\) can be calculated with the help of [12, Eq. 3.381.4] as (17), where l is the total relay number in \( \Theta_{n}\), and t = 1,2,…,l is the index of relay i in \( \Theta_{n}\), \( \upsilon_{t} = \sum\limits_{n = 1}^{t} {\frac{{m_{{\lambda_{n} }} }}{{\rho_{2} \varOmega_{{\lambda_{n} }} }}}\), \( u_{t} = \sum\limits_{n = 1}^{t} {k_{n} }\), \( \varGamma \left( \cdot \right)\) is Gamma function defined in [12, Eq. 8.310].

$$\begin{aligned} & M_{{\gamma_{{i_{sel} ,d}} |\Theta_{n} }} \left( s \right)\\ &\quad = s\int\limits_{0}^{\infty } {F_{{\gamma_{{i_{sel} ,d}} }} \left( x \right)} e^{ - xs} dx \\ &\quad = 1 + s\sum\limits_{t = 1}^{l} {\sum\limits_{{\lambda_{1} = 1}}^{l - t + 1} {\sum\limits_{{\lambda_{2} = \lambda_{1} + 1}}^{l - t + 2} { \cdots \sum\limits_{{\lambda_{t} = \lambda_{t - 1} + 1}}^{l} {\sum\limits_{{k_{1} = 0}}^{{m_{{\lambda_{1} }} - 1}} {\sum\limits_{{k_{2} = 0}}^{{m_{{\lambda_{2} }} - 1}} \cdots } \sum\limits_{{k_{t} = 0}}^{{m_{{\lambda_{t} }} - 1}} {\left( { - 1} \right)^{t} \varGamma \left( {u_{t} + 1} \right)\left( {\frac{{\upsilon_{t} }}{{\rho_{2} }} + s} \right)^{{ - u_{t} - 1}} \left( {\prod\limits_{n = 1}^{t} {\frac{{m_{{\lambda_{n} }}^{{k_{n} }} }}{{k_{n} !\rho_{2}^{{k_{n} }} \varOmega_{{\lambda_{n} }}^{{k_{n} }} }}} } \right)} } } } } \end{aligned}$$
(17)

Note that the equality in (17) is obtained from the following multinomial expansion

$$ \prod\limits_{t = 1}^{l} {\left( {1 - B_{t} } \right)} = 1 + \sum\limits_{t = 1}^{l} {\sum\limits_{{\lambda_{1} = 1}}^{l - t + 1} {\sum\limits_{{\lambda_{2} = \lambda_{1} + 1}}^{l - t + 2} { \cdots \sum\limits_{{\lambda_{t} = \lambda_{t - 1} + 1}}^{l} {\prod\limits_{n = 1}^{t} {\left( { - B_{{\lambda_{n} }} } \right)} } } } }$$

Assuming the received signals from S in the first hop and relay i in the second hop are combined with MRC at D, thus the total SNR at D is obtained as

$$ \gamma_{total}^{OMRS} = \gamma_{s,d} + \gamma_{{i_{sel} ,d}}$$
(18)

Since |h sd | is Nakagami-m random variable (RV), then the PDF of |h sd | can be written as

$$ f_{{\left| {h_{sd} } \right|}} \left( r \right) = \frac{2}{{\varGamma \left( {m_{sd} } \right)}}\left( {\frac{{m_{sd} }}{{\varOmega_{sd} }}} \right)^{{m_{sd} }} r^{{2m_{sd} - 1}} e^{{ - m_{sd} r^{2} /\varOmega_{sd} }}$$
(19)

Based on (2), the PDF and CDF of \( \gamma_{s,d}\) can be derived as following

$$ f_{{\gamma_{s,d} }} \left( r \right) = \frac{1}{{\varGamma \left( {m_{sd} } \right)}}\left( {\frac{{m_{sd} }}{{\varOmega_{sd} \rho_{1} }}} \right)^{{m_{sd} }} r^{{m_{sd} - 1}} e^{{ - \left( {\frac{{m_{sd} }}{{\varOmega_{sd} \rho_{1} }}} \right)r}}$$
(20)
$$ F_{{\gamma_{s,d} }} \left( \gamma \right) = 1 - \sum\limits_{k = 0}^{{m_{sd} - 1}} {\left( {\frac{{m_{sd} }}{{\rho_{2} \varOmega_{sd} }}} \right)^{k} \frac{{\gamma^{k} }}{k!}e^{{ - \frac{{m_{id} }}{{\rho_{2} \varOmega_{sd} }}\gamma }} }$$
(21)

Then the MGF of \( \gamma_{s,d}\) can be obtained as

$$ M_{{\gamma_{s,d} }} \left( s \right) = \left( {1 + {{\rho_{1} \varOmega_{sd} } \mathord{\left/ {\vphantom {{\rho_{1} \varOmega_{sd} } {m_{sd} }}} \right. \kern-0pt} {m_{sd} }}s} \right)^{{ - m_{sd} }}$$
(22)

Furthermore, \( \gamma_{s,d}\) and \( \gamma_{{i_{sel} ,d}}\) are independent, so the MGF of \( \gamma_{total}^{OMRS}\) can be written as

$$ M_{{\gamma_{total}^{OMRS} |\Theta_{n} }} \left( s \right) = M_{{\gamma_{s,d} }} \left( s \right)M_{{\gamma_{{i_{sel} ,d}} |\Theta_{n} }} \left( s \right)$$
(23)

By substituting (17) and (22) into (23) we obtain a closed form expression of \( M_{{\gamma_{total}^{OMRS} |\Theta_{n} }} \left( s \right)\).

$$ \begin{aligned} &\text{P}_{DF}^{OMRS} \left\{ {\gamma_{total}^{OMRS} < \gamma_{th} |\Theta_{n} } \right\}{ = }\int\limits_{0}^{{\gamma_{th} }} {\prod\limits_{{i \in \Theta_{n} }} {\Pr \left\{ {\gamma_{{i_{sel} ,d}} < \gamma_{th} - x} \right\}} } f_{{\gamma_{s,d} }} (x)dx\\ &= F_{{\gamma_{s,d} }} \left( {\gamma_{th} } \right) + \frac{{m_{sd}^{{m_{sd} }} }}{{\rho_{1}^{{m_{sd} }} \varOmega_{sd}^{{m_{sd} }} \varGamma \left( {m_{sd} } \right)}}e^{{ - \frac{{m_{sd} \gamma_{th} }}{{\rho_{1} \varOmega_{sd} }}}} \sum\limits_{t = 1}^{l} {\sum\limits_{{\lambda_{1} = 1}}^{l - t + 1} {\sum\limits_{{\lambda_{2} = \lambda_{1} + 1}}^{l - t + 2} { \cdots \sum\limits_{{\lambda_{t} = \lambda_{t - 1} + 1}}^{l} {\left( { - 1} \right)^{t} } } } } \hfill \\ & \times \, \sum\limits_{{k_{1} = 0}}^{{n_{\lambda 1} m_{{\lambda_{1} }} - 1}} {\sum\limits_{{k_{2} = 0}}^{{n_{{\lambda_{2} }} m_{{\lambda_{2} }} - 1}} \cdots } \sum\limits_{{k_{t} = 0}}^{{n_{{\lambda_{n} }} m_{{\lambda_{t} }} - 1}} {\gamma_{th}^{{m_{sd} + u_{t} }} \left( {\prod\limits_{n = 1}^{t} {\frac{{m_{{\lambda_{n} }}^{{k_{n} }} }}{{k_{n} !\rho_{2}^{{k_{n} }} \varOmega_{{\lambda_{n} }}^{{k_{n} }} }}} } \right) B\left( {m_{sd} ,u_{t} + 1} \right){}_{1}F_{1} \left( {u_{t} + 1;m_{sd} + u_{t} + 1;\frac{{m_{sd} \gamma_{th} }}{{\rho_{1} \varOmega_{sd} }} - \frac{{\upsilon_{t} \gamma_{th} }}{{\rho_{2} }}} \right)} \hfill \\ \end{aligned}$$
(24)

Then the conditional outage probability of OMRS \( \text{P}_{DF}^{OMRS} \left\{ {\gamma_{total}^{OMRS} < \gamma_{th} |\Theta_{n} } \right\}\) can be achieved with the help of [17, Eq. 3.383.1] as (24) where \( B\left( { \cdot , \cdot } \right)\) is Bata function defined in [17, Eq. 8.38],\( \varPhi \left( { \cdot , \cdot ; \cdot } \right)\) is confluent hypergeometric function defined in [17, Eq. 9.210].

Based on (12) and (24), the outage probability of OMRS in DF protocol can be obtained as

$$\begin{aligned} P_{DF}^{OMRS} (outage) = \sum\limits_{{\Theta_{n} }} {\text{P}_{DF}^{OMRS} \left\{ {\gamma_{total}^{OMRS} < \gamma_{th} |\Theta_{n} } \right\}\Pr \left\{ {\Theta_{n} } \right\}} \end{aligned}$$
(25)
  1. 2.

    Error Performance of OMRS scheme

Given \( \Theta_{n}\), the conditional error rate at D can be evaluated based on (23) for a wide variety of M-ary modulations (such as M-ary phase-shift keying (M-PSK) and M-ary quadrature amplitude modulation (M-QAM)) [18]. For instance, the average symbol error rate (SER) for M-PSK can be written as [18, Eq. 8.23]

$$ P_{{e,d|\Theta_{n} }}^{{}} = \frac{1}{\pi }\int\limits_{0}^{{{{\left( {M - 1} \right)\pi } \mathord{\left/ {\vphantom {{\left( {M - 1} \right)\pi } M}} \right. \kern-0pt} M}}} {M_{{\gamma_{total}^{OMRS} |\Theta_{n} }} \left( {\frac{{g_{PSK} }}{{\sin^{2} \left( \theta \right)}}} \right)d\theta }$$
(26)

where \( g_{PSK} = \sin^{2} \left( {\frac{\pi }{M}} \right)\).

Then the conditional bit error rate (BER) for binary phase shift keying (BPSK) modulation can be obtained with the help of [17, Eq. 3.211] and [17, Eq. 9.182] as (27), where \( {}_{2}F_{1} \left( { \cdot , \cdot ; \cdot ; \cdot } \right)\) is Gauss hypergeometric function defined in [17, Eq. 9.10].

$$ \begin{aligned} & P_{{e,d|\Theta_{n} }}^{OMRS} = \frac{1}{\pi }\int\limits_{0}^{{{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0pt} 2}}} {M_{{\gamma_{total}^{OMRS} |\Theta_{n} }} \left( {\frac{{g_{PSK} }}{{\sin^{2} \left( \theta \right)}}} \right)d\theta } \\ &= \frac{1}{2\pi }\left( {\frac{{m_{sd} }}{{\rho_{1} \varOmega_{sd} g_{PSK} }}} \right)^{{m_{sd} }} B\left( {\frac{1}{2},m_{sd} + \frac{1}{2}} \right){}_{2}F_{1} \left( {m_{sd} ,m_{sd} + \frac{1}{2};m_{sd} + 1; - \frac{{m_{sd} }}{{\rho_{1} \varOmega_{sd} g_{PSK} }}} \right) + \hfill \\ & \frac{1}{2\pi }\sum\limits_{t = 1}^{l} {\sum\limits_{{\lambda_{1} = 1}}^{l - t + 1} {\sum\limits_{{\lambda_{2} = \lambda_{1} + 1}}^{l - t + 2} { \cdots \sum\limits_{{\lambda_{t} = \lambda_{t - 1} + 1}}^{l} {\sum\limits_{{k_{1} = 0}}^{{m_{{\lambda_{1} }} - 1}} {\sum\limits_{{k_{2} = 0}}^{{m_{{\lambda_{2} }} - 1}} \cdots } \sum\limits_{{k_{t} = 0}}^{{m_{{\lambda_{t} }} - 1}} {\left( { - 1} \right)^{t} g_{{_{PSK} }}^{{ - u_{t} - m_{sd} }} \varGamma \left( {u_{t} + 1} \right)} } } } } \left( {\frac{{m_{sd} }}{{\rho_{1} \varOmega_{sd} }}} \right)^{{m_{sd} }} \left( {1 + \frac{{\upsilon_{t} }}{{\rho_{2} g_{PSK} }}} \right)^{{ - u_{t} - m_{sd} - \frac{1}{2}}} \hfill \\ & \times \left( {\prod\limits_{n = 1}^{t} {\frac{{m_{{\lambda_{n} }}^{{k_{n} }} }}{{k_{n} !\rho_{2}^{{k_{n} }} \varOmega_{{\lambda_{n} }}^{{k_{n} }} }}} } \right)B\left( {\frac{1}{2},u_{t} + m_{sd} + \frac{1}{2}} \right){}_{2}F_{1} \left( {u_{t} + m_{sd} + \frac{1}{2},m_{sd} ;u_{t} + m_{sd} + 1;\frac{{\rho_{1} \varOmega_{sd} \upsilon_{t} - \rho_{2} m_{sd} }}{{\left( {\rho_{2} g_{PSK} + \upsilon_{t} } \right)\rho_{1} \varOmega_{sd} }}} \right) \hfill \\ \end{aligned}$$
(27)

The overall end-to-end (E2E) error rate \( P_{e,E2E}^{OMRS}\) for BPSK in OMRS scheme with DF protocol can be obtained as

$$ P_{e,E2E}^{OMRS} = \sum\limits_{{\Theta_{n} }} {\Pr \left\{ {\Theta_{n} } \right\}P_{{e,d|\Theta_{n} }}^{OMRS} }$$
(28)

3.2 Performance Analysis of ABRS Scheme

  1. 1.

    Outage Probability of ABRS scheme

In contrast to our single-relay optimal rule, we consider selection of the relay that maximizes the average SNR at the destination among the decoding set:

$$ i_{sel.n} = \mathop {\arg \hbox{max} E}\limits_{{i \in \Theta_{n} }} \left\{ {\gamma_{i,d} } \right\} = \mathop {\arg \hbox{max} }\limits_{{i \in \Theta_{n} }} \left\{ {\rho_{2} n_{i} \varOmega_{id} } \right\}$$
(29)

Then the MGF of \( \gamma_{{i_{sel.n} }}\) can be obtained as

$$ M_{{\gamma_{{i_{sel,n} }} |\Theta_{n} }} \left( s \right) = \left( {1 + \rho_{2} \frac{{\varOmega_{{i_{sel,n} d}} }}{{m_{{i_{sel,n} d}} }}s} \right)^{{ - n_{{i_{sel,n} }} m_{{i_{sel,n} d}} }}$$
(30)

Thus the total SNR at D is obtained as

$$ \gamma_{total}^{ABRS} = \gamma_{s,d} + \gamma_{{i_{sel.n} }}$$
(31)

Based on (22) and (30), we can obtain a closed form expression of \( M_{{\gamma_{total}^{ABRS} |\Theta_{n} }} \left( s \right)\) as following

$$ M_{{\gamma_{total}^{ABRS} |\Theta_{n} }} \left( s \right) = \left( {1 + \frac{{\rho_{1} \varOmega_{sd} }}{{m_{sd} }}s} \right)^{{ - m_{sd} }} \left( {1 + \frac{{\rho_{2} \varOmega_{{i_{sel,n} ,d}} }}{{m_{{i_{sel,n} ,d}} }}s} \right)^{{ - n_{{i_{sel} }} m_{{i_{sel,n} ,d}} }}$$
(32)

According to (32), the conditional outage probability can be achieved as following

$$ \text{P}_{DF}^{ABRS} \left\{ {outage|\Theta_{n} } \right\} = \mathcal{\mathcal{L}}^{ - 1} \left( {s^{ - 1} M_{{\gamma_{total}^{ABRS} |\Theta_{n} }} \left( s \right)} \right)|\gamma_{th}$$
(33)

The closed form of \( \text{P}_{DF}^{ABRS} \left\{ {\gamma_{total}^{ABRS} < \gamma_{th} |\Theta_{n} } \right\}\) can also be derived as (34) where \( B\left( { \cdot , \cdot } \right)\) is Bata function defined in [17, Eq. 8.38],\( \varPhi \left( { \cdot , \cdot ; \cdot } \right)\) is confluent hypergeometric function defined in [17, Eq. 9.210].

$$ \begin{aligned} & \text{P}_{DF}^{ABRS} \left\{ {\gamma_{total}^{ABRS} < \gamma_{th} |\Theta_{n} } \right\} = L^{ - 1} \left( {s^{ - 1} M_{{\gamma_{total}^{ABRS} |\Theta_{n} }} \left( s \right)} \right)|\gamma_{th} = 1 - \sum\limits_{k = 0}^{{m_{sd} - 1}} {\left( {\frac{{m_{sd} }}{{\rho_{1} \varOmega_{sd} }}} \right)^{k} \frac{{\gamma_{th}^{k} }}{k!}e^{{ - \frac{{m_{sd} \gamma_{th} }}{{\rho_{1} \varOmega_{sd} }}}} } \hfill \\ & \quad - \frac{1}{{\varGamma \left( {m_{sd} } \right)}}\left( {\frac{{m_{sd} }}{{\rho_{1} \varOmega_{sd} }}} \right)^{{m_{sd} }} e^{{ - \frac{{m_{sd} \gamma_{th} }}{{\rho_{1} \varOmega_{sd} }}}} \sum\limits_{k = 0}^{{n_{{i_{sel.n} }} m_{{i_{sel.n} d}} - 1}} {\frac{1}{k!}} \gamma_{th}^{{m_{sd} + k}} \left( {\frac{{m_{{i_{sel.n} d}} }}{{\rho_{2} \varOmega_{{i_{sel.n} d}} }}} \right)^{k} B\left( {m_{sd} ,k + 1} \right)\varPhi \left( {k + 1,m_{sd} + k + 1;\frac{{m_{sd} \gamma_{th} }}{{\rho_{1} \varOmega_{sd} }} - \frac{{m_{{i_{sel.n} d}} \gamma_{th} }}{{\rho_{2} \varOmega_{{i_{sel.n} d}} }}} \right) \hfill \\ \end{aligned}$$
(34)

Based on (12) and (34), the outage probability can be obtained as

$$ \text{P}_{DF}^{ABRS} \left\{ {outage} \right\} = \sum\limits_{{\Theta_{n} }} {\text{P}_{DF}^{ABRS} \left\{ {outage|\Theta_{n} } \right\}\Pr \left\{ {\Theta_{n} } \right\}}$$
(35)
  1. 2.

    Error Performance of ABRS scheme

Given Θn, the conditional error rate at D in ABRS scheme for BPSK can be derived with the help of [17, Eq. 3.211] as (36), where \( F_{1} \left( { \cdot , \cdot , \cdot , \cdot ; \cdot , \cdot } \right)\) is Hypergeometric function of two variables defined in [17, Eq. 9.180].

$$ \begin{aligned} & P_{{e,d|\Theta_{n} }}^{ABRS} = \frac{1}{\pi }\int\limits_{0}^{{{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0pt} 2}}} {M_{{\gamma_{total}^{ABRS} |\Theta_{n} }} \left( {\frac{{g_{PSK} }}{{\sin^{2} \left( \theta \right)}}} \right)d\theta } \\& = \frac{1}{2\pi }\left( {\frac{{m_{sd} }}{{\rho_{1} \varOmega_{sd} g_{PSK} }}} \right)^{{m_{sd} }} \left( {\frac{{m_{{i_{sel,n} ,d}} }}{{\rho_{2} \varOmega_{{i_{sel,n} ,d}} g_{PSK} }}} \right)^{{n_{{i_{sel} }} m_{{i_{sel,n} ,d}} }} B\left( {\frac{1}{2},m_{sd} + n_{{i_{sel} ,n}} m_{{i_{sel,n} ,d}} + \frac{1}{2}} \right) \hfill \\ & \times F_{1} \left( {m_{sd} + n_{{i_{sel} ,n}} m_{{i_{sel,n} ,d}} + \frac{1}{2},m_{sd} ,n_{{i_{sel} }} m_{{i_{sel,n} ,d}} ,m_{sd} + n_{{i_{sel} ,n}} m_{{i_{sel,n} ,d}} + 1; - \frac{{m_{sd} }}{{\rho_{1} \varOmega_{sd} g_{PSK} }}, - \frac{{m_{{i_{sel,n} ,d}} }}{{\rho_{2} \varOmega_{{i_{sel,n} ,d}} g_{PSK} }}} \right) \hfill \\ \end{aligned}$$
(36)

The overall end-to-end (E2E) error rate \( P_{e,E2E}^{ABRS}\) for BPSK in ABRS scheme with DF protocol can be obtained as

$$ P_{e,E2E}^{ABRS} = \sum\limits_{{\Theta_{n} }} {\Pr \left\{ {\Theta_{n} } \right\}P_{{e,d|\Theta_{n} }}^{ABRS} }$$
(37)

3.3 Performance Analysis of BF Scheme

  1. 1.

    Outage Probability of BF scheme

Compared with relay selection methods, we consider beamforming scheme, where all the relays in the decoding subset Θ n are chosen to transmit the signal together. For the relay i \( \in\) Θ n , its corresponding beamforming weight is changed as:

$$ {\mathbf{w}}_{i}^{'} = \frac{1}{{\sqrt {\sum\limits_{{j \in \Theta_{n} }} {\left\| {{\mathbf{g}}_{j} } \right\|^{2} } } }}{\mathbf{g}}_{i}$$
(38)

The signal received at D from all the relays in Θ n is obtained as

$$ y_{n,d} = \sum\limits_{{i \in \Theta_{n} }} {{\mathbf{g}}_{i} {\mathbf{w}}_{{_{i} }}^{'H} t} + n_{n,d} = \sqrt {\sum\limits_{{j \in \Theta_{n} }} {\left\| {{\mathbf{g}}_{j} } \right\|^{2} } } t + n_{n,d}$$
(39)

Then the SNR at D in the second hop can be expressed as

$$ \gamma_{n} = \rho_{2} \sum\limits_{{j \in \Theta_{n} }} {\left\| {{\mathbf{g}}_{j} } \right\|^{2} } = \sum\limits_{{j \in \Theta_{n} }} {\gamma_{j,d} }$$
(40)

Because of the independence of \( \gamma_{j,d}\), j \( \in\) Θ n , the MGF of \( \gamma_{n}\) can be obtained as

$$ M_{{\gamma_{n} }} (s) = \prod\limits_{{j \in \Theta_{n} }} {M_{{\gamma_{j,d} }} \left( s \right)} = \prod\limits_{{j \in \Theta_{n} }} {\left( {1 + \frac{{\rho_{2} \varOmega_{id} }}{{m_{id} }}s} \right)^{{ - n_{i} m_{id} }} }$$
(41)

Assuming the received signals from S in the first hop and the decoded relays in the second hop are combined with MRC at D, thus the total SNR at D is obtained as

$$ \gamma_{total}^{BF} = \gamma_{s,d} + \gamma_{n,d}$$
(42)

Because of the independence of \( \gamma_{s,d}\) and \( \gamma_{n,d}\), j∈Θ n , the MGF of \( \gamma_{total}^{BF}\) can be written as

$$ M_{{\gamma_{total}^{BF} |\Theta_{n} }} \left( s \right) = \left( {1 + \frac{{\rho_{1} \varOmega_{sd} }}{{m_{sd} }}s} \right)^{{ - m_{sd} }} \prod\limits_{{j \in \Theta_{n} }} {\left( {1 + \frac{{\rho_{2} \varOmega_{id} }}{{m_{id} }}s} \right)^{{ - n_{i} m_{id} }} }$$
(43)

Then the conditional outage probability can be achieved as following

$$ \begin{aligned} P_{DF}^{BF} \left\{ {\gamma_{total}^{BF} < \gamma_{th} |\Theta_{n} } \right\} = L^{ - 1} \left( {s^{ - 1} M_{{\gamma_{n} }} (s)} \right)\left| {_{{\gamma_{th} }} } \right. \hfill \\ = L^{ - 1} \left( {s^{ - 1} \left( {1 + \frac{{\rho_{1} \varOmega_{sd} }}{{m_{sd} }}s} \right)^{{ - m_{sd} }} \prod\limits_{{j \in \Theta_{n} }} {\left( {1 + \frac{{\rho_{2} \varOmega_{id} }}{{m_{id} }}s} \right)^{{ - n_{i} m_{id} }} } } \right)\left| {_{{\gamma_{th} }} } \right. \hfill \\ \end{aligned}$$
(44)

where \( \mathcal{\mathcal{L}}^{ - 1}\)(·) denotes the inverse Laplace transform. The inverse Laplace transform can be done analytically or using simple numerical techniques as in [19].

Finally, the outage probability for beamforming can be written as

$$ \begin{aligned} \text{P}_{DF}^{BF} \left\{ {outage} \right\} = \sum\limits_{{\Theta_{n} }} {\left( {\text{P}_{DF}^{BF} \left\{ {\gamma_{total}^{BF} < \gamma_{th} |\Theta_{n} } \right\}\Pr \left\{ {\Theta_{n} } \right\}} \right)} \hfill \\ = \sum\limits_{{\Theta_{n} }} {\left( {L^{ - 1} \left( {s^{ - 1} \prod\limits_{{j \in \Theta_{n} }} {\left( {1 + \rho_{2} \varOmega_{jd} s} \right)^{{ - m_{j} }} } } \right)\left| {_{{\gamma_{th} }} } \right.\Pr \left\{ {\Theta_{n} } \right\}} \right)} \hfill \\ \end{aligned}$$
(45)
  1. 2.

    Error Performance of BF scheme

Given Θ n , the conditional error rate at D in BF scheme for BPSK can be obtained as

$$ P_{{e,d|\Theta_{n} }}^{BF} = \frac{1}{\pi }\int\limits_{0}^{{{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0pt} 2}}} {M_{{\gamma_{total}^{BF} |\Theta_{n} }} \left( {\frac{{g_{PSK} }}{{\sin^{2} \left( \theta \right)}}} \right)d\theta }$$

The overall end-to-end (E2E) error rate \( P_{e,E2E}^{BF}\) for BPSK in OMRS scheme with DF protocol can be obtained as

$$ P_{e,E2E}^{BF} = \sum\limits_{{\Theta_{n} }} {\Pr \left\{ {\Theta_{n} } \right\}P_{{e,d|\Theta_{n} }}^{BF} }$$
(46)

3.4 Numerical Results

In this section, we show numerical results of the analytical outage probability and BER for BPSK modulation. We consider DF cooperative network with multiple antennas multiple relays. The end-to-end spectral efficiency R is set as R = 1bit/s/Hz. For simplicity, the fading parameters of direct link are set to be m sd  = 1 and \( \varOmega_{sd}\) = 1.

Figure 2 shows the outage probability as a function of total SNR (dB) with power allocation ζ = 0.5 for the DF protocol with three 2-antenna relays (N = 3,m i  = M=2, i = 1,2,3) in symmetric channels, where the links of first hop and second hop are assumed to share the same shape fading parameters and the same average power fading parameters of Nakagami-m distribution, i.e., m si  = m id  = 1, \( \varOmega_{si}\) = \( \varOmega_{id}\) = 1, i = 1,2,3. In this figure, we show the performance of (1) OMRS DF relaying, (2) ABRS DF relaying, (3) BF transmission. In contrast to the schemes mentioned above, one can consider random relay selection (RRS), in which a relay is chosen before transmission in equal probability.

Fig. 2
figure 2

Outage probability comparison of OMRS, BF, ABRS and RRS as a function of total SNR ρ, m si  = m id  = 1 and \( \varOmega_{si}\) = \( \varOmega_{id}\) = 1, i = 1,2,3

Full size image

Figure 2 shows that the analytic results are well matched with the corresponding Monte Carlo simulations, which verifies the correctness of theoretical analysis. It also shows that BF is optimal in all the methods, and OMRS is sub-optimal and provides 1 ~ 2 dB loss in outage probability relative to BF transmission with DF protocol, while OMRS is simpler than BF. It is therefore beneficial to select the “best” one, for that it is less complex and less expensive to implement. We notice that both BF and OMRS outperform ABRS and RRS significantly especially in median and high SNR range, while ABRS has about 8–12 dB gains in outage probability compared with RRS in symmetric scenarios.

Figure 3 compares the BER performance for BPSK modulation in the same scenarios as in Fig. 2 in symmetric channels. Again, the curves obtained by the analytical and Monte Carlo simulations match very well. We can draw the similar conclusions in terms of BER as the outage probability illustrated in Fig. 2. While Fig. 3 shows that ABRS has about 15 ~ 20 dB gains in BER performance compared with RRS in symmetric scenarios.

Fig. 3
figure 3

BER comparison of OMRS, BF, ABRS and RRS as a function of total SNR ρ, m si  = m id  = 1 and \( \varOmega_{si}\) = \( \varOmega_{id}\) = 1, i = 1,2,3

Full size image

Figure 4 plots the outage probability of OMRS, BF, ABRS and RRS in the same scenarios (as in Fig. 2) in asymmetric channels with m si  = m id  = 1 and {\( \varOmega_{si}\)} = {\( \varOmega_{id}\)} = {4.5, 0.5, 0.4}, i = 1, 2, 3. It illustrates similar results as Fig. 2. Besides, we can also find that the performance of ABRS in asymmetric channels scenario is close to the outage-optimal scheme in the low and median SNR range and much better than that in symmetric scenario. This is due to the fact that ABRS always chooses the relay with the largest average channel gain in asymmetric scenario, while remove potential selection diversity benefits in symmetric channels.

Fig. 4
figure 4

Outage probability comparison of OMRS, BF, ABRS and RRS as a function of total SNR ρ, {\( \varOmega_{si}\)} = {\( \varOmega_{id}\)} = {4.5, 0.5, 0.4}, i = 1, 2, 3

Full size image

Figure 5 compares the BER performance in the same scenarios as in Fig. 4 in asymmetric channels with m si  = m id  = 1 and {\( \varOmega_{si}\)} = {\( \varOmega_{id}\)} = {4.5, 0.5, 0.4}, i = 1, 2, 3. The similar conclusions can be obtained in terms of BER as the outage probability illustrated in Fig. 4. It therefore can be concluded that OMRS is optimal among multi-antenna relay selection schemes; and ABRS is optional scheme in asymmetric scenario, for that the outage probability and BER performance of ABRS are approximate to OMRS especially in median and high SNR range.

Fig. 5
figure 5

BER comparison of OMRS, BF, ABRS and RRS as a function of total SNR ρ, {\( \varOmega_{si}\)} = {\( \varOmega_{id}\)} = {4.5, 0.5, 0.4}, i = 1, 2, 3

Full size image

Figure 6 plots outage probability of OMRS as a function of power allocation ζ for various SNR levels in the symmetric scenario with m si  = m id  = 1 and \( \varOmega_{si}\) = \( \varOmega_{id}\) = 1, i = 1, 2, 3. It shows that ζ = 0.6 is optimal in symmetric scenarios for different SNR levels. When the total end-to-end power is constrained, the optimal power allocation is that the source transmission power is allocated as 60 percents of the total power, while overall relay transmission power is allocated as 40 percents of the total power. The reason for the unequal power allocation is that the direct link between the source and destination is considered. It is observed that when ζ = 1, the outage probability of OMRS is that of the direct link from the source transmitting with all the total power to the destination.

Fig. 6
figure 6

Outage probability of OMRS as a function of power allocation ζ for OMRS, ρ = 10, 12, 14, 16, 18, and 20 dB

Full size image

Figure 7 compares the outage probability of the four schemes for two antenna levels (M = 1, 2) and relay number N ranging from 1 to 8 in the symmetric scenario with ρ = 10 dB and ζ = 0.5. We notice that when the number of antenna in relay is only one, OMRS is degraded to OR [4] scheme.

Fig. 7
figure 7

Outage probability comparison of OMRS, BF, ABRS and RRS as a function of relay number N for two antenna levels {m i } = M, i = 1, 2, 3; M = 1, 2

Full size image

It is observed that the outage probability of OMRS and BF schemes decreases exponentially to the number of relays, while the performance of ABRS gets little improvement with the increasing number of relays and RRS gets no improvement at all. Comparing the outage performance between OMRS and OR, it is clear that an increase in the number of antennas at each relays brings remarkable performance gain in the outage probability, since the performance gain is obtained by using MRC and beamforming in single multi-antenna relay. In other words, OMRS achieves more diversity gain and array gain than OR. It should further note that as the number of relays increases, OMRS provides more performance improvement than OR.

Figure 8 compares the BER performance in the same scenarios as in Fig. 7 in symmetric channels. The similar conclusions can be obtained in terms of BER as the outage probability illustrated in Fig. 7.

Fig. 8
figure 8

BER comparison of OMRS, BF, ABRS and RRS as a function of relay number N for two antenna levels {m i } = M, i = 1, 2, 3; M = 1, 2

Full size image

Figure 9, we can obtain that the performance of OMRS and BF and ABRS and RRS schemes, especially OMRS, is better than that of RRS scheme. This is because that in RRS, relays with the best channel gains obtain less resource than that with worst channel gains. The channel capacity is not fully exploited. Whereas, in OMRS, users with the best channel gains can obtain a larger amount of capacity. Unlike RRS and ABRS, OMRS scheme selects a subset of relays by selecting best instantaneous SNR to the destination in the transmission. And system performance is greatly improved since subcarriers are not distributed to the relay with bad channel gain. We also find that with higher transmit power, the performance advantage of the proposed schemes becomes more significant and the total throughput increases more quickly. In addition, the strategies with best instantaneous SNR method achieve larger capacity than that with the best average SNR.

Fig. 9
figure 9

The total capacity comparison of OMRS, BF, ABRS and RRS as a function of total power, {m i } = M, i = 1, 2, 3; M = 1, 2

Full size image

From Fig. 10 we can obtain similar conclusions with that illustrated in Fig. 9. We also find that the obtained total capacity of the proposed schemes increases with more relays. This is because the possibility of the selecting suitable relay for the destination increases when the number of relays rises.

Fig. 10
figure 10

The total capacity comparison of OMRS, BF, ABRS and RRS as a function of relay number N for two antenna levels {m i } = M, i = 1, 2, 3; M = 1, 2

Full size image

From Fig. 11 we can obtain similar conclusions with that illustrated in Fig. 10. We also observe that the required total power of all schemes decreases with more available relays, because the possibility of the distributing subcarrier to suitable relay increases when the relay number rises. As the number of relay increases further, the required total power tends to be stable. When the number of relay reached 16, the required total power of BF is basically the same as that of OMRS.

Fig. 11
figure 11

The required total power comparison of OMRS, BF, ABRS and RRS as a function of relay number N for two antenna levels {m i } = M, i = 1, 2, 3; M = 1, 2

Full size image

4 Conclusion

In this paper, we have derived the closed form expressions of outage probability and error performance for BPSK modulation of OMRS and ABRS in DF protocol under an aggregate power constraint in Nakagami-m fading channels. The analytical derivations for the outage probability and BER performance have been verified by simulation results. Simulation results prove that the proposed OMRS is outage-optimal among single-relay selection schemes and the outage performance of OMRS is close to BF, in addition that it is less complex and less expensive to implement. By comparing the performance of OMRS with OR scheme, we find that OMRS achieves lots of performance improvement, which results from the fact that the chosen relay with multiple antennas may decode the received signal with MRC and retransmit it with beamforming technique. It means that OMRS can provide more array gain and diversity order than OR when MRC and transmit beamforming are adopted in the selected multi-antenna relays. It is also observed that in symmetric channels scenarios ABRS performs much worse than OMRS, but in asymmetric channels scenarios the outage performance of ABRS is close to OMRS in low and median SNR range. Finally, we demonstrate that equal power allocation between the source and opportunistic relay gives optimal performance.

Spatial correlation properties may strongly affect the performance of multi-antenna systems. Future work should take this problem into consideration and provide more insightful perspectives.