Distributed transmit-antenna selection in variable-gain relaying systems

Abstract

Recently, distributed transmit-antenna selection schemes have attracted great interest, since they capture the essential benefits of multi-antenna systems while reducing their cost, complexity, delay, and feedback overhead. In those distributed schemes, the antenna selection is based on local channel-state information, in contrast to their optimal centralized counterparts, which require knowing the channel state of all links. Herein, we design two such distributed schemes for a dual-hop variable-gain amplify-and-forward relaying system with one multi-antenna source, one single-antenna relay, and one single-antenna destination. The two schemes differ in the diversity method used at the destination, namely, selection combining or maximal-ratio combining, and in the selection rule accordingly. In addition to conceiving these new schemes, we analyze their outage performance. Since an exact analysis proves intractable, we tackle the outage probability in terms of lower-bound expressions and their asymptotes at high signal-to-noise ratio. Importantly, the derived bounds turn out to be almost indistinguishable from the true performance, assessed via simulation. Our results reveal that the proposed distributed schemes achieve the same diversity order of their optimal centralized counterparts and perform closely to these, specially when the relay is near the source or destination.

1 Introduction

Multi-antenna cooperative communications are regarded as a key emerging paradigm for enhancing next-generation wireless networks in terms of reliability and spectral efficiency, by leveraging the fundamental benefits of multiple-input–multiple-output (MIMO) technologies, such as spatial diversity and spatial multiplexing [1, 2]. In practice, however, fully exploiting a high number of antennas increases the hardware cost and complexity, since the required multiple radio-frequency chains are expensive and power consuming. Alternatively, an attractive strategy is to lay hold of a transmit-antenna selection (TAS) scheme, as it captures the essential advantages of multi-antenna systems at a reduced cost and complexity [3]. In optimal centralized TAS schemes, the destination terminal collects the full channel-state information (CSI) of all available links and use it to choose the best antenna that the source terminal should transmit with. Afterwards, the destination feeds the selected-antenna index back to the source, which then proceeds with the transmission process [3]. Thereby, centralized TAS schemes may incur a considerable delay and feedback overhead associated with the assessment of all links. Indeed, such overhead may rapidly become prohibitive in practice, as the number of antennas increases. To alleviate the need for CSI estimation and feedback, suboptimal distributed TAS (a.k.a. DAS) schemes are of great practical interest. In these schemes, the antenna-selection mechanism is based on the partial CSI of a subset of links, usually the local ones, i.e., those links directly interfacing with the node that selects the antenna. This partial channel-state information is referred to as the local CSI. On the other hand, the TAS and DAS schemes are usually complemented by means of some diversity-combining method at the receiver side, such as maximal-ratio combining (MRC) and selection combining (SC) [4, 5]. These methods are used to merge the signals received from the direct and relaying links.

Several studies have proposed and analyzed amplify-and-forward (AF) relaying schemes with the joint use of TAS techniques at the transmitter side and diversity combining methods at the receiver side, including those in [6–18] and the references therein. In a pioneering work [6], optimal selection criteria for TAS/MRC were derived, and it was analytically demonstrated that the optimal TAS scheme achieves the same diversity order of a communication scheme that fully and simultaneously exploits all transmit antennas. The main drawback of such an optimal TAS scheme is its high complexity when performing an exhaustive search for the best transmit antenna. Aiming to reduce this complexity, some suboptimal TAS strategies have been also explored in the literature. In most cases, however, antenna selection criteria have been considered that ignore the CSI of some links [7–10]. In those works, suboptimal schemes were studied for the same basic TAS/MRC network configuration adopted in [6]. In [7], two TAS rules were considered and assessed via simulation, based on the direct-link and first-hop CSIs, respectively. In [8], the schemes in [7] have been assessed on an analytical basis. In [9], an adaptive TAS rule was considered, based either on the direct-link CSI or on the direct-link and first-hop CSIs, depending on the local channel state at the source. Finally, in [10], two TAS rules were considered and assessed analytically in terms of outage performance: the optimal one and a suboptimal one, with the latter being based on the direct-link CSI. In other cases, AF relaying schemes employing TAS techniques have been considered that ignore the direct link as a transmission path [11–16]. In [11], the error rate and outage probability were derived for a TAS/MRC relaying network with a multi-antenna source, a multi-antenna destination, and a single-antenna variable-gain AF relay. This scheme was generalized in [12] and [13], by assuming a multi-antenna relay. Based on the same network configuration, a suboptimal strategy for TAS/MRC and TAS/SC schemes was proposed in [14] and [15], by considering Nakagami-m channels. In [16], TAS/MRC and TAS/SC were investigated for Weibull channels in a multi-relay scenario.

An efficient distributed approach was introduced in [17] for a DAS/MRC scheme operating over a single-antenna fixed-gain AF relay. This approach avoids the full CSI of optimal centralized schemes while considering all the links in the antenna-selection mechanism. More recently, in [18], the new approach was applied to DAS/SC, by considering again a single-antenna fixed-gain AF relay. In this work, we extend the distributed approach used in [17] and [18] to the variable-gain scenario. More specifically, we design and analyze efficient DAS/MRC and DAS/SC schemes operating over a single-antenna variable-gain AF relay. Analytical lower bounds for the outage probability of the proposed schemes are derived, since an exact analysis proves intractable. Importantly, the obtained bounds prove to be extremely tight approximations to the exact outage performance. In addition, we provide simple closed-form asymptotic expressions for the derived bounds, which reveal that the proposed schemes achieve full diversity. Strikingly, the proposed suboptimal schemes turn out to perform very closely to their optimal centralized counterparts, mainly when the relay is located near the source or destination. Monte Carlo simulation is used to validate our analytical results. In what follows, $f_A \left( \cdot \right)$ denotes the probability density function (PDF) of a generic random variable A, $\text{E}\left[ \cdot \right]$ denotes expectation, $\Pr \left( \cdot \right)$ denotes probability, and “$\simeq$” denotes asymptotic equivalence.

2 System model

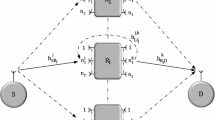
Consider the dual-hop relaying system depicted in Fig. 1, composed by one source S with $N_{t}$ antennas, one single-antenna destination D, and one single-antenna, half-duplex, variable-gain AF relay R. The system operates on a time-division multiple access basis, and all the channels undergo independent flat Rayleigh fading and additive white Gaussian noise with mean power $N_0$. Before each data transmission, an antenna selection is carried out at the source, desirably by choosing the best antenna for transmission, i.e., the one that maximizes the end-to-end signal-to-noise ratio (SNR). The selection procedure shall be presented in the next Section. Subsequently, a conventional cooperative transmission is held in two time slots. In the first time slot, S broadcasts the data stream to R and D. In the second time slot, R amplifies the received signal according to the variable-gain AF protocol and forwards it to D, which then combines the replicas from S and R via SC or MRC. Accordingly, the end-to-end SNR from the ith antenna at S to D can be formulated as

$$\begin{aligned} \text{SC:}\quad \gamma _{i}= \max \left[ Y_{i},\frac{X_{i}Z}{X_{i}+Z+1}\right] \end{aligned}$$

(1)

$$\begin{aligned} \text{MRC:}\quad \gamma _{i}= Y_{i}+\frac{X_{i} Z}{X_{i}+Z+1}, \end{aligned}$$

(2)

where $Y_i\triangleq \frac{P_S}{N_0}\vert h_{Y,i}\vert ^2$ is the direct-link received SNR from the ith antenna at S to D, $X_i\triangleq \frac{P_S}{N_0}\vert h_{X,i}\vert ^2$ is the first-hop received SNR from the ith antenna at S to R, and $Z\triangleq \frac{P_R}{N_0}\vert h_{Z}\vert ^2$ is the second-hop received SNR from R to D. Moreover, $P_S$ and $P_R$ denote the transmit powers at S and R, respectively, and $\vert h_{Y_i}\vert ^2$, $\vert h_{X,i}\vert ^2$, and $\vert h_{Z}\vert ^2$ denote the channel power coefficients of the links from the ith antenna at S to D, from the ith antenna at S to R, and from R to D, respectively. Note that, due to the Rayleigh fading condition, $X_i$, $Y_i$, and Z are exponential random variables. Herein, we assume an homogeneous network, so that all links from S to D (or to R) undergo identically distributed fading conditions, i.e., $\text{E}[X_{i}] = \bar{X}$ and $\text{E}[Y_{i}]= \bar{Y}$, $\forall i \in \{1,\ldots ,N_t\}$, and $\text{E}[Z]= \bar{Z}$.

Fig. 1

System configuration for the distributed TAS/SC and TAS/MRC schemes

3 Antenna selection scheme

In the optimal centralized scheme, the $i^*$th transmit antenna at S is selected that maximizes the end-to-end SNR, i.e.,

$$\begin{aligned} \text{Optimal TAS/MRC and TAS/SC:} \quad i^*=\arg \underset{i}{\max }\{ \gamma _{i}\}, \end{aligned}$$

(3)

where $\gamma _{i}$ is defined in (1) and (2) for TAS/SC and TAS/MRC, respectively. As mentioned before, the optimal decision requires the full knowledge of the entire system CSI, which involves a large amount of delay and feedback overhead. To reduce such impairments, we propose here efficient suboptimal DAS/SC and DAS/MRC schemes, inspired by the corresponding schemes for fixed-gain AF relaying presented in [17] and [18], respectively. In those works, the antenna-selection mechanism is based on local CSI at S, namely, $X_i$ and $Y_i$, $i \in \{1,\ldots ,N_t\}$, and on a 1-bit partial CSI related to the second hop Z. The point here is to avoid feeding back to S the full value of Z estimated at R or D—which would demand a certain number of bits—while not ignoring altogether the value of Z in the selection mechanism. Herein, we shall not discuss how $X_i$ and $Y_i$, $i \in \{1,\ldots ,N_t\}$, are made available at S, as this is also required in many suboptimal schemes proposed in the literature, thus not distinguishing those schemes from ours. Instead, we focus on showing how the addition of a minor 1-bit feedback overhead associated with Z can be used to enable a great improvement in performance.

Our DAS/SC and DAS/MRC schemes are motivated by key inequalities involving the respective end-to-end SNRs, which are obtained by replacing the known inequality $X_{i}Z/\left( {X_{i}+Z+1}\right) <\min \left[ X_{i},Z\right]$ into (1) and (2), leading to

$$\begin{aligned} \text{SC:} \quad \gamma _{i}<\max \left[ Y_{i},\min \left[ X_{i},Z\right] \right]\, \overset{\Delta }{=}\,\overset{\sim }{\gamma }_{i} \end{aligned}$$

(4)

$$\begin{aligned} \text{MRC:} \quad \gamma _{i}<Y_{i}+\min \left[ X_{i}, Z\right]\, \overset{\Delta }{=}\,\overset{\sim }{\gamma }_{i}. \end{aligned}$$

(5)

Note in (4) and (5) that the upper bound $\overset{\sim }{\gamma }_i$ of $\gamma _i$ depends on $\min \left[ X_{i},Z\right]$. From this, a DAS mechanism can be designed based on the local CSI available at S, $X_i$ and $Y_i$, $i \in \{1,\ldots ,N_t\}$, and on the whether $Z\ge \max _i \{X_i\}$ or $Z<\max _i\{X_i\}$. The latter information can be fed back from R to S by using a 1-bit message. This is the underlying rationale:

• If $Z\ge \max _i\{X_i\}$, then $\min [X_i,Z]=X_i$, $\forall i$. In this case, from (4) and (5), based on the local CSI $X_i$ and $Y_i$ available as S, a suboptimal selection rule $\max _i \{\overset{\sim }{\gamma }_{i}\}$ can be applied.

• If $Z<\max _i \{X_i\}$, then $\min [X_i,Z]=Z$ for some value(s) of i. In this case, the application of the selection rule $\max _i \{\overset{\sim }{\gamma }_{i}\}$ would require the knowledge of Z, which is unavailable at S. Instead, somewhat arbitrarily, we suggest the suboptimal selection rule $\max _i \{ Y_{i}\}$ that maximizes the direct-link received SNR.

All in all, in the proposed DAS schemes, the $i^*$th transmit antenna at S is selected as follows:

$$\begin{aligned}&\text{DAS/SC}: \\ &\quad i^*\,=\,\left\{ \begin{array}{ll} \overline{i} \triangleq\, \arg \underset{i}{\max }\left\{ \max \left[ Y_{i},X_{i} \right] \right\} , &{} \text{if }Z \,\ge\, \underset{i}{\max }\left\{ X_{i} \right\} \\ \underline{i} \triangleq \arg \underset{i}{\max }\{Y_{i}\}, &{}\text{if } Z < \underset{i}{\max }\left\{ X_{i} \right\} \end{array}\right. \end{aligned}$$

(6)

$$\begin{aligned}&\text{DAS/MRC:} \\ &\quad i^*\,=\,\left\{ \begin{array}{ll} \overline{i} \triangleq \arg \underset{i}{\max }\{ Y_{i}+X_{i} \}, &{} \text{if }Z\ge \underset{i}{\max }\left\{ X_{i} \right\} \\ \underline{i}\triangleq \arg \underset{i}{\max }\{Y_{i}\}, &{}\text{if } Z< \underset{i}{\max }\left\{ X_{i} \right\} . \end{array}\right. \end{aligned}$$

(7)

In comparison with optimal centralized schemes, the main advantage of the proposed DAS schemes is a considerably reduced delay/feedback overhead, while achieving a slightly worse performance, as discussed in [17] and [18]. Moreover, in comparison with other suboptimal TAS schemes that ignore the CSI of the second hop, the main advantage of the proposed DAS schemes is an improved outage performance at the expense of a minor additional 1-bit feedback overhead.

4 Outage analysis

In this section, we examine the outage performance of the proposed DAS/SC and DAS/MRC schemes. By definition, an outage event occurs whenever the end-to-end SNR falls below a predefined threshold $\tau$, usually obtained in terms of a target spectral efficiency $\mathfrak {R}_s$. For half-duplex relaying systems, which is the case here, $\tau =2^{2\mathfrak {R}_s}-1$. As in many related studies, an exact mathematical treatment proves intractable, since the outage event is related to the SNRs of the multiple links in a very complicated manner. Because of that, we tackle the outage probability in terms of lower bounds and handy closed-form asymptotic expressions at high SNR. Importantly, the derived bounds turn out to be highly accurate approximations to the exact outage performance. For the sake of clarity and fluidity, our analytical results shall be presented in the form of Lemmas and Propositions, all the proofs of which are postponed to appendices, even the small ones.

4.1 DAS/SC

By using (6) into (1), the outage probability $P_{\text{out}}^{\text{DAS/SC}}$ of the DAS/SC scheme can be formulated as

$$\begin{aligned} P_{\text{out}}^{\text{DAS/SC}}&= \underbrace{\text{Pr}\left( Z\ge \underset{i}{\max }\left\{ X_{i} \right\} ,\max \left[ Y_{\overline{i}}, \frac{X_{\overline{i}}Z}{X_{\overline{i}}+Z+1}\right]<\tau \right) }_{\triangleq I_1} \\&\quad +\underbrace{\text{Pr}\left( Z< \underset{i}{\max }\left\{ X_{i} \right\} ,\max \left[ Y_{\underline{i}},\frac{X_{\underline{i}}Z}{X_{\underline{i}}+Z+1}\right] <\tau \right) }_{\triangleq I_2}. \end{aligned}$$

(8)

Note in (8) that we have defined two probability terms, namely, $I_1$ and $I_2$, the sum of which gives the referred outage probability. Next we provide lower bounds for each of these terms, as well as corresponding high-SNR asymptotic expressions.

4.1.1 Bound analysis

The following lower-bound expressions are based on the key inequality presented in (4). Hereafter, $I_{1}^{\text{LB}}$, $I_{2}^{\text{LB}}$, and $P_{\text{out}}^{\text{DAS/SC,LB}}$ denote the lower bounds of $I_1$, $I_2$, and $P_{\text{out}}^{\text{DAS/SC}}$, respectively.

Lemma 1

A lower bound for the term $I_1$ defined in (8) can be elaborated as

$$\begin{aligned} I_{1}^{\text{LB}}= \Pr \left( Y_{i}<\tau \right) ^{N_t}\Pr \left( Z\ge \underset{i}{\max }\left\{ X_{i} \right\} ,\underset{i}{\max }\left\{ X_{i} \right\} <\tau \right) . \end{aligned}$$

(9)

Proof

See Appendix 1. $\square$

Lemma 2

A lower bound for the term $I_2$ defined in (8) can be elaborated as

$$\begin{aligned}&I_{2}^{\text{LB}}= \Pr \left( Y_{i}<\tau \right) ^{N_t} \\&\quad \Pr \left( Z<\underset{i}{\max }\left\{ X_{i} \right\} ,\min \left[ X_{i},Z\right] <\tau \right) . \end{aligned}$$

(10)

Proof

See Appendix 2. $\square$

Proposition 1

For independent flat Rayleigh fading, as is the case here, the lower bound $I_{1}^{\text{LB}}$ specializes to the following closed-form expression:

$$\begin{aligned} I_{1}^{\text{LB}}&=\left( 1-e^{-\frac{\tau }{\bar{Y}}}\right) ^{N_t}\left( e^{-\frac{\tau }{\bar{Z}}} \left( 1-e^{-\frac{\tau }{\bar{X}}}\right) ^{N_t} \right. \\&\qquad \left. +\sum ^{N_t}_{k=0} \left( {\begin{array}{c}N_{t}\\ k\end{array}}\right) \frac{(-1)^k \bar{X}}{\bar{X}+k\bar{Z}} \left( 1-e^{-\tau \left( \frac{k}{\bar{X}}+\frac{1}{\bar{Z}}\right) }\right) \right) . \end{aligned}$$

(11)

Proof

See Appendix 3. $\square$

Proposition 2

For independent flat Rayleigh fading, as is the case here, the lower bound $I_{2}^{\text{LB}}$ specializes to the following single-fold integral-form expression:

$$\begin{aligned} I_{2}^{\text{LB}}&=\left( 1-e^{-\frac{\tau }{\bar{Y}}}\right) ^{N_t} \left( \left( 1-e^{-\frac{\tau }{\bar{X}}}\right) \right. \\ &\quad + \left( 1-e^{-\frac{\tau }{\bar{Z}}}\right) -\left( 1-e^{-\frac{\tau }{\bar{X}}}\right) \left( 1-e^{-\frac{\tau }{\bar{Z}}}\right) \\ &\quad - \int _\tau ^\infty \frac{1}{\bar{Z}} e^{-\frac{b}{\bar{Z}}} \left( 1-e^{-\frac{b}{\bar{X}}}\right) ^{N_t-1}\left( 1-e^{-\frac{\tau }{\bar{X}}}\right) db \\ &\quad \left. - \int _0^\tau \frac{1}{\bar{Z}} e^{-\frac{z}{\bar{Z}}}\left( 1-e^{-\frac{z}{\bar{X}}}\right) ^{N_t} dz \right) . \end{aligned}$$

(12)

Proof

See Appendix 4. $\square$

By using (11) and (12) into (8), a lower-bound expression for the outage probability of the DAS/SC scheme operating over independent flat Rayleigh fading can be obtained as $P_{\text{out}}^{\text{DAS/SC,LB}} = I_{1}^{\text{LB}} + I_{2}^{\text{LB}}$.

4.1.2 Asymptotic bound analysis

In order to gain insights into the high-SNR trends of the proposed DAS/SC scheme, we now investigate the asymptotic behavior of the derived lower bounds. To this end, $\tilde{I}_1^{\text{LB}}$, $\tilde{I}_2^{\text{LB}}$, and $\tilde{P}_{\text{out}}^{\text{DAS/SC,LB}}$ denote the asymptotic lower bounds of $I_1$, $I_2$, and $P_{\text{out}}^{\text{DAS/SC}}$, respectively.

Proposition 3

A high-SNR asymptotic expression for the lower bound in (11) can be obtained as

$$\begin{aligned} \tilde{I}_1^{\text{LB}}=\left( \frac{\tau }{\bar{Y}}\right) ^{N_t} \left( \frac{\tau }{\bar{X}}\right) ^{N_t}. \end{aligned}$$

(13)

Proof

See Appendix 5. $\square$

Proposition 4

A high-SNR asymptotic expression for the lower bound in (12) can be obtained as

$$\begin{aligned} \tilde{I}_2^{\text{LB}}= \frac{\tau ^{N_t+1}}{\bar{Y}^{N_t}\bar{X}} +\frac{\tau ^{N_t+1}}{\bar{Y}^{N_t}\bar{Z}}\left( 1- B\left( \frac{\bar{X}}{\bar{Z}},N_t\right) \right) , \end{aligned}$$

(14)

where $B(\cdot ,\cdot )$ is the beta function [19, Eq. (3.312.1)].

Proof

See Appendix 6. $\square$

Proposition 5

A high-SNR asymptotic lower bound for the outage probability of the DAS/SC scheme operating over independent flat Rayleigh fading can be obtained as

$$\begin{aligned} \tilde{P}_{\text{out}}^{\text{DAS/SC,LB}} \simeq \left\{ \begin{array}{ll} \frac{2\tau ^2}{\bar{Y}\bar{X}}+\frac{\tau ^{2}}{\bar{Y}\bar{Z}}\left( 1- B\left( \frac{\bar{X}}{\bar{Z}},N_t\right) \right) &{} \text{if}\, N_t=1 \\ \frac{\tau ^{N_t+1}}{\bar{Y}^{N_t}\bar{X}}+\frac{\tau ^{N_t+1}}{\bar{Y}^{N_t}\bar{Z}}\left( 1- B\left( \frac{\bar{X}}{\bar{Z}},N_t\right) \right) &{}\text{if}\, N_t\ge 2. \end{array}\right. \end{aligned}$$

(15)

Proof

See Appendix 7. $\square$

It is noteworthy that a similar procedure can be applied to derive a corresponding upper bound for the outage probability of the proposed DAS/SC scheme. The resulting upper bound is somewhat loose, but it bears the same diversity order as the lower bound presented here. Thus, from the Pinching Theorem, it follows that our DAS/SC scheme achieves full diversity order, namely, $N_t+1$.

4.2 DAS/MRC

By using (7) into (2), the outage probability $P_{\text{out}}^{\text{DAS/MRC}}$ of the DAS/MRC scheme can be formulated as

$$\begin{aligned} P_{\text{out}}^{\text{DAS/MRC}}&= \underbrace{\text{Pr}\left( Z\ge \underset{i}{\max }\left\{ X_{i} \right\} ,Y_{\overline{i}}+ \frac{X_{\overline{i}}Z}{X_{\overline{i}}+Z+1}<\tau \right) }_{\triangleq L_1} \\&\quad +\underbrace{\text{Pr}\left( Z< \underset{i}{\max }\left\{ X_{i} \right\} ,Y_{\underline{i}}+\frac{X_{\underline{i}}Z}{X_{\underline{i}}+Z+1}<\tau \right) }_{\triangleq L_2}. \end{aligned}$$

(16)

Note in (16) that we have defined two probability terms, namely, $L_1$ and $L_2$, the sum of which gives the referred outage probability. Next we provide lower bounds for each of these terms, as well as corresponding high-SNR asymptotic expressions.

4.2.1 Bound analysis

The following lower-bound expressions are based on the key inequality presented in (5). Hereafter, $L_{1}^{\text{LB}}$, $L_{2}^{\text{LB}}$, and $P_{\text{out}}^{\text{DAS/MRC,LB}}$ denote the lower bounds of $L_1$, $L_2$, and $P_{\text{out}}^{\text{DAS/MRC}}$, respectively.

Lemma 3

A lower bound for the term $L_1$ defined in (16) can be elaborated as

$$\begin{aligned} L_{1}^{\text{LB}}=\Pr \left( Z\ge \underset{i}{\max }\left\{ X_{i} \right\} ,\underset{i}{\max }\left\{ Y_{i}+X_{i}\right\} <\tau \right) . \end{aligned}$$

(17)

Proof

See Appendix 8. $\square$

Lemma 4

A lower bound for the term $L_2$ defined in (16) can be elaborated as

$$\begin{aligned} L_{2}^{\text{LB}}=\Pr \left( Z<\underset{i}{\max }\left\{ X_{i} \right\} ,\underset{i}{\max }\left\{ Y_{i}\right\} + \min \left[ X_{i},Z\right] <\tau \right) . \end{aligned}$$

(18)

Proof

See Appendix 9. $\square$

Proposition 6

For independent flat Rayleigh fading, as is the case here, the lower bound $L_{1}^{\text{LB}}$ specializes to the following single-fold integral-form expression:

$$\begin{aligned} L_{1}^{\text{LB}}&=\int _0^\tau \frac{1}{\bar{Z}} e^{-\frac{z}{\bar{Z}}} \left( 1- e^{-\frac{z}{\bar{X}}}\right. \\&\quad \left. -\frac{\bar{Y}}{\bar{X}-\bar{Y}}e^{-\frac{\tau }{\bar{Y}}} \left( -1+e^{-z\left( \frac{1}{\bar{X}}-\frac{1}{\bar{Y}}\right) }\right) \right) ^{N_t} dz \\&\quad +\int _\tau ^\infty \frac{1}{\bar{Z}} e^{-\frac{z}{\bar{Z}}} \left( 1- e^{-\frac{\tau }{\bar{X}}}\right. \\&\quad \left. -\frac{\bar{Y}}{\bar{X}-\bar{Y}}e^{-\frac{\tau }{\bar{Y}}} \left( -1+e^{-\tau \left( \frac{1}{\bar{X}}-\frac{1}{\bar{Y}}\right) }\right) \right) ^{N_t} dz. \end{aligned}$$

(19)

Proof

See Appendix 10. $\square$

Proposition 7

For independent flat Rayleigh fading, as is the case here, the lower bound $L_{2}^{\text{LB}}$ specializes to the following two-fold integral-form expression:

$$\begin{aligned} L_{2}^{\text{LB}}&=\int _0^\tau N_t \frac{1}{\bar{Y}} e^{-\frac{y}{\bar{Y}}} \left( 1-e^{-\frac{y}{\bar{Y}}}\right) ^{N_t-1} \\&\quad \left( \left( 1-e^{-\frac{\tau -y}{\bar{X}}}\right) + \left( 1-e^{-\frac{\tau -y}{\bar{Z}}}\right) \right. \\&\quad -\left( 1-e^{-\frac{\tau -y}{\bar{X}}}\right) \left( 1-e^{-\frac{\tau -y}{\bar{Z}}}\right) \\&\quad -\int _{\tau -y}^\infty \frac{1}{\bar{Z}} e^{-\frac{b}{\bar{Z}}} \left( 1-e^{-\frac{b}{\bar{X}}}\right) ^{N_t-1} \\&\quad \times \left( 1-e^{-\frac{\tau -y}{\bar{X}}}\right) db \\&\quad \left. - \int _0^{\tau -y} \frac{1}{\bar{Z}} e^{-\frac{z}{\bar{Z}}}\left( 1-e^{-\frac{z}{\bar{X}}}\right) ^{N_t} dz \right) dy. \end{aligned}$$

(20)

Proof

See Appendix 11. $\square$

By using (19) and (20) into (16), a lower-bound expression for the outage probability of the DAS/MRC scheme operating over independent flat Rayleigh fading can be obtained as $P_{\text{out}}^{\text{DAS/MRC,LB}} = L_{1}^{\text{LB}} + L_{2}^{\text{LB}}$.

4.2.2 Asymptotic bound analysis

As for the DAS/SC case, in order to gain insights into the high-SNR trends of the proposed DAS/MRC scheme, we now investigate the asymptotic behavior of the derived lower bounds. To this end, $\tilde{L}_1^{\text{LB}}$, $\tilde{L}_2^{\text{LB}}$, and $\tilde{P}_{\text{out}}^{\text{DAS/MRC,LB}}$ denote the asymptotic lower bounds of $L_1$, $L_2$, and $P_{\text{out}}^{\text{DAS/MRC}}$, respectively.

Proposition 8

A high-SNR asymptotic expression for the lower bound in (19) can be obtained as

$$\begin{aligned} \tilde{L}_1^{\text{LB}}=\left( \frac{1}{2} \frac{\tau ^2}{\bar{X}\bar{Y}}\right) ^{N_t}. \end{aligned}$$

(21)

Proof

See Appendix 12. $\square$

Proposition 9

A high-SNR asymptotic expression for the lower bound in (20) can be obtained as

$$\begin{aligned} \tilde{L}_2^{\text{LB}}&= \left( \frac{1}{\bar{Y}}\right) ^{N_t} \frac{1}{\bar{X}} \left( \frac{\tau ^{N_t+1}}{N_t+1} \right) \\&\quad +\left( \frac{1}{\bar{Y}}\right) ^{N_t} \frac{1}{\bar{Z}} \left( \frac{\tau ^{N_t+1}}{N_t+1} \right) \left( 1-B\left( \frac{\bar{X}}{\bar{Z}},N_t\right) \right) . \end{aligned}$$

(22)

Proof

See Appendix 13. $\square$

Proposition 10

A high-SNR asymptotic lower bound for the outage probability of the DAS/MRC scheme operating over independent flat Rayleigh fading can be obtained as

$$\begin{aligned}&\tilde{P}_{\text{out}}^{\text{DAS/MRC,LB}} \\&\quad \simeq \left\{ \begin{array}{ll} \left( \frac{1}{2} \frac{\tau ^2}{\bar{X}\bar{Z}}\right) ^{N_t} e^{-\frac{\tau }{\bar{Y}}}+\frac{1}{\bar{Z}^{N_t}\bar{X}} \frac{\tau ^{N_t+1}}{(N_t+1)}+\frac{1}{\bar{Z}^{N_t}\bar{Y}}\frac{\tau ^{N_t+1}}{(N_t+1)}\\ \left( 1- B\left( \frac{\bar{X}}{\bar{Y}},N_t\right) \right) &{} \text{if}\, N_t=1 \\ \\ \frac{1}{\bar{Z}^{N_t}\bar{X}}\frac{\tau ^{N_t+1}}{(N_t+1)}+\frac{1}{\bar{Z}^{N_t}\bar{Y}}\frac{\tau ^{N_t+1}}{(N_t+1)}\left( 1- B\left( \frac{\bar{X}}{\bar{Y}},N_t\right) \right) &{}\text{if}\, N_t\ge 2. \end{array}\right. \end{aligned}$$

(23)

Proof

This proof is similar to that of Proposition 5. $\square$

As for the DAS/SC case, it is noteworthy that a similar procedure can be applied to derive a corresponding upper bound for the outage probability of the proposed DAS/MRC scheme. The resulting upper bound is somewhat loose, but it bears the same diversity order as the lower bound presented here. Thus, from the Pinching Theorem, it follows that our DAS/MRC scheme achieves full diversity order, namely, $N_t+1$.

5 Numerical results and discussions

In this section, we provide some application scenarios to verify our analytical results for the proposed DAS/MRC and DAS/SC schemes, as well as to exemplify the outage performance of these schemes in comparison with their optimal centralized counterparts TAS/MRC and TAS/SC. To this end, Monte Carlo simulation results are also included. For illustration purposes, we consider the following system configuration: the target spectral efficiency is $\mathfrak {R}_s = 1$ bit/s/Hz; the path loss exponent is $\beta =4$; the network follows a linear topology, in which $d_{SD}=d_{SR} + d_{RD}$, with $d_{SD}$, $d_{SR}$, and $d_{RD}$ being the lengths of the source-destination, source-relay, and relay-destination links, respectively; S and R have identical transmit powers, i.e., $P_S=P_R=P$; each channel mean power is $d^{-\beta }$, with d being the distance between the corresponding transceivers, so that $\bar{Y }=Pd_{SD}^{-\beta }/N_0$, $\bar{X}=Pd_{SR}^{-\beta }/N_0$, and $\bar{Z}=Pd_{RD}^{-\beta }/N_0$; and the distance between S and D is normalized to unity, i.e., $d_{SD}=1$.

Figures 2 and 3 present simulation results that show the impact of relay location on the outage performance of the proposed distributed schemes and their optimal centralized counterparts. Two scenarios are presented for each scheme, by considering two and three antennas at the source. The following can be observed from the curves:

• As expected, DAS/MRC outperforms DAS/SC in all the cases. Interestingly, the outage curves of all distributed and optimal schemes bear very similar shapes over the entire range of relay location.

• The outage performances of all investigated schemes are asymmetric functions of the relay location: for no scheme the best performance is achieved when the relay is placed at the midpoint between the source and destination. Instead, this is achieved at $d_{SR}\approx 0.72$ and $d_{SR}\approx 0.82$ with $N_t =2$ and $N_t=3$, respectively, for both DAS/SC and DAS/MRC. The best relay location is biased toward the destination because the number of transmit antennas in the first hop ($N_t$) is higher than in the second hop (one). Therefore, an optimal balance is achieved by strengthening somewhat the weakest hop, i.e., by positioning the relay a bit closer to the destination.

• As expected, the optimal centralized schemes outperform the distributed ones. However, their performances become increasingly close to each other as the relay approaches either the source ($d_{SR} \rightarrow 0$) or the destination ($d_{SR} \rightarrow 1$). This is explained as follows. On the one hand, as $d_{SR} \rightarrow 0$, $Z < \max _i \{ X_i \}$ with high probability, causing the DAS/SC and DAS/MRC rules in (6) and (7) to be both very likely $i^* = \arg \max _i \{ Y_i \}$. Also, if $Z < \max _i \{ X_i \}$, then, from (1) and (2), $\gamma _i \approx \max [Y_i,Z]$ for DAS/SC and $\gamma _i \approx Y_i+Z$ for DAS/MRC. As a result, the DAS rules tend to coincide with the optimal ones, since $\arg \max _i \{ Y_i \} = \arg \max _i \{ Y_i + Z \} = \arg \max _i \{\max [Y_i,Z] \}$, with the last equality being true iff $Z < \max _i \{ Y_i \}$, which is much probably the case. On the other hand, as $d_{SR} \rightarrow 1$, $Z \ge \max _i \{ X_i \}$ with high probability, causing the DAS/SC and DAS/MRC rules in (6) and (7) to be very likely $i^* = \arg \max _i \{ \max [ Y_i,X_i ] \}$ and $i^* = \arg \max _i \{ Y_i+X_i \}$, respectively. Also, if $Z \ge \max _i \{ X_i \}$, then, from (1) and (2), $\gamma _i \approx \max [Y_i,X_i]$ for DAS/SC and $\gamma _i \approx Y_i+X_i$ for DAS/MRC. Therefore, once again the DAS rules tend to coincide with the optimal ones.

Fig. 2

Outage probability versus normalized distance between source and relay for the proposed DAS/SC scheme and its optimal centralized counterpart ($P/N_0 = 10$ dB)

Fig. 3

Outage probability versus normalized distance between source and relay for the proposed DAS/MRC scheme and its optimal centralized counterpart ($P/N_0 = 10$ dB)

Figures 4 and 5 present simulation and analytical results for the outage probability of the proposed distributed schemes and their optimal centralized counterparts while varying the average received SNR of the source-destination link. Here again, two scenarios are presented for each scheme, by considering two and three antennas at the source and the corresponding best relay locations, estimated from Figs. 2 and 3, respectively. The following can be observed from the curves:

• Our lower bound expressions are extremely close to the exact (simulated) outage performance of the proposed distributed schemes over the entire range of SNR.

• The proposed distributed schemes achieve full diversity order, namely, $N_t+1$, which is the same of the optimal centralized schemes.

• When the relay is positioned at the best location, the performance of proposed distributed schemes is very close to that of their centralized counterparts.

Fig. 4

Outage probability versus average received SNR of the source-destination link for the proposed DAS/SC scheme, its centralized counterpart and direct-transmission

Fig. 5

Outage probability versus average received SNR of the source-destination link for the proposed  DAS/MRC scheme, its centralized counterpart and direct-transmission

For comparison, the outage probability of the direct-link transmission is also presented in Figs. 4 and 5. Note how the proposed cooperative schemes DAS/SC and DAS/MRC clearly outperform the direct-link transmission by achieving a higher diversity order. On the other hand, it is noteworthy that the (half-duplex) relaying operation brings a cost in terms of either extra time slots or extra frequency channels to accommodate the relay traffic, and such a cost reduces the achievable system throughput. This is a very important trade-off that should be taken into account in a practical engineering design.

6 Conclusions

This work proposed and analyzed a low-complexity, low-cost, distributed transmit-antenna selection approach for dual-hop variable-gain amplify-and-forward relaying systems. Two different diversity-combining methods were considered at the destination, namely, selection combining and maximal-ratio combining. Each method led to a distinct design of the antenna selection rule. We derived extremely tight lower bounds for the outage probability of each proposed scheme, as well as useful closed-form asymptotic expressions for each of the obtained bounds. In comparison with optimal centralized schemes, our distributed schemes achieve the same diversity order and a slightly worse performance, while reducing the cost, complexity, delay, and feedback overhead.

Appendices

Appendix 1: Proof of Lemma 1

By using (4) into the definition of $I_1$ in (8), a lower bound $I_{1}^{\text{LB}}$ can be derived as

$$\begin{aligned} I_{1}&\ge \Pr \left( Z\ge \underset{i}{\max }\left\{ X_{i} \right\} ,\max \left[ Y_{\overline{i}},\min \left[ X_{\overline{i}},Z\right] \right]<\tau \right) \triangleq I_{1}^{\text{LB}} \\&= \Pr \left( Z\ge \underset{i}{\max }\left\{ X_{i} \right\} ,\max \left[ Y_{\overline{i}}, X_{\overline{i}}\right]<\tau \right) \\&\overset{(a)}{=}\Pr \left( Z\ge \underset{i}{\max }\left\{ X_{i} \right\} ,\underset{i}{\max }\left\{ \max \left[ Y_{i},X_{i}\right] \right\}<\tau \right) \\&=\underbrace{\Pr \left( Z\ge \underset{i}{\max }\left\{ X_{i} \right\} ,\underset{i}{\max }\left\{ X_{i} \right\}<\tau \right) }_{\triangleq \rho } \Pr \left( Y_{i}<\tau \right) ^{N_t}, \end{aligned}$$

(24)

which coincides with the result in (9). In step (a) we have used the DAS/SC rule for $Z\ge \max _i \left\{ X_{i} \right\}$, given in (6).

Appendix 2: Proof of Lemma 2

By using (4) into the definition of $I_2$ in (8), a lower bound $I_{2}^{\text{LB}}$ can be derived as

$$\begin{aligned} I_{2}&\ge \Pr \left( Z< \underset{i}{\max }\left\{ X_{i} \right\} ,\max \left[ Y_{\underline{i}},\min \left[ X_{\underline{i}},Z\right] \right]<\tau \right) \triangleq I_{2}^{\text{LB}} \\&\overset{(a)}{=}\Pr \left( Z<\underset{i}{\max }\left\{ X_{i} \right\} ,\underset{i}{\max }\left\{ Y_{i}\right\}<\tau , \min \left[ X_{i},Z\right]<\tau \right) \\&=\,\underbrace{\Pr \left( Z<\underset{i}{\max }\left\{ X_{i} \right\} ,\min \left[ X_{i},Z\right]<\tau \right) }_{\triangleq J} \Pr \left( Y_{i}<\tau \right) ^{N_t}, \end{aligned}$$

(25)

which coincides with the result in (10). In step (a) we have used the DAS/SC rule for $Z < \max _i \left\{ X_{i} \right\}$, given in (6).

Appendix 3: Proof of Proposition 1

Relying on basic principles of the probability theory, the term $\rho$ defined in (24) can be elaborated as

$$\begin{aligned} \rho&= \Pr \left( Z\ge \underset{i}{\max }\left\{ X_{i} \right\} ,\underset{i}{\max }\left\{ X_{i} \right\}<\tau \right) \\&=\Pr \left( Z\ge \tau ,\underset{i}{\max }\left\{ X_{i} \right\}<\tau \right) \\&\quad +\Pr \left( Z<\tau ,\underset{i}{\max }\left\{ X_{i} \right\}<Z\right) \\&=\Pr \left( Z\ge \tau \right) \Pr \left( X_{i}<\tau \right) ^{N_t} \\&\quad +\int _0^\tau f_{Z}(z) \Pr \left( X_{i}<z\right) ^{N_t} dz. \end{aligned}$$

(26)

By using this into (24), as well as the exponential PDFs and cumulative distribution functions (CDFs) of $X_i$, $Y_i$, and Z, $I_{1}^{\text{LB}}$ can be rewritten as

$$\begin{aligned} I_{1}^{\text{LB}}&=\left( 1-e^{-\frac{\tau }{\bar{Y}}}\right) ^{N_t}\left( e^{-\frac{\tau }{\bar{Z}}} \left( 1-e^{-\frac{\tau }{\bar{X}}}\right) ^{N_t} \right. \\&\qquad \left. +\underbrace{\int _0^\tau \frac{1}{\bar{Z}} e^{-\frac{z}{\bar{Z}}} \left( 1-e^{-\frac{z}{\bar{X}}}\right) ^{N_t} dz}_{\triangleq \sigma }\right) . \end{aligned}$$

(27)

Finally, by using the binomial theorem [19, Eq. (1.111)] to solve the integral term $\sigma$ defined in (27), a closed-form expression for $I_{1}^{\text{LB}}$ is then obtained as in (11).

Appendix 4: Proof of Proposition 2

Relying on basic principles of the probability theory, the term J defined in (25) can be elaborated as

$$\begin{aligned} J&=\underbrace{\Pr \left( Z<\underset{i}{\max }\left\{ X_{i} \right\} , X_{i}<\tau \right) }_{\triangleq J_{1}} \\&\quad +\underbrace{\Pr \left( Z<\underset{i}{\max }\left\{ X_{i} \right\} , Z<\tau \right) }_{\triangleq J_{2}}\\ &\quad -\underbrace{\Pr \left( Z<\underset{i}{\max }\left\{ X_{i} \right\} , X_{i}<\tau ,Z<\tau \right) }_{\triangleq J_{3}}. \end{aligned}$$

(28)

Below, the component terms $J_1$, $J_2$, and $J_2$ are analyzed. The term $J_1$ can be solved as

$$\begin{aligned} J_1&=\Pr \left( X_{i}<\tau \right) -\Pr \left( \underset{i}{\max }\left\{ X_{i} \right\}<Z, X_{i}<\tau \right) \\&=\Pr \left( X_{i}<\tau \right) -\Pr \left( X_{1}<Z,X_{2}<Z,\ldots ,X_{i}<Z,\ldots ,X_{N_{t}}<Z, X_{i}<\tau \right) \\&=\Pr \left( X_{i}<\tau \right) -\Pr \left( X_{1}<Z,X_{2}<Z,\ldots ,X_{i}<\min \left[ \tau ,Z\right] ,\ldots ,X_{N_{t}}<Z\right) \\&=\Pr \left( X_{i}<\tau \right) -\Pr \left( Z<\tau ,X_{1}<Z,X_{2}<Z,\ldots ,X_{i}<Z,\ldots ,X_{N_{t}}<Z\right) \\&\quad -\Pr \left( Z>\tau ,X_{1}<Z,X_{2}<Z,\ldots ,X_{i}<\tau ,\ldots ,X_{N_{t}}<Z\right) \\&=\Pr \left( X_{i}<\tau \right) -\Pr \left( Z<\tau ,\underset{i}{\max }\left\{ X_{i} \right\}<Z \right) \\&\quad -\Pr \left( Z>\tau , \underset{i}{\max }\left\{ X_{i} \right\}<Z,X_{i}<\tau \right) \\&\overset{(a)}{=}\left( 1-e^{-\frac{\tau }{\bar{X}}}\right) -\int _0^\tau \frac{1}{\bar{Z}} e^{-\frac{a}{\bar{Z}}} \left( 1-e^{-\frac{a}{\bar{X}}}\right) ^{N_t} da \\ &\quad - \underbrace{\int _\tau ^\infty \frac{1}{\bar{Z}} e^{-\frac{b}{\bar{Z}}} \left( 1-e^{-\frac{b}{\bar{X}}}\right) ^{N_t-1}\left( 1-e^{-\frac{\tau }{\bar{X}}}\right) db}_{\triangleq \delta }, \end{aligned}$$

(29)

the term $J_2$ as

$$\begin{aligned} J_2&=\Pr \left( Z<\underset{i}{\max }\left\{ X_{i} \right\} , Z<\tau \right) \\&=\int _0^\tau f_{Z}(z) \Pr \left( z<\underset{i}{\max }\left\{ X_{i} \right\} \right) dz \\&\overset{(a)}{=}\int _0^\tau \frac{1}{\bar{Z}} e^{-\frac{z}{\bar{Z}}} \left( 1-\left( 1-e^{-\frac{z}{\bar{X}}}\right) ^{N_t}\right) dz, \end{aligned}$$

(30)

and the term $J_3$ as

$$\begin{aligned} J_3&=\text{Pr}\left( Z<\underset{i}{\max }\left\{ X_{i} \right\} , X_{i}<\tau ,Z<\tau \right) \\&=\text{Pr}\left( X_{i}<\tau ,Z<\tau \right) \\&\quad -\text{Pr}\left( Z>\underset{i}{\max }\left\{ X_{i} \right\} , X_{i}<\tau ,Z<\tau \right) \\&=\text{Pr}\left( X_{i}<\tau ,Z<\tau \right) \\&\quad -\int _0^\tau f_Z\left( z\right) \text{Pr}\left( z>\underset{i}{\max }\left\{ X_{i} \right\} , X_{i}<\tau \right) dz \\&\overset{(a)}{=}\,\left( 1-e^{-\frac{\tau }{\bar{X}}}\right) \left( 1-e^{-\frac{\tau }{\bar{Z}}}\right) \\&\quad -\int _0^\tau \frac{1}{\bar{Z}} e^{-\frac{z}{\bar{Z}}}\left( 1-e^{-\frac{z}{\bar{X}}}\right) ^{N_t}dz, \end{aligned}$$

(31)

where in step (a) of the above expressions we have used the exponential PDFs and CDFs of $X_i$ and Z. Finally, by substituting (29)–(31) into (28) and then into (25), with use of the exponential CDF of $Y_i$, a single-fold integral form expression for $I_{2}^{\text{LB}}$ is then obtained as in (12).

Appendix 5: Proof of Proposition 3

By using the MacLaurin series of the exponential function [19, Eq. (1.211.1)] into the term $\sigma$ defined in (27), we obtain

$$\begin{aligned} \sigma&\simeq \int _0^\tau \frac{1}{\bar{Z}} e^{-\frac{z}{\bar{Z}}} \left( \frac{z}{\bar{X}}\right) ^{N_t} dz \\&=\frac{1}{\bar{Z}} \left( \frac{1}{\bar{X}}\right) ^{N_t} \sum _{n=0}^{\infty } \left( \frac{1}{\bar{Z}}\right) ^{n} \frac{1}{n!} \frac{\tau ^{N_t+n+1}}{N_t+n+1}. \end{aligned}$$

(32)

Then, by substituting (32) into (27), and by using again the MacLaurin series of the exponential function, $I_1^{\text{LB}}$ can be asymptotically expressed as

$$\begin{aligned} I_{1}^{\text{LB}}\simeq \left( \frac{\tau }{\bar{Y}}\right) ^{N_t}\left( \left( 1-\frac{\tau }{\bar{Z}} \right) \left( \frac{\tau }{\bar{X}}\right) ^{N_t} +\frac{1}{\bar{Z}} \left( \frac{1}{\bar{X}}\right) ^{N_t}\frac{\tau ^{N_t+1}}{N_t+1}\right) . \end{aligned}$$

(33)

Finally, by preserving only the lowest-order terms in (33), it reduces to $\tilde{I}_1^{\text{LB}}$ as in (13).

Appendix 6: Proof of Proposition 4

By using the MacLaurin series of the exponential function into the term $\delta$ defined in (29), we obtain

$$\begin{aligned} \delta&= \left( 1-e^{-\frac{\tau }{\bar{X}}}\right) \int _\tau ^\infty \frac{1}{\bar{Z}} e^{-\frac{b}{\bar{Z}}} \left( 1-e^{-\frac{b}{\bar{X}}}\right) ^{N_t-1} db \\&= \left( 1-e^{-\frac{\tau }{\bar{X}}}\right) \left\{ \int _0^\infty \frac{1}{\bar{Z}} e^{-\frac{b}{\bar{Z}}} \left( 1-e^{-\frac{b}{\bar{X}}}\right) ^{N_t-1} db\right. \\&\quad \left. -\int _0^\tau \frac{1}{\bar{Z}} e^{-\frac{b}{\bar{Z}}} \left( 1-e^{-\frac{b}{\bar{X}}}\right) ^{N_t-1} db \right\} \\&\simeq \frac{\tau }{\bar{Z}} B\left( \frac{\bar{X}}{\bar{Z}},N_t\right) \\&\quad -\frac{\tau }{\bar{Z}} \left( \frac{1}{\bar{X}}\right) ^{N_t+1} \sum _{n=0}^{\infty } \left( \frac{1}{\bar{Z}}\right) ^{n} \frac{1}{n!} \frac{\tau ^{N_t+n}}{N_t+n}. \end{aligned}$$

(34)

Then, by substituting (32) and (34) into (12), and by using again the MacLaurin series of the exponential function, $I_2^{\text{LB}}$ can be asymptotically expressed as

$$\begin{aligned} I_{2}^{\text{LB}}&\simeq \left( \frac{\tau }{\bar{Y}}\right) ^{N_t}\left( \frac{\tau }{\bar{X}}- \frac{\tau }{\bar{Z}} B\left( \frac{\bar{X}}{\bar{Z}},N_t\right) \right. \\&\quad -\frac{1}{\bar{Z}} \left( \frac{1}{\bar{X}}\right) ^{N_t+1} \frac{\tau ^{N_t+1}}{N_t}+\frac{\tau }{\bar{Z}}\\ &\quad \left. -\frac{1}{\bar{Z}} \left( \frac{1}{\bar{X}}\right) ^{N_t} \frac{\tau ^{N_t+1}}{N_t+1}-\frac{\tau ^2}{\bar{X}\bar{Z}}\right) . \end{aligned}$$

(35)

Finally, by preserving only the lowest-order terms in (35), it reduces to $\tilde{I}_2^{\text{LB}}$ as in (14).

Appendix 7: Proof of Proposition 5

An asymptotic expression for the outage probability is obtained by preserving only the lowest-order terms in the sum $\tilde{I}_1^{\text{LB}}+\tilde{I}_2^{\text{LB}}$. From (13) and (14), it becomes apparent that the individual diversity orders of $\tilde{I}_1^{\text{LB}}$ and $\tilde{I}_2^{\text{LB}}$ are $2 N_t$ and $N_t+1$, respectively. Therefore, only for the particular case of $N_t = 1$ these two diversity orders coincide, so that the both terms must be preserved in the asymptotic outage bound. Otherwise, when $N_t \ge 2$, the diversity order of $\tilde{I}_1^{\text{LB}}$ is higher than that of $\tilde{I}_2^{\text{LB}}$, and thus $\tilde{I}_1^{\text{LB}}$ can be ignored. Taking all this into account, we arrive at (15).

Appendix 8: Proof of Lemma 3

By using (5) into the definition of $L_1$ in (16), a lower bound $L_{1}^{\text{LB}}$ can be derived as

$$\begin{aligned} L_{1}&\ge \Pr \left( Z\ge \underset{i}{\max }\left\{ X_{i} \right\} ,Y_{\overline{i}}+\min \left[ X_{\overline{i}},Z\right]<\tau \right) \triangleq I_{1}^{\text{LB}} \\&= \Pr \left( Z\ge \underset{i}{\max }\left\{ X_{i} \right\} ,Y_{\overline{i}}+ X_{\overline{i}}<\tau \right) \\&\overset{(a)}{=} \Pr \left( Z\ge \underset{i}{\max }\left\{ X_{i} \right\} ,\underset{i}{\max }\left\{ Y_{i}+X_{i}\right\} <\tau \right) , \end{aligned}$$

(36)

which coincides with the result in (17). In step (a) we have used the DAS/MRC rule for $Z\ge \max _i \left\{ X_{i} \right\}$, given in (7).

Appendix 9: Proof of Lemma 4

By using (5) into the definition of $L_2$ in (16), a lower bound $L_{2}^{\text{LB}}$ can be derived as

$$\begin{aligned} L_{2}&\ge \Pr \left( Z< \underset{i}{\max }\left\{ X_{i} \right\} ,Y_{\underline{i}}+\min \left[ X_{\underline{i}},Z\right]<\tau \right) \triangleq L_{2}^{\text{LB}} \\&\overset{(a)}{=} \Pr \left( Z<\underset{i}{\max }\left\{ X_{i} \right\} ,\underset{i}{\max }\left\{ Y_{i}\right\} + \min \left[ X_{i},Z\right] <\tau \right) , \end{aligned}$$

(37)

which coincides with the result in (18). In step (a) we have used the DAS/MRC rule for $Z < \max _i \left\{ X_{i} \right\}$, given in (7).

Appendix 10: Proof of Proposition 6

Relying on basic principles of the probability theory, the lower bound $L_{1}^{\text{LB}}$ in (36) can be elaborated as

$$\begin{aligned} L_{1}^{\text{LB}}&=\Pr \left( Z\ge \underset{i}{\max }\left\{ X_{i} \right\} ,\underset{i}{\max }\left\{ Y_{i}+X_{i}\right\}<\tau \right) \\&=\int _0^\infty f_{Z}(z) \Pr \left( \underset{i}{\max }\left\{ X_{i} \right\} \le z,\underset{i}{\max }\left\{ Y_{i}+X_{i}\right\}<\tau \right) dz \\&=\int _0^\infty f_{Z}(z) \Pr \left( \underset{i}{\max }\left\{ X_{i} \right\} \le \min \left[ z,\tau \right] ,\underset{i}{\max }\left\{ Y_{i}+X_{i}\right\}<\tau \right) dz \\&=\int _0^\tau f_{Z}(z) \Pr \left( \underset{i}{\max }\left\{ X_{i} \right\} \le z ,\underset{i}{\max }\left\{ Y_{i}+X_{i}\right\}<\tau \right) dz \\&\quad +\int _\tau ^\infty f_{Z}(z) \Pr \left( \underset{i}{\max }\left\{ X_{i} \right\} \le \tau ,\underset{i}{\max }\left\{ Y_{i}+X_{i}\right\}<\tau \right) dz \\&=\int _0^\tau f_{Z}(z) {\left( \int _0^z f_{X_i}(x) \Pr \left( Y_{i}+x<\tau \right) dx\right) } ^{N_t} dz \\&\quad +\int _\tau ^\infty f_{Z}(z) {\left( \int _0^\tau f_{X_i}(x) \Pr \left( Y_{i}+x<\tau \right) dx\right) }^{N_t} dz \\&\overset{(a)}{=}\int _0^\tau f_{Z}(z) {\underbrace{\left( 1- e^{-\frac{z}{\overline{X}}}-\frac{1}{\overline{X}}e^{-\frac{\tau }{\overline{Y}}} \int _0^z e^{-x\left( \frac{1}{\overline{X}}-\frac{1}{\overline{Y}}\right) }dx\right) }_{\triangleq \alpha _1}} ^{N_t} dz \\&\quad +\int _\tau ^\infty f_{Z}(z) {\underbrace{\left( 1- e^{-\frac{\tau }{\overline{X}}}-\frac{1}{\overline{X}}e^{-\frac{\tau }{\overline{Y}}} \int _0^\tau e^{-x\left( \frac{1}{\overline{X}}-\frac{1}{\overline{Y}}\right) }dx\right) }_{\triangleq \alpha _2}}^{N_t} dz, \end{aligned}$$

(38)

where in step (a) we have used the exponential PDFs and CDFs of $X_i$ and $Y_i$. Finally, by using the exponential PDF of Z into (38), a single-fold integral-form expression for $L_{1}^{\text{LB}}$ is then obtained as in (19).

Appendix 11: Proof of Proposition 7

Relying on basic principles of the probability theory, the lower bound $L_{2}^{\text{LB}}$ in (37) can be elaborated as

$$\begin{aligned} L_{2}^{\text{LB}}&=\Pr \left( Z<\underset{i}{\max }\left\{ X_{i} \right\} ,\underset{i}{\max }\left\{ Y_{i}\right\} + \min \left[ X_{i},Z\right]<\tau \right) \\&=\int _0^\tau f_{Y_i}(y) \underbrace{\Pr \left( Z<\underset{i}{\max }\left\{ X_{i} \right\} ,\min \left[ X_{i},Z\right] <\tau -y\right) }_{\triangleq K} dy, \end{aligned}$$

(39)

where the term K defined above can be split into three components as

$$\begin{aligned} K&=\underbrace{\Pr \left( Z<\underset{i}{\max }\left\{ X_{i} \right\} , X_{i}<\tau -y\right) }_{\triangleq K_{1}} \\&\quad +\underbrace{\Pr \left( Z<\underset{i}{\max }\left\{ X_{i} \right\} , Z<\tau -y\right) }_{\triangleq K_{2}} \\&\quad -\underbrace{\Pr \left( Z<\underset{i}{\max }\left\{ X_{i} \right\} , X_{i}<\tau -y,Z<\tau -y\right) }_{\triangleq K_{3}}. \end{aligned}$$

(40)

By comparing (40) and (28), it becomes apparent that the definitions of $K_1$, $K_2$, and $K_3$ coincide with those of $J_1$, $J_2$, and $J_3$, respectively, except that $\tau$ (in the latter) is replaced by $\tau -y$ (in the former). Therefore, expressions for $K_1$, $K_2$, and $K_3$ can be respectively obtained as in (29), (30), and (31), by substituting $\tau -y$ for $\tau$. Finally, by applying those expressions into (40) and then into (39), with use of the exponential PDF of $Y_i$, a two-fold integral form expression for $L_{2}^{\text{LB}}$ is then obtained as in (20).

Appendix 12: Proof of Proposition 8

By using the MacLaurin series of the exponential function into the term $\alpha _1$ defined in (38), we obtain

$$\begin{aligned} \alpha _1&=1- e^{-\frac{z}{\bar{X}}}-\frac{1}{\bar{X}}e^{-\frac{\tau }{\bar{Y}}} \int _0^z e^{-x\left( \frac{1}{\bar{X}}-\frac{1}{\bar{Y}}\right) }dx \\&\simeq 1-\left( 1- \frac{z}{\bar{X}}+\frac{z^2}{2\bar{X}^2}\right) \\&\quad -\frac{1}{\bar{X}}e^{-\frac{\tau }{\bar{Y}}} \int _0^z \left( 1-x\left( \frac{1}{\bar{X}}-\frac{1}{\bar{Y}}\right) \right) dx \\&\simeq \frac{1}{2} \frac{z^2}{\bar{X}\bar{Y}}. \end{aligned}$$

(41)

The term $\alpha _2$, also defined in (38), can be obtained in the same way, by substituting $\tau$ for z. Then, by using (41) into (38), $L_1^{\text{LB}}$ can be asymptotically expressed as

$$\begin{aligned} L_{1}^{\text{LB}}&\simeq \int _0^\tau \frac{1}{\bar{Z}} e^{-\frac{z}{\bar{Z}}} \left( \frac{1}{2} \frac{z^2}{\bar{X}\bar{Y}}\right) ^{N_t} dz \\&\quad +\int _\tau ^\infty \frac{1}{\bar{Z}} e^{-\frac{z}{\bar{Z}}} \left( \frac{1}{2} \frac{\tau ^2}{\bar{X}\bar{Y}}\right) ^{N_t} dz. \end{aligned}$$

(42)

Finally, by solving the integrals in (42) with use of the MacLaurin series of the exponential function, and preserving only the lowest-order terms, it reduces to $\tilde{L}_1^{\text{LB}}$ as in (21).

Appendix 13: Proof of Proposition 9

To begin with, let us rewrite the lower bound $L_2^{\text{LB}}$ in (20) as

$$\begin{aligned} L_{2}^{\text{LB}}&=\underbrace{\int _0^\tau N_t \frac{1}{\bar{Y}} e^{-\frac{y}{\bar{Y}}} \left( 1-e^{-\frac{y}{\bar{Y}}}\right) ^{N_t-1}\left( 1-e^{-\frac{\tau -y}{\bar{X}}}\right) dy}_{\triangleq \epsilon _1} \\&\quad +\underbrace{\int _0^\tau N_t \frac{1}{\bar{Y}} e^{-\frac{y}{\bar{Y}}} \left( 1-e^{-\frac{y}{\bar{Y}}}\right) ^{N_t-1} \left( 1-e^{-\frac{\tau -y}{\bar{Z}}}\right) dy}_{\triangleq \epsilon _2} \\&\quad -\underbrace{\int _0^\tau N_t \frac{1}{\bar{Y}} e^{-\frac{y}{\bar{Y}}} \left( 1-e^{-\frac{y}{\bar{Y}}}\right) ^{N_t-1}\int _{\tau -y}^\infty \frac{1}{\bar{Z}} e^{-\frac{b}{\bar{Z}}} \left( 1-e^{-\frac{b}{\bar{X}}}\right) ^{N_t-1}\left( 1-e^{-\frac{\tau -y}{\bar{X}}}\right) db dy}_{\triangleq \epsilon _3} \\&\quad -\underbrace{ \int _0^\tau N_t \frac{1}{\bar{Y}} e^{-\frac{y}{\bar{Y}}} \left( 1-e^{-\frac{y}{\bar{Y}}}\right) ^{N_t-1}\int _0^{\tau -y} \frac{1}{\bar{Z}} e^{-\frac{z}{\bar{Z}}}\left( 1-e^{-\frac{z}{\bar{X}}}\right) ^{N_t} dz dy}_{\triangleq \epsilon _4} \\&\quad -\underbrace{\int _0^\tau N_t \frac{1}{\bar{Y}} e^{-\frac{y}{\bar{Y}}} \left( 1-e^{-\frac{y}{\bar{Y}}}\right) ^{N_t-1} \left( 1-e^{-\frac{\tau -y}{\bar{X}}}\right) \left( 1-e^{-\frac{\tau -y}{\bar{Z}}}\right) dy}_{\triangleq \epsilon _5}. \end{aligned}$$

(43)

Now, high-SNR asymptotic expressions for the terms $\epsilon _1$, $\epsilon _2$, $\epsilon _3$, $\epsilon _4$, and $\epsilon _5$ defined above can be obtained by appropriately using the MacLaurin series of the exponential function into each definition. For $\epsilon _1$, we obtain

$$\begin{aligned} \epsilon _1&\simeq \int _0^\tau N_t \frac{1}{\bar{Y}} e^{-\frac{y}{\bar{Y}}} \left( \frac{y}{\bar{Y}}\right) ^{N_t-1}\left( 1-e^{-\frac{\tau -y}{\bar{X}}}\right) dy \\&=N_t \left( \frac{1}{\bar{Y}}\right) ^{N_t}\int _0^\tau \left( e^{-\frac{y}{\bar{Y}}} \left( y\right) ^{N_t-1}\right. \\&\quad \left. -e^{-\frac{y}{\bar{Y}}} \left( y\right) ^{N_t-1}e^{-\frac{\tau }{\bar{X}}}e^{\frac{y}{\bar{X}}}\right) dy \\&=N_t \left( \frac{1}{\bar{Y}}\right) ^{N_t}\int _0^\tau e^{-\frac{y}{\bar{Y}}} \left( y\right) ^{N_t-1}dy \\&\quad -N_t \left( \frac{1}{\bar{Y}}\right) ^{N_t} e^{-\frac{\tau }{\bar{X}}} \int _0^\tau e^{-\frac{y}{\bar{Y}}} \left( y\right) ^{N_t-1}e^{\frac{y}{\bar{X}}}dy \\&=N_t \left( \frac{1}{\bar{Y}}\right) ^{N_t}\sum _{n=0}^{\infty } \left( -\frac{1}{\bar{Y}}\right) ^{n} \frac{1}{n!} \frac{\tau ^{N_t+n}}{N_t+n} \\&\quad - N_t \left( \frac{1}{\bar{Y}}\right) ^{N_t} \sum _{n=0}^{\infty } \left( -\frac{1}{\bar{Y}}+\frac{1}{\bar{X}}\right) ^{n} \frac{1}{n!} \frac{\tau ^{N_t+n}}{N_t+n} \\&\quad +N_t \left( \frac{1}{\bar{Y}}\right) ^{N_t} \frac{\tau }{\bar{X}} \sum _{n=0}^{\infty } \left( -\frac{1}{\bar{Y}}+\frac{1}{\bar{X}}\right) ^{n} \frac{1}{n!} \frac{\tau ^{N_t+n}}{N_t+n} \\&\simeq \left( \frac{1}{\bar{Y}}\right) ^{N_t} \frac{1}{\bar{X}} \left( \frac{\tau ^{N_t+1}}{N_t+1} \right) . \end{aligned}$$

(44)

From (43), note that an expression for $\epsilon _2$ can be obtained by replacing $\bar{X}$ with $\bar{Z}$ into the expression for $\epsilon _1$, which gives

$$\begin{aligned} \epsilon _2\simeq \left( \frac{1}{\bar{Y}}\right) ^{N_t} \frac{1}{\bar{Z}} \left( \frac{\tau ^{N_t+1}}{N_t+1} \right) . \end{aligned}$$

(45)

In addition, expressions for $\epsilon _3$, $\epsilon _4$, and $\epsilon _5$ are obtained as follows:

$$\begin{aligned} \epsilon _3&\simeq \int _0^\tau N_t \frac{1}{\bar{Y}} e^{-\frac{y}{\bar{Y}}} \left( 1-e^{-\frac{y}{\bar{Y}}}\right) ^{N_t-1} \\&\quad \int _{\tau -y}^\infty \frac{1}{\bar{Z}} e^{-\frac{b}{\bar{Z}}} \left( 1-e^{-\frac{b}{\bar{X}}}\right) ^{N_t-1}\left( 1-e^{-\frac{\tau -y}{\bar{X}}}\right) db dy \\&\simeq \int _0^\tau N_t \frac{1}{\bar{Y}} e^{-\frac{y}{\bar{Y}}} \left( \frac{y}{\bar{Y}}\right) ^{N_t-1} \frac{\left( \tau -y\right) }{\bar{Z}} B\left( \frac{\bar{X}}{\bar{Z}},N_t\right) dy \\&\simeq \frac{1}{\bar{Z}}\left( \frac{1}{\bar{Y}}\right) ^{N_t} \left( \frac{\tau ^{N_{t}+1}}{N_t+1}\right) B\left( \frac{\bar{X}}{\bar{Z}},N_t\right) \end{aligned}$$

(46)

$$\begin{aligned} \epsilon _4&\simeq \int _0^\tau N_t \frac{1}{\bar{Y}} e^{-\frac{y}{\bar{Y}}} \left( \frac{y}{\bar{Y}}\right) ^{N_t-1} \\&\quad \int _0^{\tau -y} \frac{1}{\bar{Z}} e^{-\frac{z}{\bar{Z}}}\left( \frac{z}{\bar{X}}\right) ^{N_t} dz dy \\&=\left( \frac{1}{\bar{Y}}\right) ^{N_t} N_t \int _0^\tau e^{-\frac{y}{\bar{Y}}} \left( y\right) ^{N_t-1} \frac{1}{\bar{Z}} \left( \frac{1}{\bar{X}}\right) ^{N_t} \\&\quad \sum _{n=0}^{\infty } \left( \frac{1}{\bar{Z}}\right) ^{n} \frac{1}{n!} \frac{\left( \tau -y\right) ^{N_t+n+1}}{N_t+n+1} dy \\&\simeq \left( \frac{1}{\bar{Y} \bar{X}}\right) ^{N_t} \frac{1}{\bar{Z}}\frac{N_t}{(N_t+1)} \\&\quad \int _0^\tau e^{-\frac{y}{\bar{Y}}} \left( y\right) ^{N_t-1}\left( \tau -y\right) ^{N_t+1} dy \\&=\left( \frac{1}{\bar{Y} \bar{X}}\right) ^{N_t} \frac{1}{\bar{Z}}\frac{N_t}{(N_t+1)} \\&\quad \sum _{k=0}^{\infty } \left( {\begin{array}{c}N_{t}+1\\ k\end{array}}\right) (-1)^k\tau ^{N_t+1-k} \int _0^\tau e^{-\frac{y}{\bar{Y}}} y^{N_t-1+k} dy \\&\simeq \left( \frac{1}{\bar{Y} \bar{X}}\right) ^{N_t} \frac{1}{\bar{Z}}\frac{ \tau ^{N_t+1} }{(N_t+1)} \sum _{k=0}^{\infty } \left( {\begin{array}{c}N_{t}+1\\ k\end{array}}\right) (-1)^k \frac{N_t}{Nt+k} \\&=\left( \frac{1}{\bar{Y} \bar{X}}\right) ^{N_t} \frac{1}{\bar{Z}}\frac{ \tau ^{N_t+1} }{(N_t+1)} \frac{\Gamma (Nt+1) \Gamma (N_t+2)}{\Gamma (2Nt+2)} \end{aligned}$$

(47)

$$\begin{aligned} \epsilon _5&\simeq \int _0^\tau N_t \frac{1}{\bar{Y}} e^{-\frac{y}{\bar{Y}}} \left( \frac{y}{\bar{Y}}\right) ^{N_t-1} \left( \frac{\tau -y}{\bar{X}}\right) \left( \frac{\tau -y}{\bar{Z}}\right) dy \\&=N_t \left( \frac{1}{\bar{Y}}\right) ^{N_t} \frac{1}{\bar{X}}\frac{1}{\bar{Z}}\int _0^\tau e^{-\frac{y}{\bar{Y}}}\left( \tau ^2 y{N_t-1} -2\tau y{N_t}+y{N_t+1} \right) dy \\&\simeq \left( \frac{1}{\bar{Y}}\right) ^{N_t} \frac{1}{\bar{X}\bar{Z}}\frac{2 \tau ^{N_t+2}}{(N_t+1)(N_t+2)}. \end{aligned}$$

(48)

Finally, by using (44)–(48) into (43), and preserving only the lowest-order terms, it reduces to $\tilde{L}_2^{\text{LB}}$ as in (22).