The Design of Efficient, Low-Complexity Cooperative Diversity Schemes from Different Perspectives

Abstract

This chapter focuses on designing efficient, low-complexity cooperative diversity schemes from different perspectives, and it is divided into four parts. In the first part, assuming a general multisource, multirelay cooperative system, a new efficient scheme for the combined use of cooperative diversity and multiuser diversity is proposed. The proposed scheme significantly reduces the amount of channel estimation while achieving comparable outage performance to that using the joint selection scheme. In the second part, two spectrally efficient schemes for the diversity exploitation of downlink cooperative cellular networks are proposed. By scheduling the user with the best direct link to access the channel, an incremental decode-and-forward relaying scheme is first presented. To further enhance the transmission robustness against fading, an improved scheme is also proposed, which substantially utilizes opportunistic scheduling mechanism when the direct transmission fails. In the third part, new and efficient link selection schemes for selection relaying systems with transmit beamforming are proposed. Two distributed link selection schemes are presented that invoke a distributed decision mechanism and rely on the success/fail signaling feedback between terminals. In the fourth part, a novel distributed transmit antenna selection for dual-hop amplify-and-forward relaying systems is proposed. A multiantenna source transmits information to a single-antenna destination by using a single-antenna half-duplex relay. By invoking local channel information exploitation/decision mechanism along with decision feedback between terminals, a distributed antenna selection scheme is formulated. Compared with the optimal/suboptimal antenna selection, the proposed scheme can maintain a low and constant delay/feedback overhead irrespective of the number of transmit antennas.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

In recent years, cooperative diversity (CD) technologies have been widely investigated from industrial and academic societies. As a milestone event, the cooperative relaying technology has been incorporated into the next-generation mobile communications standard, i.e., the 3GPP LTE-Advanced, in March 2011. On the other hand, the academic studies of cooperative diversity started around 2003, during which Laneman and Sendonaris, respectively, proposed the concept of cooperative diversity in their seminal works [15, 17]. The basic idea of cooperative diversity may be summarized as follows: by exploiting the broadcasting nature of the wireless medium, a diversity order of two can be achieved by the classical source-relay-destination triplet through distributed signal processing and transmissions among terminals.

Following the above seminal works [15, 17], one line of research focuses on the design of efficient schemes to extract full diversity order of various cooperative systems. Although numerous cooperative schemes were presented to achieve system full diversity, their implementation complexity are usually too high to be deployed in realistic cooperative systems [4, 19], especially for multisource, multirelay cooperative systems. Thus, the first part of this chapter, i.e., Sect. 5.2, focuses on designing efficient, low-complexity (LC) diversity exploitation schemes for general multisource, multirelay cooperative systems. Meanwhile, even though some cooperative schemes can attain full diversity, it is achieved at the loss of transmission spectral efficiency, partially due to the nature of multiphase transmission inherent in cooperative diversity. As a result, another problem arises concerning to designing full-diversity achievable cooperative schemes with a higher spectral efficiency, which becomes quite challenging for multiuser cooperative systems. This motivates the second part of this chapter, i.e., Sect. 5.3, which aims to design spectrally-efficient diversity exploitation schemes for downlink cooperative cellular networks.

In addition to designing efficient diversity exploitation schemes for multiuser cooperative systems, another line of research concerns to a more fundamental problem for cooperative systems with selection relaying, i.e., how to avoid centralized node/link/antenna scheduling within cooperative systems? In this regard, by utilizing distributed timer techniques, Bletsas et al. proposed a distributed relay selection scheme for a single-source, multirelay, single-destination cooperative system in 2006 [3]. However, for other network topologies, low-complexity and efficient scheduling mechanisms are not well understood even for the simple source-relay-destination triplet. In view of this, the third and fourth parts of this chapter, which consist of Sects. 5.4 and 5.5, respectively, propose the concept of distributed decision and apply it to the design of efficient link/antenna scheduling schemes with a lower signaling overhead and selection delay. For such, the mechanism of local decision and decision feedback is proposed to make link/antenna selection for a typical downlink cooperative cellular system with one multiantenna source, one single-antenna relay, and one single-antenna destination. A comprehensive study is conducted to investigate the joint impacts of antenna configuration, relay placement on the transmission robustness and distributed implementation of the schemes.

In the remaining parts of this section, the basic concepts of cooperative diversity and multiuser diversity are first reviewed. Then, several typical relaying protocols, such as amplify-and-forward (AF), decode-and-forward (DF), and incremental relaying, are briefly introduced, which serves as the underlying components of the system models in the subsequent sections. Afterward, selection schemes which are used as benchmarks in our analysis will be introduced and discussed. The classical performance measures are remarked that are widely studied in typical cooperative systems. After this introductory section, the remainder of the chapter is structured as follows. In Sect. 5.2, an efficient low-complexity scheme for multisource multirelay cooperative networks is proposed. In Sect. 5.3, two spectrally efficient schemes for downlink cooperative cellular networks are presented. Section 5.4 proposes link selection schemes for selection relaying with transmit beamforming and Sect. 5.5 proposes distributed antenna selection schemes for relaying scenarios.

1.1 Cooperative Diversity

Cooperative diversity is a cooperative multiple antenna technique for improving or maximizing total network channel capacities for any given set of bandwidths, which exploits user diversity by decoding the combined signal of the relaying signal and the direct signal in wireless multihop networks. A conventional single-hop system uses direct transmission (DT) where a receiver decodes the information only based on the direct signal while regarding the relayed signal as interference, whereas the cooperative diversity considers the other signal as contribution. That is, cooperative diversity decodes the information from the combination of two signals. It can be seen that cooperative diversity is an antenna diversity that uses distributed antennas belonging to each node in a wireless network, which is also called virtual multiple-input multiple-output (MIMO) due to its equivalent effect to practical MIMO diversity.

1.2 Multiuser Diversity

Multiuser diversity (MUD) is a diversity technique using user scheduling in multiuser wireless channels where user scheduling allows the base station to select high quality channel users so as to transmit information through a relatively high quality channel in time, frequency and space domains based on the channel quality information fed back from all candidate user equipment.

1.3 Relaying Protocols

In this chapter, we describe a variety of low-complexity relaying protocols that can be utilized in the cooperative network, including fixed, selection, and incremental relaying. On the other hand, relaying protocols can also be classified as AF and DF based on whether the relay terminal recovers the original information from the source. These protocols employ different types of processing by the relay terminals, as well as different types of combining at the destination terminals. For fixed relaying, we allow the relays to either amplify their received signals subject to their power constraint, or to decode, re-encode, and retransmit the messages. Among many possible adaptive strategies, selection relaying builds upon fixed relaying by allowing transmitting terminals to select a suitable cooperative (or noncooperative) action based upon the measured signal-to-noise ratio (SNR) between them. Incremental relaying improves upon the spectral efficiency of both fixed and selection relaying by exploiting limited feedback from the destination and relaying only when necessary. In any of these cases, the radios may employ repetition or more powerful codes. We focus on repetition coding throughout the sequel, for its low implementation complexity and ease of exposition. Destination radios can appropriately combine their received signals by exploiting control information in the protocol headers.

1.4 Selection Schemes

1.4.1 Opportunistic Relay Selection Schemes

When multiple relay nodes are available to forward the information from the source to destination, it was previously deemed that all relays participate in forwarding the source’s information should be the only choice to boost the end-to-end transmission robustness. In [3], Bletsas et al. proved that opportunistic relaying is outage-optimal, that is, it is equivalent in outage behavior to the optimal DF strategy that employs all potential relays. In general, there are two modes of coordination: (i) reactive coordination among DF relays and (ii) proactive coordination among DF or AF relays. In a reactive mode, relays that successfully decode the message participate in cooperation, whereas in a proactive mode, specific relays that are selected prior to the source transmission participate in cooperation. Bletsas’s seminal works reveal that relays in cooperative communications can be viewed not only as active re-transmitters, but also as distributed sensors of the wireless channel. Cooperative relays can be useful even when they do not transmit, provided that they cooperatively listen. In that way, cooperation benefits can be cultivated with simple radio implementation.

1.4.2 Link Selection Schemes

In cooperative diversity systems, there are usually multiple links/routes available for the source to transmit its information to the destination. In this case, we can choose one best link to convey the information, which is termed as link selection in this chapter. For classical one source, multiple relay, one destination scenarios without direct link, it is clear that link selection is equivalent to relay selection and the opportunistic relay selection can be employed to perform the link/route scheduling. However, when the direct link is incorporated into the framework, the traditional opportunistic relay/node selection schemes may fail to schedule the transmit link in an efficient manner.

1.4.3 Antenna Selection Schemes

Deploying multiple antennas at cooperative node promises significant improvements in terms of spectral efficiency and link reliability since the benefits of MIMO techniques can be implemented into relay networks. For such cases, transmit antenna selection is a feasible solution to balance the transmission robustness and implementation complexity, which opportunistically schedules the most appropriate antenna to convey the information to the destination. Typically, transmit antenna selection is performed at destination by collecting the link channel quality of multiple available links. Afterwards, the transmit antenna selection is made at the destination and the chosen antenna index is then forwarded to the source. In this way, the transmit antenna selection is performed at the destination in a centralized fashion. Nonetheless, such a centralized decision may incur considerable signaling overhead and selection delay due to the comprehensive testing of all the available antenna component and the resulting direct/relaying links.

1.5 Performance Metrics

1.5.1 Outage Probability

A standard performance criterion characteristic of diversity systems operating over fading channels is the so-called outage probability-denoted by $P_\mathrm{{out}}$ and defined as the probability that the instantaneous error probability exceeds a specified value or equivalently the probability that the output SNR, $\gamma$, falls below a certain specified threshold, $\gamma _\mathrm{{th}}$. For cooperative diversity systems, one key issue to determine the outage probability is to correctly describe the spectral efficiency threshold for various relaying protocols, which becomes crucial for incremental relaying protocols.

1.5.2 Diversity and Coding Gains

In the high SNR regime, diversity and coding gains are usually utilized to characterize the high SNR behavior of the achieved performance of various cooperative diversity schemes. In some literature [18], coding gain is also called array gain since cooperative diversity systems is equivalent to a virtual MIMO array. At high SNR, the outage probability [or symbol error rate (SER), Bit Error Rate (BER)] of an uncoded (or coded) system has been observed in certain cases to be approximated by

$$\begin{aligned} P_\mathrm{{out}}\simeq (G_{c}\bar{\gamma })^{-G_{d}}, \end{aligned}$$

(5.1)

where $G_{c}$ is termed the coding gain, and $G_d$ is referred to as the diversity gain, diversity order, or, simply diversity. The diversity order determines the slope of the outage probability versus average SNR curve, at high SNR, in a log-log scale. On the other hand, the coding gain (in decibels) determines the shift of the curve in SNR relative to a benchmark outage curve of $\bar{\gamma }^{-G_d}$.

1.5.3 Diversity-Multiplexing Tradeoff

Earlier research on multiantenna coding schemes has focused either on extracting the maximal diversity gain or the maximal spatial multiplexing gain of a channel. In fact, a new point of view, proposed by Zheng and Tse [29], believes that both types of gain can be simultaneously achievable in a given channel, but there is a tradeoff between them. The Diversity-Multiplexing Tradeoff (DMT) achievable by a scheme is a more fundamental measure of its performance than just its maximal diversity gain or its maximal multiplexing gain alone. The DMT can be used to evaluate the performance of some proposed cooperative diversity schemes. The DMT measure is useful for evaluating and comparing existing schemes as well as providing insights for designing new schemes.

2 Efficient Low-Complexity Scheme for Multisource Multirelay Cooperative Networks

In this section, a new efficient scheme for the combined use of cooperative diversity and multiuser diversity is presented. Such scheme was first proposed in [8]. Assuming a DF opportunistic relaying strategy, we first analyze the outage behavior of the joint source-relay selection scheme with/without direct links, from which the significance of the direct links is recognized.¹ Motivated by the important role of these links on the system performance, a two-step selection scheme is proposed, which first chooses the best source node based on the channel quality of the direct links and then selects the best link from the selected source to destination. The proposed scheme considerably reduces the amount of channel estimation while achieving comparable performance to that using the joint selection scheme. Importantly, the achieved diversity order is the same with that using the joint selection scheme.

2.1 System Models

We focus on the same scenario as that of [19]. Specifically, we consider a cooperative wireless network with $M$ source nodes $S_m (m=1, 2,\ldots , M)$, one destination node $D$ and $N$ relays $R_n, n=1, 2,\ldots , N$. All nodes are single-antenna devices and operate in a half-duplex mode. A time-division multiple-access scheme is adopted for orthogonal channel access and the channels pertaining to each link undergo independent but not necessarily identically distributed (i.n.i.d.) Rayleigh flat fading.

Next, assuming a proactive DF opportunistic relaying strategy [3], we first analyze the joint source-relay selection scheme. For such, in each transmission process, a best source-relay pair, i.e., $(m^{\varDelta },n^{\varDelta })$, is firstly chosen among all potential ones and the detailed selection standard will be addressed in the sequel. Afterwards, the traditional two-phase transmission starts. In the first phase, $S_{m^{\varDelta }}$ broadcasts while $R_{n^{\varDelta }}$ and $D$ listen. In the second phase, $R_{n^{\varDelta }}$ forwards the signal to $D$. Regarding the signal processing at $D$, we consider two scenarios. Under the first scenario, there is no direct link between the sources and $D$, whereas under the second scenario all the direct links exist and $D$ processes the received signals during the two-phase transmission by using a selection combining technique. Next, these two scenarios are presented.

2.1.1 No Direct Link

When the direct link is unavailable, the end-to-end SNR from $S_{m}$ to $D$ is written as

$$\begin{aligned} \gamma _{m}^\mathrm{{NDL}}=\max _{n}\left[ \min \left[ \gamma _{S_{m}R_{n}},\gamma _{R_{n}D}\right] \right] , \end{aligned}$$

(5.2)

where $\gamma _{S_{m}R_{n}}\triangleq P_{S}|h_{S_{m}R_{n}}|^{2}/N_{0}$ and $\gamma _{R_{n}D}\triangleq P_{R}|h_{R_{n}D}|^{2}/N_{0}$ denote the instantaneous SNR of the links $S_{m}\rightarrow R_{n}$ and $R_{n}\rightarrow D$, respectively, with $h_{S_{m}R_{n}}$ and $h_{R_{n}D}$ being the channel coefficients of these links. Also, $P_S$ and $P_R$ indicate the transmit powers of the selected source and selected relay, respectively, and $N_0$ is the mean power of the Additive White Gaussian Noise (AWGN) arriving at the relays and destination. Without loss of generality, hereafter the system SNR is defined as $\bar{\gamma }\triangleq 1/N_{0}$ [27, 28].

2.1.2 Direct Link

When the direct links are available, the end-to-end SNR from $S_m$ to $D$ is given by

$$\begin{aligned} \gamma _{m}^\mathrm{{DL}}=\max \left[ \gamma _{S_{m}D},\max \limits _{n}\left[ \min \left[ \gamma _{S_{m}R_{n}},\gamma _{R_{n}D}\right] \right] \right] , \end{aligned}$$

(5.3)

where $\gamma _{S_{m}D}\triangleq P_{S}|h_{S_{m}D}|^{2}/N_{0}$ stands for the instantaneous SNR of the link $S_{m}\rightarrow D$, with $h_{S_{m}D}$ denoting the channel coefficient of that link.

For MUD-based mechanism, when the direct links are unavailable, we have $m^{\varDelta }=\mathrm{{arg}} \max \limits _{m}\left[ \gamma _{m}^\mathrm{{NDL}}\right]$, whereas when the direct links are available, it follows that $m^{\varDelta }=\mathrm{arg } \max \limits _{m}\left[ \gamma _{m}^\mathrm{DL }\right]$. For both cases, the selected relay satisfies

$$\begin{aligned} n^{\varDelta }= \mathrm{{arg}} \max _{n}\left[ \min \left[ \gamma _{S_{m^{\varDelta }}R_{n}},\gamma _{R_{n}D}\right] \right] . \end{aligned}$$

(5.4)

2.2 Joint Selection Scheme

2.2.1 Outage Analysis Without Direct Links

The outage probability is defined as the probability that the instantaneous capacity is below a predefined end-to-end spectral efficiency $\mathfrak {R}$ bps/Hz. More specifically, the outage probability of the system without direct link can be formulated as

$$\begin{aligned} P_\mathrm{out }^\mathrm{NDL }&= \mathrm Pr \left( \frac{1}{2}\log _{2}\left( 1+\max _{m}\left[ \gamma _{m}^\mathrm{NDL }\right] \right) <\mathfrak {R}\right) \nonumber \\&= \mathrm{Pr }\left( \max _{m}\left[ \gamma _{m}^\mathrm{NDL }\right] <2^{2\mathfrak {R}}-1\triangleq \rho \right) , \end{aligned}$$

(5.5)

where $\mathrm{Pr }(\cdot )$ denotes probability. Noting that $\gamma _{m}^\mathrm{NDL }=\max \limits _{n}\left[ \min \left[ \gamma _{S_{m}R_{n}},\gamma _{R_{n}D}\right] \right]$ and rearranging the indexes $m$ and $n$, Eq. (5.5) can be decomposed as

$$\begin{aligned} P_\mathrm{out }^\mathrm{NDL }=\,\mathrm{Pr }\left( \max _{n}\left[ \max _{m} \left[ \min \left[ \gamma _{S_{m}R_{n}},\gamma _{R_{n}D}\right] \right] \right] < \rho \right) \end{aligned}$$

$$\begin{aligned} \qquad =\prod _{n=1}^{N}\mathrm{Pr }\left( \max _{m} \left[ \min \left[ \gamma _{S_{m}R_{n}},\gamma _{R_{n}D}\right] \right] < \rho \right) . \end{aligned}$$

(5.6)

Now, let $\gamma _{n}=\max \limits _{m}\left[ \min \left[ \gamma _{S_{m}R_{n}},\gamma _{R_{n}D}\right] \right]$. To proceed further, the Cumulative Distribution Function (CDF) of $\gamma _{n}$ needs to be evaluated, which by its turn can be expressed as

$$\begin{aligned} F_{\gamma _{n}}(\rho )&=\int _{0}^{\infty }\mathrm{{Pr}}\left( \max _{m}\left[ \min \left[ \gamma _{S_{m}R_{n}},y\right] \right] < \rho \right) p_{\gamma _{R_{n}D}}(y)dy\nonumber \\&=\int _{0}^{\infty }\left( \prod _{m=1}^{M}\underbrace{\mathrm{{Pr}}\left( \min \left[ \gamma _{S_{m}R_{n}},y\right] <\rho \right) }_{\eta }\right) p_{\gamma _{R_{n}D}}(y)dy, \end{aligned}$$

(5.7)

where $p_{X}(\cdot )$ represents the Probability Density Function (PDF) of a Random Variable (RV) $X$. Relying on the relation between $y$ and $\rho$, $\eta$ can be calculated as

$$\begin{aligned} \eta =1-\mathrm{Pr }\left( \gamma _{S_{m}R_{n}}\ge \rho \right) \mathrm{Pr }(y\ge \rho )= \left\{ {\begin{array}{*{20}l} 1-e^{-\rho \,\lambda _{S_{m}R_{n}}}, \,\,\, \mathrm{if }\, y\ge \rho \\ 1,\,\,\, \mathrm{if }\, y<\rho \\ \end{array}}, \right. \end{aligned}$$

(5.8)

in which $\lambda _{S_{m}R_{n}}\triangleq 1/\mathrm{E }\{\gamma _{S_{m}R_{n}}\}$, with $\mathrm{E }\{\cdot \}$ denoting expectation. Then, by substituting Eq. (5.8) into Eq. (5.7) and after some rearrangements, we have

$$\begin{aligned} F_{\gamma _{n}}(\rho )=1-e^{-\rho \,\lambda _{R_{n}D}}+e^{-\rho \,\lambda _{R_{n}D}}\prod _{m=1}^{M}\left( 1-e^{-\rho \,\lambda _{S_{m}R_{n}}}\right) , \end{aligned}$$

(5.9)

where $\lambda _{R_{n}D}\triangleq 1/\mathrm{E }\{\gamma _{R_{n}D}\}$. Based on above, a closed-form expression for $P_\mathrm{out }^\mathrm{NDL }$ can be derived as

$$\begin{aligned} P_\mathrm{out }^\mathrm{NDL }=\prod _{n=1}^{N}\left[ 1-e^{-\rho \,\lambda _{R_{n}D}}+e^{-\rho \,\lambda _{R_{n}D}}\prod _{m=1}^{M} \left( 1-e^{-\rho \,\lambda _{S_{m}R_{n}}}\right) \right] . \end{aligned}$$

(5.10)

By using the fact that $e^{x}\approx 1+x$ when $x\rightarrow 0$, it can be concluded that, for sufficiently large system SNR, i.e., $\bar{\gamma }\rightarrow \infty$, Eq. (5.10) can be asymptotically written as

$$\begin{aligned} P_\mathrm{out }^\mathrm{NDL }\simeq \prod _{n=1}^{N}\left( \rho \,\lambda _{R_{n}D}\right) \propto \left( \frac{1}{\bar{\gamma }}\right) ^{N}. \end{aligned}$$

(5.11)

From Eq. (5.11), note that when there is no direct link between the sources and destination, the system diversity order equals to $N$, which means that MUD makes no contribution to the total diversity order.

2.2.2 Outage Analysis with Direct Links

When there are direct links from the sources to destination, the end-to-end SNR can be expressed as $\max \left[ \max \limits _{m}\gamma _{S_{m}D},\max \limits _{n}\gamma _{n}\right]$. Then, from the results above and knowing that $\gamma _{S_{m}D}$ and $\gamma _{n}$ are mutually independent, we can arrive at

$$\begin{aligned} P_\mathrm{out }^\mathrm{DL }=\left[ \prod _{m=1}^{M}F_{\gamma _{S_{m}D}}(\rho )\right] \left[ \prod _{n=1}^{N}F_{\gamma _{n}}(\rho )\right] . \end{aligned}$$

(5.12)

For high SNR regime, an asymptotic expression of Eq. (5.12) can be derived as

$$\begin{aligned} P_\mathrm{out }^\mathrm{DL }\simeq \left[ \prod _{m=1}^{M}\left( \rho \lambda _{S_{m}D}\right) \right] \left[ \prod _{n=1}^{N}\left( \rho \lambda _{R_{n}D}\right) \right] \propto \left( \frac{1}{\bar{\gamma }}\right) ^{M+N}, \end{aligned}$$

(5.13)

where $\lambda _{S_{m}D}\triangleq 1/\mathrm{E }\{\gamma _{S_{m}D}\}$. From Eq. (5.13), note that the total diversity order is $M+N$. Therefore, two parts contribute to the total diversity order, i.e., the direct links $S_{m}\rightarrow D$ ($m=1,\ldots , M$) and the relaying links $R_{n}\rightarrow D$ ($n=1,\ldots , N$). Combining this observation with that obtained in Sect. 5.2.2.1, it can be said that for MUD-based multisource multirelay cooperative systems, the direct links play an important role in the system diversity order.

2.3 The New Two-Step Selection Scheme

2.3.1 Outage Behavior

Now, an efficient low-complexity two-step selection scheme for the combination of cooperative diversity and multiuser diversity is proposed. Specifically, based on the channel quality of the direct links, the source node $S_{m^{*}}$ satisfying $m^{*}=\mathrm{arg }\max \limits _{m}\left[ \gamma _{S_{m}D}\right]$ is first chosen.² ${}^{,}$ ³ Then, the relay with the maximum dual-hop end-to-end SNR from $S_{m^{*}}$ to $D$ is selected. Afterward, the two-phase opportunistic DF relaying [3] starts and $D$ processes the received signals during the two-phase transmission using a selection combining technique. Thus, in the second phase, the best link between $S_{m^{*}}$ and $D$ is chosen so that the end-to-end SNR satisfies

$$\begin{aligned} \gamma ^\mathrm{new }=\max \left[ \max _{m}\left[ \gamma _{S_{m}D}\right] ,\max _{n}\left[ \min \left[ \gamma _{S_{m^{*}}R_{n}},\gamma _{R_{n}D}\right] \right] \right] . \end{aligned}$$

(5.14)

Next, we investigate the outage behavior of this new selection scheme. First, due to the independence between the direct links and dual-hop links, the outage probability can be formulated as

$$\begin{aligned} P_\mathrm{out }^\mathrm{new }&=\;\mathrm{Pr }\left( \gamma ^\mathrm{new }<\rho \right) =\mathrm{Pr }\left( \max _{m}\left[ \gamma _{S_{m}D}\right] <\rho \right) \nonumber \\&\quad \times \underbrace{\mathrm{Pr } \left( \max _{n}\left[ \min \left[ \gamma _{S_{m^{*}}R_{n}},\gamma _{R_{n}D}\right] \right] <\rho \right) }_{\chi }, \end{aligned}$$

(5.15)

where $\mathrm{Pr }\left( \max \limits _{m}\left[ \gamma _{S_{m}D}\right] <\rho \right)$ is readily solved as

$$\begin{aligned} \mathrm{Pr }\left( \max _{m}\left[ \gamma _{S_{m}D}\right] <\rho \right) =\prod _{m=1}^{M}\mathrm{Pr }\left( \gamma _{S_{m}D}<\rho \right) =\prod _{m=1}^{M} \left( 1-e^{-\rho \lambda _{S_{m}D}}\right) . \end{aligned}$$

(5.16)

Now, according to the total probability theorem [16], $\chi$ in Eq. (5.15) can be rewritten as

$$\begin{aligned} \chi =\sum _{m=1}^{M}\mathrm{Pr }\left( m^{*}=m\right) \underbrace{\mathrm{Pr } \left( \max _{n}\left[ \min \left[ \gamma _{S_{m}R_{n}},\gamma _{R_{n}D}\right] \right] <\rho \right) }_{\varTheta }, \end{aligned}$$

(5.17)

in which $\varTheta$ can be expressed as

$$\begin{aligned} \varTheta =\prod _{n=1}^{N}\left[ F_{\gamma _{S_{m}R_{n}}}(\rho )+F_{\gamma _{R_{n}D}}(\rho )-F_{\gamma _{S_{m}R_{n}}}(\rho ) F_{\gamma _{R_{n}D}}(\rho )\right] . \end{aligned}$$

(5.18)

In addition, $\mathrm{Pr }\left( m^{*}=m\right)$ is given by

$$\begin{aligned} \mathrm{Pr }(m^{*}=m)=1+\sum _{k=1}^{M-1}\sum _{A_{k}\subseteq \{1,2,\ldots ,m-1,m+1,\ldots ,M\}\atop {|A_k|=k}}(-1)^{k}\frac{\lambda _{S_{m}D}}{\lambda _{S_{m}D}+\sum \nolimits _{j\in A_{k}}\lambda _{S_{j}D}}, \end{aligned}$$

(5.19)

where a detailed proof of Eq. (5.19) is found in [8, Appendix]. Finally, by substituting Eqs. (5.18) and (5.19) into Eq. (5.17), and then plugging the latter into Eq. (5.15), a closed-form expression for the outage probability can be achieved as

$$\begin{aligned} P_\mathrm{out }^\mathrm{new }=&\;\left[ \prod _{m=1}^{M}\left( 1-e^{-\rho \lambda _{S_{m}D}}\right) \right] \sum _{m=1}^{M}\left( 1+\sum _{k=1}^{M-1} \sum _{A_{k}\subseteq \{1,2,\ldots ,m-1,m+1,\ldots ,M\}\atop {|A_k|=k}}(-1)^{k}\frac{\lambda _{S_{m}D}}{\lambda _{S_{m}D}+\sum \nolimits _{j\in A_{k}}\lambda _{S_{j}D}}\right) \nonumber \\&\;\times \prod _{n=1}^{N}\left[ \left( 1-e^{-\rho \lambda _{S_{m}R_{n}}}\right) +\left( 1-e^{-\rho \lambda _{R_{n}D}}\right) - \left( 1-e^{-\rho \lambda _{S_{m}R_{n}}}\right) \left( 1-e^{-\rho \lambda _{R_{n}D}}\right) \right] . \end{aligned}$$

(5.20)

Knowing that $e^{x}\approx 1+x$ when $x\rightarrow 0$, note that as $\bar{\gamma }\rightarrow \infty$, (5.20) can be asymptotically written as

$$\begin{aligned} P_\mathrm{out }^\mathrm{new }\simeq&\; \left[ \prod _{m=1}^{M}\left( \rho \lambda _{S_{m}D}\right) \right] \sum _{m=1}^{M} \left[ \left( 1+\sum _{k=1}^{M-1}\sum _{A_{k}\subseteq \{1,2,\ldots ,m-1,m+1,\ldots ,M\}\atop {|A_k|=k}}(-1)^{k}\frac{\lambda _{S_{m}D}}{\lambda _{S_{m}D}+\sum \nolimits _{j\in A_{k}}\lambda _{S_{j}D}}\right) \right. \nonumber \\&\;\times \left. \prod _{n=1}^{N}\left[ \rho \left( \lambda _{S_{m}R_{n}}+\lambda _{R_{n}D}\right) \right] \right] \propto \left( \frac{1}{\bar{\gamma }}\right) ^{M+N}. \end{aligned}$$

(5.21)

From Eq. (5.21), note that the diversity order of the proposed selection scheme is $M+N$, which is the same with the counterpart of the joint source-relay selection scheme.

2.3.2 Distributed Implementation

In this part, the distributed implementation of the proposed two-step selection scheme is presented, as illustrated in Fig. 5.1. Specifically,

(a) Selection for $S_{m^{*}}$: First, the destination $D$ broadcasts a Source Selection Request Message (SSRM), which indicates a request for the start of source selection. This message is received by all the sources $S_m (m=1,\ldots ,M)$. By overhearing SSRM, all the relays $R_n (n=1,\ldots ,N)$ are able to estimate their respective channel gains $|h_{R_{n}D}|^{2}$ , which will be utilized for the subsequent distributed relay selection. For the sources, by estimating the channel gains $|h_{S_{m}D}|^{2}$ based on SSRM, they start their respective timers and perform the distributed source selection by means of distributed timer technique [2]. Finally, the source with the best direct source-destination link has its timer expire first and broadcasts a Source Selection Acknowledge Message (SSAM) to identify its presence. Upon hearing SSAM, all the other sources back off. In addition, SSAM is also received by $D$ and is overheard by all the relays $R_n, n=1,\ldots ,N$.

(b) Selection for $R_{n^{*}}$: Once the relays $R_n (n=1,\ldots ,N)$ receive SSAM, each of them is able to estimate the channel gains $|h_{S_{m^{*}}R_{n}}|^{2}$ between $S^{*}$ and itself. Then, by combining $|h_{S_{m^{*}}R_{n}}|^{2}$ with their respective $|h_{R_{n}D}|^{2}$ attained before, each of the relays calculates its corresponding dual-hop end-to-end SNR according to the opportunistic relaying strategy employed. Specifically, for the opportunistic DF relaying strategy, the dual-hop end-to-end SNR for $R_n$ is $\min \left[ \frac{P_{S}|h_{S_{m^{*}}R_{n}}|^{2}}{N_{0}},\frac{P_{R}|h_{R_{n}D}|^{2}}{N_{0}}\right]$. Next, the end-to-end SNR is used to set the timer of each relay $R_n$ by means of distributed timer technique. Consequently, the relay $R_{n^{*}}$ with the maximum dual-hop end-to-end SNR has its timer expired first and is chosen as the selected relay. At the same time, $R_{n^{*}}$ broadcasts a Relay Selection Acknowledge Message (RSAM) to identify its presence. Upon hearing RSAM, all the other relays back off.

(c) Two-phase transmission and signal processing at $D$: Upon hearing RSAM, the selected source $S_{m^{*}}$ starts the traditional two-phase transmission process. In the first phase, $S_{m^{*}}$ broadcasts and, $R_{n^{*}}$ and $D$ listen. In the second phase, $R_{n^{*}}$ forwards the received signal to $D$. Finally, $D$ processes the received signals during the two-phase transmission by selection combining.

Fig. 5.1

Illustration of a distributed implementation for the proposed two-step selection scheme

In this way, the proposed two-step selection scheme can be implemented in a distributed manner, which does not require extensive distributed Channel State Information (CSI) knowledge. Specifically, the relays do not need the source-destination CSI and the destination (sources) does not need the source (destination)-relays CSI. Hence, it can be named as a “low-complexity” scheme.

2.4 Comparisons Between Joint Selection Scheme and Two-Step Selection Scheme

In this part, a comparison between the joint selection scheme and the proposed selection scheme is carried out. In summary, the merits of the proposed two-step selection scheme are, at least, fourfold.

Firstly, it should be noted that the joint selection scheme has the need of extensive CSI estimation and link quality comparisons, which makes it quite difficult to realize in practical systems. Indeed, the superiority in complexity and overhead of the proposed two-step scheme is very obvious compared to that of the joint selection scheme. To further clarify this, Table 5.1 shows that the complexity of the proposed two-step scheme is much lower than that of the joint selection scheme. For instance, for large-scale multisource multirelay cooperative networks, e.g., $M=100$ and $N=100$, the amounts of CSI estimation and of potential links for comparison are 10200 and 10100, respectively, for the joint selection scheme, whereas the counterparts are 300 and 200 for the proposed two-step scheme, which is a tremendous improvement over the joint selection scheme.

Table 5.1 Comparison between joint selection scheme and two-step selection scheme

Secondly, in order to select jointly the best source-relay pair from all the available ones, the CSI of the joint selection system must be handled in a centralized manner, which involves significant signaling overhead and may not allow to explore the diversity gain in fast-fading environments. This major drawback of the joint selection scheme calls therefore for low-complexity selection schemes, which can be implemented in a distributed manner. Fortunately, as shown above, the proposed selection scheme can be implemented in a distributed manner and therefore it can avoid the high signaling overhead.

Thirdly, the proposed selection scheme achieves the same diversity order with that of the joint selection one. Moreover, as stressed in the next section, the achieved outage performance of this scheme is comparable with that of the joint selection scheme, therefore making it very attractive in practical applications.

Fourthly, concerning the integration complexity into the traditional MUD-based wireless networks, the proposed two-step selection scheme is superior to the joint selection scheme. For traditional MUD-based wireless network, the source is selected based on the channel qualities of the direct source-destination links. In other words, the best direct source-destination link is available in these noncooperative networks. Now, when the relays are configured in these networks, the protocols should be modified to incorporate the cooperative diversity concept. For such, the proposed two-step scheme can be incorporated into these traditional MUD-based networks much easier since the best source-destination link is already available there and what remains to do is to choose the best link (direct or dual-hop link) between the selected source and destination. Thus, the proposed two-step selection scheme is superior to the joint selection scheme concerning the integration complexity.

2.5 Numerical Plots, Simulations, and Comparisons

Now our analytical results will be validated through Monte Carlo simulations, and a perfect concordance between the analytical curves and simulated curves will be observed. In addition, we compare the outage probability of different selection schemes. In all the cases, the nodes of the network are generated in a 2-D plane. Specifically, two scenarios are employed: (1) The destination node is located at (1, 1), and the $M$ sources and $N$ relays are uniformly distributed in the first quadrant of the $1\times 1$ rectangular coordinate region. (2) The destination is located at (1, 1), the M sources are clustered together and co-located at (0, 0), and the $N$ relays are also clustered together and co-located at (0.5, 0.5). Note that the latter case represents the scenario where all the direct links are weak, and relaying is most useful. Without loss of generality, the statistical average (mean) of the channel gain between any two nodes is determined by the distance between them, and the path loss exponent is set to 4. The total available (transmit) power of the system is normalized to unity, and equal power allocation is assumed for a fair comparison among the different selection schemes, i.e., $P_S=P_R=1/2$. In addition, the target spectral efficiency is set to $\mathfrak {R}=1$ bit/s/Hz in all cases considered.

Fig. 5.2

Scenario (1). Outage probability versus system SNR using the DF relaying strategy ($M=3, N=2$). “DL” denotes direct link

Figure 5.2 shows the outage behavior of the joint source-relay selection scheme [19] and the proposed two-step selection schemes when the DF opportunistic relaying strategy is employed. Note that the asymptotes are tight bounds in the medium- and high-SNR regions. It is also observed that the achieved outage performance of the proposed two-step selection scheme is very close to that of the joint selection scheme, with the complexity of the former being much lower. Furthermore, the large gap between the outage curve with direct link and that without direct link demonstrates the crucial role of the direct links in the MUD-based multisource multirelay cooperative systems.

Fig. 5.3

Scenario (1). Outage probability versus system SNR using AF relaying ($M=3, N=2$)

Figure 5.3 shows the outage probabilities of the joint and proposed selection schemes when the AF opportunistic relaying strategy is utilized. Note that, for the AF opportunistic relaying strategy, the outage behavior of the proposed scheme is also comparable with that of the joint selection scheme, which validates the availability of the proposed scheme again.

Figures 5.4 and 5.5 show the impacts of $M$ and $N$ on the outage performance of the joint and the proposed schemes. Herein, without loss of generality, scenario (2) is considered. From Fig. 5.4, it can be seen that, as $M$ increases, the performance gap between the joint selection scheme and the proposed scheme gradually reduces. This is due to the fact that the contribution of the direct links to the overall outage performance increases with $M$, therefore making the performance of the proposed scheme, whose MUD strategy solely depends on the direct links, very close to that of the joint selection scheme. From Fig. 5.5, we observe that the performance gap between the joint selection scheme and the proposed scheme enlarges with an increase in $N$. This is because, when $N$ increases, the joint selection scheme efficiently utilizes the contribution provided by all the dual-hop links, whereas the proposed one does not. However, we should note that, with an increase in $N$, the complexity of the joint selection scheme also significantly increases, whereas that of the proposed one is rather low. Figure 5.6 shows the outage performance for high values of $M$ and $N$ (i.e., $M=N=8$, $16$) under scenario (2). Note that, in this case, the performance of the proposed scheme is also very close to that of the joint selection scheme, therefore validating the practical interest of the former. In addition, for the AF strategy, a similar phenomenon can be observed.

Fig. 5.4

Scenario (2). Outage probability versus system SNR using DF relaying for the scenario where the direct source-destination links are weak ($N=2$)

Fig. 5.5

Scenario (2). Outage probability versus system SNR using DF relaying ($M=2$)

Fig. 5.6

Scenario (2). Outage probability versus system SNR using DF relaying ($M=N=8, 16$)

3 Spectrally-Efficient Schemes for Downlink Cooperative Cellular Networks

In this section, two spectrally efficient schemes for the diversity exploitation of downlink cooperative cellular networks are presented. Such schemes were first proposed in [5], in which one base station (source) communicates with one out of $N$ mobile users (destinations) by using a half-duplex DF relay. As in previous section, we again advocate the exploitation of direct links. Thus, by scheduling the user with the best direct link to access the channel, an Incremental DF relaying scheme is first introduced and its outage behavior is studied, revealing that this scheme can achieve full diversity order. To further enhance the transmission robustness against fading, an improved scheme is also proposed, which considerably utilizes opportunistic scheduling mechanism when the direct transmission fails. Outage analysis for this scheme shows that besides achieving full diversity order, it can also improve the transmission reliability compared with the preceding one. In addition, it is indicated that the expected spectral efficiency of the proposed schemes approaches that of direct transmission in high signal-to-noise ratio regime.

3.1 System Model

Assume a downlink cooperative cellular system in which one base station $S$ intends to transmit information to one out of $N$ mobile users $D_n (n=1,\ldots ,N)$ through the help of one half-duplex DF relay $R$. All terminals are equipped with a single antenna. Differently from [24] and [23], we consider that all the direct links $S\rightarrow D_n$ exist (even if their average channel quality may be not strong) and can be used to convey information. A time-division multiple-access scheme is adopted for orthogonal channel access. For mathematical tractability, we restrict our attentions primarily to a homogenous network topology, where the links between $S$ and $D_n$ and those between $R$ and $D_n$ are subject to independent and identically distributed (i.i.d.) Rayleigh fading, respectively.⁴ Also, we assume the link $S\rightarrow R$ undergoes Rician fading. Hereafter, we denote the channel power gain of a specified link $i\rightarrow j$ as $g_{i,j}=|h_{i,j}|^2$, with $h_{i,j}$ indicating the channel coefficient pertaining to the link $i\rightarrow j$. Accordingly, the channel power gain $g_{\text {SR}}$ of the link $S\rightarrow R$ conforms to noncentral Chi-square distribution given by [18, Eq. (2.16)] $f_{g_{{\text {SR}}}}(x)=\frac{(1+K)e^{-K}}{\varOmega _{{\text {SR}}}}\,e^{-\frac{(1+K)x}{\varOmega _{{\text {SR}}}}}I_{0}\left( 2\sqrt{\frac{K(1+K)x}{\varOmega _{\text {SR}}}}\right)$, where $I_{0}(\cdot )$ denotes the zeroth-order modified Bessel function of the first kind [1, p. 916], $K$ is the Rician K-factor, and $\varOmega _{\text {SR}}$ stands for the statistical average of $g_{\text {SR}}$. In addition, the channel power gains of the links $S\rightarrow D_{n}$ and $R\rightarrow D_{n}$ (namely, $g_{{\text {SD}}_{n}}$ and $g_{{\text {RD}}_{n}}$) follow exponential distributions with means $\varOmega _{{\text {SD}}_{n}}$ and $\varOmega _{{\text {RD}}_{n}}$, respectively. Due to the randomness of wireless channels, the instantaneous channel quality is varying from one time-frame to another.⁵ On one hand, when the instantaneous channel quality of the direct links $S\rightarrow D_{n}$ is weak, the relaying links $S\rightarrow R\rightarrow D_{n}$ can be used to enhance the transmission reliability. In this case, two time-slots will be used to transmit the information. On the other hand, when the instantaneous channel quality of the direct links $S\rightarrow D_{n}$ is strong, the direct links should make their use to convey the information. In particular, a single time-slot may be enough to accomplish the information transmission, yielding therefore improved spectral efficiency. Also, by letting only the destination with the highest instantaneous SNR occupy the channel,⁶ MUD can be readily achieved [4, 8, 19].

3.2 Protocol Descriptions

3.2.1 Incremental DF Relaying with MUD (MU-IDF)

For this scheme, the destination with the best direct link (i.e., $D_{n^{*}}$, with $n^{*}=\mathop {\text {arg max}}\limits _{n=1,\ldots ,N}[g_{{\text {SD}}_{n}}]$) is first selected out of the $N$ available ones. Afterwards, depending on the instantaneous channel quality of the selected direct link, the information transmission is performed into one or two time-slots. Specifically, in the first time-slot, $S$ broadcasts while $R$ and $D_{n^{*}}$ listen. For a given target spectral efficiency $\mathfrak {R}_{s}$ bit/s/Hz, if $D_{n^{*}}$ decodes the information correctly, it will broadcast a ‘success’ message⁷ to $S$ and $R$. Otherwise, $D_{n^{*}}$ will broadcast a ‘failure’ message to $S$ and $R$. Upon receiving the ‘success’ message, $S$ will be able to send a new information in the next time-slot. Otherwise, in the next time-slot, the relay $R$ will try to decode the previous information and retransmit it to $D_{n^{*}}$. As a result, the maximal mutual information for the MU-IDF scheme can be formulated as

$$\begin{aligned} I_\mathrm{MU-IDF }= \left\{ {\begin{array}{*{20}l} I_\mathrm{DT }, \,\,\, \mathrm{if }\, \log _{2}\left( 1+\gamma _{{\text {SD}}_{n^{*}}}\right) \ge \mathfrak {R}_{s} \\ I_\mathrm{ODF }, \,\,\, \mathrm{if }\, \log _{2}\left( 1+\gamma _{{\text {SD}}_{n^{*}}}\right) < \mathfrak {R}_{s} \\ \end{array}}, \right. \end{aligned}$$

(5.22)

where $I_\mathrm{DT }=\log _{2}\left( 1+\gamma _{{\text {SD}}_{n^{*}}}\right)$ and $I_\mathrm{ODF }=\frac{1}{2}\log _{2}\left( 1+ \min [\gamma _{\text {SR}},\gamma _{{\text {SD}}_{n^{*}}}+\gamma _{{\text {RD}}_{n^{*}}}]\right)$, with $n^{*}=\mathop {\text {arg max}}\limits _{n=1,\ldots ,N}\left[ g_{{\text {SD}}_{n}}\right]$, $\gamma _{{\text {SD}}_{n}}\triangleq P_{S}\,g_{{\text {SD}}_{n}}/N_{0}$, $\gamma _{\text {SR}}\triangleq P_{S}\,g_{\text {SR}}/N_{0}$ and $\gamma _{{\text {RD}}_{n}}\triangleq P_{R}\,g_{{\text {RD}}_{n}}/N_{0}$. As in previous section, we refer to $\bar{\gamma }\triangleq {1}/{N_0}$ as system SNR.

3.2.2 Improved Incremental DF Relaying with MUD

For MU-IIDF, similar to MU-IDF, the destination with the best direct link (i.e., $D_{n^{*}}$) is first chosen. In the first time-slot, $S$ broadcasts while $R$ and all the destinations $D_n$ listen.⁸ Then, relying on $D_{n^{*}}$ being or not being able to decode the information from $S$ correctly, $D_{n^{*}}$ will broadcast a ‘success’ or ‘failure’ message to $S$ and $R$, as in the case of MU-IDF. Upon receiving a ‘success’ message, $S$ will be able to transmit a new information in the next time-slot. Otherwise, relaying transmission will be performed. However, intuitively, $D_{n^{*}}$ may be now not the optimal choice. To address this, note that the opportunistic scheduling mechanism will be invoked. In particular, a new destination (possibly different from $D_{n^{*}}$) will be selected based on

$$\begin{aligned} n^{\varDelta }=\mathrm{arg }\,\max _{n=1,\ldots ,N}\left[ \gamma _{{\text {SD}}_{n}}+\gamma _{{\text {RD}}_{n}}\right] . \end{aligned}$$

(5.23)

Consequently, in the second time-slot, $R$ will try to decode the preceding information and forward it to the new destination $D_{n^{\varDelta }}$. Accordingly, the maximal mutual information for the MU-IIDF scheme can be expressed as

$$\begin{aligned} I_\mathrm{MU-IIDF }= \left\{ {\begin{array}{*{20}l} I_\mathrm{DT }, \,\,\, \mathrm{if }\, \log _{2}\left( 1+\gamma _{{\text {SD}}_{n^{*}}}\right) \ge \mathfrak {R}_{s} \\ \tilde{I}_\mathrm{ODF }, \,\,\, \mathrm{if }\, \log _{2}\left( 1+\gamma _{{\text {SD}}_{n^{*}}}\right) < \mathfrak {R}_{s} \\ \end{array}}, \right. \end{aligned}$$

(5.24)

where $\tilde{I}_\mathrm{ODF }=\frac{1}{2}\log _{2}\left( 1+\min \left[ \gamma _{{\text {SR}}},\gamma _{{\text {SD}}_{n^{\varDelta }}}+\gamma _{{\text {RD}}_{n^{\varDelta }}}\right] \right)$, and $I_\mathrm{DT }$ is the same as before.

3.3 User Selection Process

For each user selection process,⁹ the base station (source) first broadcasts a User Selection Requirement (USR) message to all the mobile users (destinations). Upon hearing the USR message, each mobile user can estimate its respective channel gain toward to the source. Afterwards, each mobile user returns its respective channel gain to the source in a round-robin fashion. Then, the source compares the $N$ channel gains pertaining to the direct links and selects the best one based on the criterion presented in Sect. 5.3.2.1. In this way, the best direct link can be selected and the selection process expires for the MU-IDF scheme.

For the MU-IIDF scheme, if the direct transmission is successful, the above selection process is sufficient. Otherwise, the user selection process is invoked again according to Eq. (5.23). Specifically, the relay first broadcasts a USR message to all the mobile users so that each mobile user can estimate its channel gain toward to the relay. Then, these channel gains (or equivalently, link SNRs) are returned to the base station from each mobile user in a round-robin manner. Finally, the base station chooses the best mobile user based on Eq. (5.23).

3.4 Outage Behavior

3.4.1 MU-IDF

(1) Exact Outage Behavior: We first analyze the exact outage performance of the MU-IDF scheme. From the protocol descriptions, an outage event occurs if neither the direct transmission nor the relaying transmission is successful. Specifically, for a predefined spectral efficiency $\mathfrak {R}_{s}$ bit/s/Hz, the probability to characterize such an event can be formulated as

$$\begin{aligned} P_\mathrm{{out}}^\mathrm{{IDF}}&=\mathrm{Pr }\left( \gamma _{{\text {SD}}_{n^{*}}}<2^{\mathfrak {R}_{s}}-1\triangleq \tau ,\gamma _{\text {SR}}<\tau \right) \nonumber \\&\quad +\mathrm{Pr }\left( \gamma _{{\text {SD}}_{n^{*}}}<\tau ,\gamma _{\text {SR}}>\tau ,\gamma _{{\text {SD}}_{n^{*}}}+\gamma _{{\text {RD}}_{n^{*}}}<\tau \right) \nonumber \\&=\underbrace{\mathrm{Pr }\left( \gamma _{{\text {SD}}_{n^{*}}}<\tau \right) \mathrm{Pr }\left( \gamma _{\text {SR}}<\tau \right) }_{J_1}+\underbrace{ \mathrm{Pr }\left( \gamma _{\text {SR}}>\tau , \gamma _{{\text {SD}}_{n^{*}}}+\gamma _{{\text {RD}}_{n^{*}}}<\tau \right) }_{J_2}. \end{aligned}$$

(5.25)

Next, both $J_1$ and $J_2$ will be attained. With the aid of order statistics [16] and from [18, Eq. (4.34)], $J_{1}$ can be derived in closed-form as

$$\begin{aligned} J_{1}=\left[ \prod _{n=1}^{N}\left( 1-e^{-\tau /\bar{\gamma }_{{\text {SD}}_{n}}}\right) \right] \left[ 1-Q\left( \sqrt{2K},\sqrt{\frac{2(K+1)\tau }{\bar{\gamma }_{\text {SR}}}}\right) \right] , \end{aligned}$$

(5.26)

in which $Q(\cdot ,\cdot )$ denotes the first-order Marcum $Q$-function [18, Eq. (4.34)], $\bar{\gamma }_{{\text {SD}}_{n}}\triangleq E[\gamma _{{\text {SD}}_{n}}]$ and $\bar{\gamma }_{\text {SR}}\triangleq E[\gamma _{\text {SR}}]$. Next, making use of the total probability theorem [16], $J_2$ can be rewritten as

$$\begin{aligned} J_{2}&=\mathrm{Pr }\left( \gamma _{\text {SR}}>\tau \right) \mathrm{Pr }\left( \gamma _{{\text {SD}}_{n^{*}}}+\gamma _{{\text {RD}}_{n^{*}}} <\tau \right) \nonumber \\&=Q\left( \sqrt{2K},\sqrt{\frac{2(K+1)\tau }{\bar{\gamma }_{\text {SR}}}}\right) \underbrace{ \sum _{n=1}^{N}\int _{0}^{\tau }f_{\gamma _{{\text {SD}}_{n}}}(x)F_{\gamma _{{\text {RD}}_{n}}}(\tau -x)\prod _{l=1\atop {l\ne n}}^{N}F_{\gamma _{{\text {SD}}_{l}}}(x)dx}_{J_3}, \end{aligned}$$

(5.27)

where $J_3$ can be expressed as

$$\begin{aligned} J_{3}&=\;\sum _{n=1}^{N}\frac{1}{\bar{\gamma }_{{\text {SD}}_{n}}}\int _{0}^{\tau }e^{-\frac{x}{\bar{\gamma }_{{\text {SD}}_{n}}}}\left( 1-e^{-\frac{\tau -x}{\bar{\gamma }_{{\text {RD}}_{n}}}}\right) \left[ 1+\sum _{l=1}^{N-1}\sum _{S_{l}\subseteq \{1,\ldots ,N\}\setminus n \atop {|S_l|=l}}(-1)^{l}e^ {-\sum \nolimits _{j\in S_{l}}\frac{x}{\bar{\gamma }_{{\text {SD}}_{j}}}}\right] dx\nonumber \\&=\;\sum _{n=1}^{N}\left( 1-e^{-\frac{\tau }{\bar{\gamma }_{{\text {SD}}_{n}}}}\right) +\sum _{n=1}^{N}\frac{1}{\bar{\gamma }_{{\text {SD}}_{n}}} \sum _{l=1}^{N-1}\sum _{S_{l}\subseteq \{1,\ldots ,N\}\setminus n \atop {|S_l|=l}}(-1)^{l}\frac{1-e^{-\tau \left( \frac{1}{\bar{\gamma }_{{\text {SD}}_{n}}}+\sum \nolimits _{j\in S_{l}}\frac{1}{\bar{\gamma }_{{\text {SD}}_{j}}}\right) }}{\frac{1}{\bar{\gamma }_{{\text {SD}}_{n}}}+\sum \nolimits _{j\in S_{l}}\frac{1}{\bar{\gamma }_{{\text {SD}}_{j}}}}\nonumber \\&\quad \;\; -\sum _{n=1}^{N}\frac{1}{\bar{\gamma }_{{\text {SD}}_{n}}}e^{-\frac{\tau }{\bar{\gamma }_{{\text {RD}}_{n}}}}J_{4,n}-\sum _{n=1}^{N}\frac{1}{\bar{\gamma }_{{\text {SD}}_{n}}}e^{-\frac{\tau }{\bar{\gamma }_{{\text {RD}}_{n}}}}\sum _{l=1}^{N-1}\sum _{S_{l}\subseteq \{1,\ldots ,N\}\setminus n \atop {|S_l|=l}}(-1)^{l} J_{5,l}, \end{aligned}$$

(5.28)

in which $J_{4,n}$ and $J_{5,l}$ are given, respectively, by

$$\begin{aligned} J_{4,n}=&\left\{ {\begin{array}{*{20}l} \tau , \quad \mathrm{if }\,\,\, \frac{1}{\bar{\gamma }_{{\text {SD}}_{n}}}=\frac{1}{\bar{\gamma }_{{\text {RD}}_{n}}} \\ \frac{1-e^{-\tau \left( \frac{1}{\bar{\gamma }_{{\text {SD}}_{n}}}-\frac{1}{\bar{\gamma }_{{\text {RD}}_{n}}}\right) }}{\frac{1}{\bar{\gamma }_{{\text {SD}}_{n}}}- \frac{1}{\bar{\gamma }_{{\text {RD}}_{n}}}}, \qquad \mathrm{if }\,\,\, \frac{1}{\bar{\gamma }_{{\text {SD}}_{n}}}\ne \frac{1}{\bar{\gamma }_{{\text {RD}}_{n}}} \\ \end{array}}, \right. \end{aligned}$$

(5.29)

$$\begin{aligned} J_{5,l}=&\left\{ {\begin{array}{*{20}l} \tau , \qquad \mathrm{if }\quad \frac{1}{\bar{\gamma }_{{\text {RD}}_{n}}}=\frac{1}{\bar{\gamma }_{{\text {SD}}_{n}}}+\sum \nolimits _{j\in S_{l}}\frac{1}{\bar{\gamma }_{{\text {SD}}_{j}}} \\ \frac{1-e^{-\tau \left( \frac{1}{\bar{\gamma }_{{\text {SD}}_{n}}}-\frac{1}{\bar{\gamma }_{{\text {RD}}_{n}}}+\sum \nolimits _{j\in S_{l}}\frac{1}{\bar{\gamma }_{{\text {SD}}_{j}}}\right) }}{\frac{1}{\bar{\gamma }_{{\text {SD}}_{n}}}-\frac{1}{\bar{\gamma }_{{\text {RD}}_{n}}}+\sum \nolimits _{j\in S_{l}}\frac{1}{\bar{\gamma }_{{\text {SD}}_{j}}}}, \qquad \mathrm if \,\,\, \frac{1}{\bar{\gamma }_{{\text {RD}}_{n}}}\ne \frac{1}{\bar{\gamma }_{{\text {SD}}_{n}}} +\sum \nolimits _{j\in S_{l}}\frac{1}{\bar{\gamma }_{{\text {SD}}_{j}}} \\ \end{array}}. \right. \end{aligned}$$

(5.30)

Finally, by substituting Eqs. (5.29) and (5.30) into Eq. (5.28) and plugging the latter into Eq. (5.27), a closed-form expression is achieved for $J_2$. Then, by combining Eqs. (5.26) and (5.27), one can arrive at a closed-form expression for the outage probability of MU-IDF.

(2) Asymptotic Outage Behavior: Even though the exact outage probability of MU-IDF is available, it is hard to get any insight from this formulation, due to the inherent complexity of the considered systems. In order to understand the inward nature of the outage behavior of this proposed scheme, in the sequel, we present the asymptotic outage behavior of MU-IDF in high SNR regime.

The achievable diversity order of MU-IDF is $N+1$. Particularly, at high SNR, the outage probability of MU-IDF can be asymptotically written as

$$\begin{aligned} P_\mathrm{out }^\mathrm{IDF }&\simeq (K+1)\tau ^{N+1}e^{-K}\frac{1}{\bar{\gamma }_{\text {SR}}}\left( \prod _{n=1}^{N}\frac{1}{\bar{\gamma }_{{\text {SD}}_{n}}}\right) \nonumber \\&\quad +\frac{\tau ^{N+1}}{N(N+1)}\left( \prod _{l=1}^{N}\frac{1}{\bar{\gamma }_{{\text {SD}}_{l}}}\right) \left( \sum _{n=1}^{N}\frac{1}{\bar{\gamma }_{{\text {RD}}_{n}}}\right) \propto \bar{\gamma }^{-(N+1)}. \end{aligned}$$

(5.31)

For the considered homogenous network topology, i.e., $\bar{\gamma }_{{\text {SD}}_{n}}=\bar{\gamma }_{\text {SD}}$ and $\bar{\gamma }_{{\text {RD}}_{n}}= \bar{\gamma }_{\text {RD}}$, Eq. (5.31) reduces to

$$\begin{aligned} P_\mathrm{out }^\mathrm{IDF }\simeq \tau ^{N+1}\left( \frac{1}{\bar{\gamma }_{\text {SD}}}\right) ^{N}\left[ \frac{(K+1)e^{-K}}{\bar{\gamma }_{\text {SR}}} +\frac{1}{(N+1)\bar{\gamma }_{\text {RD}}}\right] . \end{aligned}$$

(5.32)

The proof of Eq. (5.31) can be found in [5, Appendix A].

From Eqs. (5.31) and (5.32), it is clear that the proposed MU-IDF scheme can achieve full diversity order $N+1$. Furthermore, it is noteworthy that all the transmit links (including the direct links $S\rightarrow D_{n}$ and the relaying links $S\rightarrow R$ and $R\rightarrow D_{n}$) contribute to the overall system diversity order. In particular, except for the case of $N=1$, the contribution of the direct links to the overall system diversity order is always greater than that of the relaying links. This observation somewhat explains why the system diversity order reduces to unity when no direct link is available, as considered in [24]. By following a similar procedure as employed in [8, Appendix], $\mathrm{Pr }(n^{*}=n)$ can be calculated as

$$\begin{aligned} \mathrm{Pr }(n^{*}=n)&=1+\sum _{k=1}^{N-1}\sum _{A_{k}\subseteq \{1,\ldots ,N\}\setminus n \atop {|A_k|=k}}(-1)^{k}\frac{1/\varOmega _{{\text {SD}}_{n}}}{1/\varOmega _{{\text {SD}}_{n}}+\sum \nolimits _{j\in A_{k}}1/\varOmega _{{\text {SD}}_{j}}}\nonumber \\&\overset{(a)}{=}1+\sum _{k=1}^{N-1}\left( {\begin{array}{c}N-1\\ k\end{array}}\right) (-1)^{k}\frac{1}{k+1}\overset{(b)}{=}\frac{1}{N}, \end{aligned}$$

(5.33)

where step (a) is due to the homogenous (symmetrical) network topology and step (b) is due to [11, Eq. (0.155.1)]. Thus, the fairness can be guaranteed.

3.4.2 MU-IIDF

(1) Exact Outage Behavior: For a target spectral efficiency $\mathfrak {R}_{s}$ bit/s/Hz, it is shown from last section that the outage probability of MU-IIDF can be written as

$$\begin{aligned} P_\mathrm{out }^\mathrm{IIDF }=\mathrm{Pr }\left( \gamma _{{\text {SD}}_{n^{*}}}<\tau ,\gamma _{\text {SR}}<\tau \right) + \underbrace{\mathrm{Pr }\left( \gamma _{{\text {SD}}_{n^{*}}}<\tau ,\gamma _{\text {SR}}>\tau ,\gamma _{{\text {SD}}_{n^{\varDelta }}}+\gamma _{{\text {RD}}_{n^{\varDelta }}}<\tau \right) }_{J_6}, \end{aligned}$$

(5.34)

where the first term of Eq. (5.34) is exactly the same as $J_1$. On the other hand, by noting that the event $\{\gamma _{{\text {SD}}_{n^{\varDelta }}}+\gamma _{{\text {RD}}_{n^{\varDelta }}}<\tau \}$ definitely implies the event $\{\gamma _{{\text {SD}}_{n^{*}}}<\tau \}$, the second term of Eq. (5.34) can be simplified

$$\begin{aligned} J_{6}=\mathrm{Pr }(\gamma _{\text {SR}}>\tau )\underbrace{\mathrm{Pr }\left( \max _{n}\left[ \gamma _{{\text {SD}}_{n}}+\gamma _{{\text {RD}}_{n}}\right] <\tau \right) }_{J_7}, \end{aligned}$$

(5.35)

in which $\mathrm{Pr }(\gamma _{\text {SR}}>\tau )=Q\left( \sqrt{2K},\sqrt{\frac{2(K+1)\tau }{\bar{\gamma }_{\text {SR}}}}\right)$. Next, turning our attention to $J_7$, it follows from order statistics that

$$\begin{aligned} J_{7}=\prod _{n=1}^{N}\underbrace{\mathrm{Pr }\left( \gamma _{{\text {SD}}_{n}}+\gamma _{{\text {RD}}_{n}}<\tau \right) }_{\theta _n}, \end{aligned}$$

(5.36)

where $\theta _n$ can be derived, after some algebraic manipulations, as

$$\begin{aligned} \theta _{n}=1-e^{-\tau /\bar{\gamma }_{{\text {SD}}_{n}}}-\frac{1}{\bar{\gamma }_{{\text {SD}}_{n}}}e^{-\tau /\bar{\gamma }_{{\text {RD}}_{n}}} \underbrace{\int _{0}^{\tau }e^{x\left( \frac{1}{\bar{\gamma }_{{\text {RD}}_{n}}}-\frac{1}{\bar{\gamma }_{{\text {SD}}_{n}}}\right) }dx}_{\varphi }. \end{aligned}$$

(5.37)

Relying on the relation between $\bar{\gamma }_{{\text {RD}}_{n}}$ and $\bar{\gamma }_{{\text {SD}}_{n}}$, $\varphi$ can be calculated as

$$\begin{aligned} \varphi = \left\{ {\begin{array}{*{20}l} \tau , \qquad \mathrm{if }\,\,\, \bar{\gamma }_{{\text {RD}}_{n}}=\bar{\gamma }_{{\text {SD}}_{n}}, \\ \frac{e^{\tau \left( 1/\bar{\gamma }_{{\text {RD}}_{n}}-1/\bar{\gamma }_{{\text {SD}}_{n}}\right) }-1}{1/\bar{\gamma }_{{\text {RD}}_{n}}-1/\bar{\gamma }_{{\text {SD}}_{n}}}, \qquad \mathrm{if }\,\,\, \bar{\gamma }_{{\text {RD}}_{n}}\ne \bar{\gamma }_{{\text {SD}}_{n}} \\ \end{array}}. \right. \end{aligned}$$

(5.38)

Now, by summarizing the results above, a closed-form expression is achieved for the outage probability of MU-IIDF.

(2) Asymptotic Outage Behavior: The achievable diversity order of MU-IIDF is $N+1$. Particularly, for sufficiently high system SNR, the outage probability of the MU-IIDF scheme can be asymptotically expressed as

$$\begin{aligned} P_\mathrm{out }^\mathrm{IIDF }&\simeq \prod _{n=1}^{N}\left( \frac{\tau ^{2}}{2\bar{\gamma }_{{\text {SD}}_{n}} \bar{\gamma }_{{\text {RD}}_{n}}}\right) +\frac{(K+1)\tau ^{N+1}e^{-K}}{\bar{\gamma }_{\text {SR}}}\prod _{n=1}^{N}\frac{1}{\bar{\gamma }_{{\text {SD}}_{n}}}\nonumber \\&\simeq \left\{ {\begin{array}{*{20}l} \frac{\tau ^{2}}{2\bar{\gamma }_{\text {SD}}\bar{\gamma }_{\text {RD}}}+\frac{(K+1)\tau ^{2}e^{-K}}{\bar{\gamma }_{\text {SR}}\bar{\gamma }_{\text {SD}}}, \,\,\,\,\,\, \mathrm{if }\,\,\, N=1, \\ \frac{(K+1)\tau ^{N+1}e^{-K}}{\bar{\gamma }_{\text {SR}}}\prod \nolimits _{n=1}^{N}\frac{1}{\bar{\gamma }_{{\text {SD}}_{n}}}, \,\,\,\,\,\, \mathrm{if }\,\,\, N\ge 2 \\ \end{array}}. \right. \end{aligned}$$

(5.39)

The proof of Eq. (5.39) can be found in [5, Appendix B].

It is noted from Eq. (5.39) that for $N\ge 2$, the outage behavior of the MU-IIDF scheme in high SNR regime is determined by the $S\rightarrow R$ link and the $S\rightarrow D_n$ links irrespective of the fading severity pertaining to the $R\rightarrow D_n$ links. Nevertheless, for $N=1$, the outage behavior at high SNR is determined by the direct link ($S\rightarrow D$) as well as the relaying links ($S\rightarrow R$ and $R\rightarrow D$). Furthermore, it is observed from Eq. (5.39) that for $N\ge 2$, the direct links dominate the overall system diversity order, which highlights the usefulness of the direct links and the necessity of exploiting them. For arbitrary $n\in \{1,\ldots ,N\}$, we have

$$\begin{aligned}&\mathrm{Pr }(n^{\varDelta }=n)=\mathrm{Pr }\left( \bigcap _{l=1\atop {l\ne n}}^{N}(\gamma _{{\text {SD}}_{l}}+\gamma _{{\text {RD}}_{l}}<\gamma _{{\text {SD}}_{n}}+\gamma _{{\text {RD}}_{n}})\right) \nonumber \\&=\int _{0}^{\infty }\int _{0}^{\infty }f_{\gamma _{{\text {SD}}_{n}}}(x)f_{\gamma _{{\text {RD}}_{n}}}(y)\mathrm{Pr } \left( \bigcap _{l=1\atop {l\ne n}}^{N}(\gamma _{{\text {SD}}_{l}}+\gamma _{{\text {RD}}_{l}}<x+y)\right) dx dy\nonumber \\&\overset{(c)}{=}\int _{0}^{\infty }\int _{0}^{\infty }f_{\gamma _{\text {SD}}}(x)f_{\gamma _{\text {RD}}}(y) \left[ F_{\gamma _{\text {SD}}+\gamma _{\text {RD}}}(x+y)\right] ^{N-1}dx dy, \end{aligned}$$

(5.40)

where step (c) follows from the homogenous network topology, i.e., $\bar{\gamma }_{{\text {SD}}_{n}}=\bar{\gamma }_{\text {SD}}$ and $\bar{\gamma }_{{\text {RD}}_{n}}=\bar{\gamma }_{\text {RD}}$ [16]. From Eq. (5.40), it is clear that $\mathrm{Pr }(n^{\varDelta }=n)$ remains unchanged for arbitrary $n$, which guarantees the fairness of the MU-IIDF scheme.

3.5 Comparisons Between MUD-IDF and MUD-IIDF

The advantage of MU-IIDF scheme over MU-IDF scheme can be easily confirmed for the scenario where both the direct links and the links between the relay and the mobile users (destinations) are weak.¹⁰ For such a case, direct links generally fail to convey the information and the second-hop becomes the bottleneck for the dual-hop relaying transmission. Therefore, the MU-IIDF scheme, which timely re-invokes opportunistic scheduling scheme to select the potential better mobile user, achieves superior performance to MU-IDF scheme, as explicitly demonstrated in next figures. For instance, for $N=2$ or $N=3$, the SNR gain of MU-IIDF over MU-IDF is as high as $5$ dB for the outage probability lower than $10^{-3}$. Note that this advantage was also predictable from the protocol descriptions of MU-IIDF in the previous section.

Concerning to the complexity comparison between MU-IDF and MU-IIDF schemes, Table 5.2 summarizes such issues in terms of three measures, namely, the amount of CSI feedback, the number of candidates for SNR ordering, and the feedback delay required for the user selection process. In particular, the feedback delay is calculated in terms of the number of phases to complete the CSI (or link SNR) feedback, whereas the amount of CSI feedback is calculated in terms of the total amount of link SNR returned from all the mobile users to the base station. In terms of the amount of CSI feedback, it can be seen that the complexity of MU-IIDF is the same with that of MU-IDF when the direct transmission succeeds, since in this case, the CSI pertaining to the direct links is sufficient for both schemes. If the direct transmission fails, this metric will increase to $2N$ for MU-IIDF since the CSI pertaining to all the $R\rightarrow D_{n}$ links (i.e., the second-hop SNR) is now required according to Eq. (5.23). Note that even if MU-IIDF requires more CSI feedback than MU-IDF in this worst case (i.e., the direct transmission fails), the required amount of CSI feedback is actually linearly proportional to the counterpart of MU-IDF. Also, this limited increase in the amount of CSI feedback could lead to significant performance improvements, as manifested in Fig. 5.8.

Regarding the number of candidates for SNR ordering, the overhead of MU-IIDF is exactly the same with that of MU-IDF scheme when the direct transmission is successful, as before. If the direct transmission fails, according to Eq. (5.23), this metric actually increases to $2N$ due to a second round of user selection process, which is the worst case for MU-IIDF. However, this marginal increasing in the complexity of SNR ordering could harvest considerable performance enhancement, which is highly desirable in practice.

In addition, when the direct transmission succeeds, the feedback delay of MU-IIDF is also the same with that of MU-IDF, i.e., $N+1$, which consists of the delay incurred by the source broadcasting as well as that by the round-robin CSI feedback from each destination to the source. If the direct transmission fails, an additional $N+1$ feedback delay arises for MU-IIDF due to an additional relay broadcasting and a second round of CSI feedback (pertaining to the $R_{n}\rightarrow D$ links) from each destination to the source, which results in a feedback delay amounting to $2(N+1)$ for MU-IIDF. Note that for MU-IDF, the feedback delay keeps at $N+1$ for both cases.

Table 5.2 Complexity comparison of MU-IDF and MU-IIDF (DT direct transmission)

From Table 5.2, note that for MU-IIDF, the $2N$ candidates for SNR ordering consist of two groups, each group with $N$ candidates, for the two rounds of user selection. Another important performance measure to characterize the merit of incremental relaying protocols is referred to as expected spectral efficiency [15]. For the proposed two schemes, it is easy to show that both of them achieve the same expected spectral efficiency, which can be expressed as

$$\begin{aligned} {\bar{{\mathfrak {R}}}}_{s} =&\; {\mathfrak {R}}_{s}\,\mathrm{{Pr}}\left( \gamma _{{\text {SD}}_{n^{*}}}\ge \tau \right) +\frac{{\mathfrak {R}}_{s}}{2}\,\mathrm{{Pr}}\left( \gamma _{{\text {SD}}_{n^{*}}}<\tau \right) \nonumber \\ =&\; {\mathfrak {R}}_{s} \left( \sum _{l=1}^{N}\sum _{S_{l}\subseteq \{1,\ldots ,N\} \atop {|S_l|=l}}(-1)^{l+1}e^{-\tau \sum \nolimits _{j\in S_{l}}\frac{1}{{\bar{\gamma }}_{{\text {SD}}_{j}}}}\right) \nonumber \\&\; + \frac{{\mathfrak {R}}_{s}}{2} \left( 1-\sum _{l=1}^{N}\sum _{S_{l}\subseteq \{1,\ldots ,N\} \atop {|S_l|=l}}(-1)^{l+1}e^{-\tau \sum \nolimits _{j\in S_{l}}\frac{1}{{\bar{\gamma }}_{{\text {SD}}_{j}}}}\right) . \end{aligned}$$

(5.41)

In high SNR regime (as ${\bar{\gamma }}\rightarrow \infty$), by employing the Taylor’s series expansion of (5.41), one can arrive at

$$\begin{aligned} {\bar{\mathfrak {R}}}_{s}\simeq {\mathfrak {R}}_{s}\left[ 1-\prod _{n=1}^{N}\left( \frac{\tau }{{\bar{\gamma }}_{{\text {SD}}_{n}}}\right) \right] + \frac{{\mathfrak {R}}_{s}}{2}\,\prod _{n=1}^{N}\left( \frac{\tau }{{\bar{\gamma }}_{{\text {SD}}_{n}}}\right) \simeq \mathfrak {R}_{s}, \end{aligned}$$

(5.42)

which implies that the expected spectral efficiency of the proposed two schemes approaches that of direct transmission in high SNR regime.

3.6 Numerical Results, Simulations and Discussions

In this part, simulation results are presented to validate the analytical results previously attained. As will be seen, the exact theoretical results match very well with simulations, and the asymptotical results are shown to be tight bounds in the medium- and high-SNR regions. We illustrate the impacts of average channel qualities (or channel fading severity) pertaining to different links (direct links and relaying links) on the outage performance of the proposed schemes. Without loss of generality, we assume equal transmit power at base station $S$ and relay $R$, i.e., $P_{S}=P_{R}$. In addition, the target spectral efficiency is set to $\mathfrak {R}_{s}= 1$ bit/s/Hz.

Figure 5.7 plots the outage probability versus transmit SNR at $S$ for the MU-IIDF scheme. As expected, with an increase in $N$, the outage performance improves since more potential destinations are available for selection, and the MUD gain is harvested in the form of decreased outage probability and increased system diversity order. In addition, it is observed that, for $N=1$, the outage performance converges to different asymptotes as $\varOmega _{\text {RD}}$ varies. This phenomenon demonstrates the fact that, for $N=1$, the asymptotic outage behavior of MU-IIDF is determined by all the transmit links (including the direct links and the relaying links). In contrast, for $N=2,3$ ($N\ge 2$), the outage curves overlap each other in high-SNR regions, regardless of the fading severity pertaining to the $R\rightarrow D_n$ links (i.e., $\varOmega _{\text {RD}}$). However, in this case, a big performance margin appears from low- to medium-SNR regions as the fading severity of the links $R\rightarrow D_{n}$ varies.

Fig. 5.7

Outage probability of MU-IIDF versus transmit SNR $P_{S}/N_{0}$ ($K=0$ dB, $\varOmega _{\text {SR}}=1, \varOmega _{\text {SD}}=0.01$)

Figure 5.8 shows the outage behavior of the two schemes when the average channel quality of the direct links is weak, whereas the average channel quality of the $S\rightarrow R$ link is strong. It can be seen from Fig. 5.8 that, for a given system configuration, a wide performance margin exists between the two schemes in the medium- and high-SNR regions. This phenomenon can be explained as follows: For this scenario, direct transmission generally fails, and the relaying transmission will be substantially relied on. Since the $S\rightarrow R$ link is strong, the $R\rightarrow D_{n}$ links become crucial for the dual-hop relaying transmissions. Therefore, the MU-IIDF scheme, which makes full use of the opportunistic scheduling mechanism to improve the relaying transmission, achieves superior performance to the MU-IDF scheme, even if both schemes can attain the same system diversity order, as manifested in Fig. 5.8.

Fig. 5.8

Comparisons between MU-IIDF and MU-IDF when the average channel quality of the direct links is weak, whereas that of the $S\rightarrow R$ link is strong ($K=5$ dB, $\varOmega _{\text {SR}}=1$, $\varOmega _{\textit{RD}}=0.05$, $\varOmega _{\text {SD}}=0.01$)

Figure 5.9 draws a comparison between the MU-IDF scheme and the MU-IIDF scheme when the average channel quality of the direct links is strong. For such a case, it is shown that the outage performance of MU-IDF and MU-IIDF is very close to each other for any given system configuration. This is owing to the fact that, when the average channel quality of the direct links is strong (in statistics), most of the time, the direct link could accomplish the information transmission, and only one time slot is sufficient, therefore leading to very close performance for these two schemes. In addition, it is noted that, for $N=1$, the outage curves of the two schemes overlap each other since MU-IIDF degenerates into MU-IDF when only one destination is available. In addition, with an increase in $N$, the outage performance of both schemes improves, as expected.

Fig. 5.9

Comparisons between MU-IIDF and MU-IDF when the average channel quality of the direct links is strong ($K=0$ dB, $\varOmega _{\text {SR}}=\varOmega _{\text {RD}}=0.1$)

Figure 5.10 shows the outage performance of the two schemes when both the direct links and the $S\rightarrow R$ link are weak. To avoid entanglements in this figure, the simulated results are omitted. It can be seen from Fig. 5.10 that the outage performance of the two schemes is very close. This is due to the fact that, in this case, direct transmission always fails, and relaying transmission is again relied on. In particular, the $S\rightarrow R$ link becomes the bottleneck of the dual-hop relaying transmission, which makes the benefits provided by scheduling the $S\rightarrow D_n$ and $R\rightarrow D_n$ links (as done by MU-IIDF) shrink. Once again, it is observed that the full system diversity order is exploited by both the MU-IDF scheme and the MU-IIDF scheme, as expected.

Fig. 5.10

Comparisons between MU-IIDF and MU-IDF when the average channel qualities of both the direct links and the $S\rightarrow R$ link are weak ($\varOmega _{\text {RD}}=1,\varOmega _{\text {SD}}= 0.01$)

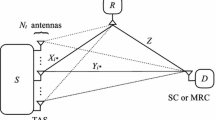
4 Link Selection Schemes for Selection Relaying Systems with Transmit Beamforming

In this part, new and efficient link selection schemes for selection relaying systems with transmit beamforming are presented. Such schemes were first proposed in [7]. Assuming variable-gain and fixed-gain relaying, two distributed link selection schemes are presented that invoke a distributed decision mechanism and rely on the success/fail signaling feedback between terminals. Our analysis considers a multiantenna Base Station (BS) that transmits messages to a single-antenna Mobile Station (MS) with the aid of a single-antenna half-duplex Relay Station (RS). For such, the distributed link selection rules are established, based on which either the direct link or the dual-hop relaying link is selected for each information transmission process. For variable-gain relaying, the proposed scheme is implemented in a perfect distributed manner, whereas for fixed-gain relaying, the proposed scheme is performed in a distributed fashion with a certain probability. In particular, when compared with the optimal scenario, both schemes can substantially reduce the CSI feedback overhead for the link selection process while achieve nearly identical outage performance, as manifested by the theoretical/numerical results. Furthermore, asymptotic analysis reveals that both the proposed schemes achieve full diversity, being validated by comprehensive Monte Carlo simulations. The impacts of RS placement and the number of antennas at BS on the probability of distributed implementation are investigated for the fixed-gain relaying case. Our results demonstrate that placing RS around MS can efficiently, concurrently guarantee the outage performance and the distributed implementation of the proposed scheme.

4.1 System Model

As in [25], consider a downlink cooperative cellular system where one BS intends to communicate with one MS by using a half-duplex AF RS. For such a case, the BS is equipped with multiple antennas in order to implement transmit beamforming, while the RS and MS are, respectively, configured with single antennas. A time-division multiple-access scheme is employed for orthogonal channel access, and all the channels undergo independent Rayleigh flat fading. For each two-phase information transmission process, either the direct link BS$\rightarrow$MS or the relaying link BS$\rightarrow$RS$\rightarrow$MS is selected. Specifically, if the direct link is selected, the transmit beamforming vector at BS is generated based on the CSI pertaining to the direct link BS$\rightarrow$MS, whereas if the relaying link is chosen, the transmit beamforming vector at BS is formed based on the first-hop relaying link BS$\rightarrow$RS. By denoting $X, Y$, and $W$, respectively, as the instantaneous SNR pertaining to the links BS$\rightarrow$RS, RS$\rightarrow$MS, and BS$\rightarrow$MS, it follows that $Y$ conforms to an exponential distribution with mean $\bar{\gamma }_{2}$, whereas $X$ and $W$ conform to gamma distributions, whose PDFs and CDFs are given as below [25]

$$\begin{aligned} f_{X}(x)=\frac{x^{N-1}}{\varGamma (N)\,\bar{\gamma }_{1}^{N}}e^{-\frac{x}{\bar{\gamma }_{1}}},\,\,\, f_{W}(w)=\frac{w^{N-1}}{\varGamma (N)\,\bar{\gamma }_{0}^{N}}e^{-\frac{w}{\bar{\gamma }_{0}}}, \end{aligned}$$

(5.43a)

$$\begin{aligned} F_{X}(x)=1-e^{-\frac{x}{\bar{\gamma }_{1}}}\sum _{i=0}^{N-1}\frac{(x/\bar{\gamma }_{1})^{i}}{i!},\,\,\, F_{W}(w)=1-e^{-\frac{w}{\bar{\gamma }_{0}}}\sum _{i=0}^{N-1}\frac{(w/\bar{\gamma }_{0})^{i}}{i!}, \end{aligned}$$

(5.43b)

in which, in this part, $N$ denotes the number of antennas at BS, $\bar{\gamma }_{1}\triangleq \frac{1}{N}E[X]$ is the average received SNR from each transmit antenna at BS to RS, and $\bar{\gamma }_{0}\triangleq \frac{1}{N}E[W]$ indicates the average received SNR from each transmit antenna at BS to MS.

4.2 Centralized Link Selection Schemes

In [25], the authors proposed an optimal link selection strategy to maximize the instantaneous end-to-end SNR, which was formulated as

$$\begin{aligned} \gamma _{\phi }=\max [W,Z_{\phi }], \end{aligned}$$

(5.44)

where $Z_{\phi }$ indicates the end-to-end SNR pertaining to the dual-hop relaying link BS$\rightarrow$RS$\rightarrow$MS. Being more specific, for variable-gain relaying, we have $Z_{\phi }=Z_\mathrm{var }\triangleq \frac{XY}{X+Y}$, whereas for fixed-gain relaying, it follows that $Z_{\phi }=Z_\mathrm{fix }\triangleq \frac{XY}{C+Y}$, with $C\triangleq 1+E[X]$. For more details, the readers can refer to [25, Sect. II].

From Eq. (5.44), note that in order to perform the optimal link selection strategy, two centralized selection schemes can be employed. As indicated by [25], the first scheme is to put the burden of link selection on the MS by transmitting test signaling through the direct link and through the dual-hop relaying link, respectively. Doing this, the instantaneous received SNRs at MS through the direct link and through the relaying link can be compared, and the stronger link is selected. However, since the direct transmission and the relaying transmission require the BS to determine different transmit beamforming vector, this scheme will consume at least three phases to accomplish the received-SNR comparison at MS before the genuine two-phase information transmission, yielding therefore considerable signaling overhead and delay.

The second centralized link selection scheme is to let BS continuously monitor the instantaneous CSI $X, Y$, and $W$, and then choose the stronger link based on (5.44). For $X$ and $W$, BS can readily acquire them by estimating the channel coefficients based on the pilot signaling from RS and MS, respectively. However, it becomes quite challenging for BS to monitor the instantaneous CSI $Y$ pertaining to the link RS$\rightarrow$MS. As a consequence, both centralized link selection schemes mentioned above demand considerable signaling overhead in practical realizations.

To address these inconveniences, next we propose two distributed link selection schemes. By efficiently exploiting the local CSI at BS and at MS, the proposed schemes can avoid (or efficiently alleviate) the need of CSI feedback (of $Y$) to BS, maintain full diversity, and achieve excellent performance.

4.3 New and Efficient Link Selection Schemes Based on a Distributed Concept

In this section, two distributed link selection schemes for the considered systems are presented assuming two types of AF relaying scenarios, i.e., variable-gain relaying and fixed-gain relaying. For each of them, we propose one link selection scheme. Next, we first clarify the basic idea and key operations of the proposed schemes, and then launch into the implementation details.

The basic idea is first to approximate the optimal link selection criterion Eq. (5.44) by its tight bounds, and then to invoke a distributed decision mechanism to realize this modified link selection criterion. In particular, if the link selection criterion is modified/designed properly, the resulting link selection scheme can be implemented in a perfect (or nearly perfect) distributed manner, which can avoid (or substantially alleviate the need of) monitoring the global CSI and only (or mainly) local CSI is sufficient to make an effective link selection.

To fulfill the distributed decision mechanism, we will introduce the success/fail signaling feedback to exchange (when necessary) the “local decision messages” between BS and MS, which leads to the proposed distributed link selection concept.

4.3.1 Variable-Gain Relaying

In this case, we have $Z_{\phi }=Z_\mathrm{var }\triangleq \frac{XY}{X+Y}$. As aforementioned, to perform the optimal link selection [25], the instantaneous CSI $Y$ has to be acquired at BS (for illustration, we take the second centralized link selection scheme for example), which may involve considerable feedback overhead. To address this, note that $Z_\mathrm{var }$ can be accurately approximated by $\min [X, Y]$, as shown in [10, 12, 14, 26]. Consequently, the selection criterion shown in Eq. (5.44) actually degenerates into Table 5.3, which can be implemented in a distributed manner (please check the flow chart in Fig. 5.11). Specifically, for each link selection process, BS first compares $X$ with $W$. If $W\ge X$, then we have $W\ge \min [X,Y]$. Thus, the direct link will be selected according to the proposed link selection criterion. Otherwise, BS simply broadcasts a ‘fail’ message and, upon hearing the ‘fail’ message from BS, MS starts the comparison between $Y$ and $W$. If $W\ge Y$, we have that $W\ge \min [X,Y]$ and MS sends a ‘success’ message to BS to infer that the direct link should be selected. Otherwise, MS merely sends a ‘fail’ message to BS and the latter will select the relaying link.

Fig. 5.11

Flowchart of distributed link selection for variable-gain relaying

Table 5.3 Distributed link selection criterion for variable-gain relaying

It is noteworthy that, for the proposed link selection criterion, the CSI $Y$ is no longer required by BS to take a decision, and MS merely sends a local decision result to BS for indicating the relation between $Y$ and $W$, which considerably reduces the feedback overhead. Then, for variable-gain relaying, the proposed link selection scheme can be implemented in a perfect distributed manner by means of ‘distributed decision’ at BS and at MS, respectively. In particular, note that in this case, only local CSI is adequate for the link selection.

4.3.2 Fixed-Gain Relaying

Firstly, note that $Z_\mathrm{fix }$ can be rewritten as

$$\begin{aligned} Z_\mathrm{fix }=\frac{XY}{C+Y}\le X\min \left[ \frac{Y}{C},1\right] , \end{aligned}$$

(5.45)

where the right hand side of the inequality was shown to be a tight bound in [6, 21]. By employing this tight bound as the equivalent end-to-end SNR, the link selection criterion for fixed-gain relaying is summarized in Table 5.4. Specifically, the link selection process starts at BS (please check the flow chart in Fig. 5.12 for details). Thus, if $W\ge X$, it follows that $W\ge X\min \left[ \frac{Y}{C},1\right]$. In this case, the direct link will be chosen according to the proposed selection criterion. Otherwise, BS sends a ‘fail’ message to MS and, upon hearing the ‘fail’ message, MS compares $Y$ with $C$. If $Y\ge C$, it follows that $W<X\min \left[ \frac{Y}{C},1\right]$. In this case, MS broadcasts a ‘success’ message to indicate that the relaying link can be selected. Otherwise, MS has to forward $Y$ to BS. Upon receiving $Y$, BS makes a comparison between $W$ and $\frac{XY}{C}$. If $W\ge \frac{XY}{C}$, the direct link is chosen. Otherwise, the relaying link will be selected.

Fig. 5.12

Flowchart of distributed link selection for fixed-gain relaying

Table 5.4 Distributed link selection criterion for fixed-gain relaying

Note that differently from variable-gain relaying, perfect distributed link selection is unavailable for fixed-gain relaying. Nonetheless, by adopting the proposed link selection criterion, BS can make a decision without acquiring $Y$ in the first two cases of Table 5.4, which substantially alleviates the need of CSI feedback. As shall be seen, deploying RS at a proper position can considerably ensure the distributed implementation as well as the outage performance of the proposed scheme.

4.4 Fixed-Gain Relaying: Distributed Implementation

As shown previously, differently from variable-gain relaying, the proposed scheme for fixed-gain relaying cannot be implemented in a perfect distributed fashion, which may jeopardize its potential applications. To address this, in this section, the implementation issues for the distributed link selection scheme will be investigated. Particularly, the probability of distributed implementation will be characterized, from which some useful RS placement rules are proposed to efficiently guarantee the distributed implementation of the proposed scheme.

4.4.1 The Probability of Distributed Implementation

The proposed scheme will be implemented in a distributed manner with probability

$$\begin{aligned}&\mathrm{Prob }^\mathrm{distributed }=\mathrm{Pr }(W\ge X)+\mathrm{Pr }\left( W<X,\frac{Y}{C}\ge 1\right) \nonumber \\&=\left( 1-e^{-\frac{C}{\bar{\gamma }_{2}}}\right) \frac{1}{\varGamma (N)\bar{\gamma }_{1}^{N}}\sum _{i=0}^{N-1} \frac{(1/\bar{\gamma }_{0})^{i}}{i!}\left( \frac{1}{\bar{\gamma }_{0}}+\frac{1}{\bar{\gamma }_{1}}\right) ^{-N-i}\varGamma (N+i)+e^{-\frac{C}{\bar{\gamma }_{2}}}. \end{aligned}$$

(5.46)

Knowing that $k_{1}=\bar{\gamma }_{1}/\bar{\gamma }_{0}$ and $k_{2}=\bar{\gamma }_{2}/(N\bar{\gamma }_{0})$, (5.46) can be rewritten as

$$\begin{aligned} \mathrm{Prob }^\mathrm{distributed }&=\left( 1-e^{-\frac{C}{\bar{\gamma }_{2}}}\right) \frac{(1+k_{1})^{-N}}{\varGamma (N)}\sum _{i=0}^{N-1} \frac{(1+k_{1}^{-1})^{-i}}{i!}\varGamma (N+i)+e^{-\frac{C}{\bar{\gamma }_{2}}}\nonumber \\&\overset{(i)}{\simeq } \left( 1-e^{-\frac{k_1}{k_2}}\right) \frac{(1+k_{1})^{-N}}{\varGamma (N)}\sum _{i=0}^{N-1} \frac{(1+k_{1}^{-1})^{-i}}{i!}\varGamma (N+i)+e^{-\frac{k_1}{k_2}}, \end{aligned}$$

(5.47)

in which step $(i)$ holds for high SNR regime. Accordingly, the proposed scheme will require the feedback of the CSI $Y$ (being therefore not operating in a distributed manner) with probability given by

$$\begin{aligned} \mathrm{Prob }^\mathrm{feedback }=\mathrm{Pr }\left( W<X,\frac{Y}{C}<1\right) =1-\mathrm{Prob }^\mathrm{distributed }. \end{aligned}$$

(5.48)

Note that, although (5.46) characterizes the exact probability of distributed implementation for the proposed scheme, it is hard to get any insight from this formulation. Alternatively, by formulating the statistical relation between the relaying links and the direct link as $\overline{X}=k_{1}\overline{W}$ and $\overline{Y}=k_{2}\overline{W}$, we note that when $k_{1}<1$, the event $\{W\ge X\}$ occurs with a higher probability. On the other hand, when $k_{1}<k_{2}$, it follows that $\overline{Y}/C=\bar{\gamma }_{2}/C\simeq k_{2}/k_{1}>1$ for sufficiently high SNR, which implies that in the case of $k_{1}\ge 1$ and $k_{1}<k_{2}$, the event $\{W<X,(Y/C)\ge 1\}$ takes place with a higher possibility. In summary, if either the condition $\{k_{1}<1\}$ or $\{k_{1}\ge 1,k_{1}<k_{2}\}$ is satisfied, the proposed scheme will be implemented in a distributed manner, with a higher probability.

4.4.2 RS Placement Issues

According to the preceding results, the role of RS placement on the distributed implementation of the proposed scheme will now be identified for fixed-gain relaying. For simplicity, we consider equal transmit SNR, namely, $P$, at BS and RS, respectively. Then, we model the average received SNR from each transmit antenna at BS to RS and to MS, respectively, as $\bar{\gamma }_{1}=({P}/{N})d_{1}^{-\beta }$ and $\bar{\gamma }_{0}=({{P}}/{N})d_{0}^{-\beta }$, with $\beta >0$ being the path loss exponent and, $d_1$ and $d_0$ denoting the distances between BS and RS, and between BS and MS, respectively. In addition, the average received SNR from RS to MS is modeled as $\bar{\gamma }_{2}={P}d_{2}^{-\beta }$, with $d_2$ representing the distance between RS and MS.

Now, we first inspect the effect of the second condition $\{k_{1}\ge 1,k_{1}<k_{2}\}$, which is equivalent to

$$\begin{aligned} d_{1}\le d_{0},\,\,\,\,\frac{d_1}{d_2}>1, \end{aligned}$$

(5.49)

which requires that: (a) RS be placed between BS and MS; (b) RS be deployed closer to MS than to BS. Note that these requirements lead to a reasonable RS configuration in practical scenarios. In this case, due to the spatial diversity induced by the transmitting beamforming in the first-hop, the second-hop link is typically weaker than the first-hop and becomes the bottleneck for the relaying transmission. As a result, placing RS closer to MS can efficiently reduce the path loss of the second-hop and then balance the dual-hop transmission, leading to stronger transmission robustness against fading. On the other hand, the condition $\{k_{1}<1\}$ signifies that

$$\begin{aligned} k_{1}=\frac{\overline{X}}{\overline{W}}=\frac{N\bar{\gamma }_{1}}{N\bar{\gamma }_{0}}=\left( \frac{d_1}{d_0}\right) ^{-\beta }<1, \end{aligned}$$

(5.50)

which yields $d_{1}>d_{0}$. In other words, the condition $\{k_{1}<1\}$ requires that RS be placed ahead of the link BS$\rightarrow$MS.¹¹ Although this RS configuration can guarantee the distributed implementation of the proposed scheme, it is not practical due to its weak transmission robustness against fading, in comparison with the RS placement aforementioned. More specifically, keeping other conditions the same, the outage performance of this RS placement will be worse than the counterpart proposed by Eq. (5.49), since the latter efficiently reduces the path loss of the first-hop link BS$\rightarrow$RS.

Fig. 5.13

Probability of distributed implementation versus the distance between BS and RS ($d_1$)

To confirm the observations above, Figs. 5.13 and 5.14 plot the probability of distributed implementation versus the distance between BS and RS ($d_1$). Herein, we consider a linear network topology, where the distance between BS and MS ($d_0$) is normalized to unity, i.e., $d_{0}=1$. For $0<d_{1}<1$, we have $d_{1}+d_{2}=1$, whereas for $d_{1}>1$, it follows that $d_{1}-d_{2}=1$. Without loss of generality, the transmit SNR is set to $P=10$ dB, and the path loss exponent is set to $\beta =3$. From Fig. 5.13, it is easy to see that with an increase of $d_1$, the probability of distributed implementation improves significantly, as expected. Interestingly, with an increase of $N$, the probability of distributed implementation decreases, although the decrease is somewhat marginal. To address this, the RS should be deployed closer to MS with an increase of $N$. Figure 5.14 depicts the case when $d_{1}>1$. From this figure, it is observed that the probability of distributed implementation is typically greater than $97\,\%$ regardless of the value of $N$. In contrary to the case of $d_{1}<1$, the probability of distributed implementation improves with an increase of $N$. These observations enable us to establish the following remarks:

Fig. 5.14

Probability of distributed implementation versus the distance between BS and RS ($d_1$)

(a) For fixed-gain relaying, placing RS around MS is certainly a good strategy to realize the distributed implementation of the proposed scheme;

(b) When $d_{1}>d_{0}$, deploying more antennas at BS is beneficial for the distributed implementation of the proposed scheme, whereas in the case of $d_{1}<d_{0}$, configuring less antennas at BS is preferable.

4.5 Feedback Overhead Comparisons Between the Centralized and Distributed Schemes

4.5.1 Variable-Gain Relaying

Let us first concentrate upon the case of variable-gain relaying. Thus, recall that the centralized link selection scheme of [25] always has the need of feeding back “$Y$” from MS to BS, whereas our proposed link selection scheme, which can be implemented in a perfect distributed manner for variable-gain relaying, does not need to feed back “$Y$” from MS to BS. As a result, in the worst case (i.e., the BS can not make a decision based on its local CSI $X$ and $W$), our distributed link selection scheme only needs 2-bit signaling overhead. Specifically, 1-bit signaling overhead (i.e., using “1” or “0” to denote the “fail” message from BS to MS) arises from the need to notify the MS that $X>W$, and the other 1-bit overhead is due to the success/fail signaling feedback from MS to BS. In the best case (i.e., the BS can make a decision based on its local CSI when $X\le W$), the BS does not need to transmit any signaling to MS, yielding therefore 0-bit overhead. Consequently, the expected amount of signaling overhead of our distributed scheme for variable-gain relaying can be calculated as

$$\begin{aligned} \varOmega _\mathrm{var }^\mathrm{distrib }=2\times \mathrm{Pr }(X>W)+0\times \mathrm{Pr }(X\le W)<2\,\mathrm{bit }. \end{aligned}$$

(5.51)

On the other hand, from the Monte Carlo simulation results (please check Figs. 5.15 and 5.16), one can notice that for both variable-gain and fixed-gain relaying, at least 4-bit quantization feedback of “$Y$” is required to achieve full diversity order for both the centralized link selection schemes and our distributed ones.¹² Consequently, Eq. (5.51) leads us to conclude that for variable-gain relaying, the feedback overhead of our distributed scheme (${<}2$ bit) is considerably smaller than that of the centralized one which requires at least 4-bit quantization feedback of “$Y$” from MS to BS.

Fig. 5.15

Outage probability of the centralized link selection scheme for variable-gain relaying when 4-bit quantization feedback is performed on the CSI “Y ”($\mathfrak {R}_{s}=1$ bit/s/Hz). Herein, $2^{4}=16$ uniform SNR quantization levels (in decibels) are adopted as in [13, Sect. III]. The first nonzero quantized value is set to 3 dB [13, Fig. 5], and the quantization interval is set to 3 dB [13, Fig. 5], and the quantization rule is the same as [13, Eq. (21)]

4.5.2 Fixed-Gain Relaying

Now, we focus on the case of fixed-gain relaying. Note that the centralized link selection scheme of [25] still has the need of feeding back “$Y$” from MS to BS as before, whereas our distributed scheme only need to feed back “$Y$” in certain cases. The worst case for the proposed distributed scheme appears when neither the BS nor the MS can determine the transmit link based on their respective local CSI. Thus, the feedback overhead is: $1+4=5$ bit, where the 1-bit overhead (e.g., a binary symbol ‘0’) arises from the “fail” message from BS to MS to notify MS that $X>W$ and the other 4-bit overhead is due to the fact that when $Y<C$, MS has to feed back the 4-bit quantization of “$Y$” to BS for link selection.

Fig. 5.16

Comparisons between the centralized scheme [25] and the distributed scheme in terms of outage probability for fixed-gain relaying when 4-bit quantization feedback is performed on the CSI “Y” ($\mathfrak {R}_{s}=1$ bit/s/Hz). Herein, the quantization rule is the same with Fig. 5.15

On the other hand, the best case happens when the BS can make a decision based on its local CSI, i.e., $X\le W$. Thus, no feedback overhead is required. Another possible case is when the BS can not determine the transmit link according to its local CSI (i.e., $X>W$), whereas the MS can make a decision based on its local CSI (i.e., $Y\ge C$). In this case, only 2-bit signaling feedback is enough for the whole distributed decision process, where the two groups of success/fail signaling feedback between BS and MS account for the 2-bit overhead. As a consequence, the expected amount of feedback overhead of our distributed scheme for fixed-gain relaying can be calculated as

$$\begin{aligned} \varOmega _\mathrm{fix }^\mathrm{distrib }=&\;2\times \mathrm{Pr }(X>W,Y\ge C)+5\times \mathrm{Pr }(X>W,Y<C)\nonumber \\&\;+0\times \mathrm{Pr }(X\le W)<5\,\mathrm{bit }. \end{aligned}$$

(5.52)

From Eq. (5.52), it is noticed that for fixed-gain relaying, the feedback overhead of our distributed scheme is not necessarily less than that of the centralized scheme which requires at least 4-bit quantization feedback of “$Y$”.

Nevertheless, in order to ensure the distributed implementation of our proposed scheme for fixed-gain relaying, RS will be deployed closer to MS than to BS (i.e., $d_{1}>d_{2}$) such that the event $\{Y\ge C\}$ occurs with a higher probability than the event $\{Y<C\}$. In this case, the probability of the event $\{X>W, Y<C\}$ will be smaller than that of the event $\{X>W, Y\ge C\}$, which will make $\varOmega _\mathrm{fix }^\mathrm{distrib }$ very low. On the other hand, when $d_{1}>d_{0}$, it follows that $\overline{X}<\overline{W}$, which means that the event $\{X>W\}$ will occur with a low probability. As such, we have from (5.52) that $\varOmega _\mathrm{fix }^\mathrm{distrib }$ will still be very low in this case.

Fig. 5.17

Expected amount of feedback overhead of our distributed scheme (fixed-gain relaying) versus the distance between BS and RS ($d_{1}=d_{0}-d_{2}$, $d_{0}=1$)

Fig. 5.18

Expected amount of feedback overhead of our distributed scheme (fixed-gain relaying) versus the distance between BS and RS ($d_{1}=d_{0}+d_{2}$, $d_{0}= 1$)

Therefore, according to (5.52), the feedback overhead of our distributed scheme can still be very low. Figures 5.17 and 5.18 plot the expected amount of feedback overhead of our distributed scheme versus the distance between BS and RS ($d_1$), in which the analytical results are derived as

$$\begin{aligned} \varOmega _\mathrm{fix }^\mathrm{distrib }&=\mathrm{Pr }(X>W)\left[ 2\,\mathrm{Pr }(Y\ge C)+5\,\mathrm{Pr }(Y<C)\right] =\left( 5-3e^{-\frac{C}{\bar{\gamma }_{2}}}\right) \mathrm{Pr }(X>W) \nonumber \\&=\left( 5-3e^{-\frac{C}{\bar{\gamma }_{2}}}\right) \left[ 1-\frac{1}{\varGamma (N)\bar{\gamma }_{1}^{N}} \sum _{i=0}^{N-1}\frac{(1/\bar{\gamma }_{0})^{i}}{i!}\int _{0}^{\infty }x^{N+i-1}e^{-x\left( \frac{1}{\bar{\gamma }_{0}}+\frac{1}{\bar{\gamma }_{1}}\right) }dx\right] \nonumber \\&\overset{(ii)}{=}\left( 5-3e^{-\frac{C}{\bar{\gamma }_{2}}}\right) \left[ 1-\frac{1}{\varGamma (N)\bar{\gamma }_{1}^{N}} \sum _{i=0}^{N-1}\frac{(1/\bar{\gamma }_{0})^{i}}{i!} \frac{\varGamma (N+i)}{(1/\bar{\gamma }_{0}+1/\bar{\gamma }_{1})^{N+i}}\right] , \end{aligned}$$

(5.53)

where step (ii) follows from [11, Eq. (3.381.4)]. Figure 5.17 considers the case when $d_{1}<d_{0}$, where the system configuration is the same as Fig. 5.12. From this figure, it is clear that placing RS closer to MS (i.e., increasing $d_1$) can efficiently reduce the amount of feedback overhead. Also, for any given $d_1$, it is numerically shown that for $d_{1}<d_{0}$ the expected amount of feedback overhead increases with the number of antennas ($N$) at BS. In contrast, Fig. 5.18 shows that when $d_1>d_0$, the inverse is true. In addition, Fig. 5.18 manifests that when $d_1>d_0$, the expected amount of feedback overhead of our distributed scheme will be less than 1 bit for arbitrary antenna deployment. Table 5.5 shows the expected amount of feedback overhead of our distributed scheme when the outage-optimal RS placement¹³ is adopted, i.e., $d_{1}=0.64, 0.73, 0.85, 0.94$ for $N=1, 2, 5, 10$, respectively. Interestingly, even if 2 antennas are deployed at BS, our distributed scheme merely requires 1.74 bit feedback overhead in statistics, which is much lower than the 4-bit feedback overhead of the centralized link selection scheme [25]. Moreover, deploying more antennas at BS can further reduce the feedback overhead, as shown by Table 5.5.

Table 5.5 Feedback overhead and outage-optimal RS placement of the distributed scheme for fixed-gain relaying with 4-bit quantization feedback of “$Y$”

4.6 Numerical Examples and Discussions

In this part, simulation results are presented to validate the analytical results. For both variable-gain and fixed-gain relaying scenarios, comprehensive comparisons between the proposed link selection and the optimal schemes will be made in terms of system outage probability and achievable diversity order. In addition, for fixed-gain relaying, the impact of relay placement on the outage performance as well as on the distributed implementation of the proposed scheme will be demonstrated via some representative cases studies. For illustration purposes and without loss of generality, the target spectral efficiency is set to $\mathfrak {R}_{s}=1$ bit/s/Hz in the following discussions.

Figure 5.19 draws a comparison between the proposed link selection scheme and the optimal scheme in terms of system outage performance for the variable-gain relaying scenario. Herein, the exact analytical results of the optimal scheme are attained from [25, Eq. (36)]. First of all, it can be seen that the analytical lower bound for the proposed scheme is very tight, and the asymptotic lower bound overlaps with the simulated curves in the medium and high SNR regions, which validates the presented analysis. In addition, the asymptotic lower bounds as well as the asymptotic upper bounds are in parallel with the simulated curves in high SNR regions, which indicates that the proposed scheme can achieve full diversity order, as expected. On the other hand, it is observed that for all the cases considered, the outage performance of the proposed scheme is very close to that of the optimal scheme, and we can hardly discern their differences over the entire SNR regions. This means that besides achieving a lower implementation complexity (due to the distributed link selection), the proposed scheme does not incur any noticeable degradation in the outage performance relative to the optimal scheme, which is definitely desirable in practice.

Fig. 5.19

Comparisons between the proposed scheme and the optimal scheme [25] in terms of outage probability for variable-gain relaying

Figure 5.20 makes a comparison of the proposed and optimal schemes for the scenario of fixed-gain relaying. Herein, the exact analytical results of the optimal scheme are attained from [25, Eq. (30)]. From this figure, we first notice that the presented asymptotic lower bound is very tight from medium to high SNR regions. In addition, the asymptotic upper bounds are in parallel with the asymptotic lower bounds and the simulated curves in high SNR regions, which means that the proposed scheme for fixed-gain relaying can also achieve full diversity order. Moreover, it is clear that the proposed scheme achieves very close performance to that of the optimal scheme over the entire SNR regions, and once again, we can hardly distinguish one from another in the plot. Therefore, as in the case of variable-gain relaying, the proposed scheme for fixed-gain relaying can also achieve competitive performance to that of the optimal scheme with a lower implementation complexity.

Fig. 5.20

Comparisons between the proposed scheme and the optimal scheme [25] in terms of outage probability for fixed-gain relaying

As stated in the previous section, for fixed-gain relaying, placing RS around MS can efficiently guarantee the distributed implementation of the proposed scheme. However, up to now, it is not clear what the impacts of this RS configuration are on the outage performance of the considered systems. In the following, we focus on such issues. Figure 5.21 depicts the outage performance of the proposed scheme versus the distance between BS and RS ($d_1$) for fixed-gain relaying scenario. Herein, we adopt the same system configurations as those in Figs. 5.13 and 5.14. For comparison purposes, the outage performance of the optimal link selection scheme is also plotted. From this figure, it can be seen that with an increase of N, the optimal RS placement (in terms of outage performance) tends toward the MS. For example, the optimal RS placements are $d_{1}=0.64, 0.73, 0.76$, and $0.85$ for $N=1, 2, 3$, and $5$, respectively. Accordingly, it follows from Fig. 5.13 [or, equivalently, Eq. (5.45)] that the probabilities of distributed implementation for these RS placements are 86.8, 95.9, 97.3, and 99.6 %, respectively. This means that when the RS is placed in an “outage-optimal” fashion for the proposed scheme, the link selection can also be performed in a nearly perfect distributed manner. In addition, by comparing Figs. 5.14 and 5.21, one can conclude that although placing RS ahead of the BS$\rightarrow$MS link (i.e., $d_{1}>1$) can efficiently guarantee the distributed implementation of the proposed scheme, doing so may considerably impair the system outage performance. For such a case, deploying more antennas onto BS can alleviate, to some extent, the negative effect of this RS placement on the system outage performance.

Fig. 5.21

Outage probability of the proposed scheme versus the distance between BS and RS ($d_1$) for fixed-gain relaying

5 Distributed Antenna Selection Schemes for Relaying Scenarios

In this section, a novel distributed transmit antenna selection for dual-hop fixed-gain AF relaying systems will be presented. Such scheme was first proposed in [9]. In this system model, a multiantenna source transmits information to a single-antenna destination by using a single-antenna half-duplex relay. By invoking local channel information exploitation/decision mechanism along with decision feedback between terminals, a distributed antenna selection scheme (DAS) is formulated. Compared with the optimal/suboptimal antenna selection, DAS can maintain a low and constant delay/feedback overhead irrespective of the number of transmit antennas. Moreover, asymptotic outage analysis reveals that DAS can still achieve full diversity order. In addition, it is numerically shown that, when the relay is deployed in an outage-optimal manner, DAS can attain very close outage performance to that of the optimal antenna selection.

5.1 System Model

Consider a cooperative system where a multiantenna source $S$ communicates with a destination $D$ through a fixed-gain AF relay $R$. Both nodes $R$ and $D$ are single-antenna devices and operate on a half-duplex mode. Differently from [20], herein we consider a fixed-gain AF relay instead of a variable-gain AF relay. Therefore, the amplifying factor relies on the statistical (and not instantaneous) CSI associated with the first-hop relaying link $S\rightarrow R$. However, as in [20], all the channels undergo independent Rayleigh flat fading.

At the beginning of each communication process, a transmit antenna selection is performed at $S$ such that only one antenna is selected out of the $N_t$ available ones. Afterwards, the traditional two-phase cooperative communications start. Following a similar signal transmission/processing procedure as employed in [20], the end-to-end SNR from the $i$th antenna at $S$ to $D$ can be written as

$$\begin{aligned} \gamma _{i}=\gamma _{{\text {SD}},i}+\frac{\gamma _{{\text {SR}},i}\,\gamma _{\text {RD}}}{\gamma _{\text {RD}}+C}, \end{aligned}$$

(5.54)

in which¹⁴ $\gamma _{{\text {SD}},i}\triangleq \frac{P_1}{N_0}|h_{{\text {SD}},i}|^{2}$, $\gamma _{{\text {SR}},i}\triangleq \frac{P_1}{N_0}|h_{{\text {SR}},i}|^{2}$, $\gamma _{\text {RD}}\triangleq \frac{P_2}{N_0}|h_{\text {RD}}|^{2}$, and $C\triangleq 1+\bar{\gamma }_{\text {SR}}$ with $\bar{\gamma }_{\text {SR}}=E[\gamma _{{\text {SR}},i}]$. Herein, $P_1$ and $P_2$ denote the transmit powers of $S$ and $R$, respectively, and $|h_{{\text {SD}},i}|^{2}$, $|h_{{\text {SR}},i}|^{2}$, and $|h_{\text {RD}}|^{2}$ stand for the exponentially-distributed channel power gains from the $i$th antenna at $S$ to $D$, from the $i$th antenna at $S$ to $R$, and from $R$ to $D$, respectively. As in [21, Eq. (8)] and [6], the fixed-gain amplifying factor at $R$ can be expressed as $G\triangleq \sqrt{P_{2}/\left( P_{1}E[|h_{{\text {SR}},i}|^{2}]+N_{0}\right) }$.

5.2 Optimal and Suboptimal Antenna Selection (AS) Schemes

5.2.1 Optimal AS Scheme

With the aim to maximize the instantaneous post-processing SNR at $D$, the authors of [20] proposed an optimal/centralized selection rule which puts the burden of antenna selection at the destination $D$ by transmitting test-signaling from each antenna at $S$ to $D$ within two orthogonal time-slots. More specifically, for every 2 time-slot process (during which only one antenna at $S$ is tested), the tested antenna at $S$ and the relay $R$ need to transmit at least 1-bit test-signaling so that the destination $D$ can estimate the direct-link and relaying-link SNR from the tested antenna. As a result, the overall test process will consume $2 N_{t}$-bit overhead since $N_t$ antennas are used at $S$ for selection. On the other hand, the second part is due to the feedback bits from $D$ to $S$ since the antenna selection is made at the destination and the source has to be informed of this fact. This amounts to an additional overhead of $\lceil \log _{2}(N_t)\rceil$ bits. Therefore, the total amount of feedback overhead is $2N_{t}+\lceil \log _{2}(N_t)\rceil$ bits (to convey the test-signaling from each antenna at $S$ to $D$ and to feedback the selected antenna index from $D$ to $S$) for each antenna selection decision [20, Sect. II]. Accordingly, the delay overhead amounts to $2N_{t}+1$ time-slots, where the $2 N_{t}$ time-slots accounts for the test process for the $N_t$ antennas at $S$ while the remaining 1 time-slot is due to the decision feedback from $D$ to inform $S$ of the selection result.

For this scheme, the selected antenna index can be written as

$$\begin{aligned} \hat{k}=\mathrm{arg }\,\max _{i}[\gamma _{i}]. \end{aligned}$$

(5.55)

5.2.2 Suboptimal AS Scheme

In order to reduce the signaling overhead, the authors of [20] also presented a suboptimal antenna selection scheme, whose decision rule relies solely on the direct links. This suboptimal antenna selection rule can be expressed as

$$\begin{aligned} \underline{k}=\mathrm{arg }\,\max _{i}[\gamma _{{\text {SD}},i}]. \end{aligned}$$

(5.56)

Similar to the scenario of optimal scheme, note that the overall feedback overhead of the suboptimal scheme is $N_{t}+\lceil \log _{2}(N_t)\rceil$ bits (to convey the test-signaling from each antenna at $S$ to $D$ and to notify $S$ of the selected antenna index), since the antenna selection is made solely based on the direct links [20]. More specifically, for every single time-slot test process (in which only one antenna at $S$ is tested), the tested antenna at $S$ needs to transmit at least 1-bit test-signaling so that the destination $D$ can estimate the direct-link SNR from the tested antenna [20]. As a result, the overall test process consumes $N_{t}$-bit overhead. In addition, as in the case of optimal scheme, an additional $\lceil \log _{2}(N_t)\rceil$-bit overhead is incurred since the antenna selection is still made at the destination and the source has to be informed of this fact. Similarly, it can be shown that the delay overhead of the suboptimal scheme is $N_{t}+1$ time-slots, where the $N_t$ time-slots accounts for the test process for the $N_t$ antennas at $S$ and the other 1 time-slot arises from the decision feedback from $D$ to inform $S$ of the selection result.

5.3 A Novel DAS Scheme

Even though the suboptimal criterion Eq. (5.56) can achieve full diversity, its achieved outage performance is inferior to that of the optimal scheme due to the limited CSI knowledge for antenna decision. Intuitively, if more CSI is available to $S$, the system performance should be potentially improved. However, acquiring more CSI may incur considerable feedback overhead. As thus, a question naturally arises: can we perform a more efficient antenna selection without incurring significant feedback overhead?

To solve this problem, herein we propose a distributed antenna selection concept. The key idea is first to substantially exploit the local CSI and then to invoke a local decision mechanism as well as the decision feedback between terminals. By conveying the CSI decision/comparison results (‘0’ or ‘1’, 1-bit signaling) instead of the CSI itself, more CSI is acquired at $S$ so that a more efficient antenna selection can be made without incurring significant feedback overhead.

The proposed distributed antenna selection concept is motivated by an important inequality given as below [6, 21]

$$\begin{aligned} \gamma _{i}<\gamma _{{\text {SD}},i}+\gamma _{{\text {SR}},i}\,\min \left[ \frac{\gamma _{\text {RD}}}{C},1\right] \triangleq \tilde{\gamma }_{i}. \end{aligned}$$

(5.57)

The following deductions will rely crucially on the tight upper bound $\tilde{\gamma }_{i}$. In particular, note that for the case of $\gamma _{\text {RD}}\ge C$, only $\gamma _{{\text {SD}},i}$ and $\gamma _{{\text {SR}},i}$ are sufficient to implement the selection rule $\max \limits _{i}[\tilde{\gamma }_{i}]$. Inspired by this important observation, a novel Distributed Antenna Selection scheme, which is referred to as DAS, is presented next:

• (i) As shown in Fig. 5.22, in the first time-slot, the destination $D$ first broadcasts a 1-bit reverse pilot signaling so that each antenna at $S$ and $R$ can estimate their respective local CSI, $\gamma _{{\text {SD}},i}$ and $\gamma _{\text {RD}}$, toward to $D$.

• (ii) In the second time-slot, the relay $R$ first compares its local CSI $\gamma _{\text {RD}}$ with¹⁵ $C$. If $\gamma _{\text {RD}}\ge C$, the relay $R$ feeds back a 1-bit message “1” to inform $S$ of the local decision “$\gamma _{\text {RD}}\ge C$”. Otherwise, a 1-bit message “0” will be broadcasted by $R$ to notify $S$ of the local decision “$\gamma _{\text {RD}}<C$”. Upon hearing the 1-bit decision feedback from $R$, $S$ will perform the following:

  • (a) Each antenna at $S$ concurrently estimates its local CSI $\gamma _{{\text {SR}},i}$ from this feedback signaling;

  • (b) Upon hearing the message “1”, $S$ will make an antenna selection according to the rule $\tilde{k}=\mathrm{arg }\,\max \limits _{i}[\gamma _{{\text {SD}},i}+\gamma _{{\text {SR}},i}]$. In contrast, when the message “0” is received, the selection rule will degenerate into that of the suboptimal scheme, i.e., $\underline{k}=\mathrm{arg }\,\max \limits _{i}[\gamma _{{\text {SD}},i}]$.

As a consequence, the antenna selection rule of DAS can be expressed as

$$\begin{aligned} \breve{k}=\left\{ {\begin{array}{*{20}l} \tilde{k}=\mathrm{arg }\,\max \limits _{i}[\gamma _{{\text {SD}},i}+\gamma _{{\text {SR}},i}], \,\,\, \mathrm{if }\, \gamma _{\text {RD}}\ge C, \\ \underline{k}=\mathrm{arg }\,\max \limits _{i}[\gamma _{{\text {SD}},i}],\,\,\, \mathrm{if }\, \gamma _{\text {RD}}<C. \\ \end{array}} \right. \end{aligned}$$

(5.58)

Fig. 5.22

Illustration of the key operations for the proposed DAS scheme

Table 5.6 draws a comparison of the delay/feedback overhead for different antenna selection schemes. From this table, it is clear that when $N_t$ increases, the overhead of the optimal and suboptimal schemes increases considerably, whereas that of DAS does not change. In particular, note that in theory, 2-bit pilot/feedback signaling is adequate for the overall antenna selection process of DAS, where 1-bit overhead accounts for the 1-bit pilot signaling broadcasted by $D$ so that $S$ and $R$ can estimate their respective local CSI $\gamma _{{\text {SD}},i}$ and $\gamma _{\text {RD}}$, and the other 1-bit overhead is due to the decision feedback signaling sent from $R$ to $S$ such that $S$ can estimate $\gamma _{{\text {SR}},i}$ and then make an antenna selection according to Eq. (5.58).

Table 5.6 Overhead comparisons for different antenna selection (AS) schemes

Remark 1:

• (a) It is worthwhile to mention that in Table 5.6 the advantage of DAS is attained at the cost of additional hardware complexity at the source. As aforementioned, the local CSI $\gamma _{{\text {SR}},i}$ and $\gamma _{{\text {SD}},i}$ of $S$ has to be exploited based on the reverse pilot signals from $R$ and $D$, respectively, within two time-slots. This may, to some extent, increase the hardware complexity at the source.

• (b) Due to the modified antenna selection criterion of DAS in comparison with the optimal selection rule Eq. (5.55), it is unclear whether DAS can achieve full diversity. Moreover, for fixed-gain relaying systems, the achievable diversity order is closely related to the form of fixed-gain relaying factor, as manifested by previous studies [21], which indeed makes the diversity order of DAS obscure. A rigorous mathematical analysis is therefore required. In the next section, we investigate the asymptotic outage behavior of this distributed antenna selection scheme.

5.4 Asymptotic Outage Analysis

The outage probability is defined as the probability that the maximum mutual information between the source and destination falls below a predefined end-to-end spectral efficiency $R_0$ bit/s/Hz, which can be mathematically formulated as

$$\begin{aligned} P_\mathrm{out }^\mathrm{DAS }=&\;\underbrace{\mathrm{Pr }\left( \gamma _{\text {RD}}\ge C,\gamma _{{\text {SD}},\tilde{k}}+\frac{\gamma _{{\text {SR}},\tilde{k}}\,\gamma _{\text {RD}}}{\gamma _{\text {RD}}+C} <\tau \triangleq 2^{2R_{0}}-1\right) }_{I_1}\nonumber \\&\;+\underbrace{\mathrm{Pr }\left( \gamma _{\text {RD}}<C,\gamma _{{\text {SD}},\underline{k}}+\frac{\gamma _{{\text {SR}},\underline{k}}\,\gamma _{\text {RD}}}{\gamma _{\text {RD}}+C} <\tau \right) }_{I_2}. \end{aligned}$$

(5.59)

Unfortunately, exact closed-form expressions for $I_1$ and $I_2$ are very difficult, if not impossible, to achieve. Alternatively, in the sequel, lower and upper bounds will be derived for these terms. First, we focus on the analysis of $I_1$, whose lower bound can be evaluated as

$$\begin{aligned} I_{1}&>\mathrm{Pr }\left( \gamma _{\text {RD}}\ge C,\gamma _{{\text {SD}},\tilde{k}}+\gamma _{{\text {SR}},\tilde{k}}\,\min \left[ \frac{\gamma _{\text {RD}}}{C},1\right] <\tau \right) \triangleq I_{1}^\mathrm{LB }\nonumber \\&=e^{-\frac{C}{\bar{\gamma }_{\text {RD}}}}\left[ \mathrm{Pr }\left( \gamma _{{\text {SD}},i}+\gamma _{{\text {SR}},i}<\tau \right) \right] ^{N_t}. \end{aligned}$$

(5.60)

On the other hand, an upper bound for $I_1$ can be derived as

$$\begin{aligned} I_{1}&<\mathrm{Pr }\left( \gamma _{\text {RD}}\ge C,\gamma _{{\text {SD}},\tilde{k}}+\frac{1}{2}\gamma _{{\text {SR}},\tilde{k}}\,\min \left[ \frac{\gamma _{\text {RD}}}{C},1\right] <\tau \right) \nonumber \\&<\mathrm{Pr }\left( \gamma _{\text {RD}}\ge C\right) \mathrm{Pr }\left( \gamma _{{\text {SD}},\tilde{k}}+\gamma _{{\text {SR}},\tilde{k}}<2\tau \right) \triangleq I_{1}^\mathrm{UB }. \end{aligned}$$

(5.61)

Next, we concentrate on the analysis of $I_2$. By following a similar procedure as employed to derive $I_{1}^\mathrm{LB }$, one can arrive at

$$\begin{aligned} I_{2}&>\mathrm{Pr }\left( \gamma _{\text {RD}}< C,\gamma _{{\text {SD}},\underline{k}}+\gamma _{{\textit{SR}},\underline{k}}\,\min \left[ \frac{\gamma _{\text {RD}}}{C},1\right] <\tau \right) \triangleq I_{2}^{\mathrm{LB }}\nonumber \\&=\mathrm{Pr }\left( \gamma _{\text {RD}}< C,\gamma _{{\text {SD}},\underline{k}}+\frac{\gamma _{{\text {SR}},\underline{k}}\,\gamma _{\text {RD}}}{C}<\tau \right) \nonumber \\&\overset{(a)}{=} \mathrm{Pr }\left( \gamma _{\text {RD}}< C,\max _{i}\left[ \gamma _{{\text {SD}},i}\right] +\frac{\gamma _{{\textit{SR}},i}\,\gamma _{\text {RD}}}{C}<\tau \right) , \end{aligned}$$

(5.62)

where step (a) is due to the fact that for $\gamma _{\text {RD}}< C$, the antenna selection of DAS relies solely on the direct links, which will incur a random selection of the channel between $S$ and $R$ [20]. Using the concepts of probability theory into Eq. (5.62), $I_{2}^\mathrm{LB }$ can be rewritten as

$$\begin{aligned} I_{2}^\mathrm{LB }&=\int _{0}^{C}f_{\gamma _{\text {RD}}}(y)\mathrm{Pr }\left( \max _{i}\left[ \gamma _{{\text {SD}},i}\right] +\frac{y}{C}\gamma _{{\text {SR}},i}<\tau \right) dy\nonumber \\&=\int _{0}^{1}\frac{C}{\bar{\gamma }_{\text {RD}}}e^{-\frac{C u}{\bar{\gamma }_{\text {RD}}}}\,\underbrace{\mathrm{Pr }\left( \max _{i}\left[ \gamma _{{\textit{SD}},i}\right] <\tau -u\gamma _{{\text {SR}},i}\right) }_{J_1}du. \end{aligned}$$

(5.63)

In what follows, we characterize the high-SNR behavior of $J_1$, which can be re-expressed as

$$\begin{aligned} J_{1}&=\int _{0}^{\infty }f_{\gamma _{{\text {SR}},i}}(\nu )\mathrm{Pr }\left( \max _{i}\left[ \gamma _{{\text {SD}},i}\right] <\tau -u\nu \right) d\nu \nonumber \\&= \int _{0}^{\tau }\frac{1}{u\bar{\gamma }_{\text {SR}}}e^{-\frac{x}{u\bar{\gamma }_{\text {SR}}}}\left( 1-e^{-\frac{\tau -x}{\bar{\gamma }_{\text {SD}}}}\right) ^{N_t}dx\nonumber \\&\simeq \frac{1}{u\bar{\gamma }_{\text {SR}}}\int _{0}^{\tau }e^{-\frac{x}{u\bar{\gamma }_{\text {SR}}}}\left( \frac{\tau -x}{\bar{\gamma }_{\text {SD}}}\right) ^{N_t}dx= \frac{1}{u\bar{\gamma }_{\text {SR}}}\left( \frac{1}{\bar{\gamma }_{\textit{SD}}}\right) ^{N_t}e^{-\frac{\tau }{u\bar{\gamma }_{\text {SR}}}}\int _{0}^{\tau } y^{N_t}e^{\frac{y}{u\bar{\gamma }_{\text {SR}}}}dy\nonumber \\&=\frac{1}{u\bar{\gamma }_{\text {SR}}}\left( \frac{1}{\bar{\gamma }_{\text {SD}}}\right) ^{N_t}e^{-\frac{\tau }{u\bar{\gamma }_{\text {SR}}}} \sum _{n=0}^{\infty }\frac{\left[ 1/(u\bar{\gamma }_{\text {SR}})\right] ^{n}}{n!}\frac{\tau ^{N_{t}+n+1}}{N_{t}+n+1}. \end{aligned}$$

(5.64)

Then, by substituting Eq. (5.64) into Eq. (5.63), $I_{2}^\mathrm{LB }$ can be asymptotically written as

$$\begin{aligned} I_{2}^\mathrm{LB }\simeq \frac{1}{\bar{\gamma }_{\textit{SR}}}\left( \frac{1}{\bar{\gamma }_{\text {SD}}}\right) ^{N_t}\sum _{n=0}^{\infty }\underbrace{ \frac{\tau ^{N_{t}+n+1}(1/\bar{\gamma }_{\text {SR}})^{n}}{n!(N_{t}+n+1)}\int _{0}^{1}\frac{C}{\bar{\gamma }_{\text {RD}}}e^{-\frac{C u}{\bar{\gamma }_{\text {RD}}}} \left( \frac{1}{u}\right) ^{n+1}e^{-\frac{\tau }{u\bar{\gamma }_{\text {SR}}}}du}_{\varPhi _{n}}. \end{aligned}$$

(5.65)

To proceed, the high-SNR behavior of $\varPhi _{n}$ needs to be characterized. With this aim, the following lemma is established.

Lemma: In the high SNR regime, $\varPhi _{n}$ can be asymptotically expressed as

$$\begin{aligned} \varPhi _{n}\simeq \left\{ {\begin{array}{*{20}l} \frac{\tau ^{N_{t}+1}}{n(N_{t}+n+1)\mu _{2}}, \,\,\, \mathrm{if }\,\,\, n\ge 1, \\ \frac{\tau ^{N_{t}+1}}{(N_{t}+1)\mu _{2}}\left[ \ln (\bar{\gamma }_{\text {RD}})-\ln (\tau )+ 2\psi (1)+\mathrm{Ei }(-1/\mu _{2})\right] ,\\ \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \mathrm{if }\,\,\, n=0, \\ \end{array}} \right. \end{aligned}$$

(5.66)

where $\mu _{2}=\bar{\gamma }_{\text {RD}}/\bar{\gamma }_{\text {SR}}$.

Based on the Lemma above, an asymptotic expression for $I_{2}^\mathrm{LB }$ can be derived as

$$\begin{aligned} I_{2}^\mathrm{LB }\simeq \frac{1}{\bar{\gamma }_{\text {SR}}}\left( \frac{1}{\bar{\gamma }_{\text {SD}}}\right) ^{N_t}\sum _{n=0}^{\infty }\varPhi _{n}. \end{aligned}$$

(5.67)

On the other hand, an upper bound for $I_2$ can be achieved as

$$\begin{aligned} I_{2}<\mathrm{Pr }\left( \gamma _{\text {RD}}<C,\gamma _{{\text {SD}},\underline{k}}+\gamma _{{\text {SR}},\underline{k}}\,\min \left[ \frac{\gamma _{\text {RD}}}{C},1\right] <2\tau \right) \triangleq I_{2}^\mathrm{UB }. \end{aligned}$$

(5.68)

Then, by replacing $\tau$ by $2\tau$ in Eq. (5.67), one can arrive at an asymptotic expression of $I_{2}^\mathrm{UB }$ as

$$\begin{aligned} I_{2}^\mathrm{UB }\simeq \frac{1}{\bar{\gamma }_{\text {SR}}}\left( \frac{1}{\bar{\gamma }_{\text {SD}}}\right) ^{N_t}\sum _{n=0}^{\infty }\varPsi _{n}, \end{aligned}$$

(5.69)

where $\varPsi _n$ is given by

$$\begin{aligned} \varPsi _{n}=\left\{ {\begin{array}{*{20}l} \frac{(2\tau )^{N_{t}+1}}{n(N_{t}+n+1)\mu _{2}}, \,\,\, \mathrm{if }\,\,\, n\ge 1, \\ \frac{(2\tau )^{N_{t}+1}}{(N_{t}+1)\mu _{2}}\left[ \ln (\bar{\gamma }_{\text {RD}})-\ln (2\tau )+ 2\psi (1)+\mathrm{Ei }(-1/\mu _{2})\right] , \,\,\,\mathrm{if }\,\,\, n=0. \\ \end{array}} \right. \end{aligned}$$

(5.70)

Now, an asymptotic analysis of $I_{1}^\mathrm{LB }$ is carried out. To this end, we first focus on the high-SNR behavior of $\mathrm{Pr }\left( \gamma _{{\text {SD}},i}+\gamma _{{\textit{SR}},i}<\tau \right)$, which can be asymptotically written as

$$\begin{aligned}&\mathrm{Pr }\left( \gamma _{{\text {SD}},i}+\gamma _{{\text {SR}},i}<\tau \right) =1-e^{-\frac{\tau }{\bar{\gamma }_{\text {SR}}}}-\frac{1}{\bar{\gamma }_{\text {SR}}}e^{-\frac{\tau }{\bar{\gamma }_{\text {SD}}}} \int _{0}^{\tau }e^{-y\left( \frac{1}{\bar{\gamma }_{\text {SR}}}-\frac{1}{\bar{\gamma }_{\text {SD}}}\right) }dy\nonumber \\&\simeq 1-\left( 1-\frac{\tau }{\bar{\gamma }_{\text {SR}}}+\frac{1}{2}\frac{\tau ^{2}}{\bar{\gamma }_{\text {SR}}^{2}}\right) -\frac{1}{\bar{\gamma }_{\text {SR}}}e^{-\frac{\tau }{\bar{\gamma }_{\text {SD}}}}\int _{0}^{\tau }\left( 1-y\left( \frac{1}{\bar{\gamma }_{\text {SR}}}-\frac{1}{\bar{\gamma }_{\text {SD}}}\right) \right) dy\nonumber \\&\simeq \frac{1}{2}\frac{\tau ^{2}}{\bar{\gamma }_{\text {SR}}\bar{\gamma }_{\text {SD}}}. \end{aligned}$$

(5.71)

By plugging Eq. (5.71) into Eq. (5.60), an asymptotic lower bound for $I_1$ can be obtained as

$$\begin{aligned} I_{1}^\mathrm{LB }\simeq e^{-\frac{1}{\mu _2}}\left( \frac{1}{2}\frac{\tau ^{2}}{\bar{\gamma }_{\text {SR}}\bar{\gamma }_{\text {SD}}}\right) ^{N_t}. \end{aligned}$$

(5.72)

Similarly, it follows from Eqs. (5.60) and (5.61) that with the replacing of $\tau$ by $2\tau$ in Eq. (5.72), an asymptotic upper bound for $I_1$ can be derived as

$$\begin{aligned} I_{1}^\mathrm{UB }\simeq e^{-\frac{1}{\mu _2}}\left( \frac{1}{2}\frac{(2\tau )^{2}}{\bar{\gamma }_{\text {SR}}\bar{\gamma }_{\text {SD}}}\right) ^{N_t}. \end{aligned}$$

(5.73)

Based on these preceding results, the following proposition is developed to characterize the outage behavior of DAS in the high SNR regime.

Proposition: For sufficiently high SNR, an asymptotic lower bound for the outage probability of DAS can be calculated as

$$\begin{aligned} P_\mathrm{out }^\mathrm{DAS,LB }\simeq \left\{ {\begin{array}{*{100}l} \frac{1}{2}e^{-\frac{1}{\mu _2}}\frac{\tau ^2}{\bar{\gamma }_{\text {SR}}\bar{\gamma }_{\text {SD}}}+\frac{1}{\bar{\gamma }_{\text {SR}}\bar{\gamma }_{\text {SD}}} \sum \nolimits _{n=0}^{\infty }\varPhi _{n}, \,\,\, \mathrm{if }\,\,\, N_{t}= 1, \\ \frac{1}{\bar{\gamma }_{\text {SR}}}\left( \frac{1}{\bar{\gamma }_{\text {SD}}}\right) ^{N_t}\sum \nolimits _{n=0}^{\infty }\varPhi _{n} ,\,\,\, \mathrm{if }\,\,\, N_{t}\ge 2. \\ \end{array}} \right. \end{aligned}$$

(5.74)

Accordingly, an asymptotic upper bound of the outage probability is given by

$$\begin{aligned} P_\mathrm{out }^\mathrm{DAS,UB }\simeq \left\{ {\begin{array}{*{100}l} e^{-\frac{1}{\mu _2}}\frac{2\tau ^2}{\bar{\gamma }_{\text {SR}}\bar{\gamma }_{\text {SD}}}+\frac{1}{\bar{\gamma }_{\text {SR}}\bar{\gamma }_{\text {SD}}} \sum \nolimits _{n=0}^{\infty }\varPsi _{n}, \,\,\, \mathrm{if }\,\,\, N_{t}= 1, \\ \frac{1}{\bar{\gamma }_{\text {SR}}}\left( \frac{1}{\bar{\gamma }_{\text {SD}}}\right) ^{N_t}\sum _{n=0}^{\infty }\varPsi _{n} ,\,\,\, \mathrm{if }\,\,\, N_{t}\ge 2. \\ \end{array}} \right. \end{aligned}$$

(5.75)

Remark 2:

• (a) As shown in Eqs. (5.74) and (5.75), the asymptotic bounds are written in terms of an infinite series, whose convergence needs to be checked. Applying the convergence test of [11, Eq. (0.223)], it can be proved that Eqs. (5.74) and (5.75) converge absolutely. In addition, it is numerically shown that Eqs. (5.74) and (5.75) converges rapidly and only 10 terms are sufficient for the most cases.

• (b) By invoking the pinching theorem, it follows from the proposition that full diversity order $N_{t}+1$ can be achieved by DAS. Besides achieving full diversity order, DAS can be implemented in a perfect distributed fashion, which makes it very attractive in practice.

Fig. 5.23

Comparison of different AS schemes in terms of outage probability ($P=8$ dB)

5.5 Numerical Examples and Discussions

Here, the impact of relay placement on the outage performance of different AS schemes is first examined via some representative cases’ studies. Based on these numerical examples, some typical relay deployments are adopted to compare the outage performance of different AS schemes. Meanwhile, Monte Carlo simulations are also invoked to validate the presented analysis. For illustration purposes and without loss of generality, hereafter, the end-to-end spectral efficiency is set to $R_{0}=1$ bit/s/Hz, the path loss exponent is assumed to be $\beta =4$, and the distance between $S$ and $D$ is normalized to unity.¹⁶

The outage performance of DAS versus $d_{\text {SR}}$ is shown in Fig. 5.23. For comparison purposes, the outage curves of the optimal and suboptimal AS schemes [20] are also plotted. Let us first focus on the case of $N_{t}=2$. For such a case, we observe that when $d_{\text {SR}}<0.5$, the outage performance of DAS overlaps that of the suboptimal scheme. However, when the relay moves toward to the destination, the outage performance of DAS dramatically improves. Particularly, at $d_{\text {SR}}\approx 0.75$, DAS achieves its best outage performance, which is very close to that of the optimal scheme. A further increase in $d_{\text {SR}}$ makes the outage curves of DAS and the optimal scheme indistinguishable from each other. The given phenomenon can be explained as follows. When $d_{\text {SR}}$ approaches unity, the inequality $\{\bar{\gamma }_{\text {RD}}\ge C\}$ always holds, which means that the event $\gamma _{\text {RD}}\ge C$ happens with a high probability. Since Eq. (55) is a tight bound, it follows from Eqs. (53) and (56) that the selection rule of DAS will tend toward that of the optimal scheme in this case. In contrary, when $d_{\text {SR}}$ approaches to zero, the event $\{\gamma _{\text {RD}}<C\}$ occurs with a high probability, which makes the selection rule of DAS tends toward the suboptimal rule Eq. (54). For $N_{t}=3$, a similar phenomenon can be observed, with the exception that the outage-optimal relay placements of DAS and the optimal scheme tend toward unity, as compared with the case of $N_{t}=2$.

Fig. 5.24

Outage probability versus average SNR of the $S{-}D$ link for different AS schemes ($d_{\text {SR}}= 0.7$, $N_{t}=2$)

Fig. 5.25

Outage probability versus average SNR of the $S{-}D$ link for different AS schemes ($d_{\text {SR}}=0.8$, $N_{t}=3$)

Fig. 5.26

Comparisons of different AS schemes in terms of outage probability with the outage-optimal relay placements

Fig. 5.27

Outage-optimal relay placements for different AS schemes and system configurations

Based on these observations, in what follows, the relay $R$ will be deployed close to destination so that the outage performance of DAS and the optimal scheme can be boosted.¹⁷ For illustration purposes, we set $d_{\text {SR}}=0.7$ or 0.8 in the subsequent numerical results. The outage performance of different AS schemes when two antennas are deployed at $S$ is compared in Fig. 5.24. From this figure, it is shown that the asymptotic outage lower bound of DAS is very tight in the medium and high-SNR regions. In addition, the asymptotic lower and upper bounds are in parallel with the simulated curves of DAS at high SNR, which validates the above diversity analysis. In addition, the outage performance of DAS and the optimal scheme are quite close to each other in the low-to-medium-SNR regions.

The case of $N_{t}=3$ is further considered in Fig. 5.25. In comparison with Fig. 5.24, it is observed that the outage performance of DAS is still very close to that of the optimal scheme in the low-to-medium-SNR regions.

A comparison of different AS schemes with outage-optimal relay placements is shown in Fig. 5.26, and the corresponding outage-optimal relay positions are plotted in Fig. 5.27. Once again, it is shown that the outage performance of DAS is extremely close to that of the optimal scheme when the outage-optimal relay placements are, respectively, adopted for them. These observations further validate the practical usefulness of the proposed DAS scheme.

6 Conclusions

This chapter focused on designing efficient, low-complexity cooperative diversity schemes from different perspectives and it was divided into four parts. In the first part, assuming a general multisource, multirelay cooperative system, a new efficient scheme for the combined use of cooperative diversity and multiuser diversity was proposed. The proposed scheme significantly reduced the amount of channel estimation while achieving comparable outage performance to that using the joint selection scheme. In the second part, two spectrally efficient schemes for the diversity exploitation of downlink cooperative cellular networks were proposed. By scheduling the user with the best direct link to access the channel, an incremental decode-and-forward relaying scheme was first presented. To further enhance the transmission robustness against fading, an improved scheme is also proposed, which substantially utilizes opportunistic scheduling mechanism when the direct transmission fails. In the third part, new and efficient link selection schemes for selection relaying systems with transmit beamforming were proposed. Two distributed link selection schemes were presented that invoke a distributed decision mechanism and rely on the success/fail signaling feedback between terminals. In the fourth part, a novel distributed transmit antenna selection for dual-hop amplify-and-forward relaying systems was proposed. A multiantenna source transmits information to a single-antenna destination by using a single-antenna half-duplex relay. By invoking local channel information exploitation/decision mechanism along with decision feedback between terminals, a distributed antenna selection scheme was formulated. Compared with the optimal/suboptimal antenna selection, the proposed scheme can maintain a low and constant delay/feedback overhead irrespective of the number of transmit antennas.