Power control and clustering in heterogeneous cellular networks

Abstract

Recently, it is widely believed that significant coverage and performance improvement can be achieved through the deployment of small cells in conjunction with the well-established macro cells. However, it is expected that the high density of base stations in such heterogeneous cellular networks will give rise to multiple design problems related to both co-tier (small-to-small) and cross-tier (between small and macro cells) interference. Fortunately, cooperation between base stations will play a major role to cope with these problems and hence to enhance the users’ data rates. In this paper, we consider a two-tier cellular network comprised of a macro cell underlaid with multiple small cells where both co-tier and cross-tier interference are taken into account. We study the scenario where the small cell base stations seek to maximize a common objective by forming multiple clusters through cooperation. These base stations have also to allocate power to their associated users and, at the same time, control the total aggregate interference caused to the macro cell user which has to be kept below a threshold prefixed by the macro cell base station. We consider two utility functions: the overall sum rate of the small cell network and the minimum data rate of the small cell users. We formulate the studied problems as mixed integer nonlinear optimization problems and we discuss their NP hardness. Therefore, due to the complexity of finding the optimal solution, we design heuristic algorithms which resolves efficiently the tradeoff between computational complexity and performance. We show through simulations that the designed heuristics approach the optimal solution (obtained using the complex exhaustive search algorithm) with highly reduced computational complexity.

1 Introduction

Heterogeneous and small cell networks (HetSNets) constitute an enormous paradigm shift affecting the way cellular networks are designed [1]. Base stations of different sizes, carrier frequencies and transmit powers are added continuously to underlay the well-established macro cell base stations. In the near future, this increase in the number of heterogeneous base stations may lead to networks where each wireless device has its own base station [1]. However, the high density of base stations will give rise to numerous research challenges. A major capacity limitation in wireless communications in general, and in HetSNets in particular, is interference. The latter can be mitigated (or reduced) through cooperative techniques [2]. In fact, in two-tiered networks adequate cooperation between small cell base stations (SBSs) can increase considerably their performance by operating as a virtual multi-input-multi-output (MIMO) array. Furthermore, when these base stations have cognitive capabilities, they can coexist (in the same frequency band) with macro cell transmissions, by limiting the degree of interference they may cause through power control [3].

Since the seminal work of Yoo and Goldsmith [4], zero forcing beamforming (ZFBF) has received a large research interest. In fact, the study in [4] showed that ZFBF can asymptotically achieve the same sum rate as the optimal dirty paper coding while reducing significantly the implementation complexity. However, the computational complexity of ZFBF significantly increases when the number of active users in the system becomes large. In fact, before the emergence of HetSNets, ZFBF was extensively investigated in the context of multiple users served by a power constrained multiantenna base station. Hence, most research efforts on ZFBF have focused on devising low complexity scheduling schemes for multiuser MIMO systems [4, 5]. When SBSs in a HetSNet are able to cooperate, they can use ZFBF in a distributed fashion. In this case, each set of SBSs willing to cooperate can form several disjoint “clusters”. Many new constraints have to be considered: (1) a per base station power constraint instead of a sum power constraint (similar to the per antenna power constraint in multiuser MIMO [6]), (2) an interference management between clusters (named as inter-cluster interference in this paper) and (3) an interference constraint imposed by the macro cell transmission.

Using distributed linear precoding, and ZFBF in particular, in HetSNets has become a hot research topic that is attracting increasing interest [7–14]. The first research work to study a per antenna power constraint is presented in [6]. The authors showed that the power allocation problem under this new constraint is a convex problem that can be hence solved in polynomial time. The work in [7] tackled a problem with the same constraint for fully cooperating multicells. The authors designed the optimal precoder for weighted sum rate maximization. Assuming a similar model, the precoder proposed in [8] maximizes the overall sum rate of the system. The authors in [9] proposed a new linear precoding scheme for sum rate maximization in cooperative multicell systems. The proposed scheme performs well for low and medium signal-to-noise ratio (SNR). More recently, Nguyen et al. [10] studied a system where the precoding is performed on a per cell basis. Two scenarios have been compared: a scenario where the base stations do not cooperate, i.e. each base station compute its precoding matrix based on its own interest, and a scenario where the base stations cooperate to compute precoding matrices that maximize a common objective. The works in [11] and [12] formulate the energy efficiency problem in multicell networks with ZFBF as a nonlinear fractional program and use the well-known Dinckelbach method to solve it. Other precoders for small cell transmissions in a two tiered network are proposed in [13] and [14]. The designed precoders aim to suppress completely the interference towards the macro cell users according to an overlay paradigm without cooperation between the base stations.

Coalitional game theory was extensively used in order to design distributed algorithms to solve the coalition formation problem. Based on the concept of recursive core, the authors of [15] propose a distributed merge-only algorithm in order to form the coalitions. The proposed algorithm tries to construct a recursive core where no SBS has an incentive to deviate from its corresponding coalition. However, the authors assume that once a base station commits to join a given coalition, it cannot change this decision in the future even if it finds a better outcome. Though this assumption simplifies the algorithm design and converges to a recursive core, it prevents the small cell network from approaching a social optimum. In [16], the authors investigate the same problem using a similar system model based on a different solution concept, namely the epsilon-core. They propose a distributed coalition formation algorithm taking into account the deviation overhead, i.e. the overhead required at base station in order to change its coalition. In [17], the authors study the coalition formation problem in a femtocell network that use interference alignment as an interference management technique. The authors design a distributed algorithm which operates iteratively in order to converge to a recursive core. In [18], the authors develop a distributed algorithm which forms overlapping coalitions in a two-tiered network. Hence, each base station may join multiple coalitions. The authors assume an orthogonal frequency-division multiple access (OFDMA) network with no precoding. Although these distributed algorithms are all shown to converge to a stable solution concept where no base station has an incentive to deviate, the final convergence state may be far from the optimal sum rate of the overall network. Therefore, centralized coalition formation and power allocation schemes are indispensable for approaching the optimal performance.

The rest of the paper is organized as follows. The contribution is summarized in Sect. 2. Section 3 presents the system model. Section 4 formulates the problem, presents the utility functions and discuss the hardness of the associated problems. Section 5 describes the proposed clustering and power allocation heuristic algorithms. Section 6 presents the numerical results and the computational complexity of the proposed algorithms and finally Sect. 7 draws some conclusions.

2 Contribution of the work

Unlike works described in the introduction, this work proposes a centralized scheme controlling a network of small cells where the SBSs are ready to form one or multiple clusters and cooperate to either maximize a common objective such as the overall sum rate of the system or ensure fairness by maximizing the minimum data rate. Therefore, we propose to use a multiuser MIMO precoding scheme in order to reduce the negative impact of co-tier interference in HetSNets. Hence, the SBSs are disposed in several clusters and the interference in each cluster is totally suppressed using the ZFBF precoding scheme. Also, the interference caused to the macro cell transmission, which is considered as a primary transmission, is kept below a prefixed interference threshold. A cluster is hence regarded as a multiuser MIMO network where SBSs form a virtual big base station with multiple antennas serving multiple users. Further, each cluster operates as a secondary transmission in a cognitive underlay scheme. The clusters are formed and the power is allocated in such a way that both inter-cluster and cross-tier interference are minimized and hence the system utility is maximized. The problem is first formulated as an optimization problem and the complexity of solving it optimally is briefly discussed. In fact, we find that the problem is $\textit{NP}$-hard which motivates us to design suboptimal but computationally efficient algorithms. Three greedy heuristics are presented and their performance is assessed through simulations. The computational complexity of the three algorithms is also evaluated and benchmarked against the complexity of finding the optimal solution.

3 System model

The considered network is made up of N small cell base stations (SBSs). Each SBS is initially associated with exactly one small cell user (SU). We denote by $\ell _n$ the link formed by SBS n and its associated SU n. The small cells coexist with a macro cell where a macro base station (MBS) is serving one user (MU) over one frequency band. We consider the downlink channel for all transmissions.

Table 1 List of notation

All the SBSs are transmitting over the same frequency band as the MBS and are distributed randomly in the same geographical area. Hence, each SU n suffers from two kinds of interference, namely co-tier interference that is caused by the SBSs other than n and cross-tier interference caused by the MBS transmission. In order to lower the impact of co-tier interference on the performance of the small cell network, SBSs seek to form clusters. The SBSs belonging to the same cluster can use a distributed beamforming so they can totally eliminate interference inside the cluster. We propose to use the well-known ZFBF [4] as the beamforming technique. When the clusters are formed each SU may be served by more than one SBS and one SBS can serve more than one SU. Unfortunately, co-tier interference is not eliminated and the SUs are still suffering from inter-cluster interference that is caused by the SBSs belonging to other clusters. On the other hand, the MU may suffer from cross-tier interference caused by the SBSs transmissions. Hence, each SBS has to control its transmit power so that the small cell network remains transparent to the macro cell transmission. It is also assumed that the SBSs are connected to the core network using a reliable and fast backhaul network. The algorithms presented in this paper are centralized. They require the availability of the parameters, on which the clustering and power allocation decisions rely, at a central entity. These parameters include the channel coefficients or the distances. Therefore, we assume that the fast and reliable backhaul allows to make these parameters available with negligible delays at this central point. Anyhow, the impact of imperfect knowledge of channel state or the distances is evaluated and discussed in Sect. 6.

The received signal at SU n can be written as:

$$\begin{aligned} y_n = {\mathbf {h}}_n {\mathbf {x}} + g^M_n \sqrt{\gamma _0} a_0 + z_n, \end{aligned}$$

(1)

where ${\mathbf {h}}_n$ is the ($1 \times N$) channel vector between the N SBSs and user n, ${\mathbf {x}}$ is the ($N \times 1$) transmitted vector of signals from all the SBSs, $g^M_n$ denotes the channel coefficient between the MBS and user n, $a_0$ and $\gamma _0$ denote respectively the transmitted signal and power to the macro user and $z_n$ is the additive white Gausssian noise (AWGN) at user n with zero mean and variance $\sigma ^2_{z_n}$.

Assuming that SBS n belongs to cluster $S_k$ (i.e. $n \in S_k$), the nth element of ${\mathbf {x}}$ is given by:

$$\begin{aligned} x_n = \sum _{m \in S_k} w_{\textit{nm}} \sqrt{\gamma _m} a_m, \end{aligned}$$

(2)

where ${\mathbf {w}}_n = [w_{\textit{nm}}]_{m \in S_k}$ is the ($1 \times |S_k|$) beamforming vector for user n ($|\cdot |$ is the cardinality of the set), $\sqrt{\gamma _m}$ is the portion of power allocated to user m and $a_m$ is the transmitted signal to user m. Since ZFBF is used, the beamforming vector ${\mathbf {w}}_n$ is the column corresponding to SBS n in matrix ${\mathbf {W}}_k$ which is the pseudo-inverse of matrix ${\mathbf {H}}_k$. Matrix ${\mathbf {H}}_k$ is formed by the channel vectors of all users in the set $S_k$, i.e. ${\mathbf {H}}_k = [{\mathbf {h}}_n]_{m \in S_k}$.

Thanks to the ZFBF, the received signal at SU n can be rewritten as:

$$\begin{aligned} y_n= & {} \sqrt{\gamma _n} a_n + \sum _{\begin{array}{c} m' \in S_j\\ j \ne k \end{array}} \mathbf {h_n} \mathbf {w_{m'}} \sqrt{\gamma _{m'}} a_{m'}\nonumber \\&+\,g^M_n \sqrt{\gamma _0} a_0 + z_n. \end{aligned}$$

(3)

The first term in the right hand side of (3) represents the desired signal whereas the second term represents the inter-cluster interference which can be reduced by adequately forming the clusters and assigning power portions. Unfortunately, this kind of interference cannot be totally suppressed and will be treated as noise. Finally, the third term represents the cross tier interference signal coming from the macro transmission. Therefore, the achievable data rate at user n is given by:

$$\begin{aligned} R_n = \log _2 \left( 1 + \frac{\gamma _n}{\sigma ^2_{z_n} + \sum _{\begin{array}{c} m' \in S_j \\ j \ne k \end{array}} |\mathbf {h_n} \mathbf {w_{m'}}|^2 \gamma _{m'} + |g^M_n|^2 \gamma _0}\right) . \end{aligned}$$

(4)

The main notations are summarized in Table 1.

4 Problem formulation

Improving the system performance cannot be realized without finding efficient solutions to the following two main problems: (1) the clustering problem, i.e. how the SBS-SU links are disposed into clusters and (2) the power control and allocation problem, i.e. how much power can be used by each SBS subject to the interference constraint imposed by the macro cell transmission and how each SBS allocates this power among the SUs belonging to its cluster.

In this section, we formulate the joint clustering and power control and allocation problem as a mixed integer nonlinear optimization problem. Two system utilities are studied, namely the system sum rate utility and the minimum rate utility.

4.1 Sum rate utility

When all SBSs seek to maximize a common interest, the objective function is the overall sum rate of the system. The problem can be formulated in this case as a problem involving both binary variables corresponding to the clustering decision and continuous variables representing the power allocation.

We first define the following binary variables:

$$\begin{aligned} x_{\textit{nm}} = \left\{ \begin{array}{ll} 1 &{} \quad \text {if} \quad \ell _n\, \text { and }\, \ell _m\, \text { are in the same cluster }\\ 0 &{} \quad \text {otherwise.} \end{array} \right. \end{aligned}$$

The achievable data rate at user n can be written as:

$$\begin{aligned} U_n = \log _2 \left( 1 + \frac{\gamma _n}{\sigma _{z_n}^2 + \sum _{m=1}^N (1-x_{\textit{nm}}) |h_{\textit{mn}}|^2 s_m + |g^M_n|^2 \gamma _0}\right) , \end{aligned}$$

(5)

where $h_{\textit{mn}}$ is the mth element of vector ${\mathbf {h}}_n$ denoting the channel coefficient between SBS m and user n with

$$\begin{aligned} s_m = \sum _{q=1}^N x_{\textit{mq}} |w_{\textit{mq}}|^2 \gamma _q. \end{aligned}$$

(6)

Each variable $\gamma _n$ denotes the power allocated to user n, and subject to the following constraint:

$$\begin{aligned} \sum _{m=1}^N x_{\textit{nm}} |w_{\textit{nm}}|^2 \gamma _m \le P^{\textit{max}}_n \quad \forall n \in \{1\dots N\} \end{aligned}$$

(7)

where $P_n^{\textit{max}}$ is the maximum amount of power available at SBS n for transmission.

Further, the portions of power allocated to SUs are subject to an interference constraint imposed by the macro transmission. Hence, the aggregate interference caused by all the SBSs to the MU must be kept below the prefixed threshold $I_{\textit{th}}$. Therefore, the following constraint has to be respected by the small cells:

$$\begin{aligned} \sum _{n=1}^N \left( \sum _{m=1}^M x_{\textit{nm}} |w_{\textit{nm}}|^2 \gamma _m \right) \cdot |g^S_n|^2 \le I_{\textit{th}} \end{aligned}$$

(8)

where $g^S_n$ denotes the channel coefficient between SBS n and the MU.

The next constraints must be added to ensure that the values of the binary variables are consistent with the formed clusters, e.g. if link n and link m are in the same cluster (i.e. $x_{\textit{nm}} = 1$) and link m and link q are in the same cluster (i.e. $x_{\textit{mq}} = 1$), then link n and link q are also in the same cluster (i.e. $x_{\textit{nq}} = 1$):

$$\begin{aligned} x_{\textit{nq}}\le & {} 1 - x_{\textit{nm}} + x_{\textit{mq}} \quad \forall n,m,q \in \{1\dots N\}^3\end{aligned}$$

(9)

$$\begin{aligned} x_{\textit{nq}}\le & {} 1 + x_{\textit{nm}} - x_{\textit{mq}} \quad \forall n,m,q \in \{1\dots N\}^3\end{aligned}$$

(10)

$$\begin{aligned} x_{\textit{nq}}\ge & {} x_{\textit{nm}} + x_{\textit{mq}} - 1 \quad \forall n,m,q \in \{1\dots N\}^3 \end{aligned}$$

(11)

The following constraints ensure that the number of links in each cluster does not exceed a prefixed limit $C_{\textit{max}}$, the maximal number of small cells admissible in each cluster:

$$\begin{aligned} \sum _{m=1}^{N} x_{\textit{nm}} \le C_{\textit{max}} \quad \forall n \in \{1\dots N\}, \end{aligned}$$

(12)

and finally, we must have:

$$\begin{aligned}&x_{\textit{nm}} = x_{\textit{mn}} \quad \forall n,m \in \{1\dots N\}^2\end{aligned}$$

(13)

$$\begin{aligned}&x_{\textit{nm}} \in \{0,1\} \quad \forall n,m \in \{1\dots N\}^2\end{aligned}$$

(14)

$$\begin{aligned}&\gamma _n \ge 0 \quad \forall n \in \{1\dots N\} \end{aligned}$$

(15)

where the first two constraints ensure the consistency of the definition of the binary variables $x_{\textit{nm}}$ while the third one ensures that no user obtains a negative amount of power.

Therefore, the sum rate maximization problem can be written as follows:

$$\begin{aligned} \text {Maximize}&\sum _{n=1}^N U_n \nonumber \\ \text {subject to }&(7) {-} (15). \end{aligned}$$

(16)

The formulation given by (16) is computationally very hard to solve since it involves both binary and continuous variables. Also, due to the nature of ZFBF, we cannot compute the matrix channel inverse before fixing the binary variables (i.e. making the clustering decision). Hence, the optimal solution to problem (16) can be only found by performing an exhaustive search over all the possible clustering decisions. For each possible formation, we must perform a separate power allocation by solving the following nonlinear optimization problem:

$$\begin{aligned} \begin{array}{lll} \text {Maximize} &{} \sum\limits_{k=1}^K \sum\limits_{n \in S_k} R_n &{}\\ \text {subject to} &{} \sum\limits_{m \in S_k} |w_{\textit{nm}}|^2 \gamma _m \le P^{\textit{max}}_n &{} \forall n \in S_k, \forall k \\ &{} \sum\limits_{k=1}^K \left( \sum\limits_{n\in S_k} \left( \sum\limits_{m\in S_k} x_{\textit{nm}} |w_{\textit{nm}}|^2 \gamma _m \right) \cdot |g^S_n|^2 \right) \le I_{\textit{th}} &{}\\ &{} \gamma _n \ge 0 &{} \forall k, \forall n \in S_k \end{array} \end{aligned}$$

(17)

where $R_n$ is given by (4) and K is the number of clusters in the considered clustering decision.

Unfortunately, the number of possible clustering decisions grows exponentially with the number of small cells in the system. Hence, such optimal solution cannot be implemented even for small numbers of SBS-user links. Furthermore, the power allocation problem can be proven to be $\textit{NP}$-hard based on a polynomial time reduction from the maximum independent set problem in a similar way to the proof of Theorem 1 in [19]. The $\textit{NP}$-hardness of the power allocation problem makes the problem of joint clustering and power allocation under the sum rate utility even more harder and an optimal brute force solution impossible to implement.

4.2 Minimum rate utility

When fairness among users is an important design issue, then maximizing the overall sum rate of the system is not suitable since some users may experience starvation. Instead, we propose to maximize the minimum user rate. The problem can hence be formulated as follows:

$$\begin{aligned} \text {Maximize}&\min _{1\le n \le N} U_n \nonumber \\ \text {subject to }&(7){-}(15). \end{aligned}$$

(18)

By introducing an auxiliary variable noted $\tau$, the minimum rate problem can be rewritten as:

$$\begin{aligned} \text{Maximize } & \quad \quad \tau \nonumber \\ \text {subject to }& \quad (7) {-} (15) \nonumber \\&\tau \left( \sigma _n^2 + \sum_{m=1}^N (1-x_{\textit{nm}}) |h_{\textit{mn}}|^2 s_m\right) \le \gamma _n \qquad \forall n \in \{1\dots N\}\nonumber \\&\tau \ge 0. \end{aligned}$$

(19)

Once again, similar to the case of sum rate utility, we have to perform an exhaustive search over an exponentially increasing number of clustering decisions. However, once the clustering is performed , the power allocation becomes polynomially solvable because of the linearity of its objective function and constraints (considering the variable $\tau$ as a parameter and performing a binary search over its value).

5 Proposed algorithms

Due to the high complexity of finding the optimal solution of the proposed problem for both utility functions, as discussed in Sect. 4, we present in this section low complexity greedy algorithms based on simple but efficient selection criteria. The proposed algorithms adopt the same main structure and differ only in the selection criteria. These algorithms start by a clustering phase by selecting in a greedy fashion one link at each iteration and adding it to its “best” choice cluster (the superlative “best” refers to a local choice due to the greedy nature of the algorithms). Once the clusters are formed, the algorithms proceed to the power allocation by solving either problem (17) for maximizing the system sum rate or problem (19) for maximizing the minimum data rate.

5.1 Greedy clustering algorithms

In the following, we detail three simple heuristic algorithms for the phase of clustering.

5.1.1 Heuristic 1: Highest SNR first (HSF)

This first heuristic algorithm starts by putting in the first cluster the link that experiences the highest SNR among all the available links. It then adds the link that causes most interference to the firstly chosen link. If the cluster is not entirely filled, the algorithm adds the link that causes the most aggregate interference to the links already in the first cluster. The algorithm continues in the same fashion until the cluster is completely filled. It then proceeds to the second iteration by putting in the second cluster the link with highest SNR chosen from the remaining links (i.e. the ones not in cluster 1). The algorithm proceeds in the same way and terminates when all the links are assigned to clusters. The different steps of heuristic 1 are detailed in Algorithm 1.

5.1.2 Heuristic 2: Highest interference first (HIF)

This heuristic starts by putting in the first cluster the two links which cause the highest amount of interference to each other. Just like HSF, the algorithm adds the link that causes the most aggregate interference to the already added links. Then, it continues in the same way until the cluster is full. The algorithm forms other clusters in the same fashion it has formed the first one and terminates when no link remains unassigned. The structure of this heuristic is similar to HSF and thus it can be described using Algorithm 1.

5.1.3 Heuristic 3: Neighbouring links first (NLF)

The third heuristic is based only on the separating distances between users and the interfering SBSs. It starts by assigning to the first cluster the two most neighboring links, i.e. the two links a and b where the distance between SBS a and user b or the distance between SBS b and user a is the smallest. If $C_{\textit{max}}>2$, the algorithm adds another neighboring link, i.e. the one having the nearest SBS to the users of the first two links or the one having the nearest user to the SBSs of the first two links. The algorithm continues adding links in the same fashion until no more places are available in the first cluster. Algorithm 1 can be easily adapted to describe the steps of NLF.

5.2 Phase 2: Iterative power allocation

The next phase is the power allocation which is common for the three proposed clustering heuristics. Once the clusters are formed, each algorithm solves the power allocation problem [given either by (17) or (19)]. As discussed before, the problem of maximizing the minimum rate utility is a parametric linear problem and thus can be optimally solved using any optimization tool in polynomial time. However, the problem of maximizing the sum rate utility is $\textit{NP}$-hard due especially to the interdependence between the clusters (i.e. making the objective function non-separable). Hence, we propose to solve the power allocation for problem (17) in an iterative fashion by computing the transmit powers of SBSs in one cluster in each new iteration. Furthermore, constraint (8) is common for all the clusters and hence it must be separated in order to solve independently the power allocation problem for each cluster. Hence, instead of constraining the aggregate interference caused by all the clusters, each cluster will have its own constraint. More specifically, its corresponding tolerable interference level must not exceed the threshold $I_{\textit{th}}/K$ (i.e. the original interference threshold divided by the number of clusters). Therefore, for each cluster $S_k$ a problem in the following form has to be solved

$$\begin{aligned} \begin{array}{lll} \text {Maximize} &{} \sum\limits_{n \in S_k} R'_n &{}\\ \text {subject to } &{} \sum\limits_{m \in S_k} |w_{\textit{nm}}|^2 \gamma _m \le P^{\textit{max}}_n &{} \forall n \in S_k \\ &{} \sum\limits_{n\in S_k} \left( \sum\limits_{m\in S_k} |w_{\textit{nm}}|^2 \gamma _m \right) \cdot |g^S_n|^2 \le \dfrac{I_{\textit{th}}}{K} &{}\\ &{} \gamma _n \ge 0 &{} \forall n \in S_k \end{array} \end{aligned}$$

(20)

where the rate $R'_n$ includes only the previously computed intra-cluster interference as it will be discussed next.

The algorithm starts by computing the transmit power of SBSs in a chosen cluster (e.g. finding $\gamma _n$ for all $n \in S_j$) by fixing the transmit power of SBSs of the other clusters to their maximal values (e.g. putting $\gamma _m$ for all $m \in S_k$ with $k \ne j$). Clearly, the problem to solve at each iteration is a convex optimization problem which can be solved using the well-known water filling method when $|S_j|~=~2$ (as presented in [6]) or requiring a numerical optimization tool when $|S_j|~>~2$. Each iteration involves solving a new convex optimization problem where the transmit power of SBSs of the already considered clusters are taken equal to their computed values, while the other values of transmit power (not computed yet) are taken equal to their maximal values. When the algorithm performs exactly K iterations and computes the transmit powers of all the SBSs, it restarts taking as input the computed portions of power. As it will be discussed in the next section, running the algorithm for only two iterations is enough to obtain a tangible sum rate improvement. Running more iterations adds only more computational complexity without significant performance improvement.

6 Simulation results

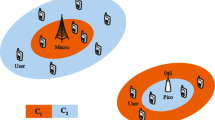
This section investigates the performance of the proposed heuristic algorithms through computer simulations performed using MATLAB where the power control optimization problem is solved using the fmincon function. As a benchmark, we use the optimal performance obtained by the highly complex exhaustive search algorithm. We consider a two tier network where the MBS is located at the center of a square area having a size of 1000 m × 1000 m. The macro cell user is located randomly within an area of 100 m × 100 m having the MBS as its center. We also consider a small cell network where N links are randomly located according to a uniform distribution in the same geographic area. An example of network made up of ten small cells disposed in four clusters is shown in Fig. 1. All the small cell links have the same separation distance between the SBS and its corresponding user which is chosen to be $d_{\textit{mm}}$ = 100 m. The channel coefficients are modeled as $h_{\textit{nm}} = \sqrt{K_0 \cdot (d_{\textit{mn}}/d_0)^{-\alpha }} \cdot \beta _{\textit{mn}}$, where $K_0 = 10^3$ is a constant capturing the system and transmission effects, $d_{\textit{mn}}$ is the distance between SBS m and user n, $d_0 = 1$ m is the reference distance, $\alpha = 4$ is the path loss exponent and $\beta _{\textit{mn}}$ is a random Gaussian variable with zero mean and unit variance (the coeffiecients $g^M_n$ and $g^S_n$ are modeled similarly). The noise spectral density at each user is chosen to be $N_0 = 10^{-10}$ W/Hz as in [20], the maximum power available at each SBS m is $P_m^{\textit{max}} = P^{\textit{max}} = 0.1$ W and the transmit power of the MBS is $\gamma _0 = 0.2$ W. We regenerate randomly the locations of the SBSs, SUs and MU at the beginning of each simulation run. The value of the objective function is obtained by averaging over $10^3$ simulation runs for the optimal solution because of its high complexity and over more than $10^4$ simulation runs for the proposed heuristics. Since we present average values, we verified that the number of simulation runs is high enough such that the resulted value converges and any additional runs will not result in any significant change to the estimated average value as presented in Fig. 2. In fact, the figure shows the convergence of two average values for the achievable sum rate presented later in Fig. 8.

Fig. 1

A two tier network example with $N=10$ links disposed in $K=4$ clusters

Fig. 2

Convergence of two average values of the achievable sum rate of HIF for $P_m^{\textit{max}} = 0.1$ and 1 W

Fig. 3

Sum rate versus the number of iterations performed in the power allocation phase

Figure 3 plots the performance of the proposed heuristics when varying the number of iterations of the power allocation phase. We notice that adding a second iteration to the power allocation phase improves the achievable sum rate independently of the employed clustering heuristic. However, adding more iterations (beyond two) does not help improving the performances as the curves stagnate after two iterations.

Fig. 4

Average rate per user comparison for different values of N with $C_{\textit{max}} = 3$ and $I_{\textit{th}} = 20N_0$

Fig. 5

Average rate per user comparison for different values of N with $C_{\textit{max}} = 3$ and no interference limit

Figures 4 and 5 compare the achievable average rate per user using the three proposed clustering heuristics to the optimal solutions found by the highly complex exhaustive search. Figure 4 shows the results for a network where the macro cell transmission imposes an interference threshold of $I_{\textit{th}} = 20 N_0$, whereas Fig. 5 shows the results for a network consisting only of small cells. We notice from the two figures that HIF outperforms the two other heuristics for all values of N. The HIF heuristic achieves sum rate close to the exhaustive search algorithm with a relatively tight performance gap between 2 and 4 %. However, in the presence of macro cell transmission, the performance gap between the optimal exhaustive search solution and HIF gets slightly larger, e.g. it goes from 2.1 (when no macro cell transmission) to 3.5 % (when $I_{\textit{th}} = 20 N_0$) for $N=6$. We can also observe from these figures that the performance gap between HIF and NLF heuristics is very small and does not exceed 1 %. NLF is based only on the information about the distances separating the SBSs and the users and does not require any information about the channel gains to obtain the clustering. Hence, this heuristic is interesting to implement thanks to its limited information requirements. Finally, we notice that as N increases, the performance of HSF degrades because the impact of interference becomes important.

Fig. 6

Sum rate comparison varying $I_{\textit{th}}$

Figure 6 shows the performance of the three proposed heuristics when varying the level of tolerable interference at the macro cell user. Two network sizes are considered: $N=6$ (lower curves) or $N=8$ (upper curves). As expected, when the macro cell communication tolerates more interference, the SBSs can increase their transmit power and hence improve the overall system sum rate. Also, we notice that when the value of $I_{\textit{th}}$ is very large, the interference constraint becomes inactive and the power portions allocated to the small users are only limited by the maximal powers available at the SBSs. Figure 6 shows also that the three heuristics performs differently when varying the value of $I_{\textit{th}}$. In fact, although for small values of $I_{\textit{th}}$, the three heuristics have almost the same performance, large values of $I_{\textit{th}}$ favors the HIF and NLF heuristics over the HSF heuristic. This advantage becomes important as N becomes larger.

Fig. 7

Average rate per small cell user versus the maximum cluster size

We plot in Fig. 7 the average rate per user of the three proposed heuristics when varying the maximal number of small cells admissible in each cluster $C_{\textit{max}}$. We consider a network with $N=20$ small cells. In the case when no interference threshold is imposed (upper curves), increasing the value of $C_{\textit{max}}$ results in a performance increase for the three heuristics. We also notice that as $C_{\textit{max}}$ increases the performance of the HSF heuristic approaches the performance of the other two heuristics. This is due to the decrease of the impact of inter-cluster interference since when $C_{\textit{max}}$ gets larger, the system forms less clusters. On the other hand, when the macro cell imposes a threshold of $I_{\textit{th}} = 20 N_0$ (lower curves), the performance of the heuristics saturate beyond $C_{\textit{max}} = 5$. Hence, forming larger clusters does not improve the achieved performance since the clustering choice is constrained by the level of interference caused to the macro cell communication.

Fig. 8

Sum rate versus maximum power at each SBS

Figure 8 plots the sum rate achieved by the three heuristics when varying the maximum transmit power available at each SBS $P^{\textit{max}}_n$, $n = 1,\dots ,N$. The figure also presents the impact of channel state estimation error that may be caused by estimation noise or outdatedness on the performance of the three heuristics. The estimation error model is similar to Wang and Lau [21] where the estimated channel coefficients are modelled as:

$$\begin{aligned} h^b_{\textit{mn}} = h_{\textit{mn}} + \Delta h_{\textit{mn}},\quad \forall (m,n) \in \{1, \dots , N\}^2 \end{aligned}$$

where $h_{\textit{mn}}$ is the actual channel coefficient and $\Delta h_{\textit{mn}}$ is the estimation error coefficient given by a complex Gaussian variable with zero mean and variance $\sigma ^2_{\Delta h}$. In Fig. 8, we consider a network composed of $N=12$, an interference threshold of $I_{\textit{th}} = 25 N_0$ and $\sigma ^2_{\Delta h} = 0$ (for the upper curves) or $\sigma ^2_{\Delta h} = 0.01$ (for the lower curves). We notice that for both values of $\sigma ^2_{\Delta h}$, the performance of the three heuristics increase as the transmit power gets larger. However, this increase saturates when $P^{\textit{max}}_n$ approaches 1W. In fact, the interference threshold imposed by the macro cell transmission prevents any performance improvement even when increasing the transmit SBS power. More precisely, at a $P^{\textit{max}}_n$ of 1W, the interference constraint is satisfied with equality and the power constraints are no longer active. Furthermore, as expected, Fig. 8 illustrates the high impact of an erroneous channel state estimation on the system performance. However, we notice that the shapes of the curves remain almost the same even with the presence of estimation errors. The performance degradation is generally due to intra-cluster interference induced by the error term $\Delta h_{\textit{mn}}$. This error impacts directly the channel inversion and prevents ZFBF from completely suppressing intra-cluster interference. Therefore, the results already presented in this section can be seen as upper bounds of the more practical model where imperfect channel state information is assumed.

Fig. 9

Average rate per user of NLF with localization estimation error

Figure 9 shows the impact of localization estimation errors on the performance of NLF when varying the number of SBSs in the network. We assume a simple error model where the erroneous coordinates of each SU n are modelled as $x^b_n = x_n + \Delta x_{n}$ and $y^b_n = y_n + \Delta y_{n}$, where $(x_n,y_n)$ are the actual coordinates of SU n and $\Delta x_{n}$ and $\Delta y_{n}$ are uniformly distributed variables taken in the interval $[-\Delta D,+\Delta D]$. As expected, algorithm NLF is sensitive to localization estimation errors since its decision relies on distances between SBSs and SUs. This sensivity becomes more important as the density of the network increases. Anyhow, the performance gap between the two curves in Fig. 9 is limited and stays below 3.5 % even for $N=12$.

Fig. 10

Execution time comparison for different values of N and $C_{\textit{max}}$

We compare in Fig. 10 the execution times of the three proposed heuristics to the exhaustive search algorithm execution time. We notice that the proposed algorithms have very similar execution times which are dominated by the time needed to perform the matrix channel inversion (which belongs to $O(N^3)$). We can also observe that even for a relatively small network with $N=10$, the exhaustive search algorithm suffers from a very high computational complexity. For $N=10$, the proposed heuristics allow a complexity reduction of more than five orders of magnitude over the exhaustive search. We also notice that as the value of $C_{\textit{max}}$ increases, the computational complexity of the exhaustive search increases dramatically as the algorithm has to explore a larger combinatorial space (e.g. when $C_{\textit{max}}$ goes from 2 to 3, the algorithm must consider in addition to the combinations of clusters of two links, the combinations of clusters of 2 and 3 links), whereas the complexity of the proposed algorithms decreases.

7 Conclusion

In this paper, we proposed efficient heuristics for clustering and power allocation in two-tier networks. We have considered a network where small cell base stations coexist and share the same frequency band with a macro cell. The small cell base stations try to form clusters in order to maximize an objective utility function. Two utility functions were considered: (1) the overall sum rate of the network and (2) the minimum data rate of the users. We have formulated the problems involving the two utility functions as optimization problems and discussed their computational complexity and hardness. Since the optimal solution can be found only with a highly computationally complex exhaustive search (for clustering) coupled with an $\textit{NP}$-hard optimization (for power allocation), we proposed three heuristic algorithms which perform the clustering phase in polynomial time and find suboptimal power allocation using an iterative scheme. Simulation results show that the proposed algorithms (especially the NLF heuristic) achieve a good tradeoff between computational complexity and performance (in terms of utility function maximization) compared to the complex optimal solution.

In future work, we will design distributed algorithms for clustering for the studied system model.