1 Introduction

Global warming is known as one of the most important threats for ecosystem services and human societies. There will be an increase in the unpredictability of water flows, linked to more frequent and extreme weather events and temporal and spatial shifts in rainfall patterns resulting in more intense floods and droughts, severe forest fires, rising sea levels, flooding, melting polar ice, catastrophic storms and declining biodiversity (Tsakiris and Loucks 2023). Precipitation is among major climatic variables that affects the hydrological regime with temporal and spatial variations. Extreme rainfall can lead to floods causing damage to buildings, farmlands, and infrastructures. Estimating future rainfall intensity is hence required in the optimal design of hydraulic structures as well as reducing the potential damage such disasters can cause (Hardy 2003).

The Intensity–Duration–Frequency (IDF) curves are widely used to capture rainfall characteristics.

The atlas of IDFs has been developed in developed countries like USA by the American National Weather Service created the National Oceanic and Atmospheric Administration (NOAA) (Perica et al. 2011). However, generating such curves in a desired area with no station is challenging and the application of regional curves instead of at-site has been suggested.

Several studies suggested that the application of regional techniques on extreme rainfalls can increasingly reduce the doubts about the estimations resulting from the at-site viewpoint (Lee and Maeng 2003; Alemaw and Chaoka 2016; Abdi et al. 2017; Mahmoudi et al. 2023). In addition, the IDF regionalization is useful in shortening the steps and required time for the calculations of the IDF curves. (Mahmoudi et al. 2023).

In the recent decades, extreme events have intensified due to global warming and human impacts (Tramblay et al. 2012; Cavanaugh et al. 2015; Xu et al. 2015). Numerous investigations indicated a significant increase in extreme precipitation over North America (Westra et al. 2014; Asadieh and Krakauer 2015), which has caused substantial structural and economic damages. Other studies reported increased extreme precipitation in Africa, Europe, and Asia (Lenderink and Van Meijgaard 2008; Singh et al. 2014; Jamali et al. 2022; Motamedi et al. 2023).

Given the importance of considering climate change and future trends in the design and construction of infrastructure, it is vital to consider the trends and nonstationary to improve the design parameters and minimize the anticipated damages to human societies (Li et al. 2018; Vasiliades et al. 2015). Therefore, a shift from stationary to nonstationary-based IDF curves is vital to capture non-monotonic trends in extreme precipitation (Veneziano and Yoon 2013; Cheng, and AghaKouchak 2014; Blanchet et al. 2016; Agilan and Umamahesh 2016).

Agilan and Umamahesh (2016) applied a multi-objective genetic algorithm (MOGA) to develop nonstationary GEV models by capturing nonlinear trends in the series. Using Bayesian inference, Ragno et al. (2019) presented a generalized framework for estimating nonstationary IDF curves and their uncertainties.

As in-site rainfall observations are sparse and have insufficient record length, the nonstationary IDFs should be regionalized to address these gaps in many regions around the world. Most of the earlier studies were focused on stationary regional IDF (Overeem and Syvitski 2010) and nonstationary IDF (Lima et al. 2016, Sarhadi and Soulis 2017), while investigations on developing regional nonstationary IDFs are generally lacking.

In this study, we developed regional nonstationary IDF curves by employing non-stationarity and clustering principles. The process-informed nonstationary extreme value analysis was applied to develop a newly-developed hybrid evolution Markov Chain Monte Carlo (MCMC) approach for numerical parameters estimation and uncertainty assessment. (Ragno et al. 2019). The present study applies a Neural Gas Network (NGN) method to cluster the hydrological data and ascertain the homogeneous regions. The NGN is one of the competitive neural networks and uses an unsupervised teaching method (Fritzke 1995). This study aims to develop regionalized nonstationary IDF curves by integrating NGN and ProNEVA as a new framework named NGN-ProNEVA. The proposed framework can describe the changes in annual maximum precipitation in response to CO2 emissions in the atmosphere and annual maximum sea levels over time.

2 Study Area

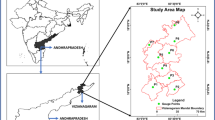
Khuzestan province is located between 47°41´ to 50°39´ eastern longitude and 29°58´ to 33°04´ northern latitude. Despite having only 4% of the Iran's total area, this province owns more than 30% of the country's surface water. The annual rainfall of the study area is 284.3 mm. The highest rainfall is recorded in Izeh station (Northeast of the province), with 614.8 mm. Khuzestan province is surrounded from the north and east by the Zagros Mountain range. Moving towards the interior of the province, the height of these mountains decreases and gives its place to the Mahor hills. Khuzestan includes two mountainous and plain regions. Two-fifths of the area of this province is mountainous, and three-fifths is plain.

3 Dataset

This study used data from 18 rain gauge stations located in Khuzestan province, Iran (Fig. 1). The data was obtained from the Khuzestan Water and Electricity Organization (KWEO). The hourly rainfall data from 1978 to 2015 were obtained to quantify the changes in the selected stations. All the selected stations consider as automatic recording stations. In addition, geographical information of the selected stations including latitude, longitude, elevation from sea level were applied to determine the number of optimal clusters (Table 1).

Fig. 1
figure 1

The study area overview and location of the selected stations

Full size image
Table 1 Characteristics of selected stations in this study
Full size table

4 Methodology

The main steps of this study include: (1) quantifying the trends in extreme precipitation of the selected stations; (2) determining the optimal number and clustering the stations; (3) defining GEV nonstationary models and select the best model; (4) developing Nonstationary IDF Curves for target clusters; (5) extracting regional stationary IDF curves. To extract the annual maximum rainfall time series for the region, the maximum rainfall for all duration and each year was extracted here to consider the same years in the stations belonging to each region,. Then, the model with the highest frequency among all duration was considered as the best one for the station.

4.1 Trend Analysis

The Mann Kendal (M–K) test (Mann 1945; Kendall 1962) is a nonparametric statistical test to detect trends in time series, that has a long tradition of application in hydrology and has been applied in the case of extremes (Villarini et al. 2009; Cheng and AghaKouchak 2014; Jamali et al. 2022; Gohari et al. 2022; Motamedi et al. 2023). The power of the M–K test depends on the pre-assigned significance level, the magnitude of the trend, the sample size, and the number of variations within the time series (Yue et al. 2002).

The M–K statistics (S) is computed as:

$$\mathrm{S}=\sum_{i=1}^{N-1}\sum_{j=i+1}^{N}sgn({x}_{j}-{x}_{i})$$
(1)

where, \(n\) is the number of data points, \(x\) is the data values in time series and the \(sgn\) function is defined as:

$$\mathrm{Sgn}\left(\uptheta \right)=\mathrm{sg}n \left({x}_{j}-{x}_{i}\right)=\left\{\begin{array}{cc}-1& \theta <0\\ 0& \theta =0\\ 1& \theta >0\end{array}\right\}$$
(2)

The standard value of the test statistics (\(Z\)) can be calculated as:

$$\mathrm{Z}=\left\{\begin{array}{cc}\frac{s-1}{\sqrt{var(s)}}& s>0\\ 0& s=0\\ \frac{s+1}{\sqrt{var(s)}}& s<0\end{array}\right\}$$
(3)

where, the \(var\) (variance) is computed as:

$$var(s)=\frac{n(n-1)(2n+5)-\sum_{i=1}^{p}{t}_{i}({t}_{i}-1)(2{t}_{i}+5)}{18}$$
(4)

where \(p\) is the number of tied groups and \({t}_{i}\) is the number of data in the \({i}^{th}\) (tied) group. Negative Z values indicate the decreasing trends while positive values show the increasing trends. This study applied the M–K test at 95% and 90% confidence levels to detect trends in the intensity of annual maximum rainfall over the selected durations.

4.2 Clustering

4.2.1 The Number of Optimal Clusters

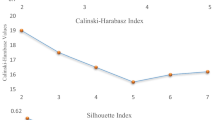
. Determining the number of optimal clusters is the first step in regionalization. Numerous methods, including Chou & Su CS (Chou et al. 2004), Silhouette (Rousseeuw 1987), and Caliński and Harabasz (1974) indices, have been widely used to determine the optimal number of clusters. The highest values in Silhouette and Calinski-Harabasz indices and the lowest one in CS indicate the optimal number of clusters.

The silhouette value calculates how similar an object is to its cluster (cohesion) compared to other clusters (separation). The silhouette ranges from − 1 to + 1, where a high value denotes that the object is well matched to its cluster and inadequately matched to neighboring clusters. The clustering configuration is appropriate if most objects have a high value. The silhouette can be calculated with any distance metric, such as the Euclidean or Manhattan distances (Rousseeuw 1987).

The Calinski-Harabasz (\(CH\)) index for \(K\) number of clusters on a dataset \(D =[ {d }_{1},{ d}_{2} ,{ d}_{3} , \dots {d}_{N} ]\) is defined as,

$$CH=\left[\frac{\sum_{k=1}^{K}{n}_{k}{\Vert {c}_{k}-c\Vert }^{2}}{K-1}\right]/\left[\frac{\sum_{k=1}^{K}{\sum }_{i=1}^{{n}_{k}}{\Vert {d}_{i}-{c}_{k}\Vert }^{2}}{N-K}\right]$$
(5)

where, \(nk\)  and \(ck\)  are the number of points and centroid of the kth cluster respectively, \(c\) is the global centroid, \(N\) is the total number of data points.

The CS measure is then defined as

$$\mathrm{CS}= \frac{\frac{1}{k}\sum_{i=1}^{k}[ \frac{1}{{N}_{i}}\sum_{{x}_{i}\in {C}_{i} }\,{max}_{{x}_{q}\in {C}_{i}} \{d({x}_{i}.{x}_{q})\} ]}{\frac{1}{k}\sum_{i=1}^{k}[{min}_{ j\in k. j\ne i }\{d({m}_{i}.{m}_{j})\} ]}=\frac{\sum_{i=1}^{k}[\frac{1}{{N}_{i}}\sum_{{x}_{i}\in {C}_{i} }\,{max}_{{x}_{q}\in {C}_{i}} \{d({x}_{i}.{x}_{q})\} ]}{\sum_{i=1}^{k}[{min}_{j\in k. j\ne i }\{d({m}_{i}.{m}_{j})\} ]}$$
(6)

where \(d\left({x}_{i}.{x}_{q}\right)\) is a function of the distance between two points in the \(i\) cluster, \(k\) is the number of clusters, \({N}_{i}\) is the number of members in each cluster, and \({m}_{i}\) is the center of each cluster.

4.2.2 Neural Gas Network (NGN)

In this study, the selected stations were divided into homogenous regions using NGN. The rule of learning in NGN is as follows:

$${w}_{i}^{new}={w}_{i}^{old}+{\alpha }_{i}(x-{w}_{i}^{old})$$
(7)
$${\alpha }_{i}=\varepsilon {e}^{\frac{{-k}_{i}}{\lambda }}$$
(8)

where \({w}_{i}\) is a gas molecule formed on data space (the number of these molecules is initially assumed as a value, and eventually, it is revised to have the logical and optimal function of the algorithm); \({\alpha }_{i}\) is a parameter that specifies the learning rate and depends on \({k}_{i}\), and \(\lambda\); \({k}_{i}\) refers to the superior neuron to the neuron \(i\); \(\varepsilon\) is a constant number that controls the learning rate. If λ tends to infinity, learning of the whole neurons would be equal, and if it tends to zero, then the nearest neuron begins to learn. The extreme modes of λ are not suitable alone, and usually, a mode between them is chosen.

An edge function is defined to create a neighborhood between the first and second neurons in terms of proximity. For each neuron, there is \({c}_{i.j}\epsilon \left\{0.1\right\}\) showing that weather there exists an edge or not. The \({t}_{i.j}\epsilon \left\{0.1.2\dots .\right\}\) also indicates the age (time intervals) from the last meeting or re-edge, if it exceeds more than one size, the neighborhood will be broken. This approach helps the neural network to learn topology. Generally, the NG algorithm can be summarized as: (Step-1) creation of A random position (\({w}_{i}\)) in the data space; (Step-2) selection of an input (x) from the expected data; (Step-3) calculation of the distance between x, and the centers of \({w}_{i}\) and \({k}_{i}\) aging for each center; (Step-4) Adaption or learning step as Eq. (9):

$${w}_{i}^{new}={w}_{i}^{old}+\varepsilon {e}^{\frac{{-k}_{i}}{\lambda }}(x-{w}_{i}^{old})$$
(9)

As the algorithm progresses, the learning speed should be reduced during the training period; otherwise, the neural network will be repeated leading to an incorrect cycle. For this purpose, the amount of \(\lambda\) and \(\varepsilon\) should be decreased as learning progresses according to Eq. (10):

$$\mathrm{G}\left(\mathrm{t}\right)={G}_{i}{\left(\frac{{G}_{f}}{{G}_{i}}\right)}^{\frac{t}{{t}_{max}}}\quad\quad{\lambda }_{i}>{\lambda }_{f},{\varepsilon }_{i}>{\varepsilon }_{f},{T}_{i}<{T}_{f}$$
(10)

where \(i\) and \(f\) show the parameter values at the beginning and the end of the learning process, respectively.

Afterwards, an edge between the first two ranks in terms of proximity and age of this edge is considered equal to zero (create a neighborhood) as Step-5. By increasing the age of all edge (\({t}_{i.j}\to {t}_{i.j}+1\)), it is assumed that \({k}_{i}=0\) and for each j when \({t}_{i.j}>T\), it is considered as \({c}_{i.j}=0\).T should be increased during the learning period to reduce the degree of rigidity, which means the edges are allowed to last longer (Step-6). If the termination conditions (e.g., the maximum quantity of neurons or any amount of performance) are not met, Step-2 is repeated, Otherwise, algorithm would be finished.

4.2.3 L-Moments

L-moments were presented by Hosking (1990), and it has been found to have great application in many regional hydro-climatic analyses. The most crucial applications of L-moments include identifying the homogeneous regions, detecting the discordant sites, and selecting the appropriate distribution function over a larger range of distributions.. They also better display the outlier events (Rao and Hamed 1997). L- moments were used here to check regional homogeneity and discordant stations and determine appropriate regional distribution.

4.3 Nonstationary IDF Curves

The time series of extreme rainfall intensity in various durations were formed based on annual maxima throughout the record. According to the extreme value theory, the behavior of these annual maxima values can generally be described by one of the three extreme value distributions, including Gumbel, Fréchet, and Weibull. The generalized extreme value (GEV) distribution, a single parametric family, represents those mentioned above three extreme distributions (Agilan and Umamahesh 2016). The cumulative distribution function of the GEV is described (Hosking and Wallis 1993) as Eq. (11):

$${F}_{GEV}\left(x|\mu ,\sigma ,\xi \right)=exp\left[{-\left(1+\xi \left(\frac{x-\mu }{\sigma }\right)\right)}^{\frac{-1}{\xi }}\right]$$
(11)
$$F_{GEV(x)}\;\mathrm{is\;defined\;for}\;\{\mathrm{x}:\;1+\upxi(\mathrm{x}-\upmu)/\upsigma>0\},\;-\infty<\upmu<\infty,\upsigma>0,\;\mathrm{and}\;-\infty<\upxi<\infty$$

where: \(\mu\), \(\sigma\), and \(\xi\) are the location, scale, and shape parameters, respectively (Smith 2001). Under stationary assumption, it is assumed that the GEV parameters, θ = {μ, σ, ξ}, are not changing over time. However, the parameters and characteristics of the GEV distribution become time-dependent under nonstationary conditions. To integrate the nonstationary effects, the nonstationary GEV model is defined by considering its parameters as a covariate of time (\({x}_{t}\)|\({\mu }_{t}\), \({\sigma }_{t}\), ~GEV (\({\mu }_{t}\), \({\sigma }_{t}\), ξ)):

$${f}_{{x}_{t}}\left({x}_{t}|{\mu }_{t},{\sigma }_{t},\xi \right)={\frac{1}{{\sigma }_{t}}\left[1+\xi \left(\frac{{x}_{t}-{\mu }_{t}}{{\sigma }_{t}}\right)\right]}^{-\frac{1}{\xi }-1}exp\left[{-\left(1+\xi \left(\frac{{x}_{t}-{\mu }_{t}}{{\sigma }_{t}}\right)\right)}^{-\frac{1}{\xi }}\right]$$
(12)

According to the Eq. (12), different nonstationary models were defined in this study to capture the non-stationarity in rainfall characteristics over the case study (Table 2).

Table 2 The defined nonstationary GEV models
Full size table

4.3.1 Parameter Estimation

In this study, the ProNEVA was applied to estimate the parameters of the extreme value distribution under both stationary and non-stationary assumptions using a Bayesian method, to address uncertainties derived from input errors and model selection.

A Bayesian Markov Chain Monte Carlo (BMCMC) approach was applied to characterized the uncertainty of time-varying IDFs. More information about BMCMC can be found in Gilks et al. (1995).

4.3.2 Model Diagnostics and Selection

We applied different metrics for Goodness Of Fit (GOF) assessment and model selection, including quantile and probability plots as a visual assessment along withthe Akaike Information Criterion (AIC) and Bayesian Information Criterion (BIC). The AIC (Akaike 1974; Aho et al. 2014) is formulated as Eq. (13):

$$AIC=2.\left(D-\widehat{L}\right)$$
(13)

where \(D\) is the number of parameters in the statistical model and \(\widehat{\text{L}}\) is the log-likelihood function evaluated at the vector of parameters. The BIC (Schwarz 1978) is also defined as:

$$BIC=D.\mathrm{ln}\left(N\right)-2.\widehat{L}$$
(14)

where \(N\) is the length of records. The model associated with a lower AIC and BIC is considered as a better fit.

5 Results and Discussions

5.1 Trend Analysis

In order to investigate the trends in the study area, all 18 stations and 11 selected durations were studied using the M–K test. Due to the negative values of Z for most time series in different stations (Table 3), it can be declared that the rainfall trend in short durations is decreasing over the study area.

Table 3 The z value for detecting trends in different time series at 90% and 95% confidence levels
Full size table

Khuzestan Province is one of the most water-rich provinces in Iran, where large rivers flow. Therefore, its water resources planning and management should be updated according to the effects of climate change. According to the results, the trend of rainfall in the most of the time duration in this region has decreased, leading to a negative effect on available water resources. Jamali et al. (2022) reported that most stations throughout Iran showing drying features with higher temperatures, which is in agreement with the presented results. Generally, most regions over Iran implied a reduction in the annual precipitation.

Due to the detected tendency in the precipitation during the different durations, extracting the IDF curves based on the nonstationary assumption is essential. Although most of the durations do not have significant trends, the recent studies highlight the need to go beyond subjective criteria for significance analysis (Rosner et al. 2014), as most ground-based stations do not exhibit a statistically significant non-stationary behavior (Westra et al. 2014; Cheng and AghaKouchak 2014).

5.2 Clustering of Rainfall Stations

Figure 2 shows the number of optimal clusters in a range of clusters. The results indicated that the optimal number of homogeneous regions under all three methods was equal to 2.

Fig. 2
figure 2

The numbers of optimal clusters under different methods a Calinski-Harabasz, b CS, and c Silhouette Index

Full size image

In this study, rainfall station clustering was performed using NGN based on the optimal number of clusters. Figure 3 shows the results of clustering the study area into two separate regions. Region 1 occupied the eastern areas, and region 2 occupied the central and western parts of the province. The results revealed that the stations with the higher altitudes in the eastern cluster and the lower stations in the western cluster were divided into separate clusters, which confirms the proper functioning of NGN in terms of topographic detection of the data space. The results of our study.

Fig. 3
figure 3

Location of stations in the cluster identified by NGN and K-means

Full size image

5.3 Nonstationary Models

According to Table 4, the best regional nonstationary model was M2 in the case of using time covariate and M5 in the case of using CO2 covariate for both homogenous regions. The scale parameter was variable in both selected models, and the location and shape parameters were constant.

Table 4 The best regional model in each region and Validation of the regional model in stations
Full size table

The uncertainty in the risk estimation of extreme precipitation in different durations because of replacing model M2 with M1 to capture non-stationarity for regions one and two are demonstrated in Fig. 4, respectively. The results showed that with an increasing return period, the values of uncertainty also increased, which is expected. As illustrated in Fig. 4, the uncertainty of ignoring M2 with M1 with a range of confidence level equal to 95 percent in region one and 85 to 95 percent in region two.

Fig. 4
figure 4

a Uncertainty of ignoring M2 with M1 with a confidence level of 95% b Uncertainty of ignoring M2 with M1 with a confidence level of (60 and 360 min; 90%, 720 min; 85%, and 1080 min; 95%)

Full size image

The uncertainty indicates that the M2 model, constructed by the scale parameter as a covariate in the GEV parameters, can capture non-stationarity effects. Gao et al. (2016) conducted a nonstationary extreme value analysis for annual maximum daily precipitation (AMP) at 631 meteorological stations over China for the period 1951–2013. They showed that the nonstationary GEV distributions performed better than their stationary equivalents. Likewise, Dixit and Jayakumar (2022) indicated that non-stationary analysis will be helpful in the accurate estimation of the drought characteristics under climate change.

To validate the results for each region, the selected model was examined for each station belonging to the homogenous regions and compared with the regional results. The results indicated that the best regional model for region one was considered the best-fitted model for all stations. However, the best regional model was M2, but the best model in some stations was considered M1 in region II (Table 4).

Comparing Fig. 4 with Table 4, it is apparent that the 95% confidence level for Region I and the average 90% confidence level for Region II are reasonable. Because in all Region I stations, the best model is M2, but for some stations in Region II, the best model is M1.

5.4 IDF Curves

The developed nonstationary and stationary IDF curves were extracted under different return periods and durations for both regions. It should be noted that the developed IDFs using time and CO2 covariates were similar. This indicates that the effect of CO2 concentration on rainfall intensity was not significant in the study area. However, it is crucial to study the effect of CO2 on rainfall intensity in different climate characteristics. The results showed that the nonstationary IDF curves have consistently overestimated precipitation values compared to the stationary curves (Figs. 5 and 6). The overestimation of nonstationary curves could be attributed to the decreasing trend in rainfall over the study area. Since, this detected trend was not considered in the stationary curves. The overestimation of regional nonstationary curves compared to the corresponding at-site nonstationary curves could be also due to the difference in climate characteristics and topography between the regions.

Fig. 5
figure 5

a Overestimation values of regional nonstationary compared to the registationary method in region 1. b Overestimation values of regional nonstationary compared to the regional stationary method in region 2

Full size image
Fig. 6
figure 6

The developed stationary and nonstationary IDF curves for return periodes of 2,10,20,50 and 100 years in Ahvaz station

Full size image

In addition, the differences between nonstationary and stationary curves were notable in the lower return period, while this difference was reduced with increasing the return periods, indicating that the nonstationary approach is more important for short-duration events. Ganguli and Coulibaly (2017) investigated non-stationarity and trends in the short-duration precipitation extremes in selected urbanized locations in Southern Ontario, Canada. They reported that the stationary vs. nonstationary models do not exhibit any significant differences in the design storm intensity despite apparent signals of non-stationarity in precipitation extremes in all locations. Yang et al. (2020) reported that rainfall depth under non-stationarity was greater for return periods less than 10 years, however, the stationary rainfall depth was higher when the return period was over 20 years.

The regional nonstationary curves had overestimated rainfall intensity compared with the corresponding in-site nonstationary curves. The regional stationary curves, on the other hand, provided more accurate estimates for the study area, which indicates the importance of considering the local characteristics in developing IDF curves.

Although the regional stationary curves are, in some cases, underestimated the values of their corresponding stationary at-site curves, their differences were insignificant. In contrast, the difference between stationary and nonstationary IDF curves decreased over higher return periods. This could be because higher return periods represent rare events that are less affected by short-term climate variability and more influenced by long-term climate trends, which are better captured by stationary curves. The average values of overestimation (regional nonstationary and regional stationary) in the return period of 2 years is equal to 50 percent, in the return period of 100 years is equal to 25 percent in region two, and in region one is equal to 20 and 43 percent, respectively (Fig. 5). The difference between the two regions is not considerable. However, the existing difference can be caused by the lower uncertainty in region one and the climate characteristics and topography between the regions. The difference between stationary and nonstationary IDF curves decreased over higher return periods. This could be because higher return periods represent rare events less affected by short-term climate variability and more influenced by long-term climate trends, better captured by stationary curves. This exactly corresponds to the result of Mohan et al. (2023). They demonstrated higher levels of non-stationarity were observed in Coastal regions and Eastern parts of India compared to the central parts. Also, the comparison of spatial patterns of rainfall intensity estimates under stationary and nonstationary showed that about 23% of grids showed an overestimation of nonstationary rainfall over their stationary counterparts by at least 15%. The nonstationary curves still show higher estimates, which will increase confidence in applying these curves in hydrological studies.

6 Conclusions

The intensity–Duration–Frequency (IDF) curve is one of the most popular tools in water resources engineering, which can be utilized as an input in designing, planning, and exploiting water resources projects. One of the fundamental problems in many countries is the scattered or inadequate networks of the required meteorological stations such that their data are considered the main bases for IDF construction. This study applied a new model of NGN and nonstationary concepts to develop the regional IDF curves. For this purpose, taking into account the characteristics of longitude, latitude, average annual rainfall, altitude, and maximum 24-h annual rainfall for each station, and using three indicators and CS, Silhouette, and Calinski-Harabasz(CH), the Khuzestan Province was clustered into two separate and possibly homogenous regions.

Regional IDF curves have been proposed based on the stationary concept in the studies published. In this research, we confirmed that most of the stations across the Khuzestan Province exhibited a nonstationary condition, so extreme rainfalls with different durations were significantly affected. The results indicated that the nonstationary IDF curves have consistently overestimated precipitation values compared to the stationary curves due to to the decreasing trend in rainfall over the study area. The difference between stationary and nonstationary IDFs decreased over higher return periods. This could be because higher return periods represent rare events that are less affected by short-term climate variability and more influenced by long-term climate trends, which are better captured by stationary curves.