A Novel Hybrid Method for River Discharge Prediction

Abstract

Accurate prediction of river discharge is essential for the planning and management of water resources. This study proposes a novel hybrid method named HD-SKA by integrating two decomposition techniques (termed as HD) with support vector regression (SVR), K-nearest neighbor (KNN) and ARIMA models (combined as SKA) respectively. Firstly, the proposed method utilizes local mean decomposition (LMD) to decompose the original river discharge series into sub-series. Next, ensemble empirical mode decomposition (EEMD) is employed to further decompose the LMD-based sub-series into intrinsic mode functions. Further, the EEMD decomposed components are used as inputs in three data-driven models to predict river discharge respectively. The prediction of all components is then aggregated to obtain the results of HD-SVR, HD-KNN and HD-ARIMA models. The final prediction is obtained by taking the average prediction of these models. The proposed method is illustrated using five rivers in Indus Basin System. In five case studies, six models were built to compare the performance of the proposed HD-SKA model. The data analysis results show that the HD-SKA model performs better than all other considered models. The Diebold-Mariano test confirms the superiority of the proposed HD-SKA model over ARIMA, SVR, KNN, EEMD-ARIMA, EEMD-KNN, and EEMD-SVR models.

1 Introduction

The prediction of river discharge is essential for the planning and management of water resources. Hydrological data prediction provides critical information on the impending drought, heatwaves, or floods which brings devastation due to its delayed and inaccurate estimation (Sehgal et al. 2014). River discharge prediction has gained attention to handle extreme events as an outcome of climate changes. Different studies on river discharge have been studied in China (Wei et al. 2013), the USA (Meshram et al. 2019), Iran (Dehghani et al. 2021) and North America (Alizadeh et al. 2021). Thus, precise river discharge estimation is necessary to construct warning systems for water management to deal with extreme events (Wang et al. 2018; Adnan et al. 2021).

Data-driven models are used to predict hydrological variables such as inflow, out-flow and discharge. These include both statistical and artificial intelligence (AI) models. Statistical models for time series include Moving Average (MA), Autoregressive (AR), ARMA and Autoregressive Integrated Moving Average (ARIMA) models and others (Bayazit 2015; Fashae et al. 2019; Bonakdari et al. 2020; Musarat et al. 2021; Aghelpour et al. 2021). However, these models are unable to capture time changes with sufficient accuracy because of linear analysis phenomena. Nowadays, AI models are widely used to model complex and non-linear time series data. For example, K-nearest Neighbor (KNN), Support Vector Regression (SVR) and Artificial Neural Network (ANN) are popular models implemented in hydrological studies (Wu et al. 2008; Nikolic and Simonovic 2015; Poul et al. 2019; Sharghi et al. 2019; Riahi-Madvar et al. 2021). However, the drawback of AI models is that they do not incorporate noise and ignore the complex multi-scale structure of hydrological variables (Rezaie-Balf et al. 2019). Therefore, using a single model to predict river discharge is challenging. Researchers in the field of hydrology have introduced hybrid methods to improve the prediction accuracy of models. This study aims to overcome the limitations on the models application and proposes a new hybrid method that helps in the precise estimation of river discharge.

Many pre-processing techniques are integrated with data-driven models to create hybrid models for predicting hydrological variables. Some pre-processing methods such as Empirical Mode Decomposition (EMD), Local Mean Decomposition (LMD) and Ensemble EMD (EEMD) are combined with data-driven models to predict river discharge (Rezaie-Balf et al. 2019; Silva et al. 2021; Vidya and Janani 2021). In this study, the focus is on improving the prediction of river discharge by using hybrid pre-processing techniques.

In this study, a novel hybrid method is proposed by combining two pre-processing techniques with data-driven models. The two pre-processing techniques used are LMD and EEMD (abbreviated as HD) and three models applied are SVR, KNN, and ARIMA models (termed as SKA). Our proposed hybrid method uses LMD to decompose the original river discharge series into sub-series. Then, EEMD is applied to decompose the obtained sub-series into different components. The HD components are used as the inputs to SVR, KNN and ARIMA models. The predictions of these components are aggregated for HD-SVR, HD-KNN and HD-ARIMA models respectively. The final forecast of HD-SKA model is obtained by taking the average of these predictions. The effectiveness of the proposed hybrid method is illustrated on the discharge data of five rivers of Indus Basin System, Pakistan. The rivers include Kabul River, Kanshi River, Kunhar River, Jhelum River (Domel station) and Jhelum River (Chattar Kallas station). The superiority of the HD-SKA method is successfully presented on five data sets where six benchmark models are used to verify the performance of the proposed hybrid model. The HD-SKA method is novel based on the combination of hybrid decomposition with data-driven models which efficiently decomposes discharge series and capture its complex features with higher prediction accuracy.

2 Methodologies

2.1 Local Mean Decomposition (LMD)

Smith (2005) introduced LMD as a tool for analyzing the time–frequency of the electroencephalogram signal. LMD is a self-adaptive time–frequency approach that is useful in capturing non-linear features of data (Liu and Han 2014; Huynh et al. 2021). LMD decomposes a signal into several product functions ($PFs$) that have a physical meaning. The time–frequency distribution of the signal is obtained by assembling the instantaneous frequency and instantaneous amplitude of all the obtained $PFs$. Given the original signal $y(t)$, it is decomposed using the following steps:

• (i) Obtain the local extrema (${n}_{i}$) from $y(t)$ and then compute the average (${m}_{i}$) of the two successive extrema as follows:

  $${m}_{i}=\frac{1}{2}\left({n}_{i}+{n}_{i+1}\right)$$

  (1)

  All the mean values (${m}_{i}^{\prime}s)$ are connected through the straight lines and the local mean function ${m}_{11}(t)$ is formed by moving averaging which smooth the ${m}_{i}^{{\prime}}s$. 

• (ii) The envelope estimate (${a}_{i}$) is defined as follows:

  $${a}_{i}=\frac{1}{2}|{n}_{i}+{n}_{i+1}|.$$

  (2)

  The estimates of the local envelope are smoothed in similar ways as the local means to derive the envelope function ${a}_{11}(t)$.

• (iii) The ${m}_{11}(t)$ is subtracted from $y\left(t\right)$ which forms the resulting signal as ${h}_{11}(t)$:

  $${h}_{11}\left(t\right)=y\left(t\right)-{m}_{11}\left(t\right).$$

  (3)

• (iv) ${h}_{11}\left(t\right)$ is amplitude demodulated by dividing it by envelope function ${a}_{11}\left(t\right)$ which forms ${s}_{11}\left(t\right)$ given as:

  $${s}_{11}\left(t\right)=\frac{{h}_{11}\left(t\right)}{{a}_{11}\left(t\right)}.$$

  (4)

  The function ${s}_{11}\left(t\right)$ is the purely frequency modulated signal known as the envelope function ${a}_{12}\left(t\right)$ of ${s}_{11}\left(t\right)$ should satisfy the condition ${a}_{12}\left(t\right)=1$. If this condition is not satisfied, then ${s}_{11}(t)$ is regarded as the original signal and the above process is repeated until the purely frequency modulated signal (${s}_{1n}\left(t\right)$) is derived that satisfies $-1\le {s}_{1n}\left(t\right)\le 1$. Therefore,

  $$\left\{\begin{array}{l}h_{11}\left(t\right)=y\left(t\right)-m_{11}\left(t\right)\\h_{12}\left(t\right)=s_{11}\left(t\right)-m_{12}\left(t\right)\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\vdots\\h_{1n}\left(t\right)=s_{1\left(n-1\right)}\left(t\right)-m_{1n}\left(t\right)\end{array}\right.,$$

  (5)

  where $\left\{\begin{array}{c}{s}_{11}\left(t\right)={h}_{11}(t)/{a}_{11}(t)\\ {s}_{12}\left(t\right)={h}_{12}(t)/{a}_{12}(t)\\ \vdots \\ {s}_{1n}\left(t\right)={h}_{1n}(t)/{a}_{1n}(t)\end{array}\right..$

• (v) The envelope signal ${a}_{1}\left(t\right)$ known as instantaneous amplitude function is obtained by taking the product of the functions of successive envelope estimate which are obtained during the iterative procedure discussed above.

  $${a}_{1}\left(t\right)={a}_{11}\left(t\right){a}_{12}\left(t\right)\dots {a}_{1n}\left(t\right)=\textstyle\prod_{l=1}^{n}{a}_{1l}\left(t\right),$$

  (6)

  where $l$ denoted the times of iterative procedure.

• (vi) The first product function $(P{F}_{1})$ is obtained by taking the product of ${a}_{1}\left(t\right)$ with the purely ${s}_{1n}\left(t\right)$ i.e., $P{F}_{1}={a}_{1}\left(t\right){s}_{1n}\left(t\right).$ The instantaneous amplitude of $P{F}_{1}$ is ${a}_{1}\left(t\right)$ and the instantaneous frequency of $P{F}_{1}$ can be obtained from ${s}_{1n}\left(t\right)$ as:

  $${f}_{1}\left(t\right)=\frac{1}{2\pi }.\frac{d\left[\mathrm{arccos}\left({s}_{1n}\left(t\right)\right)\right]}{dt}.$$

  (7)

• (vii) The difference of $y(t)$ from $P{F}_{1}$ is obtained as the new resulting signal. The whole process is repeated $k$ times until ${u}_{k}\left(t\right)$ is monotonic or constant.

  $$\left\{\begin{array}{l}u_1\left(t\right)=y\left(t\right)-PF_1\left(t\right)\\u_2\left(t\right)=u_1\left(t\right)-PF_2\left(t\right)\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\vdots\\u_k\left(t\right)=u_{(k-1)}\left(t\right)-{PF}_k(t)\end{array}\right..$$

  (8)

  Up to this point. However, the original signal can be obtained by

  $$y\left(t\right)=\textstyle\sum_{q=1}^{k}P{F}_{q}\left(t\right)+{u}_{k}\left(t\right),$$

  (9)

where $q$ is the number of $PF$ and ${u}_{k}\left(t\right)$ represents the residual term. In this study, the LMD is applied in Python through Jupyter Notebook in Anaconda Navigator using “pyLMD” package.

2.2 Ensemble Empirical Mode Decomposition

In 1998, Huang introduced empirical mode decomposition (EMD) to analyze non-linear signals. In EMD, a signal is decomposed into intrinsic mode functions ($IMFs$). To become an $IMF$, a signal needs to satisfy two conditions (a) the average of lower and upper envelopes is zero everywhere and (b) The number of extremes and zero-crossing should be equal or differ at most by 1. However, EMD has a major issue of mode-mixing (Huang et al. 1998). To overcome the drawback of EMD, Wu and Huang (2009) introduced Ensemble empirical mode decomposition (EEMD) which has a noise-assisted system. The EEMD algorithm is given as follows:

• (i) Initialize the amplitude of added white noise ($w{n}_{j}(t)$) and ensemble number $N$ to the observed series $y(t)$. The ${j}^{th}$ noise-added signal is ${y}_{j}\left(t\right)=y\left(t\right)+w{n}_{j}\left(t\right)$.

• (ii) All the local minima and maxima of ${y}_{j}\left(t\right)$ are identified as lower and upper envelopes obtained by cubic spline functions.

• (iii) Compute the average of ${m}_{1}\left(t\right)$ lower and upper envelopes.

• (iv) Compute difference of ${y}_{j}(t)$ and average value ${m}_{j}(t)$ i.e., ${h}_{1}\left(t\right)={y}_{j}\left(t\right)-{m}_{1}\left(t\right).$

• (v) Check if ${h}_{1}\left(t\right)$ is the first $IMF$ component of the signal i.e., ${h}_{1}\left(t\right)={c}_{1}\left(t\right), {r}_{1}\left(t\right)$ is defined from the remaining data by ${r}_{1}\left(t\right)={y}_{j}\left(t\right)-{c}_{1}\left(t\right).$ Otherwise, steps (ii)-(v) are repeated.

To determine the residue (${r}_{1}\left(t\right)$) as a new signal, step (ii)-(v) should be repeated $n$ times until the sift out all the $IMFs$ till the stopping criterion is met. The stopping criteria occurs when the $IMF$ component or residue becomes so small that is smaller than the predetermined value. After the sifting processing, the original signal ${y}_{j}(t)$ can be determined as the sum of all the $IMFs$ and the residual error as follows:

$${y}_{j}\left(t\right)={\sum }_{k=1}^{n}{c}_{k}\left(t\right)+{r}_{n}\left(t\right),$$

(10)

where $n$ is the number of $IMFs$, ${c}_{k}\left(t\right)$ denotes the ${k}^{th}$ $IMF$ when adding ${j}^{th}$ noise and ${r}_{n}\left(t\right)$ denotes the final residual error.

2.3 Support Vector Regression (SVR)

The SVR is a widely applied supervised learning algorithm for regression and classification problems. SVR algorithm estimates the relationship between the output and input of a system using an existing sample (Vapnik 1995). Therefore, SVR is applied to model the non-linear and complex features of the river discharge series.

Suppose we have the training set with $n$ observations $\left\{{x}_{j},{y}_{j}\right\}$, where ${y}_{j}$ represents the estimated output value of the data, ${x}_{j}$ is the corresponding lagged input vector. Then, the SVR is developed as follows:

$$g\left(x\right)={w}^{T}\Phi \left(x\right)+b,$$

(11)

where $w$ is the weights vector, $b$ is a constant which represents the bias and $\Phi \left(x\right)$ is the non-linear transfer function applied to project the input data into high dimensional space. Using the structural approach of risk minimization, Eq. (11) is solved as follows:

$$\mathrm{Minimize}:\left(\frac{\left|\left|{w}^{2}\right|\right|}{2}+C\textstyle\sum_{j=1}^{n}(\zeta +{\zeta }^{*})\right)\mathrm{ subject\;to}: \left\{\begin{array}{c}g\left({x}_{j}\right)-{y}_{j}\le \varepsilon +{\zeta }^{*}\\ {y}_{j}-g\left({x}_{j}\right)\le \varepsilon +\zeta ,\\ \zeta ,{\zeta }^{*}\ge 0\end{array}\right.$$

(12)

where $C>0$ denotes the penalty parameter, ${\zeta }^{*}$ and $\zeta$ represent the slack variables which denotes the lower and upper constraint of $g(x)$ and $\varepsilon$ represents the insensitive loss function. The Lagrangian function is further implemented which uses the regression function to replace the $\Phi \left(x\right)$ and weight vector given in the Eq. (11) as:

$$g\left({x}_{j}\right)=\textstyle\sum_{j=1}^{n}\left({\alpha }_{j}-{\alpha }_{j}^{*}\right)k\left(x,{x}_{j}\right)+b,$$

(13)

where ${\alpha }_{j}$ and ${\alpha }_{j}^{*}$ are the Lagrange coefficients and $k\left(x,{x}_{j}\right)=\langle \Phi \left(x\right), \Phi \left({x}_{j}\right)\rangle$ denotes the kernel function. There are different forms of kernel functions such as linear and radial basis. However, the choice of kernel depends upon the nature of the data. In this study, the SVR algorithm is implemented in R programming language using “e1071” package.

2.4 K-Nearest Neighbor (KNN)

Cover and Hart (1967) introduced the KNN algorithm as a non-parametric method for pattern recognition work. The KNN algorithm also has a good approximation ability for non-linear dynamics and is used for time series prediction (Martinez et al. 2018; Al-Juboor 2021). Thus, it is utilized as an efficient tool to capture non-linear dynamics of river discharge in this study.

The KNN algorithm calculates the similarity (neighborhood) of the input variables ${X}_{o}=\left\{{x}_{1o},{x}_{2o},\dots ,{x}_{no}\right\}$ with historical observations of the input variable ${X}_{t}=\left\{{x}_{1t},{x}_{2t},\dots ,{x}_{nt}\right\}$ using Euclidean distance function (${D}_{ot}$) which is given by (Araghinejad 2013):

$${D}_{ot}=\sqrt{\textstyle\sum_{j=1}^{n}{\left({x}_{jo}-{x}_{jt}\right)}^{2}}, t=\mathrm{1,2},\dots ,n.$$

(14)

The predicted variable (${Y}_{o}$) is computed by using the probabilistic function of the observed values of discharge series (${T}_{p}$):

$${Y}_{o}=\textstyle\sum_{p=1}^{K}f\left({D}_{op}\right)\times {T}_{p},$$

(15)

where $f\left({D}_{op}\right)$ denotes the kernel function of the KNN computed by using the distance (${D}_{op}$):

$$f\left({D}_{op}\right)=\frac{1/ {D}_{op}}{\sum_{p=1}^{K}\left(1/{D}_{op}\right)}.$$

(16)

The main parameter of KNN algorithm is $K$, finding an optimal value of $K$ is a practical problem. In this study, the optimal value of $K$ is computed by using metrics through the “caret” package in R.

2.5 Autoregressive Integrated Moving Average (ARIMA) Model

ARIMA model is a simple method for predicting a time series. ARIMA model is applicable for both non-stationary and stationary time series, which makes it an efficient model for predicting the uncertainty of river discharge (Wang et al. 2018). Thus, ARIMA model is used to predict river discharge which has uncertainty with time changes. Let ${y}_{t}$ be the time series and ${\varepsilon }_{t}$ represent the random error at time $t$. Then ${y}_{t}$ is considered to be the linear function of past $p$ observations ${(y}_{t-1},{y}_{t-2},\dots , {y}_{t-p})$ and $q$ random errors ${(\varepsilon }_{t}, {\varepsilon }_{t-1},$…, ${\varepsilon }_{t-q}$). The corresponding ARIMA model is given as:

$${y}_{t}={\theta }_{1}{y}_{t-1}+{\theta }_{2}{y}_{t-2}+\dots +{\theta }_{p}{y}_{t-p}+{\varepsilon }_{t}-{\beta }_{1}{\varepsilon }_{t-1}-{\beta }_{2}{\varepsilon }_{t-2}-\dots -{\beta }_{q}{\varepsilon }_{t-q},$$

(17)

where ${\theta }_{j}(j=\mathrm{0,1},2,\dots ,p)$ are the autoregressive coefficients, ${\beta }_{j}\left(j=\mathrm{0,1},2,\dots ,q\right)$ are the moving average coefficients and ${\varepsilon }_{t}$ is identically distributed with zero mean and constant variance. Similar to parameter $d$, the coefficients $q$ and $p$ are referred as the order of the ARIMA model. The main issue of ARIMA model is the determination of the appropriate order of ($p,d,q$) which is determined using correlation tools i.e., autocorrelation function (ACF) and partial ACF (Box et al. 2008).

3 Proposed Hybrid Modelling Method

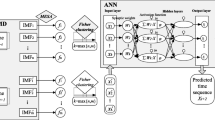
In this study, a novel hybrid method is proposed to enhance the forecasting accuracy of hydrological data. The hybrid method proposed in this study is shown in Fig. 1.

Fig. 1

Proposed Hybrid Method (HD-SKA)

The steps of the proposed hybrid method are described as follows:

• (i) The LMD algorithm is applied to decompose the original river discharge series into several product functions ($PFs$) and residual.

• (ii) The EEMD is employed to decompose the sub-series obtained in step (i). In this step, each component obtained by LMD is further decomposed into $IMFs$ and residual.

• (iii) The SVR, KNN and ARIMA models are applied to predict each $IMF$ and residual component obtained in step (ii).

• (iv) The predictions of all components is aggregated for HD-SVR, HD-KNN and HD-ARIMA models.

• (v) The average of the predictions obtained from HD-SVR, HD-KNN and HD-ARIMA models is the final prediction of the river discharge series.

4 Case Studies

In this section, the description of data and the index measures used for evaluation are provided. Program codes were written in R and Python programming language version 4.0.3 and 3.7, respectively. All the analyses were performed on a personal computer with Intel Core i9-9900 CPU and 32.0 GB of RAM.

4.1 Data Description

In this study, the discharge data of different rivers in Indus Basin System has been collected which is used for the thorough evaluation of the performance of the proposed hybrid method. The data is collected for five rivers i.e., Jhelum River (Chattar Kallas station), Jhelum River (Domel station), Kabul River (Nowshera station), Kunhar river (Talhata station) and Kanshi River (Palotte station). The daily river discharge data is obtained from the Surface Water Hydrology Project agency of Water and Power Development Authority (WAPDA) Pakistan with different hydrological periods given in Table 1.

Table 1 Hydrological stations details and descriptive summary

The river discharge series (m³/s) is denoted by S_i for i = 1, 2, 3, 4 and 5 for Jhelum River (Chattar Kallas station), Jhelum River (Domel station), Kabul River, Kunhar river and Kanshi river respectively. Initially, the data cleaning procedure was performed on the five data series and the missing values were replaced by the average discharge of the month. In Table 1, the descriptive summary of the river discharge is given. It shows that on average the discharge was highest in S₁. The standard deviation (SD) of discharge is 564.13 m³/s, 210.66 m³/s, 750.68 m³/s, 85.18 m³/s and 9.31 m³/s in S₁, S₂, S₃, S₄ and S_5, respectively. The shape of discharge of all rivers is positively skewed.

Figure 2b represents the box plot of discharge of five rivers. There is an evident difference between the discharge of rivers. The discharge of S₅ is relatively low as compared to other rivers (S₁-S₄). In Fig. 2b, some unusual discharge records are in all rivers that indicate a sign of water overflow in these rivers that is a hydrological hazard and needs proper exploration to avoid floods.

Fig. 2

(a) Pakistan Rivers Network (b) Box plot of original river discharge series (S₁-S₅)

Figure 3 represents the time series plot of river discharge. It shows that the river discharge in all cases is non-linear, volatile and has huge variability during the given years. The discharge series (S₁-S₅) is divided into the training and testing sets. The first 80% observations are used as the training set and the last 20% observations are used as the testing set.

Fig. 3

Original River Discharge series (S₁-S₅)

4.2 Evaluation Indexes

The root mean square error (RMSE), mean absolute error (MAE) and root-relative square error (RRSE) are adopted to evaluate the prediction performance of models. Several researchers have used these indicators e.g., Rezaie-Balf et al. (2019). These measures are defined as follows:

$$RMSE=\sqrt{\frac{1}{m}\textstyle\sum_{j=1}^{m}{\left({y}_{j}-{\widehat{y}}_{j}\right)}^{2}},$$

$$MAE=\frac{1}{m}\textstyle\sum_{j=1}^{m}|{y}_{j}-{\hat{y}}_{j}|,$$

$$RRSE=\sqrt{\frac{{\textstyle\sum }_{j=1}^{m}{\left({y}_{j}-{\hat{y}}_{j}\right)}^{2}}{{\textstyle\sum }_{j=1}^{m}{\left(\bar{\hat{y} }-{\hat{y}}_{j}\right)}^{2}}},$$

where ${y}_{j}$ represents the actual value, ${\hat{y}}_{j}$ represent the predicted value, $\bar{\hat{y} }$ is the mean of predicted values and $m$ is the total number of observations in the considered case. To further evaluate the performance of models, the improved percentage indicators of RMSE, MAE and RRSE are used in this study. These are defined as follows:

$${P}_{RMSE}=\frac{RMS{E}_{1}-RMS{E}_{2}}{RMS{E}_{1}}\times 100\%,$$

$${P}_{MAE}=\frac{MA{E}_{1}-MA{E}_{2}}{MA{E}_{1}}\times 100\%,$$

$${P}_{RRSE}=\frac{RRS{E}_{1}-RRS{E}_{2}}{RRS{E}_{1}}\times 100\%.$$

5 Results and Discussion

In the proposed hybrid method, LMD and EEMD algorithms are used to decompose the original river discharge series. The training set of the original discharge series of S₁ is decomposed by LMD and the resulting $PFs$ are given in Fig. 4. Then, using EEMD each $PF$ and residual is further decomposed into $IMFs$. The EEMD decomposition results of $P{F}_{1}$ to $P{F}_{4}$ are presented in Fig. 5. Similarly, all the other series are decomposed. The remaining decomposition results of S₁-S₅ are provided in the supplementary materials. Further, the EEMD decomposed components were fed to SVR, ARIMA and KNN models individually. The predictions for all components is obtained and aggregated respectively to obtain the final forecasts of the HD-SVR, HD-KNN and HD-ARIMA models. Lastly, the average prediction of these three models is computed as the final prediction of the HD-SKA model.

Fig. 4

LMD results for the original river discharge series of S₁

Fig. 5

Decomposition of $PF$ ₁-$PF$ ₄ obtained from LMD using EEMD (S₁)

Discharge data of five rivers is used to verify the prediction performance of the proposed HD-SKA model. The six benchmark models compared to the HD-SKA model are ARIMA, SVR, KNN, EEMD-ARIMA, EEMD-SVR and EEMD-KNN models. Lastly, the proposed hybrid model (HD-SKA) is applied to predict the daily river discharge of S₁-S₅.

5.1 Prediction Results

In this section, the prediction results of seven models on the S₁-S₅ series are compared and discussed. The prediction results of the training and testing phase are represented in Table 2. The detailed results are summarized as follows:

• i. The SVR, KNN and ARIMA models are close competitors of each other in predicting daily river discharge of S₁-S₅.

• ii. The EEMD-based models have better performance than single SVR, ARIMA, and KNN models except in some instances. For example, in S₄ training phase, the MAE of the EEMD-KNN model is more than the KNN model. The use of the decomposition technique improves the prediction accuracy of models for hydrological time series (Huynh et al. 2021). Therefore, EEMD has improved the prediction accuracy of SVR, ARIMA and KNN models in all five cases.

• iii. For S₁-S_5, the RMSE, MAE and RRSE of the proposed HD-SKA model are smaller compared to the other considered models. However, there are certain situations where the MAE of the proposed HD-SKA model is slightly higher than EEMD-based models but this difference is negligible. The proposed HD-SKA model has better predictive accuracy than EEMD-based ARIMA, KNN and SVR models.

• iv. Overall, the proposed HD-SKA model has better performance than all considered models in the study. The implementation of hybrid decomposition in the proposed method has enhanced the prediction capability of models. The HD-SKA model produces reliable river discharge prediction.

Table 2 Performance evaluation of training and testing prediction error of proposed model with different models for S₁- S₅ river discharge series

Figure 6a represents the prediction performance of the HD-SKA model compared to EEMD-based models in the testing phase of the S₁ and S₂ series. It can be observed that the proposed HD-SKA model precisely predicts the S₁ and S₂ series and is quite near to the original daily discharge. The remaining prediction plots for the S₃-S₅ series are provided in the supplementary material. For further verification of HD-SKA model performance, the coefficient of determination (R²) of all the seven models is represented in Fig. 6b. It is observed that the proposed HD-SKA model yields highest R² value and has produces better prediction results compared to all other considered models in both training and testing phase.

Fig. 6

Models analysis (a) Prediction performance of HD-SKA model on testing data of S₁ and S₂ series (b) Prediction accuracy plot for of seven models for S₁-S₅

5.2 Improvements by the Proposed Hybrid Model

The effectiveness of hybrid decomposition in the proposed hybrid model is illustrated in Table 3 through improved percentage indexes of RMSE, MAE and RRSE. By comparing the percentage improvements of the HD-SKA model to ARIMA, SVR and KNN models, it is observed that P_RMSE, P_MAE, and P_RRSE are all positive. The performance of the proposed HD-SKA model is superior to ARIMA, SVR, and KNN models in all five cases.

Table 3 Improved percentage of proposed model among different models for S₁-S₅

Further, the comparison of percentage improvements of the proposed HD-SKA model with EEMD-based models indicates that the HD-SKA model performs better than EEMD-ARIMA, EEMD-SVR and EEMD-KNN in all case studies. The P_RMSE, P_MAE, and P_RRSE are mostly positive except P_MAE index in some situations. For example, the MAE of the HD-SKA model compared to the EEMD-KNN model is increased by 1.38% in the training phase of the S₅ series. However, it can be observed that both models have similar performance and the difference is not much.

Overall, the proposed HD-SKA model has better performance than all other considered models. The hybrid decomposition-based models have better predictive performance than single decomposition-based models as studied in the literature see Vidya and Janani (2021). It may be deduced that the implementation of LMD with EEMD in the proposed hybrid model efficiently reduces the complexity and randomness of river discharge.

The proposed HD-SKA model in this study can serve as a helpful tool for the accurate prediction of river discharge.

5.3 Diebold-Mariano Test

The Diebold Mariano (DM) test is a well-known statistical hypothesis testing approach that helps in the identification of the degree of discrepancy among the proposed model and the compared models (Silva et al. 2021). The null hypothesis of the DM test is that the two models have similar prediction accuracy against the alternative that model 2 has lower prediction accuracy than model 1. Symbolically,

$${H}_{0}:E[L\left({e}_{t}^{1})\right]\ge E[L\left({e}_{t}^{2})\right],$$

$${H}_{1}:E[L\left({e}_{t}^{1})\right]<E[L\left({e}_{t}^{2})\right],$$

where ${e}_{t}^{1}$ and ${e}_{t}^{2}$ are the prediction errors of two comparison models and $L$ denotes the loss function of the prediction errors. The DM statistic is defined as follows:

$$DM=\frac{\bar{d}}{\sqrt{{2\pi {\widehat{f}}_{d}(0)}/{m}}}\to N\left(\mathrm{0,1}\right),$$

(18)

where ${\hat{f}}_{d}(0)$ represents the spectral density, $m$ is the length of prediction results, $2\pi {\hat{f}}_{d}(0)$ denotes the consistent estimator of the asymptotic variance and $\bar{d }=\frac{1}{m}\sum_{t=1}^{m}\left(L\left({e}_{t}^{1}\right)-L\left({e}_{t}^{2}\right)\right)$. In this study, the loss function used is mean squared error (MSE). The null hypothesis will be rejected if $DM<-{Z}_{\alpha /2}$ where $\alpha$ is the level of significance.

In this study, the DM test is applied to verify the prediction results of models at 1%, 5%, and 10% levels of significance. The null hypothesis will be rejected for S₁-S₅ if the DM statistic value is smaller than –2.58, –1.96, and –1.64 for 1%, 5% and 10% levels of significance respectively. The DM test is applied using the proposed HD-SKA model as “model 1” and benchmark models as “model 2” respectively.

In Table 4, the DM test statistic values on predictions of testing data sets are given for S₁-S₅ series. The null hypothesis is rejected for all cases except for the EEMD-SVR model in S_5. The DM test results reveals that the performance of the proposed HD-SKA model for the S₁-S₅ series is markedly diverse and superior to all considered models. However, in S₅ the EEMD-SVR model and HD-SKA model have similar prediction accuracy. Thus, the proposed HD-SKA model has higher prediction accuracy among all considered models for river discharge prediction.

Table 4 Diebold-Mariano test of different models in testing phase of S₁-S₅

6 Conclusion

In this study, a novel hybrid method is proposed to predict daily river discharge. The application of the proposed method is illustrated using discharge data of five rivers in the Indus Basin System, Pakistan. The performance of the proposed HD-SKA model is compared with six benchmark models. The models’ performance is evaluated using different performance indicators and the Diebold-Mariano test. The data analysis results show that the proposed HD-SKA model outperforms all the models considered in the study. The results of the Diebold-Mariano test revealed that the HD-SKA model possesses a higher predictive ability than benchmark models. Overall, the proposed hybrid method can be a successful tool to predict daily river discharge. The proposed method has greater accuracy when the number of components identified at the second decomposition stage is not too large. Moreover, the application of the proposed method may be checked on large data sets in future research work.