1 Introduction

Reservoirs are effective facilities to provide reliable water supplies in regions exhibiting highly fluctuating streamflow. Uneven temporal distribution of rainfall in Taiwan renders 60–90% of streamflow clustered within the wet season (May–October). Reservoirs thus become important facilities in Taiwan to store excess water during high-inflow months to compensate for the low inflow of the remaining months and provide stable water supply for agricultural, domestic, and industrial needs. However, prolonged and severe droughts may induce insufficient reservoir storage and lead to inadequate releases for projected demands.

A commonly used measure in reservoir operation to mitigate water shortage impacts during droughts is water rationing. That is, a series of smaller deficits is allowed in advance to conserve more water to avoid high-percentage water shortages in pending droughts. Many studies in the literature (e.g., Shih and ReVelle 1995; Cancelliere et al. 1998; You and Cai 2008; Shiau 2011; Ilich 2011; Taghian et al. 2014; Peng et al. 2015; Hu et al. 2016; Ahmadianfar et al. 2016; Ji et al. 2016; Ding et al. 2017; Ashofteh et al. 2017; Ahmadianfar et al. 2017; Xu et al. 2017; Wang et al. 2018; Kumar and Kasthurirengan 2018; Chang et al. 2019; Wan et al. 2019; Adeloye and Dau 2019; Men et al. 2019; Xu et al. 2019; Ahmadianfar and Zamani 2020; Li et al. 2020; Zhao et al. 2020; Ashrafi et al. 2020; Xu et al. 2020; El Harraki et al. 2021, and others) have proposed various hedging policies to determine when and how to implement hedging.

Either reservoir storage or water availability (sum of storage and inflow) are often used to guide reservoir releases in normal operation as well as in hedging rules. Since inflow is not known in advance, several techniques, such as synthetic flow (Felfelani et al. 2013; Cheng et al. 2017; Zhang et al. 2019; Wang et al. 2019), predicted flow (Karamouz and Araghinejad 2008; Wang and Liu 2013; Jin and Lee 2019), conditional expectation (Shih and ReVelle 1994) and other surrogate measures (Shiau and Lee 2005), have been proposed to formulate various hedging rules.

Reservoir storage represents the known current information and is the most reliable information for impending droughts. Inflow denotes the unknown future information and is needed to compensate for inadequate storage during droughts. In addition to the current reservoir storage and future inflow, past operation information is also known and can be used as a signal to determine reservoir releases. For example, a falling pool level implies that past inflow is insufficient to meet the demand and leads to a reduction in reservoir storage. In contrast, excess water induced by past greater-than-demand inflow is stored and results in rising storage. The falling and rising pool level (or reservoir storage) represent declining and increasing water supply ability, respectively, which is an informed factor for future reservoir releases. However, this factor is rarely addressed in reservoir operation models.

The main aim of this study is to explore the effects of past operation information and future hydrologic information on reservoir performance during droughts. These two auxiliary factors, represented by a trend statistic and a standardized streamflow index (SSI), are combined with the current storage to construct optimal hedging policies. The outcomes of these two optimal hedging policies are compared to evaluate their effects on reservoir performance in terms of shortage indices. The proposed approach is illustrated through an application to the Nanhua Reservoir located in southern Taiwan.

2 Methodology

2.1 Demand-Based Rule Curves

The traditional rule curves consider water supply and flood mitigation purposes simultaneously. The demand-based rule curves proposed in this study represent the water supply ability for future demands, which consider only the water-supply purpose. The upper and lower rule curves are defined by future NU- and ND-period demands, respectively, and expressed as

$$ {\mathrm{U}\mathrm{RC}}^{\mathrm{t}}={\sum}_{\mathrm{i}=\mathrm{t}}^{\mathrm{t}+{\mathrm{N}}_{\mathrm{U}}-1}{\mathrm{D}}^{\mathrm{i}},\kern0.5em {\mathrm{LRC}}^{\mathrm{t}}={\sum}_{\mathrm{i}=\mathrm{t}}^{\mathrm{t}+{\mathrm{N}}_{\mathrm{D}}-1}{\mathrm{D}}^{\mathrm{i}} $$
(1)

where URCt and LRCt denote the upper and lower rules curves at time t, respectively; Dt is the demand at time t; NU and ND denote the number of future periods for upper and lower rules curves, respectively, and NU > ND.

The upper and lower rules curves divide the reservoir capacity into three zones, abundant storage, normal operation, and water-stress zones, denoted as H, M, and L, respectively. Each zone identifies a specific release rule associated with a predefined rationing coefficient. That is,

$$ {\mathrm{R}}^{\mathrm{t}}=\left\{\begin{array}{c}{\upalpha}_{\mathrm{H}}{\mathrm{D}}^{\mathrm{t}}/\Delta \mathrm{t},\mathrm{if}\ {\mathrm{S}}^{\mathrm{t}}\in \mathrm{H}\ \\ {}{\upalpha}_{\mathrm{M}}{\mathrm{D}}^{\mathrm{t}}/\Delta \mathrm{t},\mathrm{if}\ {\mathrm{S}}^{\mathrm{t}}\in \mathrm{M}\\ {}{\upalpha}_{\mathrm{L}}{\mathrm{D}}^{\mathrm{t}}/\Delta \mathrm{t},\mathrm{if}\ {\mathrm{S}}^{\mathrm{t}}\in \mathrm{L}\end{array}\right. $$
(2)

where Rt, Dt, and St represent reservoir release, demand, and storage at time t, respectively; αH, αM, and αL denote the rationing coefficients for zones H, M, and L, respectively, which range between 0 and 1, and coefficients less than 1 represent hedging; and ∆t is the time interval in reservoir operation.

2.2 Fuzzified Storage and Fuzzified Rationing Coefficient

The conventional zone-based rule-curve operation described in Eq. (2) is discrete hedging, leading to the rationing coefficient abruptly changing from one zone to another. Fuzzified storage allows storage partial and simultaneous belonging to different zones and creates gradually varied rationing coefficients (Ahmadianfar et al. 2016; Shiau et al. 2018). The proposed fuzzified storage employs trapezoidal membership functions to quantify the belongingness of reservoir storage in zones H, M, and L (Fig. 1), as given by

$$ {\upmu}_{\mathrm{H}}^{\mathrm{t}}=\left\{\begin{array}{c}0,\kern0.5em \mathrm{if}\ {\mathrm{S}}^{\mathrm{t}}\le {\mathrm{LRC}}^{\mathrm{t}}\ \\ {}\frac{{\mathrm{S}}^{\mathrm{t}}-{\mathrm{LRC}}^{\mathrm{t}}}{{\mathrm{URC}}^{\mathrm{t}}-{\mathrm{LRC}}^{\mathrm{t}}},\mathrm{if}\ {\mathrm{LRC}}^{\mathrm{t}}<{\mathrm{S}}^{\mathrm{t}}\le {\mathrm{URC}}^{\mathrm{t}}\\ {}1,\kern0.5em \mathrm{if}\ {\mathrm{S}}^{\mathrm{t}}>{\mathrm{URC}}^{\mathrm{t}}\end{array}\right. $$
(3a)
$$ {\upmu}_{\mathrm{M}}^{\mathrm{t}}=\left\{\begin{array}{c}0,\kern0.5em \mathrm{if}\ {\mathrm{S}}^{\mathrm{t}}\le {\mathrm{S}}_{\mathrm{min}}\ \\ {}\frac{{\mathrm{S}}^{\mathrm{t}}-{\mathrm{S}}_{\mathrm{min}}}{{\mathrm{LRC}}^{\mathrm{t}}-{\mathrm{S}}_{\mathrm{min}}},\mathrm{if}\ {\mathrm{S}}_{\mathrm{min}}<{\mathrm{S}}^{\mathrm{t}}\le {\mathrm{LRC}}^{\mathrm{t}}\\ {}1,\kern2em \mathrm{if}\ {\mathrm{LRC}}^{\mathrm{t}}<{\mathrm{S}}^{\mathrm{t}}\le {\mathrm{URC}}^{\mathrm{t}}\\ {}\frac{{\mathrm{S}}_{\mathrm{max}}-{\mathrm{S}}^{\mathrm{t}}}{{\mathrm{S}}_{\mathrm{max}}-{\mathrm{URC}}^{\mathrm{t}}},\mathrm{if}\ {\mathrm{URC}}^{\mathrm{t}}<{\mathrm{S}}^{\mathrm{t}}\le {\mathrm{S}}_{\mathrm{max}}\\ {}0,\kern0.5em \mathrm{if}\ {\mathrm{S}}^{\mathrm{t}}>{\mathrm{S}}_{\mathrm{max}}\end{array}\right. $$
(3b)
$$ {\upmu}_{\mathrm{L}}^{\mathrm{t}}=\left\{\begin{array}{c}1,\kern0.5em \mathrm{if}\ {\mathrm{S}}^{\mathrm{t}}\le {\mathrm{L}\mathrm{RC}}^{\mathrm{t}}\ \\ {}\frac{{\mathrm{URC}}^{\mathrm{t}}-{\mathrm{S}}^{\mathrm{t}}}{{\mathrm{URC}}^{\mathrm{t}}-{\mathrm{L}\mathrm{RC}}^{\mathrm{t}}},\mathrm{if}\ {\mathrm{L}\mathrm{RC}}^{\mathrm{t}}<{\mathrm{S}}^{\mathrm{t}}\le {\mathrm{URC}}^{\mathrm{t}}\\ {}0,\kern0.5em \mathrm{if}\ {\mathrm{S}}^{\mathrm{t}}>{\mathrm{URC}}^{\mathrm{t}}\end{array}\right. $$
(3c)

where \( {\upmu}_H^t \), \( {\upmu}_M^t \), and \( {\upmu}_L^t \) are the membership values of storage St in zones H, M, and L at time t, respectively; Smax and Smin denote the reservoir capacity and dead storage, respectively.

Fig. 1
figure 1

Fuzzy membership functions for reservoir storage zones of L, M, and H (Smin: dead storage, LRC: lower rule curve, URC: upper rule curve, Smax: reservoir capacity)

Full size image

The fuzzified rationing coefficient is then defined as the membership-value weighted average of rationing coefficients of three zones, which is expressed as

$$ {\upalpha}_{\mathrm{FS}}^{\mathrm{t}}=\frac{\upalpha_{\mathrm{H}}{\upmu}_{\mathrm{H}}^{\mathrm{t}}+{\upalpha}_{\mathrm{M}}{\upmu}_{\mathrm{M}}^{\mathrm{t}}+{\upalpha}_{\mathrm{L}}{\upmu}_{\mathrm{L}}^{\mathrm{t}}}{\upmu_{\mathrm{H}}^{\mathrm{t}}+{\upmu}_{\mathrm{M}}^{\mathrm{t}}+{\upmu}_{\mathrm{L}}^{\mathrm{t}}} $$
(4a)

where \( {\upalpha}_{FS}^t \) is the fuzzified rationing coefficient at time t.

Reservoir release is determined by the fuzzified rationing coefficient simultaneously considering storage belonging to different zones, which is given by

$$ {\mathrm{R}}^{\mathrm{t}}={\upalpha}_{\mathrm{FS}}^{\mathrm{t}}\frac{{\mathrm{D}}^{\mathrm{t}}}{\Delta \mathrm{t}} $$
(4b)

2.3 Trend Statistic for Past Reservoir Operation

To evaluate variations in reservoir storage, the statistic used in the Mann-Kendall trend test (Hirsch et al. 1982) is adopted and calculated as

$$ {\mathrm{T}}_{\mathrm{n}}^{\mathrm{t}}={\sum}_{\mathrm{k}=\mathrm{t}-\mathrm{n}+1}^{\mathrm{t}-1}{\sum}_{\mathrm{j}=\mathrm{k}+1}^{\mathrm{t}}\operatorname{sgn}\left({\mathrm{x}}_{\mathrm{j}}-{\mathrm{x}}_{\mathrm{k}}\right),\kern0.5em \operatorname{sgn}\left({\mathrm{x}}_{\mathrm{j}}-{\mathrm{x}}_{\mathrm{k}}\right)=\left\{\begin{array}{c}+1\ \mathrm{if}\ {\mathrm{x}}_{\mathrm{j}}>{\mathrm{x}}_{\mathrm{k}}\\ {}0\ \mathrm{if}\ {\mathrm{x}}_{\mathrm{j}}={\mathrm{x}}_{\mathrm{k}}\\ {}1\ \mathrm{if}\ {\mathrm{x}}_{\mathrm{j}}<{\mathrm{x}}_{\mathrm{k}}\end{array}\right. $$
(5)

where xj and xk denote the reservoir storage at times j and k, respectively, and \( {T}_n^t \) is the trend statistic of storage at time t for the past n periods (time t-n + 1 to time t).

The value of \( {T}_n^t \) ranges between -n(n-1)/2 and n(n-1)/2. A positive T indicates rising storage, while a negative value denotes a falling trend. The range of \( {T}_n^t \) is equally divided into three states: falling trend F with -n(n-1)/2≤\( {T}_n^t \)<−n(n-1)/6, no trend T with -n(n-1)/6≤\( {T}_n^t \)≤n(n-1)/6, and rising trend R with n(n-1)/6<\( {T}_n^t \)≤ n(n-1)/2.

A set of nine release rules is constructed that simultaneously considers three storage zones and three storage trends. That is,

$$ {\mathrm{R}}^{\mathrm{t}}=\left\{\begin{array}{c}{\upalpha}_{\mathrm{HR}}{\mathrm{D}}^{\mathrm{t}}/\Delta \mathrm{t},\mathrm{if}\ {\mathrm{S}}^{\mathrm{t}}\in \mathrm{H}\ \mathrm{and}\ {\mathrm{T}}_{\mathrm{n}}^{\mathrm{t}}\in \mathrm{R}\\ {}{\upalpha}_{\mathrm{HT}}{\mathrm{D}}^{\mathrm{t}}/\Delta \mathrm{t},\mathrm{if}\ {\mathrm{S}}^{\mathrm{t}}\in \mathrm{H}\ \mathrm{and}\ {\mathrm{T}}_{\mathrm{n}}^{\mathrm{t}}\in \mathrm{T}\\ {}{\upalpha}_{\mathrm{HF}}{\mathrm{D}}^{\mathrm{t}}/\Delta \mathrm{t},\mathrm{if}\ {\mathrm{S}}^{\mathrm{t}}\in \mathrm{H}\ \mathrm{and}\ {\mathrm{T}}_{\mathrm{n}}^{\mathrm{t}}\in \mathrm{F}\ \\ {}{\upalpha}_{\mathrm{MR}}{\mathrm{D}}^{\mathrm{t}}/\Delta \mathrm{t},\mathrm{if}\ {\mathrm{S}}^{\mathrm{t}}\in \mathrm{M}\ \mathrm{and}\ {\mathrm{T}}_{\mathrm{n}}^{\mathrm{t}}\in \mathrm{R}\\ {}{\upalpha}_{\mathrm{MT}}{\mathrm{D}}^{\mathrm{t}}/\Delta \mathrm{t},\mathrm{if}\ {\mathrm{S}}^{\mathrm{t}}\in \mathrm{M}\ \mathrm{and}\ {\mathrm{T}}_{\mathrm{n}}^{\mathrm{t}}\in \mathrm{T}\\ {}{\upalpha}_{\mathrm{MF}}{\mathrm{D}}^{\mathrm{t}}/\Delta \mathrm{t},\mathrm{if}\ {\mathrm{S}}^{\mathrm{t}}\in \mathrm{M}\ \mathrm{and}\ {\mathrm{T}}_{\mathrm{n}}^{\mathrm{t}}\in \mathrm{F}\\ {}{\upalpha}_{\mathrm{LR}}{\mathrm{D}}^{\mathrm{t}}/\Delta \mathrm{t},\mathrm{if}\ {\mathrm{S}}^{\mathrm{t}}\in \mathrm{L}\ \mathrm{and}\ {\mathrm{T}}_{\mathrm{n}}^{\mathrm{t}}\in \mathrm{R}\\ {}{\upalpha}_{\mathrm{LT}}{\mathrm{D}}^{\mathrm{t}}/\Delta \mathrm{t},\mathrm{if}\ {\mathrm{S}}^{\mathrm{t}}\in \mathrm{L}\ \mathrm{and}\ {\mathrm{T}}_{\mathrm{n}}^{\mathrm{t}}\in \mathrm{T}\\ {}{\upalpha}_{\mathrm{LF}}{\mathrm{D}}^{\mathrm{t}}/\Delta \mathrm{t},\mathrm{if}\ {\mathrm{S}}^{\mathrm{t}}\in \mathrm{L}\ \mathrm{and}\ {\mathrm{T}}_{\mathrm{n}}^{\mathrm{t}}\in \mathrm{F}\end{array}\right. $$
(6)

where αHR, αHT, αHF, αMR, αMT, αMF, αLR, αLT, and αLF denote the rationing coefficient for various current storage zones and past storage trends, bounded between 0 and 1. These rationing coefficients are also constrained by

$$ \left\{\begin{array}{c}\begin{array}{c}{\upalpha}_{HR}\ge {\upalpha}_{MR}\ge {\upalpha}_{LR}\\ {}{\upalpha}_{HT}\ge {\upalpha}_{MT}\ge {\upalpha}_{LT}\\ {}{\upalpha}_{HF}\ge {\upalpha}_{MF}\ge {\upalpha}_{LF}\end{array}\\ {}\begin{array}{c}{\upalpha}_{HR}\ge {\upalpha}_{HT}\ge {\upalpha}_{HF}\\ {}{\upalpha}_{HR}\ge {\upalpha}_{HT}\ge {\upalpha}_{HF}\\ {}{\upalpha}_{LR}\ge {\upalpha}_{LT}\ge {\upalpha}_{LF}\end{array}\end{array}\right. $$
(7)

The trapezoidal membership functions are also used to fuzzify past storage trend with the membership values in the rising trend (R), no trend (T), and falling trend (F) expressed as

$$ {\upmu}_R^t=\left\{\begin{array}{c}0,\kern0.5em \mathrm{if}\ {T}_n^t\le \frac{n\left(n-1\right)}{6}\ \\ {}\frac{T_n^t+\frac{n\left(n-1\right)}{6}}{\frac{n\left(n-1\right)}{3}},\mathrm{if}\ \frac{n\left(n-1\right)}{6}<{T}_n^t\le \frac{n\left(n-1\right)}{6}\\ {}1,\kern0.5em \mathrm{if}\ {T}_n^t>\frac{n\left(n-1\right)}{6}\end{array}\right. $$
(8a)
$$ {\upmu}_T^t=\left\{\begin{array}{c}0,\kern0.5em \mathrm{if}\ {T}_n^t\le \frac{n\left(n-1\right)}{2}\ \\ {}\frac{T^t+\frac{n\left(n-1\right)}{2}}{\frac{n\left(n-1\right)}{3}},\mathrm{if}\ \frac{n\left(n-1\right)}{2}<{T}_n^t\le \frac{n\left(n-1\right)}{6}\\ {}1,\kern1.25em \mathrm{if}\ \frac{n\left(n-1\right)}{6}<{T}_n^t\le \frac{n\left(n-1\right)}{6}\\ {}\frac{\frac{n\left(n-1\right)}{2}-{T}^t}{\frac{n\left(n-1\right)}{3}},\mathrm{if}\ \frac{n\left(n-1\right)}{6}<{T}_n^t\le \frac{n\left(n-1\right)}{2}\\ {}0,\kern0.5em \mathrm{if}\ {T}_n^t>\frac{n\left(n-1\right)}{2}\end{array}\right. $$
(8b)
$$ {\upmu}_F^t=\left\{\begin{array}{c}1,\kern0.5em \mathrm{if}\ {T}_n^t\le \frac{n\left(n-1\right)}{6}\ \\ {}\frac{\frac{n\left(n-1\right)}{6}-{T}_n^t}{\frac{n\left(n-1\right)}{3}},\mathrm{if}\ \frac{n\left(n-1\right)}{6}<{T}_n^t\le \frac{n\left(n-1\right)}{6}\\ {}0,\kern0.5em \mathrm{if}\ {T}_n^t>\frac{n\left(n-1\right)}{6}\end{array}\right. $$
(8c)

where \( {\upmu}_R^t \), \( {\upmu}_T^t \), and \( {\upmu}_F^t \) are the membership values of trends in categories of R, T, and F at time t, respectively.

The fuzzified rationing coefficient \( {\upalpha}_{FST}^t \) simultaneously considering fuzzified storage and fuzzified past storage trends is thus defined as

$$ {\upalpha}_{\mathrm{F}\mathrm{ST}}^{\mathrm{t}}=\frac{\upalpha_{\mathrm{H}\mathrm{R}}{\upmu}_{\mathrm{H}}^{\mathrm{t}}{\upmu}_{\mathrm{R}}^{\mathrm{t}}+{\upalpha}_{\mathrm{H}\mathrm{T}}{\upmu}_{\mathrm{H}}^{\mathrm{t}}{\upmu}_{\mathrm{T}}^{\mathrm{t}}+{\upalpha}_{\mathrm{H}\mathrm{F}}{\upmu}_{\mathrm{H}}^{\mathrm{t}}{\upmu}_{\mathrm{F}}^{\mathrm{t}}+{\upalpha}_{\mathrm{M}\mathrm{R}}{\upmu}_{\mathrm{M}}^{\mathrm{t}}{\upmu}_{\mathrm{R}}^{\mathrm{t}}+{\upalpha}_{\mathrm{M}\mathrm{T}}{\upmu}_{\mathrm{M}}^{\mathrm{t}}{\upmu}_{\mathrm{T}}^{\mathrm{t}}+{\upalpha}_{\mathrm{M}\mathrm{F}}{\upmu}_{\mathrm{M}}^{\mathrm{t}}{\upmu}_{\mathrm{F}}^{\mathrm{t}}+{\upalpha}_{\mathrm{L}\mathrm{R}}{\upmu}_{\mathrm{L}}^{\mathrm{t}}{\upmu}_{\mathrm{R}}^{\mathrm{t}}+{\upalpha}_{\mathrm{L}\mathrm{T}}{\upmu}_{\mathrm{L}}^{\mathrm{t}}{\upmu}_{\mathrm{T}}^{\mathrm{t}}+{\upalpha}_{\mathrm{L}\mathrm{F}}{\upmu}_{\mathrm{L}}^{\mathrm{t}}{\upmu}_{\mathrm{F}}^{\mathrm{t}}}{\upmu_{\mathrm{H}}^{\mathrm{t}}{\upmu}_{\mathrm{R}}^{\mathrm{t}}+{\upmu}_{\mathrm{H}}^{\mathrm{t}}{\upmu}_{\mathrm{T}}^{\mathrm{t}}+{\upmu}_{\mathrm{H}}^{\mathrm{t}}{\upmu}_{\mathrm{F}}^{\mathrm{t}}+{\upmu}_{\mathrm{M}}^{\mathrm{t}}{\upmu}_{\mathrm{R}}^{\mathrm{t}}+{\upmu}_{\mathrm{M}}^{\mathrm{t}}{\upmu}_{\mathrm{T}}^{\mathrm{t}}+{\upmu}_{\mathrm{M}}^{\mathrm{t}}{\upmu}_{\mathrm{F}}^{\mathrm{t}}+{\upmu}_{\mathrm{L}}^{\mathrm{t}}{\upmu}_{\mathrm{R}}^{\mathrm{t}}+{\upmu}_{\mathrm{L}}^{\mathrm{t}}{\upmu}_{\mathrm{T}}^{\mathrm{t}}+{\upmu}_{\mathrm{L}}^{\mathrm{t}}{\upmu}_{\mathrm{F}}^{\mathrm{t}}} $$
(9)

2.4 Standardized Streamflow Index for Future Hydrologic Information

To incorporate future hydrologic information into reservoir operation rules, the standardized streamflow index (SSI) proposed by Telesca et al. (2012) is used to evaluate inflow variations and guide reservoir releases. The SSI is calculated as

$$ {\mathrm{SSI}}_{\mathrm{n}}^{\mathrm{t}}={\Phi}^{-1}\left({\mathrm{F}}_{{\mathrm{Q}}_{\mathrm{n}}^{\mathrm{t}}}\left({\mathrm{q}}_{\mathrm{n}}^{\mathrm{t}}\right)\right) $$
(10)

where \( {q}_n^t \) is the total inflow of n future periods at time t (time t to time t + n-1); \( {F}_{Q_n^t} \) is the cumulative distribution function of \( {Q}_n^t \); Φ−1 is the inverse cumulative standard normal distribution; and \( {SSI}_n^t \) is the value of SSI for n future periods at time t.

Negative and positive SSIs denote the less-than-median and greater-than-median streamflows, respectively. To have consistent category numbers with storage and storage trends, the SSI is divided into three states, wet (W), normal (N), and drought (D), when the SSI values fall within the intervals of SSI ≥ 1, −1 ≤ SSI < 1, and, SSI < -1, respectively.

Nine release rules associated with a specific rationing coefficient are constructed to simultaneously consider three storage zones and three SSI states, which are

$$ {\mathrm{R}}^{\mathrm{t}}=\left\{\begin{array}{c}{\upalpha}_{\mathrm{HW}}{\mathrm{D}}^{\mathrm{t}}/\Delta \mathrm{t},\mathrm{if}\ {\mathrm{S}}^{\mathrm{t}}\in \mathrm{H}\ \mathrm{and}\ {\mathrm{S}\mathrm{SI}}_{\mathrm{n}}^{\mathrm{t}}\in \mathrm{W}\\ {}{\upalpha}_{\mathrm{HN}}{\mathrm{D}}^{\mathrm{t}}/\Delta \mathrm{t},\mathrm{if}\ {\mathrm{S}}^{\mathrm{t}}\in \mathrm{H}\ \mathrm{and}\ {\mathrm{S}\mathrm{SI}}_{\mathrm{n}}^{\mathrm{t}}\in \mathrm{N}\\ {}{\upalpha}_{\mathrm{HD}}{\mathrm{D}}^{\mathrm{t}}/\Delta \mathrm{t},\mathrm{if}\ {\mathrm{S}}^{\mathrm{t}}\in \mathrm{H}\ \mathrm{and}\ {\mathrm{S}\mathrm{SI}}_{\mathrm{n}}^{\mathrm{t}}\in \mathrm{D}\ \\ {}{\upalpha}_{\mathrm{MW}}{\mathrm{D}}^{\mathrm{t}}/\Delta \mathrm{t},\mathrm{if}\ {\mathrm{S}}^{\mathrm{t}}\in \mathrm{M}\ \mathrm{and}\ {\mathrm{S}\mathrm{SI}}_{\mathrm{n}}^{\mathrm{t}}\in \mathrm{W}\\ {}{\upalpha}_{\mathrm{MN}}{\mathrm{D}}^{\mathrm{t}}/\Delta \mathrm{t},\mathrm{if}\ {\mathrm{S}}^{\mathrm{t}}\in \mathrm{M}\ \mathrm{and}\ {\mathrm{S}\mathrm{SI}}_{\mathrm{n}}^{\mathrm{t}}\in \mathrm{N}\\ {}{\upalpha}_{\mathrm{MD}}{\mathrm{D}}^{\mathrm{t}}/\Delta \mathrm{t},\mathrm{if}\ {\mathrm{S}}^{\mathrm{t}}\in \mathrm{M}\ \mathrm{and}\ {\mathrm{S}\mathrm{SI}}_{\mathrm{n}}^{\mathrm{t}}\in \mathrm{D}\\ {}{\upalpha}_{\mathrm{LW}}{\mathrm{D}}^{\mathrm{t}}/\Delta \mathrm{t},\mathrm{if}\ {\mathrm{S}}^{\mathrm{t}}\in \mathrm{L}\ \mathrm{and}\ {\mathrm{S}\mathrm{SI}}_{\mathrm{n}}^{\mathrm{t}}\in \mathrm{W}\\ {}{\upalpha}_{\mathrm{LN}}{\mathrm{D}}^{\mathrm{t}}/\Delta \mathrm{t},\mathrm{if}\ {\mathrm{S}}^{\mathrm{t}}\in \mathrm{L}\ \mathrm{and}\ {\mathrm{S}\mathrm{SI}}_{\mathrm{n}}^{\mathrm{t}}\in \mathrm{N}\\ {}{\upalpha}_{\mathrm{LD}}{\mathrm{D}}^{\mathrm{t}}/\Delta \mathrm{t},\mathrm{if}\ {\mathrm{S}}^{\mathrm{t}}\in \mathrm{L}\ \mathrm{and}\ {\mathrm{S}\mathrm{SI}}_{\mathrm{n}}^{\mathrm{t}}\in \mathrm{D}\end{array}\right. $$
(11)

where αHW, αHN, αHD, αMW, αMN, αMD, αLW, αLN, and αLD denote the rationing coefficient for various current storage zones and future SSI states, which are also constrained by

$$ \left\{\begin{array}{c}\begin{array}{c}{\upalpha}_{\mathrm{HW}}\ge {\upalpha}_{\mathrm{MW}}\ge {\upalpha}_{\mathrm{LW}}\\ {}{\upalpha}_{\mathrm{HN}}\ge {\upalpha}_{\mathrm{MN}}\ge {\upalpha}_{\mathrm{LN}}\\ {}{\upalpha}_{\mathrm{HD}}\ge {\upalpha}_{\mathrm{MD}}\ge {\upalpha}_{\mathrm{LD}}\end{array}\\ {}\begin{array}{c}{\upalpha}_{\mathrm{HW}}\ge {\upalpha}_{\mathrm{HN}}\ge {\upalpha}_{\mathrm{HD}}\\ {}{\upalpha}_{\mathrm{MW}}\ge {\upalpha}_{\mathrm{MN}}\ge {\upalpha}_{\mathrm{MD}}\\ {}{\upalpha}_{\mathrm{LW}}\ge {\upalpha}_{\mathrm{LN}}\ge {\upalpha}_{\mathrm{LD}}\end{array}\end{array}\right. $$
(12)

The membership values, determined by the trapezoidal membership functions, of wet (W), normal (N), and drought (D) states are, respectively expressed as

$$ {\upmu}_W^t=\left\{\begin{array}{c}0,\kern0.5em \mathrm{if}\ {SSI}_n^t\le 1\ \\ {}\frac{SSI_n^t+1}{2},\mathrm{if}\ 1<{SSI}_n^t\le 1\\ {}1,\kern0.5em \mathrm{if}\ {SSI}_n^t>1\end{array}\right. $$
(13a)
$$ {\upmu}_N^t=\left\{\begin{array}{c}0,\kern0.5em \mathrm{if}\ {SSI}_n^t\le 3\ \\ {}\frac{SSI_n^t+3}{2},\mathrm{if}\ 3<{SSI}_n^t\le 1\\ {}1,\kern0.75em \mathrm{if}\ 1<{SSI}_n^t\le 1\\ {}\frac{3-{SSI}_n^t}{2},\mathrm{if}\ 1<{SSI}_n^t\le 3\\ {}0,\kern0.5em \mathrm{if}\ {SSI}_n^t>3\end{array}\right. $$
(13b)
$$ {\upmu}_D^t=\left\{\begin{array}{c}1,\kern0.5em \mathrm{if}\ {SSI}_n^t\le 1\ \\ {}\frac{1-{SSI}_n^t}{2},\mathrm{if}\ 1<{SSI}_n^t\le 1\\ {}0,\kern0.5em \mathrm{if}\ {SSI}_n^t>1\end{array}\right. $$
(13c)

where \( {\upmu}_W^t \), \( {\upmu}_N^t \), and \( {\upmu}_D^t \) are the membership values of SSI in the W, N, and D states at time t, respectively.

The fuzzified rationing coefficient \( {\upalpha}_{FSH}^t \) is the membership-value weighted average of rationing coefficients of nine various states, which is expressed as

$$ {\upalpha}_{\mathrm{FSH}}^{\mathrm{t}}=\frac{\upalpha_{\mathrm{H}\mathrm{W}}{\upmu}_{\mathrm{H}}^{\mathrm{t}}{\upmu}_{\mathrm{W}}^{\mathrm{t}}+{\upalpha}_{\mathrm{H}\mathrm{N}}{\upmu}_{\mathrm{H}}^{\mathrm{t}}{\upmu}_{\mathrm{N}}^{\mathrm{t}}+{\upalpha}_{\mathrm{H}\mathrm{D}}{\upmu}_{\mathrm{H}}^{\mathrm{t}}{\upmu}_{\mathrm{D}}^{\mathrm{t}}+{\upalpha}_{\mathrm{M}\mathrm{W}}{\upmu}_{\mathrm{M}}^{\mathrm{t}}{\upmu}_{\mathrm{W}}^{\mathrm{t}}+{\upalpha}_{\mathrm{M}\mathrm{N}}{\upmu}_{\mathrm{M}}^{\mathrm{t}}{\upmu}_{\mathrm{N}}^{\mathrm{t}}+{\upalpha}_{\mathrm{M}\mathrm{D}}{\upmu}_{\mathrm{M}}^{\mathrm{t}}{\upmu}_{\mathrm{D}}^{\mathrm{t}}+{\upalpha}_{\mathrm{L}\mathrm{W}}{\upmu}_{\mathrm{L}}^{\mathrm{t}}{\upmu}_{\mathrm{W}}^{\mathrm{t}}+{\upalpha}_{\mathrm{L}\mathrm{N}}{\upmu}_{\mathrm{L}}^{\mathrm{t}}{\upmu}_{\mathrm{N}}^{\mathrm{t}}+{\upalpha}_{\mathrm{L}\mathrm{D}}{\upmu}_{\mathrm{L}}^{\mathrm{t}}{\upmu}_{\mathrm{D}}^{\mathrm{t}}}{\upmu_{\mathrm{H}}^{\mathrm{t}}{\upmu}_{\mathrm{W}}^{\mathrm{t}}+{\upmu}_{\mathrm{H}}^{\mathrm{t}}{\upmu}_{\mathrm{N}}^{\mathrm{t}}+{\upmu}_{\mathrm{H}}^{\mathrm{t}}{\upmu}_{\mathrm{D}}^{\mathrm{t}}+{\upmu}_{\mathrm{M}}^{\mathrm{t}}{\upmu}_{\mathrm{W}}^{\mathrm{t}}+{\upmu}_{\mathrm{M}}^{\mathrm{t}}{\upmu}_{\mathrm{N}}^{\mathrm{t}}+{\upmu}_{\mathrm{M}}^{\mathrm{t}}{\upmu}_{\mathrm{D}}^{\mathrm{t}}+{\upmu}_{\mathrm{L}}^{\mathrm{t}}{\upmu}_{\mathrm{W}}^{\mathrm{t}}+{\upmu}_{\mathrm{L}}^{\mathrm{t}}{\upmu}_{\mathrm{N}}^{\mathrm{t}}+{\upmu}_{\mathrm{L}}^{\mathrm{t}}{\upmu}_{\mathrm{D}}^{\mathrm{t}}} $$
(14)

2.5 Water-Shortage Indices-Based Reservoir Performance Evaluation

Four water-shortage indices are used to evaluate reservoir performance considering different release rules.

  1. 1.

    The maximum single-period shortage ratio (MSR) denotes the maximum shortage ratio of a single period within the total periods, which is defined as

$$ \mathrm{MSR}=\operatorname{Max}\left\{{SR}^t\right\},t=1,2,\dots, N $$
(15)

where SRt = SHt/Dt × 100% is the water-shortage ratio at time t, SHt = Max {Dt − Rt, 0} is the water shortage at time t; and N is the total period.

  1. 2.

    The total shortage ratio (TSR) denotes the ratio of total water deficits to total demands, which is defined as

$$ \mathrm{TSR}=\frac{\sum_{\mathrm{t}=1}^{\mathrm{N}}{\mathrm{SH}}^{\mathrm{t}}}{\sum_{\mathrm{t}=1}^{\mathrm{N}}{\mathrm{D}}^{\mathrm{t}}}\times 100\% $$
(16)
  1. 3.

    Average water shortage per shortage period (AWS) denotes the ratio of total water deficits to shortage periods, which is defined as

$$ \mathrm{AWS}=\frac{\sum_{\mathrm{t}=1}^{\mathrm{N}}{\mathrm{SH}}^{\mathrm{t}}}{\mathrm{SD}} $$
(17)

where \( \mathrm{SD}={\sum}_{t=1}^N\left\{\begin{array}{c}1,\kern0.5em \mathrm{if}\ {SH}^t>0\\ {}0,\mathrm{otherwise}\end{array}\right. \) is the shortage periods.

  1. 4.

    Risk (RISK) denotes the ratio of shortage periods to the total periods, which is defined as

$$ \mathrm{RISK}=\frac{SD}{N} $$
(18)

These four shortage indices reveal different water shortage characteristics and are used as objective functions in optimization models to derive the optimal hedging policies.

2.6 TOPSIS-Based Multi-Criteria Optimization

TOPSIS (technique for order performance by similarity to ideal solution)-based multicriteria optimization, proposed by Hwang and Yoon (1981), is adopted in this study to integrate four shortage indices into a single overall objective for deriving the optimal hedging policy. The following normalized scheme is first employed to ensure that the water shortage indices range between 0 and 1. The normalized water-shortage index becomes

$$ {\mathrm{WSI}}_i^{\hbox{'}}=\frac{{\mathrm{WSI}}_i-\min \left({\mathrm{WSI}}_i\right)}{\max \left({\mathrm{WSI}}_i\right)-\min \left({\mathrm{WSI}}_i\right)} $$
(19)

where WSIi and WSIi′ are original and normalized values of the ith water-shortage index (i = 1 to 4 denotes MSR, TSR, AWS, and RISK, respectively); max(WSIi) and min(WSIi) are the maximum and minimum values of the ith water-shortage index.

TOPSIS ensures that the optimal solution has the shortest distance from the positive ideal solution (PIS) and has the longest distance from the negative ideal solution (NIS). The weighted total distances of the water-shortage indices from the PIS and NIS are denoted as D+ and D− and calculated by

$$ {D}^{+}={\left[{\sum}_{i=1}^4{w}_i{\left({\mathrm{WSI}}_i^{\hbox{'}}-{\mathrm{WSI}}_i^{+}\right)}^2\right]}^{1/2},\kern0.5em {D}^{-}={\left[{\sum}_{i=1}^4{w}_i{\left({\mathrm{WSI}}_i^{\hbox{'}}-{\mathrm{WSI}}_i^{-}\right)}^2\right]}^{1/2} $$
(20)

where wi is the weighting for the ith water-shortage index and \( {\sum}_{i=1}^4{w}_i=1 \), equal weighting of 1/4 is used in this study; \( {\mathrm{WSI}}_i^{+}=0 \) and \( {\mathrm{WSI}}_i^{-}=1 \) denote PIS and NIS of the ith water-shortage index, respectively.

The overall objective D∗ represents the relative distance to the NIS and is used to search the optimal solution by maximizing D∗, which is expressed as

$$ \operatorname{Max}\ {D}^{\ast }=\operatorname{Max}\ \frac{D^{-}}{D^{+}+{D}^{-}} $$
(21)

The optimal solution is searched by the genetic algorithm (GA) with a population size of 1000, a crossover rate of 0.8, and a mutation rate of 0.05.

2.7 Optimization Models

Three types of optimization models involving different information are evaluated in this study. Model S adopts the proposed demand-based rule curves and fuzzified storage to determine reservoir releases. Model STs integrates Model S and different periods of past storage trends. Past 3, 9, and 18 10-day periods (1, 3, and 6 months) storage trends construct Models ST3, ST9, and ST18, respectively. Models SH3, SH9, and SH18 simultaneously integrate Model S and future 3, 9, and 18 10-day periods SSI to guide reservoir releases, respectively. The results of these seven optimization models are derived by TOPSIS-based multicriteria optimization and compared with the results of the current operation (Model C).

3 Case Study

3.1 An Overview of the Nanhua Reservoir

The Nanhua Reservoir located in southern Taiwan is used to illustrate the proposed approach. The Nanhua Reservoir was finished in 1995 to provide reliable domestic supplies to two major cities, Tainan and Kaohsiung. The active capacity of 99.429 million m3 (measured in 2012) of the Nanhua Reservoir is insufficient to regulate the highly fluctuating streamflow of Houku Creek (a mean annual value of 220 million m3 for the 1959–2011 period) and to meet the projected annual demand of 181.6 million m3. An interbasin transfer facility, the Chiahsien diversion weir with a maximum diversion capacity of 30 m3/s, was constructed in 1999 and diverted excess streamflow of nearby Chishan Creek to increase the water supply ability of the Nanhua Reservoir. The monthly mean values of the streamflow of Houku Creek, Chishan Creek, and the projected demand are reported in Table 1.

Table 1 Monthly mean inflow, projected demand, downstream conservation, and maximum interbasin transfer at the Nanhua Reservoir and Chiahsien diversion weir
Full size table

3.2 Parametric Representation of the Nanhua Reservoir Operation

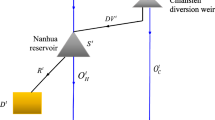
The simplified operation system of the Nanhua Reservoir and the Chiahsien diversion weir is illustrated in Fig. 2. The operation of the Nanhua Reservoir is described by the water-balance equation, i.e.

$$ {\mathrm{S}}^{\mathrm{t}+1}={\mathrm{S}}^{\mathrm{t}}+\left({\mathrm{Q}}_{\mathrm{H}}^{\mathrm{t}}+{\mathrm{DV}}^{\mathrm{t}}-{\mathrm{R}}^{\mathrm{t}}-{\mathrm{O}}_{\mathrm{H}}^{\mathrm{t}}\right)\Delta \mathrm{t}-{\mathrm{E}}^{\mathrm{t}} $$
(22)

where Δt denotes the operation interval and the 10-day period is used in this study; St and St + 1 are reservoir storage of the Nanhua reservoir at the beginning of times t and t + 1, respectively, which are constrained between dead storage Smin (= 0 million m3) and capacity Smax (= 99.429 million m3); \( {Q}_H^t \) denotes the inflow of the Nanhua Reservoir at time t; DVt denotes the interbasin diversion from the Chiahsien diversion weir, which is determined by

$$ {\mathrm{D}\mathrm{V}}^{\mathrm{t}}=\operatorname{Min}\left\{{\mathrm{RF}}_{\mathrm{C}}^{\mathrm{t}},{\mathrm{D}\mathrm{V}}_{\mathrm{max}}^{\mathrm{t}},\operatorname{Max}\left\{\frac{{\mathrm{S}}_{\mathrm{max}}-{\mathrm{S}}^{\mathrm{t}}+{\mathrm{D}}^{\mathrm{t}}+{\mathrm{E}}^{\mathrm{t}}}{\Delta \mathrm{t}}-{\mathrm{RF}}_{\mathrm{H}}^{\mathrm{t}},0\right\}\right\} $$
(23)

where \( {RF}_C^t \) and \( {RF}_H^t \) denote the remaining streamflow at time t of Chishan Creek and Houku Creek, respectively, and are determined by

$$ {\mathrm{RF}}_{\mathrm{C}}^{\mathrm{t}}=\operatorname{Max}\left\{{\mathrm{Q}}_{\mathrm{C}}^{\mathrm{t}}-{\mathrm{W}}_{\mathrm{C}}^{\mathrm{t}},0\right\},\kern0.5em {\mathrm{RF}}_{\mathrm{H}}^{\mathrm{t}}=\operatorname{Max}\left\{{\mathrm{Q}}_H^{\mathrm{t}}-{\mathrm{W}}_{\mathrm{H}}^{\mathrm{t}},0\right\} $$
(24)

where \( {W}_H^t \) and \( {W}_C^t \) are the reserved amounts of downstream uses at Houku Creek and Chishan Creek, respectively, which have a higher priority than the projected demand; \( {DV}_{\mathrm{max}}^t \) is the maximum interbasin transfer at the Chiahsien diversion weir.

Fig. 2
figure 2

Schematic layout of flow system for Nanhua Reservoir and Chiahsien diversion weir located in southern Taiwan

Full size image

Rt in Eq. (22) denotes the reservoir release for projected demand at time t and is determined by

$$ {\mathrm{R}}^{\mathrm{t}}=\operatorname{Min}\left\{{\upalpha}^{\mathrm{t}}\frac{{\mathrm{D}}^{\mathrm{t}}}{\Delta \mathrm{t}},\frac{{\mathrm{S}}^{\mathrm{t}}-{\mathrm{S}}_{\mathrm{min}}-{\mathrm{E}}^{\mathrm{t}}}{\Delta \mathrm{t}}+{\mathrm{R}\mathrm{F}}_{\mathrm{H}}^{\mathrm{t}}+{\mathrm{D}\mathrm{V}}^{\mathrm{t}}\right\} $$
(25)

where αt denotes the rationing coefficient at time t, which equals \( {\upalpha}_{FS}^t \), \( {\upalpha}_{FST}^t \), and \( {\upalpha}_{FSH}^t \), respectively, for different conditions.

Et in Eq. (22) denotes the reservoir evaporation loss at time t, which is estimated by

$$ {\mathrm{E}}^{\mathrm{t}}=0.7\times {\mathrm{e}}^{\mathrm{t}}\times \frac{1}{2}\left({\mathrm{A}}^{\mathrm{t}}+{\mathrm{A}}^{\mathrm{t}+1}\right)\Delta \mathrm{t} $$
(26)

where 0.7 is the pan coefficient; et is the daily evaporation rate; and At and At + 1 are the reservoir surface areas at times t and t + 1, respectively.

\( {O}_H^t \) in Eq. (22) denotes the reservoir outflow for downstream uses and spill flow, which is determined by

$$ {\mathrm{O}}_{\mathrm{H}}^{\mathrm{t}}=\left({\mathrm{Q}}_{\mathrm{H}}^{\mathrm{t}}-{\mathrm{R}\mathrm{F}}_{\mathrm{H}}^{\mathrm{t}}\right)+\operatorname{Max}\left\{\frac{{\mathrm{S}}^{\mathrm{t}}-{\mathrm{S}}_{\mathrm{max}}-{\mathrm{E}}^{\mathrm{t}}}{\Delta \mathrm{t}}+{\mathrm{R}\mathrm{F}}_{\mathrm{H}}^{\mathrm{t}}+{\mathrm{DV}}^{\mathrm{t}}-{\mathrm{R}}^{\mathrm{t}},0\right\} $$
(27)

The monthly values of reserved amounts of downstream uses in Houku Creek (\( {W}_H^t \)) and Chishan Creek (\( {W}_C^t \)), the maximum allowed diversion (\( {DV}_{max}^t \)), and the daily evaporation rate (et) are also reported in Table 1.

3.3 Parameters of Model C and Optimization Models

The current operation of the Nanhua Reservoir (Model C) uses the traditional rule curves (shown in Fig. 3) associated with the rationing coefficients of αH = 1, αM = 1, and αL = 0.7 to guide reservoir releases. Model S adopts the proposed demand-based rule curves of NU = 12 and ND = 6 10-day periods and αH = 1. These proposed demand-based rule curves, illustrated in Fig. 3, approximately divide the capacity of the Nanhua Reservoir (= 99.429 million m3) into three equal zones. The rationing coefficients of αM and αL of Model S are decision variables and are determined by maximizing the integrated objective D∗.

Fig. 3
figure 3

The current upper and lower rule curves for the Nanhua Reservoir and the demand-based upper and lower rule curves proposed in this study

Full size image

The rationing coefficients of αHR and αHT are assigned as 1 in Models ST3, ST9, and ST18, while the values of αHF, αMR, αMT, αMF, αLR, αLT, and αLF are determined by the optimization models. Similarly, αHW = 1 and αHN = 1 are used in Models SH3, SH9, and SH18 and the values of seven other coefficients (αHD, αMW, αMN, αMD, αLW, αLN, and αLD) are determined by the optimization models.

4 Results

4.1 Performance Evaluation of Model C

The results of the current operation of the Nanhua Reservoir-Chiahsien Weir system (Model C) based on 1959–2011 inflow series is served as a basis to compare the outcomes of other optimization models. The results of Model C in terms of the four shortage indices are MSR = 100%, TSR = 12.3%, AWS = 1.5 million m3/10-day, and RISK = 0.414, which are reported in Table 2.

Table 2 Outcomes of current operation and proposed optimization models for the Nanhua Reservoir-Chiahsien Weir system
Full size table

The most severe water shortage of Model C occurs in the period from November 1979 to May 1981 with a consecutive shortage duration of 57 10-day periods and total deficits of 105.9 million m3 due to extremely low inflow within this period. Furthermore, the shortage ratio of several periods within this shortage event exceeding 30% implies that the current operation rules with αL = 0.7 ineffectively cope with such extreme drought.

4.2 Optimal Hedging Policy of Model S

To derive the optimal solution of Model S, the maximum and minimum values of each shortage index are first determined by optimizing a single shortage index. These maximum and minimum values are also reported in Table 2. The optimal outcomes of Model S, including the optimal objective in terms of four shortage indices (associated with the corresponding normalized values) and the optimal decision variables (αM and αL), are summarized in Table 2.

Model S evidently outperforms Model C since the overall objective \( {D}_S^{\ast }=0.620>{D}_C^{\ast }=0.512 \). The better performance of Model S is attributed to the proposed demand rule curves that consider water-supply purpose only. Model S triggers water rationing when storage is below the upper rule curve (future 12 10-day periods demand). The optimal rationing coefficients of αM = 0.55 and αL = 0.5 lead to significant reductions in MSR (=49.8%) and AWS (=1.2 million m3/10-day) but at the cost of increasing TSR (=17.2%) and RISK (=0.704) when compared with the results of Model C.

To avoid severe shortages during impending droughts, early hedging associated with smaller rationing coefficients in Model S is able to reserve more water in advance. The merits of such hedging are effectively reducing the single-period shortage ratio but at the cost of increasing the shortage duration and total deficits due to early hedging. For example, the MSR decreases from 100% of Model C to 49.8% of Model S during the 1979–1981 drought. However, the shortage duration and total deficits increase from 57 and 105.9 of Model C to 61 10-day periods and 112.5 million m3 of Model S. Figure 4 illustrates the water shortages during the period of 1979–1981 for Models C and S. Early hedging and reduction of MSR in Model S are demonstrated in Fig. 4. In addition, graduate-varying shortages in Model S due to the fuzzified scheme, instead of abrupt changing shortages in Model C, are also observed in Fig. 4.

Fig. 4
figure 4

Water shortages of various models during the 1979–1981 drought

Full size image

4.3 Optimal Hedging Policies of Models ST3, ST9, and ST18

To explore the effects of past operation information on reservoir performance, three optimization models with past 3, 9, and 18 10-day periods (1, 3, and 6 months) of storage trends (Models ST3, ST9, and ST18) are analyzed in this section. The optimal outcomes of these models are reported in Table 2. Further improvements are observed for these three optimization models since \( {D}_{ST3}^{\ast } \), \( {D}_{ST9}^{\ast } \), and \( {D}_{ST18}^{\ast } \) are greater than \( {D}_S^{\ast } \). This fact indicates that past operation information is useful to assist reservoir releases and mitigate the negative impacts of droughts.

Among these models, the model with a short-term past storage trend outperforms the longer models since \( {D}_{ST3}^{\ast }=0.642>{D}_{ST9}^{\ast }=0.623>{D}_{ST18}^{\ast }=0.621 \). Illustrated in Fig. 5(a), the fluctuating variation of the normalized storage trend statistic (=\( {T}_n^t/{T}_{n,\mathit{\max}} \)) of Model ST3 reflects timely storage variation and derives a more effective hedging policy. For example, Model ST3 implementing hedging in states of MF, LT and LF significantly reduces TSR and RISK to 15.98% and 0.640, respectively, compared with TSR = 17.25% and RISK = 0.704 in Model S. In contrast, mild variation of longer past storage trends does not reflect short-term storage variation and leads to more conservative hedging rules. Early hedging implemented when storage is below the upper rule curve induces outcomes of Models ST9 and ST18 that are close to the results of Model S. That is, the effects of past storage trends on improving shortage characteristics decrease with longer past periods.

Fig. 5
figure 5

(a) The normalized statistic of past storage trends for Models ST3, ST9, and ST18, and (b) future SSIs for Models SH3, SH9, and SH18 during the 1979–1981 drought

Full size image

Model ST3 splits the consecutive shortage duration in the 1979–1981 drought obtained by Model S into two shortage events with a total shortage duration of 58 10-day periods and total deficits of 108.1 million m3, which are lower than the results of Model S. However, the effects of past storage trends on improving shortage characteristics gradually vanish when past periods become longer. The similar optimal hedging policy of Model ST18 with that of Model S results in similar outcomes and leads to a close overall performance (\( {D}_{ST18}^{\ast }=0.621 \)vs. \( {D}_S^{\ast }=0.620 \)).

4.4 Optimal Hedging Policies of Models SH3, SH9, and SH18

Since future inflow is not known in advance and certain uncertainty is involved in inflow prediction, the inflow series is assumed to be exactly known in this study to compare with the known past storage trend. The cumulative inflows of the future 3, 9, and 18 10-day periods (1, 3, and 6 months) for all periods are fitted as a probability distribution to reflect the magnitude of inflow with nearly constant demands. Then, the SSIs of the future 3, 9, and 18 10-day periods are calculated to reveal future wet or drought states.

The results of Models SH3, SH9, and SH18 are summarized in Table 2. These optimization models outperform Model S since \( {D}_{SH3}^{\ast }=0.654 \), \( {D}_{SH9}^{\ast }=0.648 \), and \( {D}_{SH18}^{\ast }=0.632 \) are greater than \( {D}_S^{\ast }=0.621 \). However, the effects on improving shortage objectives deteriorate with longer future periods. This is attributed to the fact that the short-term SSI actually reflects near-future inflow variation and results in an optimistic and effective hedging policy. Variations in various time-scale SSIs during the 1979–1981 drought are shown in Fig. 5(b) for demonstration. For instance, Model SH3 triggers water rationing when storage is below the lower rule curve due to a known future 1-month inflow. This hedging policy leads to the smallest RISK = 0.390 and TSR = 11.19% among all models. In contrast, Model SH18 uses the future 6-month SSI, which has mild variation and induces conservative hedging policy. This policy triggers hedging when storage and SSI states are categorized as MN, MD, LW, LN, and LD. Early hedging induces greater RISK = 0.710 and TSR = 13.80% in Model SH18.

It is worth noting that these three optimization models have different influences on shortage indices during the 1979–1981 drought. Illustrated in Fig. 4, Model SH3 induces the shortest shortage duration of 50 10-day periods and total deficits of 109.9 million m3. Similar to the results of Model ST3, the shortage duration is also split into two shortage events. Models SH9 and SH18 have similar outcomes, with 61 and 62 consecutive 10-day shortage periods and 108.9 and 110.1 million m3 of deficits, respectively.

5 Discussion

Two auxiliary factors, including past storage trends and future SSI, are incorporated into the proposed demand-based rule curves operation model to guide reservoir release. The results demonstrate the usefulness of these two auxiliary factors in improving reservoir performance during droughts. However, these two auxiliary factors have different impacts on the derived hedging rules and the corresponding outcomes.

The optimal hedging rules in Model SHs are generally more optimistic than those in Model STs for the same time scale. Since past storage trends used in Model STs cannot be directly extended into the future, conservative hedging rules are obtained by Model STs due to a lack of future inflow information. That is, more less-than-1 rationing coefficients in Model STs induce early hedging to conserve more water to cope with possible future droughts. This conservative hedging policy effectively reduces the MSR but at the cost of increasing the TSR and RISK. In contrast, the optimistic hedging rules derived by Model SHs have fewer rationing coefficients less than 1 since known future inflow conditions can be used to compensate for water deficits. Infrequent implementation of hedging in Model SHs leads to significant reductions in TSR and RISK. However, a greater MSR is obtained because later hedging leads to inadequate storage. These phenomena are observed in the results of 3- and 6-month time scale models. For example, hedging implemented in states of MD, LW, LN, and LD of Model SH9 leads to TSR = 12.39% and RISK = 0.680, which is lower than TSR = 16.75% and RISK = 0.704 in Model ST9 with hedging in states of MW, MN, MD, LW, LN, and LD.

The identical property in Models STs and SHs is that improvement in shortage characteristics deteriorates with longer periods in past storage trends and future SSIs. Short-term storage trends or SSIs capture the inherently fluctuating variations in reservoir storage or inflow and induce more effective hedging policies than models using long-term information. According to the overall objective D* summarized in Table 2, the favorable models for improving reservoir performance have the order of Models SH3, SH9, ST3, SH18, ST9, ST18, S, and C. Model SHs generally outperform Model STs. This fact reveals that the known future inflow is more useful than the past storage trend to achieve better reservoir performance during droughts. However, the obtained results depend on the known inflow, i.e., precise inflow prediction. Imprecise inflow prediction may induce ineffective hedging and deteriorate reservoir performance.

6 Conclusions

The results indicate that Model S outperforms Model C (\( {D}_S^{\ast }=0.620>{D}_C^{\ast }=0.512 \)), which implies that the proposed demand-based rule curve associated with fuzzified storage efficiently improves shortage characteristics during droughts. Further improvements are obtained by incorporating past storage trends (Model STs with \( {D}_{ST}^{\ast }>0.620 \)) and SSIs (Model STs with \( {D}_{SH}^{\ast }>0.620 \)) into Model S. Exactly known SSIs in Model SHs derive optimistic hedging policies that have fewer less-than-1 rationing coefficients and significantly reduce TSR and RISK. In contrast, Model STs without future inflow information lead to conservative hedging policies; that is, early hedging induced by more less-than-1 rationing coefficient effectively decrease the MSR.

Short-term storage trends and SSIs effectively capture inherent variations in storage and inflow and derive timely hedging. Mild variations in the long-term storage trends and SSIs, on the other hand, require early hedging to cope with droughts. According to the overall objective, Model SHs generally outperform Model STs, models with short-term storage trends or SSIs outperform the long-term models, and all optimization models outperform Model C. The most favorable model is Model SH3 with \( {D}_{SH3}^{\ast }=0.654 \).

Effective hedging policies depend on informed factors to trigger water rationing and ensure adequate storage and water supplies during droughts. In addition to the current storage, past storage trend and future SSI are useful auxiliary information to trigger hedging and induce significant overall performance improvements. Simultaneously, using past operation information, current storage, and future hydrologic information to construct an effective real-time hedging policy during droughts remains a topic for future studies. In addition, evaluating the effects of inflow prediction uncertainty on reservoir performance during droughts is also an important task.