1 Introduction

The risk analysis using to extreme value determination is achieved by the probability or cumulative distribution functions (PDF or CDF) in cases of stationary hydro-meteorological records. Extreme values help to design water resources systems properly, and also for their optimal management studies. Due to especially climate change impact, hydro-meteorological variables show increasing or decreasing trends, which render them into a nonstationary structure. For this objective, trend analyses are achieved mostly by the Mann-Kendall, Sperman’s Rho and sequential Mann-Kendall with Sen’s slope estimator trend tests (Kendall 1975; Mann 1945; Obeysekera and Salas 2016; Sen 1968; Spearman 1904). Each one of these methods is based on assumptions such as enough data length, serial independence, normal (Gaussian) PDF. On the other hand, Sen (2017) proposed a new trend determination approach without any assumption, namely, innovative trend analysis (ITA) method. It is originated from that a time series (parent time series) is considered as two half in ITA and this enables to researchers a comparison of second half of parent time series according to its first half unlike traditional methods. The traditional methods treat a time series as whole and there is no comparison between the first half and second. To find the comparison, they need an assumption which the time series or errors fit normal distribution. The normal distribution is universal set of the time series and the comparison is made with it. Also the normal distribution requires enough data length and serial independence assumptions. There are ITA implementation studies by different researchers showing that the method is efficient. Sonali and Kumar (2013) applied ITA on monthly, seasonal and annual maximum and minimum temperatures over all regions in India and explained that ITA outcomes match other trend test results such as Mann-Kendall, Sen’s slope, Spearman’s Rho and their derivatives. Elouissi et al. (2016) investigated Macta watershed monthly precipitation records to identify climatologically tendencies using ITA and expressed that ITA provides qualitative interpretations. Güçlü et al. (2016) used ITA and the trend possibilities of precipitation records of the Florya station in Istanbul were searched and then quantified using intensity-duration-frequency curves. Oztopal and Sen (2017) applied ITA for determining trends in seven different sub-climatological region of Turkey and mentioned that ITA enables partial trend determination in low, medium and high data ranges unlike monotonic trend. On the other hand, Salas and Obeysekera (2014); Bayazit (2015) and Obeysekera and Salas (2016) discussed nonstationary analysis usage so as to include trends in data analysis with PDF and CDF. As human intervention and anthropogenic climate change influences are becoming evident, nonstationary statistics would be better to represent the stochastic properties of the hydro-meteorological records (Rehan and Hall 2014). The nonstationary analysis is based on time varying probabilities that cannot be accounted by stationary processes. Lins and Cohn (2011) accepted the nonstationarity as a characteristic of the natural world.

The main purpose of this paper is to show the difference between the stationary and nonstationary behaviour of the hydro-meteorological data records. Stationarity works are rather old fashion methodologies and in the future the nonstationarity of the records must be taken into consideration through trend analyses.

2 Methodology

Knowledges on the temporal variation of hydrological characteristics and parameters gives one the opportunity to build a nonstationarity model, where the available information allows one to reduce the bias of the predictions (Montanari and Koutsoyiannis 2014). Herein, Innovative trend analysis (ITA) method is used to calculate the nonstationary changes in hydro-meteorological variables over time. The parent time series in hydro-meteorological record is divided into two halves and then the each half is sorted into ascending order for the implementation of the ITA as explained by Sen (2017). The first half is plotted on the horizontal and the second on vertical axis and the result is the scatter of points. Furthermore, the first half of parent time series must be plotted on the horizontal axis because the second half occurs after the first half changes with time. If the scatter of points remains wholly or partially above (below) the 1:1 (45°) straight-line then there is an increasing (decreasing) trend component in the hydro-meteorological record structure (Fig. 1a). As known, if a value on horizontal axis smaller (bigger) than a vertical value then a scatter point occurs below (above) the 45° straight-line on Cartesian coordinate system (see Fig. 1). If they are equals then the scatter point occurs over the 45° straight-line and there is no trend. In case of an increasing (decreasing) tendency on trend there is a steady increasing (decreasing) trend on data group (Fig. 1b).

Fig. 1
figure 1

a Monotonic trend. b Changing trend

Full size image

Figure 2 shows the application of ITA based on a hypothetical data which it contains a certain trend quantity and no measurement error to test the method’s efficient. To find the trend amount, first and second halves averages (μf, μs) are calculated (Fig. 2a) and the trend slope, a, is calculated by dividing the arithmetic averages difference by the half-length (n/2) of the data. Figure 2b shows the trend slope (a) and intersection point (b). All these calculations are performed using the following set of equations. In here, xi (yi) is the first (second) half group value and ti is time which is ith number. More detailed information about ITA is provided by Sen (2017).

$$ {\mu}_f=\frac{1}{\left(n/2\right)}{\sum}_{i=1}^{n/2}{x}_i $$
(1)
$$ {\mu}_s=\frac{1}{\left(n/2\right)}{\sum}_{i=1}^{n/2}{y}_i $$
(2)
$$ a=\frac{2\ast \left({\mu}_s-{\mu}_f\right)}{n} $$
(3)
$$ {y}_i=b+a\ast {t}_i $$
(4)
$$ b={\mu}_s-a\ast \overline{t} $$
(5)
Fig. 2
figure 2

Random stochastic processes (a) ITA graph (b) Time series graph

Full size image

Frequency is the occurrence probability of an event within a certain variable range. Let the first half data in order x1 < x2 < .... < xn/2 with the average, μf, and standard deviation, σf (Eqs. 1 and 6). Using Eq. (7), empirical cumulative distribution function in a stationary state (ECDF_S), F(xi,s), is simply obtained without regarded any trend and/or shift (jump, sudden change). An empirical equation is proposed in Eq. (8), where α, the trend in percent, a, the trend and μf, the mean of first half series (Eqs. 1 and 3). The trend existence in the data set implies nonstationary state. If the trend has a positive (negative) trend then with respect to the first half, the second half will have higher (smaller) extreme values. Thus a similar probability gives larger (smaller) a data value in the positive (negative) trend or the same data gives smaller (larger) a probability value. In order to import the effect of trend into the ECDF_S, these frequency values must be multiplied by (1 + α) and (1-α) as in Eq. (9) for positive and negative trend components, respectively. The equation gives an empirical cumulative frequency distribution in nonstationary state (ECDF_NS). In case of 1 ± α = 1, stationary case is valid without any trend component in the time series.

$$ {\sigma}_f=\sqrt{\frac{1}{n/2}{\sum}_{i=1}^{n/2}{\left({\mu}_x-{x}_i\right)}^2} $$
(6)
$$ F\left({x}_i,s\right)=\frac{2i}{n} $$
(7)
$$ \alpha =\frac{a}{\mu_f} $$
(8)
$$ F\left({x}_i, ns\right)=\left(1+\alpha \right)\frac{2i}{n} $$
(9)

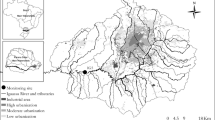
3 Study Area and Application

The methodology presented in the previous section is applied in the Oxford City, UK (Fig. 3). Monthly averages of daily maximum temperatures between 1853 and 2016 years are taken into consideration for implementing ITA and investigation of nonstationarity. A total of 164 × 12 = 1968 monthly temperature values are used and the coldest month is January (6.76 °C) and the warmest July (21.81 °C). The statistical information of the data is given in Table 1.

Fig. 3
figure 3

The location of Oxford, UK

Full size image
Table 1 A statistical summary of the monthly mean values of daily maximum temperatures(°C) for Oxford
Full size table

Average of the each half is calculated with Eqs. (1) and (2) which gave μf = 6.54 ̊C and μs = 6.98 ̊C for January and the same procedure is repeated for the other months. As an example, in January trend slope is calculated as a = 2×(6.98–6.54)/(2016–1853 + 1) = 0.0054 °C/year and trend in percent as α = a/μf = 0.0054/6.54 = 8.205 × 10−4 per year or 8.205 × 10−4 × 82 = 0.067 = 6.7% per period. The trend slope ranges from 0.002 °C/year in February to 0.013 °C/year in November. However, the trend in percent changes from 0.04 in August to 0.12 in November. The biggest trend is in November and the lowest trend takes place in February and August considered both indicators. It is observed that there is a bigger change in daily maximum temperatures in March, August, September, October and November compared to the minimum changes in February and May months (Fig. 4). Trends in winter are small amounts despite large percentages due to small temperatures. These different temperature trends can cause seasonal shifts in the future. The reason of different trends amounts among months may be local concentration differences of greenhouse gases such as water vapor, C2O, N2O, NO and CH4 among months. These greenhouse gases restrain reflection of shortwave solar radiation from the earth surface to the atmosphere (Toprak 2016). That is, the concentration differences may cause different trends on the temperatures among months.

Fig. 4
figure 4

Trend in monthly averages of daily maximum temperatures (°C)

Full size image

The ECDF_NS is obtained for January as F(xi, ns) = (1–0.067)xF(xi, s) is used according to Eq. (9). These processes are repeated for other months and ECDFs are plotted for Oxford daily maximum temperatures (see Fig. 5). Horizontal axis represents maximum temperatures and vertical axis shows ECDF_S, ECDF_NS and ECDF_A values (F(xi,s) and F(xi,ns)). In here, green, blue and red line represents first half data in stationary state, first half data in nonstationary state and all data in stationary state. It is seen that ECDF_S values are different than empirical cumulative distribution function values in all data state (ECDF_A) and this difference is bigger on March, August, September, October and November months than the other months. This difference is smaller between ECDF_NS and ECDF_A according to ECDF_S and ECDF_A. The minimum changes among ECDF_S and ECDF_A are seen in January, February and June months. Root mean square error (RMSE) method is used for testing the method’s accuracy (Eq. 10). In here, obs and calc represents observed and calculated value, and n is data length. RMSE between ECDF_NS and ECDF_A ranges from 0.02 to 0.091 whereas ECDF_S and ECDF_A from 0.027 to 0.13. The nonstationary approach makes it possible to reduce errors among 14.1% and 53.1% (Table 2).

$$ RMSE=\sqrt{\frac{\sum_{i=1}^n{\left( obs(i)-\mathrm{calc}(i)\right)}^2}{n}} $$
(10)
Fig. 5
figure 5

Empirical cumulative distribution functions for monthly averages of maximum daily temperatures on Oxford

Full size image
Table 2 Nonstationary data analysis test results and error amounts
Full size table

4 Conclusions

The main purpose of this paper is to use the innovative trend analysis (ITA) method and propose an update of the stationary frequency calculations by inclusion of the trend, and hence, nonstationary character of hydro-meteorological records. Oxford City, UK, monthly mean of daily maximum temperatures are used for testing cumulative nonstationary frequency analysis. The method is applied to monthly averages of daily maximum temperature values in Oxford, but can be used for other data and study areas. The nonstationary state is considered for frequency analysis using trend in percent. The trend obtained with ITA is added to empirical cumulative distribution function values in stationary state (ECDF_S) which are used for comparison of stationary and nonstationary states. Nonstationary empirical cumulative distribution frequency values (ECDF_NS) in first half data fits better to empirical cumulative distribution frequency in all data (ECDF_A) according to ECDF_S. Among ECDF_S and ECDF_A values, the difference is small, in where the trends have small values. This state shows that trend quantity lead to nonstationarity. Difference between ECDF_NS and ECDF_A is smaller than ECDF_S and ECDF_A values. The RMSE results support these findings and give smaller error amounts in the nonstationary state according to stationary state. It is concluded that nonstationary state gives more realistic results than stationary state. Nonstationary analysis enables qualitative forecasting of the future and thus, long-term planned hydraulic structures can be planned efficiently and resources are used more efficiently. Also, ITA can be useful for policy makers for determining risky areas with regard to flooding, drought, air temperature, sea level etc.