1 Introduction

Water loss through pipe leakage in urban water supply systems has become a continuous and global challenge for its influence to the water and energy resources as well as the public service quality (Colombo and Karney 2002). Amongst various leak detection methods developed in the past few decades, the transient-based method was proved to be efficient, economic and non-intrusive (Colombo et al. 2009; Lee et al. 2013). In summary, four typical types of transient-based methods are commonly developed in the literature, including: (1) Transient Wave Reflection (TWR) based method, such as Brunone (1999), Brunone and Ferrante (2001), Meniconi et al. (2011, 2015); (2) Transient Wave Damping (TWD) based method by Wang et al. (2002); (3) Transient Frequency Response (TFR) based method by Mpesha et al. (2001), Ferrante and Brunone (2003), Covas et al. (2005), Lee et al. (2006), Sattar and Chaudhry (2008), Duan et al. (2011), Kim (2016), Duan (2016) and Sun et al. (2016); (4) Inverse Transient Analysis (ITA) based method studied in Liggett and Chen (1994) and Vítkovský et al. (2000).

The TWR and TWD based methods, which are mainly dependent on the time domain transient information, have been successfully applied to the simple pipeline systems with signal injection of single wave front such as fast valve closure (e.g., Wang et al. 2002; Ferrante et al. 2009; Meniconi et al. 2015), but these methods may become inadequate to accurately locate and size the leakage in the pipeline due to the relatively small bandwidth of the wave injection and reflection. For example, an error of about ±400 m was generated for the field pipeline test with a total length of about 5 km conducted by Meniconi et al. (2015). The ITA-based method is the most robust and comprehensive one among these four types of method, but its accuracy and efficiency are highly dependent on the historical and available database (quantity and quality) as well as the selected inverse analysis algorithm (e.g., Liggett and Chen 1994; Vítkovský et al. 2000), so that it is so far impractical for the applications to large-scale and complex pipeline systems (Colombo et al. 2009). While for the TFR-based method, it was found to have relatively high tolerance to the system noises and data uncertainties for the applications in simple pipeline systems (Lee et al. 2013).

In a recent study of Duan (2016), the TFR-based method has been extended to relatively complex pipeline systems that may include simple branched and looped pipe junctions. The numerical tests in that study have demonstrated the feasibility of the TFR-based method in relatively more complex pipeline systems with junctions compared to previous studies in this field (e.g., Lee et al. 2006; Duan et al. 2011; Sun et al. 2016), but the results also indicated that the decreasing trend of the detection accuracy of this method with an increase of the pipe connection complexity. In other words, the application of this developed TFR-based method may be affected potentially by different factors/parameters in both the methodology development process and the practical pipeline system application process. The influences of such factors are worthy of further investigations in order to better understand and apply this efficient and non-intrusive method in practice, which is the scope of this study.

In fact, various uncertainty factors are existent and inevitable in practical transient pipe flow systems, including the system configurations, pipeline properties, initial and boundary conditions, system operations and data measurement (Duan et al. 2010). These factors may have great influences to the transient system design and analysis. For example, the study of Duan et al. (2010) indicated the uncertainty of air component in the water supply pipelines may cause the inappropriate results of the design for transient pipeline system based on the original deterministic conditions. Furthermore, the uncertainty analysis of transient-based modelling and leak detection has been conducted in Duan (2015). The results of that study have evidenced the significant impacts of different uncertainty factors in the pipe system on the accuracy of the developed transient models and leak detection methods. However, due to the limitation of the used transient model and TFR method, only the simple situation of single-pipeline systems has been considered and investigated in that former study of Duan (2015).

Based on the extended TFR method for complex pipeline systems in Duan (2016), this paper further evaluates the extended TFR-based leak detection method for the following two aspects: (1) the accuracy of the methodology development with different approximations and assumptions imposed in analytical derivation process; and (2) the sensitivity of the developed method to different uncertainties of system factors and operation conditions in practical water pipeline systems. The influence factors considered for the analysis include system properties, model incapability and data measurement. For these two purposes of investigation, the analytical analysis of the theoretical method development is firstly performed to examine the influence of the linearization approximations and assumptions on the TFR-based method obtained in Duan (2016). The First-Order-Second-Moment (FOSM) based analysis method and numerical applications are then used for sensitivity study of the developed TFR-based method to different influence factors (e.g., initial and boundary conditions) in the water pipeline system. The results obtained in this study are used to explain the validity and limitations of the TFR-based method for practical applications.

2 Models and Methods

For clarification, the developed TFR-based method of leak detection for complex pipeline systems and the analysis methods adopted for the investigation are presented in this section.

2.1 TFR-Based Leak Detection Method

The analytical form of the extended TFR-based leak detection formula obtained in the previous study of Duan (2016) can be expressed by:

$$ {\widehat{h}}_{Ln}=\frac{K_L}{C_{1n}}\left[{C}_{2n}+{C}_{3n}\sin \left(2{\mu}_n{x}_{Ln}+{C}_{4n}\right)\right], $$
(1)

where \( {\widehat{h}}_{Ln} \) is converted transient response of pressure head in the frequency domain; C1n, C2n, C3n, and C4n are intact system based known coefficients, which have been derived in Duan (2016); K L and x L are leak size and location, respectively; μn is wave propagation coefficient; and n is pipe number. Particularly, for branched pipeline case, C2n = C3n = 1; and for looped pipeline case, C2n and C3n are given in Duan (2016). The GA-based optimization framework proposed in Duan (2016) is again used here for obtaining the solution for potential leakage information. Note that in this study, the case of the branched pipeline system is used for the accuracy analysis of the TFR result derivation process, and that of the simple looped pipeline system for the FOSM-based sensitivity analysis.

2.2 FOSM-Based Sensitivity Analysis

The result of Eq. (1) shows the dependence of the system TFR on the system parameters and potential leakage information. As a result, the leakage parameters (size and location) can be obtained through inverse analysis of Eq. (1) based on the TFR data by simulations for numerical tests or measurements for experimental applications. Meanwhile, the applications in Duan (2016) indicated that the leak detection results by Eq. (1) can be potentially affected by the uncertainties of system information such as initial and boundary conditions. In this study, the FOSM analysis method is adopted for the sensitivity analysis of the developed method to different uncertainty factors and parameters in water supply pipeline systems (Ang and Tang 1975; Tung et al. 2006; Duan et al. 2010). To this end, Eq. (1) is firstly expressed as multi-variable functions for different leakage properties:

$$ {F}_p={F}_{x_L,{K}_L}={G}_p\left({\widehat{h}}_{Ln},Q,L,D,a,f\cdots \right)={G}_p\left({X}_1,{X}_2,{X}_3,\cdots {X}_k\right), $$
(2)

where F p is the information of pipe leakage to be detected (location x L and size K L ); G p () represents a function relationship; subscript p indicates each parameter of the leak (x L or K L ); Q, L, D, a and f are discharge, pipe length, diameter, wave speed and friction factor respectively; X1 to X k are uncertainty factors considered in the system; k is the number of uncertainty factors.

The stochastic characteristics of each function (F) in Eq. (2) can be approximated by the FOSM analysis as (Ang and Tang 1975; Tung et al. 2006) (with the subscript p neglected here for simplicity):

$$ {\lambda}_F\approx G\left({\mu}_{X_1},{\mu}_{X_2},{\mu}_{X_3},\cdots {\mu}_{X_k}\right), $$
(3)
$$ {\delta}_F^2\approx {\Delta}_G^2+\frac{1}{\mu_F^2}\sum \limits_{j=1}^k\sum \limits_{i=1}^k\left({\xi}_{ij}{c}_i{c}_j{\sigma}_i{\sigma}_j\right), $$
(4)

in which λ = mean value of variable X i or the function G(); δ = coefficient of variation (COV); Δ G  = bias of the model formula; c j  = ∂G/∂X j is sensitivity coefficient that is evaluated at (λ1, λ2, λ3, …, λ k ) based on Eq. (1); σ i  = μiδi representing the standard deviation of variable X i ; ξ ij  = correlation coefficient between X i and X j ; and i, j = index numbers. Since the main objective of this study is to inspect the influence of different input uncertainties on the developed TFR-based method, the bias of this model itself is not considered in this sensitivity analysis here, which is instead analyzed by the accuracy analysis of derivation approximations later in this study (i.e., the analytical analysis for achieving the first objective of this study). Therefore, it is assumed that Δ G  ≈ 0 and ξ ij  ≈ 0 for ∀(i ≠ j) in Eq. (4) for sensitivity analysis, and the contribution of each input uncertainty variable X j to the total variability of the response function can be calculated by (Tung et al. 2006),

$$ {\eta}_{X_j}\left(\%\right)\approx {\left(\frac{c_{X_j}{\sigma}_{X_j}}{\lambda_F{\delta}_F}\right)}^2\times 100, $$
(5)

in which η represents the individual contribution coefficient of each factor (X j ) to the total variability of the response, and other symbols refer to the definitions above.

Furthermore, it is necessary to note that the branched and looped pipeline systems, which are studied in Duan (2016), are used for the theoretical accuracy analysis and the sensitivity analysis respectively for illustration in this study. The similar analysis process of the TFR-based leak detection method can be referenced and applied to any other pipeline systems with different branched and looped junctions in the future work.

3 System Conditions and Influence Factors

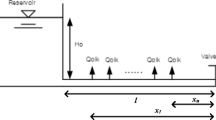
The numerical test systems with simple branched and looped junctions studied in Duan (2016) are used herein for the analysis, which are shown in Figs. 1a and b respectively. The system parameter settings are provided in the figure. In this study, however, the downstream inline valve (V1 in Fig. 1) is initially open for generating a steady-state discharge of 0.2 m3/s (i.e., Q s  = 0.2 m3/s), so as to analyze the uncertainty influence of initial conditions.

Fig. 1
figure 1

Sketches for the test pipeline systems with: (a): branched pipeline junction; (b) looped pipeline junction

Full size image

In water supply pipeline systems, many factors including pipeline system parameters and operation conditions as well as the data measurement are usually subject to uncertainties (e.g., Duan et al. 2010; Duan 2016). In this study, following uncertainty factors (X j ) are considered for the investigation,

  1. (1)

    Pipe properties (length L, diameter D, wave speed a and friction factor f);

  2. (2)

    Initial discharge condition (Q s ) at downstream valve (V1 in Fig. 1);

  3. (3)

    Data measurement (\( {\widehat{h}}_L \)) in the frequency domain.

For sensitivity analysis in this study, the mean values of these uncertainty factors are adopted as the deterministic case (as shown in Fig. 1). For simplicity and illustration, the uncertainty factors considered herein are assumed to be independent with ξ ij  = 0 for ∀(i ≠ j) and the δ Xj  = 0.1 for comparative analysis in this study. For other practical application cases of different ξ ij and δ Xj values can be conducted by using similar analysis method and procedures presented in this study. Consequently, the sensitivity results of the leak detection (x L and K L ) by the TFR-based method can then be examined to each uncertainty factor by the FOSM method described above.

4 Accuracy Evaluation of the TFR Method

As the first objective of this study, i.e., to evaluate the accuracy of the TFR-based leak detection method in Eq. (1) for complex pipeline systems, it is necessary to revisit the detailed theoretical analysis process of this method in the former study of Duan (2016). Actually, similar results have been obtained for both cases of the branched and looped pipeline systems shown in Fig. 1, since the same transfer matrix method and procedure were applied for both derivation processes (see appendix in Duan 2016). For clarification, only the case of the branched pipeline with single leakage on the pipe 1 in Fig. 1a is taken here for illustration.

Based on the transfer matrix method shown in Duan (2016), the full form of the TFR results of pressure head for branched pipeline system under intact system resonant condition is given by,

$$ {h}_L^B=\frac{\begin{array}{c}\left[\sin \left({\mu}_3{l}_3\right)\cos \left({\mu}_2{l}_2\right)\sin \left({\mu}_1{l}_1\right)+\frac{Y_2}{Y_3}\cos \left({\mu}_3{l}_3\right)\sin \left({\mu}_2{l}_2\right)\sin \left({\mu}_1{l}_1\right)+\frac{Y_2}{Y_1}\sin \left({\mu}_3{l}_3\right)\sin \left({\mu}_2{l}_2\right)\cos \left({\mu}_1{l}_1\right)\right]\\ {}-i\frac{K_L{Y}_1}{2}\left[\begin{array}{l}\left(\sin \left({\mu}_3{l}_3\right)\cos \left({\mu}_2{l}_2\right)+\frac{Y_2}{Y_3}\cos \left({\mu}_3{l}_3\right)\sin \left({\mu}_2{l}_2\right)\right)\left[\cos \left({\mu}_1{x}_1-{\mu}_1{x}_2\right)-\cos \left({\mu}_1{l}_1\right)\right]\\ {}+\frac{Y_2}{Y_1}\sin \left({\mu}_3{l}_3\right)\sin \left({\mu}_2{l}_2\right)\left[\sin \left({\mu}_1{l}_1\right)+\sin \left({\mu}_1{x}_1-{\mu}_1{x}_2\right)\right]\end{array}\right]\end{array}}{\frac{1}{2}{K}_L\frac{\cos \left({\mu}_2{l}_2\right)}{\sin \left({\mu}_1{l}_1\right)}\sin \left({\mu}_3{l}_3\right)\left[1-\cos \left(2{\mu}_1{x}_1\right)\right]}, $$
(6)

where x1 + x2 = l1; K L is the discharge impendence factor of leak orifice and K L  = QL0/2ΔHL0 with QL0 and ΔHL0 being steady state discharge and head difference at the leak orifice, respectively. For simplicity, Eq. (6) can be re-written as,

$$ {h}_L^B=\frac{R_n-{iI}_n}{\frac{1}{2}{K}_L\frac{\cos \left({\mu}_2{l}_2\right)}{\sin \left({\mu}_1{l}_1\right)}\sin \left({\mu}_3{l}_3\right)\left[1-\cos \left(2{\mu}_1{x}_1\right)\right]}, $$
(7)

where R n and I n represent the real and imaginary parts of the numerator of Eq. (6), and,

$$ {R}_n=\sqrt{{S_A}^2+{S_B}^2}\sin \left({\mu}_1{l}_1+{S}_C\right), $$
(8)
$$ {I}_n={K}_L{Y}_1\sin \left({\mu}_1{x}_1\right)\sqrt{{S_A}^2+{S_B}^2}\sin \left({\mu}_1{x}_2+{S}_C\right), $$
(9)

in which:

$$ {S}_A=\sin \left({\mu}_3{l}_3\right)\cos \left({\mu}_2{l}_2\right)+\frac{Y_2}{Y_3}\cos \left({\mu}_3{l}_3\right)\sin \left({\mu}_2{l}_2\right);{S}_B=\frac{Y_2}{Y_1}\sin \left({\mu}_3{l}_3\right)\sin \left({\mu}_2{l}_2\right);{S}_C=\mathrm{actan}\left(\frac{S_B}{S_A}\right). $$

Therefore, the relative amplitude of the imaginary part to the real part becomes,

$$ \frac{\left|{I}_n\right|}{\left|{R}_n\right|}=\left|{K}_L{Y}_1\right|\left|\frac{\sin \left({\mu}_1{x}_1\right)\sin \left({\mu}_1{x}_2+{S}_C\right)}{\sin \left({\mu}_1{l}_1+{S}_C\right)}\right|={F}_S\cdot {F}_L. $$
(10)

where F S  = |K L Y1| for representing the influence of leak size, and F L = \( \left|\frac{\sin \left({\mu}_1{x}_1\right)\sin \left({\mu}_1{x}_2+{S}_C\right)}{\sin \left({\mu}_1{l}_1+{S}_C\right)}\right| \) for the influence of leak location. Particularly, when |R n | >  > |I n |, Eq. (7) can be simplified to the result of Eq. (1) for the branched pipeline system.

4.1 Influence of Leak Size

In Eq. (10), the factor F S indicates the influence of leak size on the accuracy of the TFR-based method. It is assumed that the leak discharge can be expressed through an orifice equation,

$$ {Q}_{L0}=\left({C}_d{A}_{L0}\right)\sqrt{2g\Delta {H}_{L0}}, $$
(11)

in which C d represents the discharge coefficient of an orifice, and AL0 is the leaking area that is dependent of the leak size and shape. Therefore,

$$ {F}_S=\left|\frac{Q_{L0}}{2\Delta {H}_{L0}}\frac{a}{gA}\right|=\frac{\left({C}_d{A}_{L0}\right)}{A}\frac{a}{\sqrt{2g\Delta {H}_{Lo}}}=\frac{C_d{C}_Aa}{\sqrt{2g\Delta {H}_{Lo}}}, $$
(12)

where C A is the relative size of leak orifice area to the pipe cross-sectional area. For example, the following general orders of the parameters in water supply pipelines:

$$ a\sim 1000\ \mathrm{m}/\mathrm{s},g\sim 10\ \mathrm{m}/{\mathrm{s}}^2,\mathrm{and}\ {C}_d\kern0.5em <1, $$

which leads to,

$$ {F}_S<\frac{1000{C}_A}{\sqrt{20\Delta {H}_{Lo}}}. $$
(13)

As a result, the variation of the factor F S with C A and ΔHL0 is plotted in Fig. 2.

Fig. 2
figure 2

Influence of leak size related factor to the accuracy of TFR-based method: (a) 3D distribution surface result; (b) 2D contour line result

Full size image

The result of Fig. 2 shows that, the simplified result of Eq. (1) for the TFR-based method is preferably valid to the cases of relatively small pipe leak (i.e., the leak size is much smaller than pipe size). For example, under a common range of ΔHL0 ~ [5 m, 100 m] (which indicates of practical water supply system situations), F S  < < 1 when C A  < 0.001 (see Fig. 2b).

4.2 Influence of Leak Location

In addition to the leak size, the influence of the leak location and corresponding system configurations on the accuracy of the TFR-based method is governed by the factor F L in Eq. (10). Clearly, for different system configurations (L, D, a), the influence of this F L magnitude to the accuracy of the TFR-based method will be different. Herein, the case of branched pipeline system with single leakage on pipe 1 in Fig. 1a is examined for illustration. Based on the given system configuration and parameters in Fig. 1a, the magnitudes of F L for different leak locations and resonant peak numbers are plotted in Fig. 3.

Fig. 3
figure 3

Influence of leak location related factor to the accuracy of TFR-based method: (a) 3D distribution surface result; (b) 2D contour line result

Full size image

The result of Fig. 3 shows that the amplitudes of the leak location influence factor F L for few resonant frequencies in this studied case (e.g., the 5th, 12th and 19th peaks in Fig. 3) are comparable to or even more dominant than the influence of the leak size F S . Therefore, the accuracy of leak detection results in this case of branched pipeline system in Fig. 1a can be potentially affected by the simplification of neglecting the imaginary part in Eq. (9) for obtaining the simplified result of Eq. (1). In other words, the influence of the leak location to the validity and accuracy of the TFR-based method in Eq. (1) is dependent of the resonant peak amplitudes utilized for the analysis in the TFR-based leak detection procedure. Actually, the results of Figs. 2 and 3 on the influence of the actual leak information (location and size) to the transient responses (e.g., amplitude variation pattern in the frequency domain) and transient-based leak detection methods (e.g., TWR, TWD and TFR methods) are consistent with previous results and findings in the literature (e.g., Ferrante et al. 2014). The detailed influences of leak location and size and the improvement of the TFR-based method are further discussed later in this study.

4.3 Influence of Friction Effects

In addition to leakage, many other factors in water supply pipelines such as pipe-wall friction effect and wave-fluid-structure interactions may affect the magnitude damping of the TFR results (Duan et al. 2011). The effect of pipe-wall friction is analyzed for its influence to the TFR damping in this section, which is reflected by the following factor (Duan 2016):

$$ {F}_R=\left|\sqrt{1-i\frac{gAR}{\omega }}\right|, $$
(14)

such that the impedance coefficient and wave propagation factor can be expressed as follows:

$$ Y={Y}_0{F}_R;\mu ={\mu}_0{F}_R, $$
(15)

where F R is frictional resistance related influence factor; R = f0Q s /gDA2 is resistance factor of pipe-wall friction, with f0 being the Darcy-Weisbach friction factor; Y0 = −a/gA and μ0 = ω/a are impedance coefficient and wave propagation factor for frictionless pipelines, respectively. For the branched pipeline system in Fig. 1a, the results of the influence factor F R for typical variation ranges of pipe friction f0 and resonant frequencies ω rf (i.e., peak numbers) are shown in Fig. 4a and b for 3D surface and 2D contour distributions respectively.

Fig. 4
figure 4

Influence of pipe friction related factor to the accuracy of TFR-based method: (a) 3D distribution surface result; (b) 2D contour line result

Full size image

The results demonstrate clearly the little impact of the pipe-wall friction on the damping of the TFR results, with an order of 10−4 for the whole frequency domain focused in this study. Moreover, the influence of pipe-wall friction is increasing with the magnitude of the friction factor, but is decreasing with the peak number (resonant frequency). On this point, this result is consistent with the results from previous studies that the effect of pipe-wall friction has little influence to the validity and accuracy of the TFR-based method for pipe defect detection, which has also become one of the advantages of the TFR-based method discussed in the literature (e.g., Duan et al. 2011). It is also noted that only the quasi-steady friction effect is considered in this study and the influence of frequency dependent unsteady friction effect is not included herein because of its case-sensitive effect (e.g., transient operations, wave bandwidth injections and pipe scales) (Meniconi et al. 2014).

5 Sensitivity Analysis of the TFR Method

To examine the sensitivity of the developed TFR-based method in Duan (2016), the FOSM method is applied herein to Eq. (2) through Eq. (5). To this end, the Eq. (1) of the TFR-based method is firstly re-written in terms of leak size and location respectively as:

$$ {F}_{K_L}={K}_L=\frac{{\widehat{h}}_{Ln}{C}_{1n}}{\left[{C}_{2n}+{C}_{3n}\sin \left(2{\mu}_n{x}_{Ln}+{C}_{4n}\right)\right]}, $$
(16)
$$ {F}_{x_L}=\sin \left(2{\mu}_n{x}_{Ln}+{C}_{4n}\right)=\frac{{\widehat{h}}_{Ln}{C}_{1n}}{C_{3n}{K}_L}-\frac{C_{2n}}{C_{3n}}. $$
(17)

For illustration, the case of the looped pipeline system with single leakage on pipe 1 in Fig. 1b is taken for the analysis (i.e., n = 1 in above equations).

5.1 FOSM-Based Derivation of Sensitivity Coefficients

By following the principle given in Eq. (4), the sensitivity coefficients (c j ) of the leak detection information (size and location) to different uncertainty factors considered in this study can be derived and obtained as,

$$ {\displaystyle \begin{array}{l}{c}_{K_L}=\frac{\partial {K}_L}{\partial p}\\ {}={K}_L\left[\frac{1}{C_{11}}\frac{\partial {C}_{11}}{\partial p}+\frac{1}{{\widehat{h}}_{L1}}\frac{\partial {\widehat{h}}_{L1}}{\partial p}\right]\\ {}-\frac{K_{:L}^2}{{\widehat{h}}_{L1}{C}_{11}}\left[\frac{\partial {C}_{21}}{\partial p}+{F}_{x_L}\frac{\partial {C}_{31}}{\partial p}+{C}_{31}\cos \left(2{\mu}_1{x}_{L1}+{C}_{41}\right)\left(\frac{\partial {C}_{41}}{\partial p}+2{x}_{L1}\frac{\partial {\mu}_1}{\partial p}\right)\right]\end{array}}, $$
(19)
$$ {\displaystyle \begin{array}{l}{c}_{x_L}=\frac{\partial {x}_{L1}}{\partial p}\\ {}=-\frac{x_{L1}}{\mu_1}\frac{\partial {\mu}_1}{\partial p}-\frac{1}{2{\mu}_1}\frac{\partial {C}_{41}}{\partial p}\\ {}+\frac{1}{2{K}_L{C}_{31}{\mu}_1{F}_{x_L}}\left[{\widehat{h}}_{L1}\frac{\partial {C}_{11}}{\partial p}+{C}_{11}\frac{\partial {\widehat{h}}_{L1}}{\partial p}+\frac{K_L{C}_{21}-{\widehat{h}}_{L1}{C}_{11}}{C_{31}}\frac{\partial {C}_{31}}{\partial p}-{K}_L\frac{\partial {C}_{21}}{\partial p}\right]\end{array}}, $$
(20)

where p represents each of the six uncertainty factors (l1, D1, a1, f1, Q s , \( {\widehat{h}}_L \)) considered in this study. For the looped pipeline system in Fig. 1b, the derivative terms of parameters (C11, C21, C31, C41, μ1, \( {\widehat{h}}_L \)) in terms of each factor (p) can be obtained and calculated based on the relevant expressions given in Duan (2016). The algebraic terms are calculated based on the deterministic values for the coefficients and variables involved in the system. The final results of the derivatives in Eqs. (19) and (20) above are summarized as follows:

  1. (1)

    for parameter C11:

$$ \frac{\partial {C}_{11}}{\partial {l}_1}=-\frac{2{\mu}_1}{Y_1}\left[\begin{array}{l}-\alpha {Y}_2\sin \left({\mu}_2{l}_2\right)\sin \left({\mu}_1{l}_1\right)+\gamma {Y}_1\cos \left({\mu}_2{l}_2\right)\cos \left({\mu}_1{l}_1\right)\\ {}+ i\varphi \cos \left({\mu}_2{l}_2\right)\sin \left({\mu}_1{l}_1\right)+ i\beta {Y}_2{Y}_1\sin \left({\mu}_2{l}_2\right)\cos \left({\mu}_1{l}_1\right)\end{array}\right], $$
(21)
$$ \frac{\partial {C}_{11}}{\partial {D}_1}=\frac{\pi {D}_1{Y}_1}{4{A}_1}\left[\frac{C_{11}}{Y_1}+\frac{2}{Y_1}\left(\gamma \cos \left({\mu}_2{l}_2\right)\sin \left({\mu}_1{l}_1\right)+ i\beta {Y}_2\sin \left({\mu}_2{l}_2\right)\sin \left({\mu}_1{l}_1\right)\right)\right], $$
(22)
$$ {\displaystyle \begin{array}{c}\frac{\partial {C}_{11}}{\partial {a}_1}=-\frac{Y_1}{a_1}\left[\frac{C_{11}}{Y_1}+\frac{2}{Y_1}\left(\gamma \cos \left({\mu}_2{l}_2\right)\sin \left({\mu}_1{l}_1\right)+ i\beta {Y}_2\sin \left({\mu}_2{l}_2\right)\cos \left({\mu}_1{l}_1\right)\right)\right]\\ {}+\frac{2}{Y_1}\frac{\mu_1{l}_1}{a_1}\left[\begin{array}{l}\alpha {Y}_2\sin \left({\mu}_2{l}_2\right)\sin \left({\mu}_1{l}_1\right)+\gamma {Y}_1\cos \left({\mu}_2{l}_2\right)\cos \left({\mu}_1{l}_1\right)\\ {}+ i\varphi \cos \left({\mu}_2{l}_2\right)\sin \left({\mu}_1{l}_1\right)+ i\beta {Y}_2{Y}_1\sin \left({\mu}_2{l}_2\right)\cos \left({\mu}_1{l}_1\right)\end{array}\right]\end{array}}, $$
(23)
$$ \frac{\partial {C}_{11}}{\partial {f}_1}=i\frac{gA_1{R}_1}{\omega {f}_1{\left({F}_R\right)}^2}\left[\frac{C_{11}}{2}+\frac{\mu_1{l}_1}{Y_1}\left(-\alpha {Y}_2\sin \left({\mu}_2{l}_2\right)\sin \left({\mu}_1{l}_1\right)+ i\varphi \cos \left({\mu}_2{l}_2\right)\sin \left({\mu}_1{l}_1\right)\right)\right], $$
(24)
$$ \frac{\partial {C}_{11}}{\partial {Q}_s}=i\frac{gA_1{R}_1}{\omega {Q}_s{\left({F}_R\right)}^2}\left[\frac{C_{11}}{2}+\frac{\mu_1{l}_1}{Y_1}\left(-\alpha {Y}_2\sin \left({\mu}_2{l}_2\right)\sin \left({\mu}_1{l}_1\right)+ i\varphi \cos \left({\mu}_2{l}_2\right)\sin \left({\mu}_1{l}_1\right)\right)\right], $$
(25)
$$ \frac{\partial {C}_{11}}{\partial {\widehat{h}}_{L1}}=0; $$
(26)
  1. (2)

    for parameter C21:

$$ \frac{\partial {C}_{21}}{\partial {l}_1}={\mu}_1\left[\begin{array}{l}-\gamma \cos \left({\mu}_2{l}_2\right)\cos \left({\mu}_1{l}_1\right)+\alpha \frac{Y_1}{Y_2}\sin \left({\mu}_2{l}_2\right)\sin \left({\mu}_1{l}_1\right)\\ {}-i\frac{\varphi }{Y_2}\sin \left({\mu}_2{l}_2\right)\cos \left({\mu}_1{l}_1\right)- i\beta {Y}_1\cos \left({\mu}_2{l}_2\right)\sin \left({\mu}_1{l}_1\right)\end{array}\right], $$
(27)
$$ \frac{\partial {C}_{21}}{\partial {D}_1}=\frac{\pi {D}_1{Y}_1}{4{A}_1}\left[\alpha \frac{1}{Y_2}\sin \left({\mu}_2{l}_2\right)\cos \left({\mu}_1{l}_1\right)- i\beta \cos \left({\mu}_2{l}_2\right)\cos \left({\mu}_1{l}_1\right)\right], $$
(28)
$$ {\displaystyle \begin{array}{c}\frac{\partial {C}_{21}}{\partial {a}_1}=-\frac{\mu_1{l}_1}{a_1}\left[\begin{array}{l}-\gamma \cos \left({\mu}_2{l}_2\right)\cos \left({\mu}_1{l}_1\right)+\alpha \frac{Y_1}{Y_2}\sin \left({\mu}_2{l}_2\right)\sin \left({\mu}_1{l}_1\right)\\ {}-i\frac{\varphi }{Y_2}\sin \left({\mu}_2{l}_2\right)\cos \left({\mu}_1{l}_1\right)- i\beta {Y}_1\cos \left({\mu}_2{l}_2\right)\sin \left({\mu}_1{l}_1\right)\end{array}\right]\\ {}+\frac{Y_1}{a_1}\left[-\alpha \frac{1}{Y_2}\sin \left({\mu}_2{l}_2\right)\cos \left({\mu}_1{l}_1\right)+ i\beta \cos \left({\mu}_2{l}_2\right)\cos \left({\mu}_1{l}_1\right)\right]\end{array}}, $$
(29)
$$ \frac{\partial {C}_{21}}{\partial {f}_1}=-i\frac{gA_1{\mu}_1{R}_1{l}_1}{2\omega {f}_1{\left({F}_R\right)}^2}\left[\alpha \frac{Y_1}{Y_2}\sin \left({\mu}_2{l}_2\right)\sin \left({\mu}_1{l}_1\right)- i\beta {Y}_1\cos \left({\mu}_2{l}_2\right)\sin \left({\mu}_1{l}_1\right)\right], $$
(30)
$$ \frac{\partial {C}_{21}}{\partial {Q}_s}=-i\frac{gA_1{\mu}_1{R}_1{l}_1}{2\omega {Q}_s{\left({F}_R\right)}^2}\left[\alpha \frac{Y_1}{Y_2}\sin \left({\mu}_2{l}_2\right)\sin \left({\mu}_1{l}_1\right)- i\beta {Y}_1\cos \left({\mu}_2{l}_2\right)\sin \left({\mu}_1{l}_1\right)\right], $$
(31)
$$ \frac{\partial {C}_{21}}{\partial {\widehat{h}}_{L1}}=0; $$
(32)
  1. (3)

    for parameter C31 and C41:

$$ \frac{\partial {C}_{31}}{\partial p}=\frac{1}{C_{31}}\left[{S}_1^O\frac{\partial {S}_1^O}{\partial p}+{T}_1^O\frac{\partial {T}_1^O}{\partial p}\right], $$
(33)
$$ \frac{\partial {C}_{41}}{\partial p}=\frac{1}{{\left({T}_1^O\right)}^2+{\left({S}_1^O\right)}^2}\left({T}_1^O\frac{\partial {S}_1^O}{\partial p}-{S}_1^O\frac{\partial {T}_1^O}{\partial p}\right)-\left({\mu}_1\frac{\partial {l}_1}{\partial p}+{l}_1\frac{\partial {\mu}_1}{\partial p}\right), $$
(34)

with,

$$ {\displaystyle \begin{array}{l}\frac{\partial {S}_1^O}{\partial {l}_1}=0;\frac{\partial {S}_1^O}{\partial {D}_1}=-\frac{\pi {D}_1{S}_1^O}{4{A}_1};\frac{\partial {S}_1^O}{\partial {a}_1}=\frac{S_1^O}{a_1};\frac{\partial {S}_1^O}{\partial {f}_1}=-i\frac{gA_1{Y}_1{R}_1{S}_1^O}{2\omega {f}_1{\left({F}_R\right)}^2};\\ {}\frac{\partial {S}_1^O}{\partial {Q}_s}=-i\frac{gA_1{Y}_1{R}_1{S}_1^O}{2\omega {Q}_s{\left({F}_R\right)}^2};\frac{\partial {S}_1^O}{\partial {\widehat{h}}_{L1}}=0;\frac{\partial {T}_1^O}{\partial {l}_1}=0;\frac{\partial {T}_1^O}{\partial {D}_1}=0;\frac{\partial {T}_1^O}{\partial {a}_1}=0;\frac{\partial {T}_1^O}{\partial {f}_1}=0;\frac{\partial {T}_1^O}{\partial {Q}_s}=0;\frac{\partial {T}_1^O}{\partial {\widehat{h}}_{L1}}=0;\end{array}} $$
(35)
  1. (4)

    for parameter μ1:

$$ \frac{\partial {\mu}_1}{\partial {l}_1}=0;\frac{\partial {\mu}_1}{\partial {D}_1}=0;\frac{\partial {\mu}_1}{\partial {a}_1}=-\frac{\mu_1}{a_1};\frac{\partial {\mu}_1}{\partial {f}_1}=-i\frac{gA_1{\mu}_1{R}_1}{2\omega {f}_1{\left({F}_R\right)}^2};\frac{\partial {\mu}_1}{\partial {Q}_s}=-i\frac{gA_1{\mu}_1{R}_1}{2\omega {Q}_s{\left({F}_R\right)}^2};\frac{\partial {\mu}_1}{\partial {\widehat{h}}_{L1}}=0; $$
(36)
  1. (5)

    for parameter \( {\widehat{h}}_L \):

$$ \frac{\partial {\widehat{h}}_L}{\partial {l}_1}=0;\frac{\partial {\widehat{h}}_L}{\partial {D}_1}=0;\frac{\partial {\widehat{h}}_L}{\partial {a}_1}=0;\frac{\partial {\widehat{h}}_L}{\partial {f}_1}=0;\frac{\partial {\widehat{h}}_L}{\partial {Q}_s}=0;\frac{\partial {\widehat{h}}_L}{\partial {\widehat{h}}_L}=1 $$
(37)

where: \( Y=-\frac{a}{gA}\sqrt{1-i\frac{a}{gA}} \); \( \mu =\frac{\omega }{a}\sqrt{1-i\frac{\omega }{a}} \); R = fQ0/gDA2; α, β, γ, ϕ are coefficients relating to the system configurations. For the looped pipeline system in Fig. 1b, these coefficients can be derived as follows:

$$ {\displaystyle \begin{array}{l}\alpha =\frac{v_{11}{u}_{21}+{v}_{21}{u}_{11}}{v_{21}+{u}_{21}};\gamma =\frac{u_{22}{v}_{21}+{u}_{21}{v}_{22}}{v_{21}+{u}_{21}};\\ {}\beta =\frac{\left({v}_{12}+{u}_{12}\right)\left({v}_{21}+{u}_{21}\right)-\left({u}_{11}-{v}_{11}\right)\left({u}_{22}-{v}_{22}\right)}{v_{21}+{u}_{21}};\varphi =\frac{u_{21}{v}_{21}}{v_{21}+{u}_{21}};\end{array}} $$
(38)

in which:

$$ {\displaystyle \begin{array}{l}{v}_{11}=\cos \left({\mu}_3{l}_3\right);{v}_{12}=i\frac{1}{Y_3}\sin \left({\mu}_3{l}_3\right);{v}_{21}={iY}_3\sin \left({\mu}_3{l}_3\right);{v}_{22}=\cos \left({\mu}_3{l}_3\right);\\ {}{u}_{11}=\cos \left({\mu}_4{l}_4\right);{u}_{12}=i\frac{1}{Y_4}\sin \left({\mu}_4{l}_4\right);{u}_{21}={iY}_4\sin \left({\mu}_4{l}_4\right);{u}_{22}=\cos \left({\mu}_4{l}_4\right).\end{array}} $$
(39)

5.2 Results Analysis

The results of Eqs. (19) and (20) indicate that the sensitivity of the TFR-based leak detection (size and location) is dependent of the uncertainty factors (p) as well as the leakage information (K L and x L ). For illustration, the leakage case no. 4 in Duan (2016) (i.e., x L  = 300 m, K L  = 3 × 10−4 m2/s), and under the assumption that the COV = 0.1 and ξ ij  = 0 for ∀(i ≠ j) is used for the analysis, and the overall uncertainty of the detection results can be calculated and obtained as follows:

$$ {\delta}_{K_L}=0.1895;{\delta}_{x_L}=0.2322. $$
(40)

This result shows the potential influence and importance of the uncertainty factors to the leak detection results of the TFR-based method. For detailed inspection, the sensitivity coefficients and individual contribution coefficients based on Eq. (4) and Eq. (5) for each uncertainty factor are calculated and shown in Table 1. For clarity, the individual contributions of all the six factors to the total uncertainty of leak detection results are plotted in Fig. 5.

Table 1 Results of FOSM-based sensitivity analysis
Full size table
Fig. 5
figure 5

Individual contribution of different factors to the uncertainty of detection results for: (a) leak size; (b) leak location

Full size image

The results of Table 1 and Fig. 5 demonstrate the relative importance of different uncertainty factors to the sensitivity of the leak detection results by using the proposed TFR-based method in Eq. (1). Particularly, the influence of uncertainty factors of wave speed (a), data measurement (\( {\widehat{h}}_L \)) and pipe diameter (D) to the total uncertainty of both detection results (size and location) are more important than that of other three factors (pipe length, friction and discharge) in this system. In fact, the results of the little impacts of the pipe-wall friction and initial discharge effects to the detection results are consistent with the former accuracy analysis of this TFR-based method in this study. However, the comparison of the results also reveals that uncertainty of pipe length (L) has more influence to the leak location detection (e.g., about 10% contribution) than the leak size detection (e.g., about 0.02% contribution). Therefore, it is crucial to reduce the uncertainties of system parameters and data measurement so as to accurately apply the developed TFR-based leak detection method in practical pipeline systems.

Furthermore, the variabilities of the leak detection results with the potential leakage information based on Eqs. (19) and (20) are calculated for the looped pipeline system and shown in Fig. 6. The results imply that the uncertainty of the leak size detection is increasing with the potential leak size, but its variation is insensitive to the leak location (Fig. 6a). However, the accuracy of the leak location detection may be affected simultaneously by both the leak size and location information (Fig. 6b). Particularly, the TFR-based method is more accurate to locate relatively large-size leaks (Fig. 6b), but with relatively large uncertainty of sizing such leaks in the pipeline (Fig. 6a). Consequently, it can be concluded from the results and analysis in Figs. 5 and 6 that the accuracy and validity of the developed TFR-based method can be influenced by both the uncertainty factors and the pipe leakage information to be detected in the system.

Fig. 6
figure 6

Variability of detection results with uncertainty of the leakage information for: (a) Top: leak size; (b) Bottom: leak location

Full size image

6 Results Discussion and Method Improvement

Despite the successful applications of the developed TFR-based method for the leak detection in branched and looped pipeline systems such as the numerical applications in Duan (2016), the accuracy and sensitivity analysis of this study also indicate the validity range of this method and potential influences of different uncertainty factors in the system. From this perspective, on the one hand, it is necessary to understand better the investigated pipeline system for its physical parameters and operation conditions prior to the applications of the TFR-based method for pipe diagnosis. For example, the accurate data acquisition and measurement as well as the system calibration for the pipeline properties (e.g., pipe length and diameter, wave speed, friction factor) and hydraulic parameters (e.g., flow discharge, energy dissipation and water consumption) are essentially known as the inputs of the TFR-based leak detection analysis procedure. Meanwhile, with understanding the sensitivity of this TFR-based method to various practical factors, it is explainable for the ranges of the possible difference and errors of the leak detection by using this method in the practical applications.

On the other hand, further improvement and extension of the developed TFR-based method is another important and essential way to accurate and efficient applications of this method for practical leak detection problems. Based on the accuracy analysis in this study, the consideration and inclusion of both the real and imaginary parts in Eq. (7) may improve the accuracy of the method for relaxing the approximation assumption made in original derivation process in Eq. (1) (i.e., approximation of neglecting the imaginary part). To this end, for the branched pipeline system in the former analysis, the following general form of the TFR-based method is considered for the improvement in this study:

$$ {\widehat{h}}_{Ln}=\frac{K_L}{C_{1n}{C}_{Sn}}\left[{C}_{2n}+{C}_{3n}\sin \left(2{\mu}_n{x}_{Ln}+{C}_{4n}\right)\right], $$
(41)

where \( {C}_{Sn}=\sqrt{1+{\left({F}_S{F}_L\right)}^2} \) is a lumped coefficient by considering the influence of the leak size and location information to be detected as shown in Eq. (7). The expressions of F S and F L are given in Eq. (10) in this study.

Note that for the improved TFR-based method in Eq. (19), the introduced new coefficient C Sn is leak information related, and therefore, it must be figured out through the solution process such as in the GA-based optimization process proposed in Duan (2016). Consequently, a pre-judgment step based on the magnitude comparison of |R n | and |I n | for the given pipeline system with known configuration parameters is preferably added for the selection of the appropriate leak detection equation (i.e., Eq. (1) or (41)) prior to predict the leakage information by the GA-based optimization proposed in Duan (2016). That is, when |R n | > > |I n |, the simplified form of Eq. (1) is valid and used for the leak detection (as conducted in Duan 2016); otherwise, the general form of Eq. (41) is applied for the analysis. It is also noted that, with the increased accuracy by the improved TFR-based method, the application efficiency of the general form in Eq. (41) is also reduced accordingly due to the more complicated solution process, especially for complex pipeline systems. For example, compared to the simplified form of the method in Duan (2016), about 30% more analysis time consumption is required for the improved method for the branched pipeline case of Fig. 1a in this study. Therefore, it is necessary for the modeler and analyst to make appropriate decision of the method utilization for different practical purposes.

7 Summary and Conclusions

This paper investigates the accuracy and sensitivity analysis of the TFR-based leak detection method developed in the literature for multiple-pipeline systems with simple branched and looped pipe junctions. The theoretical analysis results for the multiple-pipeline system with branched junction demonstrate clearly the potential influence of the approximations and assumptions made in the original derivation for the method development to the accuracy of the TFR-based leak detection method. Particularly, the influences of the leak size, location, as well as the pipe friction are systematically analyzed for the studied cases. The results show that leak information (size and location) to be determined may have significant impacts on the accuracy and validity of the derivation approximation, but the results also indicate that the used approximation is valid for a relatively large and typical range of the pipe-wall friction.

Furthermore, based on the FOSM analysis, the variability of the TFR-based leak detection method may be induced by many different factors in the system. The simple looped pipeline system has been taken in this study for the illustration of sensitivity analysis of the developed TFR-based method. The results and analysis imply that the uncertainty of the pipe wave speed, diameter and data measurement can contribute dominantly to the variability of the detection results (both leak size and leak location). Meanwhile, the sensitivity of the TFR-based method to different uncertainty factors is also affected by the leak information to be detected in the pipeline system. Specifically, the variation of the detection results is more sensitive to the leak size than the leak location. Moreover, under the influence of the studied uncertainty factors in the pipeline system, the variability of sizing pipe leakage is increasing with, while that of locating pipe leakage is decreasing with, the potential leak size to be detected in the system.

With the results and findings of the accuracy and sensitivity analysis in this study, the practical implications and method improvements are suggested in the paper. In particular, it is essential to accurately estimate and measure the properties and parameters of the system under investigation that act as known inputs of the detection procedure by the TFR-based method. Moreover, the inclusion of some approximations and assumptions such as the original ignorance of the imaginary part during the theoretical derivations could increase the detection accuracy of the developed method, but at the same time, would decrease accordingly the efficiency of the detection process.