1 Introduction

The study of flow through porous media is received great attention by many scientists because of its application in many fields such as environmental science and groundwater hydrology (Krajnc et al. 2007; Jasrotia and Kumar 2014; Tsakiris and Alexakis 2014; Sidiropoulos et al. 2016). Mathematical models are widely utilized to predict aquifer behavior in groundwater problems. Mathematical models include numerical and analytical models. Numerical models can solve practical problems with complex geometries and varying material properties. Numerical techniques have been used to investigate several problems. For example, to describe 2D unsaturated flow in irregularly shaped regions using a finite volume method (Tsakiris et al. 1991), to predict the unsteady two-dimensional groundwater flow over a sloping bed in unconfined aquifer (Kalaidzidou-Paikou et al. 1997), to modejl contaminants in aquifers (Tatalovich et al. 2000), to describe the stream depletion rates caused by pumping of a well from an aquifer (Darama 2001), to estimate stream depletion by a well pumping (Di Matteo and Dragoni 2005), to analyze groundwater flow response to tidal fluctuation in coastal aquifers (Saeedpanah et al. 2011), to determine aquifer parameters (Yidana and Chegbeleh 2013), to deal with groundwater flows in heterogeneous porous media (Xie et al. 2014), to model the transport of aqueous benzene concentration along a fracture in a saturated fracture-matrix system (Renu and Kumar 2016), and to model interactions between seawater and groundwater (Sherif et al. 2012; Yihdego and Al-Weshah 2016). Analytical solutions are constructed on rather simplified assumptions and used only for idealized problems. However, they can provide quick answers based on a few basic parameters. In addition, analytical methods can solve the problems with rather less expenses than numerical methods. Therefore, numerous researchers are interested to analyze analytically the groundwater problems. For example, analytical models of problems such as water table fluctuation in response to transient recharge (Rai et al. 2001), groundwater flow to horizontal or slanted well (Zhan and Zlotnik 2002), groundwater flow to horizontal drains (Emikh 2008), associated studies of coastal aquifers (Li and Jiao 2002; Kim et al. 2003; Dong et al. 2012), and flow to partially penetrating wells (Fen and Yeh 2012; Feng and Wen 2016; Wen et al. 2016). There are also recent developments in analytical modeling of water table fluctuations in aquifers due to time varying recharge from multiple basins (Rai and Manglik 2012). In addition, several three-dimensional analytical and semi-analytical solutions are developed for flow to a well in a leaky aquifer with storative semi confining layers (Sepúlveda 2008), and in a sloping fault zone unconfined aquifer (Huang et al. 2014a).

Groundwater-surface water interactions have been received great attention by scientists and hydrologists. Prediction of aquifer behavior in groundwater-surface water systems is a hot topic among researchers. Rassam and Werner (2008) categorizes the processes affecting groundwater-surface water interactions into flooding recharge, evapotranspiration from shallow water tables, groundwater interception by wetlands, parafluvial flow, hyporheic exchange, bank storage effects caused by fluctuating river levels, groundwater extraction and structural features causing heterogeneity of flow. For the cases, such as interactions between aquifer and stream, numerous works have been done. Haushild and Kruse (1962) studied unsteady flow of groundwater into a surface reservoir and obtained an expression for the water-table fluctuation in a stream-aquifer system. Yeh (1970) obtained a numerical solution for the shape of the water table in a stream-aquifer system. Hall and Moench (1972) obtained flow and head variations in stationary linear stream-aquifer systems through application of the convolution equation. Barlow et al. (2000) developed analytical step-response functions, for several cases of transient hydraulic interaction between a fully penetrating stream and a confined, leaky, or water-table aquifer and used them in the convolution integral to calculate aquifer heads, stream bank seepage rates, and bank storage that occur in response to stream stage fluctuations and basin wide recharge or evapotranspiration. Hantush (2005) presented closed-form solutions using Laplace transform to stream–aquifer interactions during storm events and base-flow periods. Chen et al. (2010) used the stream-flow estimation model and the groundwater flow numerical software MODFLOW to estimate the stream infiltration with consideration to the variation of the river water level in the Hsinhuwei River. In addition, several analytical solutions are presented to investigate interactions between an aquifer and a time-varying stream (Boufadel and Peridier 2002; Srivastava 2003; Bansal and Das 2009, 2010, 2011). Huang et al. (2014b) provided a general Laplace-domain solution for describing the temporal distribution of stream depletion rate induced by a fully-penetrating vertical well in an aquifer bounded by two parallel streams. Xie et al. (2016) examined stream chemistry changes during flow events in a synthetic 3D stream–aquifer model. They used numerical modelling to show that, at any particular monitoring location: (i) the increase in stream stage associated with a flow event will precede the decrease in solute concentration; and (ii) the decrease in stream stage following the flow peak will usually precede the subsequent return (increase) in solute concentration. Also, Saeedpanah and Golmohamadi Azar (2017) presented analytical solutions of a confined aquifer bounded with streams of varying water level.

In the present paper, we attempt to analyze analytically the variations of the hydraulic heads in a one-dimensional leaky confined aquifer subjected to one constant head and one varying head. The governing equation with boundary conditions is solved by means of the Laplace transform. It is assumed that the stream level changes exponentially. Since our objective is to investigate differences in aquifer response to stream level changes, two cases of descending and ascending water levels are considered. In addition, the flow rates at the boundaries are quantified for both cases. In fact, the novelty of this paper is to developing new analytical solutions as well as comparing the aquifer response for different cases. Such information can be useful for selection of proper schemes for groundwater resources management. One of the useful applications of the analytical expressions is to analyze the sensitivity of hydraulic heads to aquifer parameters. Hence, we have evaluated the sensitivity of hydraulic heads to aquifer parameters by application of the presented solution to a hypothetical example.

2 Solution Methodology

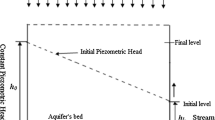
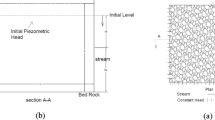
The leaky confined aquifer interacting with two parallel streams considered here is shown diagrammatically in Fig. 1. The aquifer is assumed to be homogeneous, isotropic, incompressible fluid and with constant recharge from the aquifer upper boundary. This aquifer has a constant thickness, a leaky layer and an underlying bed as presented in Fig. 1. The underlying bed is impermeable and horizontal. Furthermore, the aquifer is in contact with a constant piezometric head at one end and a stream of varying water level at the other end. As presented in Fig. 1, to investigate the aquifer response with different change rates two cases are considered, namely case (I) and case (II). In case (I), h 0 is considered greater than h c and the stream water level declines exponentially with time from the initial level of h 0 to the final level of h c . In case (II), h c is considered greater than h 0 and the stream water level rises exponentially with time from the initial level of h c to the final level of h 0. Therefore, the governing equation with boundary conditions for the one-dimensional streams- leaky confined aquifer interactions are the following.

$$ K\frac{\partial^2 h}{\partial {x}^2}+\frac{w}{b}={S}_s\frac{\partial h}{\partial t} $$
(1)
$$ h\kern0.1em \left( x, t=0\right)={h}_0-\frac{h_0-{h}_c}{L} x $$
(2)
$$ h\kern0.1em \left( x=0, t\right)={h}_c+\left({h}_0-{h}_c\right){e}^{-\psi \kern0.5em t} $$
(3)
$$ h\left( x= L, t\right)={h}_c $$
(4)
Fig. 1
figure 1

Diagrammatic representation of a leaky confined aquifer interacting with two parallel streams under recharge condition a case (I); b case (II)

Full size image

where h is hydraulic head, S s is specific storage, K is the saturated hydraulic conductivity of the aquifer, b is the constant thickness of the aquifer, h c is constant head at the right boundary and final level of the stream at the left boundary, h 0 is the initial level of the stream, L is length of the aquifer and parameter ψ is a positive constant signifying the rate of the water variation in the stream.

Based on the following dimensionless variables:

$$ X=\frac{x}{L};\kern1em \eta =\frac{K}{S_S\kern0.1em {L}^2} t;\kern1em \lambda =\frac{S_S{L}^2}{K}\psi; \kern1em H=\frac{h-{h}_c}{h_c-{h}_0};\kern1em R=\frac{wL^2}{\left({h}_c-{h}_0\right) Kb} $$
(5)

Equations (1) to (4) can be expressed in dimensionless form as:

$$ \frac{\partial^2 H}{\partial {X}^2}+ R=\frac{\partial H}{\partial \eta} $$
(6)
$$ H\kern0.1em \left( X,\eta =0\right)= X-1 $$
(7)
$$ H\left( X=0,\eta \right)=-{e}^{-\lambda \eta} $$
(8)
$$ H\kern0.1em \left( X=1,\eta \right)=0 $$
(9)

After taking the Laplace transform of governing equation and following the procedure as in Appendix results the following dimensionless domain solution:

$$ H\left( X,\eta \right)=-{e}^{-\lambda \eta}\left( \cos X\sqrt{\lambda}-\mathrm{cotg}\sqrt{\lambda} \sin X\sqrt{\lambda}\right)-2\sum_{n=1}^{\infty }{e}^{-{n}^2{\pi}^2\eta}\frac{\lambda \sin n\pi X}{ n\pi \left(\lambda -{n}^2{\pi}^2\right)}-2 R\sum_{n=1}^{\infty }{e}^{-{n}^2{\pi}^2\eta}\frac{ \sin n\pi X}{n^3{\pi}^3}+2 R\sum_{n=1}^{\infty }{e}^{-{n}^2{\pi}^2\eta}\frac{{\left(-1\right)}^n}{n^3{\pi}^3} \sin n\pi X+ R\frac{X-{X}^2}{2} $$
(10)

Equation (10) calculates the piezometric heads in the aquifer under the aforementioned initial and boundary conditions. The steady-state values of hydraulic heads can be calculated by taking η → ∞ in Eq. (10)

$$ H\left( X,\eta \to \infty \right)= R\frac{X-{X}^2}{2} $$
(11)

It can be noticed that the steady-state values of hydraulic heads are dependent to R. Differentiating Eq. (11) with respect to X gives us:

$$ \frac{d}{ d x} H\left( X,\eta \to \infty \right)= R\frac{1-2 X}{2} $$
(12)

From Eq. (12), it can be deduced that the water divide positions take place at point X = 0.5 as time goes to infinity.

The flow through the one-dimensional aquifer is expressed as:

$$ q=- K\frac{\partial h}{\partial x} $$
(13)

Using Eq. (8), the Eq. (13) can be rewritten as below:

$$ q=- K\frac{h_c-{h}_0}{L}\frac{\partial H}{\partial X} $$
(14)

Then, dimensionless flow rate Q can be expressed as:

$$ Q=\frac{\partial H}{\partial X}=\frac{qL}{K\left({h}_0-{h}_c\right)} $$
(15)

Hence, the flow rates can be calculated by the following solutions:

$$ Q\left( X,\eta \right)=-{e}^{-\lambda \eta}\left(-\sqrt{\lambda} \sin X\sqrt{\lambda}-\sqrt{\lambda}\mathrm{cotg}\sqrt{\lambda} \cos X\sqrt{\lambda}\right)-2\sum_{n=1}^{\infty }{e}^{-{n}^2{\pi}^2\eta}\frac{\lambda \cos n\pi X}{\left(\lambda -{n}^2{\pi}^2\right)}-2 R\sum_{n=1}^{\infty }{e}^{-{n}^2{\pi}^2\eta}\frac{ \cos n\pi X}{n^2{\pi}^2}+2 R\sum_{n=1}^{\infty }{e}^{-{n}^2{\pi}^2\eta}\frac{{\left(-1\right)}^n}{n^2{\pi}^2} \cos n\pi X+ R\frac{1-2 X}{2} $$
(16)

3 Discussion of Results

The capability of the presented analytical solution to predict the hydraulic heads can be demonstrated by application to a hypothetical aquifer. Equation (12) is utilized for simulation of the hydraulic heads. To verify the presented analytical solution the model is then simulated in MODFLOW. The computational time interval for MODFLOW is 1 h. PCG2 solver solves the flow equations and the flow package is Layer-Property Flow (LPF). The type of boundary conditions is considered as specified head. The domain is discretized into 400 cells with the grid spacing of Δx = 0.25 m. Figure 2 demonstrates the dimensionless hydraulic heads H against dimensionless distance X at different times (t) for three values of recharge rate (w = 2 , 3 and 6 mm/hr). For case (I) h 0 = 26 m and h c  = 22 m, and for case (II) h 0 = 22 m and h c  = 26 m. The other parameters are as given in Table 1. It can be seen that the results of numerical solution are in good agreement with those results obtained from the analytical solution. It can be observed that the recharge rate has a significant impact on the aquifer response. In case (I), the average difference in dimensionless hydraulic heads between recharge rate of 3 and 2 mm/h was about −0.0099, and between recharge rate of 6 and 3 mm/h was about −0.0297 (−0.0099 × 3) for both time steps of 60 and 80 h; and for case (II) such these differences were 0.0099 and 0.0297, respectively. Also, it can be seen that with a rise in recharge rate the hydraulic heads in the middle of the aquifer (X = 0.5) grows faster than that of the other points of the aquifer. Respectively, decreasing the recharge rate from 6 to 3 mm/h and from 3 to 2 mm/h in case (I) resulted in −0.15 and −0.1 movements of the water divide positions in time step of 60 h, and −0.05 and −0.05 movements of the water divide positions in time step of 80 h (Fig. 2a) . In case (II), decreasing the recharge rate from 6 to 3 mm/h and from 3 to 2 mm/h resulted in 0.15 and 0.1 movements of the water divide positions in time step of 60 h, and 0.05 and 0.05 movements of the water divide positions in time step of 80 h, respectively (Fig. 2b).

Fig. 2
figure 2

Hydraulic heads in the aquifer for a case (I); b case (II)

Full size image
Table 1 Parameter values used in the hypothetical aquifer
Full size table

3.1 Analysis of Flow Rates

The flow rates at the left and right boundaries of the aquifer can be calculated by setting X = 0 and X = 1 in Eq. (16). The derived expressions can be stated as below:

$$ Q\left(0,\eta \right)=-{e}^{-\lambda \eta}\left(-\sqrt{\lambda}\mathrm{cotg}\sqrt{\lambda}\right)-2\sum_{n=1}^{\infty }{e}^{-{n}^2{\pi}^2\eta}\frac{\lambda}{\left(\lambda -{n}^2{\pi}^2\right)}-2 R\sum_{n=1}^{\infty }{e}^{-{n}^2{\pi}^2\eta}\frac{1}{n^2{\pi}^2}+2 R\sum_{n=1}^{\infty }{e}^{-{n}^2{\pi}^2\eta}\frac{{\left(-1\right)}^n}{n^2{\pi}^2}+ R\frac{1}{2} $$
(17)
$$ Q\left(1,\eta \right)=-{e}^{-\lambda \eta}\left(-\sqrt{\lambda} \sin \sqrt{\lambda}-\sqrt{\lambda}\mathrm{cotg}\sqrt{\lambda} \cos \sqrt{\lambda}\right)-2\sum_{n=1}^{\infty }{e}^{-{n}^2{\pi}^2\eta}\frac{\lambda \cos n\pi}{\left(\lambda -{n}^2{\pi}^2\right)}-2 R\sum_{n=1}^{\infty }{e}^{-{n}^2{\pi}^2\eta}\frac{ \cos n\pi}{n^2{\pi}^2}+2 R\sum_{n=1}^{\infty }{e}^{-{n}^2{\pi}^2\eta}\frac{{\left(-1\right)}^n}{n^2{\pi}^2} \cos n\pi - R\frac{1}{2} $$
(18)

Equations (17) and (18) calculate the flow rates at the left and right boundaries. Figures 3 and 4 show the values of dimensionless flow rates against dimensionless time with different w for case (I) and case (II), respectively. It can be observed that the dimensionless flow rates decrease gradually until attaining a steady state value. The steady state values can be obtained by setting η → ∞ in Eqs. (17) and (18)

$$ Q\left(0,\eta \to \infty \right)= R\frac{1}{2} $$
(19)
$$ Q\left(1,\eta \to \infty \right)=- R\frac{1}{2} $$
(20)
Fig. 3
figure 3

Values of the flow rates with different recharge rates in case (I)

Full size image
Fig. 4
figure 4

Values of the flow rates with different recharge rates in case (II)

Full size image

From Eqs. (19) and (20) it can be deduced that in the absence of recharge, there is no flow rate at the steady state condition and a higher recharge rate increases the outflow through the boundaries.

In case (I), h 0 > h c and due to the available hydraulic gradient the water moves towards the right side and in case (II), h 0 < h c and the water moves towards the left side; although a higher recharge rate changes the directions of flow rates at the left boundary in case (I) and at the right boundary in case (II). The times at which flow rates changed from positive to negative values decrease as recharge rate increases. Figures 5 and 6 show the values of dimensionless flow rates against dimensionless time with different ψ for case (I) and case (II), respectively. It can be observed that a higher ψ reduces the values of dimensionless flow rates. In addition, the times at which flow rates changed from positive to negative values decrease with rises inψ.

Fig. 5
figure 5

Values of the flow rates in case (I) at the a left boundary; b right boundary

Full size image
Fig. 6
figure 6

Values of the flow rates in case (II) at the a left boundary; b right boundary

Full size image

3.2 Sensitivity Analysis

In this part of the research, sensitivity of hydraulic heads to aquifer parameters is analyzed. Figure 7 shows the sensitivity of hydraulic heads to the aquifer hydraulic conductivity. For this purpose, three values of K are considered, namely K = 0.8 m/hr, K = 1 m/hr and K = 1.2 m/hr. Respectively, the average differences in dimensionless hydraulic heads between hydraulic conductivity of 0.8 and 1 m/h and between hydraulic conductivity of 1 and 1.2 m/h were about 0.008 and 0.005 for case (I), and about −0.008 and −0.005 for case (II). For case (I), the movements of water divide positions from K = 0.8 m/hr to K = 1 m/hr and from K = 1 m/hr to K = 1.2 m/hr were −0.02 and −0.0225, respectively, while such these movements for case (II) were 0.02 and 0.0225.

Fig. 7
figure 7

Sensitivity of hydraulic heads to K at t = 80 hr for a case (I); b case (II)

Full size image

Figure 8 shows the sensitivity of hydraulic heads to the specific storage. Therefore, three values of S s are considered, namely S s  = 1 × 10−6  m −1, S s  = 1 × 10−5  m −1 and S s  = 1 × 10−4  m −1. For both cases, the average differences in dimensionless hydraulic heads between specific storage of 1 × 10−6 and 1 × 10−5  m −1 and between specific storage of 1 × 10−5 and 1 × 10−4  m −1 were about 6 × 10−5 and6 × 10−6, respectively.

Fig. 8
figure 8

Sensitivity of hydraulic heads to S s at t = 80 hr for a case (I); b case (II)

Full size image

Figure 9 shows the sensitivity of hydraulic heads to the aquifer thickness. Hence, three values of b are considered, namely b = 18 m, b = 16 m and b = 14 m. Respectively, the average differences in dimensionless hydraulic heads between thickness of 14 and 16 m and between thickness of 16 and 18 m were about 0.0056 and 0.0043 for case (I), and about −0.0056 and −0.0043 for case (II). For case (I), the movements of water divide positions from b = 14 m to b = 16 m and from b = 16 m to b = 18 m, were −0.0125 and −0.01, respectively, while such these movements for case (II) were 0.0125 and 0.01.

Fig. 9
figure 9

Sensitivity of hydraulic heads to b at t = 80 hr for a case (I); b case (II)

Full size image

The sensitivity of hydraulic heads to the changes in recharge rate with different values of the hydraulic conductivity, thickness, and length of the aquifer is analyzed. For this purpose, dimensionless hydraulic heads (H) versus recharge rate (w) are depicted in Fig. 10. A numerical example is introduced (called Model 1) in which the parameters are as given in Table 1. Three other models have been adopted, namely, Model 2, Model 3, and Model 4 in which b ′ = 0.75b = 15 m for Model 2, L ′ = 0.75L = 75 m for Model 3, and K ′ = 0.75K = 0.75 m/hr for Model 4, the other parameters are as given in Table 1. For case (I), Fig. 10a shows that with a rise in recharge rate from 0 to 10 mm/h, the dimensionless hydraulic heads change about −0.16 in Model 1, −0.21 in an aquifer with a smaller thickness (Model 2), −0.09 in an aquifer with a smaller length (Model 3), and −0.21 in an aquifer with a less hydraulic conductivity (Model 4). Also, for case (II), Fig. 10b shows that with a rise in recharge rate from 0 to 10 mm/h, the dimensionless hydraulic heads change about 0.16, 0.21, 0.09, and 0.21 for Model 1, Model 2, Model 3, and Model 4, respectively.

Fig. 10
figure 10

Sensitivity of hydraulic heads to the recharge rate variations at X = 0.5 and t = 100 hr with different values of K, b and L in a case (I); and b case (II)

Full size image

4 Conclusion

In this research, new analytical solutions of unsteady one-dimensional groundwater flow in a leaky confined aquifer between two parallel streams, one with constant and the other with exponentially changing water level have been presented. The governing equation with boundary conditions is solved by application of the Laplace transform method. The results of the presented analytical solutions were verified with those results obtained from MODFLOW. An exponential function of time is adopted for describing the stream level changes. The aquifer responses for two cases of ascending and descending water levels are compared to each other. In addition, the sensitivity of hydraulic heads and flow rates to different aquifer parameter were determined. The locations of water divide and how they change by change in hydraulic conductivity, thickness, recharge rate, and water level change rates were also discussed. Considering a hypothetical aquifer, the following conclusions can be drawn:

  1. I.

    It is shown that with a rise in w the water divide positions move towards right boundary in case (I). In addition, as time passes, the positions of water divide move towards the right boundary. Also, with a rise in w the water divide positions move towards left boundary in case (II). Furthermore, as time passes, the positions of water divide move towards the left boundary.

  2. II.

    The hydraulic heads in the middle of the aquifer are more influenced by a constant recharge than that of the rest of the aquifer.

  3. III.

    A rise in thickness caused lower hydraulic heads for both cases. Actually, a higher thickness provides a higher storage capacity that causes lower hydraulic heads in the aquifer.

  4. IV.

    The hydraulic heads rise with increase in the aquifer length.

  5. V.

    Changes in specific storage have had a little impact on the hydraulic heads.

  6. VI.

    The steady state values of hydraulic heads are also quantified and it is shown that they depend jointly on the value of the parameterR.

  7. VII.

    The sensitivity of hydraulic heads to the changes in recharge rate with different values of hydraulic conductivity, thickness, and length of the aquifer is analyzed. It demonstrates that among these parameters the length of the aquifer is the most important parameter affecting the hydraulic heads.

  8. VIII.

    In the absence of recharge, there is no flow rate at the steady state condition and a higher recharge rate increases the outflow through the boundaries.

  9. IX.

    The times at which flow rates changed from positive to negative values decrease as recharge rate increases.

  10. X.

    A higher ψ reduces the values of dimensionless flow rates. In addition, the times at which flow rates changed from positive to negative values decrease with rises in ψ.

  11. XI.

    The movements of water divide positions in cases (I) and (II) are the same in magnitude, but not in direction; as it can generally be claimed that an increase in either hydraulic conductivity or thickness results in movement of water divide positions towards left side in case (I) while such these movements of water divide positions are towards right side in case (II).

The main objective of this paper is to develop new analytical solutions to predict aquifer response for different scenarios in stream-aquifer systems. It should be mentioned that the presented solutions could be used in many practical problems. One of the important problems in stream-aquifer systems is to quantify contaminant exchange between stream and aquifer. The presented analytical solutions can be developed to investigate contaminant exchanges and how they change by change in aquifer parameters. Calculation of transit time is another important problem in groundwater systems. Therefore, the presented solutions can also be used to determine the transit time.