1 Introduction

Flood frequency analysis (FFA) is concerned with determining the probability of occurrence of extreme runoff events in rivers, and is open to a number of approaches (e.g. Vogel et al. 1993; Katz et al. 2002; Kwon et al. 2008; Gilroy and McCuen 2012; Katz 2012; Li et al. 2015a). FFA is conventionally conducted under the assumptions of: (i) independence of the flood series, which means that the probability distribution parameters to be estimated come from independent and identically distributed observations, and (ii) stationarity of the flood series, which means that the environmental factors that generate or modify floods, such as climate and land cover, are the same in the past, present and future (Khaliq et al. 2006; Gilroy and McCuen 2012; Li et al. 2015b). Under the conditions of climate change, land use change and river regulation, acting individually or together, the assumption of stationarity is suspect (Katz et al. 2002; Xiong and Guo 2004; Milly et al. 2005, 2008; Gilroy and McCuen 2012; Salas and Obeysekera 2014; Vasiliades et al. 2015), and design flood predictions made on this basis would be questionable. Climate change and human activities impacting flood runoff is a global phenomenon. There is a need then for development of effective non-stationary FFA methods.

Non-stationary FFA is most commonly approached using the method of time-varying moments (Strupczewski et al. 2001a, b; Strupczewski and Kaczmarek 2001; Coles 2001; Katz et al. 2002; Khaliq et al. 2006; Leclerc and Ouarda 2007; Villarini et al. 2009b, 2010; Gilroy and McCuen 2012; Salas and Obeysekera 2014). Strupczewski et al. (2001a) introduced a linear or quadratic time trend into the first two moments (mean and standard deviation) of the observed Vistula River flood series over the period of 1921–1990 with six candidate probability distributions. In this case, non-stationarity was expressed based on the relationships between the distribution parameters and the time-dependent moments, the maximum likelihood method was adopted for parameter estimation, and the Akaike Information Criterion (AIC) optimizing criterion (Akaike 1974) used for model selection. In other studies by these authors, trends in 39 annual maximum flow series in Polish Rivers were investigated using the non-stationary at-site FFA method of weighted least squares (Strupczewski and Kaczmarek 2001), and using the maximum likelihood method (Strupczewski et al. 2001b). Katz et al. (2002) fitted the Generalized Pareto distribution by maximum likelihood estimation to the US annual damage from flood series with a linear trend in the log-transformed scale parameter. A detailed review of the time-varying moments approach applied to non-stationary FFA was provided by Khaliq et al. (2006). Leclerc and Ouarda (2007) presented a method to perform regional FFA at ungauged sites when the assumption of stationarity was not valid. A non-stationary approach using the Generalized Additive Models for Location, Scale and Shape parameters (GAMLSS) (Rigby and Stasinopoulos 2005) was applied to seasonal precipitation and temperature data from Rome (Villarini et al. 2010) and peak discharge data from the Little Sugar Creek in Charlotte (Villarini et al. 2009b). Gilroy and McCuen (2012) developed a non-stationary FFA method that accounts for climate change and urbanization influences, and applied it to the Little Patuxent River in Guilford. Salas and Obeysekera (2014) suggested placing the concepts of return period and risk as they apply in the stationary world into a non-stationary framework by extending the geometric distribution to allow for changing exceeding probabilities over time. Although the literature on non-stationary FFA contains variety in certain aspects of the methodology, one common factor is exclusive reliance on the annual maximum flood series. The innovation presented in this paper is to also make use of the annual daily flow series for non-stationary FFA.

In seasonal rivers, generation of the maximum flood in a year is very closely related to hydrological processes during the flood season in that year, so non-stationarity in the annual daily flow series is likely to have some impact on non-stationarity in the annual maximum daily flood (AMDF) series. The central theme of this paper is development of an approach for incorporating non-stationarity information in the annual daily flow series in the non-stationary FFA of the AMDF series. We did this using the norming constants method (NCM), which is based on the Fisher-Tippett theory (Fisher and Tippett 1928). The core theory of NCM is that the statistical parameters of the annual maximum flood distribution for a year can be mathematically derived from the daily flow series within the year in terms of the maximum domain of attraction of the annual maximum flood distribution. We elaborate our NCM-based approach in this paper and illustrate its practical application using a case study of the Wei River, China. FFA often makes use of maximum instantaneous flow data, which is particularly important in small and medium size rivers, where the instantaneous peak daily flow can be much higher than the mean daily flow. Due to limitations on data availability, we used mean daily flow data, but the NCM applies equally well to instantaneous peak flow series.

This paper is organized as follows. First the NCM methodology is described, along with a description of methods for calculation of the statistical characteristics of the annual daily flow series, and covariate analysis to establish relationships between statistical parameters of the annual maximum flood distribution and meteorological factors. Then, relevant information about the Wei River basin is provided, and the data sets used in this case study are described. The results and discussion of the case study follow, and finally we make conclusions about application of NCM to the problem of non-stationary FFA.

2 Proposed Norming Constants Method (NCM) of Non-Stationary FFA

We suggest a four-step framework, termed the norming constants method (NCM) of non-stationary FFA, for incorporating non-stationarity information in the annual daily flow series in the non-stationary FFA of the AMDF series:

  1. 1.

    The AMDF series is tested for statistically significant non-stationarity, which is the basis for then proceeding with non-stationary FFA.

  2. 2.

    Statistical characterization and non-stationarity detection is undertaken on the series of the mean and variance of the annual daily flow series.

  3. 3.

    If non-stationarity is detected in both the AMDF and the annual daily flow series in Steps 1 and 2, then non-stationary FFA based on the NCM is carried out.

  4. 4.

    If non-stationarity is present, meteorological covariate analysis is carried out to establish relationships between the statistical parameters of the annual maximum flood distribution and the meteorological factors for the NCM. All the models are compared by the AIC criterion and assessed using residual plots and statistics.

2.1 Detection of Non-Stationarity in Hydrological Time Series

Incorporation of non-stationarity information in the annual daily flow series does not depend on the form of non-stationarity, whether it be monotonic, non-monotonic, linear, non-linear or step-change trend. A number of tests are available for the purpose of testing for non-stationarity in hydrological time series (Chiew and McMahon 1993; Xu et al. 2004) and one or more of these might be appropriate, depending on the nature of the data.

2.2 Probability Distributions of the Annual Daily Flow Series

The annual daily flow series refers to the hydrograph of all mean daily flows for a year, and is denoted by X t  = (x d ,t ), d = 1,2,...,v, where x d,t represents the flow rate of day d in year t and v is the number of days in the year, referred to as the block length. When the annual daily flow series is serially independent, the block length is 365 for non-leap years or 366 for leap years. In essence, frequency analysis of the annual daily flow series fits the flow-duration curve based on X t with a probability distribution F X t (x). With respect to the distribution of the annual maximum daily flood series, the distribution F X t (x) of X t is normally referred to as the parent distribution (PD). The daily flows are often assumed to follow a Lognormal or Gamma distribution (Fennessey and Vogel 1990; LeBoutillier and Waylen 1993; Krasovskaia et al. 2006; Gottschalk et al. 2013a, b). For the annual daily flow series of different years, although the distribution function type is assumed to be the same, the statistical parameters might be different due to the non-stationarity of the annual daily flow series.

When F X t (x) is a Lognormal distribution, its probability density function and the mean and variance of X t are (Johnson et al. 1994; Stasinopoulos et al. 2008):

$$ {f}_t^X(x)=\frac{1}{{\left(2\pi \right)}^{1/2}{\sigma}_tx} \exp \left\{-\frac{{\left[ ln(x)-{\mu}_t\right]}^2}{2{\sigma}_t^2}\right\},x>0,{\mu}_t\kern.3em \in \Re, {\sigma}_t>0 $$
(1)
$$ E\left({X}_t\right)={\omega}^{1/2} \exp \left({\mu}_t\right) $$
(2)
$$ Var\left({X}_t\right)=\omega \left(\omega -1\right) \exp \left(2{\mu}_t\right) $$
(3)

where μ t and σ t are the mean and standard deviation of the log-transformed annual daily flow series X t for the year t, and ω = exp(σ 2 t ).

When F X t (x) is a Gamma distribution, its probability density function and the mean and variance of X t are:

$$ {f}_t^X(x)=\frac{1}{\beta_t^{\gamma_t}\varGamma \left({\gamma}_t\right)}{x}^{\gamma_t-1} \exp \left(-\frac{x}{\beta_t}\right),x>0,{\gamma}_t>0,{\beta}_t>0 $$
(4)
$$ E\left({X}_t\right)={\gamma}_t{\beta}_t $$
(5)
$$ Var\left({X}_t\right)={\gamma}_t{\beta}_t^2 $$
(6)

where γ t and β t are the shape and scale parameters.

As the mean E(X t ) and variance Var(X t ) of X t are derived from the parameters of the PD by Eqs. (2)–(3) or (5)–(6), the character of the PD should be determined before investigating the non-stationarity in the series of E(X t ) and Var(X t ) of the annual daily flow series.

We suggest adoption of both the maximum likelihood and L-moments (Hosking 1990) techniques to estimate the statistical parameters (μ t , σ t ) and (γ t , β t ) of the PD for each year. This results in four optional scenarios for the annual daily flow series: Lognormal PD with maximum likelihood method, Lognormal PD with L-moments method, Gamma PD with maximum likelihood method, and Gamma PD with L-moments method. In order to determine the optimal PD and parameter estimation method, these four scenarios are considered for fitting the annual daily flow series of each year, and the Chi-squared test (Greenwood 1996), the Nash-Sutcliffe efficiency between modelled and empirical probabilities (NSE pp ), and the Nash-Sutcliffe efficiency between modelled and empirical daily flows (NSE qq ) are calculated to assess the goodness-of-fit of each scenario.

2.3 Norming Constants Method (NCM)

The maximum statistic of a sample of random variables is also a random variable and has its own probability distribution. For the annual daily flow series X t  = (x d,t ), d = 1, 2, ⋯, v of the year t, the corresponding annual maximum daily flood statistic Z v t of the year is derived as:

$$ {Z}_t^v= \max \left({X}_t\right)=\underset{1\le d\le v}{ \max}\left({x}_{d,t}\right) $$
(7)

The extreme value distribution of Z v t approaches one of three limiting forms, i.e. the Fréchet, Weibull or Gumbel distribution, as the sample size increases (Fisher and Tippett 1928). These three extreme value distributions can be further combined into a single distribution function, the well-known Generalized Extreme Value (GEV) distribution. The Gumbel distribution is more widely employed as the probability distribution of the annual maximum flood event than the other two extreme value distributions (Kwon et al. 2008; Villarini et al. 2009a, b; Mujere 2011; Gottschalk et al. 2013a). The cumulative distribution function of the Gumbel is given by:

$$ {F}_t^{Z^v}\left(\left.{z}_t^v\right|{d}_t^v,{c}_t^v\right)= \exp \left\{- \exp \left[-\frac{\left({z}_t^v-{d}_t^v\right)}{c_t^v}\right]\right\} $$
(8)

where d v t and c v t are the norming constants of the year t satisfying the maximum domain of attraction of the Gumbel distribution. From a theoretical perspective, the corresponding norming constants d v t and c v t can be derived from the statistical parameters of the parent distribution F X t (x) of the annual daily flow series of year t (Cramér 1999; Embrechts et al. 1997).

When F X t (x) is a Lognormal distribution, the expressions of the norming constants d v t and c v t by the Lognormal parameters (μ t and σ t ) can be derived as:

$$ {d}_t^v= \exp \left\{{\mu}_t+{\sigma}_t\left[{\left(2 \ln v\right)}^{1/2}-\frac{ \ln \left(4\pi \right)+ \ln \left( \ln v\right)}{2{\left(2 \ln v\right)}^{1/2}}\right]\right\} $$
(9)
$$ {c}_t^v={\sigma}_t{\left(2 \ln v\right)}^{-1/2}{d}_t^v $$
(10)

When F X t (x) is a Gamma distribution, the expressions of the norming constants d v t and c v t by the Gamma parameters (γ t and β t ) can be derived as:

$$ {d}_t^v={\beta}_t\left[ \ln v+\left({\gamma}_t-1\right) \ln \left( \ln v\right)- \ln \varGamma \left({\gamma}_t\right)\right] $$
(11)
$$ {c}_t^v={\beta}_t $$
(12)

After either the Lognormal or the Gamma distribution is selected as the PD that best fits the daily flows of year t, and the corresponding PD parameters are estimated, the Gumbel norming constants d v t and c v t for year t are calculated using Eqs. (9)–(10) or (11)–(12). The non-stationary FFA can then be conducted using the norming constants for each year.

An observed annual daily flow series would not normally be expected to satisfy the assumption of independence. We followed other authors who have relaxed the requirement for independence when fitting the daily flow series to probability distributions (e.g. Fennessey and Vogel 1990; LeBoutillier and Waylen 1993; Krasovskaia et al. 2006; Gottschalk et al. 2013a). In this situation, the block length v should be a value less than 365 (or 366) days. When the NCM is applied in practice, v should be calibrated to take an effective value reflecting the real independence among the annual daily flow series, denoted here by v eff . The optimal value of v eff can be derived in terms of the AIC criterion. When v eff is determined, it replaces v in Eqs. (9)–(12).

2.4 Meteorological Covariate Analysis

The main mechanism for flood runoff generation in most places is infiltration-excess runoff generation. In this case, flood events are closely associated with heavy rainfall events, which in turn can be related to other climatic variables. Thus, climate variables often at least partially explain non-stationarity in a flood series. Including climatic factors as explanatory variables in non-stationary FFA might have two benefits. First, it could help to provide physical meaning to the non-stationary design flood prediction, and second, the results could be interpreted in the context of runoff changes predicted by application of global circulation models and downscaling techniques.

In the proposed NCM, the estimated PD parameters are firstly expressed as linear functions of covariates, and these functions are then substituted into Eqs. (9)–(10) or (11)–(12) for calculating the time-varying norming constants d v t and c v t and conducting non-stationary FFA.

2.5 Model Selection and Assessment Criteria

The established models are compared using AIC criterion, where the maximum likelihood value is penalized by the effective degrees of freedom (Akaike 1974; Rigby and Stasinopoulos 2005). While a smaller AIC value indicates better model performance, which identifies the optimal model, there is no indication of how well the selected model captures the variability of the non-stationary flood series. Examination of the normalized quantile residuals (subsequently referred to here as residuals) (Dunn and Smyth 1996) is an effective way for testing the efficiency of the selected model. Thus, we suggest use of a combination of qualitative and quantitative assessment criteria to assess the overall performance of the selected model. The qualitative assessment involves visual inspection of the diagnostic residual plots, specifically, residual versus observed year plot, ACF (Autocorrelation Function) plot (Guang-Te and Singh 1994), normal Q-Q plot, or the more effective worm plot (Buuren and Fredriks 2001; Stasinopoulos et al. 2008). The worm plot is a de-trended Q-Q plot with the difference between the empirical and theoretical quantile residuals on the vertical axis and the theoretical quantile residuals on the horizontal axis. Quantitative assessment relies on statistics of the Filliben correlation coefficient (Filliben 1975) and KS test (Massey 1951) of the residuals. Centile curve plots can indicate how well the selected model captures the variability of the observed flood series, and to assess how the observed flood events fall in relation to each centile curve and the corresponding theoretical probability.

3 Study Area and Data

3.1 General Characteristics of the Study Area

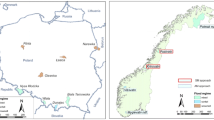
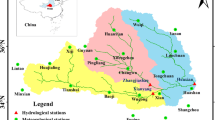
The Wei River, the largest tributary of the Yellow River, originates from the Niaoshu Mountain at an elevation of 3 485 m above sea level in the Weiyuan county of Gansu province. Located between the coordinates 33°40′-37°26′N and 103°57′-110°27′E in the southeastern part of the loess plateau, the river has a length of 818 km and a drainage area of 134 800 km2 (Fig. 1). After flowing west to east through the three provinces (autonomous region) of Gansu, Ningxia and Shaanxi the Wei River joins the Yellow River at Tongguan in Shaanxi province. Two large tributaries, the Jing River and the Beiluo River, join the Wei River in the middle and lower reaches of the basin respectively. The Wei River is known regionally as the ‘Mother River’ of the Guanzhong Plain of the southern part of the loess plateau because of its key role in the economic development of western China (Song et al. 2007; Huang et al. 2014).

Fig. 1
figure 1

Location, topography, hydro-meteorological stations and river systems of the Wei River basin

Full size image

The Wei River basin is characterized by semi-arid and sub-humid continental monsoon climate. Mean annual precipitation of the basin is about 570 mm but there is a strong decreasing gradient from south to north. The southern region has a sub-humid climate with mean annual precipitation of about 800–1000 mm, whereas the northern region has a semi-arid climate with mean annual precipitation of about 400–700 mm. The annual mean temperature over the entire basin is about 6–14 °C. The range in the annual potential evapotranspiration is about 660–1600 mm, and the mean annual actual evapotranspiration from the land surface is about 500 mm (Zuo et al. 2014).

The mean annual natural discharge of the Wei River is about 10 × 109 m3, contributing approximately 17 % of the discharge of Yellow River. The Wei River basin is one of the most important industrial and agricultural production zones in China, which has led to large scale exploitation of the surface and groundwater resources. The annual discharge of the Wei River at Linjiacun station during the decade 1991–2000 was 53.9 % less than that during the preceding decade, while at Huaxian station it was 50.3 % less (McVicar et al. 2007; Song et al. 2007).

3.2 Data

The observed mean daily flow series from Huaxian gauging station over the period 1954–2009, provided by the Hydrology Bureau of the Yellow River Conservancy Commission, was the source of the AMDF series. Huaxian hydrological station, located at 109°46′E, 34°35′N, is about 70 km upstream of the junction of the Wei and Yellow rivers (Fig. 1). The catchment area upstream of this station is 106 500 km2, or about 80 % of the total basin area (Fig. 1).

Meteorological data from 22 stations (Fig. 1) for the period 1954–2009 was provided by the National Climate Center of the China Meteorological Administration (source: http://cdc.cma.gov.cn). The data included five observed daily variables: daily precipitation (rain, mm), daily maximum temperature (TMAX, °C), daily minimum temperature (TMIN, °C), daily mean temperature (TMEAN, °C) and daily mean relative humidity (H, %). Time series of the areal mean values of these daily climate variables for the basin above the Huaxian station were generated using the Thiessen polygon method. From these data series, eight statistics were calculated: annual maximum daily precipitation (rain 1 max), annual maximum 3-day precipitation (rain 3 max), annual maximum 7-day precipitation (rain 7 max), annual total precipitation (rain year ), annual mean of daily maximum temperature (TMAX mean ), annual mean of daily minimum temperature (TMIN mean ), annual mean of daily mean temperature (TMEAN mean ) and annual mean of daily mean relative humidity (H mean ).

4 Results of Case Study

4.1 Step 1. Temporal Trends in the AMDF Series

The lag-1 ACF value of the AMDF series was not significantly different from 0 at α = 0.05, meaning that the AMDF series was serially independent. We used the Mann-Kendall (MK) test (Mann 1945; Kendall 1975; Yue and Wang 2004; Li et al. 2014) to test for the presence of non-stationarity in the flood series. In non-stationary analysis of extreme value series, the focus is commonly on non-stationarity in the mean. However, non-stationarity in the variance of the distribution of the extreme value series may also have significant impacts on non-stationary modelling (Katz and Brown 1992; Villarini et al. 2009a, b). Vinnikov and Robock (2002) provided a technique for investigating temporal trends in the variance and higher moments of the distribution of extreme value series. Their method constructs time series of the squares, cubes and any higher powers of the residuals (anomalies) after the trend in the expected value is subtracted from the observed time series. Trend analysis of these created series can then be used to examine the variability of the series over time. The MK test detected significant decreasing trends in both the mean and the variance of the distribution of the AMDF series (Table 1).

Table 1 Mann-Kendall (MK) test results of the moments considered in this study. The critical value of the MK statistic is Z 1 − α/2 = 1.960, at α = 0.05; all trends were decreasing
Full size table

4.2 Step 2. Temporal Trends in the E(X t ) and Var(X t ) Series

The PD and corresponding parameter estimation method were applied to the annual daily flow series of different years from Huaxian station under the four scenarios described earlier: Lognormal PD with maximum likelihood method, Lognormal PD with L-moments method, Gamma PD with maximum likelihood method, and Gamma PD with L-moments method. Examination of the assumption of independence for each of the observed annual daily flow series unsurprisingly indicated that most of the annual daily flow series did not satisfy the independence assumption. In this situation we relaxed the requirement for independence, as explained previously.

When taking the Lognormal distribution as the PD, no rejection at the significance level of α = 0.05 using the Chi-squared test was detected for both the maximum likelihood and the L-moments methods, which means that the scenarios of Lognormal PD with maximum likelihood and L-moments techniques both satisfactorily fitted the 56 observed annual daily flow series. For the Gamma distribution, there were rejections in 20 and 9 out of 56 years for the maximum likelihood and the L-moments methods respectively. Thus, the Lognormal performed better than the Gamma distribution as the PD. Boxplots of the NSE pp and NSE qq for the period of 1954–2009 (Fig. 2) indicated that the L-moments was superior to the maximum likelihood method, with almost all the NSE pp and NSE qq higher than 0.9. This data exploration led us to select the Lognormal distribution as the PD of the annual daily flow series, and employ the L-moments technique to estimate the parameters of the PD. Examples of the frequency analysis of annual daily flow series with corresponding NSE pp and NSE qq under the four scenarios (Fig. 3) illustrate the differences in the distributions and parameter estimation methods. Finally, the E(X t ) and Var(X t ) series for the period of 1954–2009, calculated by Eqs. (2)–(3), both had significant decreasing trends indicated by the MK test (Table 1).

Fig. 2
figure 2

Boxplots of the a Nash-Sutcliffe efficiency between modelled and empirical probabilities (NSE pp ) and b Nash-Sutcliffe efficiency between modelled and empirical daily flows (NSE qq ) of the four scenarios applied to the 56 annual daily flow series of Huaxian station. The four scenarios are (S1) Lognormal parent distribution (PD) with maximum likelihood method, (S2) Lognormal PD with L-moments method, (S3) Gamma PD with maximum likelihood method, and (S4) Gamma PD with L-moments method

Full size image
Fig. 3
figure 3

Six examples of frequency analysis of the annual daily flow series with corresponding NSE pp and NSE qq under the four scenarios used in the study

Full size image

4.3 Step 3. Non-Stationary Flood Series Modelling with NCM

As significant non-stationarity was detected in both the annual daily flow series and the AMDF series, we could progress to investigating the impact of the non-stationarity in the annual daily flow series on the non-stationarity in the AMDF series using NCM. The estimated shape parameter κ of the GEV distribution fitted to the observed AMDF series from Huaxian station was close to zero (0.039), suggesting that the Gumbel distribution was more appropriate (Stedinger et al. 1993; Gilroy and McCuen 2012). For any year t, the Gumbel norming constants d v t and c v t can be theoretically derived by Eqs. (9)–(10) given the corresponding fitted PD parameters (μ t and σ t ) and the block length v. The block length for an annual maximum flood event is ostensibly 1 year, whereby v = 365 (or 366). As the annual daily flow series in most years was not serially independent, v should take a value lower than this, which might explain the sporadically poor model fits by the Lognormal and Gamma distributions, expressed by outliers in the boxplots of both NSE pp and NSE qq , even for the optimal scenario of Lognormal PD with L-moments parameter estimation method (Fig. 2). For the observed AMDF series, we derived an optimal value of v eff  = 343 days in terms of the AIC criterion (Fig. 4a). Time-varying norming constants \( {d}_t^{v_{eff}} \) and \( {c}_t^{v_{eff}} \) for the period of 1954–2009 were then calculated by Eqs. (9)–(10) with the estimated μ t and σ t series and the optimal v eff . The result indicated decreasing trends for both \( {d}_t^{v_{eff}} \) and \( {c}_t^{v_{eff}} \) (Fig. 4b).

Fig. 4
figure 4

a Calibration of v eff in terms of the AIC criterion and b calculated time-varying norming constants series \( {d}_t^{v_{eff}} \) and \( {c}_t^{v_{eff}} \); the series were derived by Eqs. (9) and (10) respectively with the Lognormal μ t and σ t series estimated from the annual daily flow series by the L-moments method and the v eff  = 343

Full size image

In application of non-stationary FFA by NCM, the residuals should theoretically be approximately independent and normally distributed if the fit of the model is correct. The independence and normality of the residuals indicate that the selected model describes all the systematic information and the remaining part (residuals) are independent and normally distributed random noise. For the Wei River data, the model residuals were found to be randomly distributed and serially independent (Fig. 5a, b). Most of the points in the normal Q-Q plot (not illustrated in this paper) were evenly distributed on or around the 1:1 line—a pattern also revealed by the worm plot (Fig. 5c). Almost all of the worm points were within the 95 % confidence intervals, indicating good consistency between the selected model and the observed flood data. The statistics of the model residuals (Table 2) indicated no significant departure from normality of the residuals. The centile curves plot (Fig. 5d) showed most of the points within the region between the 5 and 95 % centile curves and the decreasing trend was also captured. The empirical frequency was within 5 % of the theoretical probability for all centile curves, except for the 50th percentile, which had a difference of 7.1 % (Table 3). The above qualitative and quantitative assessment criteria together suggested that: (i) the model residuals were approximately independent and identically distributed random noise, and (ii) the NCM provided a reasonably good fit to the non-stationary AMDF series by considering the relationship of the non-stationarities in the annual maximum floods to the non-stationarities in the annual daily flow series.

Fig. 5
figure 5

Residual plots and the centile curves plot for the NCM (time-varying \( {d}_t^{v_{eff}} \) and \( {c}_t^{v_{eff}} \) series were calculated as described in Fig. 4b). a Residual versus observed year plot, b ACF plot, c worm plot, and d centile curves plot; the blue points are the observed AMDF series, the red line is the 50 % centile curve, the dark grey region is the area between the 25 and 75 % centile curves and the light grey region is the area between the 5 and 95 % centile curves

Full size image
Table 2 Summary of the AIC values and statistics of the residuals for the NCM, the stationary model and the optimal NCM with meteorological covariates (NCM-MC)
Full size table
Table 3 Comparison between the empirical frequency of the observed flood events falling below each centile curve and the corresponding theoretical probability for the NCM, the stationary model and the optimal NCM with meteorological covariates (NCM-MC)
Full size table

As a comparison with the NCM, the conventional stationary FFA model was also applied to the AMDF series by fitting the Gumbel distribution and estimating the invariable norming constants d v and c v by the L-moments technique over the entire AMDF series. A decreasing trend of the residuals was indicated (Fig. 6a), and a serial correlation could not be rejected (Fig. 6b). The worm plot indicated an acceptable result, with almost all the points falling within the 95 % confidence intervals (Fig. 6c), but the stationary model had a larger AIC value than the NCM, and the normality of the residuals was just unacceptable in terms of the Filliben correlation coefficient (Table 2). Furthermore, all the centile curves were horizontal (Fig. 6d), which does not describe the variability of the AMDF series, and there were discrepancies of 5 % or more for three of the centile curves (Table 3).

Fig. 6
figure 6

Residual plots and the centile curves plot for the stationary model. a Residual versus observed year plot, b ACF plot, c worm plot, and d centile curves plot; the blue points are the observed AMDF series, the red line is the 50 % centile curve, the dark grey region is the area between the 25 and 75 % centile curves and the light grey region is the area between the 5 and 95 % centile curves

Full size image

4.4 Step 4. Meteorological Covariate Analysis for the NCM

The estimated μ t and σ t sequences for the period of 1954–2009 were expressed as multivariate linear functions of the meteorological covariates. The fitted expressions were then substituted into Eqs. (9)–(10) for calculating the time-varying norming constants (with v eff  = 343) and the covariate combinations for both PD parameter sequences were optimized in terms of the AIC criterion. This produced significant covariates for μ t and σ t , the optimal AIC value and the statistics of the residuals (Table 2, Fig. 7). The optimal fitted expressions of μ t and σ t by meteorological covariates were:

$$ {\mu}_t=3.5751+0.0819{H}_{mean}-0.4496 TMEA{N}_{mean} $$
(13)
$$ {\sigma}_t=2.6093-0.0376{H}_{mean}+0.0056rai{n}_{3 \max }+0.0012rai{n}_{year} $$
(14)
Fig. 7
figure 7

Residual plots and the centile curves plot for the optimal NCM with meteorological covariates (time-varying \( {d}_t^{v_{eff}} \) and \( {c}_t^{v_{eff}} \) series were calculated by Eqs. (9) and (10) respectively after a procedure of expressing the estimated Lognormal μ t and σ t series as linear functions of meteorological covariates and v eff  = 343). a Residual versus observed year plot, b ACF plot, c worm plot, and d centile curves plot; the blue points are the observed AMDF series, the red line is the 50 % centile curve, the dark grey region is the area between the 25 and 75 % centile curves and the light grey region is the area between the 5 and 95 % centile curves

Full size image

For the NCM with meteorological covariates (NCM-MC) a slightly smaller AIC value was observed compared to that of the NCM without considering the relation of the PD parameters (μ t and σ t ) to meteorological factors (Table 2). The residuals were randomly distributed and serially independent, and without outliers (Fig. 7a, b). The normal Q-Q plot (not illustrated in this paper) had almost all the points distributed on the 1:1 line—a pattern also revealed by the worm plot (Fig. 7c), where all the points were located within the 95 % confidence intervals and aligned on or around the fitted cubic polynomial line. The statistics of both the Filliben correlation coefficient and the KS test of the residuals (Table 2) indicated that the residuals were normally distributed random noise. The centile curves plot (Fig. 7d) showed the majority of the points falling within the 5–95 % region, and the centiles captured the decreasing trend of the flood series. The empirical frequency was within 5 % of the theoretical probability for all centile curves (Table 3).

4.5 Implication of NCM for Design Flood Estimation

The NCM with meteorological covariates (NCM-MC) takes full advantage of the non-stationarity in the annual daily flow series and closely related climate factors. For the Wei River, this method produced the most reliable estimate of the magnitude of a design flood under non-stationary conditions. Flood magnitudes with a 0.01 annual exceedance probability (corresponding to 100-year flood events under stationary conditions) were estimated for each observed year for the NCM-MC. The 0.01-probability flood quantile of the stationary FFA model was also estimated and compared with that from the NCM-MC. The 95 % confidence intervals of the 0.01-probability flood quantiles were evaluated with the parametric bootstrap technique (Kyselý 2010; Tramblay et al. 2013) for both the stationary and the NCM-MC models.

For the stationary FFA model, the estimated 100-year flood event was a constant magnitude of 7 300 m3/s (Fig. 8). For the NCM-MC, a great range of variability was apparent in the estimated design flood (Fig. 8). The flood magnitudes under the 0.01-probability ranged from a minimum of 2 000 m3/s (in 1997) to a maximum of 14 100 m3/s (in 1983). In this case, the assumption of stationarity would seem to over-estimate design flood magnitudes for the future. In the case of increasing trend in the flood series (e.g. Robson 2002), design floods could be under-estimated, potentially increasing risk of flood damage or dam failure into the future. On the other hand, where the trend is decreasing (e.g. Ishak et al. 2013, and our Wei River case study) design floods could be over-estimated, possibly imposing unnecessarily high costs on society for future flood protection. The NCM proposed here for non-stationary FFA has application to both of these cases.

Fig. 8
figure 8

Flood quantiles for the 0.01 annual exceedance probability for both the stationary model and the optimal NCM with meteorological covariates (NCM-MC). CI is the confidence interval of the corresponding flood quantile

Full size image

5 Conclusions

The fundamental assumption of stationarity for flood frequency analysis is suspect under the conditions of climate change and large-scale anthropogenic activities that affect flood runoff. Recognizing this problem, we developed a solution termed the norming constants method (NCM) of non-stationary flood frequency analysis (FFA). Our approach was to incorporate non-stationarity information in the annual daily flow series into the non-stationary FFA of the AMDF series.

A four-step framework is appropriate for applying the NCM of non-stationary FFA. The basis of applying the NCM is testing the presence of non-stationarity in the hydrological time series. As the time-varying statistical parameters of the AMDF distribution are mathematically derived from the annual daily flow series, the form of non-stationarity of the AMDF series is unimportant, and any suitable test for non-stationarity can be employed.

In applying the NCM, we suggest that both Lognormal and Gamma distributions be fitted to annual daily flow series, and both the maximum likelihood and L-moments techniques be used to estimate the statistical parameters of the distributions. Statistical tests will determine the most appropriate scenario for the annual daily flow series. Our suggested solution to the serial correlation apparent in most annual daily flow series is to calibrate the value of block length v in terms of the AIC criterion, to reflect the real independence within the annual daily flow series. Application of the suggested NCM to data from Huaxian hydrological station on the Wei River, China, found that by considering information concerning the non-stationarity in the annual daily flow series, the NCM performed better than a model based on the assumption of stationarity. Incorporating climate factors as explanatory variables further improved the model performance, and made the non-stationary FFA more physically meaningful. On this basis, estimation of design flood magnitude should be more reliable using the NCM approach than a method that assumes stationarity. While our test application of the NCM approach was limited to only one study site, the results were sufficiently promising to suggest that the method could have widespread global application in providing more realistic information for flood risk assessment.