Introduction

Water, a blessed gift bestowed by God that covers ~ 70% of our planet’s surface, is found all around the earth, in lakes, rivers, oceans, icebergs and even under the ground, and beyond the earth in clouds and the atmosphere. However, 97.5% of this amount is comprised of saline waters and thus only 2.5% is fresh, and the latter is not distributed equally across the planet (Shiklomanov 1998). Moreover, only 0.4% of the total volume of freshwater available to humans is in the form of lakes and rivers, and unlike other resources such as oil, which can be utilized in different forms, there are no substitutes (Guo et al. 2010).

Water scarcity is a serious concern in many countries that limits the development of the industrial and agricultural sectors as well as the overall aspects of human life (Li et al. 2015). Water shortage occurs due to the population growth, global economic development, urbanization and industrialization, climate change, water infrastructure destruction, and poor water quality (Sophocleous 2004; Xie et al. 2013). Today, many parts of the planet face scarcity of water resources. Based on statistics released by the United Nations, ~ 700 million people in 43 different countries are suffering from water shortage. It is predicted that by 2025, 1.8 billion people who live in regions and countries faced with water shortages and 3–4 million people die annually due to water shortage or related diseases (Wang and Huang 2015). Moreover, it is reported that the agriculture sector will likely face the problem of reduced water availability and the need to produce more food in the near future (Dogra et al. 2014).

Over the past decades, optimal and efficient water allocation has challenged many water resource managers. Ineffective allocation of water resources and farmland further aggravated the conflict among the water users (Dong et al. 2018). This ineffective allocation exacerbated the problem of water pollution (Dong et al. 2018). Water allocation planning is an essential component of managing water uses, and it involves deciding how much water is available from a particular resource and how much water can be taken (Sophocleous 2004; Shao et al. 2011). In other words, equity in water allocation is a significant challenge that needs to be considered by authorities and decision makers (Shukla and Gedam 2018).

Optimization techniques play a vital role in helping the decision makers optimally allocate water resources to different users. The variety of uncertainties existing in water resources management may intensify the complexity in decision-making process; therefore, conventional optimization techniques such as linear programming, quadratic programming, and integer programming would become ineffective (Wang and Huang 2015).

Among the variety of methods used in water resources management for dealing with uncertainties, two-stage stochastic programming (TSP), as a kind of stochastic optimization method, was widely used for dealing with randomness in such systems and has the ability to take corrective actions after a random event occurs (Brige and Louveaux 1988; Tajeddini et al. 2014; Parisio and Jones 2015). TSP is a scenario-based approach and is useful in analyzing long-term and midterm schemes. In TSP, at first, a decision is made before the realization of random variables; then, the second decision can be determined to minimize penalties after the random event has taken place, and their values are known. The process of making the first decision is called the first stage, and the relevant variables are called first-stage variables. The process of making other decisions is called the second stage, and the relevant variables are called second-stage variables.

Pereira and Pinto (1985) proposed a stochastic optimization approach for the planning of a multi-reservoir hydroelectric system under uncertainty. Wang and Adams (1986) introduced a two-stage optimization framework for optimal water reservoir operations. In their research, periodic Markov processes were used to describe seasonality of water resources inflows. Ferrero et al. (1998) examined the hydrothermal scheduling of multi-reservoir systems using a two-stage dynamic programming approach. Seifi and Hipel (2001) proposed a method for the long-term planning of reservoirs with stochastic inflows. They used TSP and an interior-point method for optimizing reservoir operation. Ahmed et al. (2003) also used a limited branch and boundary algorithm to solve the two-stage stochastic planning.

Previous research on the TSP method does not reflect the dynamic changes in system conditions (especially in high-volume systems). Thus, multistage stochastic programming (MSP) method has been developed by the recent researchers (Yin and Han 2015; Hu and Hu 2018; Zahiri et al. 2018). In MSP, recourse actions are permitted for each period based on uncertainties related to specified values. The most prominent advantage of MSP is its flexibility in the decision-making and scenario-setting process, although period information should be investigated. Among the conducted research, quantitative researchers have implemented this method independently in the field of water resources management. For example, Pereira and Pinto (1991) introduced a multistage stochastic optimization method in hydrological energy system planning. Watkins et al. (2000) presented an MSP model to utilize water from mountain lakes. Modeling with MSP to manage water resources is identical to the two-stage approach.

The role of wastewater in today’s world where the demand for water is rising sharply, and the earth’s water resources are consequently decreasing, is becoming more and more prominent. Under such circumstances, the use of unconventional water including sewage from refinement plants in various sectors—particularly for the agricultural industry that uses the majority of water—is inevitable. The year 2017 was named the Year of Wastewater by the World Water Forum, which indicates the importance of wastewater about water reuse and quality of wastewater discharges. Therefore, this research aims to optimally manage and allocate water resources by considering the uncertainty and vague parameters. This research focuses on the city of Zarand, Kerman province, Iran, as a case study (which consists of three kinds of consumers and three water resources where no wastewater refinement is carried out). In addition, in the form of a scenario, refined wastewater was considered as an allocable water supply and then compared with the case where refined wastewater was not considered as a water supplier. Hence, a designated wastewater refinement plant with specified volume was considered and applied within the model where wastewater that can be refined was collected from all areas, and subsequent refinement operations were carried out and re-transferred to applicant sections.

Water Allocation Modeling

The world today is witnessed to increasing demand for water due to population growth, industrial and agricultural development, urbanization, and climate changes (Wang et al. 2016). In order to develop the agricultural and industrial sectors, these disparate groups of water users need to be aware of how much water they can expect for their activities and economic investments. This information is extremely necessary for planning because, if the promised water cannot be delivered, they will have to obtain water from higher priced alternatives or make negative changes in their development plans. In other words, there is inherent complexity and uncertainty in water resource decision making that placed them beyond the conventional deterministic optimization methods (Maqsood et al. 2005).

Water Allocation Modeling by TSP

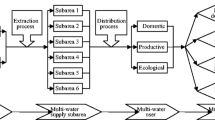
A region is considered that contains a number of water resources and water managers, which are responsible for allocating water to different consumers including agricultural, industrial, and municipal sectors. This problem can be formulated as (Loucks et al. 1981):

$$ \hbox{max} \;f = \mathop \sum \limits_{i = 1}^{m} {{NB}}_{i} T_{i} - E\left[ {\mathop \sum \limits_{i = 1}^{m} C_{i} D_{iQ} } \right] $$
(1)

subject to:

$$ Q \ge \mathop \sum \limits_{i = 1}^{m} \left( {T_{i} - D_{iQ} } \right) $$
(2)
$$ T_{i\;\hbox{max} } \ge T_{i} \ge D_{iQ} \ge 0 $$
(3)

In this model, \( {{NB}}_{i} \) is the net benefit of consumer i per unit of water allocated, \( T_{i} \) is allocation target of water that is promised to consumer i (cubic meter), \( C_{i} \) is reduction in net benefit to user i per unit of water not allocated, \( D_{iQ} \) is amount by which water allocation target is not met when seasonal flow is Q, E [0] is the expected value of a random variable, f is net system benefit, m is number of water consumers, Q is random variable equal to total water available, and \( T_{i\;\hbox{max} } \) is maximum allowable allocation amount for consumer i.

Equation 1 is an objective function that maximizes the expected value of a region’s economic activity such that if the promised amount is delivered, it will lead to the net benefit for the local economy. However, if not delivered, it leads to penalties in the local economy. Equation 2 shows the first constraint that water allocated from different resource is less than the amount of water available; and Eq. 3 shows the second constraint that the maximum allowable allocation amount is more than the initial allocation target and the optimal shortage of consumers.

In order to solve this model by linear programming, the probability distribution of Q must be approximated by a discrete function. If Q takes q values with probability P, then:

$$ E\left[ {\mathop \sum \limits_{i = 1}^{m} C_{i} D_{iQ} } \right] = \mathop \sum \limits_{i = 1}^{m} C_{i} \left( {\mathop \sum \limits_{j = 1}^{n} P_{j} D_{ij} } \right) $$
(4)

where \( D_{ij} \) is water shortage for consumer i, when seasonal flow is \( q_{j} \) with probability of \( P_{j} \), n is number of different flow levels (low, medium, high), \( P_{j} \) is probability of occurrence flow level j (low, medium, high).

By using Eq. 4 in Eq. 1, the TSP is formulated as:

$$ \hbox{max} \;f = \mathop \sum \limits_{i = 1}^{m} {{NB}}_{i} T_{i} - \mathop \sum \limits_{i = 1}^{m} C_{i} \left( {\mathop \sum \limits_{j = 1}^{n} P_{j} D_{ij} } \right) $$
(5)

subject to:

$$ q_{j} \ge \mathop \sum \limits_{i = 1}^{m} \left( {T_{i} - D_{ij} } \right) \quad \forall j $$
(6)
$$ T_{i\;\hbox{max} } \ge T_{i} \ge D_{ij} \ge 0\quad \forall i.j $$
(7)

TSP is not easily implemented in the real-world cases of water resources management because it is difficult for a planner to determine a deterministic value of parameters such as allocation targets \( T_{i} \), the net benefit of water allocated \( {{NB}}_{i} \) or the penalty of water not delivered \( C_{i} \). In addition, the inadequate quality of the information to present them as probability distribution has made TSP a challenging method (Birge and Louveaux 1988). Therefore, incorporating interval-parameter programming (IPP) within a TSP framework is a practical approach to better reflecting uncertainties. IPP was introduced by Huang et al. (1995), and it has been widely used in various fields, especially in water resources management. Huang and Loucks (2000) have used IPP in the TSP framework since 2000. The reasons for using such method in water resources management can be summarized as follows:

  • The quality of data obtained from uncertain parameters is not satisfactory enough to be used to obtain the probability distribution function. Besides, even if these distributions are available, their reflection in large-scale TSP models can be extremely challenging (Huang and Loucks 2000). In other words, in order to obtain the probability distribution function of an uncertain parameter, accurate and reliable information is required (Fan et al. 2011).

  • It is hard to solve the TSP model with all uncertain parameters being expressed as a probability density function (Fan et al. 2015).

  • Using and presenting information as interval and fuzzy parameters is more favorable than deterministic parameters (Fan et al. 2011).

If x is a closed set of real numbers, then \( x^{ \pm } \) is a gray number with upper and lower bounds but with unknown distribution; thus,

$$ x^{ \pm } = \left[ {x^{ - },\,x^{ + } } \right] = \left\{ {t \in x|x^{ - } \le t \le x^{ + } } \right\} $$
(8)

where \( x^{ - } \), \( x^{ + } \) represent the lower and upper bounds of \( x^{ \pm } \), respectively.

Huang and Loucks (2000) presented a TSP method with interval parameters or inexact two-stage stochastic programming (ITSP) approach to allocate water to different consumers. Their research has been used extensively for water resources management and environmental planning, and provides solutions for generating decision alternatives and identifies and analyzes significant factors that affect a system’s performance (Huang and Loucks 2000). ITSP is an effective measure for addressing problems where an analysis of policy scenarios is desired periodically over time and uncertain parameters have probability distribution functions and interval numbers (Xie et al. 2018). Huang et al. (1993, 1995) proposed an IPP to manage water resources in an agricultural environment. Li and Huang (2008) also combined TSP and IPP in a nonlinear programming framework. Their model considers several water resources, demand regions and a bunch of water end users, and responses as interval parameters maximize economic benefit and minimize failure risks. Xie et al. (2013) applied ITSP by considering multiple water resources and several consumers. Various scenarios corresponding to different river inflow levels were evaluated. The results indicated that different inflow levels could lead to different water allocation schemes with variation in system benefit and system failure risk. Zhang and Li (2014) used ITSP for sustainable development and water resources management and applied it to an area in China that includes multiple water resources and some regions and users. Fu et al. (2016) presented an ITSP method based on adaptive water resource management (AWRM). In their model, the cost of water exchange between different regions is considered, and results indicated that optimistic water policies lead to higher income but may be subject to higher risk of system failure, and the results can be used by managers to adjust investment activities and avoid making inappropriate decisions. Ji et al. (2017) applied the ITSP model to manage water resources in Tianjin, China (a coastal city facing severe water shortage). In their optimization model, water supply cost and sewage treatment cost were considered besides water utilization benefits and water shortage penalty. Liu et al. (2017) proposed a two-stage regional multi-water source allocation model by considering surface, ground, and transit water. By solving the model of Liu et al. (2017), optimized water supply target and shortage, optimized water allocation, and satisfaction of supply targets in each user sector have been obtained.

Modeling Optimal Water Resources Allocation Using ITSP

Water resources allocation within ITSP framework is modeled as follows:

$$ \hbox{max} \;f^{ \pm } = \mathop \sum \limits_{i = 1}^{m} {{NB}}_{i}^{ \pm } T_{i}^{ \pm } - \mathop \sum \limits_{i = 1}^{m} \mathop \sum \limits_{j = 1}^{n} P_{j} C_{i}^{ \pm } D_{ij}^{ \pm } $$
(9)

subject to:

$$ q_{j}^{ \pm } \ge \mathop \sum \limits_{i = 1}^{m} \left( {T_{i}^{ \pm } - D_{ij}^{ \pm } } \right) \quad \forall j $$
(10)
$$ T_{i\;\hbox{max} }^{ \pm } \ge T_{i}^{ \pm } \ge D_{ij}^{ \pm } \ge 0\quad \forall i.j $$
(11)

where \( T_{i\;\hbox{max} }^{ \pm } .C_{i}^{ \pm } . D_{ij}^{ \pm } . {{NB}}_{i}^{ \pm } . T_{i}^{ \pm } \) are interval variables and parameters. If \( T_{i}^{ \pm } \) represents promised water allocation targets for different consumers, which are considered as uncertain parameters, it would be difficult to determine which parameter bounds (\( T_{i}^{ + } \) as the upper bound or \( T_{i}^{ - } \) as the lower bound) will correspond to the upper bound of system benefit (\( f^{ + } \)). In these circumstances, the existing methods will not be applicable for solving the interval linear programming problems (Huang and Loucks 2000). Therefore, an optimized set of allocation targets can be obtained by including \( y_{i} \) in the model as decision variables such as below:

$$ T_{i}^{ \pm } = T_{i}^{ - } + \Delta T_{i} y_{i} $$
(12)
$$ \Delta T_{i} = T_{i}^{ + } - T_{i}^{ - } $$
(13)

By incorporating Eqs. (12) and (13) in Eq. (9), ITSP can be formulated:

$$ \hbox{max} \;f^{ \pm } = \mathop \sum \limits_{i = 1}^{m} {{NB}}_{i}^{ \pm } \left( {T_{i}^{ - } + \Delta T_{i} y_{i} } \right) - \mathop \sum \limits_{i = 1}^{m} \mathop \sum \limits_{j = 1}^{n} P_{j} C_{i}^{ \pm } D_{ij}^{ \pm } $$
(14)

subject to:

$$ q_{j}^{ \pm } \ge \mathop \sum \limits_{i = 1}^{m} \left( {T_{i}^{ - } + \Delta T_{i} y_{i} - D_{ij}^{ \pm } } \right)\quad \forall j $$
(15)
$$ T_{i\;\hbox{max} }^{ \pm } \ge T_{i}^{ - } + \Delta T_{i} y_{i} \ge D_{ij}^{ \pm } \ge 0\quad \forall i.j $$
(16)
$$ 0 \le y_{i} \le 1 $$
(17)

where \( y_{i} \) is the decision variable. On this basis, when \( T_{i}^{ \pm } \) reaches its upper bound (\( y_{i} = 1 \)), higher benefits will be obtained while the risk of unsatisfying promised allocation targets reaches upper bound. Conversely, if \( T_{i}^{ \pm } \) reaches its lower bound (\( y_{i} = 0 \)), there will be a lower benefit but with lower risks of the system.

Modeling Optimal Water Resources Allocation Using Interval Fuzzy TSP

Although ITSP has been used extensively in many studies (Huang and Loucks 2000; Xie et al. 2018), IPP is not applicable in many real-world problems, because vague information may exist in the optimization model (objective function and constraints). Moreover, in IPP, uncertainties in parameters are presented as discrete intervals; thus, the upper and lower bounds of these intervals may be known with uncertainty that results in dual uncertainties. An effective way to overcome these complexities is to incorporate fuzzy programming (FP) with type 2 membership function within the framework of ITSP (Maqsood et al. 2005) that leads to an interval fuzzy TSP (IFTSP).

FP is applicable when the information of the problem is vague. In other words, the system impreciseness can be addressed by FP. It is also useful to be used in decision-making problems with the fuzzy objective function and constraints (Zimmermann 1985). If G is fuzzy objective and C is fuzzy constraint in X decision alternative, then fuzzy decision set D will be the intersection between G and C (Fig. 1) and is shown by the following equations:

Figure 1
figure 1

Fuzzy decision theory (Wang and Huang 2013)

Full size image
$$ D = G\;\cap C $$
(18)
$$ \mu_{D} = \hbox{min} \left\{ {\mu_{G},\,\mu_{C} } \right\} $$
(19)

where \( \mu_{D},\,\mu_{G},\,\mu_{C} \) are fuzzy decision membership functions, fuzzy goal, and fuzzy constraints, respectively. The desired decision is the one with the highest \( \mu_{D} \) value:

$$ \hbox{max} \;\mu_{D} = \hbox{max} \;\hbox{min} \left\{ {\mu_{G} .\mu_{C} } \right\} $$
(20)

Ordinary fuzzy sets are not applicable if the membership functions are given imprecisely. Therefore, in practical problems, the appropriate choice of membership functions for fuzzy goal and constraints is one of the critical issues. To reflect such issues, the concept of type 2 fuzzy sets is effective in addressing such uncertainties. The concept of type 2 fuzzy sets is shown in Figure 2.

Figure 2
figure 2

Fuzzy decision theory with type 2 membership function (Wang and Huang 2013)

Full size image

Maqsood et al. (2005) proposed an IFTSP to manage water resources for allocating water optimally to different consumers. In their optimization model, type 2 fuzzy membership function has been used. Wang and Huang (2013) used IFTSP to reflect uncertainties in the objective function and right-hand side of constraints as fuzzy and interval parameters. The results indicate that several interval solutions can be obtained under various scenarios, which enhances the diversity of solutions for supporting decisions of water resources allocation.

Fan et al. (2015) also used IFTSP in their study and obtained a series of fuzzy interval solutions under different α-cut levels. Zhou et al. (2016) proposed an IFTSP approach to support water resources management under dual uncertainties. They took into account uncertainties as fuzzy parameters and variability of α-cut levels. Their results showed that any change in α-cut level could affect the solutions. Therefore, fuzzy sets are highly applicable in the water resource management where many of its information have uncertainties. Zeng et al. (2017) applied IFTSP for water resources allocation and water quality management in a river basin in China by considering sever water deficit and water quality degradation. In their model, water allocation pattern, pollution mitigation scheme, and system benefit under various scenarios were analyzed.

Optimal water resource allocation can be modeled using FP within the ITSP framework as follows:

$$ \hbox{max} \;\alpha^{ \pm } $$
(21)

subject to:

$$ \mathop \sum \limits_{i = 1}^{m} {{NB}}_{i}^{ \pm } \left( {T_{i}^{ - } + \Delta T_{i} y_{i} } \right) - \mathop \sum \limits_{i = 1}^{m} \mathop \sum \limits_{j = 1}^{n} P_{j} C_{i}^{ \pm } D_{ij}^{ \pm } \ge \underline{f}^{ \pm } + \widetilde{\Delta f}\alpha $$
(22)
$$ \underline{q}_{j}^{ \pm } - \widetilde{{\Delta q_{j} }}\alpha \ge \mathop \sum \limits_{i = 1}^{m} \left( {T_{i}^{ - } + \Delta T_{i} y_{i} - D_{ij}^{ \pm } } \right) \quad \forall j $$
(23)
$$ T_{i\;\hbox{max} }^{ \pm } - \Delta T_{i\;\hbox{max} } \alpha \ge T_{i}^{ - } + \Delta T_{i} y_{i} $$
(24)
$$ T_{i}^{ - } + \Delta T_{i} y_{i} \ge D_{ij}^{ \pm } \quad \forall i.j $$
(25)
$$ D_{ij}^{ \pm } \ge 0\quad \forall i.j $$
(26)
$$ 0 \le y_{i} \le 1\quad \forall i $$
(27)
$$ 0 \le \alpha \le 1 $$
(28)

In this model, \( \alpha^{ \pm } \) is degree of satisfaction of the fuzzy objective or constraints (optimal system reliability), \( \underline{f}^{ \pm } \) is lower bound of net system benefit where it is expressed as intervals, \( \overline{f}^{ \pm } \) is upper bound of net system benefit, \( \overline{q}^{ \pm } \) is upper bound of water inflow, \( \underline{q}^{ \pm } \) is lower bound of water inflow, \( \overline{f}^{ - } \) is lower interval of upper-bound net system benefit, \( \underline{f}^{ - } \) is lower interval of lower-bound net system benefit, \( \overline{f}^{ + } \) is upper interval of upper-bound net system benefit, \( \underline{f}^{ + } \) is upper interval of lower-bound net system benefit. Equation 29 is established for this model; thus,

$$ \widetilde{\Delta f} = \overline{f}^{ \pm } - \underline{f}^{ \pm } = \left[ {\overline{f}^{ - } ,\,\overline{f}^{ + } } \right] - \left[ {\underline{f}^{ - } ,\,\underline{f}^{ + } :} \right] = \left[ {\overline{f}^{ - } - \underline{f}^{ + } ,\,\overline{f}^{ + } - \underline{f}^{ - } } \right] $$
(29)

IFTSP Solution Method

To solve model’s objective \( (\hbox{max} \;\alpha^{ \pm } ) \), we should transform it into two deterministic sub-models. Initially, the sub-model corresponding to the most desirable system objective value \( (f^{ + } ) \) is solved, and then, the results are used to solve the sub-model corresponding to \( f^{ - } \). The sub-model to find \( f^{ + } \) is:

$$ \hbox{max} \;\alpha^{ + } $$
(30)

subject to:

$$ \mathop \sum \limits_{i = 1}^{m} {{NB}}_{i}^{ + } \left( {T_{i}^{ - } + \Delta T_{i} y_{i} } \right) - \mathop \sum \limits_{i = 1}^{m} \mathop \sum \limits_{j = 1}^{n} P_{j} C_{i}^{ - } D_{ij}^{ - } \ge \underline{f}^{ + } + \widetilde{\Delta f}\alpha $$
(31)
$$ \overline{{q_{j}^{ + } }} - \widetilde{{\Delta q_{j} }}\alpha \ge \mathop \sum \limits_{i = 1}^{m} \left( {T_{i}^{ - } + \Delta T_{i} y_{i} - D_{ij}^{ - } } \right)\quad \forall j $$
(32)
$$ T_{i\;\hbox{max} }^{ + } - \Delta T_{i\;\hbox{max} } \alpha \ge T_{i}^{ - } + \Delta T_{i} y_{i} $$
(33)
$$ T_{i}^{ - } + \Delta T_{i} y_{i} \ge D_{ij}^{ - } \quad \forall i.j $$
(34)
$$ D_{ij}^{ - } \ge 0\quad \forall i.j $$
(35)
$$ 0 \le y_{i} \le 1\quad \forall i $$
(36)
$$ 0 \le \alpha^{ + } \le 1 $$
(37)

In this sub-model, \( D_{ij}^{ - } \) and \( y_{i} \) are decision variables, and \( \alpha^{ + } \) is upper system reliability bound. Optimized targets allocation values \( T_{{i\;{\text{opt}}}}^{ \pm } \) can be obtained as:

$$ T_{{i\;{\text{opt}}}}^{ \pm } = T_{i}^{ - } + \Delta T_{i} y_{i} $$
(38)

The next step is to solve the sub-model corresponding to \( f^{ - } \):

$$ \hbox{max} \;\alpha^{ - } $$
(39)

subject to:

$$ \mathop \sum \limits_{i = 1}^{m} {{NB}}_{i}^{ - } \left( {T_{i}^{ - } + \Delta T_{i} y_{{i\;{\text{opt}}}} } \right) - \mathop \sum \limits_{i = 1}^{m} \mathop \sum \limits_{j = 1}^{n} P_{j} C_{i}^{ + } D_{ij}^{ + } \ge \underline{{f^{ - } }} + \widetilde{\Delta f}\alpha $$
(40)
$$ \overline{{q_{j}^{ - } }} - \widetilde{{\Delta q_{j} }}\alpha \ge \mathop \sum \limits_{i = 1}^{m} \left( {T_{i}^{ - } + \Delta T_{i} y_{{i\;{\text{opt}}}} - D_{ij}^{ + } } \right)\quad \forall j $$
(41)
$$ T_{i\;\hbox{max} }^{ - } - \Delta T_{i\;\hbox{max} } \alpha \ge T_{i}^{ - } + \Delta T_{i} y_{{i\;{\text{opt}}}} $$
(42)
$$ T_{i}^{ - } + \Delta T_{i} y_{{i\;{\text{opt}}}} \ge D_{ij}^{ + } \quad \forall i.j $$
(43)
$$ D_{ij}^{ + } \ge D_{{ij\;{\text{opt}}}}^{ - } \quad \forall i.j $$
(44)
$$ 0 \le \alpha^{ - } \le 1 $$
(45)

In this sub-model, \( D_{ij}^{ + } \) is the decision variable; thus, all optimal solutions for model’s objective \( (\hbox{max} \;\alpha^{ \pm } ) \) are as follows:

$$ D_{{ij\;{\text{opt}}}}^{ \pm } = \left[ {D_{{ij\;{\text{opt}}}}^{ - } ,\,D_{{ij\;{\text{opt}}}}^{ + } } \right] $$
(46)
$$ f_{\text{opt}}^{ \pm } = \left[ {f_{\text{opt}}^{ - } ,\,f_{\text{opt}}^{ + } } \right] $$
(47)
$$ A_{{ij\;{\text{opt}}}}^{ \pm } = T_{{i\;{\text{opt}}}}^{ \pm } - D_{{ij\;{\text{opt}}}}^{ \pm } $$
(48)

where \( D_{{ij\;{\text{opt}}}}^{ \pm } \) is optimal shortage for consumers under different flow levels, \( f_{\text{opt}}^{ \pm } \) is optimal objective function value that is net system benefit, and \( A_{{ij\;{\text{opt}}}}^{ \pm } \) is optimal water resources allocation to consumers under different water flow levels.

In summary, IFTSP can be overcome by the uncertainty embodied in water resources management by using the interval and vague parameters. Table 1 represents the comparison among TSP, ITSP, and IFTSP.

Table 1 Comparison of the TSP, ITSP, and IFTSP
Full size table

Case Study

Problem Statement

This research aims to use IFTSP for optimally managing and allocating water resources. In this optimization model, treated wastewater was considered as allocable water. Therefore, the related parameters have been incorporated into the model. In addition, loss rate of water during transportation and surplus water in the reservoirs have been considered. In order to develop the agricultural and industrial sectors, these disparate groups of water users need to be aware of how much water they can expect for their activities and economic investments. This information is essential for planning because, if the promised water cannot be delivered, they will have to obtain water from higher priced alternatives or make negative changes in their development plans.

Study Area Overview

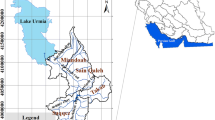
In this research, Zarand city located in the Kerman province of Iran was selected as a case study. This area is part of the Bafq swamp southern basin that has been surrounded from the north and east by Kerman hills, from the west by Davaran hills, and from the south by Kerman plain. The area is about 8420 square meters. It is located in a hot and dry region that has mining sites and industries besides huge pistachio gardens. Therefore, these industrial and agricultural sectors consume the major assigned water to this region. In recent years, this region faced water shortage due to the leak of precipitation besides the agricultural and a rise in industrial sectors’ water demand. Statistical reports gathered by Kerman regional water company show that the annual precipitation of Zarand city was less than 130 mm. In this research, according to the conditions of the case study and based on the opinions of water resources experts in Kerman province, a mathematical programming model is presented using the IFTSP method. In this region, there are three water resources including wellhead, spring, and qanat. The water consumers are the agriculture, industry, and municipal sectors. The model proposed in this study is described in following subsections.

Problem Formulation

Objective Function

This problem can be formulated as an IFTSP model:

$$ \hbox{max} \;\alpha^{ \pm } $$
(49)

Constraints

  • Desirable system benefit constraint

$$ \begin{aligned} & \mathop \sum \limits_{i = 1}^{m} {{NB}}_{i}^{ \pm } \left( {Ta_{i}^{ - } + \left( {\Delta Ta_{i} .ya_{i} } \right)} \right) - \mathop \sum \limits_{i = 1}^{m} \mathop \sum \limits_{j = 1}^{n} Pa_{j} .C_{i}^{ \pm } .Da_{ij}^{ \pm } \\ & + \mathop \sum \limits_{i = 1}^{m} {{NB}}_{i}^{ \pm } \left( {Tb_{i}^{ - } + \left( {\Delta Tb_{i} .yb_{i} } \right)} \right) - \mathop \sum \limits_{i = 1}^{m} \mathop \sum \limits_{j = 1}^{n} Pb_{j} .C_{i}^{ \pm } .Db_{ij}^{ \pm } \\ & + \mathop \sum \limits_{i = 1}^{m} {{NB}}_{i}^{ \pm } \left( {Tc_{i}^{ - } + \left( {\Delta Tc_{i} .yc_{i} } \right)} \right) - \mathop \sum \limits_{i = 1}^{m} \mathop \sum \limits_{j = 1}^{n} Pc_{j} .C_{i}^{ \pm } .Dc_{ij}^{ \pm } \\ & + \mathop \sum \limits_{i = 1}^{m} {{NB}}_{i}^{ \pm } \left( {Tw_{i}^{ - } + \left( {\Delta Tw_{i} .yw_{i} } \right)} \right) - \mathop \sum \limits_{i = 1}^{m} \mathop \sum \limits_{j = 1}^{n} Pw_{j} .C_{i}^{ \pm } .Dw_{ij}^{ \pm } - \alpha \widetilde{\Delta f} \ge \underline{f}^{ \pm } ; \\ \end{aligned} $$
(50)

Equation 50 shows that the net benefit for various consumers minus the penalties (because of not meeting the promised amount of water) should be higher than the desired system benefit.

  • Available water quantity constraints

$$ \mathop \sum \limits_{i = 1}^{m} \left[ {\left( {Ta_{i}^{ - } + \left( {\Delta Ta_{i} .ya_{i} } \right) - Da_{ij}^{ \pm } } \right)} \right]\left( {1 + \varepsilon } \right) + \alpha \Delta \widetilde{qa}_{j} \le \overline{qa}_{j}^{ \pm } + sa0_{j}^{ \pm } \quad \forall j = 1.2.3 $$
(51)
$$ \mathop \sum \limits_{i = 1}^{m} \left[ {\left( {Tb_{i}^{ - } + \left( {\Delta Tb_{i} .yb_{i} } \right) - Db_{ij}^{ \pm } } \right)} \right]\left( {1 + \varepsilon } \right) + \alpha \Delta \widetilde{qb}_{j} \le \overline{qb}_{j}^{ \pm } \quad \forall j = 1.2.3 $$
(52)
$$ \mathop \sum \limits_{i = 1}^{m} \left[ {\left( {Tc_{i}^{ - } + \left( {\Delta Tc_{i} .yc_{i} } \right) - Dc_{ij}^{ \pm } } \right)} \right]\left( {1 + \varepsilon } \right) + \alpha \Delta \widetilde{qc}_{j} \le \overline{qc}_{j}^{ \pm } \quad \forall j = 1.2.3 $$
(53)

Equations 51–53 illustrate that the total water allocated to all water users should be less than the available water flows of the water resources in order to balance the relationship between water supply and demand.

  • Constraint of available water in wellhead

$$ Sa1_{j}^{ \pm } = \overline{qa}_{j}^{ \pm } - \alpha \Delta \widetilde{qa}_{j} - \left[ {\mathop \sum \limits_{i = 1}^{m} \left[ {\left( {Ta_{i}^{ - } + \left( {\Delta Ta_{i} .ya_{i} } \right) - Da_{ij}^{ \pm } } \right)} \right]\left( {1 + \varepsilon } \right)} \right] + Sa0_{j}^{ \pm } \quad \forall j = 1.2.3 $$
(54)

Equation 54 expresses that the surplus water in the resource in the present period is equal to total available water in the reservoir plus the surplus water in resource in the previous period minus the allocated water to various consumers.

  • Wastewater treatment constraints

$$ \begin{aligned} & \mathop \sum \limits_{i = 1}^{m} \left[ {\left( {Tw_{i}^{ - } + \left( {\Delta Tw_{i} .yw_{i} } \right) - Dw_{ij}^{ \pm } } \right)} \right]\left( {1 + \varepsilon } \right) \le \theta_{1} \cdot \beta_{1} \left[ {\left( {\left( {Ta_{1}^{ - } + \left( {\Delta Ta_{1} .ya_{1} } \right) - Da_{1j}^{ \pm } } \right)} \right)} \right. \\ & + \left( {\left( {Tb_{1}^{ - } + \left( {\Delta Tb_{1} .yb_{1} } \right) - Db_{1j}^{ \pm } } \right)} \right) + \left( {\left( {Tc_{1}^{ - } + \left( {\Delta Tc_{1} .yc_{1} } \right) - Dc_{1j}^{ \pm } } \right)} \right) \\ & \left. { + \left( {Tw_{1}^{ - } + \left( {\Delta Tw_{1} .yw_{1} } \right) - Dw_{1j}^{ \pm } } \right)} \right] + \theta_{2} \cdot \beta_{2} \left[ {\left( {\left( {Ta_{2}^{ - } + \left( {\Delta Ta_{2} .ya_{2} } \right) - Da_{2j}^{ \pm } } \right)} \right)} \right. \\ & + \left( {\left( {Tb_{2}^{ - } + \left( {\Delta Tb_{2} .yb_{2} } \right) - Db_{2j}^{ \pm } } \right)} \right) + \left( {\left( {Tc_{2}^{ - } + \left( {\Delta Tc_{2} .yc_{2} } \right) - Dc_{2j}^{ \pm } } \right)} \right) \\ & \left. { + \left( {Tw_{2}^{ - } + \left( {\Delta Tw_{2} .yw_{2} } \right) - Dw_{2j}^{ \pm } } \right)} \right] + \theta_{3} \cdot \beta_{3} \left[ {\left( {\left( {Ta_{3}^{ - } + \left( {\Delta Ta_{3} .ya_{3} } \right) - Da_{3j}^{ \pm } } \right)} \right)} \right. \\ & + \left( {\left( {Tb_{3}^{ - } + \left( {\Delta Tb_{3} .yb_{3} } \right) - Db_{3j}^{ \pm } } \right)} \right) + \left( {\left( {Tc_{3}^{ - } + \left( {\Delta Tc_{3} .yc_{3} } \right) - Dc_{3j}^{ \pm } } \right)} \right) \\ & \left. { + \left( {Tw_{3}^{ - } + \left( {\Delta Tw_{3} .yw_{3} } \right) - Dw_{3j}^{ \pm } } \right)} \right] \le \overline{\text{Swt}}^{ \pm }_{1} - \alpha \Delta \widetilde{{{\text{Swt}}_{1} }}\quad \forall j = 1.2.3 \\ \end{aligned} $$
(55)

Equation 55 demonstrates that total wastewater allocated for various consumptions should be less than the obtained wastewater from various uses and the total capacity of the wastewater treatment station.

  • Water demand, water shortage, and nonnegativity constraints

$$ Ta^{ \pm }_{i\;\hbox{max} } \ge \left( {Ta_{i}^{ - } + \left( {\Delta Ta_{i} .ya_{i} } \right) - Da_{ij}^{ \pm } } \right) \ge Da_{ij}^{ \pm } \ge 0 \quad \forall j = 1.2.3 $$
(56)
$$ Tb^{ \pm }_{i\;\hbox{max} } \ge \left( {Tb_{i}^{ - } + \left( {\Delta Tb_{i} .yb_{i} } \right) - Db_{ij}^{ \pm } } \right) \ge Db_{ij}^{ \pm } \ge 0 \quad \forall j = 1.2.3 $$
(57)
$$ Tc^{ \pm }_{i\;\hbox{max} } \ge \left( {Tc_{i}^{ - } + \left( {\Delta Tc_{i} .yc_{i} } \right) - Dc_{ij}^{ \pm } } \right) \ge Dc_{ij}^{ \pm } \ge 0\quad \forall j = 1.2.3 $$
(58)
$$ Tw^{ \pm }_{i\;\hbox{max} } \ge \left( {Tw_{i}^{ - } + \left( {\Delta Tw_{i} .yw_{i} } \right) - Dw_{ij}^{ \pm } } \right) \ge Dw_{ij}^{ \pm } \ge 0\quad \forall j = 1.2.3 $$
(59)

Equations 56–59 show that the maximum allowable allocation target should be greater than the water allocated and greater than shortages of each consumer under all water inflow levels.

  • Technical constraints

$$ 0 \le \alpha^{ \pm } \le 1 $$
(60)
$$ 0 \le ya_{i} .yb_{i} .yc_{i} .yw_{i} \le 1\quad \forall i = 1.2.3 $$
(61)

Equations 60–61 are technical constraints.

In this model, \( Ta_{i}^{ \pm } \) is allocation target for consumer i from wellheads, \( Tb_{i}^{ \pm } \) is allocation target for consumer i from springs, \( Tc_{i}^{ \pm } \) is allocation target for consumer i from the qanats, \( Tw_{i}^{ \pm } \) is allocation target for consumer i from treated wastewater, \( ya_{i} .yb_{i} .yc_{i} .yw_{i} \) are decision variables with zero to one values from well, springs, qanats, treated wastewater to determine the optimal set of allocation targets, \( Da_{ij}^{ \pm } ,Db_{ij}^{ \pm } ,Dc_{ij}^{ \pm } \), \( Dw_{ij}^{ \pm } \) are optimal water shortages for consumer i from wellheads, springs, qanats, and refined wastewater under water inflow level j, \( Pw_{j} .Pc_{j} .Pb_{j} .Pa_{j} \) are probability of occurrence of flow level for wellheads, springs, and treated wastewater, \( \varepsilon \) is loss rate of water during distribution, \( \overline{qa}^{ - } .\overline{qb}^{ - } .\overline{qc}^{ - } \) are lower interval of the upper-bound wellhead, spring, and qanat water flow, \( \underline{qa}^{ + } . \underline{qb}^{ + } . \underline{qc}^{ + } \) are upper interval of the lower-bound wellhead, spring, and qanat water flow, \( \overline{qa}^{ + } .\overline{qb}^{ + } .\overline{qc}^{ + } \) are upper interval of the upper-bound wellhead, spring, and qanat water flow, \( \underline{qa}^{ - } . \underline{qb}^{ - } . \underline{qc}^{ - } \) are lower interval of the lower-bound wellhead, spring, and qanat water flow, \( sa0_{j}^{ \pm } \) is surplus water remaining in wellhead in the previous period, \( Sa1_{j}^{ \pm } \) is surplus water in wellhead for the next period. \( \theta_{i} \) is discharge of wastewater per unit of consumption for different consumers, \( \overline{{{\text{Swt}}^{ + } }} \) is upper interval of upper-bound wastewater treatment station capacity, \( \underline{{{\text{Swt}}^{ - } }} \) is lower interval of lower-bound wastewater treatment station capacity, \( \underline{{{\text{Swt}}^{ + } }} \) is upper interval of lower-bound wastewater treatment station capacity, \( \underline{{{\text{Swt}}^{ - } }} \) is lower interval of lower-bound wastewater treatment station capacity, \( Ta_{i\;\hbox{max} } .Tb_{i\;\hbox{max} } .Tc_{i\;\hbox{max} } \).\( Tw_{i\;\hbox{max} } \) are maximum allowable allocation target from wellheads, springs, qanats, and treated wastewater to different consumers, \( \beta_{i} \) is rate of recycling per unit of wastewater created. i is water consumers (1: municipal, 2: industrial, 3: agricultural), j is various water flow levels (1: low, 2: medium, 3: high).

Model Scenarios

In fact, this research answers the question of “how to allocate water resources to various consumers in order to obtain maximum economic benefits for the region.” This study examined two scenarios:

  • Scenario 1:

Taking into account the current conditions of the case study (all parameter models except the parameters related to wastewater treatment)

  • Scenario 2:

Considering treated wastewater as an allocable resource (all model parameters)

Scenario 1

In this scenario, the current conditions of Zarand city are considered. There are three consumer sectors—agricultural, industrial, and municipal—that utilize water from wellheads, springs and qanats. The information required for scenario 1 is presented in Tables 2 and 3, respectively. By considering the water loss rate \( (\varepsilon) \) to be 30% and using the data of Tables 2 and 3 and according to the section IFTSP Solution Method, the model is constructed and solved in GAMS software.

Table 2 Description of water flow distribution
Full size table
Table 3 Water resources and economic data
Full size table

Scenario 2

This scenario improves the current conditions of the case study by establishing a wastewater treatment station. All data are same as scenario 1, except the allocation target of wellhead \( (Ta_{i}^{ \pm } ) \) and maximum allowable allocation target from wellhead \((Ta^{ \pm }_{i\;\hbox{max} }) \). Moreover, some parameters related to wastewater are incorporated into the model. The model’s parameters are represented in Tables 4 and 5.

Table 4 Information required for scenario 2
Full size table
Table 5 Parameters related to wastewater treatment
Full size table

Results

Results of Scenario 1

Results of the sub-model corresponding to \( f^{ + } \) in scenario 1 are presented in Table 6.

Table 6 Solution of the sub-model corresponding to maximum net benefit
Full size table

By incorporating above results into the other sub-model, overall results based on scenario 1 obtained. The results shown in Table 7 present the optimized water allocation, water shortage amount, and related system benefits. In case of insufficient water, the industry use should be first guaranteed because it brings the highest benefit. Municipal usage has the second priority and the agriculture sector has the last priority. In Table 7, the solutions \( Da^{ \pm }_{11} = Da^{ \pm }_{12} = Da^{ \pm }_{13} = 0 \)\( Da^{ \pm }_{21} = Da^{ \pm }_{21} = Da^{ \pm }_{21} = 0 \) indicate that there will be no shortage of water for municipal and industrial users. However, under low flow level of wellhead with a probability of 49%, there should be a shortage of \( 60.646 \times 10^{6} {\text{m}}^{3} \) for the agricultural sector. Even if the flow level of wellhead is high, the optimal shortage for the agricultural sector will be (0, 1.213) × 106 m3 with probability of 20%. It can be concluded that under high water flow level, when the available water is over 280 million cubic meters, the shortages for all consumers will be zero. Similarly, for other sources, if there are high levels of water flow for the qanat (with probability of 77%), then there will be no shortages for consumers.

Table 7 Overall results of scenario 1
Full size table

In this scenario, the system net benefit is (217604.361, 3578184.443) million Rials with reliability of (0.284, 0.6712). The upper bound of the system net benefit is corresponding to 0.6712, and the lower bound of the system net benefit is corresponding to 0.284.

Results of Scenario 2

Table 8 shows the results of solving the model in scenario 2 by considering all parameters and variables of model. Results show that with 49% probability for wellhead under low flow level, agricultural sector will face a shortage of 38.126 million cubic meters, while the other sectors will not face any shortages. In the previous scenario (lack of treated wastewater resource), the optimal shortage was 60.647 million cubic meters for the agricultural sector. Moreover, under medium flow level there is lower shortage than the previous scenario, whereas under high flow level there is no shortage for agricultural sector. As shown in Table 8, the total water allocated would be \( 173.5 \)\( (Aa^{ \pm }_{33} = 173.5) \), and optimal allocation target is 173.5 \( (Ta_{{3\;{\text{opt}}}}^{ \pm } = 173.5) \); thus, there is no shortage for agricultural sector under high flow level. Treated wastewater satisfies industry and municipal sectors’ demands, while the agricultural sector will face shortage under different flow levels. There is also improvements in system net benefit and system reliability \((f^{ \pm } = \left( {5270477.738,\, 6865883.395} \right) \) million Rials and \( \alpha^{ \pm } = \left( {0.3013,\, 0.6851} \right) \)).

Table 8 Overall results of scenario 2
Full size table

Figure 3 shows that there is more surplus water in wellhead for the next period in scenario 2 than in scenario 1. As shown in Figure 4, the system net benefit in scenario 2 is significantly higher than in scenario 1. This indicates that establishing a wastewater treatment station in Zarand can reduce the usage of natural water resources while maximizing regional economic benefits.

Figure 3
figure 3

Comparison of surplus water in the wellhead for the next period for scenarios 1 and 2

Full size image
Figure 4
figure 4

Comparison of the net benefit resulting from the implementation of scenarios 1 and 2

Full size image

Sensitivity Analysis of Water Loss Rate

Today, among the important and critical issues in water resources management in Kerman province are the old water pipelines and the lack of scientific methods of transforming water. Currently, water loss rate is estimated to be 30%. In Zarand, such high water loss rate entails high volume of water extraction from groundwater resources and causes reservoir drainage as well as serious problems for agricultural and industrial economic schemes. Therefore, as a scenario, the water loss rate is set at 20% and the results (Table 9) are compared with scenarios 1 and 2. As shown in Figures 5 and 6, when water loss rate is set at 20%, there are improvements especially in net benefit and the surplus water remaining in the wellhead for the next period.

Figure 5
figure 5

Comparison of the net benefit considering reduction in water loss rate

Full size image
Figure 6
figure 6

Comparison of surplus water remaining in wellhead for the next period considering reduction in water loss rate

Full size image
Table 9 Overall results of a scenario considering 20% water loss rate
Full size table

Discussion and Conclusion

Today, issues regarding water resources have become one of the most prominent challenges facing humanity, and there is a need to find improved ways of making optimal uses of these resources. Water resources management provides a set of methods, tools, and optimization models to prevent reservoir shortages, water waste, water shortage, loss of water quality and to deliver optimally high-quality water to consumers. One of the main issues in this field is the optimal allocation of water resources to various consumers, which becomes increasingly important every year because water resources are decreasing while demands are increasing. Therefore, considering the importance of this issue, the aim of this study was based on optimal water resources allocation, and research results of a case study (Zarand region, Kerman province) were presented and discussed to identify the differences between scientific allocation methods and current management methods. In this research, a two-stage stochastic method with interval and fuzzy parameters was used. One of the advantages of this method is that before the identification of uncertainties relevant to the model parameters (especially water available from sources), objectives are set for various sectors, and the optimization model is solved upon identifying uncertainties. Then, each sector will be informed of the shortages they will face and the quantity of water they will receive. Therefore, the agricultural consumer will know the quantity of water that they will receive in the future to make suitable investments on farmland while knowing when to compensate water shortages from other sources or to limit plantation and cultivation. Similarly, if the industry sector is informed of future water shortages, it will reduce its production or plan to purchase water from the more expensive sources. However, in current management conditions, consumers are unaware of their received water quantity and cannot design economic schemes. Under these conditions, facing scarcities will entail crisis for various sectors especially municipal, agricultural, and industrial consumers. Therefore, there is a need for scientific methods to become involved in policy making and management to maximize the economic benefits of societies while preventing consumers from facing the crisis.

The model presented in this research can help regional water managers to provide equity for distributing water among different consumers with various limitations. Besides, the results of this study indicate a substantial improvement in system profits and water resources conservation and maintenance. Thus, it can be concluded that regional water managers have this opportunity to develop their regions from three perspectives including social, environmental, and economic. For the future, this model can be applied to other case studies, and the economic results can be compared with the results of this study. For extending the application of this model in other regions and making it more comfortable for the users, a decision support system can be designed by providing a graphical user interface that can be developed by programs such as MATLAB, C#, and Java. Moreover, models with better accuracy can be presented by considering costs for wastewater refinement maintenance.