1 Introduction

The wavelet filterbanks (FBs) have gained considerable popularity in the signal and image processing applications, such as feature extraction, pattern recognition, compression, denoising, classification and watermarking. The filterbanks can be classified as either orthogonal or bi-orthogonal. The biorthogonal FBs are generally chosen for the image processing applications, due to its linear phase criterion. It is desirable that wavelet filters should have the properties such as regularity, tight frame bound ratio, high frequency selectivity and symmetry. It is important to consider higher regularity measure in the FBs design and it is obtained by imposing zeros at ω = π or z = − 1 (aliasing frequency) for the low-pass filters. The zeros are referred as vanishing moments (VMs). In theory, maximum VMs give the smoother scaling function which represents the complex signals accurately. Therefore, the selection of VMs is a desirable criterion to take into consideration for designing the PR FBs [1,2,3,4,5].

In this direction several filterbank design methods have been proposed in [5,6,7,8,9,10,11,12,13,14,15,16,17,18]. The commonly used method for designing different wavelet FBs is by using factorization of halfband polynomials [6]. The well known biorthogonal FBs, such as spline wavelet FBs, CDF-9/7 [19,20,21] have been designed by the factorization method. The Lagrange halfband polynomial (LHBP) has been factorized to design filters. This polynomial has maximum number of zeros at z = − 1, which give higher regularity measure. However, the wavelet filters designed from this method do not have any free parameter (degree of design freedom) which have control on the frequency response of filters. Therefore, to have some control on the frequency response of wavelet filters Patil et al. have used some independent parameters to design generalized halfband polynomial (GHBP) [6]. The factorization method is used to obtain bi-orthogonal wavelet filters from GHBP [6]. However, it is observed that factorization is mathematically complicated for higher order HBPs. The lifting scheme design is well known and attractive schemes for designing FBs as it provides PR structurally. Phoong et al. [22] found a new halfband filterbank structure using lifting scheme with two kernels. However, the drawback of this design is that, frequency response magnitude of filters at ω = π/2 is restricted to values 0.5 and 1.0 only. To overcome this problem [23], the triplet halfband structure (THFB) have been proposed by Ansari et al. [23] using three lifting kernels. The tunable parameter used in their work gives higher flexibility for shaping the frequency response of the filters.

In this paper, we propose a method to design bi-orthogonal filterbank using generalized lifting scheme. Here, we use the Euler Frobenius polynomial (EFP) to design a maximally flat Euler Frobenius halfband polynomial (EFHP). The EFHP is obtained from EFP by imposing PR and VMs constraint structurally. This new EFHP is used to obtain lifting halfband kernels. The analysis and synthesis wavelet filters are designed by employing three and four step lifting structure. The proposed filters preserve PR property structurally and have frame bound ratio close to unity. The proposed filters comparatively give better property measures than existing methods.

The paper is organized as follows. Section 2 gives preliminaries of two channel FBs. Section 3 explains the proposed method with lifting scheme and selection of lifting parameters. This section also demonstrates few design examples. The properties of proposed and existing wavelet filters are compared in Section 4. Conclusion is given in Section 5.

2 Background of Two Channel Filterbanks

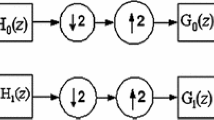
Figure 1 shows the general structure for two channel bi-orthogonal filterbanks. The four filters that form two channel filterbanks are analysis low-pass (H0(z)), analysis high-pass (H1(z)), synthesis low-pass (F0(z)) and synthesis high-pass (F1(z)). The two channel FBs is called PR FBs if it satisfy the following equation

$$ H_{0}(z)F_{0}(z)+H_{0}(-z)F_{0}(-z)=cz^{l} $$
(1)

where, l is the amount of delay. The PR condition can always be met if alias cancellation is achieved. This can be achieved by selecting the following analysis and synthesis high-pass filters as

$$ \begin{array}{@{}rcl@{}} H_{1}(z)&&=z^{-1}F_{0}(-z)\qquad \text{and} \end{array} $$
(2)
$$ \begin{array}{@{}rcl@{}} \qquad F_{1}(z)&&=zH_{0}(-z) \end{array} $$
(3)

The product filter is defined as P(z) = H0(z)F0(z). This product filter is related to special class halfband filters. The scaling and wavelet functions of analysis filters are given by

$$ \phi(t)=\frac{2}{H_{0}(\omega)\vert_{\omega=0}} \sum\limits_{n}h_{0}(n)\phi(2t-n) $$
(4)
$$ \psi(t)=\frac{2}{H_{1}(\omega)\vert_{\omega=0}} \sum\limits_{n}h_{1}(n)\phi(2t-n) $$
(5)

where, h0(n) and h1(n) are the analysis low-pass and high-pass filters coefficients respectively.

Figure 1
figure 1

A general structure of two channel filterbanks.

Full size image

3 Proposed FBs Design using Euler Frobenius Polynomials (EFP) and Generalized Lifting Scheme

In this section, the design of biorthogonal two channel PR filterbank is proposed using EFP and lifting construction.

3.1 Design of Euler Frobenius Halfband polynomial

The Euler Frobenius Polynomials (EFP) are well known and have been used in the design of spline wavelets [24]. The main advantage of using EFP is that, its coefficients are integers and polynomial is symmetric. Also, these coefficients are determined recursively. The generalized Euler Frobenius Polynomials (EFP) are defined as

$$ \mathcal{E}_{f}(z) =\sum\limits_{i=0}^{m}\hat{e}(i +1)z^{-i} $$
(6)

where m represents the order of EFP and coefficients are obtained by

$$ \hat{e}(i +1) =\sum\limits_{\ell=0}^{i}(-1)^{\ell}\binom{m+2}{\ell}(i +1-\ell)^{m+1}. $$
(7)

In this work, we have used EFP to design the required halfband polynomial. The odd-length EFP are combined with VMs (zeros at z = − 1) and introduced some independent parameters βi so as to convert them into halfband polynomial. This new polynomial is called as Euler Frobenius halfband polynomial (EFHP) and given by

$$ P(z)=(1+z^{-1})^{\eta}\mathcal{E}_{f}(z)\sum\limits_{i=0}^{L}{\upbeta}_{i}z^{-i} $$
(8)

where, η represents the number of VMs. The mth order EFP is represented by \(\mathcal {E}_{f}(z)\). The product filter P(z) have order K = η + m + L. The order of free polynomial is L = K/2 − 1. The free parameters βi are formulated such that the PR condition given in Eq. 1 is satisfied. The required Kth order kernel of the lifting scheme is given by

$$ \hat{T}(z)=z^{K/2}P(z)-1 $$
(9)

We consider above equation to design the lifting kernels.

3.2 Generalized Lifting Construction

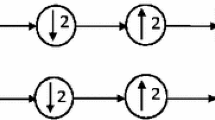
The proposed filters are constructed via three-step and four-step lifting structure. Figure 2 shows the lifting structure for analysis filters. It is parametrized with three and four halfband filters. The analysis filterbank can be expressed in the polyphase matrix form

$$ \mathcal{R}=\left[\begin{array}{cc} H_{0even} & H_{0odd} \\ H_{1even} & H_{1odd} \end{array}\right]. $$
(10)

From polyphase matrix, we can find the filters H0 and H1 as

$$ \begin{array}{@{}rcl@{}} H_{0}(z)=H_{0even}(z^{2}) + z^{-1}H_{0odd}(z^{2}) \end{array} $$
(11)
$$ \begin{array}{@{}rcl@{}} H_{1}(z)=H_{1even}(z^{2}) + z^{-1}H_{1odd}(z^{2}). \end{array} $$
(12)

The inverse of polyphase matrix \( \mathcal {R}\) represents the synthesis polyphase matrix \( \mathcal {S}\). To satisfy the PR, it is necessary to have \(\mathcal {R}\mathcal {S}= I\). The general prediction step is always given by multiplication by matrix of the form \( {P}(z)= \left [\begin {array}{cc} 1 &0 \\ -p_{2}\hat {T_{1}}(z) & 1 \end {array}\right ]\) and update step is given by \( {U}(z)= \left [\begin {array}{cc} 1 &p_{1}\hat {T_{0}}(z)\\0& 1 \end {array}\right ]\). The polyphase representation for generalized lifting scheme is given by

$$ \begin{array}{@{}rcl@{}} {\mathcal{P}} &=& \left[\begin{array}{cc} C_{0} &0 \\ 0 & C_{1} \end{array}\right] \left[\begin{array}{cc} 1 &0 \\-p_{L}P_{L}(z) & 1 \end{array}\right] \left[\begin{array}{cc} 1 &p_{L-1}U_{L}(z) \\0& 1 \end{array}\right] \dots\\\small &&\left[\begin{array}{cc} 1 &0 \\ -p_{4}P_{2}(z) & 1 \end{array}\right] \left[\begin{array}{cc} 1 &p_{3}U_{2}(z) \\ 0& 1 \end{array}\right] \left[\begin{array}{cc} 1 &0 \\ -p_{2}P_{1}(z) & 1 \end{array}\right] \left[\begin{array}{cc} 1 &p_{1}U_{1}(z) \\ 0& 1 \end{array}\right] \end{array} $$
(13)

where, pi for i = 1,2,3,...,L represents non-zero lifting parameters. The constants C0 and C1 denotes normalization constants. The prediction and update kernels are designed from Kth order halfband polynomial \(1+\hat {T}(z)\), \( \text {where } \hat {T}(z)=-\hat {T}(-z)\).

We have chosen \(P_{i}(z)=U_{i}(z)=\hat {T}_{i}(z)=\hat {T}(z)\) where (i = 1,...,L). The objective is to design these kernels, such that the resultant analysis and synthesis filters have good frequency selectivity, almost tight frame bound ratio and desired regularity.

Figure 2
figure 2

Generalized lifting structure.

Full size image

3.2.1 Three-Step Lifting Scheme:

The analysis and synthesis low pass filters constructed with three lifting steps are given by

$$ \begin{array}{@{}rcl@{}} \small H_{0}(z)&=&C_{0}\{\frac{1+p}{2}+\frac{1}{2}\hat{T}_{1}(z)(1-p\hat{T}_{0}(z))\} \end{array} $$
(14)
$$ \begin{array}{@{}rcl@{}} F_{0}(z)&=&C_{1}\{(\frac{1+p\hat{T}_{0}(z)}{1+p}+\frac{1-p}{1+p}\hat{T}_{2}(z)\\&&\times(\frac{1+p}{2}-\frac{1}{2}\hat{T}_{1}(z)(1+p\hat{T}_{0}(z)))\} \end{array} $$
(15)

where, the kernels \(\hat {T}_{0}(z)\), \(\hat {T}_{1}(z)\) and \(\hat {T}_{2}(z)\) are designed from Kth order proposed halfband polynomial.

3.2.2 Four-Step Lifting Scheme:

The analysis filters are constructed with four lifting steps are given by

$$ \begin{array}{@{}rcl@{}}\small H_{0}(z)&=&C_{0}\{1+(p_{1}+p_{3})\hat{T}(z)+p_{2}p_{3}\hat{T}^{2}(z)\\ &&+p_{1}p_{2}p_{3}\hat{T}^{3}(z)\} \end{array} $$
(16)
$$ \begin{array}{@{}rcl@{}} F_{0}(z)&=&z^{-1}C_{1}\{1+(p_{2}+p_{4})\hat{T}(z)+p_{1}p_{2}p_{3}p_{4}\hat{T}^{4}(z) \ \ \ \\ && +(p_{1}p_{2}+p_{1}p_{4}+p_{3}p_{4})\hat{T}^{2}(z)+p_{2}p_{3}p_{4}\hat{T}^{3}(z)\} \ \ \ \ \end{array} $$
(17)

where, the kernels \(\hat {T}(z)\) are designed from Kth order halfband polynomial. The aim is to design lifting kernels \(\hat {T}(z)\) with good frequency selectivity and regularity. The high-pass filters are obtained by using Eq. 3. The lifting parameter p is the degree of freedom which provides the flexibility for choosing the magnitude at ω = π/2.

3.3 Choice of lifting parameters

For three-step lifting scheme, we have selected same parameter values given in [23]. For four-step lifting scheme, the lifting parameters p1, p2, p3 and p4 are obtained by choosing some constraints on analysis filters. The values of halfband kernel at ω = 0, ω = π/2 and ω = π are \( \hat {T}(1) = 1 \), \( \hat {T}(e^{j\pi /2}) = 0 \), \( \hat {T}(-1) = -1 \) respectively. The first two constraints are H0(− 1) = 0 and H1(1) = 0, which ensures at least one vanishing moment and gives no dc-leakage. This gives the parameters relationship as below

$$ \begin{array}{@{}rcl@{}} p_{3}&=&\frac{1-p_{1}}{(1-p_{1}+p_{1}p_{2})} \end{array} $$
(18)
$$ \begin{array}{@{}rcl@{}} p_{4}&=&0.5(-1-2p_{1}p_{2}+{p_{2}^{2}}-{p_{1}^{2}}{p_{2}^{2}}). \end{array} $$
(19)

By considering the equal dc gain H0(1) = F0(1) and using equation (18-19), we get the normalization constants as

$$ \begin{array}{@{}rcl@{}} C_{0}&=&G_{dc}(1-p_{2} + p_{1}p_{2} ) \end{array} $$
(20)
$$ \begin{array}{@{}rcl@{}} C_{1}& = &G_{dc}(1-p_{2} + p_{1}p_{2} )^{-1} \end{array} $$
(21)

where Gdc is the desired dc gain. The constraint of orthogonality H0(ejπ/2) = F0(ejπ/2) is imposed which leads to C0 = C1. By equating this and solving for p2, we get

$$ p_{2}=(\sqrt2-1)(p_{1}-1)^{-1}. $$
(22)

The free parameters p2, p3, p4 are determined in terms of p1. This free parameter is useful for controlling the shape of frequency response of filter at π/2.

3.4 Design Examples

This section demonstrates few examples to illustrate the proposed design method. We consider the dc gain Gdc = 1.

Example 1

We consider η = 3, m = 1 and L = 2 to design 9/15 length filters. The three independent parameters are imposed as halfband PR constraints to obtain halfband filters. This results in three linear equations as

$$ \begin{array}{@{}rcl@{}} 4{\upbeta}_{0}+4{\upbeta}_{1}=0 \end{array} $$
(23)
$$ \begin{array}{@{}rcl@{}} 4{\upbeta}_{0}+24{\upbeta}_{1}+4{\upbeta}_{2}=1 \end{array} $$
(24)
$$ \begin{array}{@{}rcl@{}} 4{\upbeta}_{1}+4{\upbeta}_{2}=0 \end{array} $$
(25)

By solving this linear equations simultaneously, we get β0 = − 1/16, β1 = 1/4, β2 = − 1/16. By substituting these values in the Eq. 8, we get the resultant halfband product filter. This resultant P(z) is used to design lifting kernel \( \hat {T}(z)\). For 9/15 length filters we choose the lifting kernels as below

$$ \begin{array}{@{}rcl@{}} \hat{T}_{0}(z)&=&(z+z^{-1})/2 \end{array} $$
(26)
$$ \begin{array}{@{}rcl@{}} \hat{T}_{1}(z)&=&z^{-K/2} P(z)-1 \end{array} $$
(27)
$$ \begin{array}{@{}rcl@{}} \hat{T}_{2}(z)&=&z^{-K/2} P(z)-1. \end{array} $$
(28)

These kernels are substituted in (14) and (15), to obtain the analysis and synthesis low-pass filters. The frequency response for proposed 9/15 length wavelet filters is shown in Fig. 3. The analysis scaling and wavelet functions are shown in Figs. 4 and 5.

Figure 3
figure 3

Frequency Response of Filters: Dotted line: 9/11 Filters given in [25], Solid Line: Proposed 9/15 filter pair (Example-1).

Full size image
Figure 4
figure 4

Plot of analysis scaling functions (Example-1).

Full size image
Figure 5
figure 5

Plot of analysis wavelet functions (Example-1).

Full size image

Example 2

The 6th order EFHP is used to design halfband kernel \(\hat {T}(z) \). The resulted filters H0 and F0 have length 19 and 25 respectively. Select η = 3 to achieve maximum regularity and L = 2 for imposing the PR constraints. This results in three linear equations as

$$ \begin{array}{@{}rcl@{}} 4{\upbeta}_{0}+4{\upbeta}_{1}=0 \end{array} $$
(29)
$$ \begin{array}{@{}rcl@{}} 4{\upbeta}_{0}+24{\upbeta}_{1}+4{\upbeta}_{2}=1 \end{array} $$
(30)
$$ \begin{array}{@{}rcl@{}} 4{\upbeta}_{1}+4{\upbeta}_{2}=0 \end{array} $$
(31)

By solving this linear equations simultaneously, we get β0 = − 1/16, β1 = 1/4, β2 = − 1/16. By substituting these values in the Eq. 8, we get the resultant halfband product filter. This resultant P(z) is used in equation to design kernel \(\hat { T}(z)\). We have considered identical kernels to design 19/25 filters as below

$$ \begin{array}{@{}rcl@{}} \hat{T}_{0}(z)=\hat{T}_{1}(z)=\hat{T}_{2}(z)=\hat{T}_{3}(z)=z^{-K/2} P(z)-1. \end{array} $$
(32)

These kernels are substituted in (16) and (17), to obtain the analysis and synthesis low-pass filters. The frequency response for proposed 19/25 length wavelet filters is shown in Fig. 6. Ripples are observed in stopband regions of frequency response for filters given in [25]. This can be easily seen from Fig. 6.

Figure 6
figure 6

Frequency Response of 19/25 Filters: Dotted line: Filters given in [25], Solid Line: Proposed filter pair.

Full size image

In image compression application, ripples occurred in stopband region of filter response causes information to be spilled into high-pass subbands. This reduces the compression efficiency. This ripples also reduces regularity of filters as its corresponding scaling and wavelet functions are comparatively irregular. This effect is shown in Figs. 7 and 8. However, proposed filters do not have any ripples and hence are useful in such applications. It is seen that proposed filters give more degree of smoothness. Wavelets having more smoothness gives acceptable reconstruction quality for different image processing applications.

Figure 7
figure 7

Plot of analysis scaling functions.

Full size image
Figure 8
figure 8

Plot of analysis wavelet functions.

Full size image

4 Properties of the Proposed FBs and Comparison with Existing Methods

This section discusses the comparison of proposed and existing wavelet FBs in terms of desirable properties. We have computed properties, such as symmetry, frame bound ratio, time-frequency localization, regularity, and frequency selectivity. The values of measures for different properties are presented in Table 1.

Table 1 Comparison of proposed filters with existing filters in terms of Property Measures.
Full size table

4.1 Symmetry

Symmetry is one of the important property of wavelet FBs. Symmetry is defined to measure dissimilarity of the proposed filters. We define \( \left \lVert (H_{0}-F_{0} )\right \rVert ^{2} \) to measure the symmetry. The proposed filters give better symmetry than existing filters and values are given in Table 1.

4.2 Regularity

Regularity property is a measure of smoothness for scaling and wavelet functions. It is obtained by imposing maximum number of zeros at ω = π/2. We compute sobelov index [1] to measure the regularity. The values given in Table 1 shows that proposed filters have more regularity than existing filters.

4.3 Energy of the error

The energy of the error is an error between ideal and designed low-pass filter. This measure can also be referred as frequency selectivity. It is expressed as

$$ E ={\int}_{0}^{\pi/2}|1-H(e^{j\omega})|^{2}d\omega +{\int}_{\pi/2}^{\pi}|H(e^{j\omega})|^{2}d\omega $$
(33)

Table 1 shows the values of frequency selectivity.

4.4 Frame Bound Ratio

The frame bound ratio Rb can be defined as

$$ R_{b} =\frac{\max_{\omega\in[0,\pi]}\sqrt{B(e^{j\omega})}}{\min_{\omega\in[0,\pi]}\sqrt{B(e^{j\omega})}} $$

where B(ejω) = |H0(ejω)|2 + |H1(ejω)|2. It is observed that the proposed filter have frame bound ratio very closed to unity. Hence they are called as almost tight wavelet filters.

4.5 Time frequency product

We use Heisenberg uncertainty relation to define time frequency localization and it is expressed with inequality relation as: △ ω ×△t ≥ 1/2. The time and frequency localization measure are tabulated in Table 1. It have been observed that proposed filters have good time frequency localization.

5 Energy Distribution of Proposed Wavelets

The selection of suitable wavelet filters for different applications is generally dependent on energy distribution in wavelet decomposition subbands (LL, LH, HL and HH). The LL subband corresponds to low frequency parts of row and column while LH relates to low frequency parts of row and high frequency parts of column. Similarly, HL subband is linked to high frequency parts of row and low frequency parts of column whereas HH to high frequency parts in both row and column. Here Ehi, Evi and Edi denote the percentages of energy corresponding to HL, LH and HH subbands for ith level of decomposition. Ea represents the percentage of energy related to LL subband. The energy of wavelet subbands are calculated as follows

$$ \begin{array}{@{}rcl@{}} E_{ai}=\Big(\frac{\sum C_{ai}^{2}}{E_{t}}\Big)\times 100 \end{array} $$
(34)
$$ \begin{array}{@{}rcl@{}} E_{hi}=\Big(\frac{\sum C_{hi}^{2}}{E_{t}}\Big)\times 100 \end{array} $$
(35)
$$ \begin{array}{@{}rcl@{}} E_{vi}=\Big(\frac{\sum C_{vi}^{2}}{E_{t}}\Big)\times 100 \end{array} $$
(36)
$$ \begin{array}{@{}rcl@{}} E_{di}=\Big(\frac{\sum C_{di}^{2}}{E_{t}}\Big)\times 100. \end{array} $$
(37)

The total energy Et is given by

$$ E_{t}=\sum{{C_{t}^{2}}} $$
(38)

where C denotes magnitude of coefficients for corresponding subbands. For image compression applications it is desired to have higher energy in average (LL) subband whereas for feature extraction applications a small amount of energy in (LH, HL and HH) the detail subbands is also required.

Table 2 depicts the percentage energy obtained for proposed filters and existing methods. These values are obtained by decomposing image at first level. The neurological brain MRI image is considered for first level decomposition to verify the energy retention in subbands. The proposed filters retains maximum energy in average subband in comparison with [10]. Also, it is seen that the more amount of energy is present in (LH, HL and HH) subbands as compared to proposed method. This can be seen visually from Fig. 9 for detail subbands. This is due to the ripples present in the stopband region of analysis filters of [10] which passes more information to highpass subbands. However, proposed filters do not have such a ripples and hence gives satisfactory performance in image compression applications. The coefficients of approximation subband (LL) are only retained in compression. Since the maximum energy is retained in approximation subband (LL), the retention of coefficients in this subband leads to better reconstruction quality. However, JPEG2000 standard restricts the users choice to two wavelet transforms: Daubechies 9/7 for lossy compression, and the 5/3 LeGall wavelet, which has rational coefficients, for reversible or lossless compression [26].

Table 2 Percentage energy distribution of subbands for different wavelets.
Full size table
Figure 9
figure 9

First level wavelet decomposition of neurological MRI image a LL Subband with our filters b LL Subband of filters given in [10] c LH Subband of with our filters d LH Subband of filters given in [10] e HL Subband of with our filters f HL Subband of filters given in [10] g HH Subband of with our filters h HH Subband of filters given in [10].

Full size image

6 Conclusion

In this paper, a new technique has been presented to design biorthogonal halfband filterbank. The Euler Frobenius polynomial has been used to construct maximally flat Euler Frobenius halfband polynomial (EEHP) by imposing PR and VM constraints. The proposed EEHP has been used in three and four step lifting structure to construct a new class of sharp biorthogonal filters. Proposed method gives more degree of freedom to control the frequency response of filter with free parameters. The design examples illustrates that the proposed filters are comparable with existing methods. In addition, proposed filters give better frequency selectivity, more regularity, less time-frequency localization and almost unit frame bound ratio as compared to existing filterbanks. The designed filters also satisfy the PR criterion.