Design of Biorthogonal Wavelet Filters of DTCWT Using Factorization of Halfband Polynomials

Abstract

In this paper, we propose a new approach for designing the biorthogonal wavelet filters (BWFs) of Dual-Tree Complex Wavelet Transform (DTCWT). Proposed approach provides an effective way to handle the frequency response characteristics of these filters. This is done by optimizing the free variables obtained using factorization of generalized halfband polynomial (GHBP). The designed filters using proposed approach have better frequency response characteristics than those obtained by using binomial spectral factorization approach. Also, their associated wavelets show improved analyticity in terms of qualitative and quantitative measures. Transform-based image denoising using the proposed filters shows better visual as well as quantitative performance.

1 Introduction

In recent years, Dual-Tree Complex Wavelet Transform (DTCWT) has gained popularity as one of the important transform-domain processing tools in wide range of multimedia applications such as image [1] and video denoising [2], fusion [3], watermarking [4] to name a few. Unlike discrete wavelet transform (DWT), it offers better directionality, near-shift invariance and phase information with limited redundancy. In practice, DTCWT is implemented using two branches of DWT referred to as primal (filter bank: h) and dual (filter bank: g) tree and outputs of these are considered as the real and imaginary parts of the complex coefficient representation of an input signal. With the use of orthogonal/biorthogonal finite impulse response (FIR) filters in these trees, the transform is approximately analytic with a redundancy factor of just $2^m$ for an input of m-dimensional (m-D) signal, while the directionality is $2^{(m-1)} \times (2^{m} - 1)$. The idea for constructing dual-tree complex wavelet transform (DTCWT) was first proposed by Nick Kingsbury [5, 6] and subsequently developed by Selesnick in [7, 8]. We refer to [9] as an excellent tutorial paper on various aspects of DTCWT.

Although, DTCWT output representation is complex valued, real-valued filter coefficients are used in the construction and no complex arithmetic is required which is very much advantageous. However, design of such filters is quite challenging [10], since the filter coefficients need to satisfy various constraints. Selesnick [7] was the first researcher to arrive at certain conditions that must be satisfied by the DTCWT filters in order to have desired analyticity property. He showed that if the wavelet functions associated with the two trees of DTCWT are Hilbert transform pairs, the transform is completely analytic and shift-invariant. Since, obtaining perfect analyticity is difficult using compactly supported filters, approximate analyticity and near shift-invariance can be achieved using FIR orthogonal/biorthogonal wavelet filters [8]. In order to have these properties, filters must satisfy perfect reconstruction (PR), vanishing moment (VM) and half-sample delay (HSD) constraints as minimum requirements. HSD condition plays the role of coupling between two trees of DTCWT to have approximate Hilbert transform relationship. Intuitively, the HSD requirement given by Selesnick is equivalent to Kingsbury’s [6] idea of doubling the sampling rate at each scale thus largely removing the aliasing caused by downsamplers and making the transform nearly shift-invariant [9]. The concept of generalized HSD is used in [11, 12] to obtain M-band extensions of orthogonal and biorthogonal DTCWT, respectively. Theoretical details about the necessary and sufficient conditions in case of orthogonal and biorthogonal DTCWT filters can be found in [13, 14], respectively.

Traditional wavelet filter design techniques cannot be used directly to design DTCWT filters since they only consider PR and VM conditions. Considering the much needed HSD requirement, various approaches are proposed in the literature to obtain orthogonal/biorthogonal DTCWT filters [9, 10].

In this paper, we only consider the design of biorthogonal FIR filters by modifying the common factor approach [8]. The filters designed using common factor approach [8] have poor frequency response since it uses maximum number of vanishing moments i.e., zeros at $z = -1$ or $\omega = \pi$ resulting in zero degrees of freedom to shape the filter response characteristics. Hence, it is desired to have filters with good frequency response characteristics to minimize the inherent residual amplitude distortion present in the maximally decimated filter banks used in the two trees of DTCWT.

The paper is organized as follows. In Sect. 2, we give the background to understand the DTCWT basics and briefly describe the common factor technique. In Sect. 3, proposed approach is described while Sect. 4 details the design examples of the proposed approach along with their qualitative and quantitative measures. In Sect. 5, we discuss image denoising application using the designed filters. Section 6 concludes the paper.

Fig. 1.

Two trees of 2-channel filter banks used in DTCWT construction

2 Background Review

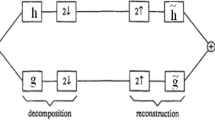
Figure 1 shows core structure of the DTCWT. It has two trees consisting of 2-channel filter banks that use 1-D biorthogonal wavelet filters.

In Tree-1, the filters $\tilde{h}_{0}(n)$ and $\tilde{h}_{1}(n)$ represent the analysis lowpass and highpass filters, respectively. Similarly, the $h_{0}(n)$ and $h_{1}(n)$ represent the same on the synthesis side referred to as synthesis lowpass and highpass filters. They are related to each other as follows

$$\begin{aligned} \begin{aligned} \tilde{h}_{1}(n)&= -(-1)^{n}h_{0}(n),\; \;0 \le n \le N-1\\ h_{1}(n)&= (-1)^{n}\tilde{h}_{0}(n),\; \;0 \le n \le \tilde{N}-1. \end{aligned} \end{aligned}$$

(1)

Here, $\tilde{N}$ and N represent lengths of the filters $\tilde{h}_{0}(n)$ and $h_{0}(n)$, respectively. Similar relations hold good in the case of filters in Tree-2.

Let, $\phi _{h}(t)$ and $\phi _{g}(t)$ be the synthesis scaling functions of Tree-1 and Tree-2, respectively and $\psi _{h}(t)$ and $\psi _{g}(t)$ be their corresponding wavelet functions. Then the two-scale equations associated with these are given as

$$\begin{aligned} \begin{aligned} \phi _{h}(t)&= \sqrt{2}\sum _{n} h_{0}(n)\phi _{h}(2t-n)\\ \psi _{h}(t)&= \sqrt{2}\sum _{n} h_{1}(n)\phi _{h}(2t-n)\\ \phi _{g}(t)&= \sqrt{2}\sum _{n} g_{0}(n)\phi _{g}(2t-n)\\ \psi _{g}(t)&= \sqrt{2}\sum _{n} g_{1}(n)\phi _{g}(2t-n). \end{aligned} \end{aligned}$$

(2)

In a similar way one can define analysis wavelet functions $\tilde{\psi }_{h}(t)$ and $\tilde{\psi }_{g}(t)$. In order to have approximate analyticity of DTCWT, we require that $\psi _{g}(t) \approx \mathcal {H}\left\{ \psi _{h}(t) \right\}$ and $\tilde{\psi }_{g}(t) \approx \mathcal {H}\left\{ \tilde{\psi }_{h}(t) \right\}$ [7, 8] representing Hilbert transform pairs criteria. This indicates that the synthesis and analysis wavelet functions of Tree-2 are approximately Hilbert transforms of Tree-1 wavelet functions. In Fourier domain, these relations are given as

$$\begin{aligned} \varPsi _{g}(\omega ) \approx {\left\{ \begin{array}{ll} \begin{aligned} -j\varPsi _{h}(\omega ),\; &{} \;\omega > 0\\ j\varPsi _{h}(\omega ), \; &{} \;\omega < 0. \end{aligned} \end{array}\right. } \end{aligned}$$

(3)

Similar expressions exist for $\tilde{\varPsi }_{g}(\omega )$. Here, $\varPsi _{h}(\omega )$, $\varPsi _{g}(\omega )$, $\tilde{\varPsi }_{h}(\omega )$ and $\tilde{\varPsi }_{g}(\omega )$ represent Fourier transforms of $\psi _{h}(t)$, $\psi _{g}(t)$, $\tilde{\psi }_{h}(t)$ and $\tilde{\psi }_{g}(t)$, respectively. Since, wavelet functions depend on the scaling functions which in turn depend on the lowpass filters associated with that scaling function, the problem of designing the Hilbert transform pairs of wavelet bases reduces to designing the lowpass filters that satisfy $g_{0}(n) \approx h_{0}(n - 0.5)$ which is known as half-sample delay (HSD) constraint [9]. In Fourier domain, this can be expressed as

$$\begin{aligned} G_{0}(\omega ) \approx e^{-j\frac{\omega }{2}}H_{0}(\omega ) \end{aligned}$$

(4)

where, $G_{0}(\omega )$ and $H_{0}(\omega )$ are Fourier transforms of $g_{0}(n)$ and $h_{0}(n)$, respectively. One can design these filters by approximating the magnitude and phase responses as

$$\begin{aligned} |G_{0}(\omega )|&= |H_{0}(\omega )| \end{aligned}$$

(5)

$$\begin{aligned} \angle G_{0}(\omega )&= -\frac{\omega }{2} + \angle H_{0}(\omega ) . \end{aligned}$$

(6)

Due to the nature of the Eq. (4), one of the two conditions given in Eqs. (5) and (6) is satisfied exactly or both are approximated. Common factor design method satisfies the magnitude condition exactly while phase condition is approximately met by using maximally flat all pass filters which is reviewed in the next subsection since proposed approach is based on the same.

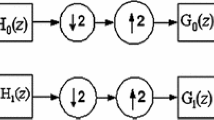
2.1 Common Factor Technique

Common factor technique [8] proposed by Selesnick uses a two stage design process to approximate the relation given in Eq. (4) and finally obtains the required filters of DTCWT shown in Fig. 1. In the first stage, half-sample delay constraint is approximated using Thiran’s maximally flat allpass filters [15]. Perfect reconstruction and vanishing moment constraints are imposed in the second stage by considering the use of maxflat halfband polynomial factorization approach. Both the stages are combined to obtain the final product filter P(z) to design the biorthogonal wavelet filters. Here, we only need to design the product filter of one of the two trees i.e., either of the following two Eqs. (7) and (8) can be used.

$$\begin{aligned} P(z)&= \tilde{H}_{0}(z)H_{0}(z) \end{aligned}$$

(7)

$$\begin{aligned}&= \tilde{G}_{0}(z)G_{0}(z) . \end{aligned}$$

(8)

Here, $\tilde{H}_{0}(z)$, $H_{0}(z)$, $\tilde{G}_{0}(z)$ and $G_{0}(z)$ are the $z-$transforms of $\tilde{h}_{0}(n)$, $h_{0}(n)$, $\tilde{g}_{0}(n)$ and $g_{0}(n)$, respectively. If the lengths of the filters $\tilde{h}_{0}(n)$ and $h_{0}(n)$ are $\tilde{N}$ and N, respectively, the filters of Tree-2 can be obtained using time-reversal relationship as

$$\begin{aligned} \tilde{g}_{0}(n)&= \tilde{h}_{0}(\tilde{N} - 1 - n),\; \; 0\le n \le \tilde{N}-1 \end{aligned}$$

(9)

$$\begin{aligned} g_{0}(n)&= h_{0}(N - 1 - n),\; \; 0\le n \le N-1. \end{aligned}$$

(10)

The filters $\tilde{h}_{0}(n)$ and $h_{0}(n)$ are obtained using polynomial factorization of the form $\tilde{H}_{0}(z) = \tilde{F}_{0}(z)D(z)$ and $H_{0}(z) = F_{0}(z)D(z^{-1})z^{-L}$, where D(z) and $D(z^{-1})z^{-L}$ are chosen such that

$$\begin{aligned} A(z) = \frac{D(z^{-1})z^{-L}}{D(z)} = z^{-1/2}|_{z = 1}. \end{aligned}$$

(11)

which represents an all pass filter approximation of half-sample delay. Here, $D(z)\overset{\mathcal {Z}}{\longleftrightarrow }d(n)$ represents a z-transform pair and L represents order of the filter d(n) obtained using Eq. (12).

$$\begin{aligned} d(n+1) = d(n).\frac{(L-n)(L-n-0.5)}{(n+1)(n+1+0.5)},\; \;0\le n\le L-1 \end{aligned}$$

(12)

where, $d(0)=1$. Factors $\tilde{F}_{0}(z)$ and $F_{0}(z)$ are maxflat or binomial filters used in order to satisfy the perfect reconstruction and vanishing moments criteria and are of the form $\tilde{Q}(z)(1+{z^{-1}})^{\tilde{K}}$ and $Q(z)(1+z^{-1})^{K}$, respectively. The polynomials $\tilde{Q}(z)$ and Q(z) are obtained by solving a set of linear equations by imposing halfband constraint on P(z). Here, $\tilde{K}$ and K represent the number of VMs for $\tilde{h}_{0}(n)$ and $h_{0}(n)$, respectively. Since the filters are chosen to satisfy Eqs. (9) and (10), the magnitude condition given in Eq. (5) is exactly satisfied, whereas the phase condition given in Eq. (6) is approximated since the order L used is finite. Ideally L should be $\infty$ to satisfy the Eq. (11) exactly.

3 Proposed Approach

In the proposed approach, we use factorization of generalized halfband polynomial (GHBP) [16]. Here, we propose and design generalized halfband polynomial such that perfect reconstruction (PR) and vanishing moment (VM) and half-sample delay (HSD) constraints are satisfied for any values of the free variables. Given Eq. (7) or (8), we obtain the generalized halfband polynomial for P(z) that satisfies PR, VM and HSD constraints in order to design the DTCWT filters. Let us choose Eq. (7) for designing DTCWT filters of Tree-1 i.e., $\tilde{h}_{0}(n)$ and $h_{0}(n)$. There are three input parameters $\tilde{K}$, K and L. Here, $\tilde{K}$ and K represent number of vanishing moments for $\tilde{h}_{0}(n)$ and $h_{0}(n)$, respectively while L represents order of d(n) i.e., denominator polynomial of an allpass filter used to approximate the HSD condition. Since, we wish to design $\tilde{h}_{0}(n)$ and $h_{0}(n)$ as real symmetric odd-length filters of arbitrary lengths, all the input parameters must be even. Let, $n_{f}$ be the number of free variables used in the optimization to shape the frequency response characteristics. We then select the GHBP of order D given by

$$\begin{aligned} \begin{aligned} P^{D}(z) = a_{0} + a_{2}z^{-2}&+ \dots + a_{(D/2)-1}z^{-(D/2)-1} + z^{-(D/2)}\\&+ a_{(D/2)-1}z^{-(D/2)+1} + \dots + a_{0}z^{-D}, \end{aligned} \end{aligned}$$

(13)

where the polynomial order D is chosen as $D = 2(M-1) + 4L + 8n_{f}$. Note that, order D is chosen such that it includes desired number of VMs, $L^{th}$ order all-pass HSD approximation with $n_{f}$ degrees of freedom available to shape the frequency responses of the filters. Here, $M = \tilde{K} + K$ represents total number of VMs required in the design. For $P^{D}(z)$ of order D, there exist maximum $(\frac{D}{2} + 1)$ zeros at $z = -1$ and $\frac{(D+2)}{4}$ unknown variables i.e., $a_{i}$, $i = 0, 2, \dots , (\frac{D}{2}-1)$. By imposing M number of zeros at $z = -1$, the $P^{D}(z)$ can then be expressed as

$$\begin{aligned} \begin{aligned} P^{D}(z) = (1+z^{-1})^{M}R(z)&= (1+z^{-1})^{\tilde{K}+K}R(z)\\&= \tilde{F}_{0}(z)F_{0}(z), \end{aligned} \end{aligned}$$

(14)

where, the term $(1+z^{-1})$ represents the condition on vanishing moments i.e., zero at $z = -1$ or $\omega = \pi$ which decides smoothness or regularity of the wavelet functions and R(z) is a remainder polynomial expressed in terms of free variables. Here, a double zero at $z = -1$ eliminates one degree of freedom from $P^{D}(z)$, thus $\frac{M}{2}$ unknown variables are expressed in terms of $n_{f} = \left( \frac{D+2}{4} - \frac{M}{2} \right)$ free variables in the remainder polynomial R(z). With this, our modified product filter to design the lowpass filters of Tree-1 i.e., $\tilde{h}_{0}(n)$ and $h_{0}(n)$ can be chosen as

$$\begin{aligned} P(z)&= P^{D}(z)D(z)D(z^{-1})z^{-L}\end{aligned}$$

(15)

$$\begin{aligned} P(z)&= P^{D}(z)D_{L}(z). \end{aligned}$$

(16)

The polynomial factor $D_{L}(z) = D(z)D(z^{-1})z^{-L}$ used here represents half-sample delay constraint. Due to this, P(z) is no longer a halfband polynomial and perfect reconstruction property of the designed filters is lost. Therefore, we impose halfband constraints on P(z) to make it a halfband polynomial before the factorization step. Using Eq. (14), P(z) can be then written as

$$\begin{aligned} P(z)&= (1+z^{-1})^{\tilde{K}+K}R(z)D_{L}(z) \end{aligned}$$

(17)

$$\begin{aligned} P(z)&= B(z)R(z). \end{aligned}$$

(18)

Imposing Halfband Constraints: In Eq. (18), coefficients of the B(z) polynomial are exactly known while R(z) is a symmetric polynomial having unknown variables $a_{i}, i = 0, 2, \dots , (D/2)-1$ as coefficients. After collecting the terms of the product B(z)R(z), we get P(z) which has both odd and even powers of z i.e., it violates the halfband condition. Hence, coefficients of even powers of z are made 0 while the center term (or constant term) is chosen to be 1 in order to obtain the halfband polynomial P(z). Remainder polynomial R(z) in Eq. (18) is now expressed in terms of desired $n_{f}$ number of free variables.

We use MATLAB optimization toolbox routine fminunc to obtain the filters $\tilde{H}_{0}(z)$ and $H_{0}(z)$ by minimizing the following objective function with respect to $n_{f}$ number of free variables as

$$\begin{aligned} \begin{aligned} F_{obj}&= \int \limits _{0}^{\omega _{p}}\left| 1 - \tilde{H}_{0}(\omega )\right| ^{2}d\omega + \int \limits _{\omega _{s}}^{\pi }\left| \tilde{H}_{0}(\omega )\right| ^{2}d\omega \\ {}&+ \int \limits _{0}^{\omega _{p}}\left| 1 - H_{0}(\omega )\right| ^{2}d\omega + \int \limits _{\omega _{s}}^{\pi }\left| H_{0}(\omega )\right| ^{2}d\omega . \end{aligned} \end{aligned}$$

(19)

Here, $\omega _{p}$ and $\omega _{s}$ represent passband and stopband cut-off frequencies (in radian), respectively. Expressions for $\tilde{H}_{0}(\omega )$ and $H_{0}(\omega )$ are given as:

$$\begin{aligned} \tilde{H}_{0}(\omega )&= (1+z^{-1})^{\tilde{K}}R_{1}(z)D(z)|_{z = e^{j\omega }}\end{aligned}$$

(20)

$$\begin{aligned} H_{0}(\omega )&= (1+z^{-1})^{K}R_{2}(z)D(z^{-1})z^{-L}|_{z = e^{j\omega }}. \end{aligned}$$

(21)

During the optimization, for given values of the free variables polynomial R(z) is first evaluated and factorized into polynomials $R_{1}(z)$ and $R_{2}(z)$. Since, this factorization is not unique the objective function value is then computed for all possible combinations of real-valued symmetric polynomials $R_{1}(z)$ and $R_{2}(z)$. We choose them to be symmetric polynomials such that $\tilde{h}_{0}(n)$ and $h_{0}(n)$ obtained are real-valued biorthogonal filters having near-orthogonal frequency response characteristics. Due to approximation of the HSD condition using finite length polynomial, the designed filters have approximate linear-phase property.

4 Design Example

Input parameters chosen are $\tilde{K} = 2$, $K = 4$, $L = 2$ and $n_{f} = 1$. The lengths of the designed filters $\tilde{h}_{0}(n)$ and $h_{0}(n)$ is 11 and 13, respectively. Biorthogonal filters given in Table 3 of [8] also have the same lengths for the filters $\tilde{h}_{0}(n)$ and $h_{0}(n)$. These filters were obtained using max-flat factorization approach of Daubechies [17] with input parameters $\tilde{K} = K = 4$ and $L=2$. We see from Table 1 that the filter coefficients obtained in our case are entirely different from [8]. Due to same lengths of the obtained filters and Selesnick’s 11/13 filters [8], we compare the frequency response characteristics of both the filters. Figure 2 shows magnitude response comparison between proposed and Selesnick’s 11/13 filters. It is clear that frequency response characteristics of the proposed filters are much better and closely mimic near-orthogonal filter response characteristics than those designed using maxflat approach. Wavelet plots for the proposed filters are shown in Fig. 3. Here, one can observe that apart from near-orthogonal frequency response characteristics of the designed filters, analyticity of their associated wavelets is also good. For $\omega <0$, one see that the magnitude frequency plots of $|\tilde{\varPsi }_{h}(\omega ) + j\tilde{\varPsi }_{g}(\omega )|$ and $|\varPsi _{h}(\omega ) + j\varPsi _{g}(\omega )|$ have negligible frequency contents. Wavelets of the two trees are approximately Hilbert transform pairs of each other.

Table 1. Coefficients of the designed filters.

Fig. 2.

Magnitude response comparison between Tree-1 analysis filters of the proposed 11/13 filters and Selesnick’s 11/13 filters.

Fig. 3.

Plots for the designed example (a) magnitude responses for analysis filters of Tree-1 i.e., $\tilde{H}_{0}(\omega )$ and $\tilde{H}_{1}(\omega )$ (b) magnitude responses for synthesis filters of Tree-1 i.e., $H_{0}(\omega )$ and $H_{1}(\omega )$. (c) Analysis wavelet functions $\tilde{\psi }_{h}(t)$, $\tilde{\psi }_{g}(t)$ and $|\tilde{\psi }_{h}(t) + j\tilde{\psi }_{g}(t)|$ (d) Magnitude frequency spectrum for $|\tilde{\varPsi }_{h}(\omega ) + j\tilde{\varPsi }_{g}(\omega )|$ (e) Synthesis wavelet functions $\psi _{h}(t)$, $\psi _{g}(t)$ and $|\psi _{h}(t) + j\psi _{g}(t)|$ (f) Magnitude frequency spectrum for $|\varPsi _{h}(\omega ) + j\varPsi _{g}(\omega )|$.

Apart from qualitative results, we also give quantitative evaluation of the designed filters using proposed approach to measure analyticity of their associated wavelets as well as orthogonality of their frequency response characteristics. The error measuring analyticity is quantified using two quantitative measures $E_{1}$ and $E_{2}$ given by Tay et al. in [18]. Ideally, $E_{1}$ and $E_{2}$ must be 0. For qualitative evaluation of the frequency response characteristics of the proposed filters, we use two orthogonality measures given in [19, 20]. They indicate how good the response characteristics match to the orthogonal filters which have ideal value of 0. Expression for the first measure used is $ON1 = \frac{1}{\pi }\int _{0}^{\pi } (2-O(\omega ))^2 d\omega$, where $O(\omega ) = O(z)|_{z = e^{j\omega }}$ with $O(z) = H_{0}(z)H_{0}(z^{-1})+H_{1}(z)H_{1}(z^{-1})$. Expression for the second measure is $ON2 = \left| \left| H_{0}\left( \frac{\pi }{2} \right) \right| - \left| H_{1}\left( \frac{\pi }{2} \right) \right| \right|$. Here, $H_{0}(z)$ and $H_{1}(z)$ denote analysis lowpass and highpass filters, respectively. Table 2 shows quantitative comparison of the filters designed using the proposed approach and common factor technique.

Table 2. Quantitative comparison of the filters.

5 Image Denoising Application

In this section, we show the performance of the proposed filter set for the image denoising application. We have used filters of the proposed set to obtain the 2-D DTCWT by using the construction given [9]. For comparing the image denoising performance, we have used the MATLAB software provided by Ivan W. Selesnick on his website [21]. We have compared our results with 2-D DTCWT obtained using Selesnick’s 11/13 filters [8]. Additive white Gaussian noise (AWGN) of standard deviation $\sigma$ is added to the original image in order to test the performance on noisy images. We have used bivariate shrinkage method [22] to obtain the denoised results. MATLAB implementation of the same can be found in the software mentioned above. Figure 4 shows image denoising results on widely used Lena image for AWGN of standard deviation $\sigma = 30$. It can be observed that image denoising performance of 2-D DTCWT obtained using proposed filter set outperforms Selesnick’s 11/13 filters [8] in terms of Peak Signal-to-Noise Ratio (PSNR) value while considerable improvement is observed in case of recent image quality indicator values namely Structural Similarity Index Measure (SSIM) [23] and Feature Similarity Index Measure (FSIM) [24]. Both SSIM and FSIM have ideal value of 1. Denoising output shown in Fig. 4(d) for proposed filter set have better visual performance when compared to the output for Selesnick’s filters shown in Fig. 4(c). Directional image features are better captured using the proposed filters due to better directional selectivity of their 2-D dual-tree directional wavelets. Also, due to near-orthogonality of the proposed filters, noise is better removed than that of Selesnick’s filters.

Fig. 4.

Image denoising using 2-D DTCWT (a) original image (b) noisy image with $\sigma = 30$, PSNR = 18.59 dB. Denoising using (c) Selesnick’s 11/13 filters [8], PSNR = 28.73 dB, SSIM [23] = 0.73 and FSIM [24] = 0.90. (d) proposed filters, PSNR = 29.52 dB, SSIM [23] = 0.77 and FSIM [24] = 0.92.

6 Conclusion

In this paper, we proposed a new approach to design the biorthogonal wavelet filters of DTCWT. The proposed approach is based on optimization of free variables obtained through factorization of generalized halfband polynomial. The designed filters using the proposed approach have better frequency response characteristics. Also, their associated wavelets show better analyticity in terms of qualitative as well as quantitative evaluation. Transform-based image denoising experiment using the proposed filters shows better performance in terms of qualitative and quantitative evaluation when compared to the filters designed using common factor approach.