1 Introduction

In multiview geometry, the essential matrix describes the relative orientation of two calibrated cameras. It was first introduced by Longuet-Higgins (1981), where the essential matrix was used for the scene reconstruction from point correspondences in two views. Later, the algebraic properties of essential matrices have been investigated in detail in Faugeras and Maybank (1990), Horn (1990), Huang and Faugeras (1989). The well-known characterization of the algebraic variety of essential matrices, which is the closure of the set of essential matrices in the corresponding projective space, consists of a unique matrix equation of degree three (Demazure 1988; Maybank 1993). Based on this equation, a number of efficient algorithmic solutions to different relative pose estimation problems have been proposed in the last two decades, e.g. Nistér (2004), Stewénius et al. (2006, 2008), Kukelova and Pajdla (2007).

The relative orientation of three calibrated cameras can be naturally described by the so-called calibrated trifocal tensor. It first appeared in Spetsakis and Aloimonos (1990), Weng et al. (1992) as a tool of scene reconstruction from line correspondences. The algebraic properties of calibrated trifocal tensors were recently investigated in Martyushev (2017), where some necessary and sufficient polynomial constraints on a real calibrated trifocal tensor have been derived. A 3-view analog of the variety of essential matrices—the calibrated trifocal variety—has been introduced in Kileel (2017), where it was used to compute algebraic degrees of various 3-view relative pose problems. The complete characterization of the calibrated trifocal variety is an open and challenging problem. For the uncalibrated case such characterization consists of 10 cubic, 81 quintic, and 1980 sextic polynomial equations (Aholt and Oeding 2014).

Another way to describe the geometry of three calibrated cameras comes from considering the compatible triplets of essential matrices. The compatibility means that a triplet must correspond to a certain configuration of three calibrated cameras. In the recent paper (Kasten et al. 2019a), the authors considered compatible n-view multiplets of essential matrices, which are the natural n-view generalization of the triplets, and proposed their algebraic characterization in terms of the spectral (or singular value) decomposition of a symmetric \(3n\times 3n\) matrix constructed from the multiplet.

On the other hand, the polynomial constraints on compatible triplets of essential matrices have not previously been studied. The present paper is a step in this direction. Its main contribution is a set of polynomial constraints such that any triplet of real and rank-two essential matrices that fulfils these constraints is guaranteed to be compatible. An important advantage of the introduced constraints is their sufficiency even in the case of cameras with collinear centers. The results of the paper may be applied to different computer vision problems including relative camera pose estimation from three and more views, averaging of essential matrices for incremental structure from motion, multiview camera auto-calibration, etc.

The rest of the paper is organized as follows. In Sect. 2, we recall some definitions and results from multiview geometry. In Sect. 3, we propose our necessary and sufficient constraints on compatible triplets of essential matrices. The constraints have the form of 82 cubic, one quartic, and one sextic homogeneous polynomial equations in the entries of essential matrices. Section 4 outlines two possible applications of the proposed constraints. In Sect. 5, we discuss the results of the paper and make conclusions. The “Appendix” includes some auxiliary lemmas that we used throughout the proof of our main Theorem 5.

2 Preliminaries

2.1 Notation

We preferably use \(\alpha \), \(\beta , \ldots \) for scalars, a, \(b, \ldots \) for column 3-vectors or polynomials, and A, \(B, \ldots \) both for matrices and column 4-vectors. For a matrix A, the entries are \((A)_{ij}\), the transpose is \(A^\top \), and the adjugate (i.e. the transposed matrix of cofactors) is \(A^*\). The determinant of A is \(\det A\) and the trace is \({{\,\mathrm{tr}\,}}A\). For two 3-vectors a and b, the cross product is \(a\times b\). For a vector a, the entries are \((a)_i\). The notation \([a]_\times \) stands for the skew-symmetric matrix such that \([a]_\times b = a \times b\) for any vector b. We use I for the identity matrix and \(\Vert \cdot \Vert \) for the Frobenius norm.

2.2 Fundamental Matrix

We briefly recall some definitions and results from multiview geometry, see Faugeras (1993), Faugeras and Maybank (1990), Hartley and Zisserman (2003), Maybank (1993) for details.

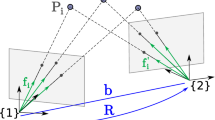
A matrix \(P = \begin{bmatrix}A&a\end{bmatrix}\), where A is an invertible \(3\times 3\) matrix and a is a 3-vector, is called the finite projective camera. A camera P represents a perspective projection of 3-space onto the image plane, which is the image of P, through the camera center, which is the right null vector of P.

Let \(P_1 = \begin{bmatrix}A_1&a_1\end{bmatrix}\) and \(P_2 = \begin{bmatrix}A_2&a_2\end{bmatrix}\) be finite projective cameras. Let Q be a point in 3-space represented by its homogeneous coordinates and \(q_j\) be its jth perspective image. Then,

$$\begin{aligned} q_j \sim P_j Q, \end{aligned}$$
(1)

where \(\sim \) means an equality up to a non-zero scale. The epipolar constraint for a pair \((q_1, q_2)\) says

$$\begin{aligned} q_2^\top F_{21} q_1 = 0, \end{aligned}$$
(2)

where Sengupta et al. (2017), Kasten et al. (2019a)

$$\begin{aligned} F_{21} = (A_2^*)^\top [A_2^{-1}a_2 - A_1^{-1} a_1]_\times A_1^* \end{aligned}$$
(3)

is called the fundamental matrix. By definition, \(F_{21}\) must be of rank two. The left and right null vectors of \(F_{21}\), that is the vectors

$$\begin{aligned} e_{21} = A_2A_1^{-1}a_1 - a_2 \quad \text {and}\quad e_{12} = A_1A_2^{-1}a_2 - a_1 \end{aligned}$$
(4)

respectively, are called the epipoles. Geometrically, \(e_{ij}\) is the perspective projection of the jth camera center onto the ith image plane.

The following theorem gives an algebraic characterization of the set of fundamental matrices.

Theorem 1

(Hartley and Zisserman 2003) Any real \(3\times 3\) matrix of rank two is a fundamental matrix.

2.3 Essential Matrix

The essential matrix \(E_{21}\) is the fundamental matrix for calibrated cameras \({{\hat{P}}}_1 = \begin{bmatrix} R_1&t_1 \end{bmatrix}\) and \({{\hat{P}}}_2 = \begin{bmatrix} R_2&t_2\end{bmatrix}\), where \(R_1, R_2 \in \mathrm {SO}(3)\) and \(t_1\), \(t_2\) are 3-vectors, that is

$$\begin{aligned} E_{21} = R_2[R_2^\top t_2 - R_1^\top t_1]_\times R_1^\top . \end{aligned}$$
(5)

The proof of formula (5) can be found in Arie-Nachimson et al. (2012).

In general, the calibrated and uncalibrated camera matrices are related by

$$\begin{aligned} P_j \sim K_j {{\hat{P}}}_j H, \end{aligned}$$
(6)

where \(K_j\) is an invertible upper-triangular matrix known as the calibration matrix of the jth camera and H is a certain invertible \(4\times 4\) matrix. Then it can be shown that

$$\begin{aligned} F_{21} \sim K_2^{-\top } E_{21} K_1^{-1}. \end{aligned}$$
(7)

Hence, the epipolar constraint for the essential matrix becomes

$$\begin{aligned} {{\hat{q}}}_2^\top E_{21} {{\hat{q}}}_1 = 0, \end{aligned}$$
(8)

where \({{\hat{q}}}_j = K_j^{-1} q_j\).

The following theorem gives an algebraic characterization of the set of essential matrices.

Theorem 2

(Demazure 1988; Faugeras and Maybank 1990; Maybank 1993) A real \(3\times 3\) matrix E of rank two is an essential matrix if and only if E satisfies

$$\begin{aligned} E^\top EE^\top - \frac{1}{2}{{\,\mathrm{tr}\,}}(E^\top E)\, E^\top = 0_{3\times 3}. \end{aligned}$$
(9)

2.4 Compatible Triplets of Fundamental Matrices

A triplet of fundamental matrices \(\{F_{12}, F_{23}, F_{31}\}\) is said to be compatible if there exist matrices \(B_1, B_2, B_3 \in \mathrm {GL}(3)\) and 3-vectors \(b_1\), \(b_2\), \(b_3\) such that

$$\begin{aligned} F_{ij} = B_i^\top [b_i - b_j]_\times B_j \end{aligned}$$
(10)

for all distinct \(i, j \in \{1, 2, 3\}\). It follows from (10) that \(F_{ji} = F_{ij}^\top \).

Theorem 3

Let \({\mathcal {F}} = \{F_{12}, F_{23}, F_{31}\}\) be a triplet of real rank-two fundamental matrices with non-collinear epipoles, i.e. \(e_{ki} \not \sim e_{kj}\) for all distinct \(i, j, k \in \{1, 2, 3\}\). Then, \({\mathcal {F}}\) is compatible if and only if it satisfies

$$\begin{aligned} F_{ij}^* F_{ik} F_{jk}^* = 0_{3\times 3}. \end{aligned}$$
(11)

Proof

By the definition of epipoles, constraints (11) imply (and are implied by)

$$\begin{aligned} e_{ij}^\top F_{ik} e_{kj} = 0 \end{aligned}$$
(12)

for all distinct indices \(i, j, k \in \{1, 2, 3\}\). Geometrically, constraints (12) mean that the epipoles \(e_{ij}\) and \(e_{kj}\) are matched and correspond to the projections of the jth camera center onto the ith and kth image plane respectively. The proof of compatibility of three fundamental matrices with non-collinear epipoles satisfying (12) can be found in Hartley and Zisserman (2003). \(\square \)

The main goal of this paper is to propose a generalized analog of Theorem 3 for a triplet of essential matrices with possibly collinear epipoles.

3 Compatible Triplets of Essential Matrices

A triplet of essential matrices \(\{E_{12}, E_{23}, E_{31}\}\) is said to be compatible if there exist matrices \(R_1, R_2, R_3 \in \mathrm {SO}(3)\) and 3-vectors \(b_1\), \(b_2\), \(b_3\) such that

$$\begin{aligned} E_{ij} = R_i[b_i - b_j]_\times R_j^\top \end{aligned}$$
(13)

for all distinct \(i, j \in \{1, 2, 3\}\).

Given a triplet of essential matrices \(\{E_{12}, E_{23}, E_{31}\}\), let us denote

$$\begin{aligned} E = \begin{bmatrix} 0_{3\times 3} &{} E_{12} &{} E_{13} \\ E_{21} &{} 0_{3\times 3} &{} E_{23} \\ E_{31} &{} E_{32} &{} 0_{3\times 3} \end{bmatrix}. \end{aligned}$$
(14)

The symmetric \(9\times 9\) matrix E (as well as its analog for fundamental matrices) has been previously introduced in Sengupta et al. (2017), Kasten et al. (2019a, b) where some of its spectral properties were investigated. The matrix E is called compatible if it is constructed from a compatible triplet. In Kasten et al. (2019a), the authors propose necessary and sufficient conditions on the compatibility of matrix E (more precisely, of an n-view generalization of matrix E) in terms of its spectral or singular value decomposition. In particular, these conditions imply that the characteristic polynomial of a compatible matrix E must be of the form

$$\begin{aligned} p_E(\lambda ) = \lambda ^3(\lambda ^2 - \lambda _1^2)(\lambda ^2 - \lambda _2^2)(\lambda ^2 - \lambda _3^2), \end{aligned}$$
(15)

where \(\lambda _1\), \(\lambda _2\), and \(\lambda _3\) are possibly non-zero eigenvalues of E.

Condition (15) induces polynomial constraints on the entries of matrix E. Namely, the coefficients of \(p_E(\lambda )\) in \(\lambda ^6\), \(\lambda ^4\), \(\lambda ^2\), \(\lambda ^1\), and \(\lambda ^0\) must vanish. It is clear that these coefficients are polynomials in the entries of matrices \(E_{12}\), \(E_{23}\), \(E_{31}\) of degree 3, 5, 7, 8, and 9 respectively. For example, the coefficient in \(\lambda ^6\) equals \(-2{{\,\mathrm{tr}\,}}(E_{12}E_{23}E_{31})\). Below we propose a set of cubic polynomial equations on matrix E such that constraint (15) is implied by these equations, see Eqs. (26)–(28).

Apart from condition (15), there exists an additional quadratic constraint on the eigenvalues of matrix E. Let \(|\lambda _1| > |\lambda _2|\) and \(|\lambda _1| > |\lambda _3|\). Then, by a straightforward computation, one verifies that

$$\begin{aligned} \lambda _1^2 - \lambda _2^2 - \lambda _3^2 = 0. \end{aligned}$$
(16)

A symmetrized version of Eq. (16), which is independent of the ordering on the set of eigenvalues, has the form

$$\begin{aligned} (\lambda _1^2 - \lambda _2^2 - \lambda _3^2)(\lambda _2^2 - \lambda _3^2 - \lambda _1^2)(\lambda _3^2 - \lambda _1^2 - \lambda _2^2) = 0. \end{aligned}$$
(17)

Since the l.h.s. of Eq. (17) is a symmetric function in values \(\lambda _1^2\), \(\lambda _2^2\), and \(\lambda _3^2\), it can be expanded in terms of the elementary symmetric functions, which are the coefficients in (15). On the other hand, these coefficients can be represented as polynomials in \({{\,\mathrm{tr}\,}}(E^{2k})\) for \(k = 1, 2, 3\). Thus we obtain an additional sixth degree scalar equation on matrix E, see Eq. (30).

Finally, some of our polynomial constraints are easier to formulate using a specific binary operation on the space of \(3\times 3\) matrices. Let \(A^*\) be the adjugate of a matrix A, i.e. the transposed matrix of its cofactors. Then for a pair of \(3\times 3\) matrices A and B we define

$$\begin{aligned} A\diamond B = (A - B)^* - A^* - B^*. \end{aligned}$$
(18)

An alternative expression for \(A\diamond B\) can be derived using the well-known formula

$$\begin{aligned} A^* = \frac{1}{2}\,({{\,\mathrm{tr}\,}}^2 A - {{\,\mathrm{tr}\,}}A^2)I - A{{\,\mathrm{tr}\,}}A + A^2. \end{aligned}$$
(19)

Thus we get

$$\begin{aligned} A\diamond B&= ({{\,\mathrm{tr}\,}}(AB) - {{\,\mathrm{tr}\,}}A{{\,\mathrm{tr}\,}}B)I + A{{\,\mathrm{tr}\,}}B\nonumber \\&\quad + B{{\,\mathrm{tr}\,}}A - AB - BA. \end{aligned}$$
(20)

It is straightforward to show that for any \(3\times 3\) matrices A, B, C, D and any scalars \(\beta \) and \(\gamma \) the following identities hold:

$$\begin{aligned}&A\diamond B = B\diamond A, \end{aligned}$$
(21)
$$\begin{aligned}&A\diamond (\beta B + \gamma C) = \beta (A\diamond B) + \gamma (A\diamond C), \end{aligned}$$
(22)
$$\begin{aligned}&(A\diamond B)^\top = A^\top \diamond B^\top , \end{aligned}$$
(23)
$$\begin{aligned}&(CAD)\diamond (CBD) = D^*(A\diamond B)C^*, \end{aligned}$$
(24)
$$\begin{aligned}&A\diamond I = A - {{\,\mathrm{tr}\,}}(A)I. \end{aligned}$$
(25)

Now we can formulate our polynomial constraints.

Theorem 4

Let \(\{E_{12}, E_{23}, E_{31}\}\) be a compatible triplet of essential matrices, matrix E be defined in (14). Then the following equations hold:

$$\begin{aligned}&{{\,\mathrm{tr}\,}}(E_{12}E_{23}E_{31}) = 0, \end{aligned}$$
(26)
$$\begin{aligned}&E_{ij}^\top E_{ij}E_{jk} - \frac{1}{2}{{\,\mathrm{tr}\,}}(E_{ij}^\top E_{ij})\, E_{jk} + E_{ij}^*E_{ki}^\top = 0_{3\times 3}, \end{aligned}$$
(27)
$$\begin{aligned}&E_{jk}^\top E_{ij}^* + E_{jk}^*E_{ij}^\top + (E_{ij}E_{jk}) \diamond E_{ki}^\top = 0_{3\times 3}, \end{aligned}$$
(28)
$$\begin{aligned}&{{\,\mathrm{tr}\,}}^2(E^2) - 16{{\,\mathrm{tr}\,}}(E^4) + 24\sum \limits _{i < j}{{\,\mathrm{tr}\,}}^2(E_{ij}^\top E_{ij}) = 0, \end{aligned}$$
(29)
$$\begin{aligned}&{{\,\mathrm{tr}\,}}^3(E^2) - 12{{\,\mathrm{tr}\,}}(E^2){{\,\mathrm{tr}\,}}(E^4) + 32{{\,\mathrm{tr}\,}}(E^6) = 0 \end{aligned}$$
(30)

for all distinct \(i, j, k \in \{1, 2, 3\}\). There are in total \(1 + 6\cdot 9 + 3\cdot 9 = 82\) linearly independent cubic equations of type (26)–(28).

Proof

Let

$$\begin{aligned} {\widetilde{E}}_{ij} = U_i E_{ij}U_j^\top , \end{aligned}$$
(31)

where \(U_i \in \mathrm {SO}(3)\). It is clear that \({\mathcal {E}} = \{E_{12}, E_{23}, E_{31}\}\) is a compatible triplet if and only if so is \(\widetilde{{\mathcal {E}}} = \{{{\widetilde{E}}}_{12}, \widetilde{E}_{23}, {{\widetilde{E}}}_{31}\}\). Also it can be readily seen that \({\mathcal {E}}\) fulfils Eqs. (26)–(30) if and only if so does \(\widetilde{{\mathcal {E}}}\).

Given a compatible triplet \(\{E_{12}, E_{23}, E_{31}\}\), where each \(E_{ij}\) is represented by (13), we set \(U_i = R_i^\top \). Then essential matrices \({{\widetilde{E}}}_{ij} = U_i E_{ij}U_j^\top \) become skew-symmetric and can be written in form

$$\begin{aligned}&\!\!\!\!{{\widetilde{E}}}_{ij} = [b_i - b_j]_\times , \quad {{\widetilde{E}}}_{jk} = [b_j - b_k]_\times ,\nonumber \\ \quad&{{\widetilde{E}}}_{ki} = [b_k - b_i]_\times , \end{aligned}$$
(32)

where indices i, j, k are intended to be distinct. Denoting \(b_i - b_j = c\), \(b_j - b_k = d\) yields \(b_k - b_i = -c - d\) and hence we can write

$$\begin{aligned} {{\widetilde{E}}}_{ij} = [c]_\times , \quad {{\widetilde{E}}}_{jk} = [d]_\times , \quad {{\widetilde{E}}}_{ki} = -[c]_\times - [d]_\times . \end{aligned}$$
(33)

By substituting this into Eqs. (26)–(28), we get

$$\begin{aligned}&{{\,\mathrm{tr}\,}}({{\widetilde{E}}}_{ij}{{\widetilde{E}}}_{jk}{{\widetilde{E}}}_{ki}) = -{{\,\mathrm{tr}\,}}([c]_\times [d]_\times [c]_\times + [c]_\times [d]_\times [d]_\times ) \nonumber \\&\quad = -{{\,\mathrm{tr}\,}}([c]_\times (cd^\top - (d^\top c)I) + (cd^\top - (d^\top c)I)[d]_\times ) \nonumber \\&\quad = (d^\top c){{\,\mathrm{tr}\,}}([c + d]_\times ) = 0, \end{aligned}$$
(34)
$$\begin{aligned}&\bigl ({{\widetilde{E}}}_{ij}^\top {{\widetilde{E}}}_{ij} - \frac{1}{2}\, {{\,\mathrm{tr}\,}}({{\widetilde{E}}}_{ij}^\top {{\widetilde{E}}}_{ij}) I\bigr )\widetilde{E}_{jk} + {{\widetilde{E}}}_{ij}^* {{\widetilde{E}}}_{ki}^\top \nonumber \\&\quad = \bigl (-[c]_\times [c]_\times + \frac{1}{2}\, {{\,\mathrm{tr}\,}}([c]_\times [c]_\times ) I\bigr )[d]_\times + cc^\top ([c]_\times + [d]_\times ) \nonumber \\&\quad = \bigl (-cc^\top + (c^\top c)I - \frac{1}{2}\, 2(c^\top c)I\bigr )[d]_\times + cc^\top [d]_\times \nonumber \\&\quad = -cc^\top [d]_\times + cc^\top [d]_\times = 0_{3\times 3}, \end{aligned}$$
(35)
$$\begin{aligned}&{{\widetilde{E}}}_{jk}^\top {{\widetilde{E}}}_{ij}^* + {{\widetilde{E}}}_{jk}^* {{\widetilde{E}}}_{ij}^\top + ({{\widetilde{E}}}_{ij}{{\widetilde{E}}}_{jk}) \diamond {{\widetilde{E}}}_{ki}^\top \nonumber \\&\quad = -[d]_\times cc^\top - dd^\top [c]_\times + (dc^\top - (c^\top d)I) \diamond ([c]_\times + [d]_\times ) \nonumber \\&\quad = -[d]_\times cc^\top - dd^\top [c]_\times + (dc^\top )\diamond [c]_\times + (dc^\top )\diamond [d]_\times \nonumber \\&\qquad - (c^\top d)([c]_\times + [d]_\times ) = -[d]_\times cc^\top - dd^\top [c]_\times \nonumber \\&\qquad - [c]_\times dc^\top - dc^\top [d]_\times = 0_{3\times 3}. \end{aligned}$$
(36)

We used that \([a]_\times [b]_\times = ba^\top - (a^\top b)I\) and \(([a]_\times )^* = aa^\top \) for arbitrary 3-vectors a and b. Equations (29)–(30) can be verified in a similar manner, but the computation is more complicated. Theorem 4 is proved. \(\square \)

Remark 1

Constraint (11) for essential matrices is implied by Eq. (27). Namely, multiplying (27) on the right by \(E_{jk}^*\) gives (11).

We also note that Eq. (27) is a generalization of Eq. (9). Setting \(k = i\) in (27) and taking into account that \(E_{ii} = 0_{3\times 3}\) gives (9).

Theorem 5

Let \({\mathcal {E}} = \{E_{12}, E_{23}, E_{31}\}\) be a triplet of real rank-two essential matrices. Then \({\mathcal {E}}\) is compatible if and only if it satisfies Eqs. (26)–(30) from Theorem 4.

Proof

The “only if” part is by Theorem 4. Let us prove the “if” part.

First of all, we simplify the triplet \({\mathcal {E}}\) by using transform (31). Each essential matrix from \(\mathcal E\) can be represented in form \(E_{ij} = [b_{ij}]_\times R_{ij}\), where \(R_{ij} \in \mathrm {SO}(3)\) and \(b_{ij}\) is a 3-vector. We set \(U_2 = U_1 R_{12}\) and \(U_3 = U_2 R_{23} = U_1 R_{12}R_{23}\). Then,

$$\begin{aligned} \begin{aligned} {{\widetilde{E}}}_{12}&= U_1[b_{12}]_\times R_{12} U_2^\top = [U_1b_{12}]_\times ,\\ {{\widetilde{E}}}_{23}&= U_2[b_{23}]_\times R_{23} U_3^\top = [U_1R_{12}b_{23}]_\times ,\\ {{\widetilde{E}}}_{31}&= U_3[b_{31}]_\times R_{31} U_1^\top = [U_1 R_{12}R_{23}b_{31}]_\times U_1 R U_1^\top , \end{aligned} \end{aligned}$$
(37)

where \(R = R_{12}R_{23}R_{31}\). The matrix \(U_1\) is chosen so thatFootnote 1

$$\begin{aligned} U_1RU_1^\top = \begin{bmatrix}\lambda &{} \mu &{} 0 \\ -\mu &{} \lambda &{} 0 \\ 0 &{} 0 &{} 1 \end{bmatrix}, \end{aligned}$$
(38)

where \(\lambda ^2 + \mu ^2 = 1\) and also \((U_1R_{12}R_{23}b_{31})_1 = 0\). As a result, it suffices to prove the “if” part for the following triplet:

$$\begin{aligned} {{\widetilde{E}}}_{12}= & {} \begin{bmatrix} 0 &{} -\gamma _1 &{} \beta _1 \\ \gamma _1 &{} 0 &{} -\alpha _1 \\ -\beta _1 &{} \alpha _1 &{} 0 \end{bmatrix},\quad {{\widetilde{E}}}_{23} = \begin{bmatrix} 0 &{} -\gamma _2 &{} \beta _2 \\ \gamma _2 &{} 0 &{} -\alpha _2 \\ -\beta _2 &{} \alpha _2 &{} 0 \end{bmatrix},\nonumber \\ {{\widetilde{E}}}_{31}= & {} \begin{bmatrix}\gamma _3\mu &{} -\gamma _3\lambda &{} \beta _3 \\ \gamma _3\lambda &{} \gamma _3\mu &{} 0 \\ -\beta _3\lambda &{} -\beta _3\mu &{} 0 \end{bmatrix}, \end{aligned}$$
(39)

where \(\lambda , \mu , \alpha _1, \ldots , \gamma _3\) are some scalars. For the purpose of completeness, we also write down the epipoles corresponding to triplet (39):

$$\begin{aligned} \begin{aligned} e_{12}&= \begin{bmatrix} \alpha _1&\beta _1&\gamma _1 \end{bmatrix}^\top ,&e_{13}&= \begin{bmatrix} -\beta _3\mu&\beta _3\lambda&\gamma _3 \end{bmatrix}^\top ,\\ e_{21}&= \begin{bmatrix} \alpha _1&\beta _1&\gamma _1 \end{bmatrix}^\top ,&e_{23}&= \begin{bmatrix} \alpha _2&\beta _2&\gamma _2 \end{bmatrix}^\top ,\\ e_{31}&= \begin{bmatrix} 0&\beta _3&\gamma _3 \end{bmatrix}^\top ,&e_{32}&= \begin{bmatrix} \alpha _2&\beta _2&\gamma _2 \end{bmatrix}^\top . \end{aligned} \end{aligned}$$
(40)

Let us define an ideal \(J \subset {\mathbb {C}}[\lambda , \mu , \alpha _1, \ldots , \gamma _3]\) generated by all polynomials from (26)–(30) for triplet \(\{\widetilde{E}_{12}, {{\widetilde{E}}}_{23}, {{\widetilde{E}}}_{31}\}\) and also by \(\lambda ^2 + \mu ^2 - 1\). The ideal J determines an affine variety \({\mathcal {V}}(J) \subset {\mathbb {C}}^{10}\). The rest of the proof consists in showing that each point of \({\mathcal {V}}(J)\) is either a compatible or degenerate triplet of essential matrices. By degeneration we mean that at least one essential matrix from the triplet is a zero matrix. For the reader’s convenience, the main steps of the further proof are schematically shown in Fig. 1.

Fig. 1
figure 1

To the proof of Theorem 5. Every real point of the variety defined by the ideal J is either a compatible triplet or a degenerate triplet with at least one \({{\widetilde{E}}}_{ij} = 0_{3\times 3}\). The dashed arrow means correspondence to a particular case

Full size image

We consider the three main cases: (i) \(\mu = 0\), \(\lambda = 1\); (ii) \(\mu = 0\), \(\lambda = -1\); (iii) \(\mu \ne 0\).

Case I: \(\mu = 0\), \(\lambda = 1\).

First we note that a polynomial ideal and its radical define the same affine variety, whereas the algebraic structure of the radical may be much easier. For example, the Gröbner bases of the ideal J and its radical \(\sqrt{J}\) w.r.t. the same monomial ordering consist of 217 and 62 polynomials respectively. Besides, there exist a simple radical membership test allowing to check whether a given polynomial belongs to the radical or not, see Lemma 1 from the “Appendix”. The above arguments should explain the use of radicals throughout the further proof.

Let us define the polynomials

$$\begin{aligned} \begin{aligned} f_1&= \alpha _1 + \alpha _2,&\quad g_3&= \alpha _2\beta _3,\\ f_2&= \beta _1 + \beta _2 + \beta _3,&\quad g_4&= \alpha _2\gamma _3,\\ f_3&= \gamma _1 + \gamma _2 + \gamma _3,&\quad g_5&= \beta _1\gamma _2 - \beta _2\gamma _1,\\ g_1&= \alpha _1\beta _3,&\quad g_6&= \beta _2\gamma _3 - \beta _3\gamma _2,\\ g_2&= \alpha _1\gamma _3,&\quad g_7&= \beta _1\gamma _3 - \beta _3\gamma _1. \end{aligned} \end{aligned}$$
(41)

Then, by the radical membership test, we get

$$\begin{aligned} f_ig_j \in \sqrt{J + \langle \mu , \lambda - 1 \rangle } \end{aligned}$$
(42)

for all indices i and j.

First suppose that \(f_i \ne 0\) for a certain i. Then it follows from (42) that \(\alpha _1\beta _3 = \alpha _1\gamma _3 = \alpha _2\beta _3 = \alpha _2\gamma _3 = 0\). If \(\alpha _1 \ne 0\) or \(\alpha _2 \ne 0\), then \(\beta _3 = \gamma _3 = 0\) and we get \({{\widetilde{E}}}_{31} = 0_{3\times 3}\) in contradiction with the rank-two condition. Therefore \(\alpha _1 = \alpha _2 = 0\) and it follows from (42) that

$$\begin{aligned} \beta _1\gamma _2 - \beta _2\gamma _1 = \beta _2\gamma _3 - \beta _3\gamma _2 = \beta _1\gamma _3 - \beta _3\gamma _1 = 0. \end{aligned}$$
(43)

The variables \(\beta _3\) and \(\gamma _3\) cannot be zero simultaneously. Without loss of generality, assume that \(\gamma _3 \ne 0\) and introduce parameter \(\delta = \beta _3/\gamma _3\). Then Eqs. (43) imply \(\beta _i = \delta \gamma _i\) for all i. Using the radical membership test, one verifies that the variables \(\gamma _i\) are constrained by

$$\begin{aligned}&(\gamma _1 + \gamma _2 + \gamma _3)(-\gamma _1 + \gamma _2 + \gamma _3)\nonumber \\&\quad (\gamma _1 - \gamma _2 + \gamma _3)(\gamma _1 + \gamma _2 - \gamma _3) = 0, \end{aligned}$$
(44)

that is \(\gamma _3 = \epsilon _1\gamma _1 + \epsilon _2\gamma _2\) with \(\epsilon _i = {\pm } 1\). The triplet of essential matrices has the form (67) and is compatible by Lemma 3.Footnote 2

Now consider the case \(f_1 = f_2 = f_3 = 0\), that is

$$\begin{aligned} \alpha _1 + \alpha _2 = \beta _1 + \beta _2 + \beta _3 = \gamma _1 + \gamma _2 + \gamma _3 = 0. \end{aligned}$$
(45)

The triplet of essential matrices has the form (69) and is compatible by Lemma 4.

Case II: \(\mu = 0\), \(\lambda = -1\).

Let \(J' = J + \langle \mu , \lambda + 1 \rangle \). The ideal \(\sqrt{J'}\) contains the following polynomials:

$$\begin{aligned} \begin{aligned}&\alpha _i\beta _3\gamma _1,&\quad&\alpha _i\beta _3(\alpha _1 - \alpha _2),\\&\alpha _i\beta _3\gamma _2,&\quad&\alpha _i\beta _3(\beta _1 - \beta _2 + \beta _3),\\&\alpha _i\beta _3\gamma _3,&\quad&\alpha _i\beta _3\beta _1\beta _2(\beta _1\beta _2 + \alpha _1^2), \end{aligned} \end{aligned}$$
(46)

where \(i = 1, 2\). Supposing that \(\alpha _1\beta _3 \ne 0\) or \(\alpha _2\beta _3 \ne 0\) yields

$$\begin{aligned} \gamma _1= & {} \gamma _2 = \gamma _3 = \alpha _1 - \alpha _2 = \beta _1 - \beta _2 + \beta _3 \nonumber \\= & {} \beta _1\beta _2(\beta _1\beta _2 + \alpha _1^2) = \beta _1\beta _2(\beta _1\beta _2 + \alpha _2^2) = 0. \end{aligned}$$
(47)

The case \(\beta _1 = \beta _2 = 0\) contradicts to the rank-two condition, since leads to \({{\widetilde{E}}}_{31} = 0_{3\times 3}\). If \(\beta _1 = 0\) and \(\beta _2 \ne 0\), then triplet \(\{\widetilde{E}_{12}, {{\widetilde{E}}}_{23}, {{\widetilde{E}}}_{31}\}\) has the form (70) and is compatible by Lemma 4. Similarly, we get compatible triplet (71) in the case \(\beta _2 = 0\) and \(\beta _1 \ne 0\). Finally, if \(\beta _1\beta _2 \ne 0\), then it follows from (47) that \(\beta _1\beta _2 + \alpha _1^2 = 0\) and so \(\beta _2 = -\alpha _1^2/\beta _1\). The triplet \(\{\widetilde{E}_{12}, {{\widetilde{E}}}_{23}, {{\widetilde{E}}}_{31}\}\) has the form (72) and is compatible by Lemma 4.

Now consider the case \(\alpha _1\beta _3 = \alpha _2\beta _3 = 0\). There are two possibilities. If \(\beta _3 = 0\), then ideal \(\sqrt{J' + \langle \beta _3 \rangle }\) contains the following polynomials:

$$\begin{aligned} \begin{aligned}&\gamma _3(\alpha _1 + \alpha _2),&\quad&\alpha _2\gamma _3(\gamma _1 + \gamma _2 - \gamma _3), \\&\gamma _3(\beta _1 + \beta _2),&\quad&\beta _2\gamma _3(\gamma _1 + \gamma _2 - \gamma _3). \end{aligned} \end{aligned}$$
(48)

The case \(\gamma _3 = 0\) contradicts to the rank-two condition. Thus, \(\alpha _1 + \alpha _2 = \beta _1 + \beta _2 = 0\). It follows that, if \(\alpha _2 = \beta _2 = 0\), then \(\alpha _1 = \beta _1 = 0\). By the radical membership test, the variables \(\gamma _1\), \(\gamma _2\), and \(\gamma _3\) are constrained by (44) and hence we get a particular case (\(\delta = 0\)) of triplet (67) which is compatible by Lemma 3. On the other hand, if \(\alpha _2 \ne 0\) or \(\beta _2 \ne 0\), then we get

$$\begin{aligned} \alpha _1 + \alpha _2 = \beta _1 + \beta _2 = \gamma _1 + \gamma _2 - \gamma _3 = 0. \end{aligned}$$
(49)

The triplet \(\{{{\widetilde{E}}}_{12}, {{\widetilde{E}}}_{23}, \widetilde{E}_{31}\}\) is a particular case (\(\beta _3 = 0\)) of (69) which is compatible by Lemma 4.

The second possibility is \(\beta _3 \ne 0\) and \(\alpha _1 = \alpha _2 = 0\). Denote \(J'' = J' + \langle \alpha _1, \alpha _2 \rangle \) and define the polynomials

$$\begin{aligned} \begin{aligned} h_1&= \beta _1\beta _2\beta _3\,(\beta _1(\beta _1 + \beta _2 - \beta _3) + \gamma _1(\gamma _1 + \gamma _2 + \gamma _3)),\\ h_2&= \beta _1\beta _2\beta _3\,(\beta _2(\beta _1 + \beta _2 + \beta _3) + \gamma _2(\gamma _1 + \gamma _2 + \gamma _3)),\\ h_3&= \beta _1\beta _2\beta _3\,(\beta _3(-\beta _1 + \beta _2 + \beta _3) + \gamma _3(\gamma _1 + \gamma _2 + \gamma _3)). \end{aligned} \end{aligned}$$
(50)

Then, the radical membership test yields

$$\begin{aligned} h_i \in \sqrt{J''} \end{aligned}$$
(51)

for all i.

Consider the case \(\beta _1\beta _2 = 0\). If \(\beta _1 = 0\), then ideal \(\sqrt{J'' + \langle \beta _1 \rangle }\) contains the polynomials

$$\begin{aligned} \gamma _1(\beta _2 + \beta _3), \quad \gamma _1\beta _3(\gamma _1 - \gamma _2 - \gamma _3). \end{aligned}$$
(52)

The case \(\gamma _1 = 0\) leads to \({{\widetilde{E}}}_{12} = 0_{3\times 3}\) and hence contradicts to the rank-two condition. Therefore we get

$$\begin{aligned} \alpha _1 = \alpha _2 = \beta _1 = \beta _2 + \beta _3 = \gamma _1 - \gamma _2 - \gamma _3 = 0. \end{aligned}$$
(53)

The triplet \(\{{{\widetilde{E}}}_{12}, {{\widetilde{E}}}_{23}, \widetilde{E}_{31}\}\) has the form (73) and is compatible by Lemma 4. Similarly we get compatible triplet (74) if \(\beta _2 = 0\).

Finally, let \(\beta _1\beta _2 \ne 0\). The case \(\gamma _1 + \gamma _2 + \gamma _3 = 0\) is impossible, since ideal \(\sqrt{J'' + \langle \gamma _1 + \gamma _2 + \gamma _3 \rangle }\) contains \(\beta _1\beta _2\beta _3 \ne 0\). Let us denote \(\delta = -1/(\gamma _1 + \gamma _2 + \gamma _3)\). Then it follows from (51) that

$$\begin{aligned} \begin{aligned} \gamma _1&= \delta \beta _1(\beta _1 + \beta _2 - \beta _3),\\ \gamma _2&= \delta \beta _2(\beta _1 + \beta _2 + \beta _3),\\ \gamma _3&= \delta \beta _3(-\beta _1 + \beta _2 + \beta _3). \end{aligned} \end{aligned}$$
(54)

The triplet \(\{{{\widetilde{E}}}_{12}, {{\widetilde{E}}}_{23}, \widetilde{E}_{31}\}\) has the form (75) and is compatible by Lemma 4.

Case III: \(\mu \ne 0\).

The ideal \(\sqrt{J}\) contains the following polynomials:

$$\begin{aligned} \mu \alpha _2\beta _3\gamma _1, \quad \mu \alpha _2\gamma _3, \quad \mu \alpha _2\beta _3\gamma _2. \end{aligned}$$
(55)

Since \(\mu \ne 0\), we have \(\alpha _2\gamma _3 = \beta _2\gamma _3 - \beta _3\gamma _2 = 0\).

First, supposing that \(\gamma _i \ne 0\) for a certain i gives \(\alpha _2\beta _3 = 0\). If \(\alpha _2 \ne 0\), then \(\beta _3 = \gamma _3 = 0\) and hence \({{\widetilde{E}}}_{31} = 0_{3\times 3}\) in contradiction with the rank-two condition. If \(\alpha _2 = 0\), then ideal \(\sqrt{J + \langle \alpha _2 \rangle }\) contains \(\alpha _1\beta _2\) and \(\alpha _1\gamma _2\). If \(\alpha _1 \ne 0\), then \({{\widetilde{E}}}_{23} = 0_{3\times 3}\) in contradiction with the rank-two condition. Continuing this way, one concludes that \(\beta _1 = \beta _2 = \beta _3 = 0\). The ideal \(\sqrt{J + \langle \alpha _1, \alpha _2, \beta _1, \beta _2, \beta _3 \rangle }\) contains \(\mu \gamma _1\gamma _2\gamma _3\). The condition \(\mu \ne 0\) implies that at least one \(\gamma _i = 0\) and so at least one essential matrix \({{\widetilde{E}}}_{ij}\) is a zero matrix. This contradicts to the rank-two condition.

Let \(\gamma _i = 0\) for all i. The ideal \(\sqrt{J + \langle \gamma _1, \gamma _2, \gamma _3 \rangle }\) contains \(\beta _3(\alpha _1\lambda + \beta _1\mu + \alpha _2)\). Since \(\beta _3 \ne 0\) (otherwise \({{\widetilde{E}}}_{31} = 0_{3\times 3}\)), we conclude that \(\alpha _1\lambda + \beta _1\mu + \alpha _2 = 0\). Denote \(J' = J + \langle \gamma _1, \gamma _2, \gamma _3, \alpha _1\lambda + \beta _1\mu + \alpha _2\rangle \) and define the polynomials

$$\begin{aligned} p_1&= \alpha _1 - \alpha _2,&\quad q_3&= \beta _3\lambda - \beta _1 + \beta _2,\nonumber \\ p_2&= \beta _1 - \beta _2 + \beta _3,&\quad r_1&= \mu (\alpha _1\mu - \beta _1\lambda - \beta _2 + \beta _3),\nonumber \\ p_3&= \alpha _1\mu - \beta _1(\lambda - 1),&\quad r_2&= \alpha _2\beta _3 + \beta _1\alpha _2 - \alpha _1\beta _2,\nonumber \\ q_1&= \alpha _2\mu - \beta _2(\lambda - 1),&\quad r_3&= \mu (\alpha _2(\alpha _1 + \alpha _2)\nonumber \\ q_2&= \beta _3\mu + \alpha _1 - \alpha _2,&\qquad + \beta _2(\beta _1 + \beta _2 - \beta _3)).\nonumber \\ \end{aligned}$$
(56)

Then, by the radical membership test, we get

$$\begin{aligned} \alpha _2\beta _3p_iq_jr_k \in \sqrt{J'} \end{aligned}$$
(57)

for all indices i, j, and k.

Suppose that \(\alpha _2\beta _3 = 0\). Since \(\beta _3 \ne 0\) (otherwise \({{\widetilde{E}}}_{31} = 0_{3\times 3}\)), we conclude that \(\alpha _2 = 0\). The ideal \(\sqrt{J' + \langle \alpha _2 \rangle }\) contains \(\alpha _1\beta _2\). Since \(\beta _2 \ne 0\) (otherwise \({{\widetilde{E}}}_{23} = 0_{3\times 3}\)), we have \(\alpha _1 = 0\). The ideal \(\sqrt{J' + \langle \alpha _1, \alpha _2 \rangle }\) contains \(\mu \beta _1\). Since \(\mu \ne 0\), we have \(\beta _1 = 0\) and thus \({{\widetilde{E}}}_{12} = 0_{3\times 3}\) in contradiction with the rank-two condition.

Let \(\alpha _2\beta _3 \ne 0\). Then it follows from (57) that

$$\begin{aligned} p_1q_1r_1 = 0. \end{aligned}$$
(58)

Each of the three cases \(p_1 = q_1 = 0\), \(p_1 = r_1 = 0\), and \(q_1 = r_1 = 0\) is impossible, since leads to \(\mu \alpha _2\beta _3 = 0\) in contradiction with \(\mu \ne 0\) and \(\alpha _2\beta _3 \ne 0\).

Assume that \(p_1 = 0\), \(q_1 \ne 0\), and \(r_1 \ne 0\). Then it follows from (57) that \(p_i = 0\) for all i. The triplet \(\{{{\widetilde{E}}}_{12}, {{\widetilde{E}}}_{23}, \widetilde{E}_{31}\}\) has the form (86) and is compatible by Lemma 5.

Let \(q_1 = 0\), \(p_1 \ne 0\), and \(r_1 \ne 0\). Then we have \(q_j = 0\) for all j. The triplet \(\{{{\widetilde{E}}}_{12}, {{\widetilde{E}}}_{23}, {{\widetilde{E}}}_{31}\}\) has the form (87) and is compatible by Lemma 5.

Finally, if \(r_1 = 0\), \(p_1 \ne 0\), and \(q_1 \ne 0\), then \(r_k = 0\) for all k. Taking into account that \(\mu \ne 0\), after some computation, we conclude that the triplet \(\{{{\widetilde{E}}}_{12}, {{\widetilde{E}}}_{23}, {{\widetilde{E}}}_{31}\}\) has the form (88) and is compatible by Lemma 5. We note that the denominator \(p_3 = \alpha _1\mu - \beta _1(\lambda - 1)\) in (89) does not vanish, since otherwise \(\sqrt{J' + \langle r_1, r_2, r_3, p_3 \rangle }\) contains \(\mu \alpha _2\beta _3 \ne 0\).

To summarize, we have shown that a triplet of real rank-two essential matrices \(\{{{\widetilde{E}}}_{12}, {{\widetilde{E}}}_{23}, {{\widetilde{E}}}_{31}\}\) that has the form (39) and fulfils Eqs. (26)–(30) is compatible. Formula (31) implies that the triplet \(\{E_{12}, E_{23}, E_{31}\}\) is compatible too as required. Theorem 5 is proved. \(\square \)

Remark 2

Although the 82 cubic equations from Theorem 5 are linearly independent, some of them may be algebraically dependent and therefore redundant for some applications. It is clear that if an ideal generated by a certain subset of Eqs. (26)–(30) equals the ideal J defined in the proof, then Theorem 5 remains valid for this subset. The equality of ideals is readily verified by computing their reduced Gröbner bases. In this way we found that Eq. (26) and the 27 equations of type (27) for indices \((i, j, k) \in \{(1, 3, 2), (3, 2, 1), (2, 1, 3)\}\) are redundant and may be omitted. Theorem 5 holds for the remaining 56 equations.

We also note that Eq. (29) only affects the compatibility of triplets with collinear epipoles, that is without Eq. (29) Theorem 5 remains valid for a triplet of real rank-two essential matrices with non-collinear epipoles.

4 Applications

Among the possible applications of Theorem 5 we outline the following two ones.

4.1 Incremental Structure from Motion

In incremental structure from motion a set of essential matrices arises from independently solved two-view relative pose estimation problems. Due to the noise in input data, scale ambiguity, and other factors, the estimated essential matrices are hardly compatible. Their rectification (averaging) is one of the possible approaches to overcome the incompatibility. In Kasten et al. (2019a), the authors proposed a novel solution to the essential matrix averaging problem based on their own algebraic characterization of compatible sets of essential matrices. Although the method from Kasten et al. (2019a) demonstrates good results outperforming the existing state-of-the-art solutions both in accuracy and in speed, it is not applicable to the practically important case of cameras with collinear centers.

Fig. 2
figure 2

Left: residuals \(\Vert {\mathcal {E}} - \hat{{\mathcal {E}}}_\Lambda \Vert \) at varying levels of Gaussian image noise. Here, \(\hat{\mathcal E}_\Lambda \) is the triplet of pairwise estimated essential matrices each of which is scaled with respective \(\lambda _{ij} \in \Lambda \), \({\mathcal {E}}\) is the averaged compatible triplet. Both triplets are normalized to the unit Frobenius norm. For each noise level, the box shows values from lower to upper quartile, the line inside indicates the median, the whiskers show data within \(1.5\times \) interquartile range, and the dots outside the whiskers are outliers. Right: average rotational and translational errors against Gaussian image noise. Each point on the diagram is a median of \(10^3\) trials. The absolute rotations \(R_i\) and translations \(t_i\), with \(R_1 = I\) and \(t_1 = 0_{3\times 1}\), are recovered from the compatible triplet \({\mathcal {E}}\). The rotational and translational errors are averaged over the 2nd and 3rd views

Full size image

The introduced polynomial constraints (26)–(30) can also be used to solve the rectification problem. In the simplest form it can be stated as follows: given a triplet of essential matrices \(\hat{{\mathcal {E}}} = \{{{\hat{E}}}_{12}, {{\hat{E}}}_{23}, {{\hat{E}}}_{31}\}\), find a compatible triplet \({\mathcal {E}}\) and scale factors \(\Lambda = \{\lambda _{12}, \lambda _{23}, \lambda _{31}\}\) so that \(\Vert \Lambda \Vert ^2 = 1\) and \({\mathcal {E}}\) is the closest to \(\hat{{\mathcal {E}}}_\Lambda = \{\lambda _{12}{{\hat{E}}}_{12}, \lambda _{23}{{\hat{E}}}_{23}, \lambda _{31}{{\hat{E}}}_{31}\}\) w.r.t. the Frobenius norm. Thus, we arrive at the following polynomial optimization problem:

$$\begin{aligned} \begin{aligned}&\min \limits _{\Lambda , {\mathcal {E}}}\, \Vert {\mathcal {E}} - \hat{{\mathcal {E}}}_\Lambda \Vert ^2\\&\text {subject to}\quad {\mathcal {E}} \in {\mathcal {V}}(J), \quad \Vert \Lambda \Vert ^2 = 1, \end{aligned} \end{aligned}$$
(59)

where J is the homogeneous ideal generated by all forms from (9), (26)–(30) and \({\mathcal {V}}(J)\) is the corresponding projective variety. Problem (59) can be further solved by using iterative methods for constrained optimization, e.g. sequential quadratic programming (SQP), augmented Lagrangian method, etc.

To confirm the proposed approach, we modeled a scene consisting of six points viewed by three fully calibrated cameras with collinear centers. The scene and camera configuration is detailed in the following table:

Distance to the scene

1

Scene depth

0.5

Baseline length

0.2

Image dimensions

\(752 \times 480\)

Field of view

\(60^{\circ }\)

Here, the baseline length is the distance between the first and third camera centers. The second camera center varies randomly around the baseline middle point with an amplitude of 0.02. To each image we added a zero-mean Gaussian noise of standard deviation varying from 0 to 1 pixels.

First, the standard 5-point algorithm (Stewénius et al. 2006) was applied to each image pair to estimate the triplet of essential matrices \(\hat{{\mathcal {E}}}\). The sixth point was used to resolve the multiplicity. Each essential matrix from \(\hat{{\mathcal {E}}}\) was normalized to the unit Frobenius norm. Then, problem (59) was solved by the SQP resulting in a compatible triplet \({\mathcal {E}}\) and a set of scale factors \(\Lambda = \{\lambda _{ij}\}\). The results for \(10^3\) trials per each noise level are shown in Fig. 2. Note that the estimated essential matrices for the noise-free case are guaranteed to have collinear epipoles as they differ from the ground truth only by scales. As it can be seen, the algorithm handles the collinear case without a modification.

4.2 Three-View Auto-Calibration

Let \(\{F_{12}, F_{23}, F_{31}\}\) be a compatible triplet of fundamental matrices and \(K_i\) be the calibration matrix of the ith camera. Then we can write \(\lambda _i \lambda _j E_{ij} = K_i^\top F_{ij} K_j\) for certain scalars \(\lambda _1\), \(\lambda _2\), and \(\lambda _3\), cf. (7). Substituting this into Eqs. (26)–(30), we get by a straightforward computation the following equations:

$$\begin{aligned}&{{\,\mathrm{tr}\,}}(C_1F_{12}C_2F_{23}C_3F_{31}) = 0, \end{aligned}$$
(60)
$$\begin{aligned}&F_{ij}^\top C_i F_{ij} C_j F_{jk} - \frac{1}{2} {{\,\mathrm{tr}\,}}(C_j F_{ij}^\top C_i F_{ij})\, F_{jk}\qquad \nonumber \\&\quad + C_j^*\, F_{ij}^* F_{ki}^\top = 0_{3\times 3}, \end{aligned}$$
(61)
$$\begin{aligned}&C_kF_{jk}^\top F_{ij}^* + F_{jk}^* F_{ij}^\top C_i + (F_{ij} C_j F_{jk}) \diamond F_{ki}^\top = 0_{3\times 3}, \end{aligned}$$
(62)
$$\begin{aligned}&{{\,\mathrm{tr}\,}}^3((CF)^2) - 12{{\,\mathrm{tr}\,}}((CF)^2){{\,\mathrm{tr}\,}}((CF)^4)\qquad \nonumber \\&\quad + 32{{\,\mathrm{tr}\,}}((CF)^6) = 0, \end{aligned}$$
(63)

where \(C_i = \lambda _i(\det K_i)^{-1}(K_iK_i^\top )\), \(C = {{\,\mathrm{diag}\,}}(C_1, C_2, C_3)\), and F is the symmetric \(9\times 9\) matrix constructed from \(F_{12}\), \(F_{23}\), and \(F_{31}\) similarly as in formula (14). It is clear that \(K_iK_i^\top = C_i/(C_i)_{33}\) and therefore the calibration matrix can be estimated from \(C_i\) by the Cholesky factorization.

Given \(F_{12}\), \(F_{23}\), and \(F_{31}\), only matrices \(C_i\) are constrained by Eqs. (60)–(63) and hence these equations can be used to solve the camera auto-calibration problem in three and more views. We note that Eq. (63) is sextic, Eq. (60) is cubic, Eq. (61) is quadratic, and Eq. (62) is linear in the entries of matrix C. The auto-calibration constraint corresponding to Eq. (29) is of degree 10 in the entries of C. We do not write it here.

5 Discussion

In this paper we propose new necessary and sufficient conditions on the compatibility of three real rank-two essential matrices (Theorems 4 and 5 ). By compatibility we mean the correspondence of the essential matrices to a certain configuration of three calibrated cameras. The conditions have form of 82 cubic, one quartic, and one sextic homogeneous polynomial equations. We would like to emphasize that (i) these equations relate to the calibrated case only and in general do not hold for compatible triplets of fundamental matrices; (ii) the sufficiency of the equations covers the case of cameras with collinear centers.

The possible applications of the constraints may include multiview relative pose estimation, essential matrix averaging for incremental structure from motion, multiview auto-calibration, etc. Regarding the auto-calibration, it is worth mentioning that some of our equations [Eq. (62)] turn out to be linear in the entries of matrix incorporating the calibration parameters. This unexpected result could be useful in developing novel auto-calibration solutions.