1 Introduction

Understanding the contact behavior of elastic body with finite thickness is of crucial interest in the fields of mechanical engineering and material science. For example, a large number of experiment studies have demonstrated that the thickness of elastic layer can significantly affect the mechanical and tribological properties in rigid substrate [1,2,3,4]. On the other hand, it also leads to an adjustment in adhesion by design if the thickness of the elastic layer is well chosen [5, 6].

As a fundamental and one of the most important issues in contact mechanics, how thickness affects the dependence of relative contact area \(a_{{\mathrm{r}}}\) on pressure p has been discussed in depth and made great progress in the last decades [7,8,9]. For contact problems of elastic half-space, many advanced simulation studies reported that the relative contact area \(a_{{\mathrm{r}}}\) increases linearly with pressure p from very small but non-zero \(a_{{\mathrm{r}}}\) up to \(a_{{\mathrm{r}}} \approx 0.1\) in randomly rough surface contact simulations [10,11,12,13,14]. This linearity can be rationalized with Persson theory, which, not only predicts the area–pressure relation reasonably well [15, 16], but also finds a highly accurate pressure-dependence of the interfacial stiffness along with accurate distribution functions of the interfacial separation and correct spatial stress correlations [17, 18].

It has also been noticed that the linearity not only holds in randomly rough surfaces but also in periodic repeated indenter with harmonic height profiles [19,20,21]. Unfortunately, the linearity breaks down when the thickness of the elastic layer is reduced from infinity to a finite value [7]. To solve this type of problem, especially in Hertzian contact model, the semi-analytical methods [8, 22] as well as the Green’s function method [9] were proposed in some studies and successfully managed to find a stable solution. However, considering that most of the indenters in practice are not of the Hertzian profile, more general indenters, such as the periodic repeated indenter with harmonic height profiles and randomly rough surfaces should be investigated.

Green’s function molecular dynamics (GFMD) is a boundary element method that allows us to address the linear elastic response of solids to boundary conditions [23, 24]. Considerable studies have demonstrated that it is an efficient and reliable technique to study those contact problems of isotropic elastic bodies with infinite or finite thickness [25,26,27]. On the other hand, the fast inertial relaxation engine (FIRE), which has been demonstrated several times to be an efficient optimization method in both particle based simulations and boundary value problems, can also be applied in this study to speedup the GFMD simulations, details of the procedure have been discussed elsewhere [28, 29]. In light of these facts, it is reasonable to expect that the optimized GFMD technique can contribute to determining the thickness effect of elastic body on the relation between contact area and pressure.

The main intention of this study is to identify the thickness effects on the area–pressure relation for smooth indenter with harmonic height profiles and randomly rough surfaces. Towards this end, the dependence of prefactor \(\kappa\) on the reduced thickness \({\tilde{d}} \equiv d/a_{{\mathrm{r}}}\) and Poisson ratio \(\nu\) will be addressed in the framework of GFMD and the asymptotic behavior for small \({\tilde{d}}\) will be discussed in detail. For randomly rough surface contacts, the effects of Hurst exponent H on the area–pressure relation will be addressed.

In the remaining part of this paper, the model and method are described in Sect. 2. Numerical results are presented in Sect. 3 and conclusions are drawn in the final Sect. 4.

2 Model and Method

In this study, we restrict our attention on the (1 + 1) dimensional elastic contact problems as the computational cost is much less than (2 + 1) dimensional contact simulations. On the other hand, the results obtained from (1 + 1) dimensional contact simulations still remain meaningful to practice, because they can give a true picture of those contact problems with strong anisotropic indenters such as the polished and scratched surfaces.

The elastic body is assumed to be homogeneous, isotropic elastic body so that the Hooke’s law can be applied. The thickness of the elastic body d can be either finite or infinite in the framework of GFMD and is considered as finite value in this study if not mentioned explicitly. The bottom of the elastic layer is fixed in space and the top is placed such that the normal displacement u(x) equals to zero as long as no external forces acting on the body.

Fig. 1
figure 1

Schematic figure of the elastic body with finite thickness d and the rigid indenter with a harmonic height profile and b randomly rough surface. Normal pressure p is acting on the rigid indenter, the elastic body is confined on the rigid substrate, so that the displacement of the bottom layer is fixed to zero

Full size image

The rigid indenter is modeled as either harmonic height profile or randomly rough surface. As shown in Fig. 1a, the harmonic height profile of the indenter is given by

$$\begin{aligned} h(x) = \left( \frac{R_{{\mathrm{c}}}}{n}\right) \left( \frac{x}{R_{{\mathrm{c}}}}\right) ^n, \end{aligned},$$
(1)

where \(n>0\), \(R_{{\mathrm{c}}}\) denotes the variable of unit length and x the in-plane distance from a point to the center of the indenter. The value of n used in this study are restricted to \(n = 1.5\) (sharp indenter), \(n = 2\) (Hertzian geometry) and \(n = 4\) (blunt indenter).

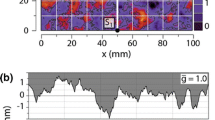
As to the randomly rough surface, which sketched in Fig. 1b, the height profile h(x) is generated by assuming the random-phase approximation for the associated Fourier transform \({\hat{h}}(q)\), that is, \({\hat{h}}(q) \propto \sqrt{C(q)}\exp (i2\pi \xi _q)\), where \(\xi _q\) is a (pseudo) random number generator, which produces random numbers uniformly distributed between [0, 1], q denotes the wave number. The proportional factor is chosen so that the root mean square height gradient equals to unity. The power spectrum C(q) applied in this study reads

$$\begin{aligned} C(q) = \frac{C_0 {\Theta }(q_{{\mathrm{s}}} - q)}{[1+(q/q_{{\mathrm{r}}})^2]^{0.5+H}}, \end{aligned}$$
(2)

where H is the Hurst exponent and \(\Theta (\bullet )\) the Heaviside step function. \(q_{{\mathrm{r}}} = 2\pi /\lambda _{{\mathrm{r}}}\) and \(q_{{\mathrm{s}}} = 2\pi /\lambda _{{\mathrm{s}}}\) represent the wave numbers associated with the roll-off wavelength \(\lambda _{{\mathrm{r}}}\) and short wavelength \(\lambda _{{\mathrm{s}}}\), respectively. The default surface used in this study is defined as follows: the thermodynamic limit \(\varepsilon _{{\mathrm{t}}} = \lambda _{{\mathrm{r}}}/L\) is fixed to 1/8 as it has been demonstrated that any \(\varepsilon _{{\mathrm{t}}} \le 1/4\) can provide an acceptable probability density of heights for randomly rough surfaces [30], where L denotes the length of the elastic body and is set to be unity throughout this study. The continuum limit \(\varepsilon _{{\mathrm{c}}} = \varDelta a / \lambda _{{\mathrm{s}}}\) is chosen to be 1/64 to guarantee the achievement of numerical convergence, where \(\varDelta a\) denotes the discretization. The fractal limit \(\varepsilon _{{\mathrm{f}}} = \lambda _{{\mathrm{s}}}/\lambda _{{\mathrm{r}}}\) is set to be 1/512 so that small roughness is considered.

The hard-wall constraint, which is the oldest and most commonly used model, is applied here to describe the interaction between the indenter and the elastic layer. This can be stated as a non-holonomic boundary condition, namely,

$$\begin{aligned} g(x) = h(x) - u(x) \ge 0, \end{aligned},$$
(3)

where g(x) denotes the gap at the interface of indenter and elastic layer. The contact area therefore is defined by \(a_{{\mathrm{r}}} = N^{g(x)=0}_x/N^{\mathrm{total}}_x\), where \(N^{g(x)=0}_x\) represents the number of discretization with \(g(x) = 0\) and \(N^{\mathrm{total}}_x\) the total number of discretization. The displacement u(x) as well as the normal stress \(\sigma (x)\) are not only expressed in real space, but also in Fourier space. Hence the following convention for the Fourier transform should be applied.

$$\begin{aligned} {\hat{f}}(q)&= \frac{1}{L} \sum _x f(x) \exp (iqx), \\ f(x)&= \sum _q {\hat{f}}(q) \exp (-iqx). \end{aligned}$$

The elastic energy of the layer with finite thickness can be formulated in Fourier space as below simply by following the work proposed by Carbone et al. [31],

$$\begin{aligned} V_{\mathrm{ela}}&= \sum _q \frac{qE^*}{4} |{\hat{u}}(q) |^2 \nonumber \\&\quad \times \frac{(3-4\nu )\cos h (2qd) + 2(qd)^2 - 4\nu (3-2\nu ) + 5}{(3-4\nu )\sin h (2qd) - 2qd}, \end{aligned}$$
(4)

where \(E^* = E/(1-\nu ^2)\) denotes the contact modulus of the elastic layer, E represents elastic modulus and \(\nu\) the Poisson ratio.

Throughout this study, the contact model mentioned above will be solved numerically using the Green’s function molecular dynamics simulations so that the Newton’s equation of motion for the displacement can be solved by locating the local minimum of the total potential energy. The central idea and corresponding equilibrium condition can be revisited in many related studies  [20, 23, 32,33,34]. A slightly modification in this study is that the damping term is replaced by the FIRE optimizer so that the minimum potential can be located quickly.

3 Numerical Results

For contacts of elastic half-space and periodic repeated indenter with harmonic height profile, the area–pressure relation can be given by

$$\begin{aligned} a_{{\mathrm{r}}} = \kappa _{\infty } p^*, \end{aligned},$$
(5)

where the reduced pressure \(p^* \equiv p/(E^*{{\bar{g}}}_c)\) assumes to be small compared to unity. To discriminate the contacts of elastic half-space from the elastic layer with finite thickness, the subscript notation “d” will be used in this study to indicate the finite thickness case and the subscript notation “\(\infty\)” the elastic half-space case. As a result, \(\kappa _{\infty }\) represents the proportionality coefficient when the thickness of elastic body is infinity large.

For (2 + 1) dimensional elastic contacts, the expression of \(\kappa\) is given by Müser [19]. In the case of (1 + 1) dimensional elastic contacts, a similar expression for the proportionality coefficient can be obtained by following the spirit of the calculations presented in previous studies [19, 35], the result reads,

$$\begin{aligned} \kappa _{\infty } = \sqrt{\frac{16}{\pi (2n-1)}}\frac{\varGamma (\frac{n}{2} + 1)}{\varGamma (\frac{n}{2} + \frac{1}{2})}, \end{aligned},$$
(6)

where \(\varGamma (\bullet )\) denotes the gamma function. When \(n = 2\), \(\kappa _{\infty } = 8/(\sqrt{3}\pi ) \approx 1.47\), which has been reported by Dokkum et al. [20].

However, when the elastic half-space is replaced by elastic layer with finite thickness, especially the value of thickness d is relatively small, the linearity of the area–pressure relation cannot hold anymore and the thickness d as well as the Poisson ratio \(\nu\) start to dominate the area–pressure relation.

According to previous studies on contact mechanics of elastic layer with finite thickness [8, 9, 22], the central quantities that matter the asymptotic behavior of small thickness should be the reduced thickness \({\tilde{d}} = d / a_{{\mathrm{r}}}\) and Poisson ratio \(\nu\). In this case, we expect that the area–pressure relation can still be described by Eq. (5), while the coefficient should be replaced by \(\kappa _{{\mathrm{d}}}\) and should be fully determined by the reduced thickness \({\tilde{d}}\) and the Poisson ratio \(\nu\) for a given indenter geometry.

Fig. 2
figure 2

Reduced coefficient \({\tilde{\kappa }}_{{\mathrm{d}}} / {\tilde{d}}\) as a function of the reduced thickness \({\tilde{d}}\) for different Poisson ratio \(\nu\) in the case of Hertzian geometry. Symbols represent the GFMD simulation results and the solid lines in the same color as the symbols indicate the asymptotic limits obtained from Eq. (9)

Full size image

Considering that the proportionality coefficient \(\kappa _{\infty }\) is only a constant for a given indenter geometry, the reduced coefficient \({\tilde{\kappa }} \equiv \kappa _{{\mathrm{d}}} / \kappa _{\infty }\) should yield

$$\begin{aligned} {\tilde{\kappa }}_{{\mathrm{d}}} = {\tilde{\kappa }}_{{\mathrm{d}}}({\tilde{d}}, \nu ). \end{aligned}$$
(7)

In the case of Hertzian contacts, the asymptotic behavior of area–pressure relation when the reduced thickness \({\tilde{d}} \ll 1\) can be given by [8]

$$\begin{aligned} \frac{4R_{{\mathrm{c}}}p}{E^*a_{{\mathrm{r}}}^2} = \frac{1}{3} \frac{a_{{\mathrm{r}}}}{d} \frac{(1-\nu )^2}{1-2\nu }. \end{aligned}$$
(8)

Furthermore, the root mean square gradient height determined over the actual contact area in Hertzian geometry reads \({{\bar{g}}}_{{\mathrm{c}}} = a_{{\mathrm{r}}}/(2\sqrt{3}R_{{\mathrm{c}}})\). It gives

$$\begin{aligned} {\tilde{\kappa }}_{{\mathrm{d}}} = \alpha \frac{1-2\nu }{(1-\nu )^2} {\tilde{d}}, \end{aligned}$$
(9)

where \(\alpha\) is a dimensionless prefactor that only depends on the height profile of rigid indenter. For Hertzian geometry, it equals to \(3\pi /4 \simeq 2.36\).

Results are shown in Fig. 2, for which we chose \(N_x^{\mathrm{total}} = 2^{18}\) and \(p/(E^*R_{{\mathrm{c}}}) = 2 \times 10^{-3}\) while \(E^*\) and \(R_{{\mathrm{c}}}\) are fixed to unity. It reveals that the reduced coefficient \({\tilde{\kappa }}_{{\mathrm{d}}}\) changes quite noticeably with decreasing reduced thickness \({\tilde{d}}\) for different Poisson ratio, while it essentially plateaus at small \({\tilde{d}}\). A qualitative difference at small \({\tilde{d}}\) between different Poisson ratio would be realized and the difference can be rationalized by Eq. (9).

Fig. 3
figure 3

Same as Fig. 2, however, this time for sharp indenter with \(n = 1.5\)

Full size image
Fig. 4
figure 4

Same as Fig. 2, however, this time for blunt indenter with \(n = 4.0\)

Full size image

If the Hertzian indenter is replaced by a sharp (\(n=1.5\)) or blunt (\(n=4.0\)) geometry, we get similar results. As shown in Figs. 3 and 4, for both sharp and blunt indenter, the reduced coefficient \({\tilde{\kappa }}_{{\mathrm{d}}}\) converges to unity for large \({\tilde{d}}\), which corresponds to the solution of elastic half-space. On the other hand, the asymptotic behavior at small \({\tilde{d}}\) can also be well rationalized by Eq. (9), as long as the prefactor \(\alpha\) be replaced by 2.20 for sharp geometry and 2.94 for blunt case.

Based on this fact, it is reasonable to expect that for all single asperity contacts, the linearity between \({\tilde{\kappa }}_{{\mathrm{d}}}\) and \({\tilde{d}}\) in the limit of small \({\tilde{d}}\) holds as long as the Poisson ratio \(\nu\) is given and not equals to 0.5. This motivates us to investigate the contact between elastic body of finite thickness and randomly rough surface. Basically, in the case of elastic layer with finite thickness confined on a rigid substrate, the small value of thickness leads to large value of contact stiffness [36, 37]. As a result, for a given external load p, the thinner elastic layer leads to a smaller contact area \(a_{{\mathrm{r}}}\), and if the thickness is small enough, the single asperity contact should be realized essentially. In this case, considering that the area–pressure relation of single asperity contacts at small \({\tilde{d}}\) can be well rationalized by Eq. (9), by adjusting the prefactor \(\alpha\) accordingly, the relation should also work for randomly rough surface contacts.

Fig. 5
figure 5

The reduced coefficient \({\tilde{\kappa }}_{{\mathrm{d}}} / {\tilde{d}}\) as a function of reduced thickness \({\tilde{d}}\) with varying Hurst exponent H and Poisson ratio \(\nu\). Symbols represent the GFMD results, solid lines in the same color as the symbols indicate the asymptotic limits, and the dashed lines are drawn to guide the eye. The parameters used to determine the randomly rough surface are presented in Sect. 2 and the applied pressure is fixed as \(p \equiv 0.01 E^*{\bar{g}}\), where \({\bar{g}}\) is the root mean square gradient height of the randomly rough surface and is set to be unity

Full size image

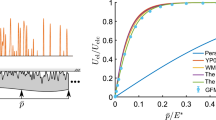
Figure 5 shows the results of the ratio \({\tilde{\kappa }}_{{\mathrm{d}}} / {\tilde{d}}\) versus the reduced thickness \({\tilde{d}}\). All GFMD data points are averaged over more than 32 different realizations, so that the random nature of the roughness can be captured. This figure confirms that for large \({\tilde{d}}\), simulations results of \({\tilde{\kappa }}_{{\mathrm{d}}} / {\tilde{d}}\) with different Hurst exponent and different Poisson ratio converge to a single curve \(1 / {\tilde{d}}\), which means that \(\kappa _{{\mathrm{d}}} = \kappa _{\infty } \simeq 1.75\) [20]. This limit is nothing but the elastic contacts between randomly rough surface and the half-space, which has been discussed many times. The interesting part is located in the limit case where \({\tilde{d}}\) fairly small. In this limit, different Poisson ratio \(\nu\) leads to different \({\tilde{\kappa }}_{{\mathrm{d}}} / {\tilde{d}}\), while for a given Poisson ratio, the curves for different H converge to an identical limit, which is identical to the results of Eq. (9) with \(\alpha \simeq 2\pi /3\).

The data between these two limits should also be noticed. As shown in Fig. 5, with decreasing of the reduced thickness \({\tilde{d}}\), the Hurst exponent H and Poisson ratio \(\nu\) starts to play an important role on \({\tilde{\kappa }}_{{\mathrm{d}}} / {\tilde{d}}\). Hence the deviation of \({\tilde{\kappa }}_{{\mathrm{d}}} / {\tilde{d}}\) with different H and \(\nu\) are observed. For a given Poisson ratio, small H leads to large \({\tilde{\kappa }}_{{\mathrm{d}}}\) at the beginning, and the deviation increases with the decreasing of \({\tilde{d}}\). However, as \({\tilde{d}}\) even smaller, the deviation of \({\tilde{\kappa }}_{{\mathrm{d}}} / {\tilde{d}}\) eventually decreases and finally the curves converge to a constant which can be fully determined by Poisson ratio.

The reason for this trend can be potentially linked to the distribution of contact patch areas and the characteristic contact patch size \(A_{{\mathrm{c}}}\), which we define to be the expected patch size that a randomly picked contact point belongs to. As mentioned in previous studies, for \(H < 0.5\), the characteristic contact areas are fairly small, so that large contact patches are not possible, In contrast, for \(H > 0.5\), typically for \(H = 0.8\), large contact patches can be realized easily for a small pressure [21, 38]. Therefore, large value of \({\tilde{\kappa }}_{{\mathrm{d}}} / {\tilde{d}}\) for small H can be observed at medium reduced thickness \({\tilde{d}}\). As reduced thickness decreases smaller and smaller, considering that the bottom of elastic layer is fixed in space, the effect of applied load on the stress and contact area is fully confined in a fairly small range of the same order of d and therefore cannot have any effect to neighbor patches. In this case, the effect of Hurst exponent on \({\tilde{\kappa }}_{{\mathrm{d}}} / {\tilde{d}}\) is attenuated and finally eliminated.

4 Conclusions

For elastic contacts of either smooth indenter with harmonic height profiles or randomly rough surfaces, the relative contact area \(a_{{\mathrm{r}}}\) depends linearly on reduced pressure \(p^*\) if the thickness of the elastic body is infinitely large, and the root mean square gradient height is evaluated over the actual contact area. Hence the linearity coefficient \(\kappa _{\infty } \equiv a_{{\mathrm{r}}} / p^*\) can be realized.

In this study, using Green’s function molecular dynamics simulations, we shown that for contacts of elastic layer with finite thickness, the linearity between relative contact area \(a_{{\mathrm{r}}}\) and reduced pressure \(p^*\) cannot hold anymore. Instead, for a given indenter, the reduced coefficient \({\tilde{\kappa }}_{{\mathrm{d}}} \equiv \kappa _{{\mathrm{d}}} / \kappa _{\infty }\) depends strongly on the reduced thickness \({\tilde{d}}\) and the Poisson ratio.

For a given Poisson ratio \(\nu \ne 0.5\), because the dependence of \({\tilde{\kappa }}_{{\mathrm{d}}}\) on reduced thickness \({\tilde{d}}\) exhibits strong nonlinearity, it is difficult to determine the analytical expression to describe the area–pressure relation, especially for randomly rough surface contacts. Nevertheless, the limit case for both large and small \({\tilde{d}}\) still can be addressed. For large limit of \({\tilde{d}}\), the area–pressure relation is reduced to the solution of contacts between elastic half-space and rigid indenter. While for the small limit of \({\tilde{d}}\), the linearity between the reduced coefficient \({\tilde{\kappa }}_{{\mathrm{d}}}\) and the reduced \({\tilde{d}}\) is obtained, which is given in Eq. (9). This linearity not only holds for Hertzian contacts, but also for any smooth indenter with harmonic height profiles and randomly rough surfaces. It also should be noticed that for randomly rough contacts, in the limit of small \({\tilde{d}}\), the effect of Hurst exponent eventually died out as long as the root mean square gradient height is evaluated over the actual contact area, so that the linearity between \({\tilde{\kappa }}_{{\mathrm{d}}}\) and \({\tilde{d}}\) only depends on the Poisson ratio and the prefactor \(\alpha\).