1 Introduction

Generalised Reynolds equations are largely used to determine elastohydrodynamic film thickness for shear-thinning lubricants [1, 2]. Very often, the rheological behaviour of the lubricants is properly described by the Carreau model [3], which is formulated in Eq. (1)

$$\eta = \mu \left( {1 + \left( {\frac{{\mu \dot{\gamma }}}{G}} \right)^{2} } \right)^{{\frac{{\left( {n - 1} \right)}}{2}}}$$
(1)

When dealing with generalised Reynolds equations for non-Newtonian fluids, a modified version is frequently used, with τ being the independent variable. Bair [4, 5] proposed Eq. (2), valid for 0.2 < n<1, which is therefore applicable to most non-Newtonian fluids that follow the Carreau model

$$\eta = \mu \left( {1 + \left( {\frac{\tau }{G}} \right)^{2} } \right)^{{\frac{{\left( {1 - \left(1/n\right)} \right)}}{2}}}$$
(2)

where low-shear viscosity is assumed to vary exponentially with pressure and temperature [6], according to Eq. (3)

$$\mu = \mu_{0} {\text{e}}^{{\left( {\alpha p - \beta \left( {T - T_{0} } \right)} \right)}}$$
(3)

The Carreau equation incorporates the variation in the viscosity–temperature and the viscosity–pressure coefficients under shear-thinning conditions.

De la Guerra et al. [7] presented a new analytical form (4) of the one-dimensional Reynolds equation for lubricants whose rheological behaviour fits the modified Carreau model proposed by Bair

$$\begin{aligned} Q & = u_{1} h - \frac{{G^{(n-1)/n} n\left( {G^{2} + \left( {\tau_{m} - \frac{\partial p}{\partial x}\frac{h}{2}} \right)^{2} } \right)^{{\frac{1 + n}{2n}}} h}}{{\left( {1 + n} \right)\mu \frac{\partial p}{\partial x}}} \\ & \quad + \frac{{nG^{2} \left( {\tau_{m} + \frac{\partial p}{\partial x}\frac{h}{2}} \right)}}{{\left( {1 + n} \right)\mu \left( {\frac{\partial p}{\partial x}} \right)^{2} }}{\text{hypergeom}}\left( {\left[ {\frac{1}{2},\quad - \frac{1 + n}{2n}} \right],\quad \left[ {\frac{3}{2}} \right], - \frac{{\left( {\tau_{m} + \frac{\partial p}{\partial x}\frac{h}{2}} \right)^{2} }}{{G^{2} }}} \right) \\ & \quad - \frac{{nG^{2} \left( {\tau_{m} - \frac{\partial p}{\partial x}\frac{h}{2}} \right)}}{{\left( {1 + n} \right)\mu \left( {\frac{\partial p}{\partial x}} \right)^{2} }}{\text{hypergeom}}\left( {\left[ {\frac{1}{2},\quad - \frac{1 + n}{2n}} \right],\quad \left[ {\frac{3}{2}} \right],\quad - \frac{{\left( {\tau_{m} - \frac{\partial p}{\partial x}\frac{h}{2}} \right)^{2} }}{{G^{2} }}} \right) \\ \end{aligned}$$
(4)

where hypergeom denotes the Gauss hypergeometric function. Equation (4) is a function of τ m (the value of the shear stress at the lubricant mid-plane), which is calculated with Eq. (5)

$$\frac{{\left( {u_{2} - u_{1} } \right)\mu \frac{\partial p}{\partial x}\left( {1 + n} \right)}}{{G^{{1 - \left(1/n\right)}} n}} = \left( {G^{2} + \tau_{m}^{2} + \tau_{m} h\frac{\partial p}{\partial x} + \frac{1}{4}\left( {h\frac{\partial p}{\partial x}} \right)^{2} } \right)^{{\frac{1 + n}{2n}}} - \left( {G^{2} + \tau_{m}^{2} - \tau_{m} h\frac{\partial p}{\partial x} + \frac{1}{4}\left( {h\frac{\partial p}{\partial x}} \right)^{2} } \right)^{{\frac{1 + n}{2n}}}$$
(5)

Other forms of Reynolds–Carreau equations have also been developed for line contacts [6, 8]. The formulation proposed by Bair [8] is based on numerical adjustment of the equations for flow-rate and mid-plane shear stress through simulations under different operating conditions. Unlike the approximate expression attained in that way, the new Reynolds–Carreau equation [7] was obtained in a general manner by adding the shear-thinning influence to a procedure similar to that used for deducing the classic Reynolds equation.

All these approaches greatly simplify the solving process. The use of Grubin-style calculations [9] has shown to provide quick and reasonably accurate results of the shear-thinned central film thickness under isothermal conditions [8, 10]. In contrast, the use of full EHL solving methods involves a very high computational cost.

On the other hand, bearing in mind a practical use of the film thickness results, several formulae have been deducted from a regression using data from full EHL calculations. By the way of example, Anuradha and Kumar developed accurate expressions for the central film thickness [2, 10] shown in Eqs. (6–9), which are used as reference values in the present article

$$\frac{{h_{0} }}{R} = 1.904093\overline{U}^{0.696} \overline{G}^{0.562} \overline{W}^{ - 0.144} \overline{R} \overline{S}$$
(6)

where

$$\overline{U} = \frac{{\mu_{0} u_{m} }}{E'R};\quad \overline{G} = \alpha E^{\prime } ;\quad \overline{W} = \frac{W}{{E^{\prime } R}}$$
(7)
$$\overline{R} = \left( {1 + 0.122459\frac{{\overline{U}^{0.453} \overline{W}^{0.27} }}{{\overline{G}^{0.22} \left( {G/E^{\prime } } \right)^{1.288} }}} \right)^{{ - 1.2\left( {1 - n} \right)^{1.44} }}$$
(8)
$$\overline{S} = \left( {1 + 1.08\frac{{\varSigma^{2.22} \overline{U}^{0.047} \overline{W}^{ - 0.03} }}{{\overline{G}^{0.176} \left( {G/E^{\prime } } \right)^{0.11} }}} \right)^{{ - 1.3\left( {1 - n} \right)^{1.6} }}$$
(9)

Another remarkable approach based on numerical EHL calculations and the ensuing regression analysis is the shear-thinning parameter κ proposed by Bair [6] and shown in Eq. (10), which divides the Newtonian central film thickness to obtain the corresponding value under shear-thinning conditions

$$\kappa = \left[ {1 + 0.79\left( {\left( {1 + \varSigma } \right)\frac{{u_{m} \mu_{0} }}{{h_{\text{N}} G}}} \right)^{{\frac{1}{1 + 0.2\varSigma }}} } \right]^{{3.6(1 - n)^{1.7} }}$$
(10)

In addition, the heat generated in the contact can cause a local rise in the lubricant temperature, especially for high slide-to-roll ratios (SRRs), leading to a reduction in film thickness. Based on Cheng, Gupta and other authors, Hamrock proposed a correction factor (11) that can be applied to the isothermal film thickness to take into account the thermal effects [11, 12]

$$\varphi_{\text{T}} = \frac{{1 - 13.2\left( {p_{0} /E^{{\prime }} } \right)L_{\text{T}}^{0.42} }}{{1 + 0.213\left[ {1 + 2.23\left( {\frac{{\Delta u}}{{u_{m} }}} \right)^{0.83} } \right]L_{\text{T}}^{0.64} }};\quad {\text{where}}\quad L_{\text{T}} = \frac{{\beta \mu_{0} u_{m}^{2} }}{{k_{\text{l}} }}$$
(11)

More recently, Anuradha and Kumar [13] analysed several cases and reported a significant influence not only of shear-thinning but also of thermal effects on film thickness.

Besides the existing predictions for thermal film thickness based on simple formulae, the thermal influence is frequently considered by means of the energy equation [14], solved together with generalised Reynolds equations. This involves an additional increase in the computational cost. The general expression for the energy equation in line contact is as follows [14]

$$\frac{\partial }{\partial x}\left( {k_{\text{l}} \frac{\partial T}{\partial x}} \right) + \frac{\partial }{\partial z}\left( {k_{\text{l}} \frac{\partial T}{\partial z}} \right) + \varepsilon Tu\frac{\partial p}{\partial x} + \eta \left( {\frac{\partial u}{\partial z}} \right)^{2} = \rho_{\text{l}} c_{\text{l}} u\frac{\partial T}{\partial x}$$
(12)

The thermal balance for each contacting body i (i = 1,2) is given by Eq. (13),

$$\frac{{\partial^{2} T_{1,2} }}{{\partial x^{2} }} + \frac{{\partial^{2} T_{1,2} }}{{\partial z^{2} }} = \frac{{\rho_{\text{b}} c_{\text{b}} }}{{k_{\text{b}} }}u_{1,2} \frac{{\partial T_{1,2} }}{\partial x}$$
(13)

The following assumptions are frequently made:

  • Couette flow, with a negligible Poiseuille component [6].

  • All heat generated by fluid shear (none by compression) [15].

  • Absence of heat conduction in the x-direction within the lubricant film and the contacting bodies [16, 17].

  • Thermal properties of the lubricant and contacting bodies constant with temperature [18].

Thus, Eqs. (12) and (13) are simplified as follows

$$k_{\text{l}} \frac{{\partial^{2} T}}{{\partial z^{2} }} + \eta \left( {\frac{\partial u}{\partial z}} \right)^{2} = \rho_{\text{l}} c_{\text{l}} u\frac{\partial T}{\partial x}$$
(14)
$$\frac{{\partial^{2} T_{1,2} }}{{\partial z^{2} }} = \frac{{\rho_{\text{b}} c_{\text{b}} }}{{k_{\text{b}} }}u_{1,2} \frac{{\partial T_{1,2} }}{\partial x}$$
(15)

In this article, central film thickness and temperature distribution are calculated by adding thermal considerations to the Reynolds–Carreau equations proposed in references [8, 10] for line contacts.

It is generally accepted that the central film thickness is essentially determined by the fluid dynamics of the inlet zone, irrespective of the lubricant behaviour within the Hertz region [6, 14]. This characteristic greatly simplifies the solving process when compared with full thermal EHL simulations thanks to the Grubin inlet zone approximation for solving the Reynolds–Carreau equation, subsequently only requiring the need to solve the energy equation in the inlet zone.

Taking into account the results obtained, the new approach allows for a new formula to be developed to predict film thickness considering both shear-thinning and thermal effects. The new equation attempts to provide fast and reliable film thickness results by means of easy-to-use factors.

2 Calculating Film Thickness and Temperature Distribution

Reference [10] discloses the calculation of the isothermal film thickness, i.e. the equations involved, their discretization and the solving method. Hereby we aim to use an analogous process for calculating thermal film thickness. Consequently, a similar grid is selected in the flow direction x, from x = − 6a to the inlet x = 0. Each x-coordinate in the grid includes thirteen nodes in the z-direction: nine within the lubricant, two more in the fluid–solid interfaces and one additional node inside each contacting body at a depth equal to the thermally affected distance. Figure 1 shows the non-uniform grid selected for the lubricant.

Fig. 1
figure 1

Distribution of the nodes in the non-uniform grid

Full size image

The thermally affected distance represents the depth to which there is a thermal gradient in each body [19]. These depths can be calculated with Eq. (16)

$$d_{1,2} = \sqrt {\frac{{k_{\text{b}} }}{{\rho_{\text{b}} c_{\text{b}} }}\frac{dx}{{u_{1,2} }}}$$
(16)

Regarding the boundary conditions, the temperatures of the lubricant and the bodies are considered equal to the bath temperature Tb sufficiently far upstream (at a distance 6a to the inlet) and also for the bodies at depths equal to the thermally affected distances (d1, d2). Thus, the boundary conditions can be written as follows [20]

$$\begin{aligned} & T(x = - \,6a,z) = T_{1} (x = - \,6a,z) = T_{2} (x = - \,6a,z) = T_{b} ,\quad \forall z \\ & T_{1} (x,z = h/2 + d_{1} ) = T_{\text{b}} ,\quad \forall x \\ & T_{2} (x,z = - \,h/2 - d_{2} ) = T_{\text{b}} ,\quad \forall x \\ \end{aligned}$$
(17)

Continuity of heat flux and temperature is imposed across the two lubricant–solid interfaces. When the heat flow has reached the bodies in contact, it is diffused to the inside of the bodies

$$\begin{aligned} k_{\text{l}} \left( {\frac{\partial T(x,z)}{\partial z}} \right)_{z = h/2} & = k_{\text{b}} \frac{{T_{1} (x,z = h/2) - T_{\text{b}} }}{{d_{1} }},\quad \forall x \\ k_{\text{l}} \left( {\frac{\partial T(x,z)}{\partial z}} \right)_{z = - h/2} & = k_{\text{b}} \frac{{T_{2} (x,z = - h/2) - T_{\text{b}} }}{{d_{2} }},\quad \forall x \\ \end{aligned}$$
(18)

where

$$\begin{aligned} & T_{1} (x,z = h/2) = T(x,z = h/2),\quad \forall x \\ & T_{2} (x,z = - h/2) = T(x,z = - h/2),\quad \forall x \\ \end{aligned}$$
(19)

Temperature gradients inside the bodies are not analysed in detail, as they are not relevant for the film thickness determination. However, the calculation process ensures that the energy equations are satisfied.

In addition to the equations exposed in Ref. [10], the discretization of the energy Eqs. (12, 13), together with their boundary conditions, is performed in line with Ref. [20].

Later on, we can solve the system of equations following the flow chart depicted in Fig. 2, attaining the temperature field and the thermal film thickness h0.

Fig. 2
figure 2

Flow chart for calculating thermal film thickness

Full size image

In the first step, the temperature is set equal to that of the lubricant bath, i.e. the temperature at a distance L sufficiently remote from the inlet: L = 6a. Applying the calculation method disclosed in Ref. [10], a velocity field and a film thickness are attained for the isothermal case, which are used to solve the energy Eqs. (14, 15) and find a new temperature distribution. Then, the viscosity of each point is updated with this temperature field to start an iterative solving process that gives the thermal film thickness and the temperature distribution. The termination criterion of this process is defined as a difference below 0.1 nm in the film thickness calculated in two consecutive iterations.

3 Relevance of the Thermal Effects on Film Thickness

The described methodology for numerically solving the thermal EHL problem has been applied to a typical lubricant under EHL operating conditions [8]: steel–steel contact with R = 0.02 m, p m  = 0.8 GPa, u m  = 1 m/s, μ0 = 0.08 Pa s, α = 15 GPa−1, β = 0.076 K−1, G = 10 MPa, n = 0.75, kl = 0.1515 W/m K, ρl = 975 kg/m3, cl = 2000 J/kg K. Figure 3 shows temperature distributions of the lubricant and the contacting surfaces in two cases: low slide-to-roll ratio (Ʃ = 0.5) and medium slide-to-roll ratio (Ʃ = 1.0).

Fig. 3
figure 3

Film thickness and temperature distribution of the lubricant and the upper/faster surface and the lower/slower surface. a Ʃ = 0.5; b Ʃ = 1.0

Full size image

The thermal solving process has been performed for the two Reynolds–Carreau equations presented in references [8, 10]. In both cases, analogous temperature distributions are attained. Hence, the results are shown only for the new model (Eq. 4).

As the SRR increases, more heat is generated in the inlet zone due to the difference in velocities between the layers of fluid. For a low slide-to-roll ratio (Σ = 0.5), the inlet temperature is 10% higher to that of the lubricant bath, there being a 34% jump in the case of a medium slide-to-roll ratio (Σ = 1.0), something which shows how important it is to include the energy equation during the resolution when the SRR reaches significant values. As far as film thickness is concerned, the rise in SRR causes an increasing loss of viscosity due to the pseudoplastic and thermal effects on the lubricant, with the ensuing reduction in film thickness (Fig. 3). These results are in line with references [21, 22].

4 New Film Thickness Formula

A new film thickness formula is determined from the results of the aforementioned Reynolds–Carreau equations [8, 10] for the thermal case. The process aims to obtain easy-to-use expressions following a methodology used by Anuradha and Kumar in [2], to which a new thermal factor is added. This process consists of the following stages:

  • Selecting the range of input parameters and the types of equations to fit.

  • Fitting an equation for the Newtonian film thickness hN.

  • Fitting a factor to incorporate the shear-thinning effect under pure rolling conditions: φNN.

  • Fitting a factor to incorporate the shear-thinning effect under rolling and sliding conditions: φSRR.

  • Fitting a thermal correction factor for film thickness: φT.

Figure 4 outlines the effect of each of the factors in a film thickness versus SRR graph. When using all the factors, the film thickness is obtained with Eq. (20)

Fig. 4
figure 4

Influence of the correction factors on the film thickness

Full size image
$$h_{0} = h_{\text{N}} \cdot\varphi_{\text{NN}} \cdot\varphi_{\text{SRR}} \cdot\varphi_{\text{T}}$$
(20)

Expressions are presented as a function of the usual dimensionless parameters for velocity \(\bar{U}\), load \(\bar{W}\), material \(\bar{G}\) and Newtonian limit G/E′. Based on [2], the range of input dimensionless parameters used for determining the equations is shown in Table 1.

Table 1 Range of input dimensionless parameters
Full size table

Several materials with different mechanical and thermal properties are considered in order to obtain more general equations, with a broader range of applicability.

For the Newtonian film thickness, the equation model is (21), where k1–k4 are adjustable constants to be obtained

$$\frac{{h_{\text{N}} }}{R} = k_{1} \bar{U}^{{k_{2} }} \bar{G}^{{k_{3} }} \bar{W}^{{k_{4} }}$$
(21)

After fitting the Newtonian formula, Eq. (22) provides a shear-thinning correction under pure rolling conditions, where k5–k11 are constants to be adjusted. This expression is based on the non-Newtonian viscosity corrector of Carreau

$$\varphi_{\text{NN}} = \left( {1 + k_{5} \frac{{\bar{U}^{{k_{6} }} \bar{W}^{{k_{7} }} }}{{\bar{G}^{{k_{8} }} \left( {G/E^{{\prime }} } \right)^{{k_{9} }} }}} \right)^{{k_{10} (1 - n)^{{k_{11} }} }}$$
(22)

As for the shear-thinning correction factor under rolling and sliding conditions, a similar type of equation is considered (23), but taking into account SRR:

$$\varphi_{\text{SRR}} = \left( {1 + k_{12} \frac{{\varSigma^{{k_{13} }} \bar{U}^{{k_{14} }} \bar{W}^{{k_{15} }} }}{{\bar{G}^{{k_{16} }} \left( {G/E^{{\prime }} } \right)^{{k_{17} }} }}} \right)^{{k_{18} (1 - n)^{{k_{19} }} }}$$
(23)

It is worth noting that both φNN and φSRR are equal to one for the Newtonian case (n = 1).

To take account of the film thickness reduction due to thermal effects, the equation used (24) is based on the empirical expression (11). In order to broaden the application range, additional factors are added, such as thermal conductivity, specific heat and density of the contacting bodies

$$\varphi_{\text{T}} = \frac{{1 - k_{20} \frac{{p_{m} }}{{E^{{\prime }} }}\left( {\frac{{\mu_{0} u_{m}^{2} }}{{\beta T_{\text{b}}^{2} k_{\text{l}} }}} \right)^{{k_{21} }} \left( {\frac{{k_{\text{b}} }}{{k_{\text{l}} }}} \right)^{{k_{22} }} \left( {\frac{G}{{E^{{\prime }} }}} \right)^{{k_{23} n}} \left( {\frac{{c_{\text{b}} }}{{c_{\text{l}} }}} \right)^{{k_{24} }} \left( {\frac{{\rho_{\text{l}} }}{{\rho_{\text{b}} }}} \right)^{{k_{25} }} }}{{1 + k_{26} \,\left( {1 + k_{27} \varSigma^{{k_{28} }} } \right)\left( {\frac{{\mu_{0} u_{m}^{2} }}{{\beta T_{\text{b}}^{2} k_{\text{l}} }}} \right)^{{k_{29} }} }}$$
(24)

The constants in Eqs. (21–24) are determined by using the GRG algorithm [23] to minimise the sum of squared deviations of the fitted equation with respect to the results of the simulations using Reynolds–Carreau equations with thermal effects.

In this way, the fitted expression for Newtonian film thickness is presented in Eq. (25). Likewise, Eqs. (26–28) show the corresponding correction factors obtained when performing thermal calculations with the new model described by the authors in [10]

$$\frac{{h_{\text{N}} }}{R} = 1.9983\bar{U}^{0.7376} \bar{G}^{0.7385} \bar{W}^{ - 0.1091}$$
(25)
$$\varphi_{\text{NN,New}} = \left( {1 + \frac{{\bar{U}^{0.3960} \bar{W}^{0.2212} }}{{\bar{G}^{1.3541} \left( {G/E^{{\prime }} } \right)^{1.7724} }}} \right)^{{ - 0.9447(1 - n)^{1.6978} }}$$
(26)
$$\varphi_{\text{SRR,New}} = \left( {1 + 0.2335\frac{{\varSigma^{1.0620} \bar{U}^{0.1045} \bar{W}^{0.2706} }}{{\bar{G}^{0.5225} \left( {G/E^{{\prime }} } \right)^{0.5150} }}} \right)^{ - 36.8638(1 - n)}$$
(27)
$$\varphi_{\text{T,New}} = \frac{{1 - 424.4448\frac{{p_{m} }}{{E^{{\prime }} }}\left( {\frac{{\mu_{0} u_{m}^{2} }}{{\beta T_{\text{b}}^{2} k_{\text{l}} }}} \right)^{0.3053} \left( {\frac{{k_{\text{b}} }}{{k_{\text{l}} }}} \right)^{ - 1.0458} \left( {\frac{G}{{E^{{\prime }} }}} \right)^{0.0195n} \left( {\frac{{c_{\text{b}} }}{{c_{\text{l}} }}} \right)^{ - 3.5064} \left( {\frac{{\rho_{\text{l}} }}{{\rho_{\text{b}} }}} \right)^{0.0492} }}{{1 + 6.4127\,\left( {1 + 1.3148\varSigma^{1.6814} } \right)\left( {\frac{{\mu_{0} u_{m}^{2} }}{{\beta T_{\text{b}}^{2} k_{\text{l}} }}} \right)^{0.6098} }}$$
(28)

An advantage of the structure of these equations is that all the factors are completely independent. Therefore, they can be applied in any order.

Table 2 compares the film thickness results obtained using expressions (25–28) “h0,New formula”, with the equivalent results calculated numerically with the new Reynolds–Carreau equation “h0,New numerical”, showing an average error lower than 2%. This indicates that the fitting process followed leads to a very good agreement between the adjusted formula and the numerical results.

Table 2 Film thickness results for the new Reynolds–Carreau model
Full size table

On the other hand, analogous Eqs. (29, 30) are obtained for the shear-thinning factors from the Reynolds–Carreau equation proposed by Bair [8]. However, identical equations are considered to obtain the Newtonian film thickness (25) and the thermal correction factor (28), as they are not influenced by the model in Ref. [8]

$$\varphi_{\text{NN,New}}^{\text{Bair}} = \left( {1 + 3.5061 \times 10^{ - 8} \frac{{\bar{U}^{0.6902} \bar{W}^{0.3495} }}{{\bar{G}^{2.0181} (G/E^{{\prime }} )^{4.4027} }}} \right)^{ - 0.1199(1 - n)}$$
(29)
$$\varphi_{\text{SRR,New}}^{\text{Bair}} = \left( {1 + 4.2163 \times 10^{ - 6} \frac{{\varSigma^{0.6235} \bar{U}^{0.5256} \bar{W}^{0.1918} }}{{\bar{G}^{1.7568} \left( {G/E^{{\prime }} } \right)^{3.0968} }}} \right)^{ - 1.6580(1 - n)}$$
(30)

By comparing the results of this model with those of the model proposed in [10], average deviations of lower than 3% are found (Table 3). The numerical results presented are attained by means of the calculation process described in the present article in order to obtain results that can be compared.

Table 3 Film thickness results for the model proposed by Bair
Full size table

5 Results of the New Formula and the New Factors

Having verified that the new formula provides results equivalent to those of the numerical simulations within the range specified in Table 1, the new correction factors for shear-thinning and thermal effects have been compared with results of other authors.

Table 4 compares several film thickness corrections due to shear-thinning under isothermal conditions for the model proposed by Bair (Eqs. 29, 30), Anuradha and Kumar (Eqs. 8, 9) and the new Eqs. (26, 27). The correlation between the new formulae and those of Anuradha and Kumar “A&K” is shown in Fig. 5 and in the last column of Table 4, with percentage differences less than 20% in all cases (usually less than 10%). These variations are explained by the fact that Newtonian film thickness differs from one model to another, as noted in references [7, 10]. Indeed, Anuradha and Kumar tend to obtain a lower Newtonian film thickness and therefore the corresponding factors apply a lesser shear-thinning correction to match the numerical simulations, leading to negative differences in most cases.

Table 4 Film thickness corrections due to shear-thinning under isothermal conditions
Full size table
Fig. 5
figure 5

Comparison of shear-thinning factors under isothermal conditions. Steel–steel contact with R = 0.1 m, μ0 = 0.08 Pa s, α = 18.9 GPa−1, G = 1.0 MPa, n = 0.3. a Ʃ = 0.75; b Ʃ = 1.5

Full size image

In Table 5 and Fig. 6, the thermal factor (11) is compared with the new formula (28). Both expressions give similar results (differences lower than 9%), with values slightly higher for the new factor. Hence, the new model predicts a less significant thermal influence on film thickness.

Table 5 Film thickness corrections due to thermal effects
Full size table
Fig. 6
figure 6

Comparison of thermal factors. Steel–steel contact with R = 0.1 m, μ0 = 0.08 Pa s, α = 18.9 GPa−1, β = 0.076 K−1, Tb = 313 K, G = 1.0 MPa, n = 0.3, kl = 0.15 W/m K, ρl = 975 kg/m3, cl = 2000 J/kg K. a Ʃ = 0.75; b Ʃ = 1.5

Full size image

After the analysis of the individual effect of shear-thinning and thermal factors, film thickness calculations have been done taking into account all the factors. Figure 7 shows the results of the formulae developed for the Bair model (Eqs. 25, 28, 29, 30) and the new formula (Eqs. 25, 26, 27, 28), together with the results of Anuradha and Kumar (Eqs. 6, 8, 9) modified with the thermal factor of Eq. (11) to be able to compare the predictions [denoted by “A&K + Eq. (11)”].

Fig. 7
figure 7

Film thickness calculations using different formulae. Steel–steel contact with R = 0.1 m, kl = 0.15 W/m K, cl = 2000 J/kg K. a p m  = 1.0 GPa, μ0 = 0.08 Pa s, α = 18.9 GPa−1, β = 0.076 K−1, Tb = 313 K, G = 1.0 MPa, n = 0.3, ρl = 975 kg/m3; b base oil M100, Tb = 298 K, p m  = 1.5 GPa, ρl = 900 kg/m3; c base oil N100, Tb = 298 K, p m  = 2.0 GPa, ρl = 900 kg/m3. The parameters of these base oils are given in Table 6

Full size image

The results of the film thickness formula developed for the new model present a clear agreement with those of Anuradha and Kumar throughout the range compared, showing average deviations of 12% and a similar decreasing trend as SRR rises. This is in line with the simulations presented in the article [10] for the isothermal case, where the new model shows a film thickness variation with SRR close to the results of Anuradha and Kumar, which are based on full EHL simulations. In contrast, the formula obtained for the Bair model shows lower sensitivity to SRR.

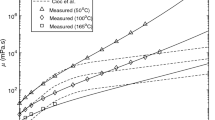
Bearing in mind the lack of film thickness measurements for line contacts, it is interesting to compare the results of the new formula with experimental data under thermal conditions, Ref. [24]. For this purpose, approximate values of the rheological parameters have been taken (Table 6), utilising information available for lubricants of a similar nature.

Table 6 Rheological parameters considered for the lubricants
Full size table

Figure 8 depicts the calculated film thickness as a function of SRR for diverse lubricants, together with the experimental results. In these cases, the input parameters move away from the range specified in Table 1 and the new formula only allows a rough estimate. The results can be improved by using a more general Newtonian formula instead of Eq. (25), such as the Hamrock formula for line contact [6]:

$$h_{\text{Nc}} = 2.154\alpha^{0.47} \left( {\mu_{0} u_{m} } \right)^{0.692} E^{{{\prime }0.110}} R^{0.308} p_{0}^{ - 0.332}$$
(31)
Fig. 8
figure 8

Comparison between predicted results and experimental data from Ref. [24]. Steel–steel contact with p m  = 0.785 GPa, u m  = 8 m/s, R = 0.02 m, kl = 0.15 W/m K, ρl = 900 kg/m3, cl = 2000 J/kg K. a PAO; b M100; c N100

Full size image

Figure 8 also presents the predictions attained by applying the new correction factors in Eqs. (26–28) to the Hamrock formula. The results show a better agreement with the experimental data, and the new correction factors properly estimate the variation of film thickness with regard to SRR and lubricant type.

6 Conclusions

The authors have improved their previous model to determine film thickness by considering thermal effects in the calculation process of the Reynolds–Carreau equation. Solving the energy equation has allowed for the determination of the temperature distributions in the lubricant and the contacting surfaces in the inlet zone. In this way, the results with different working conditions have been discussed.

As a result of the application of the model developed over a wide range of conditions, a new film thickness formula is proposed for EHL line contacts, which can be used for fast and easy calculations. The new formula consists of an equation for the Newtonian film thickness, a shear-thinning factor under pure rolling, a shear-thinning factor under rolling and sliding conditions and a thermal factor:

$$\begin{aligned} \frac{{h_{\text{N}} }}{R} & = 1.9983\bar{U}^{0.7376} \bar{G}^{0.7385} \bar{W}^{ - 0.1091} \\ \varphi_{\text{NN,New}} & = \left( {1 + \frac{{\bar{U}^{0.3960} \bar{W}^{0.2212} }}{{\bar{G}^{1.3541} \left( {G/E^{{\prime }} } \right)^{1.7724} }}} \right)^{{ - 0.9447(1 - n)^{1.6978} }} \\ \varphi_{\text{SRR,New}} & = \left( {1 + 0.2335\frac{{\varSigma^{1.0620} \bar{U}^{0.1045} \bar{W}^{0.2706} }}{{\bar{G}^{0.5225} \left( {G/E^{{\prime }} } \right)^{0.5150} }}} \right)^{ - 36.8638(1 - n)} \\ \varphi_{\text{T,New}} & = \frac{{1 - 424.4448\frac{{p_{m} }}{{E^{{\prime }} }}\left( {\frac{{\mu_{0} u_{m}^{2} }}{{\beta T_{\text{b}}^{2} k_{\text{l}} }}} \right)^{0.3053} \left( {\frac{{k_{\text{b}} }}{{k_{\text{l}} }}} \right)^{ - 1.0458} \left( {\frac{G}{{E^{{\prime }} }}} \right)^{0.0195n} \left( {\frac{{c_{\text{b}} }}{{c_{\text{l}} }}} \right)^{ - 3.5064} \left( {\frac{{\rho_{\text{l}} }}{{\rho_{\text{b}} }}} \right)^{0.0492} }}{{1 + 6.4127\,\left( {1 + 1.3148\varSigma^{1.6814} } \right)\left( {\frac{{\mu_{0} u_{m}^{2} }}{{\beta T_{\text{b}}^{2} k_{\text{l}} }}} \right)^{0.6098} }} \\ \end{aligned}$$

Therefore, the complete film thickness equation can be expressed as follows

$$h_{0} = h_{\text{N}} \cdot\varphi_{\text{NN}} \cdot\varphi_{\text{SRR}} \cdot\varphi_{\text{T}}$$

This expression has shown to provide reasonably good accuracy for predicting the film thickness when compared to numerical calculations using Reynolds–Carreau equations, to full EHL simulations and to experimental results.