1 Introduction

In elastohydrodynamic lubricated (EHL) conjunctions, minimum film thickness is regarded as a critical parameter, used in assessing whether or not the corresponding machine element would operate safely, without direct contact between surface asperities [1,2,3,4,5,6]. This emphasis makes it all the more surprising that the most widely accepted film thickness formulas do not accurately predict the minimum thickness [7] even when the viscosity has been measured to be Newtonian at the stress magnitude of the inlet zone. In fact, by comparing such analytical predictions to numerical ones (generated using a finite element framework [8]; validated against experiments), Wheeler et al. [9] pointed out that most analytical film thickness formulae are capable of predicting central film thickness within 10%. However, when it comes to minimum film thickness, deviations can exceed 50%; reaching 90% in some extreme cases. What is even more problematic is that the formulae overestimated the numerical predictions.

It has been universally accepted that the influence of the piezoviscous response of the liquid on the film thickness depends only on a pressure-viscosity coefficient which can be quantified by knowledge of the piezoviscous function at pressures from ambient to some low pressure. Up until recently, the required pressure for determination of the coefficient was believed to be constant, with significant disparities in the literature for its corresponding value. Some works consider it to be as low as 70 MPa [10], while others consider it to be as high as 545 MPa [11]. Only recently, Habchi and Bair [12] quantified the inlet pressure and showed it to be dependent on the contact configuration (i.e., line or point contact), and the operating conditions. It was found to range from 50 to 185 MPa. The belief that the viscosity at pressures greater than those existing in the inlet zone has no effect upon the film thickness and film shape has persisted, in spite of the absence of a generally accepted definition of the pressure-viscosity coefficient which applies to all lubricants (there have been roughly six different definitions [13]). Though Habchi and Bair [12] showed this belief to be true for central film thickness, their results revealed that minimum film thickness in circular contacts is also affected by the high-pressure viscosity response of the lubricant, in the central part of the contact. This is probably the main reason behind the lack of accuracy of classical minimum film thickness formulae, and the emergence of new formulae that quantify minimum thickness by means of a ratio of central-to-minimum film thickness, instead of a direct quantification [14, 15]. Similarly, the effect of the shear-dependence of viscosity on film thickness has been ignored until the mid-nineties [16]. It has simply been absorbed into a pressure-viscosity coefficient that was fitted to a film thickness measurement [17].

Much of the recent lack of progress in classical EHL can be attributed to the adoption of fictitious pressure-viscosity models. An example is shown in Fig. 1 for a helicopter transmission fluid. The viscosity of Royco 555® measured with a falling cylinder viscometer is shown as the points and the improved Yasutomi model [18] is shown as the solid curves. The representation of the viscosity of a helicopter transmission fluid employed in a classical numerical simulation [19] is shown as the broken curves. Clearly, progress in understanding the mechanisms of EHL which require shear response at EHL pressures will not come from the techniques of the classical analyses.

Fig. 1
figure 1

Comparison of the measured viscosity of a transmission oil and the improved Yasutomi correlation with a representation of the viscosity in classical EHL [19]

Full size image

In an experimental investigation of the film thickness of fresh and degraded hydraulic oil [20], the central film thickness was precisely predicted from primary viscosity measurements for both oils using a quantitative EHL formula [21]. However, the minimum film thickness was overestimated although the relative thicknesses of the two oils were correct. This difficulty in predicting the minimum film thickness is not unusual.

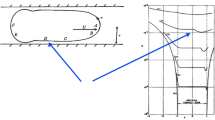
To validate predictions of the scale and load sensitivities of the central film thickness using measured pressure and shear dependent viscosities, experimental measurements were made of the complete EHL film shape in circular contacts [22, 23] at Brno University of Technology. Over the course of these film measurements many profiles of the exit restriction and the side lobe minimum were captured. An example is shown in Fig. 2. SRBS is solvent refined mineral bright stock oil and PG460 is a polyglycol gear oil. Common conditions are oil temperature of 40 °C and maximum Hertz pressure of 518 MPa in a circular contact between a 25.4 mm steel ball and glass disc. The central thicknesses are made equal to 200 nm for both oils by selecting rolling velocities of 0.071 m/s for PG460 and for SRBS, 0.053 m/s. The differences are striking in the shapes of the exit restriction along the x-direction of motion in Fig. 2a and the side lobe minimum thickness shown in Fig. 2b, in profile across the direction of motion, y-direction. The polyglycol gives the thinner film on the contact exit along the central line in the entrainment direction, while the mineral oil gives the thinner minimum thickness.

Fig. 2
figure 2

Measured film profiles for a mineral oil, SRBS and a polyglycol, PG460 in the a) x-direction, and b) y-direction

Full size image

The rheology of the two oils is characterized in Fig. 3 for piezoviscous response and in Fig. 4 the shear-dependent viscosity, \(\eta\), is normalized by the low-shear viscosity, μ and plotted versus shear stress. There are clear differences between the two oils in terms of both properties, with the mineral oil being more viscous under both high pressure and high shear.

Fig. 3
figure 3

Low-shear viscosity versus pressure of SRBS and PG460, at 40 °C

Full size image
Fig. 4
figure 4

Relative shear-dependent viscosity as a function of shear stress of SRBS and PG460

Full size image

The issue addressed in this article is the governing mechanisms of EHL minimum film thickness, which cause the differences observed in Fig. 2. As a first step, the focus here will be on the influence of pressure-viscosity response, while shear response will be left out for later.

2 Numerical Model

The numerical model employed in this work is based on the full-system finite element approach [8]. Smooth steady-state line and circular contacts are considered, under isothermal Newtonian considerations. The modeling approach consists of a fully-coupled resolution of the governing equations of elastohydrodynamic lubrication: Reynolds, linear elasticity, and load balance. The full-system resolution guarantees extremely fast convergence rates. All field variables are discretized using second-order Lagrange finite elements. The free cavitation boundary arising in the solution of Reynolds equation on the contact outlet side is handled using a penalty method, as proposed by Wu [24]. It consists in adding a penalty term that forces any arising negative pressures in the solution to zero, since such pressures cannot be tolerated by the lubricant, which will cavitate. In addition, spurious numerical oscillations arising in the pressure field under highly loaded conditions are cured through the use of special stabilized finite element formulations [25]. This relates to the convection–diffusion-reaction nature of Reynolds equation, which becomes convection-dominated under high loads. As such, the Galerkin formulation—typically employed in standard finite elements—fails to capture all inherent error scales of the problem. Non-regular non-structured meshing is employed, with the projection of sub-surface elements on the contact domain being used as the mesh of the latter. This prevents any unnecessary and computationally expensive mapping operations between the two meshes. In addition, the mesh size is optimized such that it is the smallest over the contact domain, where the highest precision is required, and it increases when moving towards the peripheral areas. This significantly reduces the size of the arising algebraic system of equations. Further reductions are attained through the use of Model Order Reduction techniques [26], statically condensing non-needed subsurface elastic deformations. The mesh size is calibrated with sufficient refinements to guarantee grid-independence. Given the highly non-linear character of Reynolds equation, a damped-Newton [27] procedure is required to solve the overall arising algebraic system of equations. For the fluid density-pressure dependence, the universal equation of state proposed by Bair [28] is employed, based on the Tait relation:

$$\rho = \frac{{\rho_{0} }}{{1 - \frac{1}{{1 + K^{\prime}_{0} }}\ln \left[ {1 + \frac{p}{{K_{0} }}\left( {1 + K^{\prime}_{0} } \right)} \right]}}$$
(1)

with \(K_{0} = 1.28\;{\text{GPa}}\) and \(K^{\prime}_{0} = 11\). The value of the ambient-pressure density \(\rho_{0}\) is not specified, since it is not needed in the simulations (it cancels out from all Reynolds equation terms). As for the viscosity–pressure dependence it will be described in detail in Sect. 3. For further details about the employed numerical model, interested readers are referred to [8].

3 Procedure for Investigating Minimum Film Thickness Governing Mechanisms

In order to investigate the governing mechanisms of minimum film thickness in elastohydrodynamic lubricated contacts, numerical simulations of smooth steel-steel line and circular contacts are carried out, under steady-state pure-rolling isothermal Newtonian conditions. Given that only pure-rolling conditions are considered, thermal effects are expected to be minimal, and they are thus neglected. The influence of lubricant viscosity dependence on shear will also be ignored, out of simplicity, and in order to isolate the influence of piezoviscous effects. Such a dependence will be considered in future works.

It is well-known in the EHL literature that central film thickness is influenced by lubricant viscosity up to inlet pressure. The latter parameter was only quantified recently by Habchi and Bair [12], who revealed its dependence on operating conditions. In addition, it was shown to range from 50 to 150 MPa for line contacts, or 185 MPa for circular contacts. Therefore, in order to restrict the analysis to minimum film thickness, three hypothetical lubricant viscosity–pressure responses are considered (A, B, and C), with the exact same low-pressure dependence, up to 300 MPa. Beyond this value, the three responses diverge into increasingly higher viscosity values, respectively. For the low-pressure response, the McEwen model was chosen for its high suitability to low pressures [28]. As for high-pressures, a newly devised 6-parameter exponential-polynomial function is adopted. Its parameters are chosen such that they would lead to a continuous viscosity–pressure response at 300 MPa, and that the first derivative would be continuous at this pressure. The McEwen and exponential-polynomial functions describe viscosity variations \(\mu\) as a function of pressure \(p\) as follows:

$$\mu = \left\{ {\begin{array}{*{20}c} {\mu_{0} \left( {1 + \frac{{\alpha_{0} }}{q}p} \right)^{q} } & {for\;\;p \le 300MPa} \\ {\exp \left( {a_{0} + a_{1} \,p + a_{2} \,p^{2} + a_{3} \,p^{3} + a_{4} \,p^{4} + a_{5} \,p^{5} } \right)} & {for\;\;p > 300MPa} \\ \end{array} } \right.$$
(2)

where \(\mu_{0}\) and \(\alpha_{0}\) are the ambient-pressure viscosity, and viscosity–pressure coefficient. The employed values for the McEwen model parameters are \(\mu_{0} = 1.878\;mPa \cdot s\), \(\alpha_{0} = 11.7\;GPa^{ - 1}\), and \(q = 2.616\), which are the actual values of a typical jet oil. As for the exponential-polynomial model, the values of the 6 parameters for the three considered high-pressure viscosity responses (A, B, and C) are given in Table 1. The viscosity–pressure responses of the three fluids are plotted in Fig. 5.

Table 1 Parameters of the exponential-polynomial viscosity–pressure model of fluids A, B and C
Full size table
Fig. 5
figure 5

Viscosity–pressure responses of the fluids A, B and C

Full size image

Given that the viscosity–pressure responses of fluids A, B, and C are the same, up to a pressure of 300 MPa, which exceeds inlet pressures of line and circular contacts, they are expected to produce similar central film thicknesses, within less than 1% [12]. Any differences in minimum film thickness (under the same operating conditions and solid material parameters) can then only be attributed to high-pressure rheology.

4 Results

Smooth steel-steel circular contacts are considered with a roller radius \(R = 15mm\), and a constant mean entrainment speed \(u_{m}\) in the x-direction, varied from 0.5 to 10 m/s. Two external applied loads \(F\) are considered; a moderate one with \(F = 30N\) (\(p_{h} = 0.7GPa\)), and a high one with \(F = 300N\) (\(p_{h} = 1.5GPa\)). The three hypothetical fluid responses (A, B, and C) detailed in Sect. 3 are considered, with the same density-pressure response as described in Sect. 2. Figure 6 shows the ratio of the central film thickness \(h_{c}\) to the minimum film thickness \(h_{m}\) (usually located at the side lobes) as the mean entrainment speed \(u_{m}\) is varied for both considered loads, for all three fluid responses.

Fig. 6
figure 6

Variations of hc/hm with um in circular contacts, for all three considered pressure-viscosity responses, with a) F = 30N (ph = 0.7GPa), and b) F = 300N (ph = 1.5GPa)

Full size image

The results of Fig. 6, reveal that the ratio \({{h_{c} } \mathord{\left/ {\vphantom {{h_{c} } {h_{m} }}} \right. \kern-0pt} {h_{m} }}\) increases as the fluid viscosity in the high-pressure central part of the contact is increased. But, \(h_{c}\) is virtually identical for all three fluids, given that they share the same exact low-pressure viscosity. Thus, it is clear that \(h_{m}\) decreases as the high-pressure fluid viscosity is increased. This is consistent with the experimental observations reported in Fig. 2. Note that the deviation between the three fluid responses increases with both load, and mean entrainment speed.

The ratio of the central film thickness \(h_{c}\) to the minimum film thickness along the central line of the contact in the entrainment direction \(h_{c,m}\) (usually located at the exit restriction) for the same conditions is plotted in Fig. 7. It is clear that the trend is now reversed, with \(h_{c,m}\) increasing as the high-pressure fluid viscosity is increased. This is also consistent with the experimental observations of Fig. 2. The latter are not to be directly compared though in a quantitative manner to the numerical results provided in this section, given that they are not carried out under similar conditions. In fact, for the experimental results of Fig. 2, entrainment speeds are different, the two fluids only have a similar ambient-pressure viscosity \(\mu_{0}\), and they have different shear responses. However, the reason why these results are discussed in the introduction is because they instigate the current study, and they do hint towards the main conclusions that are drawn here. That is, fluids with a higher viscosity in the central part of the contact tend to exhibit a higher drop in film thickness between the central part and the side lobes, and that this tendency is inverted on the exit side in the entrainment direction. Through the viscosity data provided in Figs. 3 and 4, it can be seen that SRBS would have a higher viscosity in the high-pressure high-shear central part of the contact, compared to PG460. Finding real lubricants that have the exact same low-pressure viscosity–pressure dependence and a different high-pressure response, with the same shear response is virtually impossible. This is why the current study had to be restricted to hypothetical fluids with such features.

Fig. 7
figure 7

Variations of hc/hc,m with um in circular contacts, for all three considered pressure-viscosity responses, with a) F = 30N (ph = 0.7GPa), and b) F = 300N (ph = 1.5GPa)

Full size image

Remark:

For the results presented in Figs. 6 and 7, it was verified that, under similar operating conditions, central film thicknesses are virtually the same (within less than 1%) for all three fluids. This being said, any discrepancies in \({{h_{c} } \mathord{\left/ {\vphantom {{h_{c} } {h_{m} }}} \right. \kern-0pt} {h_{m} }}\) or \({{h_{c} } \mathord{\left/ {\vphantom {{h_{c} } {h_{c,m} }}} \right. \kern-0pt} {h_{c,m} }}\) amongst the three fluids must result from differences in \(h_{m}\) or \(h_{c,m}\), respectively.

5 Discussion

Given the differences among the three considered fluid responses in minimum film thickness responses (both \(h_{m}\) and \(h_{{{\text{c}},{\text{m}}}}\)), and given that the three fluids share the exact same density and low-pressure viscosity, it becomes clear that minimum film thickness is not entirely governed by the inlet rheology of the lubricant, as was previously believed. Inlet rheology governs central film thickness; and by proxy, it indirectly affects minimum film thickness by simple translation. That is, as inlet viscosity is increased, central film thickness increases, and minimum film thickness would follow. But then, the drop in thickness between \(h_{c}\), and \(h_{m}\) or \(h_{c,m}\), and thus the shape of the high-pressure central conjunction is governed by the high-pressure rheology of the lubricant. In order to understand the underlying physical mechanisms behind these observations, one must examine the mass flows in and out of a circular EHL contact. These are illustrated in Fig. 8.

Fig. 8
figure 8

Mass flows into and out of an EHL circular contact

Full size image

Given that the surface velocities are unidirectional in the x-direction, the lubricant is entrained from left to right. As it reaches the central part of the contact (i.e. the high-pressure region), it is driven out of the contact both in the lateral (y-) and entrainment (x-) directions. However, the mechanisms differ. In the lateral direction, given that surface speeds are nil, the flow out of the contact is driven solely by a pressure gradient in that direction (Poiseuille flow). In the entrainment direction on the other hand, it is driven by both a pressure gradient in that direction (Poiseuille component), and the solid surface velocities (Couette component), with the latter being usually more dominant. Under isothermal Newtonian considerations, the fluid velocity \(v_{f}\) in the y-direction is expressed as follows, as a function of the z-position within the film thickness (\(z = 0\), or \(z = h\) correspond to the solid surfaces, while \(z = {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0pt} 2}\) corresponds to the mid-layer of the film):

$$v_{f} = \frac{1}{2\mu }\frac{\partial p}{{\partial y}}z\left( {z - h} \right)$$
(3)

Clearly, \(v_{f}\) is inversely proportional to viscosity. That is, for a higher viscosity in the high-pressure central part of the contact, the mass flow out of the contact in the lateral direction would be reduced, resulting in reduced minimum film thickness \(h_{m}\) at the side lobes, as reported in Figs. 2(b) or 6. Conservation of mass requires then that the mass flow out on the exit side in the entrainment direction be increased to compensate. This results in increased minimum film thickness along the central line of the contact in the x-direction \(h_{c,m}\), as reported in Figs. 2(a) and 7. In order to verify the pertinence of this proposed explanation, it would be interesting to consider the case of line contacts, since these are infinitely long in the y-direction, with no mass flow out in that direction (mass only flows out of the contact in the entrainment direction).

Figure 9 shows variations of \({{h_{{\text{c}}} } \mathord{\left/ {\vphantom {{h_{{\text{c}}} } {h_{{\text{m}}} }}} \right. \kern-0pt} {h_{{\text{m}}} }}\) for line contacts, under similar conditions as those considered for circular contacts (i.e., similar contact pressures and entrainment speeds). These are, smooth steel-steel contacts with a roller radius \(R = 15\;{\text{mm}}\) and Hertzian contact pressures of 0.7GPa (\(F = 0.2\;{\text{MN}}/{\text{m}}\)) and 1.5GPa (\(F = 0.92\;{\text{MN}}/{\text{m}}\)). The mean entrainment speed is also varied from 0.5 to 10 m/s, and the three fluid responses (A, B, and C) are considered. Note that for line contacts \(h_{{\text{m}}} \; = \;h_{{{\text{c}},\;{\text{m}}}}\). It is clear from the results of Fig. 9 that high-pressure rheology has little-to-no influence on minimum film thickness. In this case, the latter is truly governed by inlet rheology. This is attributed to the absence of lateral flow out of the contact. But remember that line contacts are only theoretical and do not exist in any real-life machine component. Nonetheless, one can draw an important conclusion from the observations made here. That is, minimum film thickness in wide elliptical contacts (i.e., the closest possible configuration to the line contact one) would be expected to exhibit a lower sensitivity to high-pressure rheology than circular contacts, while for slender contacts, the sensitivity is expected to be higher.

Fig. 9
figure 9

Variations of hc/hm with um in line contacts, for all three considered pressure-viscosity responses, with a F = 0.2MN/m (ph = 0.7GPa), and b F = 0.92MN/m (ph = 1.5GPa)

Full size image

6 Conclusion

This work investigates the governing mechanisms of minimum film thickness in elastohydrodynamic lubricated contacts. Up until now, it was thought to be governed by lubricant rheology in the low-pressure contact inlet. Through numerical simulations of EHL line and circular contacts, lubricated with fluids having the same low-pressure viscosity, but a very different response at high-pressure, minimum film thickness is shown to be governed by lubricant inlet rheology only in the theoretical line contact configuration. In real contacts however, it is not only governed by inlet rheology, but also by the high-pressure viscosity response of the lubricant. It is observed that the greater the viscosity at high pressure, the lower the minimum film thickness would be, as a result of reduced lateral flow out of the contact. Conservation of mass requires that a higher minimum film thickness would be attained along the central line of the contact, in the entrainment direction. These findings corroborate well with experimental observations.

The shear response of the fluid was not considered here, in order to isolate the influence of the pressure response. However, to fully understand the governing mechanisms of minimum film thickness, this topic is left to be addressed in future works, in addition to thermal effects. An additional interesting perspective would be to derive a high-pressure pressure-viscosity parameter that would allow a proper quantification of the minimum film thickness behavior reported in this work, through the use of analytical formulae. Despite a relatively good accuracy in predicting central film thicknesses, analytical formulae have historically suffered in quantifying minimum film thickness. This is probably due to a lack of understanding of its governing mechanisms, which have led to the development of formulae that are based on a pressure–viscosity parameter describing the lubricant behavior only on the inlet side of the contact. This is also due to the use of inappropriate piezoviscous functions, Barus and Roelands, for which the viscosity at high pressure is fixed by the viscosity and its pressure derivative at ambient pressure. The findings reported here, clearly highlight the impertinence of such an approach, given that minimum film thickness is not only governed by inlet rheology, but also by the high-pressure one. This is also probably why recent formulae, quantifying minimum film thickness through a ratio of central-to-minimum thickness have been more successful than traditional ones, which attempt a direct quantification of minimum thickness.

It has been necessary to alter the viscosity at the highest pressures of the contact to an unreasonably low value to cause the Eyring sinh-law to appear to be an accurate model for traction [29]. Not only is the sinh-law unacceptable for describing the effect of shear-thinning on central film thickness [17], but the altered viscosity at high pressure has also prevented an understanding of the minimum thickness.