A Computational Study of the Effects of Strain Hardening in Micro-asperity Friction Models

Abstract

In this paper, we study the effects of plastic strain hardening and damage on the friction response of a surface at the microscopic and macroscopic scales. At the microscale, the role played by hardening and damage in the response of a single asperity is determined using three-dimensional finite element analysis. The sample materials for the asperity are Al 2024-T3 and Ti6Al4V, which are modeled as isotropic bilinear plastic and include Johnson–Cook damage. The friction responses for two different damage models (Johnson–Cook and Bao–Wierzbicki) are also compared for the perfectly plastic case. In the simulations the asperity is initially compressed in order to induce a normal preload and then sheared to study the friction response. Then a statistical homogenization approach is used to propagate these effects to the macroscale. Toward this end, the surface is modeled as an isotropic Gaussian random process. The computed microscale responses are parameterized, and the overall macroscopic response of the surface is determined. Results of this study show that, at the microscale, strain hardening increases the coefficient of friction, particularly at low interference values. Similarly, material response plays a significant role at the macroscale over a wide range of normal force values.

1 Introduction

Friction between surfaces is affected by various factors such as geometry, mechanical action, chemical reactions. Though friction is not fully understood, considerable progress has been made since Amonton and Coulomb initiated the formal study of the subject by defining constant static and kinetic friction coefficients. Of particular interest is the role of surface and material properties on friction at the microscopic and macroscopic levels.

A number of researchers have developed models of the interaction between a single deformable asperity and a rigid plane. On the analytical side, Chang et al. [1] propose a model of an elastic-perfectly plastic asperity that assumes a rectangular pressure distribution in the contact zone. Among the modifications and improvements to this approach, we mention the use of elliptical contact pressure distribution by Evseev et al. [2], linear interpolation between elastic and plastic results by Chang [3] and mathematical smoothing of results by Zhao et al. [4].

With advances in computing power in recent decades, many researchers have proposed computational approaches as a means to simulate the response of an asperity and to verify analytical approaches. This includes the works by Kucharski et al. [5], Vu-Quoc et al. [6], and Kogut and Etsion [7]. Notably, Kogut and Etsion [7] develop an empirical relationship for the normal and shear force response of an asperity as a function of interference value. This relationship is independent of the material properties and shows discontinuities when the asperity transitions from a purely elastic regime to an elastic–plastic regime, and from an elastic–plastic regime to a fully plastic regime. Jackson and Green [8] also develop empirical formulations based on the finite element analysis of an elasto-plastic asperity, but their model shows no discontinuities and captures the dependence of the response on the material’s yield strength and Poisson’s ratio. More recently, the study by Shankar and Mayuram [9] on the role of yield strength and tangent modulus suggests that both quantities influence the transition from elastic–plastic contact to the fully plastic contact. Chatterjee and Sahoo [10] conclude that during the compression stage, the contact parameters are greatly influenced by strain hardening but negligibly by the contact conditions (full stick or perfect slip).

Another line of research has been the response and failure of an asperity under combined normal and tangential loading [11,12,13,14]. Kogut and Etsion [15] (KE model) present a semi-analytical friction model based on the hypothesis that sliding begins when there is elastic–plastic contact between the contacting bodies. Brizmer et al. [16] (BKE model) assume a full stick contact condition and hypothesize that failure occurs when the asperity contact stiffness (ratio of shear force to lateral displacement) reaches 10% of its initial value. Wu et al. [17] use the maximum shear stress criterion for sliding inception. Their model transitions from the KE model at low compressive interference to the BKE model at high compressive interference. This model is similar to the Coulomb friction model in terms of partial slip in that no-slip contact is maintained until a certain criterion is met, beyond which localized sliding is assumed.

The role of material damage has been receiving more attention in recent years. Wu et al. [18] study the flake-like wear particle formation in a two-dimensional plane strain cylinder upon shearing. Their work compares three material damage models to study fracture behavior and the friction coefficient of the asperity: the Bao–Wierzbicki criterion [19], the Johnson–Cook criterion [20] and shear band localization [21].

Much of the work on asperity shearing assumes elastic-perfectly plastic material behavior, and the effects of hardening and material damage have not been explored in great detail. Our goal in this work is to understand how hardening and material damage affect the friction response at both micro- and macro-levels using three-dimensional computational models. Toward this end, we use a statistical homogenization-based approach proposed by Sista and Vemaganti [22], shown in a schematic form in Fig. 1, consisting of three components: (a) a mathematical model of the surface roughness, generally in the form of a joint probability distribution of asperity heights and curvatures, (b) the normal and shear responses of a single asperity in a parametric form and (c) the homogenization procedure. The result is a prediction of the overall macroscopic normal, shear and friction responses of the surface.

Fig. 1

Statistical homogenization approach for calculating macroscopic friction coefficient from the micro-asperity friction response [22]

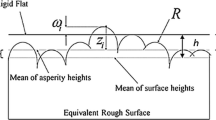
In the current research, the surface is modeled as an isotropic Gaussian random process following [23,24,25]. The autocorrelation function (ACF) for the surface heights is assumed to be Gaussian, though other forms can be used without affecting the overall approach adopted here. The Gaussian ACF filters out the smaller asperities that do not contribute to the overall friction but can significantly skew the surface parameters [26]. Consequently, the surface and its spectral moments are completely defined by two ACF parameters: the RMS roughness $\sigma$ and the correlation length $\lambda$.

To understand the role of hardening in the response of a single asperity, we investigate the role of isotropic strain hardening and rate hardening on the asperity’s normal contact and friction responses. Two alloys are considered: Al 2024-T3 and Ti6Al4V. The Y / E (yield strength-to-Young’s modulus) ratio of the Al alloy is about 1.6 times that of the Ti alloy (see Table 1), and this ratio plays an important role in the friction response of the material [22]. The alloys are modeled as bilinear plastic materials. Additionally, the effects of material damage on the coefficient of friction are studied for the case of an elastic-perfectly plastic asperity. Here, we use the damage models proposed by Bao and Wierzbicki [19], and Johnson and Cook [20].

The contact area between the asperity and the rigid plane supports the normal and shear loads until the asperity fails. Rather than assuming a partial slip contact model, this failure is controlled in this study by a maximum shear force resistance criterion proposed by Wu et al. [17]. But because of the presence of material damage in our model, our results for the shear response of the asperity differ significantly from those reported by Wu et al. [17]. The results of the single asperity study are parameterized and statistically homogenized to predict the overall friction response of the surface for various values of surface roughness and asperity aspect ratios.

The remaining article is structured as follows: After Introduction, Sect. 2 describes the computational methods used for the microscale single asperity problem. The statistical homogenization approach for the macroscale is described in Sect. 3. This is followed by results and discussion in Sect. 4, and some concluding remarks in Sect. 5.

2 Computational Methods for the Microscale Problem

2.1 Problem Description and Finite Element Mesh

This study examines the compression and friction behavior of a hemispherical asperity for various normal preloads, material parameters, loading rates and material damage models by initially compressing and subsequently shearing an asperity, as shown in Fig. 2. A two-dimensional computational model is used to find the normal force–displacement responses of a deformable asperity under compression, and a three-dimensional model is used to find its friction response under combined normal and shear loading.

Fig. 2

Schematic diagram of a hemispherical asperity under compressive (P) and shear (Q) forces

The two-dimensional axisymmetric model used to compute the normal force–displacement response of an asperity under compression alone is shown in Fig. 3. The three-dimensional half-hemisphere model used to simulate the friction response of the asperity is shown in Fig. 4. This half-hemisphere model takes into consideration the planar symmetry of the problem. For each case, the figure shows the finite element discretization of the asperity along with a close-up of the area where contact occurs with the rigid plane.

Fig. 3

Axisymmetric finite element mesh for a hemispherical asperity under compression alone

Fig. 4

Symmetric finite element mesh for a hemispherical asperity under compression and shear

The computational results reported in this work are obtained using the commercial finite element package ABAQUS/EXPLICIT 6.12-3. The rigid body compressing and shearing the asperity is represented by a flat rigid surface.

The two-dimensional axisymmetric model consists of 28,528 nodes and 28,152 bilinear axisymmetric quadrilateral, reduced integration (CAX4R) elements as shown in Fig. 3. The three-dimensional half-hemisphere model is partitioned similar to the two-dimensional model and consists of 240,357 nodes and 229,600 linear hexahedral reduced integration (C3D8R) elements as shown in Fig. 4.

A mesh sensitivity study is used to determine the appropriate discretization level. These details are discussed in Results section.

2.2 Boundary Conditions and Contact Interactions

The boundary conditions for the two- and three-dimensional models are shown in the insets of Figs. 3 and 4, respectively. The displacements of the base nodes are completely constrained for both cases, representing the asperity’s connection to a larger bulk of material that is unaffected by the compression and shearing effects.

The normal and shear movements of the rigid plane are displacement-controlled. For the compression-only simulations, the normal displacement is linearly ramped. But for the combined normal and shear loading simulations, the normal displacement is applied in the form of a fifth-order polynomial with zero slope and curvature at the beginning and end of loading. This helps reduce any inertial effects when the loading changes from normal displacement to a constant velocity tangential displacement.

Lagrangian contact constraints control the interaction between the rigid surface and the asperity, allowing no inter-element penetration. A frictionless contact condition is used during the normal loading as friction has negligible effect on the normal load [27]. On the other hand, a full stick contact condition is used during tangential loading. This choice is motivated by the strong adhesive junctions between contacting bodies [28].

2.3 Establishing a Quasistatic Loading Rate

An explicit dynamic solver is used to solve the microscale problem, which requires the specification of a velocity for the rigid plane compressing the asperity. This velocity should be low enough to represent a quasistatic process, while simultaneously keeping the computational costs reasonable. Wu and Shi [18] determine an optimal velocity based on simulations comparing the normal force, shear force, contact pressure distribution and kinetic-to-internal energy ratio for various velocities. A similar study is performed here. Based on the results (discussed in Results section), and taking into consideration the trade-off between computational cost and accuracy, 0.1 m/s is chosen as the optimum velocity for all the quasistatic simulations.

2.4 Material Models

2.4.1 Plasticity Model

The asperities undergo severe deformations during gross sliding. The material behavior under such deformations is far from linear elastic, so it is important to model the material response accurately in the studies on a single asperity. In this work, we explore the importance of the material constitutive model by including strain hardening and material failure to determine how the macroscopic friction behavior is affected by these factors.

For each material under study, we consider two models of plasticity: (a) elastic-perfectly plastic and (b) bilinear elastic–plastic with isotropic hardening. The Young’s modulus (E), Poisson’s ratio ($\nu$) and yield strength (Y) for the materials are shown in Table 1. For the case of bilinear plasticity, the tangent modulus value is varied from 0.005E to 0.02E, based on the experimental data reported by [29].

Table 1 Young’s moduli, Poisson’s ratios, yield strengths and tangent moduli used in this study

2.4.2 Material Damage Models

While the plasticity model governs the bulk mechanical response of the asperity, the damage model governs the loss of its stiffness (load-bearing capacity) after the inception of damage. Two such damage models are considered in our work. These are described here only briefly, and the details can be found in the literature [20, 30].

Johnson–Cook damage model Material failure in the Johnson–Cook model [20] is derived from the following damage law governing a scalar damage variable D:

$$\begin{aligned} D=\int {\frac{{\mathrm{d}}\varepsilon }{\varepsilon _f}} \end{aligned}$$

(1)

in which ${\mathrm{d}}\varepsilon$ is the increment in effective plastic strain during an increment in loading and the fracture strain, $\varepsilon _f$ is given by

$$\begin{aligned} \varepsilon _f=\big (D_1+D_2\exp \left( D_3{\sigma ^{*}}\right) \big )\big (1+D_4\text{ ln } ({\dot{\varepsilon }}^*)\big )\big (1+D_5T^*\big ), \end{aligned}$$

(2)

where $\dot{\varepsilon }^*$ is the normalized effective plastic strain rate (typically normalized to a strain rate of 1 s$^{-1}$), and $T^*$ is defined as

$$\begin{aligned} T^*=\frac{T-T_0}{T_{\mathrm {melt}}-T_0}, \end{aligned}$$

(3)

where T is the temperature of the body, $T_0$ is the reference temperature, and $T_{\mathrm {melt}}$ is the melting temperature of the material. The parameters $D_1,~D_2,~D_3,~D_4,~D_5$ are material constants obtained experimentally, and $\sigma ^*$ is the stress triaxiality defined as the mean stress normalized by the effective stress. In terms of the principal stresses, $\sigma _i~(i=1,2,3)$, the stress triaxiality can be defined as

$$\begin{aligned} {\sigma ^{*}}=\frac{\sigma _m}{\overline{\sigma }} = \frac{(\sigma _1+\sigma _2+\sigma _3)/3}{\sqrt{\frac{1}{2} \left[ (\sigma _1-\sigma _2)^2+(\sigma _2-\sigma _3)^2+(\sigma _3-\sigma _1)^2\right] }} \end{aligned}$$

(4)

Table 2 shows the values of the damage parameters $D_1$ to $D_5$ for Al 2024-T3 and Ti6Al4V used in this study [31].

The cumulative effect of this equivalent plastic fracture strain $\varepsilon _f$ causes the parameter D to increase from 0 to 1. Fracture is assumed to occur when D reaches 1.

Table 2 Johnson–Cook material damage parameters used in this study

Bao–Wierzbicki damage model According to Bao and Wierzbicki [30] a single function cannot predict fracture criteria over the whole stress triaxiality range due to the complex processes leading to crack formation. In the low (negative) stress triaxiality range crack formation is caused by shear fracture; in the high stress triaxiality range it is caused by the growth and linkage of void nucleations, while in the intermediate region a mixed fracture mode develops.

Using a series of upsetting, shear and tensile tests validated by numerical simulations Bao–Wierzbicki construct a fracture locus for the Al 2024-T351 alloy relating equivalent fracture strain to stress triaxiality:

$$\begin{aligned} \varepsilon _f=\left\{ \begin{array}{ll} 0.1225\left( {\sigma ^{*}}+\dfrac{1}{3}\right) ^{-0.46}, &{} -1/3\le {\sigma ^{*}}<0\\ 1.9{\sigma ^{*}}^2-0.18{\sigma ^{*}}+0.21, &{} 0\le {\sigma ^{*}}<0.4\\ 0.15{\sigma ^{*}}^{-1}, &{} 0.4\le {\sigma ^{*}}<0.95.\\ \end{array} \right. \end{aligned}$$

(5)

Due to the similarities between Al 2024-T3 and Al 2024-T351, the model in Eq. (5) is used in this study.

Giglio et al. [32] carry out a similar exercise and calibrate the fracture locus for the Ti6Al4V alloy:

$$\begin{aligned} \varepsilon _f=\left\{ \begin{array}{ll} \dfrac{0.164}{1+3{\sigma ^{*}}}+0.292, &{} -1/3<{\sigma ^{*}}\le 0\\ 1.376{\sigma ^{*}}^2-0.052{\sigma ^{*}}+0.461, &{} 0<{\sigma ^{*}}\le 0.4\\ 1.853\exp (-1.89{\sigma ^{*}}), &{} 0.4<{\sigma ^{*}}\le 0.95.\\ \end{array} \right. \end{aligned}$$

(6)

Figure 5 shows the comparison of the fracture strain versus stress triaxiality response for the Johnson–Cook and Bao–Wierzbicki damage models for the two materials under consideration. The models show very different fracture strain responses, especially for small values of triaxiality.

Fig. 5

Comparison of Johnson–Cook and Bao–Wierzbicki damage models: fracture strain as a function of triaxiality

2.5 Critical Normal Interference and Force

Upon application of normal load, the asperity shows plastic yielding at a certain interference. The displacement and reaction force at this initial yield point are defined as the critical interference, $\omega _{\mathrm{c}}$, and critical load, $P_{\mathrm{c}}$, respectively. Analytical models for the critical interference have been proposed by various authors including Chang, Etsion, Bogy (CEB) [1], Bhushan [33], Zhao, Maietta, Chang (ZMC) [4], and Jackson and Green [8].

$$\begin{aligned} \omega _{\mathrm{c}}=\left\{ \begin{array}{ll} \left( \dfrac{\pi KH}{2E^\prime }\right) ^2R &{} \text{ CEB }\,[1]\\ 6.32\left( \dfrac{Y}{E^\prime }\right) ^2R &{} \text{ Bhushan }\,[33]\\ \left( \dfrac{3\pi kH}{4E^\prime }\right) ^2R &{} \text{ ZMC }\,[4]\\ \left( \dfrac{\pi \cdot c\cdot Y}{2E^\prime }\right) ^2R &{} \text{ Jackson-Green }\,[8], \end{array} \right. \end{aligned}$$

(7)

where Y is the yield strength of the softer material and $E^\prime$ is the Hertz elastic modulus defined as

$$\begin{aligned} \frac{1}{E^\prime }=\frac{1-{\nu _1}^2}{E_1}+\frac{1-{\nu _2}^2}{E_2}. \end{aligned}$$

(8)

Here $E_1$, $E_2$ and $\nu _1$, $\nu _2$ are the Young’s moduli and the Poisson’s ratios of the contacting materials, respectively. The CEB model defines $K=0.454+0.41\nu$ as the maximum contact pressure factor $(\text{ pressure }_\mathrm {max}/H)$, H as the hardness of the softer material and the hemispherical asperity radius as R. In the ZMC model, k is the mean contact pressure factor $(\text{ pressure }_{\mathrm {mean}}/H)$, and in the Jackson–Green model, $c=1.295\exp (0.736\nu )$ is the yield strength coefficient $(\text{ pressure }_\mathrm {max}/H)$.

The Jackson–Green critical interference equation is a notable improvement compared to the previous models because (a) it is independent of the hardness and (b) its dependence on the Poisson’s ratio is derived numerically, as opposed to [1] where it is derived analytically by making volume conservation assumptions.

All these models follow the Hertzian solution for the critical normal force, $P_{\mathrm{c}}$ [34]:

$$\begin{aligned} P_{\mathrm{c}}=\frac{4}{3}E\sqrt{R {\omega _{\mathrm{c}}}^{3} } \end{aligned}$$

(9)

The critical interference and critical load formulations of Jackson and Green [8] are used in this study to normalize the displacements and forces, respectively.

2.6 Single Asperity Failure Criterion

The current literature provides many different models for the limiting shear load that asperity can support. Some of the commonly used criteria include local yielding [35], complete plastic contact [15], minimum relative tangent stiffness value [16] or von Mises shear strength limit [17].

During tangential loading, the shear force supported by the asperity initially increases and then decreases as extensive damage sets in around the contact region. In this work, the asperity shear failure is assumed to occur at that lateral displacement $u_x$ when the shear resistance Q takes on its maximum value $Q_{\mathrm {max}}$. The motivation behind this is that if a shear force greater than $Q_{\mathrm {max}}$ is applied, then the asperity cannot support this load and will proceed to complete failure. Therefore, the final asperity static friction coefficient is defined as

$$\begin{aligned} \mu ^* = \frac{Q_{\mathrm {max}}}{P}, \end{aligned}$$

(10)

where P is the normal force experienced by the asperity corresponding to the combined normal and tangential loading.

3 Computational Methods for the Macroscale Problem

Sista and Vemaganti [22] (SV) use a computational model to extrapolate micro-asperity friction results to the macroscale using the following components: (a) a parametric representation of the normal and shear responses of a single asperity, (b) a statistical model of the surface based on a known autocorrelation function (ACF) and (c) a statistical homogenization procedure to compute the overall friction response. These components are briefly described below.

3.1 Parameterization of Single Asperity Friction Response

The SV model originally uses the KE model for the single asperity response. Here, we use the results from the single asperity results of this study in order to better represent the effects of material damage and hardening at the micro-level. The top center and right boxes in Fig. 1 show the normal reaction force $P^*$ and shear reaction force $Q^*$, respectively, of a single asperity that has a normalized height $\xi$ and a normalized curvature $\eta$.

For static friction, the FEA responses of Al 2024-T3 and Ti6Al4V with Johnson–Cook damage are parameterized by the following equation for use in the SV model:

$$\begin{aligned} \mu ^*\left( \dfrac{\omega }{\omega _{\mathrm{c}}}\right) = \gamma _1~\mathrm {coth} \left( \left( \dfrac{\omega }{\omega _{\mathrm{c}}}\right) ^{\gamma _2}\right) + \gamma _3, \end{aligned}$$

(11)

where $\gamma _k$ are constants to be estimated from the FEA response using, for example, a least squares fit. For comparison, the KE model [7] for the single asperity response used by Sista and Vemaganti [22] is

$$\begin{aligned} \mu ^* = \left\{ \begin{array}{l} 0.516\left( \dfrac{P^*}{P_{\mathrm{c}}^*}\right) ^{-0.345}, \quad 0 < \omega \le \omega _{\mathrm{c}}\\ -0.007\left( \dfrac{P^*}{P_{\mathrm{c}}^*}\right) ^{2.104}+0.083\left( \dfrac{P^*}{P_{\mathrm{c}}^*}\right) ^{1.405}\\ -0.380\left( \dfrac{P^*}{P_{\mathrm{c}}^*}\right) ^{0.701}+ 0.822, \,\,\,\,\,\, \omega _{\mathrm{c}} \le \omega \le 6\omega _{\mathrm{c}}\\ 0, \quad 6\omega _{\mathrm{c}} \le \omega \le 110\omega _{\mathrm{c}}\\ \end{array} \right. \end{aligned}$$

(12)

where the dimensionless normal force $\frac{P^*}{P^*_{\mathrm{c}}}$ is given by

$$\begin{aligned} \frac{P^*}{P^*_{\mathrm{c}}} = \left\{ \begin{array}{ll} \left( \dfrac{\omega }{\omega _{\mathrm{c}}}\right) ^{3/2}, &{} \omega \le \omega _{\mathrm{c}}\\ 1.03\left( \dfrac{\omega }{\omega _{\mathrm{c}}}\right) ^{1.425}, &{} 1\le \omega \le 6\omega _{\mathrm{c}}\\ 0.93\left( \dfrac{\omega }{\omega _{\mathrm{c}}}\right) ^{1.136}, &{} 6\le \omega \le 110\omega _{\mathrm{c}}.\\ \end{array} \right. \end{aligned}$$

(13)

3.2 Statistical Model of Surface

The surface is modeled as an isotropic Gaussian random process with the surface height as the random variable. Following Longuet-Higgins [23], Nayak [24], and Francis [25], the statistical distribution of asperity height and curvature of an isotropic surface is represented using a function $f(\xi ,\eta )$ that gives the joint probability of finding an asperity with normalized height $\xi$ and normalized curvature $\eta$ on the surface:

$$\begin{aligned} \begin{array}{rcl} f(\xi ,\eta )&{}=&{}\dfrac{\sqrt{3}}{\pi \sqrt{1-\beta ^2}}\{\eta ^2-1+\mathrm {exp} \left( -\eta ^2\right) \}\\ &{}&{}\times \mathrm {exp}\left[ -\dfrac{1}{2\left( 1-\beta ^2\right) } \{\xi ^2-2\beta \xi \eta +\eta ^2\}\right], \end{array} \end{aligned}$$

(14)

where $\beta =\sqrt{\dfrac{1.5{m_2}^2}{\left( m_0m_4\right) }},$ where $m_0$, $m_2$ and $m_4$ are the radial spectral moments of the surface. The autocorrelation function (ACF) for the surface heights is assumed to be Gaussian with the form

$$\begin{aligned} R(x) = \frac{1}{\sigma ^2} \exp {-\left( \frac{x^2}{\lambda ^2}\right) }, \end{aligned}$$

(15)

where $\sigma$ is the root-mean-square (RMS) roughness of the surface and $\lambda$ is correlation length. Then the radial spectral moments of the surface (and therefore the joint probability density function f) are completely specified by the ACF parameters $\sigma$ and $\lambda$:

$$\begin{aligned} m_0=\sigma ^2,\,\,\,\, m_2=\dfrac{2\sigma ^2}{\lambda ^2},\,\,\,\, m_4=\dfrac{12\sigma ^2}{\lambda ^4}. \end{aligned}$$

(16)

Sista and Vemaganti [22] define a parameter known as the surface aspect ratio:

$$\begin{aligned} \mathrm {Aspect~ratio}=\frac{\sigma }{\lambda } \end{aligned}.$$

(17)

For a constant aspect ratio, as the RMS roughness of the surface increases, the correlation length increases proportionally. This results in asperities that are tall and broad with gradually changing heights. For a constant RMS roughness and increasing aspect ratio the overall asperity heights remain the same, although the asperities become narrower, almost spiky in nature due to the proportional drop in correlation length. These changes in the nature of the surface are shown in Fig. 6.

Fig. 6

Surface asperity distribution for various values of surface roughness and aspect ratio [22]

3.3 Statistical Homogenization

The third component of the SV model deals with summing the contributions from all the asperities on a surface using statistical homogenization. This is shown in the center box of Fig. 1. The macroscopic normal force $\langle P\rangle$, macroscopic shear force $\langle Q\rangle$ and the macroscopic coefficient of friction $\langle \mu \rangle$ are given by:

$$\begin{aligned} \langle P\rangle= & {} D_p \displaystyle \int _{\eta =0}^\infty \displaystyle \int _{\xi =h}^\infty P^*\left( \xi ,\eta \right) f\left( \xi ,\eta \right) \,\,\mathrm {d}\xi \,\,\mathrm {d}\eta \nonumber \\ \langle Q\rangle= & {} D_p\displaystyle \int _{\eta =0}^\infty \displaystyle \int _{\xi =h}^\infty \mu ^*P^*\left( \xi ,\eta \right) f\left( \xi ,\eta \right) \,\,\mathrm {d}\xi \,\,\mathrm {d}\eta \nonumber \\ \langle \mu \rangle= & {} \dfrac{\langle Q\rangle }{\langle P\rangle },\end{aligned}$$

(18)

where $D_p=m_4/(6\sqrt{3}\pi m_2)$ is the density of asperities on the surface and $\mu ^*$ is the parameterized single asperity static friction coefficient. A recursive adaptive Simpson quadrature method in the software MATLAB [36] is used to evaluate the integrals in Eq. (18).

4 Results and Discussion

This section is divided into four subsections. First, we describe the mesh convergence studies carried out to ensure the accuracy of the simulations. Then, the normal force behavior of a single asperity under compression alone is discussed. The third part discusses results of combined normal and tangential loading on a single asperity. Finally, the results of the macroscopic friction studies are discussed.

4.1 Mesh Convergence Study

A mesh sensitivity study is conducted prior to the analysis wherein the dimensionless normal force versus dimensionless normal displacement responses ($P/P_{\mathrm{c}}$ vs. $\omega /\omega _{\mathrm{c}}$) from three meshes are compared to the Hertzian response and the dimensionless shear force versus dimensionless lateral displacement responses ($Q/P_{\mathrm{c}}$ vs. $u_x/\omega _{\mathrm{c}}$) are compared to each other in Fig. 7. The legend denotes the smallest element size of a particular mesh in terms of the asperity radius R. The normal force results for the two-dimensional axisymmetric and the three-dimensional half-hemisphere model both agree very closely with the Hertzian solution. The difference between the final and intermediate meshes is 0.16% and that between the Hertzian solution and the finest mesh is 0.32%. In the case of the shear force, the difference between the intermediate and finest meshes is 2.65%. The finest mesh is used in the rest of the studies reported here.

Fig. 7

Mesh convergence study: normal and shear force responses for various mesh sizes

4.2 Asperity Compression Response

4.2.1 Quasistatic Linear Elastic-Perfectly Plastic Material

In Figs. 8 and 9, we show the normal force–displacement response for Al 2024-T3 and Ti6Al4V using the elastic-perfectly plastic material model. For interference values up to $2\omega _{\mathrm{c}}$, the computed response follows the Hertzian response (as seen from the mesh convergence studies). At high interference values, when the material undergoes extensive plastic deformation, the response transforms into a linear curve with a smaller slope.

Fig. 8

Comparison of computed FEA results with various normal force models in the literature for elastic-perfectly plastic Al 2024-T3. Insets show the discontinuity in the KE and CEB models

Fig. 9

Comparison of computed FEA results with various normal force models in the literature for elastic-perfectly plastic Ti6Al4V. Insets show the discontinuity in the KE and CEB models

As shown in the insets of Figs. 8 and 9, the CEB model [1] has a discontinuity at $\omega _{\mathrm{c}}$. Also, up to a compression of $14\omega _{\mathrm{c}}$, the normal force predicted by the CEB model is more than that predicted by the current finite element simulation. Beyond $14\omega _{\mathrm{c}}$, the CEB response is lower than the current one. This is because the CEB model assumes that the entire contact region turns plastic beyond the critical interference and that the hardness (or average indentation pressure) of the material is constant regardless of the change in geometry. This limitation of the CEB model is also discussed by Evseev et al. [2].

The piecewise KE model, which is a power law model, shows good agreement with our FEA response up to a compression of $60\omega _{\mathrm{c}}$ for both Al 20204-T3 and Ti6Al4V metals. This is shown in Figs. 8 and 9. Beyond that value, it predicts a higher force than that predicted by the current model. The piecewise KE model [7] also shows discontinuities in its results in terms of slope and magnitude at $\omega _{\mathrm{c}}$ and $6\omega _{\mathrm{c}}$ compression ratios. On the other hand, the Jackson–Green model [8] shows good agreement with our FEA results and also does not suffer from any discontinuities.

4.2.2 Quasistatic Linear Strain-Hardened Material

Next, we introduce linear strain hardening into the material model for the asperity. As expected, the normal force–displacement response increases in terms of magnitude and slope, nearly proportional to the tangent modulus, as shown in Figs. 10 and 11.

Fig. 10

Effects of strain hardening: computed normal force responses of isotropic strain-hardened Al 2024-T3 under compression for various values of the tangent modulus

Fig. 11

Effects of strain hardening: computed normal force responses of isotropic strain-hardened Ti6Al4V under compression for various values of the tangent modulus

4.2.3 Linearly Elastic-Perfectly Plastic Material with Varying Loading Rates

The effects of different loading rates (0.1, 1, 5 and 10 m/s) are studied next. The results for the Al alloy assuming perfect plasticity are shown in Fig. 12. Velocities higher than 10 m/s are not included in the study as the FE model begins to show numerical instabilities at high loading rates leading to non-physical results. The increase in compression loading rate leads to a very negligible increase in the normal force response for the Al 2024-T3 alloy. This increase caused by greater inertial forces at non-quasistatic velocities is so small that one can assume these responses to be approximately equal up to a velocity of 10  m/s. The corresponding results for the Ti6Al4V alloy are very similar and are not shown for the sake of brevity.

Fig. 12

Effects of loading rate: computed normal force response for elastic-perfectly plastic Al 2024-T3 under compression at different rates. Insets show smooth responses at low compressions but increasing oscillations at high compression values

4.3 Single Asperity Shearing Response

4.3.1 Quasistatic Linearly Elastic-Perfectly Plastic Material

Subsequent to the normal loading, a shear load is applied to the asperity. Assuming elastic-perfectly plastic behavior, the shear force responses for the Al 2024-T3 alloy at different compressive preloads are shown in Fig. 13. For low compression preloads the failure limit occurs at smaller tangential displacements, while at high compression preloads a larger tangential displacement is required for failure. This happens because the contact area for the low compression case is small and the shear load is supported by this small area, which fails rapidly leading to a quick decrease in the shear force resistance. On the other hand, an asperity with a large preload has a larger contact area with the rigid surface and therefore many elements are required to fail before the net shear force resistance drops.

Fig. 13

Asperity shearing response: change in shear force with lateral displacement for various levels of compressive preload. Elastic-perfectly plastic Al 2024-T3 asperity. Inset: a closer look at the responses for preloads of $0.25\omega _{\mathrm{c}}$, $0.5\omega _{\mathrm{c}}$ and $1.0\omega _{\mathrm{c}}$. Note the much smaller scale on the force axis compared to the main figure

The shear force, normal force and static friction responses of the Ti6Al4V alloy assuming elastic-perfectly plastic behavior are qualitatively very similar to the Al 2024-T3 responses and therefore not shown. Likewise, these responses for both materials, including isotropic strain hardening and rate hardening behavior or even with different damage models, are qualitatively very similar and hence not repeated.

Next, the static coefficient of friction for the asperity as a function of the interference is shown in Fig. 14. For each alloy considered here, we see that the material parameters as well as the choice of the damage model significantly impact the friction response. For the purpose of comparison, the figure also shows the responses predicted by the BKE model [16], the WSP model [17] and the KE model [15]. The BKE model response is for a hypothetical material with $Y/E= 10^{-3}$, while the WSP model response represents Al 2024-T351 with $Y/E=4.4 \times 10^{-3}$. The KE model is developed for the range $10^{-2} \ge Y/E \ge 10^{-3}$ [15].

Fig. 14

Asperity coefficient of friction as a function of compression for Al 2024-T3 and Ti6Al4V using various quasistatic elastic-perfectly plastic models. FEA refers to the results of the current study

The KE model assumes that asperity shear failure occurs when there is plastic inception in the contact region. Their semi-analytical friction model also does not consider the softening of the normal resistance provided by the asperity as it is sheared; instead, the model uses the normal force from the compression-only results. Due to these assumptions the KE model underestimates friction considerably. In reality, the asperity does support shear loads beyond the inception of plasticity in the contact area and fails at a later stage. The BKE response is similar to our FEA response for both alloys with the Johnson–Cook damage model. Both the BKE and WSP models agree with the computational results for JC damage at high interference values.

4.3.2 Quasistatic Bilinear Isotropic Strain-Hardened Material

Strain hardening has different effects on Al 2024-T3 and Ti6Al4V, as shown in Figs. 15 and 16, respectively. For the Al 2024-T3 alloy, there is a large increase in the friction response, especially at low interference values, as the tangent modulus is increased. This is in contrast to the nominal increase in the friction coefficient for the Ti6Al4V alloy.

Being more ductile, the Al 2024-T3 alloy undergoes considerable plastic deformation and strain hardening before damage. Thus, at high plastic strains it provides more resistance, leading to a larger coefficient of friction. On the other hand, the Ti6Al4V alloy fails more quickly and is unable to achieve a large amount of plastic deformation.

Fig. 15

Asperity coefficient of friction as a function of the tangent modulus: Al 2024-T3

Fig. 16

Asperity coefficient of friction as a function of the tangent modulus: Ti6Al4V

4.3.3 Linearly Elastic-Perfectly Plastic Material with Varying Loading Rates

We now consider the friction responses of the alloys at various shearing rates. Note that the non-quasistatic shear loading rate is not the slip velocity between the contacting bodies. Rather, it is the rate at which the junction between the bodies is broken. As such, the friction parameter being observed in this scenario is still the static coefficient of friction.

Fig. 17

Asperity coefficient of friction as a function of the shearing rate

Similar to the rate-dependent normal force response, the rate-dependent friction response shows a negligible increase over the quasistatic results as shown in Fig. 17. This negligible increase is due to the very small inertial effects at or below 10 m/s shearing velocity and the strain rate-dependent parameters in the Johnson–Cook damage model, which are very small in magnitude compared to the other parameters. Thus, their effect at such low velocities is almost undetectable.

4.4 Macroscopic Friction

4.4.1 Parameterization of Single Asperity Response

The computed FEA responses of Al 2024-T3 and Ti6Al4V with JC damage are parameterized by Eq. (11). The resulting values for the coefficients $\gamma _k$ are shown in Table 3. The corresponding fits are shown in Fig. 18, where very good agreement is observed between the data and the parametric representations.

Fig. 18

Parameterization of computed single asperity responses by Eq. (11) for Al 2024-T3 and Ti6Al4V

Table 3 Parameterization of an asperity’s response: coefficients $\gamma _k$ in Eq. (11) for Al 2024-T3 and Ti6Al4V

4.4.2 Effect of Surface Roughness and Aspect Ratio

Figure 19 shows the macroscopic friction coefficient as a function of the average normal stress on the surface for various aspect ratios as well as different asperity materials. As the aspect ratio of the surface increases the coefficient of friction decreases. This is because a surface with a high aspect ratio is more likely to have tall spiky asperities that easily come into contact with the rigid plane, undergo higher compression and reach failure sooner. A surface with a low aspect ratio has broader asperities that provide more resistance to loading and result in a higher coefficient of friction. Thus, in Fig. 19 the macroscopic friction coefficient nearly doubles as the aspect ratio is halved. There is significant difference between the friction coefficients calculated from the single asperity FEA results of Al 2024-T3, Ti6Al4V and the semi-analytical KE model. This is because the semi-analytical KE friction model does not consider the softening of the normal resistance provided by the asperity. Consequently, macroscopic friction is highly dependent on the material and failure models chosen for the asperity.

Fig. 19

Macroscopic friction variation with surface aspect ratio for Al 2024-T3 and Ti6Al4V

Figure 19 captures the essence of the micro-to-macro-approach used in this work. Knowing the constitutive response of the asperity material and knowing the surface characteristics, the statistical homogenization procedure allows us to obtain the overall friction response of the surface in a form that can readily be used in, say, a finite element analysis to simulate macroscopic friction more realistically.

5 Conclusions

In this study, finite element models of a hemispherical asperity are employed to study the normal force–displacement response in compression and the friction response in full stick shear. These responses are computed for various material models at multiple loading rates. The Johnson–Cook damage model and the Bao–Wierzbicki damage model control the material deterioration in the shearing simulations. This study limits the simulation velocities to a magnitude less than or equal to 10 m/s to ensure convergence in the transient simulations and to avoid non-physical results.

The results from the single microscale asperity study are scaled up to the macroscale using a statistical homogenization procedure, which uses the single asperity response and a model of the surface roughness to determine the overall friction response. The main outcomes of the study are summarized as follows.

• The Jackson–Green model for the normal force response of an asperity shows very good agreement with the results of our very detailed two- and three-dimensional finite element analyses. This response shows a significant increase in magnitude with strain hardening. This relationship needs to be studied extensively for a variety of materials before general expressions can be developed.

• Increasing the compression rate leads to a negligible increase in the normal force up to velocities of 10 m/s and can be ignored at low velocities. Similarly, an asperity’s friction response varies very little at low shearing rates and can be assumed to be approximately constant up to a rate of 10 m/s.

• Depending on the material, an increase in an asperity’s tangent modulus can lead to a considerable increase in its coefficient of friction, especially at lower compressions. Additional studies over a wider range of materials are needed to quantify and further generalize our results.

• The choice of the material damage model significantly changes the static friction coefficient of an asperity for a given set of elastic and plastic material parameters. Therefore, the availability of material damage data that can guide the calibration and selection of an appropriate damage model plays an important role. Material characteristics that may affect an asperity’s friction response are also important to consider (e.g., temperature dependency, low triaxiality range, strain rate dependency).

• Macroscopic friction is highly dependent on the material and failure models chosen for the asperity. A good understanding of material behavior and careful experimentation are therefore necessary to facilitate accurate modeling and simulation of macroscopic friction.