On the Linearity of Contact Area and Reduced Pressure

Abstract

Computer simulations, Persson theory, and dimensional analysis find that the relative contact area between nominally flat surfaces grows linearly with the reduced pressure $p^*$ at small loads, where $p^*$ is the ratio of the macroscopic pressure p to the contact modulus times the root-mean-square height gradient $\bar{g}$. Here, we show that it also holds for Hertzian and other harmonic, axisymmetric indenters—as long as $\bar{g}$ is determined over the true contact area and p is defined as the load divided by an arbitrary but fixed reference area. For a Hertzian indenter, the value for the proportionality coefficient $\kappa$ turns out to be $\kappa = 3\pi /\sqrt{32}$. The analysis explains why mathematically rigorous treatments of Greenwood–Williamson type models identify a sublinear dependence of contact area on load.

1 Introduction

The recent past has seen much work on the linear elasticity of solids with nominally flat surfaces. It is now well established [1,2,3,4,5,6,7] that the equation

$$\begin{aligned} a_\mathrm{rel} = \kappa p^* \end{aligned}$$

(1)

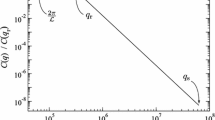
describes the dependence of the relative contact area on the reduced pressure $p^*$ quite well, where $p^* \equiv p/E^* \bar{g}$ is assumed to be small compared to unity. In this definition, $E^*$ is the contact modulus, and $\bar{g}$ the root-mean-square gradient of the air gap between the two solids before they touch. If the height topographies are randomly rough (to be precise, if the Fourier components of the height topography satisfy the random-phase approximation), the value of $\kappa$ turns out to be slightly greater than two with a rather weak dependence on the Hurst roughness exponent [2, 3, 7].

Since Eq. (1) was also obtained from dimensional analysis [7], the question arises why it does not appear to hold for those cases, where analytical relations are known such as Hertzian or other axisymmetric indenters. In this Letter, it is shown that this perception is erroneous and that Eq. (1) also applies to certain single-asperity contacts.

2 Theory

We start our calculation by assuming that

$$\begin{aligned} a_\mathrm{rel} = \kappa {p}/{\bar{g}E^*} \end{aligned}$$

(2)

is satisfied for an axisymmetric indenter with a harmonic height profile

$$\begin{aligned} h(\rho ) = \frac{R}{n} \left( \frac{\rho }{R}\right) ^n \end{aligned}$$

(3)

for $n > 0$. Here $\rho$ gives the distance from the symmetry axis, and R is a variable of unit length. For a Hertzian indenter ($n=2$), R is the radius of curvature. Assuming an arbitrary but fixed apparent contact area over which the pressure is averaged, Eq. (2) can be rewritten as

$$\begin{aligned} \pi a_\mathrm{c}^2 = \frac{\kappa L}{\bar{g} E^*}. \end{aligned}$$

(4)

The root-mean-square gradient of the undeformed gap profile, averaged over the true contact, is

$$\begin{aligned} \bar{g} = \frac{1}{\sqrt{n}} \left( \frac{a_\mathrm{c}}{R} \right) ^{n-1}. \end{aligned}$$

(5)

Replacing $\bar{g}$ in Eq. (4) leads to the equality

$$\begin{aligned} L = \frac{\pi E^*}{\kappa \sqrt{n}} a_\mathrm{c}^2 \left( \frac{a_\mathrm{c}}{R} \right) ^{n-1} , \end{aligned}$$

(6)

which reduces to the well known $L \propto a_\mathrm{c}^3$ relation for a Hertzian contact.

From Sneddon’s analytical solution for axisymmetric indenters, see Eqs. (4.3) and (7.3) in Ref. [8], one obtains

$$\begin{aligned} L = c_n E^* a_\mathrm{c}^2 \left( \frac{a_\mathrm{c}}{R} \right) ^{n-1} \end{aligned}$$

(7)

with

$$\begin{aligned} c_n = \frac{\sqrt{\pi }\Gamma \left( \frac{n}{2}+1\right) }{\Gamma \left( \frac{n}{2}+\frac{3}{2}\right) } , \end{aligned}$$

(8)

where $\Gamma (\bullet )$ represents the gamma function. Thus, for Eq. (6) to be correct, we need to set

$$\begin{aligned} \kappa = \frac{\pi }{c_n \sqrt{n}}. \end{aligned}$$

(9)

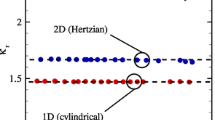
Evaluating $\kappa$ at $n = 2$ yields

$$\begin{aligned} \kappa _\mathrm{H} = \frac{3\pi }{\sqrt{32}} \end{aligned}$$

(10)

for a Hertzian indenter.

3 Discussion and Conclusions

In this letter, it is demonstrated that Eq. (2) does not only apply to randomly rough surfaces but also to axisymmetric punches whose height profile is a harmonic function of degree n in the distance from the symmetry axis. Equation (2) must therefore also hold for a collection of indenters if the patch-area distribution function does not change with load. The numerical value for an individual Hertzian indenter, $\kappa _\mathrm{H} \approx 1.67$, is markedly different from that obtained in the famous paper by Bush et al. [9], $\kappa _\mathrm{BGT} = \sqrt{2\pi } \approx 2.52$, but close to Persson’s original estimate [1] of $\kappa$, namely $\kappa _\mathrm{P} = \sqrt{8/\pi } \approx 1.60$. One difference between our and these previous treatments is that we determine $\bar{g}$ solely over the real contact area, while the usual definition of $\bar{g}$ considers the full surface. However, this difference is not significant for randomly rough surfaces, which we tested numerically.

Simulations reveal that there must be a characteristic (maximum) cluster size in real contacts, which increases with load [10]. As a consequence the mean value of $\bar{g}$ also increases with load for $n > 1$ and decreases for $n < 1$, and thus, a rigorous treatment of the Greenwood–Williamson model [11] model must lead to a slightly sublinear dependence of $a_\mathrm{r}$ with p for $n>1$. Given the computational resources in the mid-1960s, it might be understandable that GW did not realize the deviation of the true $a_\mathrm{rel}(p)$ relation in their model from linearity. However, it is astounding to notice that since then only one numerical GW study [4] appears to have been sufficiently carefully designed to unravel that discrepancy. This adds to our previous criticism that bearing-area models predict contacts to be much too clustered near the highest peak [12, 13] and to substantially underestimate the mean displacement at small loads [14].