1 Introduction

The highly complex manufacturing processes required for integrated circuits (ICs) or computer chips lead to systematic variations which decrease the manufacturing yield of the product. As technology scales down, these systematic variations have increased, leading to more failures in the form of increased parasitics, short circuits, and open circuits [1]. Chemical mechanical polishing (CMP) has allowed tighter and more aggressive design rules to be used by improving the uniformity of deposition and lithography by reducing surface roughness.

CMP is a specialized polishing process in which the surface of a wafer is planarized by mounting it on a rotating chuck and pressing it against a rotating pad that is flooded with slurry consisting of a fluid and abrasive nanoparticles [2]. Scanning electron microscope (SEM) images from industry have shown that the wafer is non-uniformly polished. This occurs at the wafer, die, and feature scale [3, 4]. The feature-scale non-uniform polish causes systematic defects found in manufacturing commonly referred to as dishing and erosion. Dishing (the removal of metal faster than the surrounding oxide) and erosion (the excess wear of dielectric materials in regions where there are densely patterned metal lines) are two types of defects that arise during manufacturing when a composite, typically two alternating materials, surface is polished as seen in Fig. 1a, b. This non-uniformity leads to multiple undesired effects on the circuit. It affects the resistance, capacitance, and inductance (RLC) parasitics, and accurate extraction becomes a difficult task even for commercial tools [5]. Statistical timing analysis (STA) is performed using these electrical parameters in order to compute critical path delay and operating frequency. If the parasitics are not accurately modeled, it is possible for the system to no longer be able to operate at the desired frequency since timing, such as the critical path delay, may significantly differ from the STA simulations post-manufacturing. Additionally, the non-uniformity affects the subsequent layers and causes large topographical variation and undesired effects for lithography. This can lead to hard failure due to open and short circuits as shown by Mekkoth [6]. These complexities and variations cause it to be a major barrier which must be addressed in design for manufacturability (DFM) rules [2].

Fig. 1
figure 1

a Dishing and erosion are two common systematic defects that occur during the CMP process. b SEM showing severe dishing and erosion across multiple layers in an integrated circuit

Full size image

To circumvent time-consuming fundamental physics-based computer models, designers often follow rules, use empirical models, and employ fix methods such as dummy fill in order to minimize the defects of CMP [7]. However, the variation in topography is not deterministic at the feature scale, the dummy fill causes an increase in capacitance, and the empirical data are costly and take months to generate and analyze, causing lead products not to benefit [8].

Seminal models such as the MIT pattern density model [9–13] are semi-empirical, typically focusing on the die and feature scales. They use a modified version of the Preston material removal rate equation in combination with an effective pattern density and the fitted parameters such as the interaction distance of the pad in order to predict the effects of CMP. MIT models have been verified and validated with profilometer, electron microscope, and electrical data from CMP test wafers, which consist of blocks of simple layout with different spacing, densities, areas, and line widths [14] (see Fig. 2). The model has progressed over time and now incorporates filtering functions for more realistic effective pattern densities, contact mechanics for better determining the pressure at the die scale, and more accurate empirical formulations.

Fig. 2
figure 2

CMP test mask illustration from D. Boning 2003 [14]. Pitch, density, and area are varied across the layout

Full size image

Alternatively, die and feature-scale physics-based models have been presented in the literature [8, 15–20]. The high-fidelity models use contact mechanics combined with the Preston material removal rate equation to predict the CMP evolution. However, they have focused on periodic features due to model limitations and computational resources [15–18]. Others have presented statistical treatments of contact mechanics coupled with the Preston equation sacrificing fidelity for speed [19, 20]. Terrell and Higgs developed a full multi-physics (i.e., fluid dynamics, particle dynamics, and contact mechanics) model in order to predict CMP [8] at the feature scale. While this feature-scale model has one of the highest fidelities, it is hampered by being computationally expensive and too slow for regions of interest larger than a few features.

Contact mechanics-based approaches to modeling pad deformation have been developed to operate at the feature scale using the Winkler or elastic foundation model. Similar to the field of computer graphics, surfaces can be represented as discrete cuboid elements called “voxels” (i.e., volume pixels [21]). The Winkler model in essence treats the voxel-represented surface as a set of springs. The Winkler model’s use of voxel on voxel contact has been shown to represent the real contact area in micro-/nanoscale applications with reasonable accuracy [22, 23]. However, the lack of coupling between voxels in the Winkler model leads to the over-prediction or under-prediction of wear. Sawyer circumvented this issue by introducing a 2D numerical model [24] which captures the pressure evolution between two surfaces by coupling spatial elements through the introduction of a second-order fitting parameter. This parameter introduces curvature into the Winkler elastic foundation model while ensuring the dishing profile takes on a parabolic shape. The novelty in their work was being able to produce dishing and erosion effects from two initially flat surfaces, where one is composed of two different materials. This model was also a computationally inexpensive method for simulating dishing and erosion profiles without the use of filtering/weighting functions associated with pattern density. However, their model cannot be re-formulated in three dimensions (3D) and uses fitting parameters which are not physical material properties.

In this paper, a 3D physics-based model and methodology is presented for feature-scale CMP evaluation of an arbitrary layout. This model and methodology addresses the shortcomings of empirical models while keeping the fidelity of previous physics-based models with reduced computational burden. In addition, it minimizes error that arises as a natural consequence of the mathematics near the boundaries of the domain being simulated, and it is able to simulate CMP on aperiodic layouts. Dishing and erosion are captured without utilizing fluid and particle dynamics. Such high fidelity, and allowance of aperiodicity, may be important when dealing with application-specific integrated circuits (ASICs) in leading-edge technology nodes such as 22 nm, where data may not be available a priori and changes in resistance and capacitance (RC) are critical to manufacturing yield and chip performance.

2 Theory

Polishing rates depend on numerous parameters such as material hardness, applied pressure, number of abrasive particles, slurry pH levels, and other tribological, material, and chemical parameters. As mentioned, the non-uniformity of the surface can lead to changes in critical electrical parameters such as resistance, inductance, and capacitance due to increased parasitic effects. It is therefore crucial to accurately model the effects of CMP and other manufacturing processes. The Preston material removal rate Eq. (1) is a semi-empirical physics-based model which determines the material remove rate (MRR), as follows:

$${\text{MRR}} = \frac{{{\text{d}}h}}{{{\text{d}}t}} = K \times V \times P$$
(1)

where K is the empirical “Preston’s coefficient,” a proportionality constant determined from CMP experiments designed to account for the mechanical and chemical uncertainties, P is the applied pressure on the wafer, V is relative velocity between the wafer and pad during CMP, and h is the surface height which changes with time, t, due to polishing.

Dishing and erosion occur at the feature scale where the relative velocity can be assumed uniform. The Preston coefficient K can be treated as a constant for a given pair of rubbing materials and process set. Studies have shown that the pressure is strongly a function of position, which would lead to varying levels of dishing and erosion from the Preston equation [25–27]. If the surfaces are very smooth, as is the case in the polishing segment of CMP where dishing and erosion occur, the spatially dependent pressure would emerge from the influence from neighboring elements on the surface. This would be difficult to capture in the Winkler elastic model which excludes shear between neighboring surface elements. Thus, a 3D elastic half-space contact mechanics model, derived from the Boussinesq and Cerruti potential functions, is used in this study as shown below:

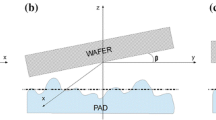
$$u_{z} (x,y) = \frac{{1 - \nu^{2} }}{{\pi E_{{}} }}\int {da\int {db\frac{p(a,b)}{{\sqrt {(x - a)^{2} + (y - b)^{2} } }}} }$$
(2)

A discussion and derivation can be found in Johnson [28]. A solution, expressed below, was formulated by Love [29] relating a uniform pressure p, acting on a rectangular area of 2a × 2b, on an elastic half-space, to the deflection u z , at a general point, a distance (x, y) away.

$$u_{z} = \frac{{(1 - v^{2} )}}{\pi E}\left\{ \begin{aligned} (x + a)\ln \left[ {\frac{{(y + b) + \sqrt {\left\{ {(y + b)^{2} + (x + a)^{2} } \right\}} }}{{(y - b) + \sqrt {\left\{ {(y - b)^{2} + (x + a)^{2} } \right\}} }}} \right] \hfill \\ + (y + b)\ln \left[ {\frac{{(x + a) + \sqrt {\left\{ {(y + b)^{2} + (x + a)^{2} } \right\}} }}{{(x - a) + \sqrt {\left\{ {(y + b)^{2} + (x - a)^{2} } \right\}} }}} \right] \hfill \\ + (x - a)\ln \left[ {\frac{{(y - b) + \sqrt {\left\{ {(y - b)^{2} + (x - a)^{2} } \right\}} }}{{(y + b) + \sqrt {\left\{ {(y + b)^{2} + (x - a)^{2} } \right\}} }}} \right] \hfill \\ + (y - b)\ln \left[ {\frac{{(x - a) + \sqrt {\left\{ {(y - b)^{2} + (x - a)^{2} } \right\}} }}{{(x + a) + \sqrt {\left\{ {(y - b)^{2} + (x + a)^{2} } \right\}} }}} \right] \hfill \\ \end{aligned} \right\}p$$
(3)

This formulation, herein referred to as Love’s formulation, couples neighboring elements as would physically happen in an elastic half-space such as a CMP pad. Coupled surface elements are important for capturing phenomena such as dishing and erosion which are highly sensitive to the composition of the surrounding layout areas. Further, since layout is deterministic, a framework which allows specific materials and geometrical properties to be assigned to specific surface regions is of importance. This fits in well with voxel surface representation since properties can be assigned to specific voxel coordinates, albeit the pressure is assumed to be uniform over the voxel. Figure 3 illustrates the formulation parameters. When the pressure profile p is known, the surface deflection u z may be determined (and vice versa) by simultaneously solving the coupled system of equations:

$${\mathbf{u}}_{{\mathbf{z}}} = {\mathbf{Cp}}$$
(4)

where u z and p are vectors composed of each of the elements in the domain and C is a matrix composed of the influence coefficients from (3).

Fig. 3
figure 3

Love’s formulation determines the deflection caused by an applied pressure, p, at any point in the domain at a distance (x, y) from the pressure. The domain is split into a square grid with a size of (2a × 2b) per element

Full size image

Alternatively, the system can be solved using Fourier transforms in order to improve computational efficiency [30]. The matrix multiplication solution differs from the Fourier transform-based solution presented by Chekina and Keer [31]. It does not require the domain to be periodic allowing for the study of layouts which are both heterogeneous (i.e., multiple materials) and deterministic (i.e., irregular patterns). In addition, an error-reducing scheme is introduced as shown in “2D Model Implementation” section.

3 Methodology, Experimentation, and Results

3.1 2D Model Implementation

The 3D Love’s formulation (3) can also be represented in 2D. The Love’s formulation was coupled with the Preston Eq. (1) in order to calculate the wafer and pressure evolution over time. Both the pad and wafer are assumed to be perfectly flat before wear occurs. It is also assumed that the pad is not worn down during the simulation. This methodology leads to results with spikes in pressure on the edge of the domain, referred to as “pressure edge effects,” as seen in Fig. 4 near a normalized length of 0 and 1. This is due to the derivation of (3), which is a discrete solution for a finite region located within a semi-infinite spatial domain, as the solution to (2), which is the continuous solution for an entire semi-infinite domain. Simply put, the domain is not just the area accounted for in the influence coefficient matrix C, but the entire elastic half-space. One can only have control over the area specified by the size of the influence coefficient matrix C. This area lies on some arbitrary point in this elastic half-space which by definition is infinitely large. Thus, if all the elements in an arbitrarily prescribed circle are uniformly displaced, the half-space sees a flat punch being pressed in, and the pressure edge effects are expected. Thus, the half-space goes from some deflection uz in the area spanned by the influence coefficient matrix C to a deflection of zero in the area which is not covered by the influence coefficient matrix. The internal spikes in pressure are also caused by a difference in height between adjacent voxels, and one can show by trial and error that the difference in height is proportional to the magnitude of the pressure spike. Since the time step used in (1) determines the magnitude of the differential height, the time step must be chosen wisely so that the pressure evolves in a realistic fashion and does not diverge from a steady-state solution. Overall, the coupling of (3) and (1) is elegant in the sense that an entire wafer could be modeled limited only by the resolution (i.e., the size of the rectangular voxel elements) permitted by computational resources. Figure 5 shows the wear and pressure seen in a wafer containing three metal lines. In addition, the methodology can capture phenomena such as the increased dishing of wider metal lines as seen in Fig. 6. Figure 7a illustrates a flowchart for this methodology, herein referred to as the wafer-scale methodology. However, the scale of interest is in the nanometer range and current resources make this prohibitive. Thus, a different methodology using (3) was developed in order to be able to perform focused or localized analysis in the range of interest without the use of Fourier transforms and the associated error and periodicity conditions that come with it. Instead of allowing for deflection in the entire area represented by the influence coefficient matrix, only deflections which vary from the original mean deflection are considered. A temporary pressure matrix is created from this new treatment of deflection and combined with the average pressure for the localized region. A flowchart illustrating this methodology, referred to as the localized methodology, is presented in Fig. 7b.

Fig. 4
figure 4

Pressure (top) and wafer height (bottom) profiles after simulating CMP for a wafer with a centered metal line

Full size image
Fig. 5
figure 5

Pressure (top) and wafer height (bottom) profiles for three centered lines on a wafer during CMP simulation

Full size image
Fig. 6
figure 6

Pressure and wafer height evolution profiles for a wafer containing two metal lines of different widths

Full size image
Fig. 7
figure 7

a Wafer-scale methodology for pressure and wear evolution during CMP. b Localized methodology for pressure and wear evolution during CMP

Full size image

3.2 2D Localized Comparison

The 2D localized methodology was compared against work done by Sawyer [24] and experiments from the MIT group [32–36]. Comparisons can be seen in Figs. 8, 9, 10, 11, 12 and 13. Table 1 lists the parameters used during the simulation.

Fig. 8
figure 8

Pressure and local height evolution for a single copper line using the localized methodology

Full size image
Fig. 9
figure 9

Steady-state pressure magnitude vs. copper area fraction

Full size image
Fig. 10
figure 10

Wafer height and pressure after 500 time cycles for a 30 % metal/oxide array with eleven metal lines

Full size image
Fig. 11
figure 11

Wafer height and pressure after 500 time cycles for a 70 % metal/oxide array with eleven metal lines

Full size image
Fig. 12
figure 12

Wafer height and pressure after 500 time cycles for a 50 % metal/oxide array with eleven metal lines

Full size image
Fig. 13
figure 13

Wafer height and pressure after 500 time cycles for a 50 % metal/oxide array with fifteen metal lines

Full size image
Table 1 Parameters used during CMP simulation
Full size table

Figure 8 illustrates the evolution of wafer height and pressure for a single line. Edge effects are essentially nonexistent, though some numerical error can be seen after 3000 cycles. Some other interesting things can be noticed from this Fig. 8. For example, a steady-state condition is reached, the final pressure ratio is equal to the ratio of the Preston coefficients, the magnitude of pressure is dependent on the ratio of copper to silicon dioxide, and the copper section reaches equilibrium much sooner than the silicon dioxide. Steady state is expected due to the surface evolving in a non-uniform fashion due to the non-uniform pressure caused by the deformation pad which is assumed to conform to the wafer surface. Once enough time has passed, the pressure will evolve in such a way that the oxide will be removed at the same rate as the copper as described by (5). This same steady-state condition was found and used by Noh et al. [25] in order to develop his dishing and erosion model. Our model arrived at this condition naturally from the transient simulation without a priori knowledge of dishing and erosion behavior. The faster evolution of the copper area is not immediately apparent by looking at our governing equation. However, it does make sense when considering the Preston coefficients and magnitude of the pressure peaks. The lower wear (i.e., polish) resistance of the copper causes the copper to conform to the shape which will allows the elements with higher loads to decompress, resulting in less pressure until equilibrium is reached with its neighbors.

$$\frac{{P_{{oxide_{SS} }} }}{{P_{copperSS} }} = \frac{{K_{oxide} }}{{K_{copper} }}$$
(5)

The steady-state pressure is a function of the fraction of area covered by copper, referred to as the area fraction in [24].

The steady-state normalized pressure from the localized methodology was compared against the linear rule of mixture model determined by Sawyer [24]. The results follow roughly the same trend; however, they diverge as the area fraction increases. We believe that this divergence is due to the difference between the half-space approximation and the elastic foundation approximation of the pad behavior. Elastic foundation models such as the Winkler model have been shown to be a reasonable match [23], but there is some discrepancy as compared with classical elastic deformation solutions such as Hertz [28]. This is attributed to the thickness of the voxel which is more arbitrary than rigorously chosen. This uncertain parameter does not exist for an approach like ours. Thus, as copper area increases, the discrepancy caused by the dubious voxel thickness becomes larger. Results are shown in Fig. 9.

Figures 10, 11, 12, and 13 are direct comparisons against the figures presented in Sawyer [24], since Sawyer’s model was validated by the experiments of [37]. The localized methodology’s results capture the pressure effects at the material interfaces leading to the dishing- and erosion-like profiles encountered during manufacturing. The pressure and wafer height results are a close match with the corresponding results, shown in Fig. 14 from Sawyer’s modeling work [24]. The pressure from Fig. 14 has been non-dimensionalized by the mean applied pressure (6a), while the wear death (highest wafer height–worn wafer height) has been non-dimensionalized by the deflection of the pad under a uniform applied load (6b).

Fig. 14
figure 14

Wafer height and pressure evolution for 40 cycles using Sawyer method. Wear is less than 1 angstrom after 40 cycles

Full size image
$$p^{*} = \frac{p}{{p_{m} }}$$
(6a)
$$w_{h}^{*} = \frac{{w_{h} }}{{z_{0} }}$$
(6b)
$$z_{0} = \frac{{p_{m} }}{{k_{p} }}$$
(6c)

Quantitatively and qualitatively, the local methodology results, Figs. 10, 11, 12, and 13 show good agreement when compared to Fig. 15. The magnitude of pressure during evolution is shown to be dependent on the area fraction, as shown in Figs. 10, 11, and 12, and a spread from ~9 kPa (Fig. 10) to ~15 kPa (Fig. 11) can be seen. Area fraction varies across chip even with tight design rules; thus, there can be CMP-sensitive pieces of layout which may exhibit too large of pressure magnitudes leading to manufacturing defects. Another important observation is that the localized methodology allows the pressure to evolve in a realistic fashion, especially during the early cycles. Figure 14 illustrates the initial evolution of pressure and height using Sawyer’s empirical formula. As shown in Fig. 14, the pressure needs numerous cycles to evolve into the expected pressure profile and initially evolves in a step-like fashion. This is a consequence of the differential term in Sawyer’s formula. This is nonexistent when using the elastic half-space model. The pressure profile is immediately present and evolves in a natural fashion as time progresses. The differential term also requires the time step to be much smaller in order to maintain a stable solution.

Fig. 15
figure 15

Results from numerical simulation by [24] for variation in copper area fraction (a–c) and line width (d). Simulations were run for 5000 cycles. The variable \(\widetilde{\theta }^{b}\) represents the copper area fraction, and all variables have been non-dimensionalized

Full size image

3.3 3D Model Results

The main advantage of the current model is that it is inherently three-dimensional (3D). It can be implemented in 3D in order to capture dishing and erosion effects, since elastic foundation model is 3D to begin with, leaving no complications in transitioning into the 3D domain. Figures 16, 17, 18, and 19 show two simulations done in 3D. The pressure profile and wafer height are shown after five cycles, Fig. 16, and after steady state has been reached, Fig. 17, for a layout composed of three metal lines. We can see that at steady state, the height of the wafer has evolved such that every element is subject to a pressure which causes the exact amount of wear in all voxels. The same simulation was performed on a layout composed of a 3 × 3 via array with transient and steady-state results shown in Figs. 18 and 19, respectively. A random asymmetric layout was also simulated as shown in Fig. 20. As can be seen, pressure behaves in a complex manner. Specifically, bends in lines and the effects of neighboring lines should be of concern to designers during manufacturing. Currently, there are no experiments to compare these results. Mostly, these experiments would serve to more accurately assign parameters as it is difficult to select terms such as elastic modulus and the Preston coefficients which have been shown to have significant variance over time [38, 39]. The 3D results give good high-fidelity height evolutions allowing for exploration of manufacturing run times, material properties, and loads. In addition, post-manufacturing changes such as electric parasitic effects can be measured and studied. Effects such as larger dishing and erosion in the center of via arrays naturally arise using the Love’s formulation allowing for further studies of layout patterns.

Fig. 16
figure 16

3D pressure and height profiles after five cycles for three copper lines surrounded by silicon dioxide

Full size image
Fig. 17
figure 17

3D pressure and height profiles at steady state for three copper lines surrounded by silicon dioxide

Full size image
Fig. 18
figure 18

3D pressure and height profiles after five cycles for a 3 × 3 via array surrounded by silicon dioxide

Full size image
Fig. 19
figure 19

3D pressure and height profiles at steady state for a 3 × 3 via array surrounded by silicon dioxide

Full size image
Fig. 20
figure 20

3D pressure and height profiles after five cycles for an asymmetrical design of copper lines surrounded by silicon dioxide

Full size image

4 Conclusion

A three-dimensional contact mechanics formulation with a wafer and localized methodology is presented for both two and three dimensions. It captures dishing and erosion effects at both the wafer and feature scale. The localized methodology allows for the study of local wear without the need to discard large amounts of edge data. Unlike Fourier transform methods which introduce error and have periodicity constraints which need to be met, the current model allows for high accuracy. The formulation fits well with the voxel surface elements representation which is well suited for nanoscale applications and deterministic surfaces such as those born from IC layouts. Results are compared against an empirical feature-scale model which had been experimentally validated. The methodology and model offer physics-based results that further the understanding of CMP for any given layout.