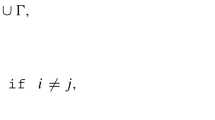1 Introduction

In slow flow through a porous medium the dynamic, frequency-dependent permeability is defined by generalizing the Darcy’s law to the frequency domain:

$$\begin{aligned} \mathbf{v}(\omega )=-\frac{K(\omega )}{\mu }{\varvec{\nabla }}P(\omega )\;, \end{aligned}$$
(1)

where v and \(\mu \) are, respectively, the fluid’s velocity and viscosity, \(K(\omega )\) is the frequency-dependent permeability, P is the pressure, and \(\omega \) is the frequency. Dynamics is introduced into the system by setting \(P(\mathbf{x},\omega )=P(\mathbf{x})\exp (-i\omega t)\) as the alternating-current (AC) pressure between two opposite faces of a porous medium at time t, i.e., the oscillatory pressure drop. Equivalently, one can inject a fluid into the pore space whose speed is an oscillatory function of time. The usual static permeability of the pore space is then, \(K_0=K(\omega =0)\).

Fig. 1
figure 1

Complex hydraulic conductance of a pore between nodes j and m, with g being the real conductivity and \(iC\omega \) representing the capacitance effect

Full size image

The dynamic permeability is a complex function of the frequency. Its real part characterizes the flow generated by the viscous forces, and is a decreasing function of frequency. The imaginary part of \(K(\omega )\) characterizes the phase shift caused by fluid inertia, and goes through a maximum at a frequency \(\omega _m\) at which a transition from the viscous-dominated flow to an inertia-dominated regime occurs, and the viscous penetration depth, the region in which the viscous effects are concentrated, is on the order of the pore sizes. The roughness of the pore surfaces also affects the dynamics permeability (Cortis et al. 2003).

Oscillatory flow and the resulting dynamic permeability provide an efficient way of characterizing the (linear) response of a fluid to an oscillating pressure gradient \({\varvec{\nabla }}P\), because the frequency-dependent permeability quantifies the resistance to flow for each of the modes present in \({\varvec{\nabla }}P\), and contains information about the porous medium, or any system in which the oscillatory flow is occurring (Johnson et al. 1987; Charlaix et al. 1988; Sheng and Zhou 1988; Zhou and Sheng 1989; Chapman and Higdon 1992; Glover et al. 2020). In addition, the dynamic permeability is used to obtain information on the acoustic properties of a porous medium. If the fluid or the medium is elastic, then the dynamics of the system is modified profoundly (Auriault et al. 1985; del Rió et al. 1998, 2001; Corvera Poiré and Hernández-Machado 2010; Mueller and Sahay 2011).

In addition to being interesting from a scientific view point and the aforementioned properties, oscillatory flows in a porous medium have many important applications. For example, controlling the flow of immiscible fluids in microscale channels is of fundamental importance for a wide range of problems in biological and medical sciences, physics, engineering, and chemistry (see, for example, Bringer et al. 2004; Atencia and Beebe 2005; Squires and Quake 2005; Jo et al. 2009; Vijayakumar et al. 2010; Zhang et al. 2017; Lombard et al. 2020). One example is continuous flow of droplets or slug arrays, which has received much attention because one has precise control on chemical and biochemical reactions that can occur there. Each slug behaves as an individual reaction chamber of submicron volume, independent of the others (Stone et al. 2004; Joanicot and Ajdari 2005; Srisa-Art et al. 2007; Huebner et al. 2008). The problem is that even in slug–based reactions, mixing between reagents is slow and, thus, problematic. One way to overcome this is by using oscillatory flow (Glasgow and Aubry 2003; Glasgow et al. 2004; Khoshmanesh et al. 2015; Xie et al. 2015).

Numerical simulation of oscillatory flow in porous media has been carried out by several groups. Kutay and Aydilek (2007) utilized a lattice-Boltzmann approach to simulate oscillatory flow in asphalt and the resulting dynamic permeability. Pazdniakou and Adler (2013) utilized the same method to carry out a comprehensive study of the problem. Much earlier, Knackstedt et al. (1993) used the lattice-gas method to address the issue of the universality of the rescaled dynamic permeability (see below). Analytical studies of the problem have also been undertaken. Derivation of the dynamic permeability of porous media based on simple models of pore space, such as cylindrical pores, or pores between two parallel flat surfaces (see below) is straighforward. Using a spatially-periodic model of porous media, Perrot et al. (2008) analyzed the symmetry of the viscous dynamic permeability tensor. Chapman and Higdon (1992) carried out numerical and analytical studies of the problem in models of porous media studied by Perrot et al. (2008).

All the numerical simulations, as well as the analytical works, indicate that if the dynamic permeability is rescaled by its static value \(K_0\), then it is a universal function of the rescaled frequency \(\omega /\omega _0\), where \(\omega _0\) is a characteristic frequency given by (Johnson et al. 1987)

$$\begin{aligned} \omega _0=\frac{\mu }{FK_0\rho }=\frac{\mu \phi }{\rho K_0\tau }\;, \end{aligned}$$
(2)

where F is the porous medium’s formation factor, \(\rho \) is the fluid’s density, \(\phi \) is the porosity, and \(\tau \) is the static tortuosity. Therefore,

$$\begin{aligned} \tilde{K}=f(\tilde{\omega })\;, \end{aligned}$$
(3)

where, \(\tilde{K}(\tilde{\omega })=K(\omega )/K_0\), \(\tilde{\omega }= \omega /\omega _0\), and \(f(\tilde{\omega })\) is the universal function that expresses the frequency-dependence of the dynamic permeability. Note that the characteristic frequency \(\omega _0\) contains the porosity \(\phi \), and that Eq. (3) implies that the universality of rescaled permeability holds for any \(\phi \).

Although, as mentioned earlier, numerical simulation and analytical expression for the dynamic permeability of simple models of porous media do support the idea of universal rescaled dynamic permeability, to author’s knowledge there has never been any general derivation of this most interesting result. The purpose of the present paper is to derive Eq. (3) by two distinct approaches. One is based on the effective-medium approximation (EMA), while the second approach utilizes what is referred to as the critical-path analysis (CPA). The former is accurate when the heterogeneity of the pore space is not very strong (see Sahimi 2003 for a comprehensive discussion), whereas the latter provides accurate predictions if the heterogeneity of the pore space is strong (Ghanbarian et al. 2016; Hunt and Sahimi 2017; Ghanbarian 2020a, b). Thus, the results derived by the two approaches essentially cover any type of porous media and, therefore, establish the validity of the apparent universality of \(\tilde{K}\).

The rest of this paper is organized as follows. The preliminary aspects of the problem at the pore scale are described in Sect. 2, followed by the EMA for the macroscopic dynamic flow conductance, or the permeability, in Sect. 3. The CPA is described in Sect. 4, while the results and significance of the dynamic permeability are discussed further in Sect. 5. The last section summarizes the paper.

2 Pore Conductance and Admittance

Let us assume that a porous medium is represented by a network of interconnected pore throats to which we do not attribute any particular shape, but assume only that their length is \(\ell \). Consider the dynamic permeability \(k(\omega )\) for slow flow through a pore represented by two flat parallel surfaces separated by a distance a, which is given by

$$\begin{aligned} k(\omega )=-\frac{1}{\chi ^2}\left[ 1-\frac{\tan (a\chi /2)}{a\chi /2}\right] \;, \end{aligned}$$
(4)

which reduces to \(a^2/12\) in the static limit, as it should, and for a cylindrical pore of radius a,

$$\begin{aligned} k(\omega )=\frac{i}{\omega }\left[ 1-\frac{2}{\beta a}\frac{J_1(\beta a)}{J_0(\beta a)}\right] \;, \end{aligned}$$
(5)

where \(\chi =\sqrt{i\omega /\nu }\), with \(\nu =\mu /\rho \) being the fluid’s kinematic viscosity, \(\beta =\sqrt{i\omega }\), and \(J_m\) being the Bessel function of first kind and order m. Both equations indicate, as already mentioned, that \(k(\omega )\) is a complex function of the frequency. To use the language of electrical networks, each pore throat between nodes i and j is characterized by an admittance \(k_{ij}\), which is the sum of a flow conductance \(g_{ij}\)—its real part—in parallel with a capacitor - its imaginary part—see Fig. 1. Thus, the goal is to determine the effective macroscopic admittance of the entire pore space.

Suppose that \(I_{ij}=Cg\Delta P_{ij}\) is the fluid current in a pore throat ij, where C is a constant, and \(\Delta P_{ij}\) is the pressure drop along the pore. Then, the flux is \(q_{ij}=I_{ij}/\ell ^{d-1}=g_{ij}\Delta P_{ij}/\ell \) and, therefore, \(C=\ell ^{d-1}\), with the pore admittance being simply, \(k_{ij}= \ell ^{d-2}(g_{ij}+i\omega )=\ell ^{d-2}(g_{ij}+\beta ^2)\), where d is the spatial dimension.

3 Effective–Medium Approximation

As is well-known, the continuity equation for slow flow of a fluid of density \(\rho \) in a disordered porous medium of porosity \(\phi \) is given by

$$\begin{aligned} \phi \frac{\partial \rho }{\partial t}=\varvec{\nabla }\cdot (\rho \mathbf{v}) \;. \end{aligned}$$
(6)

where v is the fluid’s velocity. We assume that the fluid is Newtonian and slightly compressible, so that we can write, \(\rho \approx \rho _0+c\rho _0 (P-P_0)\), where \(\rho _0\) is the density at some reference pressure \(P_0\), P is the pressure, and c is a constant. Thus, using Darcy’s law and the expression for the density in Eq. (6), we obtain the governing equation for the dynamic pressure distribution in the pore space (Barenblatt and Zheltov 1960),

$$\begin{aligned} \frac{\partial P}{\partial t}=\varvec{\nabla }\cdot (W{\varvec{\nabla }}P)\;, \end{aligned}$$
(7)

with \(W=k/(c\mu \phi )\), where k is the spatially-varying permeability, with \(\mu \) being the fluid’s viscosity. Discretizing Eq. (7) by finite difference or finite element, one obtains the following master equation for pressure \(P_i\) at node i at time t,

$$\begin{aligned} \frac{\partial P_i}{\partial t}=\sum _{j\in \{i\}}W_{ij}\left[ P_j(t)-P_i(t) \right] \;, \end{aligned}$$
(8)

which is equivalent to a standard pore network in which the “conductance” is \(W_{ij}\), which is related to the local permeabilities at i and j, and \(\{i\}\) denotes the set of the pore throats connected to pore body or node j. For example, for a one-dimensional medium, \(W_{ij}=(k_i+k_j)/(2c\ell ^2\mu \phi ) \). We rescale the pressure by its initial value \(P_0\). Then, Eq. (8) may be interpreted probabilistically: \(P_i\) is the probability of a fluid molecule being at i at time t, given that it was at the origin at time \(t=0\). Given this interpretation, \(W_{ij}\) is the transition rate, i.e., the probability of moving from i to j, and has the units (time)\(^{-1}\). Equation (8) has been solved numerically for a variety of porous and composite materials (see Sahimi 2003 for a comprehensive review), as well as analytically by various approximations in order to determine the macroscopic transition rate \(W_e\) and, therefore, the macroscopic conductivity or permeability.

If we take the Fourier transform of Eq. (8), we obtain,

$$\begin{aligned} i\omega \hat{P_i}(\omega )=\sum _{j\in \{i\}}W_{ij}\left[ \hat{P_j}(\omega ) -\hat{P_i}(\omega )\right] \;. \end{aligned}$$
(9)

As shown by Sahimi et al. (1983) and Odagaki and Lax (1983), the macroscopic admittance \(W_e\) depends on the frequency . Thus, if we demonstrate that a suitably rescaled \(W_e\) follows a universal law for all the rescaled frequencies, then so will also the rescaled macroscopic permeability \(\tilde{K}\). Except in one-dimensional media, Eq. (9) cannot be solved exactly. Thus, analytical methods have been developed for deriving approximate solution of Eq. (9).

One such analytical approximation is the EMA, first derived by Bruggeman (1935) for the permittivity of disordered materials, and derived independently by Landauer (1952) for the effectve electrical conductivity. Kirkpatrick (1971) extended the EMA to resistor networks of coordination number or connectivity Z. The EMA derived by these authors was for the static limit, \(\omega =0\), and was derived as follows. One considers a pore conductance in the network, embedded in an “effective medium” in which all the pore conductances are \(W_e\) and is constructed such that it mimics, under the assumptions made, the behavior of average surroundings of the particular conductance that one is focused on. To do so, one requires that the potential field around the particular conductance to be, on average, equal to the far-field homogeneous field of the effective medium. Thus, suppose the pore conducttances are distributed randomly and independently according to a probability distribution function (PDF) \(f(W_{ij})\). For simplicity, we write, \(w=W_{ij}\). Then, the EMA predicts that

$$\begin{aligned} \left\langle \frac{w-W_e}{w+(Z/2-1)W_e}\right\rangle =0\;, \end{aligned}$$
(10)

where \(\langle \cdot \rangle \) denotes an average over the PDF f(w) of w, so that,

$$\begin{aligned} \int \frac{w-W_e}{w+(Z/2-1)W_e}f(w)dw=0\;. \end{aligned}$$
(11)

In Landuaer’s formulation of the problem, Z/2 is replaced by d, the spatial dimension of the network, and thus,

$$\begin{aligned} \int \frac{w-W_e}{w+(d-1)W_e}f(w)dw=0\;. \end{aligned}$$
(12)

We now use a dynamic EMA to analyze the macroscopic admittance of the network for \(\omega \ne 0\). There are two ways of analyzing the problem.

3.1 Formulation as an Admittance Network

In the first method w is viewed as the admittance of a pore throat, similar to what has been done for the admittance of semi-conducting materials with a similar analysis (Dyre 1993). Therefore, we write, \(W_e=\ell ^{d-2} (\sigma +\beta ^2)\), where \(\sigma \) is the macroscopic conductance of the porous medium. Then, Eq. (11) becomes

$$\begin{aligned} \int \frac{2(g-\sigma )}{2g+(Z-2)\sigma +Z\beta ^2}\;h(g)dg=0\;, \end{aligned}$$
(13)

with h(g) being the PDF of the pore conductance g. Note that for \(\beta =0\), i.e., in the static limit \(\omega =0\), Eq. (13) reduces to the standard Landauer-Kirkpatrick EMA. Next, we note that, \(g-\sigma =\frac{1}{2}[g+(Z-2) \sigma +Z\beta ^2-Z(\sigma +\beta ^2)]\). Thus, if we substitute for \(g-\sigma \) in Eq. (13), and rearrange the equation, we obtain

$$\begin{aligned} \frac{1}{Z(\sigma +\beta ^2)}=\int \frac{1}{2g+(Z-2)\sigma +Z\beta ^2}\;h(g)dg\;. \end{aligned}$$
(14)

Moreover, with \(\tilde{\sigma }=\sigma /\sigma _0\) and \(\tilde{\beta ^2}=\beta ^2/ \sigma _0=i\omega /\sigma _0\), Eq. (14) is rewritten as

$$\begin{aligned} \frac{1}{Z(\tilde{\sigma }+\tilde{\beta ^2})}=\sigma _0\int \frac{1}{2x+(Z-2) \tilde{\beta ^2}+Z\tilde{\beta ^2}}h(x\sigma _0)dx\;, \end{aligned}$$
(15)

where \(\sigma _0\) is the static (flow) conductance at \(\omega =0\). The solution of Eq. (15) yields \(\tilde{\sigma }(\tilde{\beta ^2})=\tilde{\sigma } (\tilde{\omega })\), i.e., the frequency-dependent conductance. Note, however, that regardless of the functional form of h(x), Eq. (15) indicates already that the rescaled conductance \(\tilde{\sigma }\) is a universal function of the rescaled frequency \(\tilde{\beta ^2}=\beta ^2/\sigma _0=i\omega /\sigma _0\), independent of the morphology of the pore space.

Equations (14) or (15) is our working formulation for determining frequency-dependent macroscopic flow conductance within the framework of the EMA. Consider, for example, the conductance distribution, \(h(g)=(1-\alpha ) g^{-\alpha }\), with \(0\le \alpha < 1\), which was shown by Halperin et al. (1985) to describe the distribution of the pore flow conductances in a packing of overlapping spheres, a reasonable model of consolidated sandstones (Roberts and Schwartz 1985). Substituting h(g) in Eq. (14) and integrating we obtain

$$\begin{aligned} \frac{2}{Z(\sigma +\beta ^2)}=\frac{g_\mathrm{max}^{1-\alpha }}{c}\;_2F_1(1,1-\alpha ; 2-\alpha ;-g_\mathrm{max}/c)-\frac{g_\mathrm{min}^{1-\alpha }}{c}\;_2F_1(1,1-\alpha ; 2-\alpha ;-g_\mathrm{min}/c)\;, \end{aligned}$$
(16)

where \(c=\frac{1}{2}[(Z-2)\sigma +Z\beta ^2]\), \(_2F_1\) is the hypergeometric function, and \(g_\mathrm{max}\) and \(g_\mathrm{min}\) are, respectively, the maximum and minimum conductances. Equation (16) may be solved numerically in order to determine \(\sigma (\beta ^2)=\sigma (i\omega )\).

To make the universal function more explicit, we further simplify Eqs. (14), or (14) by considering some limiting cases, and making reasonable assumptions that are valid for many heterogeneous porous media. Suppose, for example, that the pore conductances g vary rapidly, which is normally the case in many heterogeneous porous media. Heterogeneous semi-conducting materials, in which the microscopic conductivity varies over sixteen orders of magnitude (Pazhoohesh et al. 2006), also exhibit such rapid variations (Dyre 1993). Then, for a given \(\sigma (\omega )\) one has two regimes: (a) \(g\ll (d-1)\sigma +d\beta ^2 \), in which case g can be ignored, and (b) \(g\gg (d-1)\sigma +d\beta ^2\), so that the denominator on the right side of Eq. (14) will become very large, and the integral vanishes. Thus, only regime (a) is of interest to us. The boundary between the two regimes is set by a particular conductance \(2g_s=(Z-2)\sigma + Z\beta ^2\), which depends on the frequency, so that regime (a) is defined by \(g\ll g_s\).

Therefore, Eq, (14) is simplified to

$$\begin{aligned} \frac{1}{Z(\sigma +\beta ^2)}=\frac{1}{(Z-2)\sigma +Z\beta ^2}\int _0^{g_s}h(x)dx\;. \end{aligned}$$
(17)

Consider the static case, \(\omega =0\) or \(\beta =0\). Then, \(g_s(\omega =0)=g_0= \frac{1}{2}(Z-2)\sigma _0\), and Eq. (17) becomes

$$\begin{aligned} \frac{1}{Z\sigma _0}=\frac{1}{(Z-2)\sigma _0}\int _0^{g_0} h(x)dx\;, \end{aligned}$$
(18)

which, when subtracted from Eq. (17), results in

$$\begin{aligned} \frac{2\beta ^2}{Z(\sigma +\beta ^2)}=\int _{g_0}^{g_s}h(x)dx\;. \end{aligned}$$
(19)

In this limit too we may also consider various distributions h(g) in order to assess the functional form of the universal function of the rescaled frequency for the flow conductance. Consider, first, the aforementioned distribution, \(h(g)=(1-\alpha )g^{-\alpha }\). Substituting h(g) in Eq. (19), yields,

$$\begin{aligned} \frac{2\beta ^2}{Z(\sigma +\beta ^2)}=\left( g_s^{1-\alpha }-g_0^{1-\alpha } \right) \;, \end{aligned}$$
(20)

which, after substituting for \(g_0\) and \(g_s\) and some algebra, yields

$$\begin{aligned} \tilde{\sigma }(\tilde{\omega })=\left\{ \left( \frac{2}{Z\sigma _0^{1-\alpha }} \right) \left[ \frac{2^{1-\alpha }}{[(Z-2)\tilde{\sigma }(\tilde{\omega })-Z \tilde{\beta ^2}]^{1-\alpha }-(Z-2)^{1-\alpha }}\right] -1\right\} (i\omega /\sigma _0);. \end{aligned}$$
(21)

Equation (21) is an algebraic equation for \(\tilde{\sigma }\), whose solution provides the functional dependence of \(\tilde{\sigma }\) on \(\omega \). Note that Eq. (21) contains only rescaled frequency and some numerical constants. Therefore, the solution depends only on \(\tilde{\omega }\), independent of h(g).

Next, consider the case in which the pore flow conductances vary rapidly. In this case \(g_s\) and \(g_0\) are close to each other, so that we may write,

$$\begin{aligned} \int _{g_0}^{g_s}h(x)dx\approx h(g_s)(g_s-g_0)=\frac{1}{2}h(g_s)[(Z-2)\sigma (s) -Z\beta ^2-(Z-2)\sigma _0]\;, \end{aligned}$$
(22)

and, therefore,

$$\begin{aligned} \sigma (\omega )=\left[ \frac{2i\omega }{Z\sigma _0h(g_s)}\right] \left[ \frac{2}{(Z-2)\sigma (\beta ^2)-Z\beta ^2-(Z-2)\sigma _0}\right] -i\omega \;, \end{aligned}$$
(23)

so that in terms of the rescaled conductance and frequency we obtain

$$\begin{aligned} \tilde{\sigma }(\tilde{\beta ^2})=\left\{ \left[ \frac{2}{Zh(g_s)}\right] \left[ \frac{2}{(Z-2)\tilde{\sigma }(\tilde{\beta ^2})-Z\tilde{\beta ^2}-(Z-2)}\right] -1 \right\} \tilde{\beta }^2\;. \end{aligned}$$
(24)

Under the assumptions made, Eq. (24) is a quadratic equation for \(\tilde{\sigma }\) whose solution provides the frequency-dependence of the rescaled flow conductance. Note that Eq. (24) and, therefore, the solution for the macroscopic conductance contains nothing but \(\tilde{\omega }\) and some constants.

3.2 Formulation in Terms of the Green Function

In the second EMA formulation of the problem, we use the Green function formulation and perturbation expansion to develop the solution of Eq. (9). This was already done by Sahimi et al. (1983) a in the context of diffusion in disordered media. Thus, we only present the final equation:

$$\begin{aligned} \int _0^\infty \frac{f(w)}{1-\gamma (w-W_e)/W_e}\;dw=1\;, \end{aligned}$$
(25)

where

$$\begin{aligned} \gamma =-\frac{2}{Z}+\frac{2i\omega }{ZW_e}G_0\;. \end{aligned}$$
(26)

Note that in the static limit, \(\omega =0\), Eq. (25) reduces to Eq. (11). Here, \(G_0\) is a Green function that, for a d-dimensional simple-cubic network is given by (Sahimi et al. 1983)

$$\begin{aligned} G_0=-\frac{1}{2}\int _0^\infty \exp [-\frac{1}{2}(Zx+\epsilon )]I_0^2(x)dx\;, \end{aligned}$$
(27)

with \(I_0(x)\) being the modified Bessel function of order zero, and \(\epsilon = i\omega /W_e\). The corresponding Green function for the BCC and FCC networks are given by (Sahimi et al. 1983)

$$\begin{aligned} G_0=-\frac{1}{(2\pi )^3}\int _{-\pi }^\pi \int _{-\pi }^\pi \int _{-\pi }^\pi \frac{1}{8+\epsilon -8\cos x\cos y\cos z}\;dxdydz\;, \end{aligned}$$
(28)

for the BCC network and

$$\begin{aligned} G_0=-\frac{1}{(2\pi )^3}\int _{-\pi }^\pi \int _{-\pi }^\pi \int _{-\pi }^\pi \frac{1}{12+\epsilon -4(\cos x\cos y+\cos x\cos z+\cos y\cos z)}dxdydz\;, \end{aligned}$$
(29)

for the FCC lattice. Equation (25) was also derived by Odagaki and Lax (1981) and Summerfield (1981) for the problem of hopping transport in heterogeneous semiconductors. In the condensed matter literature, Eq. (25) is referred to as the coherent-potential approximation.

If a heterogeneous porous medium is represented by a pore network in which a fraction p of the pore throats are open to flow, while the rest are too small to accomodate it, then, more explicit expression can be obtained. As discussed above, the problem can be mapped onto a conductance network and, thus, one must determine the effective admittance of the network. Using the coherent-potential approximation, or the EMA, Odagaki and Lax (1983) derived the following equations for \(\tilde{W_e}(\omega )\) in the low-frequency limit:

$$\begin{aligned} \tilde{W_e}(\omega )=W_0+\frac{\displaystyle \pi c(1-p)}{\displaystyle (Z-2) (p-p_c)}\omega -\frac{\displaystyle 2c(1-p)}{\displaystyle Z(Z-2)(p-p_c)} (\omega \ln \omega )i \end{aligned}$$
(30)

for 2D networks, and

$$\begin{aligned} \tilde{W_e}=W_0+\frac{\displaystyle \pi c(1-p)}{\displaystyle 2\sqrt{2}Z^2 (Z-2)^{1/2}(p-p_c)^{3/2}}\omega ^{3/2}+\frac{\displaystyle 2I_w(1-p)}{\displaystyle Z(Z-2)(p-p_c)}\omega i \end{aligned}$$
(31)

for 3D networks. Here, \(W_0=\tilde{W_e}(\omega =0)\), c is a constant of order unity, \(p_c\) is the percolation threshold of the network that the coherent-potential apprpoximation or the EMA predicts, \(p_c=2/Z\), and \(I_w\) is the Watson integral (Hughes 1995), which represent the limit \(\omega =0\) of the Green function \(G_0\). The numerical values of \(I_w\) for the three main 3D latticess, namely, the simple-cubic, and body-centered and face-centered cubic networks, are given by

$$\begin{aligned} I_w=\left\{ \begin{array}{cc} \displaystyle \frac{\sqrt{6}}{96\pi ^3}\Gamma (1/24)\Gamma (5/24)\Gamma (7/24) \Gamma (11/24)\simeq 0.50546 &{} \text{ simple-cubic } \text{ network }\\ \displaystyle \frac{1}{4\pi ^3}\Gamma (1/4)^4\simeq 1.3932 &{} \text{ body-centered } \text{ cubic } \text{ network }\\ \displaystyle \frac{3}{2^{14/3}\pi ^4}\Gamma (1/3)^6 \simeq 0.4482 &{} \text{ face-centered } \text{ cubic } \text{ network } \end{array}\right. \end{aligned}$$
(32)

where \(\Gamma (x)\) is the gamma function. Extension of these approaximations to higher-order EMA that is more accurate than Eqs. (30) and (31) was described by Sahimi (1984) and Sahimi and Tsotsis (1997). Note that both Eqs. (30) and (31), which provide explicit expressions for the real and imaginary parts of the effective admittance or the effective frequency-dependent flow conductance of the network, indicate that the imaginary part increases with \(\omega \) in the low-frequency regime, which is in agreement with the aforementioned numerical simulations. In addition, they both indicate that the rescaled complex conductance \(\tilde{W_e}/W_0\) depends mainly on \(\omega /W_0\).

4 The Critical-Path Analysis

The CPA was first proposed by Ambegaokar et al. (1971) in order to estimate hopping conductivity of extremely disordered semiconductors, and was proven rigorously later on by Ty̆c and Halperin (1989); see Hunt and Sahimi (2017) for a comnprehensive review. The CPA is based on the following concept. Consider, first, the static case, i.e., the limit \(\omega =0\), and suppose as before that the porous medium is represented by a pore network in which the pore flow conductances follow a PDF h(g). We remove all the pore conductances from the network and, then, begin to fill up the network again by replacing the conductances, in their original locations, in the order of decreasing pore conductance by starting from the largest conductance. Clearly, at the beginning there is no sample-spanning cluster of pore flow conductances, but as percolation theory (Stauffer and Aharony 1994; Sahimi 1994) has taught us, after we reinstate a sufficiently large fraction of the pores’ conductances, a sample-spanning cluster is formed, and the macroscopic conductivity and, thus, the permeability of the network rises from zero. The first pore conductance that completes the formation of the sample-spanning cluster is referred to as the critical conductance \(g_c\), while the just formed cluster is called the critical cluster. Therefore, \(p_c\), the bond percolation threshold of the pore network, is related to \(g_c\) by

$$\begin{aligned} p_c=\int _{g_c}^\infty h(g)dg\;. \end{aligned}$$
(33)

We point out that for a \(d-\)dimensional pore network of average connectivity Z, the relation \(p_c\approx d/[Z(d-1)]\) provides very accurate estimates of \(p_c\), so that for a given h(g) one can estimate the critical conductance \(g_c\).

If h(g) is very broad, varying over rders of magnitude, then, all the pore conductances that were reinstated before \(g_c\) are much larger than \(g_c\), and are effectively in series with it, since it is \(g_c\) that controls the flow, as all the fluids passing through the pores with conductances much larger \(g_c\) must eventually pass through \(g_c\) and, therefore, the resistance of the larger conductors can be neglected. On the other hand, all the pore conductances that are reinstated with values smaller than \(g_c\), i.e., after formation of the sample-spanning cluster, will be much smaller than \(g_c\). After the remaining pore conductances are reinstated, we recognize that since they all are much smaller than \(g_c\), they are essentially in parallel with \(g_c\) and play no significant role in the flow process and, hence, they can also be neglected. Therefore, the macroscopic conductivity is essentially \(g_c\).

Numerical simulation of Berman et al. (1986) confirmed the accuracy of the CPA. Katz and Thompson (1986) applied the CPA to estimate the static permeability of porous media, followed by others (Le Doussal 1989; Friedman and Seaton 1998; Skaggs 2011; Ghanbarian et al. 2016; Ghanbarian 2020a, b). Sahimi (1993) used the CPA to estimate the effective permeability of porous media during the flow of power-law fluids.

The same arguments are applicable to the frequency-dependent permeability or flow conductance. Since the critical cluster, made of the pores with admittances, \(w=g+s=g+i\omega \) is a linear or quasi-linear chain in which the admittances are in series, the macroscopic admittance of the network, according to the CPA, is given by

$$\begin{aligned} \frac{1}{\sigma +i\omega }=\int _{g_c}^\infty \frac{h(g)}{g+i\omega }dg\;, \end{aligned}$$
(34)

which is obtained by substituting \(d=1\) in Eq. (12). In practice, the upper limit of the integral in Eq. (34) is, of course, cut off at some conductance \(g_\mathrm{max}\). It is known (Sahimi et al. 1983) that the dynamic EMA is exact for \(d=1\) and, thus, if the critical cluster is also one dimnsional or quasi-one dimensional, it is not surprising that the two approximations become identical. It is also worth noting, as pointed out earlier, that the EMA is accurate when the heterogeneity of the pore space is mild, whereas the CPA provides accurate estimates of the transport properties when the heterogeneity is very strong. Despite this, the two approximations coincide in the particular problem and limits that we consider.

We note that Eq. (34) can be rewritten in terms of the rescaled flow conductance \(\tilde{\sigma }=\sigma /\sigma _0\) and frequency \(\tilde{s}= i\omega /\sigma _0\):

$$\begin{aligned} \frac{1}{\tilde{\sigma }+\tilde{\beta ^2}}=\sigma _0\int \frac{h(x\sigma _0)}{x+\tilde{\beta ^2}}dx\;. \end{aligned}$$
(35)

Equation (35) indicates that the CPA also predicts that the rescaled macroscopic flow conductance \(\tilde{\sigma }\) is a universal function of \(\tilde{\beta ^2}=i\omega /\sigma _0\). Thus, one may use Eq. (34) or (35) to examine the type of predictions that the CPA provides for the dynamic flow conductance and, hence, for the frequency-dependent permeability. As a simple example, suppose that the pore flow conductances are distributed uniformly in \(g_c\le g\le g_\mathrm{max}\), with \(g_c\ll g_\mathrm{max}\). Therefore, \(h(g)= (g_\mathrm{max}-g_c)^{-1}\), which after substituting in Eq. (35) yields,

$$\begin{aligned} \frac{1}{\tilde{\sigma }+\tilde{\beta ^2}}=\frac{1}{\tilde{g}_\mathrm{max} -\tilde{g_c}}\ln \left( \frac{\tilde{g}_\mathrm{max}+\tilde{\beta ^2}}{\tilde{g_c}+\tilde{\beta ^2}}\right) \;, \end{aligned}$$
(36)

with \(\tilde{g}_\mathrm{max}=g_\mathrm{max}/\sigma _0\), and similarly for \(\tilde{g_c}\). If we use the identities, \(\ln (1+ix)=\frac{1}{2}\ln (1+x^2)+i \arctan (x)\), and \(\arctan (x)-\arctan (y)=\arctan [(x-y)/(1+xy)]\), we finally obtain

$$\begin{aligned} \frac{1}{\tilde{\sigma }+\tilde{\beta ^2}}=\frac{1}{2}\left( \frac{\tilde{g}_\mathrm{max}^2-\tilde{\beta ^2}^2}{\tilde{g_c}^2-\tilde{\beta ^2}^2}\right) +i\arctan \left( \frac{\omega /g_\mathrm{max}-\omega /g_c}{1+\omega ^2/g_\mathrm{max}g_c}\right) \;. \end{aligned}$$
(37)

We may refine the prediction of the CPA, Eq. (34), by the following analysis (Sahimi 2022).. Let us view of flow of a liquid through a porous medium as a “two-phase flow” problem in which the second phase is air. Let \(P_{cij}\) be the capillary pressure associated with bond ij of the pore network. We define the minimum spanning tree (MST) (Dobrin and Duxbury 2001) as a cluster that visits every node in the network such that the total “energy,” \(E= \sum _{ij}P_{cij}\), is minimum, with the constraint that visit to any node cannot create a closed loop. To construct the tree, one begins at a node i and selects a bond b connected to i with the lowest \(P_{cij}\) . Then, among all the unvisited bonds connected to b, the one with the lowest \(P_{cij}\) is selected, and so on. But, this is also the physical basis for the bond invasion percolation clusters (BIPCs) (Sahimi et al. 1998), if invasion is from a single node, i.e., if we inject the fluid into the pore space from a single node. The MST, or the BIPC, is a fractal object with (Sahimi et al. 1998; Knackstedt et al. 2000), \(D_f\simeq 1.22\) and 1.37 in two and three dimensions, respectively.

The analysis implies that, instead of substituting \(d=1\) in Eq. (12) to obtain Eq. (34), we should replace d with the aforementioned \(D_f\) of the BIPC. Thus, in that case, we obtain

$$\begin{aligned} \frac{1}{D_f(\sigma +i\omega )}=\int \frac{1}{g+(D_f-1)\sigma +D_f(i\omega )}\;h(g) dg\;, \end{aligned}$$
(38)

instead of Eq. (34). The rest of the analysis of Eq. (38) is the same as before.

The structure of the BIPC is universal, because only the order of \(P_{cij}\) matters, not their numerical values or their statistical distribution. Therefore, the universality of the rescaled frequency-dependent permeability is due to the universality of the structure of the BIPC. This also explains why the EMA provides accurate predictions for \(\tilde{K}\): the cluster through which flow occurs is a low-dimensional, quasi-one-dimensional cluster, even in three dimensions, and it is well-known that the EMA is very accurate for low-dimensional systems.

5 Discussion

The universality of \(K(\omega )\) may seem to be a bit disappointing, because it implies that experimental data for it may not provide any additional information about the microstructure of the porous medium for which the data were collected. Frequency-dependent permeability is, however, still useful for understanding flow in porous media. One reason is that the characteristic frequency \(\omega _c\) is typically large, whereas \(K_0\) is the permeability at low (strictly speaking, zero) frequencies. It is due to such a contrast between the two rescaling variables that the universality is produced, and it is useful because there is always uncertainty in the precision of the instruments and experimental data. In particular, if the fluid is Newtonian, the real part of \(K(\omega )/K_0\) is a monotonically decreasing function of \(\omega /\omega _c\), so that if we take two distinct porous media (say, with different porosities) and force the rescaled permeability curves coincide in the very low and very high frequencies, it will produce universality for intermediate frequencies.

In addition, the frequency-dependent permeability represents a response function that relates, in the frequency domain, the imposed pressure gradient to the fluid velocity. According to Eqs. (16), (21), and (24)–(26), the relation is simple, and any value of \(K(\omega )\) in the frequency domain provides insight into how the flow system in the pore space would respond in the time domain to every frequency imposed by the frequency-dependent pressure gradient, without any need for actually solving the governing flow equations for every frequency mode.

Although not studied in this paper, the frequency-dependent permeability of a Newtonian fluid in an elastic (deformable) tube (Torres Rojas et al. 2017), or that of viscoelastic fluids in rigid porous media (Lombard et al. 2020), provides even more insight into the behavior of the system. For example, Torres Rojas et al. (2017) showed that the interplay between the viscosity of the fluid, the elasticity of the wall, and the characteristic length scale of a confining medium gives rise to many interesting phenomena, including resonances, implying that the flow amplitude of a fluid system in a zero–mean flow may be optimized at certain frequencies. The resonances are relevant when the confining medium is small and its Young’s modulus is also low, which is typical of elastomeric materials in microfluidic systems. But, for a specific tube radius, Young’s modulus, and fluid viscosity less than a critical value, the resonances disappear. An even richer behavior was reported by Lombard et al. (2020) for the dynamic permeability in two-phase flow of a viscoelastic fluid.

The formulation developed here was based on a flow conductance network. Clearly, a similar formulation that completely parallels what was described above can also be developed for the electrical conductivity of saturated porous media in an oscillatory potential field. As a result, we predict that the rescaled frequency-dependent electrical conductivity (for experimental data see, Lerot and Revil, 2009; Woodrull et al. 2014; Revil et al. 2013, 2015) of porous media should be a universal function of the suitably-rescaled frequency. Given that the formation factor is essentially the inverse of the conductivity, and that gas diffusivity of porous media is also closely related to the electrical conductivity through the Einstein relation, our formulation of the problem enables us to study the same quantities under oscillatory conditions, and to establish that they too are universal functions of the rescaled frequency. We will soon report on these issues.

Finally, we believe that frequency-dependent dispersion coefficients (Valdés-Parada and Alvarez-Ramirez 2011), i.e., the dispersion coefficients in oscillatory flows in porous media, should exhibit universal scaling, if the coefficients are rescaled by their static values, or another suitably-selected parameter. This will be demonstrated in a future paper.

6 Summary

Experimental data and numerical simulation of flow of a Newtonian fluid in a porous medium, subject to a pulsatile pressure gradient, had indicated that the frequency-dependent permeability of the medium, when rescaled with its static value, is a universal or quasi-universal function of the frequency, if it is rescaled with a characteristic frequency. Analytical models of flow in such simple geometries as cylindrical pores had also supported the same. No derivation of this important result for a general model of porous media had, however, been presented before. Using two approximate theories, one very accurate for porous media with mild heterogeneties, and a second one that is accurate for highly heterogeneous porous media, we demonstrated that the rescaled effective frequency-dependent flow conductance and, therefore, permeability of the porous media do indeed follow universal dependence on a rescaled frequency. We also discussed the relevance of this result to gaining more insights into the dynamics of flow in porous media that are subject to an oscillatory pressure gradient.