An Experimental Study on the Slippage Effect of Gas Flow in a Compact Rock

Abstract

Gas flow in small pore throats in compact rocks is usually affected by the gas slippage effect due to the dense structure and low porosity of the rocks. In this study, permeability and porosity of two granitic gneiss specimens under different pore and confining pressures are measured. Petrographic studies are also performed using X-ray diffraction, optical microscopy, and scanning electron microscopy coupled with an energy-dispersive spectrometer. Test data indicate that the gas flow in the compact rock does not follow Darcy’s law due to the effect of gas slippage, and the measured permeability needs to be corrected by the gas slippage effect. The test results show that the gas slippage effect increases subsequently when the pore pressure is low, which leads to the measured permeability higher than the absolute permeability. The influence of confining pressure on the impact rate of the slippage effect appears to approach an upper limit symptomatically. It is found that a power law describes well the relationship between the absolute permeability and the effective porosity. A correlation of the slippage factor and the absolute permeability is provided. When the confining pressure is high and the pore pressure is low, the flows are slip flow and transitional flow and traditional fluid dynamics N–S equations are not applicable and Knudsen’s diffusion equations should be used.

1 Introduction

Natural compact rock formations are ideal for underground storage of oil, gas, $\mathrm{CO}_{2}$, and nuclear wastes due to their extremely low permeability and high mechanical strength (Jones and Owens 1980; Skoczylas and Henry 1995; Croise’ et al. 2004; Tsang et al. 2005; Davy et al. 2007; Boulin et al. 2012). For example, several large underground oil and gas storage depots are being built in China. The main lithology for these storage depots is the late Proterozoic compact granite gneiss. The flow characteristics of gas in small pore throats in compact rocks and other tight formations and the change in permeability with pressure need to be determined in the design of these excavations.

Gas is often used as the flow medium to carry out laboratory tests to measure permeability of compact rocks (Wang et al. 2014a, b). Owing to its dense structure, the flow channels in a compact rock are very small. The mean free path of gas molecules varies noticeably compared with the pore-throat radius; as a result, the Knudsen number ($K_{n}$, which is the ratio of the mean free path of gas molecules to the characteristic dimension of the flow channels) varies considerably. If a gas flows through the medium, the microscale effect will be obvious, which makes the tangential speed of the gas flow in the boundary wall of the rock medium nonzero, resulting in the Klinkenberg effect or the slippage effect (Klinkenberg 1941). The slip of gas near a solid wall was first reported by Maxwell (1867). Knudsen (1909)’s formulation of diffusion of gas molecules is one of the most important achievements in this study area; however, gas slippage in porous media and its effect on the permeability of the media were first addressed by Klinkenberg (1941) (Ziarani and Aguilera 2012).

It has been observed that when the mean free path of molecules is within two orders of the magnitude of the pore-throat diameter (i.e. $0.1 < K_{n} < 10$), gas molecules tend to “slip” on the surface of the pores. Under such a condition, Darcy’s law is no longer applicable and the measured gas permeability of a rock specimen is greater than its absolute permeability (Ziarani and Aguilera 2012). Some research results show that the smaller the pore radius of a rock is, the lower the permeability is, and there is a more noticeable Klinkenberg effect of gas flow (Jones and Owens 1980; Sampath and Keighin 1982; Wu et al. 1998). Klinkenberg (1941) proposed a linear correlation between the measured gas permeability and the absolute permeability:

$$\begin{aligned} k_g =k_{g\infty } \left( {1+\frac{b}{p_m }} \right) \end{aligned}$$

(1)

where $k_g$ is the gas permeability under the mean pressure $p_m$, $k_{g\infty }$ is the absolute permeability (also known as the Klinkenberg’s corrected permeability), and b is the Klinkenberg’s slippage factor. When $b= 0$, the flow is Darcy’s flow. b depends on the molecule’s mean free path ($\lambda )$, the pore-throat radius (r), and the mean pressure $(p_m)$ (Javadpour et al. 2007):

$$\begin{aligned} b=\frac{4c\lambda }{\gamma }p_m \end{aligned}$$

(2)

where b and $p_m$ are in psi, $\lambda$ and $\gamma$ are in nm, and c is a constant close to unity.

Some researchers have carried out gas flow tests under different conditions to obtain the Klinkenberg’s slippage factor. Heid et al. (1950) developed an empirical equation for determining the Klinkenberg’s slippage factor based on the test results of 164 core specimens. Jones and Owens (1980) studied the permeability of tight sands and found that the gas slippage effect was more pronounced in low permeability rocks; they also provided an empirical formula for the slippage factor. Cosenza and Ghoreychi (1999) discussed the relationship between the mean free path and the pressure of molecules based on gas flow tests on rock salt and found that when the gas pressure was increased from 0.06 to 6 MPa, the mean free path of molecules was close to the characteristic dimension of the rock and the Klinkenberg effect was apparent. Florence et al. (2007) and Civan (2010) proposed empirical equations for the Klinkenberg’s slippage factor using their test data. Ziarani and Aguilera (2012) studied Knudsen’s permeability correction number for tight porous media and concluded that the Knudsen’s permeability correlation is more accurate than Klinkenberg’s model, especially for extremely tight porous media with transitional and free molecular flows.

It is observed that Klinkenberg’s model and its various extensions developed so far may underestimate the permeability correction especially for fluid flows in media with high Knudsen numbers. To confirm this hypothesis, a detailed experimental study is carried out and the results are presented in the following sections.

2 Experimental Set Up

2.1 Specimen Preparation and Test Conditions

Two rock samples were collected from the late Proterozoic granite gneiss of an underground oil and gas storage depot (120 m below the ground surface) in China. Two cylinder specimens (marked QDC-5 and QDC-6, see Fig. 1), with a length of 50 mm and a diameter of 50 mm, were prepared. There are no visible cracks on the rock surface. Petrographic studies were performed using X-ray diffraction, optical microscopy, and scanning electron microscopy coupled with an energy-dispersive spectrometer. The main minerals of the rock are: (1) 37 % of K-feldspar with granular structure; (2) about 30 % of plagioclase; (3) about 25 % of quartz with large phenocryst particles of about 2 mm in diameter and small matrix particles; (4) about 8 % of biotite with fine particles. The strength of the specimens is high, with an average uniaxial compressive strength of 185 MPa. Table 1 presents the basic physical properties and the dimensions of the specimens. Compared with other rocks such as altered rocks (Wang et al. 2014c) and porous chalks (Xie and Shao 2006) with large porosities, the porosity of the rock in this study is very small, and a low permeability behaviour is expected. It is expected that the fluid flow properties of the rock should be very different from that of rocks with high porosities.

Fig. 1

Test specimens of granite gneiss

Table 1 Basic physical parameters and dimensions of the rock specimens

Using argon gas as the flow medium, permeability test was performed under different pore and confining pressures and in a constant temperature ($22\,^{\circ }\hbox {C}$) environment. Table 2 shows the ranges of the pore and confining pressures. The pore pressure is set from low (0.2 MPa) to high (2.5 MPa) to study the influence of the pore pressure on the slippage effect. During each test, a predetermined confining pressure is applied first and then the pore pressure is changed from 0.2 to 2.5 MPa in the steps shown in Table 2, and gas flow is recorded under each pore pressure until all the tests are completed.

Table 2 Test programs

2.2 Experimental Facility and Principles

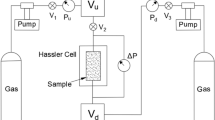
A gas permeability test system was jointly developed by the Rock Mechanics Laboratory of Geotechnical Research Institute of Hohai University in China and Lille University of Science and Technology in France in 2012. A schematic diagram of the test system is shown in Fig. 2. The system, which is used mainly for testing compact rocks, consists of a pressure chamber I, a gas pressure loading system II, a gas pressure control panel III, and a confining pressure loading system IV. The gas pressure control panel consists of a gas tank, gas pipes, and valves. $\mathrm{p}_{1}$ and $\mathrm{p}_{2}$ are the pressures of the gas tank at the ends of the inlet and outlet, respectively.

The confining pressure and the gas flow pressure in the pressure chamber can be adjusted by the confining pressure loading system IV and the gas pressure control panel III, respectively. The maximum confining pressure of the test system is 60 MPa, and the lowest permeability that can be practically measured is $10^{-22}\hbox { m}^{2}$. If the permeability of a rock specimen is lower than $10^{-22}\hbox { m}^{2}$, the measuring time will be too long for each test at a given pore pressure (in the order of a few hours to a day), which can lead to a low precision of the measured results. The test system can be used to measure porosity using a precision gas pressure sensor, which has a pressure range of 0–2 MPa and a resolution of 0.0001 MPa. During a test, permeability measurement is carried out by maintaining a constant confining pressure while the pore pressure is increased progressively. For each measurement, gas pressure equilibrium must be reached before recording the data. During a measurement, the gas flow is considered to be in a steady state when the pressure remains constant in 3–5 min. For each pore pressure change, it normally takes about 3–30 min to reach the pressure equilibrium.

Fig. 2

Schematic diagram of the test system: 1 gas pressure tank, 2 inert argon gas, and 3 rock specimen

The general principle of the test is to carry out a continuous gas flow through the specimen under steady conditions (Fig. 3). In order to record time variation t to get a small drop in pressure $\Delta p$ , a high-precision manometer is installed in the downstream side of the specimen; Gas flow $Q_{\mathrm{s}}$ at the end of outlet of the chamber is deduced from the perfect gas assumption (Loosveldt et al. 2002):

$$\begin{aligned} Q_s =\frac{V_s \Delta p}{t\left( p_0+ {\frac{\Delta p}{2}} \right) } \end{aligned}$$

(3)

where $Q_{s}$ is the gas flow at the end of the outlet of the chamber ($\hbox {m}^{3}/\hbox {s}$), $V_{s}$ is the internal volume of the gas gauge, $\Delta p$ is the change of gas pressure (MPa) at high-precision manometer within time t, and $p_{0}$ is the atmospheric pressure (0.1 MPa).

Fig. 3

Principles of permeability test

If the gas flow follows Darcy’s law during a test, according to the test conditions shown in Fig. 3 the permeability can be expressed as:

$$\begin{aligned} k_g =\frac{2Q_s \mu Lp_0 }{A\left( {p^{2}-p_0 ^{2}} \right) } \end{aligned}$$

(4)

where $k_{g}$ is the gas permeability $(\hbox {m}^{2})$ of the rock specimen, $\mu$ is the gas viscosity ($\hbox {Pa}\cdot \hbox {s}$), p is the gas pressure (MPa) at the inlet end of chamber, and L and A are length (m) and the cross-sectional area $(\hbox {m}^{2})$ of the rock specimen. It is seen that if the gas flow follows Darcy’s law, the gas flow rate $Q_s$ is linearly proportional to the difference of squared pressures $\left( {p^{2}-p_0 ^{2}} \right)$.

A similar method for measuring gas permeability can be found by Loosveldt et al. (2002) under more complex conditions.

$k_{g}$ depends on many factors such as fluid, solid structure and temperature. To reduce experimental errors caused by temperature change, all tests were conducted in a thermally insulated room at a constant temperature of ($22\pm 0.5\,^{\circ }\hbox {C}$) maintained by an air conditioner.

3 Experimental Results

3.1 Characteristics of Gas Flow in Granite Gneiss

Using the experimental facility and the test method described above, for a predetermined confining pressure the gas flow under different fluid flow pressures is obtained; then curves showing the relationship between the gas flow rate $Q_s$ and the difference of squared pressures $\left( {p^{2}-p_0 ^{2}} \right)$ are plotted and the results are presented in Figs. 4 and 5 for specimens QDC-5 and QDC-6, respectively.

Fig. 4

Curves of gas flow in specimen QDC-5

Fig. 5

Curves of gas flow in specimen QDC-6

It is found that as the pore pressure changes under a constant confining pressure, the relationship between the gas flow and the difference of squared pressures is not linear as described by Eq. (4). Instead, the curves are nonlinear and convex, especially when the pore pressure is low and the confining pressure is high. Thus, the gas flow in the granite gneiss is affected by the Klinkenberg effect.

Reda (1987) and Baehr and Hult (1991) provided experimental evidence showing that the Klinkenberg effect cannot be neglected in low permeability media. Wu et al. (1998) developed a set of analytical solutions for the steady state and transient gas flows in porous media including the Klinkenberg effect. We identified from our laboratory test that pore pressure, confining pressure, rock permeability, and pore radius are the main factors that affect the gas slippage effect and detailed discussions of our test results are presented in the following subsections.

3.2 Influence of Pore Pressure on Gas Slippage Effect

The no-slip condition on the pore walls may break down at a low gas pressure. The wall-slip flow occurs because the mean free path of a molecule $\lambda$, i.e. the mean distance that it travels before it collides with another molecule, is inversely proportional to the pore pressure as:

$$\begin{aligned} \lambda =\frac{\mu }{p}\sqrt{\frac{\pi RT}{2M}} \end{aligned}$$

(5)

where $\mu$ is the viscosity of gas in $\hbox {Pa}\cdot \hbox {s}, p$ is the pore pressure in Pa, $R= 8314\hbox { J}/(\hbox {k}\cdot \hbox {mol})$ is a gas constant, T is temperature in k, and M is the molecular mass in kg/k mol.

According to Eqs. (5) and (2), the mean free path of molecule ($\lambda$) increases as the pore pressure (p) decreases, and the Klinkenberg’s slippage effect increases, which will lead to a measured permeability ($k_{g}$) larger than the absolute permeability ($k_{g\infty }$). On the other hand, the mean free path of molecule ($\lambda$) decreases as the pore pressure (p) increases, and the Klinkenberg’s slippage effect will be suppressed.

Based on the test data, the relationships between the reciprocal of the average pore pressure $\left( p_m =\frac{p+p_0 }{2}\right)$ and the gas permeability $(k_{g})$ are plotted, and the results are shown in Figs. 6 and 7 for specimens QDC-5 and QDC-6, respectively. It is seen from Figs. 6 and 7 that the experimental results agree with the theoretical ones, both showing that the average pore pressure and gas permeability have a good correlation. Under the same confining pressure, the measured gas permeability increases with the increase in the reciprocal of the average pore pressure $(1/p_{m})$. When the average pore pressure is small and the mean free path of molecule is large, the measured gas permeability increases. It is observed that the Klinkenberg effect plays a key role in this phenomenon.

Fig. 6

Relationship between $1/p_{m}$ and $k_{g}$ of specimen QDC-5

Fig. 7

Relationship between $1/p_{m}$ and $k_{g}$ of specimen QDC-6

The absolute permeability ($k_{\mathrm{g}\infty }$) and the Klinkenberg’s slippage factor (b) can be obtained by correlating $k_{g}$ and $1/p_{m}$ (Figs. 6, 7) using Eq. (1). The regression curves of $k_{g}\sim 1/p_{m}$ for specimens QDC-5 and QDC-6 are presented in Figs. 8 and 9, respectively. The calculated absolute permeability $(k_{\mathrm{g}\infty })$ and slippage factors (b) for each confining pressure are listed in Tables 3 and 4. Most of the curves show a linear relationship between $k_{g}$ and $1/p_{m}$, and the correlation coefficients of fitting $(R^{2})$ are high ($>$0.97). For QDC-6, at $p_{c}$ equals to 2 and 3 MPa, the relation between $k_{g}$ and $1/p_{m}$ is not a linear. Adding a term of 1/ $(p_{m})^{2}$ to the fitting equation results in a better fit for this two cases. The fitting expressions are also listed in Table 4. The porosities of the rock specimens under different confining pressures are measured, and the results are listed in Tables 3 and 4.

Fig. 8

Regression curves of $1/p_{m}$ and $k_{g}$ of specimen QDC-5

Fig. 9

Regression curves of $1/p_{m}$ and $k_{g}$ of specimen QDC-6

Once the measured permeability $(k_{g})$ is corrected by the gas slippage effect, the absolute permeability $(k_{\mathrm{g}\infty })$ under different confining pressures can be obtained. With the increase in confining pressure, both the porosity and the absolute permeability decrease, and the slippage factor increases. For specimens QDC-5 and QDC-6, the slippage factors change from 0.1 to 0.3 and from 0.0004 to 0.8 MPa for confining pressure ranges of 2–25 and 2–30 MPa, respectively.

3.3 Relationship Between Absolute Permeability and Effective Porosity

For a porosity reduction of about 1 % caused by the closure of microcracks in Westerly granite specimens, the permeability of the rock can be reduced by as much as two orders of magnitude (Brace et al. 1968). It is of interests to find out the relationship between porosity and permeability.

Table 3 Regression results of specimen QDC-5

Table 4 Regression results of specimen QDC-6

The effective porosity was measured under different confining pressures in this test and the results are listed in Tables 3 and 4. The effective porosity decreases with the increase in the confining pressure, and as a result the absolute permeability decreases. Figure 10 presents the relationship between the absolute permeability and the effective porosity. A power law is used to fit the data:

$$\begin{aligned} k_{g\infty } =k_{g\infty }^0 \times \left( {\frac{\varphi }{\varphi _0 }} \right) ^{n} \end{aligned}$$

(6)

where $k_{g\infty }^0$ is the initial absolute permeability, $\varphi _0$ is the initial effective porosity, and n is a regression parameter. The fitting parameters and their correlation coefficients of fitting are listed in Table 5. After comparing with the fitting results by the power law with that by the exponential law, we find that the power law describes well the relationship between the absolute permeability and the effective porosity. This conclusion is consistent with the results by Walder and Nur (1984), David et al. (1994), and Civan (2002a).

3.4 Relative Impact of Gas Slippage Effect on the Measured Permeability

To analyse the influence of the slippage effect on the measured permeability, we define an impact rate $\eta$ of the gas slippage effect as:

$$\begin{aligned} \eta =\frac{\left| {k_g -k_{g\infty } } \right| }{k_g}\times 100\% \end{aligned}$$

(7)

The impact rates of the gas slippage effect are calculated and plotted in Figs. 11 and 12, and the data are listed in Tables 6 and 7 (in “Appendix”). It is shown that for a given confining pressure, the impact rates of the gas slippage effect decrease with the increase in the pore pressure. Therefore, the gas slippage effect is large when the pore pressure is low. This is due to the fact that when the pore pressure is low, the density of the gas molecules in the rock specimens will increase, and the interaction between the gas molecules and the pore walls will be enhanced, leading to an increase in the measured permeability. For specimens QDC-5 and QDC-6, when the pore pressure is lower than 0.4 MPa, the impact rate is $<$50 %. Thus, the influence of the gas slippage effect on the measured permeability of the rocks should be considered when the pore pressure is low for an underground oil and gas or $\mathrm{CO}_{2}$ storage project. When the pore pressure is equal to 2.0 MPa or higher, the impact rate of the gas slippage effect is small and negligible.

Fig. 10

Fitting curves of the absolute permeability and the effective porosity for specimens a QDC-5; b QDC-6

Table 5 Fitting parameters of specimens QDC-5 and QDC-6

Fig. 11

Impact rates of gas slippage effect for specimen QDC-5

Fig. 12

Impact rates of gas slippage effect for specimen QDC-6

The impact rate of the slippage effect is also affected by confining pressure. For specimen QDC-5, when the pore pressure is stable and the confining pressure increases from 2 to 12 MPa, the impact rate of the slippage effect increases gradually. When the confining pressure is $>$12 MPa, the impact rate change is small, which means that the pore volume in the rock is reduced, and the influence of the confining pressure on the permeability decreases. It seems that there is a threshold confining pressure below which the influence of the slippage effect on the measured permeability is large. For specimen QDC-6, as the confining pressure changes from 2 to 25 MPa, the impact rate of the slippage effect increases continuously. When the confining pressure is relatively low (2–3 MPa) and the pore pressure is higher than 0.4 MPa, the impact rate of the slippage effect is small.

3.5 The Relationship Between Slippage Factor and Absolute Permeability

Civan (2010) proposed an equation that relates the slippage factor b and the absolute permeability through theoretical analysis:

$$\begin{aligned} b=\beta \left( \frac{k_{g\infty } }{\phi }\right) ^{-1/2} \end{aligned}$$

(8)

where $k_{g\infty }$ is the absolute permeability, $\varphi$ is the effective porosity, and the coefficient $\beta$ is defined by

$$\begin{aligned} \beta =p\lambda \sqrt{\frac{2}{\tau _h }} \end{aligned}$$

(9)

where $\tau _{h}$ is the tortuosity factor and is a ratio of the length of the tortuous flow paths to the length of bulk porous media, P is fluid pressure, and $\lambda$ is the molecule’s mean free path.

Sampath and Keighin (1982) proposed an improved correlation for the Klinkenberg coefficient of the $N_2$ gas in the presence of water in porous media, which is expressed below in SI unit.

$$\begin{aligned} b=0.0414\left( \frac{k_{g\infty } }{\phi }\right) ^{-0.53} \end{aligned}$$

(10)

The significance of this correlation is that its exponent is very close to the $-0.50$ exponent value obtained by the theoretical analysis of Civan (2010) in Eq. (8).

Based on the test results, empirical power law relations between the slippage factor and the absolute permeability are obtained for the two specimens, and the results are presented in Fig. 13. The b factors for specimens QDC-5 and QDC-6 are:

$$\begin{aligned} b= & {} 0.2232k_{g\infty } ^{-0.201}\qquad (\hbox {QDC-}5)\nonumber \\ b= & {} 0.2861k_{g\infty } ^{-0.5319}\qquad (\hbox {QDC-}6) \end{aligned}$$

(11)

For specimen QDC-6, the $-0.5319$ exponent is very close to the theoretical value obtained by Civan (2010). The large difference between the two specimens may be caused by the difference in porosity and pore-throat of two rock specimens.

Fig. 13

Fitting curves of slippage factor and absolute permeability for specimens a QDC-5, b QDC-6

3.6 Knudsen Number ($\hbox {K}_{n}$) and Flow Regimes

The Knudsen number $(K_{n})$, which is a dimensionless parameter, is the ratio of the mean free path $(\lambda )$ of a gas molecule to the characteristic dimension (L) of the flow channel. Gas flow in small pores is generally divided into four regimes according to the Knudsen number (Schaaf and Chambre 1961). When $K_{n} <0.01$, the flow is the viscous flow and continuum and thermodynamic equilibrium assumptions are appropriate and conventional fluid dynamic equations such as Darcy’s equation are applicable. When $0.01 < K_{n} < 0.1$, the flow is in the slippage flow regime. The non-equilibrium effects dominate near the pore walls. The no-slip boundary condition fails to provide an agreement between theoretical predictions and experimental results. In this type of flow, the conventional flow equations such as Darcy’s equation can be employed with a modification such as the Klinkenberg correction. When $0.1 < K_{n} < 10$, the flow is in the transitional flow regime, which includes both the slippage and diffusion flows. Traditional fluid dynamics Navier–Stokes equations start to fail, and it is better to use Knudsen’s diffusion equations especially for the flows with high Knudsen numbers (Ziarani and Aguilera 2012). When $K_{n} >10$, the flow is in the Knudsen’s (free molecular) flow regime. Continuum fluid flow equations are not applicable, and alternative techniques such as direct numerical simulations using the Monte Carlo method (Bird 1994) or the lattice Boltzmann method (Lilley and Sader 2008) can be used. This classification of flows, which is based on the Knudsen number, is based on pipe flow experiments and may vary in other cases (Beskok and Karniadakis 1999). It is very important for choosing the methods used for modelling and predicting gas micro-flows.

The Knudsen number $(K_{n})$ is expressed as:

$$\begin{aligned} k_n =\frac{\lambda }{L} \end{aligned}$$

(12)

In porous media, L represents the equivalent hydraulic radius r (Civan 2010). Thus, Eq. (12) can be written as:

$$\begin{aligned} k_n =\frac{\lambda }{r} \end{aligned}$$

(13)

Comparing Eqs. 2 and 13 yields an expression as:

$$\begin{aligned} k_n =\frac{b}{4p_m } \end{aligned}$$

(14)

Based on Eq. (14) and b values presented in Tables 3 and 4, the Knudsen numbers $(K_{n})$ under different pore and confining pressures can be obtained. The relationships between the Knudsen numbers $(K_{n})$ and the pore pressure are plotted in Figs. 14 and 15, and the numbers are listed in Tables 8 and 9 in “Appendix”.

Fig. 14

Relationship between the Knudsen numbers $(K_{n})$ and pore pressure for specimen QDC-5

Fig. 15

Relationship between the Knudsen numbers $(K_{n})$ and pore pressure for specimen QDC-6

It can be seen from Figs. 14 and 15 as well as the data in Tables 7 and 8 that for a given confining pressure, the Knudsen numbers depend on the pore pressure. The higher the pore pressure is, the lower the Knudsen numbers are. When the pore pressure changes from 0.2 to 2.5 MPa and the confining pressure changes from 2 to 30 MPa, the Knudsen numbers $(K_{n})$ vary between 0.0001 and 0.9. As described by Schaaf and Chambre (1961), when the Knudsen numbers $<$0.01, the gas flow can be described by Darcy’s law and the assumption of continuum flow remains valid. When the Knudsen numbers are higher than 0.01, an effective permeability must be computed to correct the Knudsen diffusion and/or slip flow.

For QDC-5, when the pore pressure varies from 0.8 to 2.5 MPa, the Knudsen numbers $(K_{n})$ are between 0.01 and 0.1 (see Table 7 in “Appendix”) and the flow regime is slippage flow. Ziarani and Aguilera (2012) suggest that under this condition a model of Darcy’s equation with Klinkenberg or Knudsen’s correction should be applied. Although Knudsen’s correction is more accurate, Klinkenberg’s correction is easier to be applied and hence is widely used. Ma et al. (2014) also indicated that when the Knudsen number is $<$0.1, the Knudsen diffusion is much smaller than the slip flow, and therefore it should contribute less to the gas permeability. When the pore pressure is in the range of 0.2–0.6, the Knudsen numbers $(K_{n})$ vary between 0.1 and 0.9, and the flow should be transitional flow. Agarwal et al. (2001) suggested that Darcy’s law with a Knudsen’s correction can be applied in this case, and an alternative method is Burnett’s equation with slip boundary conditions. Ziarani and Aguilera (2012) stated that the Knudsen’s diffusion equation is more reliable, especially when the Kn value is close to 10.

For QDC-6, the Knudsen numbers $(K_{n})$ are $<$0.01 for confining pressures equal to 2 and 3 MPa; in this case the flow is in the viscous flow regime and Darcy’s equation is applicable. When the confining pressure is between 4 and 8 MPa and the pore pressure is higher than 1.8 MPa, the Knudsen numbers are between 0.01 and 0.1 (see Table 8 in “Appendix”) and the flow is in the slippage flow regime. When the confining pressure is higher than 6 MPa and pore pressure is $<$0.8 MPa, the flow is in the transitional flow regime because the Knudsen numbers are between 0.1 and 0.9. The tested granitic gneiss has shown viscous flow, slippage flow, and transitional flow in the pressure range of testing.

The gas used in this study is considered as the ideal gas. Ma et al. (2014) proposed to compare test results using ideal gas and non-ideal gas and hypothesized that the ideal gas may over- or underestimate the apparent permeability depending on the flow regimes. In addition, it would be interesting to compare the test result using gas with that using water (e.g. Boulin et al. 2012). These outstanding issues will be addressed in our future research.

4 Conclusions

The flow characteristics of gas in small pore throats in a compact rock (granitic gneiss) are investigated, and the permeability and the porosity under different pore and confining pressures are measured. The influence of the gas slippage effect on the measured permeability is discussed. The test results show that the relationship between the gas flow rate and the difference of squared pressures is not linear and exhibits the nonlinear flow characteristic. The gas flow in the compact rock is affected by the Klinkenberg’s slippage effect. When the pore pressure is low, the mean free path of molecules increases and the Klinkenberg’s slippage effect increases subsequently, leading to a measured permeability that is higher than the absolute permeability of the rock.

For a given confining pressure, the gas slippage effect is more obvious when the pore pressure is low. When the pore pressure is lower than 0.4 MPa, the impact rate of the gas slippage effect is generally ${}{>}$50 %. Thus, the influence of the gas slippage effect on the measured permeability of rocks should be considered when the pore pressure is low. The influence of confining pressure on the impact rate of the slippage effect has an upper bound. When the confining pressure reaches a certain value, the impact rate of the slippage effect no longer increases.

A power law describes well the relationship between the absolute permeability and the effective porosity. A correlation of the slippage factor and the absolute permeability is provided based on the test results. At low confining pressures of 2 and 3 MPa, the Knudsen numbers (Kn) of specimen QDC-6 are $<$0.01, and Darcy’s equation is applicable. When the confining pressure increases from 4 to 30 MPa and the pore pressure is in the range of 0.2 to 3 MPa, the Knudsen numbers (Kn) are between 0.01 and 0.9, indicating that the flows are slip flow and transitional flow. Under those conditions, traditional fluid dynamics and Navier–Stokes equations are no longer applicable, and it is recommended to use Knudsen’s diffusion equations, especially for the flows with high Knudsen numbers.

Appendix

See Tables 6, 7, 8, and 9.

Table 6 Impact rates of gas slippage effect for specimen QDC-5

Table 7 Impact rates of gas slippage effect for specimen QDC-6

Table 8 Knudsen numbers $(K_{n})$ for specimen QDC-5

Table 9 Knudsen numbers $(K_{n})$ for specimen QDC-6