Flow and Transport Properties of Deforming Porous Media. I. Permeability

Abstract

Estimating flow and transport properties of porous media that undergo deformation as a result of applying an external pressure or force is important to a wide variety of processes, ranging from injecting a fracking liquid into shale formations, to CO$_2$ sequestration in spent oil reservoirs. We propose a novel model for estimating the effective flow and transport properties of such porous media. Assuming that the solid matrix of a porous medium undergoes elastic deformation, and given its initial porosity before deformation, as well as the Young’s modulus of its grains, the model uses an extension of the Hertz–Mindlin theory of contact between grains to compute the new PSD that results from applying an external pressure P to the medium, and utilizes the updated PSD in the effective-medium approximation (EMA) to estimate the effective flow and transport properties at pressure P. In the present part of this series, we use the theory to predict the effective permeability as a function of the applied pressure. Comparison between the predictions and experimental data for twenty-four types of sandstones indicates excellent agreement between the two.

1 Introduction

The focus of this paper is on the effect of deformation of porous media on their flow and transport properties, a problem that is encountered in a wide variety of contexts, and is of fundamental interest to geologists, reservoir engineers, and groundwater scientists. Examples include deformation of consolidating clays (Brown and Brindley 1980), geological formations deep underground where the pressure is large (Iliev et al. 2008; Fagbemi et al. 2018), geothermal, coal-bed methane, oil and gas reservoirs, as well as unconventional energy resources, such as shale formations. For example, to extract hot water from geothermal reservoirs at economically attractive rates, their porosity and permeability must be such that the volume flow rate of water is on the order of tens of m$^3$/hr or larger (Heiland 2003). Often though, such reservoirs have low permeability and, therefore, they need stimulation by, for example, hydraulic fracturing in order to produce hot water economically.

Aside from laboratory experiments on the effect of deformation on the effective permeability (Zoback and Byerlee 1975), one also needs a predictive model that can provide accurate estimates for the pressure- or stress-dependence of the effective flow and transport properties. Although the problem has been studied experimentally by numerous groups (see, for example, Zhu and Wong 1997; Keaney et al. 1998; Ruisten et al. 1999; Ngwenya et al. 2003; Fossein et al. 2007; Baud et al. 2012; Ballas et al. 2015; Liu et al. 2018; Meng et al. 2019; Yang and Hu 2020), an accurate model for predicting the pressure-dependence of flow and transport properties of deforming porous media is still lacking.

A related phenomenon is deformation of shale formations (Ibanez and Kronenberg 1993) under compression and varying confining pressure. When shale gas accumulates in rock, the pressure rises significantly as a result of the action of high-pressure gas, coupled with ground stress in the seam, implying that the surrounding rock is always under high confining stress. Due to their low porosity and permeability, shale formations will not produce, unless they are subject to hydraulic fracturing that generates a fracture network, with the induced fractures intersecting the natural ones (Osborn et al. 2011). After producing for a while, gas production decreases, leading to repeated fracturing. At the end, the pressures of the shale gas and the fracturing fluid both decrease, as the high-pressure fracturing fluid is discharged. Therefore, during the entire process, shale formations are subject to cyclic loading and water pressure, hence giving rise to stress–permeability coupling (Jiang et al. 2018).

Deformation of coal-bed methane reservoirs represents another example in which the permeability of the formations varies under uniaxial or triaxial stress. Several groups have developed theoretical models for the effect of an external load on the porosity and permeability of coals (see, for example, Liu and Harpalani 2013; Wu et al. 2018; Mathias et al. 2019). The cleats in coal formations contribute most to their permeability. Reducing the pore pressure increases the effective stress, leading to a reduction in the apertures of the coal cleats and, hence, a reduction in the porosity and permeability.

Deformation of solid materials is not, however, confined to rock, as there is a wide class of deformable porous materials whose flow and transport properties, when they are subject to an external load, vary with the magnitude of the load - pressure or stress. They range anywhere from polymers and hydrogels (Iritani et al. 2006; Karada 2010; Sweijen et al. 2017), the “cake” that is built up on the external surface of filters (Sahimi and Imdakm 1991; Imdakm and Sahimi 1987, 1991), and printing papers (Ghassemzadeh et al. 2001; Ghassemzadeh and Sahimi 2004; Masoudi and Pillai 2010), to diapers (Savoji and Pourjavadi 2006; Salimi et al. 2010), and foams (Koehler et al. 2000; Pitois et al. 2009). Another important example of much current interest is deformation and swelling of geological formations, such as oil and gas reservoirs that no longer produce, as a result of injecting CO$_2$ into their pore space. As recent molecular dynamics simulations indicated (Rahromostaqim and Sahimi 2018, 2019), in the presence of brine, CO$_2$ causes swelling of pure and mixed clays that may eventually lead to earthquakes (Maxwell et al. 2008; Tafti et al. 2013; Rother et al. 2013; Lee et al. 2016).

The physical properties of porous media depend strongly on their morphology, namely, their pore shape, pore-size distribution (PSD), and pore connectivity. Deformation changes the morphology and, therefore, the macroscopic properties. Therefore, a main goal of studying deformation of porous media is predicting such properties as a function of the driving force for deformation, such as an external pressure or stress. In particular, one is interested in understanding the relation between the effective flow and transport properties of deforming porous media, which is typically smaller than the initial properties before deformation, and the external pressure; see for example, the aforementioned references, as well as Khoei and Mohammadnejad (2011), Bhandari et al. (2015), and Pesavento et al. (2017).

The foundation for modeling of flow and transport in deforming porous medium is provided by the momentum balance and the equations that govern elastic deformation of solids, together with mass balance and appropriate constitutive and state equations. In a macroscopic approach to the problem, one averages the microscopic conservation laws over a suitable volume of a porous formation and supplements the theory with empirical or semi-empirical constitutive relations for flow, transport and mechanical properties. Biot (1941, 1956) pioneered this approach, which has also been extended in order to study the same phenomena involving nonlinear material behavior (see, for example, Zienkiewicz and Shiomi 1994; Zienkiewicz et al. 1990; Schrefler et al. 1998; Li et al. 2004; Zhang et al. 2009), as well as when the pore space is only partially saturated by a fluid in the presence of a second fluid (see, for example, Khoei and Mohammadnejad 2011; Pesavento et al. 2017).

Another macroscopic approach is the so-called mixture theory (see, for example, Atkin and Craine 1976a, b; Bowen 1982; Murad and Cushman 1996; Huyghe and Janssen 1997; Cowin and Cardoso 2012; Huyghe et al. 2017), which was derived by averaging the microscopic equations of mass, momentum and energy over a suitable length scale. The entropy inequality that describes the direction of dissipation of energy due to deformation was not, however, invoked for deriving the macroscale equations. As a result, the relationships that link macroscopic thermodynamic variables to the properties of porous media could not be derived directly. Hassanizadeh and Gray (1979a, b, 1990) combined the two aforementioned macroscopic approaches together with the entropy inequality in order to derive a generalization of Darcy’s law for the flow field in a deformable porous medium (see also Weinstein et al. 2008; Zhu et al. 2010).

Since flow and transport in heterogeneous porous media are controlled by their morphology, a few computational approaches have also been developed that carry out numerical simulations, either in the image of porous media, or in a model of them (see, for example, Zhu and Wong 1999; Boutt and McPherson 2002; Arns et al. 2001, 2002; Dautriat et al. 2009; Thovert and Adler 2011; Jasinski et al. 2015; Bakhshian and Sahimi 2016; Bakhshian et al. 2018; Fagbemi et al. 2018; Aljasmi and Sahimi 2020) in order to simulate the changes in the morphology of porous media as they undergo deformation.

The goal of our study is developing a relatively simple, and to our knowledge, new, theoretical model for predicting the effective flow and transport properties of porous media that deform under an external hydrostatic pressure P. The model that we develop combines a theory of deformation of contacting grains under an external force with the effective-medium approximation (EMA) in order to predict the effective flow and transport properties as a function of P. Bruggeman (1935) was the first to develop an EMA for estimating the macroscopic properties of heterogeneous media. The same formulation was developed independently by Landauer (1952) for computing electrical conductivity of composite solids. The EMA was used by Koplik et al. (1984) to predict the effective permeability and conductivity of a porous medium.

In addition, other theories have been suggested for predicting the permeability. For example, Wadsworth et al. (2016) proposed a universal scaling of the permeability, which is based on the power laws of percolation theory. But all the past works, including those that utilized the EMA, were for predicting physical properties of rigid heterogeneous media (for comprehensive reviews see Sahimi 2003, 2011). What we present is, however, the application of a novel combination of the EMA and a theory of deformation for computing the macroscopic permeability and electrical conductivity of porous media that undergo deformation, when a hydrostatic pressure P is applied to them. In the present paper, Part I of a series, we develop the essential theory and utilize it to predict the effective permeability. In subsequent parts, the theory will be utilized for predicting the effective electrical conductivity of fluid-saturated porous media and other properties.

The organization of this paper is as follows. In Sect.2, we derive the new theoretical model for estimating the change in the size of the pores when the pressure P is applied to a porous medium. The theory is then used in Sect. 3 to determine the evolution of the PSD during deformation. Section 4 describes the EMA for estimating the effective permeability. The proposed theory involves the elastic modulus of the grains or the solid matrix, and, therefore, Sect. 5 describes the various approaches for estimating the modulus. The computational procedure is described in Sect. 6, while Sect. 7 presents the theoretical predictions for the permeability of a wide variety of sandstones and compares them with experimental data. Section 8 discusses a few aspects of the model, while the paper is summarized in Sect. 9.

2 Theory of Elastic Deformation of Porous Media Under an Applied Force

As mentioned in the Introduction, we employ the EMA to predict the effective permeability of porous media that deform as a result of applying an external pressure or stress. The EMA is a sort of mean-field approximation (MFA) that replaces a heterogeneous porous medium by an effective one in which all the pores have the same effective size $r_e$. The solution of the flow and transport problem in the uniform system is straightforward. Then, one pore in the effective medium is selected at random and its radius in the original disordered medium is restored, with the rest of the pores still having the same size $r_e$. This generates a perturbation in the solution of the uniform system, whose magnitude is the difference between the solution for the uniform medium and one that is uniform everywhere, but in one pore. The perturbation is calculated, and since the single pore is selected at random and its size follows a PSD, in order to be able to still represent the disordered medium with one with an effective pore radius $r_e$ and an effective flow or transport property, one insists that the average of the perturbation, when the averaging is taken over the PSD, should be zero. In effect, only the interaction of a single pore with the rest of the effective medium is taken into account, and the influence of the remaining part of the disordered porous medium is represented by the far-field external pressure gradient. Extensions of the EMA that account for interactions of a pore with those that are farther than the nearest-neighbor ones were also developed (Sahimi et al. 1983, 1984), but we ignore them in this work.

We assume that the deformation is elastic. At very high pressures, the inelastic effects may become important, but the range of pressure over which the experimental data that we use with the theoretical predictions is in the range of elastic deformation. Thus, in the spirit of the EMA, and for the sake of developing a tractable theoretical approach that is consistent with the mean-field nature of the EMA, we consider the interaction between two grains, the minimum number of grains in a MFA, subject to an external force F or the corresponding hydrostatic pressure P applied to the medium, and determine the deformation that it causes in the pore between the two grains that changes its size. The effect of the deformation of the rest of a porous medium is represented by the far-field applied pressure P or force. The pressure P changes the PSD of the pore space that, in turn, influences its effective flow and transport properties, and in particular its effective permeability $K_e$. Since one important input to the EMA is the PSD of the pore space, the first step toward the goal of predicting the dependence of $K_e$ on the external pressure P is to determine the changes in the PSD as P is gradually increased.

To determine the interaction between two neighboring grains and the deformation of the pore space between them, we derive a theory of deformation of contacting grains, first studied by Hertz (1882) who assumed no friction between the grains. Goodman (1962) studied the same problem, but with friction between the two grains, while (Mindlin 1949) considered the case in which tangential forces and twisting were coupled at the contact point between two grains. The derivation that we present is similar to the analysis of Timonshenko and Goodier (1970), but we present the complete details, simplify the analysis, and our final results were not actually presented by them.

Fig. 1

a Configuration of two grains and the pore between them for estimating the new pore radius. b The loaded zone for computing the pressure distribution, with point A being on the contact surface

We consider a typical, or average, grain size $R_g$, and normalize all the length scale with respect to it. Consider, then, Fig. 1a that shows two grains, 1 and 2, which, in the absence of any applied external pressure, are in contact at point C along the Z axis. We assume that the grains’ surfaces at the point of contact have radii of curvature $R_1$ and $R_2$. If the grains are roughly spherical, then, $R_1$ and $R_2$ also represent roughly their radii. Consider the plane tangent at C, and two points A and B that are on the front sections of the surfaces 1 and 2 at a small distance x from the Z axis. The distances $z_1$ and $z_2$ of A and B from the tangent plane satisfy the relations, $(R_1-z_1)^2+x^2=R_1^2$, and $(R_2-z_2)^2+x^2=R_2^2$. Assuming that $z_1$ and $z_2$ are small enough that $z_1^2$ and $z_2^2$ can be ignored, we obtain, $z_1=x^2/(2R_1)$ and $z_2=x^2/(2R_2)$. Therefore, the distance $D=z_1+z_2$ between A and B is given by

$$\begin{aligned} D=\left( \frac{R_1+R_2}{2R_1R_2}\right) x^2\;. \end{aligned}$$

(1)

An external force F is applied to the porous medium to press the grains together, which causes local deformation near C over a small, roughly circular (spherical) surface, which we refer to as the contact surface (CS). If the deformation is small, we may assume that both $R_1$ and $R_2$ are much larger than the radius of the CS. Suppose that $u_A$ and $u_B$ are, respectively, the displacements of A and B due to the local deformation along the Z axis. Then, if the tangent plane at C is held fixed, the local compression causes any two points on the surface of the two grains, which are far from C, to move toward each other by an amount u, implying that the distance between A and B decreases by $u-(u_A+u_B)$ and, therefore, the effective pore radius between the two grains also decreases by u/2. Thus, if the compression caused by applying the force F brings A and B into the CS, we must have,

$$\begin{aligned} u-(u_A+u_B)=\alpha x^2\;,\;\;\mathrm{with}\;\;\alpha =\frac{R_1+R_2}{2R_1R_2}\;, \end{aligned}$$

(2)

if we use Eq. (1). Thus,

$$\begin{aligned} u=u_A+u_B+\alpha x^2\;. \end{aligned}$$

(3)

Therefore, we must determine $u_A$ and $u_B$ in order to compute u, i.e., the decrease in the distance between non-contacting surfaces of two grains, which leads directly to the change in the size of the pore between them and, hence, the change in the PSD of the deforming porous medium can be determined.

Consider a small element of the loaded zone, shown by the shaded area in Fig. 1b that is bounded between radii s and $s+\text {d}s$ and angle $\text {d}\theta$ where, as shown in Fig. 1a, A is a point on the CS. If p is the local pressure in the CS, then, the displacement $u_A$ is given by (Timoshenko and Goodier 1970),

$$\begin{aligned} u_A=\left( \frac{1-\nu _1^2}{\pi E_1}\right) \int \int p\;\text {d}s\text {d}\theta \;, \end{aligned}$$

(4)

which follows directly from the theory of displacement of a spherical grain, where $E_1$ and $\nu _1$ are, respectively, the elastic (Young’s) modulus and Poisson’s ratio of the grain. A similar equation also holds for $u_B$:

$$\begin{aligned} u_B=\left( \frac{1-\nu _2^2}{\pi E_2}\right) \int \int p\;\text {d}s\text {d}\theta \;. \end{aligned}$$

(5)

Note that the two equations for $u_A$ and $u_B$ are subject to the condition that both A and B are on the CS. Therefore, by substituting the expressions for $u_A$ and $u_B$ in Eq. (3), we obtain

$$\begin{aligned} \frac{1}{\pi }\left( \frac{1-\nu _1^2}{E_1}+\frac{1-\nu _2^2}{E_2}\right) \int \int p\;\text {d}s\text {d}\theta =u-\alpha x^2\;. \end{aligned}$$

(6)

It remains to calculate p, the local pressure distribution over the CS. If a hemisphere of radius $R_c$ is constructed on the CS, then building on the Hertz–Mindlin work, we argue that the pressure distribution is represented by the hemisphere’s ordinates. This implies that the pressure $p_0$ at the center of the CS, i.e., the maximum pressure in the CS, is simply proportional to $R_c$ and is given by, $p_0=aR_c$, where a is a scale factor. As shown in Fig. 1b, the local pressure p varies over a chord mn, shown by the dashed semicircle. Therefore, $\int pds=p_0S/R_c$, with S being the area of the semicircle. Since

$$\begin{aligned} S=\frac{1}{2}\pi (R_c^2-x^2\sin ^2\theta )\;, \end{aligned}$$

(7)

then, substituting for $\int p\;ds$ and S in Eq. (6), yields

$$\begin{aligned} \left( \frac{p_0}{R_c}\right) \left( \frac{1-\nu _1^2}{E_1}+\frac{1-\nu _2^2}{E_2} \right) \int _0^{\pi /2}(R_c^2-x^2\sin ^2\theta )\text {d}\theta =u-\alpha x^2\;. \end{aligned}$$

(8)

Carrying out the integration, we obtain

$$\begin{aligned} \left( \frac{\pi p_0}{4R_c}\right) (2R_c^2-x^2)\left( \frac{1-\nu _1^2}{E_1}+ \frac{1-\nu _2^2}{E_2}\right) =u-\alpha x^2\;. \end{aligned}$$

(9)

Equation (9) is an identity in terms of x that must be valid for any of its values. This would be possible if

$$\begin{aligned}&R_c=\left( \frac{\pi p_0}{4\alpha }\right) \left( \frac{1-\nu _1^2}{E_1}+ \frac{1-\nu _2^2}{E_2}\right) \;, \end{aligned}$$

(10)

$$\begin{aligned}&u=\left( \frac{1}{2}\;\pi p_0R_c\right) \left( \frac{1-\nu _1^2}{E_1}+ \frac{1-\nu _2^2}{E_2}\right) \;. \end{aligned}$$

(11)

To relate $p_0$ to the applied force F, we note that the sum of the pressures in the contact area multiplied by its surface should be equal to F. Thus, $(p_0/R_c)(\frac{2}{3}\pi R_c^3)=F$, or, $p_0=3F/(2\pi R_c^2)$, which, after substituting in Eq. (10) and solving for $R_c$, yields,

$$\begin{aligned} R_c=\left[ \frac{3F}{8\alpha }\left( \frac{1-\nu _1^2}{E_1}+\frac{1-\nu _2^2}{E_2} \right) \right] ^{1/3}\;. \end{aligned}$$

(12)

If we substitute Eq. (12) and the result for $p_0$ in Eq. (11), we find that

$$\begin{aligned} u=\frac{1}{2}\left[ 3F\left( \frac{1-\nu _1^2}{E_1}+\frac{1-\nu _2^2}{E_2}\right) \left( \frac{R_1+R_2}{2R_1R_2}\right) ^{1/2}\right] ^{2/3}\;. \end{aligned}$$

(13)

Assuming that the two grains are composed of the same materials, we have, $\nu _1=\nu _2=\nu$ and $E_1=E_2=E_e$. We also assume that the two grains have roughly the same radii of curvature, $R_1\approx R_2=R$. With the assumption of local isotropy, the local force is isotropic and homothetic, i.e., it is a monotonic transformation of F. Thus, F and the hydrostatic pressure P are related by, $F=\sqrt{2}\;R_g^2P=\sqrt{2}P$, with the second equation being due to normalization of lengths by $R_g$ (i.e., $R_g\rightarrow R_g/R_g=1$), where $\sqrt{2}$ is due to the geometrical considerations, as shown by Deresiewicz (1958). Under these conditions, Eqs. (12) and (13) are simplified to

$$\begin{aligned}&R_c=(R)^{1/3}\left[ \frac{3\sqrt{2}P(1-\nu ^2)}{4E_e}\right] ^{1/3}\;, \end{aligned}$$

(14)

$$\begin{aligned}&u=\left( \frac{1}{R}\right) ^{1/3}\left[ \frac{3P(1-\nu ^2)}{E_e} \right] ^{2/3}\;. \end{aligned}$$

(15)

Thus, writing u and R in un-normalized units, Eqs. (14) and (15) become,

$$\begin{aligned}&R_c=R_g\left( \frac{R}{R_g}\right) ^{1/3}\left[ \frac{3\sqrt{2}P(1-\nu ^2)}{4E_e}\right] ^{1/3}\;, \end{aligned}$$

(16)

$$\begin{aligned}&u=R_g\left( \frac{R_g}{R}\right) ^{1/3}\left[ \frac{3P(1-\nu ^2)}{E_e} \right] ^{2/3}\;. \end{aligned}$$

(17)

Note that, $R_g\approx R$, if the grains are roughly spherical, which we assume to be the case or, at the minimum, we can define a radius for an equivalent spherical particle.

3 Evolution of the Pore-Size Distribution Under an External Hydrostatic Pressure

Within the framework of a MFA in which the interactions of two neighboring grains with other grains farther away are ignored, the pore between the two grains does not also interact with the pores farther away. Thus, as pointed out earlier, to a first-order approximation, the effective radius of a pore under an external hydrostatic pressure P decreases by u/2, where u is given by Eq. (17). In other words, the initial PSD distribution $f_0(r_0)$ before any pressure is applied is transformed to a new PSD $f_P(r_P)$ at pressure P where, $r_P=r_0-u/2$. If $f_0(r_0)$ is given, either analytically or numerically, then, since, $f_P(r_P)=f_0(r_0-u/2)$, one either has an analytical expression for $f_P(r_P)$, or constructs it numerically for any pressure P.

4 The EMA for the Effective Permeability

A porous medium consists of pore throats connected together at the pore bodies. The effective sizes of both the pore throats and pore bodies are distributed according to statistical distributions $f_t(r_t)$ and $f_b(r_b)$. It is, however, not straightforward to measure $f_b(r_b)$, which is why it is usually not available. Thus, since the macroscopic permeability is controlled by the pore throats, for convenience we refer to the pore throats as pores, and their distribution f(r) as the PSD. As described in Sect. 2, in the EMA a heterogeneous pore space is represented by a uniform medium with the size of all the pores being $r_e$. We assume that the pores are cylindrical. Then, for slow flow the flow conductance $K_f$ is given by, $K_f\propto r^4$ (other pore shapes may also be considered). Note that it is possible to consider other pore shapes. The EMA predicts that the macroscopic permeability $K_e$ is given by (Doyen 1988; David et al. 1990)

$$\begin{aligned} K_e=\frac{\phi }{C_s\tau }\frac{r_e^4}{\langle r_b^2\rangle }\;, \end{aligned}$$

(18)

with $\phi$ being the porosity, $\tau$ is the flow tortuosity for which various theories, as well as empirical and semi-empirical relations have been developed (for a review see Ghanbarian-Alavijeh et al. 2013), $C_s$ is a geometrical factor with $C_s=8$ for cylindrical pores in Hagen–Poiseuille (slow or laminar) flow, and $r_b$ is the size of the pore bodies. Since the distribution $f_b(r_b)$ of the size of the pore bodies is typically not available, David et al. (1990) suggested that one should use, $\langle r_b^2\rangle \simeq \langle r^2\rangle =\int _{r_m}^{r_M}r^2f(r)\text {d}r$, with $r_m$ and $r_M$ being, respectively, the minimum and maximum pore radii; we do the same in this paper. $r_e^4$ is computed by the EMA:

$$\begin{aligned} \int _{r_m}^{r_M}\frac{r_e^4-r^4}{r^4+(D-1)r_e^4}f(r)\text {d}r=0\;, \end{aligned}$$

(19)

Here, D is the Euclidean dimensionality of the porous medium ($D=3$ in our calculations). If the porosity of the porous medium is low enough that the pore space is near its critical porosity $\phi _c$ or the percolation threshold, i.e., the porosity at which the sample-spanning cluster of the pores is barely connected, and the macroscopic permeability and electrical conductivity vanish for $\phi \le \phi _c$, then, as first derived by Kirkpatrick (1971), one may use Z/2 in Eq. (19), instead of D, where Z is the mean connectivity of the pore space.

Mukhopadhyay and Sahimi (2000) derived an EMA for predicting the direction-dependent macroscopic permeabilities of anisotropic porous media; Stroud (1975) presented a continuum EMA for anisotropic media in which the local conductivity or permeability was a tensor; Ghanbarian et al. (2016) utilized Eq. (19) to predict the relative permeability of water in soil in the presence of air; Ghanbarian and Javadpour (2017) invoked Eq. (19) to estimate the gas permeability in shales, while saturation-dependent electrical conductivity of partially saturated packings of spherical particles was computed by Ghanbarian and Sahimi (2017) using Eq. (19).

5 Estimating the Parameters of the Model

Let us first point out that the model presented in Sect. 4 is a MFA. Therefore, similar to any MFA, the fluctuations in the local properties are ignored, allowing one to analyze the behavior of the system based on only two grains, the minimum number for a meaningful analysis. Similar to all the MFAs, the approach has its limitations and strengths, which we will discuss in Sect. 8. For now, it suffices to mention that since this is a two-grain MFA and, as a result, only an average grain size is required. We will return to this point in Sect. 8.

5.1 The Poisson’s Ratio and the Pore-Size Distribution

According to Eqs. (17) and (19), the parameters of the model are the Young’s modulus $E_e$, the Poisson’s ratio $\nu$, and the PSD f(r). If experimental data are available for the three parameters, they can be used directly in the theory. Unfortunately, for the sandstones that we analyze, the information is not available. Thus, we need to make judicious choice of the parameters. Our preliminary computations indicated that while the predictions of the model are sensitive to the value of the Young’s modulus, they only change mildly when $\nu$ and the PSD are varied, which we now demonstrate.

Consider, first, the sensitivity of the predictions to the PSD. To study this, we used the following theoretical PSD distribution,

$$\begin{aligned} f(r)=\left[ \frac{r-r_m}{(r_0-r_m)^2}\right] \exp \left[ -\frac{1}{2} \left( \frac{r-r_m}{r_0-r_m}\right) ^2\right] \;, \end{aligned}$$

(20)

Fig. 2

a The PSD distributions generated by Eq. (20) with $r_m$ held constant at $0.18\;\mu$m. b The PSD that was utilized in most of the computations, which was reported by Lindquist et al. (2000). The units of r are $\mu$m

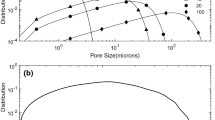
where $r_0$ is a parameter related to the average pore size $r_a$ through, $r_a =(r_0-r_m)\sqrt{\pi /2}+r_m$. We fixed the minimum pore size $r_m$ at $0.18\; \mu$m, the lowest pore sizes that we could identify in the published PSDs for sandstones, and varied $r_0$ over two orders of magnitude. Figure 2a presents the type of the PSD that Eq. (20) generates. The distribution generated by the lowest $r_0$ in Fig. 2 has striking similarities with what was reported by Fredrich et al. (1993) for a Fontainebleau sandstone, while those generated by other values of $r_0$ are qualitatively similar to those reported by others for other types of sandstone. We then computed the effective permeability for one of the sandstones that we analyze later in this paper, namely, the Tensleep sandstone (see Sect. 7), fixing all the parameters, but varying the PSD.

Figure 3 presents the results, where the permeability is normalized by its value before deformation (see also Sect. 7). The results do not indicate great sensitivity to the PSD. Calculations for all the sandstones that we analyzed (see Sect. 7) indicated the same trends. Thus, in the absence of any experimental data for the PSDs of the sandstones that we analyzer below, we used in all the cases described below the distribution presented in Fig. 2b as the initial PSD, $f_0(r_0)$, which was reported by Lindquist et al. (2000) for a Fontainebleau sandstone, and is similar to those for many other sandstones reported by others (see, for example, Cheung et al. 2012 for Bleurswiller and Boise sandstones). Note that the distribution is also similar to what Eq. (20) generates, and that the pore sizes vary over about two orders of magnitude, a relatively broad range.

Fig. 3

Effect of the PSD on the predicted permeabilities. $r_0$ is the parameter related to the average pore size $r_a$ (see the text), while $r_m= 0.16\;\mu$m

Next, we studied the sensitivity of the predictions to the value of the Poisson’s ratio, $\nu$. Once again, all the parameters but $\nu$ were fixed, and the model was used to predict the dependence on the applied pressure of the permeability of the sandstone of Fig. 3. Figure 4 presents the results. The Poisson’s ratio was varied by a factor of 4, and yet the predictions vary by at most 2 percent. Calculations with all the other sandstones that we analyze below (see Sect. 7) indicated the same trends. Thus, we fixed the Poisson’s ratio at $\nu \approx 0.3$, which is in the middle of the range for sandstones.

Fig. 4

Effect of the Poisson’s ratio $\nu$ on the predicted permeabilities

5.2 The Young’s Modulus of the Grains

Let us first emphasize that the Young’s modulus $E_e$ in Eq. (17) is not that of the porous medium as a whole, which depends on its porosity and for which an EMA has been developed (Makse et al. 2001), but rather it is that of the grains, or the solid matrix of the porous medium in the MFA, which should either be measured, estimated theoretically, or is treated as an adjustable parameter. The grains are, however, hardly pure materials; they usually represent composites of several components. If the composition of the solid matrix or grains is known, then there are at least two theoretical approaches that can be used to estimate $E_e$.

One method of estimating the elastic moduli of the solid matrix is through rigorous upper and lower bounds. Over the years, relatively tight bounds have been derived that provide reasonable estimates of the elastic moduli of solid composites. These are described in detail by Torquato (2002) and Sahimi (2003), to whom the interested reader is referred. The second approach is based on the so-called self-consistent approximation (SCA) for the effective elastic moduli of a composite material, first developed by Budiansky (1965), Hill (1965), and Wu (1966), and developed further by Berryman (1980), which is the analog of the EMA for the elastic moduli. For example, if we assume that the solid matrix is composed of two components, say quartz and clay as in many sandstones, such that the spatial distribution of clay (component 1) with volume fraction $\phi _1$ is represented by identical spheres dispersed in the background matrix made of quartz—component 2 with volume fraction $\phi _2$—then, according to the SCA the effective bulk modulus $B_e$ and shear modulus $\mu _e$ of the matrix are the solution of the following nonlinear coupled equations:

$$\begin{aligned} \phi _1\frac{B_e-B_1}{4\mu _e/3+B_1}+\phi _2\frac{B_e-B_2}{4\mu _e/3+B_2}=0\;, \end{aligned}$$

(21)

and

$$\begin{aligned} \phi _1\frac{\mu _e-\mu _1}{C_e\mu _e+\mu _1}+\phi _2\frac{\mu _e-\mu _2}{C_e\mu _e+ \mu _2}=0\;, \end{aligned}$$

(22)

where $C_e=(9B_e+8\mu _e)/(6B_e+12\mu _e)$. The case in which component 1 is spatially distributed in the background matrix as elliptical particles has also been studied (Berrymnan 1980). Equation (21) and (22) are accurate, provided that $\phi _1\ll \phi _2$.

Suppose, for example, that the matrix consists of clay with a volume fraction of $\phi _1=0.22$, for which $\mu _1=6.85$ GPa and $B_1=21$ GPa, and quartz with volume fraction of $\phi _2=0.78$ with $B_2=138$ GPa and $\mu _2=44$ GPa. Then, Eqs. (21) and (22) yield, $\mu _e\approx 30.5$ GPa and $B_e\approx 33.5$ GPa. Thus, since the Poisson’s ratio is given by, $\nu =(DB_e-2\mu _e)/[D(D-1)B_e+ 2\mu _e]$, with $D=3$ being the dimensionality of the space, we obtain, $\nu \approx 0.15$. The effective Young’s modulus is then given by, $E_e=2\mu _e(1 +\nu )\approx 70$ GPA. On the other hand, suppose that a sandstone is composed of about 24 percent quartz (component 1), the same as Fahler 154 and close to the Boise sandstone, both analyzed in Sect. 7, while the rest is made of clay (or any other compound much softer than quartz) as component 2. Then, Eqs. (21) and (22) predict that, $B_e\approx 28.7$ and $\mu _e\approx 10.3$, both in GPa, so that $\nu \approx 0.28$ and $E_e\approx 26$ GPa, much smaller than that of pure quartz, $E_e\approx 106$ GPa. These are, of course, approximations, but they do indicate that the Young’s modulus of the grains depends strongly on their compositions.

The information on the exact composition of the solid matrix of the deforming sandstones that we analyze in the present paper is not available. Therefore, in the absence of such information that we could have used in, for example, Eqs. (21) and (22) to estimate $E_e$ for each deforming porous medium that we analyze, we utilize a single experimental data point for the permeability at a given pressure P in order to calibrate the model and estimate $E_e$. We typically took the point in the middle of the pressure range for each set of the data. The estimate is then utilized for predicting $K_e(P)$ at all other pressures.

It is, of course, well-known that the elastic moduli of composite materials, including porous media’s solid matrix, are functions of the applied pressure P. Consider, however, the elastic moduli of quartz, which is typically a main component of sandstones. Its elastic moduli do depend on P (Kondo et al. 1981; Wang et al. 2015), but only at pressures much higher than those considered in the experiments described below. Thus, ignoring the pressure-dependence of $E_e$ is justified. For the predictions that we present below, we used a data point at a pressure in the middle of the range of the pressures at which $K_e$ had been measured.

6 Computational Procedure

Having developed the necessary theoretical tools for predicting the effective permeability of deforming porous media, the computational procedure is as follows.

• (i) We begin with an initial PSD $f_0(r_0)$ of the porous medium to be deformed and estimate its initial permeability using Eqs. (18) and (19).

• (ii) For an applied hydrostatic pressure P, we construct the PSD $f_P(r_P)$ corresponding to P by selecting the pore sizes from $f_0(r_0)$, calculating their updated values using Eq. (17) and $r_P=r_0-u/2$, and repeating it for a large number of pore sizes selected from $f_0(r_0)$, in order to construct a representative $f_P(r_P)$.

• (iii) The resulting $f_P(r_P)$ is then utilized to first update the value of $\langle r_b^2(P)\rangle =\langle r_P^2\rangle$ and then is used together with $f_P(r_P)$ in Eqs. (18) and (19) to compute $K_e(P)$ at the given pressure P.

As pointed out earlier, if the PSD $f_0(r_0)$ can be expressed by an analytical expression, such as Eq. (20), then, so can also $f_P(r_P)$ for any P in which case the computations are very fast.

7 Results and Comparison with Experimental Data

Let us first emphasize again that Eqs. (16)–(19) are not exact, but represent only MFAs to the problem, which we now utilize to predict the pressure-dependence of the effective permeability $K_e(P)$ of a large number of sandstones, and to compare the predictions with the experimental data. Almost all the experimental data are given by Yale (1984), although as noted below, some of them were not his measurements, but he had included them in his Doctoral Thesis for comparison and completeness. Yale (1984) did not provide the sandstones’ initial PSD and, therefore, as mentioned earlier, we used in all the cases described below the PSD presented in Fig. 2b as the initial PSD, $f_0(r_0)$, which was reported by Lindquist et al. (2000). The qualitative aspects of the PSD that we utilize are similar to those for many sandstones, namely, that the distribution is skewed; it has a maximum close to the smallest pores, and that it also has a relatively long tail. Clearly, any PSD can be used in the theoretical formulation that we have developed.

Let us also emphasize that since the PSD and the Poisson’s ratio are fixed in all the cases, only the initial porosity of each sample and the fitted value of the Young’s modulus are used as the parameters of the model. Despite this, as the comparison between the predictions and the experimental data indicates, the theory provides accurate predictions for almost all the cases. In the discussions that follows all the percentages and fractions that are mentioned are volumetric.

7.1 Fontainebleau Sandstone

Before presenting the predictions for the sandstones that Yale (1984) experimented on, we present the results for a Fontainebleau sandstone, since its PSD was reported by Lindquist et al. (2000), while the data for its pressure-dependent $K_e(P)$ were reported by Song and Renner (2008). The initial porosity of the samples was between 0.025 and 0.09 (several samples were experimented on). We found the best estimate for the Young’s modulus of the sandstone that provides accurate predictions for the permeability to be, $E_e\approx 30$ GPa. Figure 5 compares the predictions with the experimental data.

Fig. 5

Comparison of the predicted permeabilities with the experimental data for the Fontainebleau sandstone. The estimate value of the Young’s modulus $E_e$ of the grains is $\approx 30$ GPa

One may reasonably argue that the predictions are not as accurate as one would expect, since the “universal” PSD that we used for all the cases was taken from the data for this Fontainebleau sandstone. Indeed, in this case the model is actually the least successful (see below), since normalized permeability is under- or over-predicted for small or large P, with the overall slope being about half of the experimental data. If, as a reviewer pointed out, we simply model $K_e(P)/K_e(0)=1$, we will have an error of about 15 percent over the wide range of pressures used in the experiments, which should be compared with the maximum error of about 4.4 percent, produced by the model, which is definitely an improvement but, perhaps, one might expect a better performance by the model.

It is, however, noteworthy to point out that the data are considerably scattered. Moreover, the normalized permeability at a pressure of about 180 MPa (the second data point from the left) is larger than 1, hence, indicating that, during the experiments, something might have happened to the sample that the theory cannot account for. Note also that the data vary in a narrow range of (0.85,1) and, therefore, the apparent disagreement between the predictions and the data is a bit superficial. In fact, as mentioned earlier, the maximum error of the predictions is only 4.4 percent, while the average error is only 2 percent.

Let us also point out that Fredrich et al. (1993) also reported experimental data for the PSD and pressure-dependence of the permeability of a Fontainebleau sandstone. Their PSD has striking similarity with the distribution that Eq. (20) produces for $r_0=1$. However, their data for $K_e(P)$ have some peculiar features. In particular (see their Fig. 4), $K_e(P)$ sharply drops when what is referred to as the “effective pressure” is increased from zero to only 4 MPa. It then stays essentially constant for 4 MPa $<P<$ 40 MPa, and then it increases for $P>40$ MPa. Fredrich et al. (1993) remarked that their data have considerable scattering due to inelastic deformations; that some data may be “artifacts” at the higher pressures due to errors in the opening and closing valves, and that the core sample that they experimented on split in half when they removed it from the experimental setup. Thus, we did not try to predict their data.

Yale (1984) stated that in all cases that he experimented on the pore pressure $P_p$ was constant. Thus, in what follows the pressure P may be replaced by $P-P_p$.

7.2 Beaver River Sandstone

Fig. 6

Comparison of the predicted permeabilities with the experimental data for the Beaver sandstone. The estimated value of the Young’s modulus $E_e$ of the grains is 2.7 GPa

The Beaver River sandstone (BRS) is a formation on the west side of the Athabasca River near Mildred Lake and the Beaver River (in Alberta, Canada) and has been identified as quartzite (Kristensen et al. 2015) with fine- to medium-size and well-sorted grains, 78 percent of which was quartz. Its pore space was cemented by 16 percent quartz overgrowth and also contained clay. Its initial porosity (before deformation) was $\phi _0\approx 0.076$. Figure 6 compares the predicted permeabilities, normalized by the initial permeability of the sandstone before deformation (as also presented by Yale (1984)) as a function of the applied pressure, with the experimental data of Yale (1984). The agreement between the two is excellent. Because the sandstone is mostly quartz, its porosity and, thus, PSD do not change much over the range of the applied pressure. This is confirmed by the inset of Fig. 6 that shows that the porosity is reduced by only 5 percent of its initial value, as well as Fig. 7 that presents the PSD of the sandstone at higher pressures, indicating only small changes.

Fig. 7

Evolution of the pore-size distribution of the Beaver sandstone as a result of applying the external hydrostatic pressure P to the sandstone

7.3 Berea Sandstones

Yale (1984) presented experimental data for two Berea sandstone. One was Berea 100H (with H implying that the bedding was horizontal in the experiments) with a sublitharenite environment—one in which the sandstone is characterized by the presence of less than 15 percent mud matrix—with 5–25% of the grains being rock fragments, more than the feldspar content. The sandstone consisted of 53% quartz and had fine to very fine, well-sorted grains with an initial porosity of 0.165. Its cement contained 11% quartz overgrowth, as well as clay. Figure 8a compares the predicted permeabilities with the experimental data; the agreement is excellent.

Fig. 8

Comparison of the predicted permeabilities with the experimental data for two Berea sandstones. a Berea 100H with fitted value of the Young’s modulus $E_e\approx 25$ GPa, and b Berea 500 with $E_e\approx 13$ GPa

Fig. 9

Comparison of the predicted permeabilities with the experimental data for Boise sandstone with the fitted value of the Young’s modulus $E_e \approx 38.5$ GPa

The second Berea sandstone that Yale (1984) experimented on was Berea 500, a quartzenite-type porous medium composed of up to 90 percent detrital quartz, with limited amounts of other framework grains, such as feldspar and lithic fragments. Such sandstone can have higher-than-average amounts of resistant grains, such as chert and minerals. Sixty six percent of Berea 500 was quartz. Its initial porosity was $\phi _0\approx 0.2$, while its cement consisted of 5 percent quartz overgrowth, 8 percent Fe oxide, and 1 percent clay, with the rest being other types of materials. Figure 8b presents a comparison of the pressure-dependence of the permeability with the experimental data, indicating excellent agreement. In both sandstones, the porosity was reduced by only 5-6 percent of its initial value over the entire range of pressure and, therefore, the change in the PSDs was small.

7.4 Boise Sandstone

The Boise sandstone used in the experiments by Yale (1984) was of arkosic arenite, or arkose type, a detrital sedimentary rock that contains at least 25% feldspar, which is why it is sometimes referred to loosely as feldspathic sandstone. The sandstone was fine to medium grained, very well sorted, with initial porosity of about 0.26 and minor carbonate-clay cement. Its grains consisted of 28 percent quartz and 44 percent feldspar. Figure 9 compares the predicted permeabilities w the estimated $E_e\approx 38.5$ GPa is close to what the SCA, Eqs. (21) and (22), predict, $E_e\approx 26$ GPa. is close to what the SCA, Eq.s (21) and (22), predict, $E_e\approx 26$ GPa.

7.5 Cambrian Sandstone

Fig. 10

Comparison of the predicted permeabilities with the experimental data for three Cambrian sandstones with the fitted value of the Young’s modulus being a $E_e\approx 10$; b 12, and c 2, all in GPa

Chierici et al. (1967) presented experimental data for the pressure-dependence of the permeability of three Cambrian sandstones. These are low-porosity sandstones from the Cambrian era that consist of sand-size quartz grains held together by quartz cement. The three were referred to as Cambrian 6, Cambrian 14 and Cambrian 16 by Yale (1984) and had initial porosities of 0.08, 0.11, and 0.13, respectively. Figure 10a–c presents comparison of the predicted pressure-dependence of the effective permeability with the experimental data. In all cases, the agreement between the predictions and the data is good, with the largest difference being about 12 percent at 45 MPa, applied to Cambrian 16. Note that the fact that in the cases of Cambrian 6 and Cambrian 14 the final porosities of the sandstones at the highest pressure applied were about 95 percent of their initial values indicates the rigidity of their structure. In addition, the lower value of the Young’s modulus $E_e$ for the Cambrian 16 is consistent with a larger reduction in its initial porosity.

7.6 Fahler Sandstones

Fig. 11

Comparison of the predicted permeabilities with the experimental data for the four Fahler sandstones with the fitted value of the Young’s modulus being a $E_e\approx 0.12$; b 0.15; c 0.11, and d 0.17, all in GPa

Yale (1984) presented experimental data for pressure-dependence of the effective permeabilities of four Fahler sandstones, which he referred to them as Falher 142, Fahler 154, Fahler 162, and Fahler 189. Of the four, Fahler 142 was of quartzarenite type, whereas the other three were sublitharenite sandstones. Moreover, the initial porosity of Fahler 142 was $\phi _0\approx 0.08$. It was fine grained, very well sorted, with quartz outgrowth, and clay and carbonate cement. It consisted of 35 percent quartz, 8 percent chert, and 3 percent feldspar, with the rest being various other types of rock materials. Its cement contained 23 percent carbonate. Fahler 154 with an initial porosity of 0.044 was very fine to fine grained and very well sorted, 24 percent of which was quartz, 8 percent chert, 4 percent lithics, and 2 percent feldspar, with the rest being other rock materials. Its cement contained chalcedony (a cryptocrystalline form of silica), Fe oxide and carbonate. Likewise, Fahler 162 was a sandstone with an initial porosity of 0.03, fine to medium grained, consisting of 46 percent quartz, 8 percent various lithics, and 6 percent chert, with the rest being other types of rock materials. Its cement consisted of 25 percent quartz overgrowth, 8 percent Fe oxide, and 8 percent clay. Finally, Fahler 189 had an initial porosity of 0.02, medium grained, and contained 27 percent quartz, 27 percent chert, 11 percent various lithics, and 3 percent feldspar. Its cement consisted of 13 percent quartz overgrowth, 9 percent carbonate, 4 percent chalcedony, and 2 percent clay.

Figure 11a–d presents the predictions and compares them with the experimental data. We first note the consistency between the estimated values of $E_e$ for the four sandstones, which indicates the internal consistency of the theoretical model. As Figure 11 indicate, in all cases the agreement between the predictions and the data is excellent for pressures as high as 25 MPa, but they deviate from the data at higher pressures. We will come back to this point in Sect. 8.

Fig. 12

Comparison of the predicted permeabilities with the experimental data for the Indiana DH sandstone with the fitted value of the Young’s modulus being $E_e\approx 30$ GPa

7.7 Indiana Dark Sandstone

The next sandstone whose pressure-dependent permeability we predicted is the Indiana Dark sandstone, referred to as the Indiana DH, with DH indicating that the sample was taken after drilling horizontally. The sandstone was of subarkose type, one in which feldspar sand grains exceed rock fragments, but make up 5 to 15 percent of the rock. Its initial porosity was relatively high, 0.27, with its major components being 57 percent quartz and 7 percent feldspar. Its cement contained clay, as well as 22 percent hematite, Fe$_2$O$_3$. Figure 12 compares the predictions with the experimental data of Yale (1984); the agreement is excellent. Note that since the initial porosity of the sandstone was high and it reduced by only 4 percent even at the highest pressure, then, consistent with our arguments about the Fahler sandstone, the porous medium remained well connected, precisely in the range of porosity in which the EMA is highly accurate.

7.8 Massillon Dark Sandstone

Fig. 13

Comparison of the predicted permeabilities with the experimental data for the Massillon DH sandstone with the fitted value of the Young’s modulus being $E_e\approx 9.5$ GPa

The sandstone, referred to as Massillon DH (from Massillon, Stark County, Ohio) by Yale (1984), was of quatzarenite type with an initial porosity of 0.161, and medium-size and well-sorted grains. Sixty-one percent of it was quartz, with feldspar, chert, and lithics each contributing 1 percent, and the rest being other types of rock material. Its cement contained Fe oxide at 15 percent and clay at 5 percent. Figure 13 compares the predictions with the experimental data of Yale (1984). The largest difference between the two sets is about 6 percent at a pressure of 40 MPa.

7.9 Miocene Sandstone

Fig. 14

Comparison of the predicted permeabilities with the experimental data for the Miocene 7 sandstone with the fitted value of the Young’s modulus being $E_e\approx 5$ GPa

Chierici et al. (1967) reported experimental data for the pressure-dependence of Miocene sandstone, a low-porosity rock that is of the feldspathic arenite type. Its initial porosity was 0.083. The roundness and sorting of the grains of such sandstones are typically high, implying the existence of long flow and transport distances (Saitoh and Masuda 2004). Figure 14 presents the comparison between the predictions for the pressure-dependent permeability and the experimental data. The agreement is excellent. The existence of well-connected and long transport and flow paths practically guarantees that the predictions would be accurate, because it is precisely under such conditions that the EMA is accurate.

7.10 Pliocene Sandstone

Fig. 15

Comparison of the predicted permeabilities with the experimental data for the Pliocene 35 sandstone with the fitted value of the Young’s modulus being $E_e\approx 4$ GPa

Chierici et al. (1967) also reported experimental data for the pressure-dependence of the permeability of a Pliocene sandstone, which Yale (1984) referred to it as Pliocene 35. Similar to Miocene sandstones, Pliocene sandstones also have round grains. The initial porosity of the sample was 0.2. Figure 15 compares the predictions with the data. The agreement between the two is excellent.

7.11 Tensleep Sandstone

Fatt (1957) reported on his measurements of the pressure-dependence of the permeability of Tensleep sandstone. The porous medium represents a geological formation from the entire Pennsylvanian sequence in central and northern Wyoming in the very early Permian age (Branson and Branson 1941). Such rocks are predominantly crossbedded sandstone and have thin limestone and dolomite beds (Kerr et al. 1986). The initial porosity of the sample was 0.146. In Fig. 16, we compare the predictions with the experimental data of Fatt (1957), also reported by Yale (1984). The agreement is excellent over much of the range of the applied pressure. The largest difference, at the highest pressure, is about 10 percent.

Fig. 16

Comparison of the predicted permeabilities with the experimental data for the Tensleep 35 sandstone with the fitted value of the Young’s modulus being $E_e\approx 2.6$ GPa

Fig. 17

Comparison of the predicted permeabilities with the experimental data for the Tertiary 807 sandstone with the fitted value of the Young’s modulus being $E_e\approx 6.4$ GPa

Fig. 18

Comparison of the predicted permeabilities with the experimental data for the Torpedo sandstone with the fitted value of the Young’s modulus being $E_e\approx 3$ GPa

7.12 Gulf Coast Sandstone

The experimental data for this sandstone were reported by Yale (1984), who referred to the rock as Tertiary 807. In general, tertiary rocks are those that were formed during part of the Cenozoic era, covering the Paleogene and Neogene periods. The sample with which the experiments were carried out was of the subarkose type, with fine, well-sorted grains and high intergranular porosity. It contained 52 percent quartz, 9 percent feldspar, 5 percent chert, and 3 percent lithics with an initial porosity of 0.22. Figure 17 compares the theoretical predictions with the experimental data. Once again, over much of the pressure range the agreement between the predictions and the data is excellent. The theory predicts slightly higher permeabilities at the two highest pressures, with the largest deviation from the data being, however, about 5 percent at 40 MPa.

7.13 Torpedo Sandstone

Dobrynin (1962) reported permeability data for the Torpedo sandstone from Kansas. The initial porosity of the sample was 0.202, and it contained about 5 percent clay minerals that consisted mostly of kaolinite and chlorite, distributed evenly throughout the sample. As Figure 18 indicates, except at 45 MPa where the predicted permeability is larger than the measured value by 5 percent, the agreement between the predictions and the experimental data is excellent.

7.14 Triassic Sandstones

Yale (1984) reported measurements of the pressure-dependence of the permeability of five Triassic sandstones. Such rocks were formed in the Triassic period, between 200 and 251 million years ago. The morphology of such sandstones varies greatly, from very fine- to very coarse-grained. They represent porous formations with low- or ultra-low permeability, but they often contain both tectonic and diagenetic fractures that provide flow paths. The five sandstones studied by Yale (1984) were referred to as Triassic 26, 27, 34, 38, and 41 with initial porosities that were, respectively, 0.18, 0.18, 0.2, 0.2, and 0.21. Figure 19a–e compare the predictions of the permeabilities with the experimental data. Except for Triassic 27 sandstone, the agreement between the predictions and the data is uniformly excellent. Even in the case of Triassic 27, the maximum difference between the predictions and the data at high pressures is only about 5 percent.

Fig. 19

Comparison of the predicted permeabilities with the experimental data for the Triassic sandstone with the fitted value of the Young’s modulus $E_e$ being a 8; b 6.5; c 83; d 40, and e 2.8, all in GPa

8 Discussion

Let us first point out that in a previous paper (Richesson and Sahimi 2019), we used the radius of contact $R_c$, given by Eq. (16) (originally presented by Yale (1984), without derivation) in order to develop an expression for the PSD of a deforming porous medium. Within the MFA that we have developed, $\ell _p(P)$, the pore length at pressure P, is given by (Yale 1984)

$$\begin{aligned} \ell _p(P)=\ell _0-R_c(P)=\ell _0\left[ 1-\frac{R_c(P)}{\ell _0}\right] \;, \end{aligned}$$

(23)

where $\ell _0$ is the length of the pore before deformation. If $r_0/\ell _0$ is the aspect ratio of a pore before it is deformed, then, within the MFA the pore size at pressure P is given by

$$\begin{aligned} r_P(P)=\ell _p(P)\left( \frac{r_0}{\ell _0}\right). \end{aligned}$$

(24)

Thus, if a hydrostatic pressure P is applied to a porous medium, the change in any pore size can be computed by Eq. (24), implying that the initial PSD can be updated. However, although as we demonstrated previously (Richesson and Sahimi 2019), we obtained excellent agreement between the predicted permeabilities and the experimental data for five sandstones, when we used Eq. (24) for updating the PSDs of the sandstones considered in this paper, good agreement between the theoretical predictions and the data could often be obtained only when the Young’s modulus $E_e$ of the grains or the solid matrix was unphysically very high, ranging from hundreds of GPa to even thousands. Thus, we believe that only when the change in the PSD is determined through the quantity u, given by Eq. (17), can one expect physically acceptable fitted values of $E_e$ and good agreement between the predictions and the experimental data.

Several other aspects of our proposed model deserve discussions, which we now present.

8.1 The Fitted Values of the Young’s Modulus

As discussed in detail earlier, if for each sandstone that we examined the composition of the grains are available, then, there are a variety of theoretical methods by which their effective Young’s modulus can be estimated. In the absence of such information, we used a single point to estimate the modulus, which is similar to calibrating an experimental system. Table 1 presented the fitted values of the Young’s moduli for the sandstones considered in this paper.

As Table 1 indicates, in many cases the fitted values of the Young’s modulus are smaller than what one would expect, particularly for sandstones in which quartz is a major component. The reason is, however, clear: we fit the permeability at one point for a sandstone as a whole in order to estimate the modulus for its grains or the solid matrix. Clearly, the datum represents and is influenced by, a variety of morphological factors and, therefore, the estimate of the modulus should be smaller than the actual value because, for example, the datum is influenced by the porosity, whereas the grain themselves are solid particles. We shall comeback to this point in Sect. 8.6

Table 1 Fitted values of the Young’s modulus $E_e$ of the sandstones’ grains

8.2 Limits of Validity of the EMA

An important question is the range of the validity of the EMA, as well as the MFA that we developed for the deformation. Comprehensive discussions of the strengths and shortcomings of the EMA are provided by Sahimi (2003) and Hunt and Sahimi (2017). Koplik (1981), Adler and Berkowitz (2000), and others (see Sahimi 2003) studied the limit of the accuracy of the EMA. Generally speaking, the EMA is (i) accurate if a porous medium is not near its percolation threshold, i.e., the critical porosity at which the permeability and electrical conductivity vanish; (ii) more accurate for two-dimensional (2D) media than for 3D if they are close to the percolation threshold, and (iii) not very accurate for 3D porous media in what is called the critical region. In random media, the critical region is defined roughly by (Sahimi 1994), $\phi -\phi _c\le 1/Z$, where Z is the mean pore connectivity, and $\phi _c$ is the critical porosity. (iv) If there are extended correlations between the pores’ sizes, then the EMA is less accurate than in completely random porous media, although Mukhopadhyay and Sahimi (2000) suggested ways of taking into account the effect of such correlations. The extensive comparison between the theoretical predictions and the experimental data presented earlier is consistent with this picture, namely, if the porosity of a porous medium is not extremely low, to the extent that it is barely connected, the MFA developed in this paper together with the EMA provide accurate predictions for the effective permeability of porous media.

8.3 Effect of Structural Changes in the Pore Space

In some cases, such as the Cambrian and Fahler sandstones, the effective permeability at high pressures decreases a bit more slowly than the predictions. One possible reason for this is that the morphology of the porous media undergoes fundamental changes at high pressures, such as opening up new cracks that provide new flow paths for the fluid and, hence, arrest to some extent the decline in the permeability at high pressures. If such changes do occur, the approach that we propose in the present paper would not be applicable.

8.4 Effect of Microcracks

If the porous medium contains, in addition to pores, microcracks, then, two approaches may be taken to take their effect into account. One is by simply assuming that the cracks are large pores and use a bimodal PSD to represent both pores and microcracks. This is, of course, a crude approximation whose accuracy remains to be tested.

The second method is based on treating the microcracks as completely distinct from the pores such that they may, for example, have their own “network.” In that case an EMA, developed by Hughes and Sahimi (1993a, b) for flow and transport in porous media with two distinct types of flow and transport paths—pores and microcracks—may be used. One would need, of course, not only the PSD, but also the distribution of the cracks’ flow properties. In addition, hydrostatic deformation of a porous medium with cracks typically involves an initial nonlinear elastic crack closure, followed by pore deformation. This implies that one should also develop an expression for the way the microcracks close, since it is different from that for pores that we presented here.

8.5 Effect of Clay on Pore-Pressure Dependence of the Permeability

It has been suggested that the permeability of sandstones that are rich in their clay content may be sensitive to pore pressure (Al-Wandy and Zimmerman 2004; Meng et al. 2020). For example, Al-Wandy and Zimmerman (2004) reported that the permeability is more sensitive to changes in the pore pressure than to variations in the confining pressure, and that it increases with increasing pore pressure, but decreases with increasing confining pressure (which is the case in the data that we present and discuss). The model that we have proposed in this paper cannot, in its present form, take this effect into account. If, however, the dependence on the pre pressure of the permeability of a pore and, therefore, the pore’s flow velocity, can be expressed by a functional form, then, the EMA can be extended to include such effects (see, for example, Sahimi 2003). This will be described in a future paper.

8.6 Effect of Contact Law for the Grains

The theory that was developed in Section 2 in order to determine the change in the size of a pore as a result of deformation of a porous medium was based on the Hertz–Mindlin theory of contacting grains in unconsolidated porous media. The experimental data that were compared with the theoretical predictions were, however, for mostly consolidated sandstones that have been cemented. It is known (Dvorking and Yin 1995) that cementation influences strongly the contact laws. This could provide an explanation as to why the fitted Young’s moduli of the various sandstones (see above) did not often agree with what one might expect for such porous media, which contain a significant amount of quartz.

Thus, one way to address the shortcoming is to use the Hertz–Mindlin theory for cemented sandstones, rederive the expression for the change in the effective size of the pores, and recompute everything. An alternative, and perhaps simpler, approach would be to determine the change in the radius of a hollow cylinder (a pore throat), embedded in a solid material of a given Young’s modulus, as a result of exposing the system to a hydrostatic pressure. This would indeed represent a MFA. The result can then be used to determine the modified PSD and, hence, the effective permeability. We will report on both approaches in a future paper.

8.7 The Effect of a Grain-Size Distribution

As described earlier, the present theory of grain deformation, Eqs. (16) and (17), requires an average grain size $R_g$. This is due to the fact that, as emphasized earlier, the present theory of deformation is a MFA and, as such, it considers the deformation of only two neighboring grains and the change in the effective radius of the pore between them. Thus, if a grain-size distribution (GSD) is available (see, for example, Cheung et al. 2012), one can compute $R_g$. Beyond that, and in order to take into account the effect of a GSD of a collection of grains, the MFA must be refined, and the effect of the interactions between a collection of grains must be taken into account. While numerical simulations in this direction have been made in the past (see, for example, Bakhshian and Sahimi 2016; Das and Singh 2017), to our knowledge none has produced a tractable theory for the evolution of the PSD. This is an issue that we are currently studying.

8.8 Effect of the Deformation Mode

Deformation of porous geological formations, such as depleted oil reservoirs, is often caused by uniaxial stress. What we have studied is the case in which the confining pressure is applied hydrostatically. It is clear that the deformations that result from the two types of the boundary conditions are different, because the spatial distributions of pressure in the two systems are different. But, when, for example, the overburden pressure exerts itself uniaxially in an oil reservoir, the surrounding rock limits the resulting lateral deformation. This implies that one obtains mostly vertical compaction, which represents smaller changes in the pore sizes than what is caused by hydrostatic pressure. Section 7 demonstrated that our theory provides accurate predictions for the macroscopic permeability as a function of the hydrostatic pressure, and such a pressure deforms the pore space much more extensively than a uniaxial stress would. We therefore believe that a slightly modified theory would be at least equally accurate for the case in which a uniaxial stress is exerted on a porous medium.

8.9 Universal Curves for Rescaled Permeability versus Rescaled Pressure

We have observed that, for at least some of the sandstones that we describe earlier, if we consider the $K_e(P)/K_0$ curves and rescale the pressure to a suitably selected rescaled form, we obtain a single, more or less universal curve, often referred to as the master curve. Physically, the master curve represents essentially the dimensionless response of a porous medium to the changes in the pressure, since the initial PSD and the Poisson’s ratio are all set to constant values. One clue to the proper rescaling of P is provided by Eq. (17), since it implies that, with $R\approx R_g$, the quantity $u/R_g$ is a function only of $P/E_e$.

The existence of such a master curve implies that it can predict the measurements by rescaling the pressure axis to generate a dimensionless form based on the input data—the initial porosity and an experimental data point that provides an estimate for the effective Young’s modulus $E_e$. Other mechanical models than the HM theory of point-contact that we utilized in this paper may provide a different master curve (based on different rescaled variables). But, the general implication is clear: with proper rescaling of the main variables, one may obtain a universal curve that provides accurate predictions for a variety of deforming porous media. In fact, such a master curve was proposed much earlier (Rassamdana et al. 1996) for another property of oil reservoirs that represent large-scale porous media.

9 Summary

Predicting physical properties of deforming porous media, and in particular their permeability and transport characteristics, such as their electrical conductivity when they are saturated with brine, is important to many physical processes. They include shale formations undergoing fracking, and oil, gas, and coal-bed reservoirs, as well as composite materials that are used in everyday life. We presented a new theoretical model for predicting the permeability $K_e$ of such porous media and materials. The theory, a mean-field approximation, determines the change in the size of a pore between two grains that deform when a hydrostatic pressure is applied to them. Then, given the initial PSD of a porous medium before deformation and the Young’s modulus of the grains as the input, the theory determines the PSD of a porous medium that is deformed by applying an external pressure P, which is then used with the effective-medium approximation to predict the effective permeability of the porous medium at the same pressure. Extensive comparison between the theoretical predictions and experimental data for the pressure-dependence of the effective permeabilities of twenty four sandstones indicated agreement between the two in almost all cases, ranging from very good to excellent.

With some modifications, the same approach can be used for predicting the electrical conductivity of brine-saturated porous media that undergo deformation, as well as their relative permeabilities to two-phase flows. Work in this direction is in progress. The results will be reported in Part II of this series (Richesson and Sahimi 2021).