1 Introduction

The migration of gas bubbles in porous media has important implications for remediation of contaminated soil and recovery of resources in various applications such as in situ air sparging (ISAS) (Pankow et al. 1993), supersaturated water injection (SWI) for groundwater remediation and recovery of volatile, light non-aqueous phase liquids (LNAPLs) (Li 2004; Nelson et al. 2009), mobilization of residual oil blobs in water-wet reservoirs (Chatzis 2011), evolution of gas bubbles from oil in saturated reservoirs when the pressure declines below the bubble point pressure (McCain 1990), ebullition of biogenic gas bubbles and the transport of methane-containing gases from contaminated sediments (Baird et al. 2004; Ostrovsky et al. 2008), and geological CO2 sequestration (Oldenburg and Lewicki 2006; Jafari et al. 2017; Dejam and Hassanzadeh 2018a, b). Fluidized beds and packed bed flow reactors are also well-known chemical processes in which gas bubbles flow through porous media (Iliuta et al. 1999; Wu et al. 2017). The buoyancy-driven migration of gas bubbles from sediments makes an important contribution to the transport of gas within aquifers and from aquifers up to the atmosphere. Ebullition of gas bubbles from sediments affects biogeochemical processes and increases the emission of greenhouse gases into the atmosphere (Amos and Mayer 2006). Microbial decomposition of the organic substances in sediments produces gases, which move through saturated sediments into overlying water and ultimately escape to the atmosphere. Whalen (2005) reported that methane (CH4) as an important greenhouse gas comprises 37% of total emissions from natural wetlands. Ebullition is a major mechanism for CH4 transport to the atmosphere, as gas bubbles bypass the unsaturated, oxidized zone of CH4 consumption. Figure 1 shows a conceptual model of gas bubble migration in CO2-supersaturated water injection (SWI) technology.

Fig. 1
figure 1

A conceptual schematic of CO2-supersaturated water injection (SWI) technology for NAPL recovery

Full size image

Understanding the flow patterns of gas phase in liquid-saturated porous media has been the subject matter of many studies. In the in situ air sparging literature, three types of flow patterns for a gas phase injected into a saturated porous medium have been reported: bubble flow, percolation networks and air channels. It has been found that the critical parameter affecting the flow pattern is the grain size of the porous medium, with bubble flow occurring in porous media with pore size greater than 4 mm, air channels forming when the pore size is smaller than 0.5 mm and dendritic invasion happening in media with the intermediate grain size (Selker et al. 2007). Sandnes et al. (2011) conducted an extensive study on the fluid dynamics and pattern-forming processes in simple fluids and suspensions and found that gravity-induced frictional forces have a profound impact on the fluid dynamics. They characterized new dynamic modes ranging from stick–slip bubbles at low rate to destabilized viscous fingers at high rate and classified the fluid dynamics into frictional and viscous regimes.

Roosevelt and Corapcioglu (1998) were the first to do a quantitative study to measure the terminal velocity of air bubbles rising in a stationary granular porous medium by video recordings. They injected single air bubbles of varying sizes into the bottom of two columns packed with 4-mm glass beads in random packing order. Velocities measured for bubbles with equivalent radius varying from 0.2 to 0.5 cm were found to be within the range of 16.7–20.2 cm s−1. Their results showed a linear time dependency for the rise velocity of bubbles in the porous medium. They also found that the data measured for the velocity of air bubbles in the porous medium were 17.4–27.4% smaller than those obtained for single bubbles rising in a column filled with only water. Ma et al. (2015) systematically investigated the flow of discrete microbubbles and the induced water circulation in a 2D water-saturated porous medium. Combining the experimental results with scaling analysis, they quantified the behaviors between the gas bubble release rates at the bottom of a flume filled with transparent water-based gelbeads and various characteristics of the formed bubble plume. Luo et al. (2011) studied the flow of supercritical CO2 and water injected into the sintered glass porous media structure by different CO2–water ratios, using MRI as the visualization method. Their results demonstrated that the CO2 saturation increases with elevation in CO2–water ratio, and the CO2 distribution is significantly influenced by the buoyancy force. Kim et al. (2018) conducted visualization experiments using a rectangular transparent acrylic cell containing glass beads saturated with alkaline solution, to investigate the migration behaviors of gas and dissolved CO2 in water-saturated porous media. While many studies have focused on two-phase flow (gas–liquid) patterns in constrained porous media (in which the grains are fixed in the bed), Varas et al. (2015) reported an experimental investigation of the dynamics of air rising through a water-saturated, unconstrained granular bed (three-phase systems). Their results showed the dependency of the fluidized zone shape, for larger grains, on the injection flow rate and grain size.

To better understand the dynamics of gas bubble migration and two-phase flow in porous media, experimental studies have been conducted using micromodels (Tohidi et al. 2001; Lago et al. 2002; Gutiérrez et al. 2008; Buchgraber et al. 2012) and Hele–Shaw cells (Johann and Siekmann 1978; Maruvada and Park 1996; Selva et al. 2011). The micromodels are two-dimensional network patterns composed of relatively large pore bodies connected by smaller pore throats etched on glass or silicone plates (Chatzis 1982; Mckellar and Warldlaw 1982). A Hele–Shaw cell refers to a narrow microfluidic slot sandwiched between two parallel glass walls (Bear 1972). These glass models are useful tools for studying the multi-phase fluid flow in porous media, with controlled parameters and high precision; however, the effects of the pore network are neglected in Hele–Shaw models (Roosevelt and Corapcioglu 1998). Mashayekhizadeh et al. (2011) made observations of free gravity drainage of air–crude oil system in fractured porous media in pore level using glass micromodels and calculated the oil recovery factors. Mashayekhizadeh et al. (2012) also investigated the effects of fracture tilt angle on frequency and stability of liquid bridges in fractured porous media through micromodel visualization experiments. Buchgraber et al. (2012) conducted CO2–water imbibition experiments in silicon micromodels to investigate the mechanisms of immobilization and trapping of carbon dioxide in sandstones.

Corapcioglu et al. (2004) developed a theoretical model to estimate the rise velocity of an air bubble in coarse porous media based on the experimental results of Roosevelt and Corapcioglu (1998). Oldenburg and Lewicki (2006) applied the model of Corapcioglu et al. (2004) for incompressible bubbles to predict the rise velocity of CO2 bubbles in porous media. Their results showed that the rise of CO2 bubbles in saturated porous media is more likely to occur as channel flow rather than bubble flow. In their work, a maximum velocity of 30 cm s−1 was calculated for buoyancy-driven rise of CO2 bubbles in surface water. Cihan and Corapcioglu (2008) developed another model by combining Newton’s second law of motion and the ideal gas law to analyze the effect of air compressibility on the bubble rise velocity in porous media. Their results showed a strong dependency of the rise velocity of a compressible air bubble on the depth at which the air phase was injected. Stark and Manga (2000) conducted a numerical study to simulate the flow of discrete bubbles through porous media using a network model. Mahabadi et al. (2018) investigated the effect of gas bubble size on the residual gas saturation and hydraulic conductivity reduction through numerical simulation using a pore network model. They found changes in bubble size distribution during migration due to coalescence of gas bubbles, with larger bubbles found in the upper parts of the pore network model due to the upward migration. It was also reported that the fraction of trapped bubbles and the residual gas increased with an increase in the bubble size.

Despite previous research on gas transport in porous media, not enough attention has been paid to the influence of the wetting liquid and porous medium size characteristics on the bubble rise velocity. The reported works that have studied fluid flow in an inclined porous medium in lateral pathways have been focused on the oil bubbles as the migrating fluid (Mashayekhizadeh et al. 2012; Yan et al. 2012). To the best knowledge of authors, no study of the velocity of gas bubbles traveling in a porous medium with different inclination angles and saturated with different wetting liquids has been reported in the literature. Here we present a study on the buoyancy-driven migration of single air bubbles and displacement events as a function of the bubble length, pathway inclination angle and wetting liquid properties through a saturated porous medium with uniform geometry using a glass micromodel. The experiments were designed based on the available video technology to visualize and quantify the motion of air bubbles through the micromodel. In analyzing the experimental data, we aimed to understand and quantify the critical inclination angle and effective length for a bubble migrating in a porous medium. Analyses were conducted, and a theoretical model was developed to obtain the migration velocity of a gas bubble in a saturated porous medium for one-dimensional flow. Further, we modified a MATLAB® code that had already been developed in our laboratory, to simulate the motion of discrete air bubbles in pore networks consisting of pore bodies interconnected by tubes of given diameters. The comparisons were made between the experimental and simulation results.

2 Theory Development

For a porous medium with uniform pore geometry saturated with a fluid of density ρ and viscosity µ, the velocity of the single phase within the medium is governed by Darcy’s law for one-dimensional single-phase flow, as

$$u_{ } = \frac{K}{\mu } \frac{\Delta P}{L}$$
(1)

where K is the intrinsic permeability of the medium and ∆P/L is the pressure drop over sample length L.

Now, we consider a gas bubble of length Lb, density ρg and viscosity µg trapped in a porous medium already saturated with a liquid (as shown in Fig. 2). The velocity of the gas bubble can be described by the extension of Darcy’s law for two-phase flow in porous media (Hubert 1956) as (Niessner et al. 2011)

$$u_{\text{b }} = \frac{{K_{\text{g}} }}{{\mu_{\text{g}} }} \cdot \left( {\nabla p_{\text{g}} - \rho_{\text{g}} g} \right)$$
(2)

where Kg is the saturation-dependent two-phase permeability of the medium for the gas phase (also known as effective permeability). Using the concept of relative permeability, Kg is described as

$$K_{\text{g }} = k_{\text{rg}} K$$
(3)

where krg = krg (Sg) is the saturation-dependent relative permeability of the gas phase. Similarly, for liquid phase, Kl = krlK and krl = krl (Sl). Sg and Sl are saturations of gas and liquid phases, respectively, and are constrained by

$$S_{{{\text{g}} }} + S_{\text{l}} = 1$$
(4)
Fig. 2
figure 2

Schematic of an air bubble surrounded by oil in a pore network

Full size image

For locally constant density (incompressible) gas invasion, the total pressure difference across the gas bubble trapped in a pore network with inclination angle αinc saturated with a liquid (Fig. 2), also called “bubble pressure,” is given by

$$\Delta P_{{{\text{b}} }} = \left( {\rho_{\text{l}} - \rho_{\text{g}} } \right) g L_{\text{b}} \sin \alpha_{\text{inc}} - \left( {P_{{{\text{c}}1}} - P_{{{\text{c}}2}} } \right)$$
(5)

where g is the gravitational acceleration and Pc1 and Pc2 are capillary pressures at the meniscuses of the bubble front and bubble tailing end, respectively. For immiscible displacement in porous media, ΔPb refers to the capillary pressure required for the gas bubble to penetrate through a capillary tube with an equivalent diameter (Smith et al. 2005).

For bubble migration in a porous medium, the liquid displaced by the motion of the bubble does not travel a particular distance as in the capillary tube, but rather travels along a generally unknown route over a length termed the “effective length,” Leff. The effective length is a measure of the path length over which the liquid displaced by the bubble front must travel to reach the bubble tail. Leff varies with the structure of the porous medium and the bubble length. From the aforementioned definition and substituting Eq. (5) into Eq. (2), the bubble velocity can be expressed as

$$u_{\text{b }} = \frac{{K_{\text{g}} }}{{\mu_{\text{g}} }} \left[ {\frac{{\left( {\rho_{\text{l}} - \rho_{\text{g}} } \right) g L_{\text{b}} \sin \alpha_{\text{inc}} - \left( {P_{{{\text{c}}1}} - P_{{{\text{c}}2}} } \right)}}{{L_{\text{eff}} }} - \rho_{\text{g}} g} \right]$$
(6)

In a study by Ma et al. (2015), it was shown that for gas volume fractions below 3% and as ρg ≪ ρl, the effective viscosity of liquid–bubble mixture changed little from the liquid viscosity (i.e., µmix ≈ µl). Therefore, the bubble velocity expressed in Eq. (6) can be approximated as

$$u_{\text{b }} { = } \frac{{K_{\text{g}} }}{{\mu_{\text{l}} L_{\text{eff}} }}\left[ {\rho_{\text{l}} g L_{\text{b}} \sin \alpha_{\text{inc}} - \left( {P_{{{\text{c}}1}} - P_{{{\text{c}}2}} } \right)} \right]$$
(7)

Rearranging Eq. (7) yields

$$u_{\text{b }} = \frac{{ K_{\text{g}} \rho_{\text{l}} g \sin \alpha_{\text{inc}} }}{{\mu_{\text{l}} }}\left( {\frac{{L_{\text{b}} }}{{L_{\text{eff}} }}} \right) - \frac{{K \left( {P_{{{\text{c}}1}} - P_{{{\text{c}}2}} } \right)}}{{\mu_{\text{l}} L_{\text{eff}} }}$$
(8)

In the calculation of the capillary pressures at the front and at the rear of a moving bubble in a porous medium (Pc1 and Pc2, respectively), it should be noted that, unlike bubble rise in a capillary tube, the pore diameters in which the advancing and receding menisci are formed, DA and DR in Fig. 2, are not necessarily the same. Accordingly, Eq. (8) can be rewritten as

$$u_{\text{b }} = \frac{{ K_{\text{g}} \rho_{\text{l}} g \sin \alpha_{\text{inc}} }}{{\mu_{\text{l}} }}\left( {\frac{{L_{\text{b}} }}{{L_{\text{eff}} }}} \right) - \frac{K}{{\mu_{\text{l}} L_{\text{eff}} }} \left[ {4\sigma \left( {\frac{{\cos \theta_{\text{R}} }}{{D_{\text{R}} }} - \frac{{\cos \theta_{\text{A}} }}{{D_{\text{A}} }}} \right)} \right]$$
(9)

where σ is the interfacial tension between the liquid and gas and θR and θA are receding and advancing contact angles at the bubble front and bubble tail, respectively (as shown in Fig. 2). Two different interface configurations in a network of pore bodies and pore throats for a gas bubble rising upwards are shown in Fig. 3. Figure 3a shows the configuration of minimum driving force, in that the receding meniscus is located in a pore throat and thus produces maximum capillary pressure resisting the upward motion of the bubble, while the advancing interface is located in a pore body and produces minimum force acting in the direction of the bubble motion. On the other hand, Fig. 3b represents a condition in that maximum driving force for the bubble motion is produced. In configuration (a), the net surface tension force opposes buoyancy forces, whereas in configuration (b), it acts in the same direction as buoyancy forces and facilitates upward motion of the bubble.

Fig. 3
figure 3

Configurations for the interface position leading to a minimum and b maximum capillary driving force during bubble motion (edited after Smith 2005)

Full size image

3 Experimental

3.1 Method and Materials

Experiments were conducted in a water-wet micromodel with a pore network pattern etched into the glass to represent an actual porous medium in two dimensions (3.2 cm × 27.8 cm). The micromodel had a series of channels with relatively equal sizes interconnected by smaller-sized pore throats on either side of the central channel. Figure 4 shows the microstructure pattern of the micromodel. The liquids were injected into the pore network through the access holes drilled at both ends of the micromodel. The micromodel was 9 pores wide (3.2 cm) by 100 pores long (27.8 cm), and the pattern had been designed such that the liquid displaced from the main channel could travel along multi-side channels during bubble migration. Micromodel characterization is discussed in Section 3.2.

Fig. 4
figure 4

Pattern etched in the micromodel

Full size image

Fluids used as the wetting phase to saturate the micromodel were kerosene, Soltrol 170 and white oil dyed red. These liquids are relatively nonvolatile so that they do not influence bubble size due to vaporization. The densities of the liquids were measured by using volumetric flasks and a digital scale over a period of days in order to gain data at different temperatures. Viscosity of test liquids was measured by using Cannon–Fenske Routine glass viscometers in a constant temperature bath at different set temperatures. Surface tension of the liquids was measured by a Video Contact Angle System (VCA 2500XE) in an open atmosphere. The physical properties of the test fluids at 25 °C are given in Table 1. The values of equilibrium contact angle are taken from the work of Dong and Chatzis (2004).

Table 1 Physical properties of test liquids at 25 °C
Full size table

To perform an experiment, the micromodel was cleaned, dried and saturated with the test liquid by using a glass syringe through either of the two access ports. An air bubble was created by slightly tilting up the model from one end imposing the drainage of the liquid from the other end. This allows air to enter the model through the access hole at the elevated side. Since the micromodel structure was such that the central passageway was a bit larger than the pore throats connecting the central passage to the side passages, the air invaded preferentially into the central row of pore bodies and pore throats. Once a bubble with an arbitrary length was formed, the micromodel was set in a horizontal position and both access ports were closed with small pieces of septum to ensure an airtight seal and prevent further drainage of the liquid. The micromodel was fixed horizontally on the top flat surface of the setup and oriented such that the bubble was positioned near one end immediately behind a specific line marked at a small distance (1.2 cm) behind the start line. This allowed bubbles to begin traveling before timing was started in order to get close to their steady-state velocity (Garrettson 1973; Corapcioglu et al. 2004). The length of the bubble (i.e., the shortest distance between the bubble front and bubble tail end positions) was measured via video recording and further image analysis. The opposite end of the micromodel was then elevated gently by an unknown angle with respect to its horizontal position causing the bubble to start moving under the action of buoyancy. The critical inclination angle of the model, αcr, at which the air bubble started to move, was recorded for each experiment. The ambient temperature was measured to correct for any possible changes in temperature during experiments. The angle of inclination, αinc, was calculated by measuring both horizontal and vertical sides of the right triangle. For each inclination angle above the critical angle (αcr < αinc < 90°), the time of the bubble displacement over a set distance (10 cm) was recorded using a stopwatch once it passed the start line. Both bubble length and the inclination angle of the micromodel were altered during experiments for each test fluid; and the velocity measurements were made by varying the inclination angle for a given bubble length. This procedure has the advantage of collecting several data points without changing the bubble length. Two runs of each experiment were performed to ensure accurate measurements and repeatability. The data collected for both runs were close enough so that their average value was reported as the measured bubble velocity. Experiments were repeated for different bubble lengths, inclination angles and wetting liquids.

The limitations of the experiments in this study were: (a) the inclination angles were varied within the range of 3°–38°, so that the bubbles migration could be accurately recorded using our video camera, (b) the bubbles travel distance was 10 cm, and (c) bubbles did not reach their steady-state velocity. In this study, it is assumed that pore structure and geometry are uniform throughout the micromodel. This assumption could be a reason for possible differences between the results of this work and the results reported in the literature for bubbles rising through in situ sediments. For example, (a) the in situ sediments can have irregular shapes of pore bodies and throats; thus, the capillary pressure that the bubble overcomes will not be a constant value, and (b) as a bubble rises, it experiences a pressure change, mainly reduction. The pressure reduction may cause an increase in interfacial tension, resulting in some changes in rising velocity (Zheng et al. 2018).

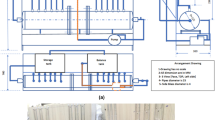
To visualize the flow of bubbles migrating in a porous medium, the bubble motion through the micromodel was video recorded by a digital camera with 12× optical zoom. A schematic of the setup configuration is shown in Fig. 5. White oil (dyed red) was the only test liquid for which the experiments were video recorded, as its viscosity is about 12 times higher than kerosene and Soltrol 170, and thus, the inclination angles were varied in a wider range and the bubble velocities in the saturated medium were within the range that could be accurately measured with our recording equipment. When an inclination angle was set for the micromodel and the bubble started to move, video recording was initiated immediately, and timing was started once the bubble front passed the marked start line. Video recording continued even after the leading edge of the bubble crossed the end line (i.e., timing was stopped) until the tailing end of the bubble passed the end line.

Fig. 5
figure 5

Schematic of the experimental setup

Full size image

The videos were then reviewed on the computer, and the analysis was performed using the PowerDVD 11 software. To obtain images of an air bubble migrating through the micromodel, the frames were captured from the video at the same time intervals of 1, 2 or 3 s and magnified up to 5 times. The time of the bubble traverse over the set distance, exact locations of the bubble front and bubble tail ends at different times during motion, the dynamic bubble lengths (i.e., length of bubbles during motion) and the instantaneous bubble velocities were determined by the image analysis.

3.2 Micromodel Characterization

The micromodel used in this study was characterized for its pore structure information to predict the permeability of the model and analyze the experimental results. A photograph of pore geometry of this micromodel taken by a microscope is shown in Fig. 6. Pore structure characteristics were measured over several pores in the medium to yield the average data given in Table 2.

Fig. 6
figure 6

Photograph of pore geometry of the micromodel

Full size image
Table 2 Pore characteristics of the micromodel in mm
Full size table

Drainage and imbibition capillary height tests were performed to calculate the depth of etching for pores and throats. For drainage capillary height tests, a tube filled with the wetting liquid was connected to the liquid-saturated micromodel at one end and placed inside a sufficiently large beaker full of the liquid at the other end. The micromodel was then held in a vertical position and lifted up to cause the liquid to drain under gravity. The elevation of the micromodel over the liquid level in the beaker was gradually increased, and the heights of new capillary interfaces established in the micromodel were recorded after allowing the system some time to equilibrate. The drainage capillary pressure, Pc,dr, at each elevation was calculated from the difference between the lowest height recorded for the interface in the micromodel and the level of the liquid in the beaker by

$$P_{\text{c,dr}} = h_{\text{c,dr}} \,\rho g$$
(10)

where ρ is the liquid density. The same procedure was repeated for imbibition capillary height measurements, except that the top end of the vertically positioned micromodel was lowered forcing the liquid to push the air upwards in the model. The heights of the newly established capillary interfaces were measured, and the imbibition capillary pressure of the model, Pc,imb, was calculated from the difference in heights between the highest interface level recorded during the test and the level of the liquid in the beaker. Similar to Eq. (10), we have

$$P_{\text{c,imb}} = h_{\text{c,imb}} \,\rho g$$
(11)

Knowing drainage and imbibition capillary pressures, the depth of pores, DP, and the depth of throats, DT, of the micromodel were obtained from the relations suggested by Lenormand et al. (1983) and Ioannidis et al. (1991) as for θA = 0°:

$$P_{\text{c,dr}} = 2\sigma \left( {\frac{1}{{D_{\text{T}} }} + \frac{1}{{W_{\text{T}} }}} \right)$$
(12)
$$P_{\text{c,imb}} = 2\sigma \left( {\frac{1}{{D_{\text{P}} }} + \frac{1}{{W_{\text{P}} }}} \right)$$
(13)

where σ is the surface tension of the liquid used for the capillary height tests. WP and WT are the width of pores and throats, respectively.

4 Numerical Model

Smith (2005) carried out a numerical simulation for a rising bubble in a porous medium. He used a model consisting of a two-dimensional network of pores connected to their neighbors by four circular tubes (coordination number = 4) of uniform length. The bubble was placed at the central pores of the network. A schematic of the network used in the simulation is illustrated in Fig. 7a. Following the work of Smith (2005), a MATLAB® code was developed in this study to investigate the effects of different pore and tube sizes, bubble length and liquid properties on bubble velocity. Assumptions on which the modeling was based are

Fig. 7
figure 7

Schematic of a tube network used in bubble velocity simulation, b nodal arrangement

Full size image
  1. (1)

    the bubble migrates at steady-state condition in the direction opposite to gravity,

  2. (2)

    the bubble is incompressible, and thus, the energy associated with the expansion and contraction of the bubble while invading pore bodies and pore throats is neglected,

  3. (3)

    the energy loss due to the fluid flow through the elbows in the tube network is negligible,

  4. (4)

    no energy loss occurs due to friction between the rising bubble and the liquid.

To calculate the flow inside the tube network, the buoyancy pressure is calculated by

$$P_{\text{buoyancy }} = \left( {\rho_{\text{l}} - \rho_{\text{g}} } \right) g \sin \alpha_{\text{inc}} L_{\text{t}} N_{\text{b}}$$
(14)

where Lt is the tube length and Nb is the number of nodes occupied by the bubble. The net capillary pressure is calculated by

$$\Delta P_{\text{c }} = \frac{4\sigma }{{D_{\text{t}} }}\left( {\cos \theta_{\text{R}} - \cos \theta_{\text{A}} } \right)$$
(15)

where σ is the gas–liquid surface tension, Dt is the tube diameter and θR and θA are the receding and advancing contact angles, respectively. The migration process will continue only if Pbuoyancy > ∆Pc which is the necessary condition for bubble movement. An initial value is then assumed for the bubble velocity and is reduced by a constant coefficient (0.8 is considered in this work) in each step. Based on the value of bubble velocity ub at each step, the values of pressure at all nodes are evaluated, and accordingly, the total dissipation of power due to all liquid flows inside the entire network of tubes is calculated. The bubble reaches its steady-state velocity when the total power dissipation is equal to the power introduced into the system by the bubble motion, Powerin, defined as

$${\text{Power}}_{{{\text{in}} }} = u_{b} \cdot \frac{{\pi D_{\text{T}}^{2} }}{4}\left( {P_{\text{buoyancy}} - P_{\text{c}} } \right)$$
(16)

and the total dissipated power by viscosity, Powerloss, is calculated from

$${\text{Power}}_{\text{loss }} = \sum Q_{i} \Delta P_{{{\text{total}}, i}}$$
(17)

where summation, Σ, is performed over all connecting tubes, ∆Ptotal,i is the pressure drop for a laminar flow inside the ith tube connecting two neighbor nodes (e.g., M and N) and Q is the volumetric flow rate of the liquid calculated by

$$Q = \frac{{\pi D_{\text{t}}^{4} }}{{128 \mu_{\text{l}} L_{\text{t}} }}\left( {P_{\text{M}} - P_{\text{N}} + \rho_{\text{l}} g \sin \alpha_{\text{inc}} \Delta z - P_{\text{Loss,f}} } \right)$$
(18a)
$$P_{\text{Loss,f}} = f\frac{L}{D}\frac{{\rho V^{2} }}{2}$$
(18b)

where ∆z is the difference in heights between nodes M and N and \(P_{\text{Loss,f}}\) is the pressure drop due to friction and is calculated by Eq. (18b). Since flows in the connecting tubes are by far in laminar regime (Re ≪ 2300), where Re is the Reynolds number, the friction coefficient \(f\) is calculated from 64/Re. Substituting this into Eq. (18b) and then Eq. (18a) results in

$$P_{\text{Loss,f}} = \frac{64}{Re}\frac{{L_{\text{t}} }}{D}\frac{{\rho V^{2} }}{2} = 32\mu \frac{{L_{\text{t}} V}}{{D^{2} }} = 128\mu \frac{{L_{\text{t}} Q}}{{\pi D^{4} }}$$
(18c)
$$Q = \frac{{\pi D_{\text{t}}^{4} }}{{256 \mu L_{\text{t}} }}\left( {P_{\text{M}} - P_{\text{N}} + \rho g\sin \left( {\alpha_{\text{inc}} } \right) \Delta Z} \right)$$
(18d)

Nodal pressure values are calculated by applying the mass conservation law on each node (as illustrated in Fig. 7b)

$$\mathop \sum \limits_{i = 1}^{4} Q_{i} = 0$$
(19)

substituting Eq. (18a) into Eq. (19) yields

$$A_{i,j} P_{i,j} - A_{i + 1,j} P_{i + 1,j} - A_{i - 1,j} P_{i - 1,j} - A_{i,j + 1} P_{i,j + 1} - A_{i,j - 1} P_{i,j - 1} = B_{i,j}$$
(20)

where

$$B_{i,j} = \rho g \sin \alpha_{\text{inc}} \left[ {A_{i,j} z_{i,j} - A_{i + 1,j} z_{i + 1,j} - A_{i - 1,j} z_{i - 1,j} - A_{i,j + 1} z_{i,j + 1} - A_{i,j - 1} z_{i,j - 1} } \right]$$
(21)

Equations (20) and (21) form a system of linear equations when are written for all nodes in the network.

The values of \(A_{\text{m,n}}\) are calculated from

$$A_{\text{m,n}} = \frac{{\pi D_{\text{t}}^{4} }}{{256\mu L_{\text{t}} }}$$
(22)

where \(D_{\text{t}}\) and \(L_{\text{t}}\) are the diameter and length of the tube connecting pores M and N. Since all the vertical tubes have the same diameter and length and all the horizontal tubes have the same diameter and length in the pore network of this study, values of \(A_{\text{m,n}}\) for vertical and horizontal tubes are \(A_{\text{v}}\) and \(A_{\text{h}}\), respectively. This results in zero value for Bi,j as the hydrostatic pressure terms cancel out each other. For boundary nodes, including the nodes next to the bubble, the component of the matrix A associated with the node located either outside of the domain or on a bubble node is set as zero. Therefore, Eqs. (20) and (21) are rearranged correspondingly and values of Bi,j for this case are not necessarily zero. The resulting system of equations is then solved for values of pressure nodes. To improve the convergence of the program and find the bubble velocity with any required tolerance, a simple half-division method is employed when the sign of (Powerloss − Powerin) changes due to reduction in ub (i.e., when the value of ub is close to the desired steady-state velocity). The solution is terminated when (Powerloss − Powerin)/Powerin is less than a given tolerance value (set as 0.001 in this work).

5 Results and Discussion

5.1 Experimental

Figure 8a–c shows the average bubble velocity as a function of sin αinc for bubbles of different lengths moving in kerosene, Soltrol 170 and white oil, respectively. As expected from Eq. (9), the bubble velocity increases with increasing sin αinc linearly for a given fluid (i.e., constant ρ and µ); the larger the inclination angle, the higher is the velocity of the bubble, due to the increase in the pressure gradient. Figure 8d shows the variations in bubble velocity with the initial bubble length, Lb0, for different test liquids measured at a particular inclination angle (αinc = 18°). Lb0 refers to the bubble length measured at the beginning of each experiment at static condition. The data show linear dependency of the bubble rise velocity on the bubble length for the three test liquids (R2 = 0.98).

Fig. 8
figure 8figure 8

Variations in average bubble velocity with sin αinc for a kerosene, b Soltrol 170, and c white oil. d Variations in average bubble velocity with the initial bubble length, Lb0, for different test liquids (αinc = 18°)

Full size image

The slope of trendlines in Fig. 8a–c represents [(K krgρlg/µl) (Lb/Leff)) from which values of the gas bubble permeability, Kg,cal = K krg, were calculated for different bubble lengths and test liquids assuming Lb = Leff. The highest calculated permeability values were obtained for bubbles moving in the porous medium saturated with Soltrol 170. For all wetting liquids, the calculated permeability of the medium for the gas bubble increased with increasing the bubble length, as shown in Fig. 9. This can be explained by the fact that for longer bubbles, the shape of the bubble becomes more or less flatten, especially at the tailing end, resulting in less drag force against bubble motion from the wall of pore bodies. The observed changes suggest the existence of an effective bubble length that is different from the apparent length of the bubble (i.e., Leff ≠ Lb) and is responsible for the flow around the bubble during its upward motion.

Fig. 9
figure 9

Variations in the calculated permeability of micromodel for the gas bubble, Kg,cal, with initial bubble length Lb0, assuming Leff = Lb

Full size image

Assuming that the micromodel permeability for the gas phase is constant and equal to the largest value of the calculated permeabilities at different inclination angels, the values of Leff/Lb were calculated from the slope of plots in Fig. 8a–c for different bubble lengths. This assumption was made based on the definition of the effective length, which implies that the effective length for a bubble moving through a porous medium is equal or greater than the apparent length of the bubble measured as the difference between the bubble front and tail positions (i.e., Leff ≥ Lb). Therefore, when Leff ≠ Lb, we have Leff > Lb; consequently, Sg [Leff > Lb] > Sg [Leff = Lb] and krg [Leff > Lb] > krg [Leff = Lb]. Therefore, gas-phase saturation and permeability are higher when Leff ≠ Lb rather than when Leff = Lb. The results show that the difference between the values of Leff and Lb0 is more noticeable for smaller bubbles, and as the length of bubbles increases and their shape flattens, the two values become closer and their ratio approaches 1, as illustrated in Fig. 10. This finding is consistent with the observed changes in bubble shape for longer bubbles at higher inclination angles. Effective length is also a function of medium permeability, pore geometry and connectivity, and the presence or absence of other pore bodies in the vicinity of the bubble (Smith 2005).

Fig. 10
figure 10

Changes in the ratio of effective length to apparent bubble length, Leff/Lb0, versus apparent (initial) bubble length

Full size image

The results from the visualization experiments indicate that bubbles do not migrate at a constant velocity through a porous medium, but their velocity constantly changes with time and bubble position, implying unsteady-state flow conditions. These observations could be explained by the existence of locally non-uniform flow conditions being affected by pressure, temperature, pore structure and saturation-dependent permeability of the medium along the bubble pathway, resulting in the local variations in the values of individual forces acting on the rising bubble (Corapcioglu et al. 2004). Figure 11 shows the variations in the local bubble velocity measured for a bubble with 2.5 cm static length over a 10 cm travel distance in 1-second time intervals as a function of time and the bubble front position, Xf, for white oil. As seen, the local velocity of the bubble is significantly higher at the beginning (i.e., around Xf = 1.5 cm) and reaches its minimum at some points close to the end of the traverse distance, due to flow inducing pressure drop. This was seen for all experiments, suggesting that there is some non-uniformity in the pore sizes and depth of etching throughout the model. Therefore, some pore throats are larger, and some are smaller relative to the neighbors through which the air bubble invasion is easier or more difficult, respectively.

Fig. 11
figure 11

Variations in local bubble velocity with time and bubble front position for Lb0 = 2.5 cm and αinc = 25° (white oil)

Full size image

Plot of the bubble front, Xf, and bubble tail, Xt, positions versus time (as shown in Fig. 12a) illustrates that both the front and tail positions vary linearly with time. This was seen for various bubble lengths and inclination angles. The difference between Xf and Xt represents the actual bubble length in dynamic condition (hereinafter referred to as the dynamic bubble length, Lb,dynamic) at every moment. The variations in Lb,dynamic with time for a bubble with the static bubble length of 1.9 cm are shown in Fig. 12b for the same experimental condition. As seen, the dynamic bubble length fluctuates slightly over an average value of 2.2 for a bubble with initial length of 1.9 cm, and thus, it verifies the assumption of constant bubble length during experiments.

Fig. 12
figure 12

Variations in a bubble front and tail positions and b dynamic bubble length with time (Lb,dynamic = 2.2 ± 0.1). The data here are for Lb0 = 1.9 cm and αinc = 32° (white oil)

Full size image

Figure 13 shows photographs of the moving bubbles with different lengths and inclination angles. It is seen that bubbles with the same static lengths, as shown in Fig. 13a, b or c, d, exhibited slightly different dynamic lengths during upward movement due to different angles of inclination. Moreover, the dynamic lengths were always larger than their initial length over the range of inclination angles in this work. Another interesting observation was that the shape of the bubble tail ends remarkably changed for larger bubbles moving at higher speeds. Moving bubbles stretched in length and their tail deformed in shape and became very narrow during upward migration through an inclined porous medium. These changes were most significant for longer bubbles during fast motion and nearly nonexistent for bubbles moving at low speeds. These observations were in agreement with those reported in the literature (Haberman and Morton 1953; Yang et al. 2007). The deformation of the bubble tail was such that the curvature of the interface at the back of the bubble increased significantly. This rear interface stopped expanding and could not occupy the pore space upon reaching a pore body. As Yang et al. 2007 stated in their review, the shape of a bubble is governed by the interaction of surface tension and viscous and hydrodynamic forces. The reason for the flattened bubble tail may be explained by the fact that some of the liquid displaced from the front of the bubble returned back to the rear of the bubble through the side passageways and accumulated between the bubble and the pore walls, resulting in a narrowing of the shape of the tail end. Another possible explanation of this phenomenon is that a pressure buildup occurred at the top of the fast-moving bubbles, which would be relatively large in comparison with its pressure under static conditions. Therefore, the shape and the curvature of the bubble tail change in order to create the same pressure inside the bubble. According to Ajaev and Homsy (2006), both capillary and viscous effects are important at the leading edge of the bubble. However, near the sides of the bubble at the tail end, the dominant effect is the capillary pressure gradient, which causes a draining flow from the top of the bubble (low curvature) to the rear end of the bubble (higher curvature). Another type of deformation was observed for bubbles moving very quickly (i.e., very long bubbles). In this case, the tail of the bubble became flattened, but the very end tip grew a little bit such that the size of the bubble at the tail section decreased from normal size to very thin and then increased again. A photograph of a long bubble with this type of deformation in the shape of the tail section is shown in Fig. 13e. The bubbles with long enough lengths showed such shape deformations and were more likely to cause breakup during fast motion, leaving behind a portion of immobile bubble. The reason for this change in the tail shape of very long bubbles is that the bubble tends to keep its continuity and prevent division by shrinkage.

Fig. 13
figure 13

Photographs of moving bubbles showing the dynamic lengths and shapes for aLb0 = 1.9 cm and αinc = 12°, bLb0 = 1.9 cm and αinc = 25°, cLb0 = 2.5 cm and αinc = 12°, and dLb0 = 2.5 cm and αinc = 25°, eLb0 = 4.7 cm and αinc = 11° (white oil dyed red)

Full size image

A linear relationship was found between the various Lb0 and their corresponding value of Lb,dynamic for bubbles rising in white oil as illustrated in Fig. 14 for αinc = 13°. Such correlation was also obtained for bubbles traveling at other employed inclination angles and found to be useful to predict the actual length of the rising bubbles within a common range of sizes.

Fig. 14
figure 14

Relationship between the dynamic and static bubble lengths (αinc = 13°; white oil)

Full size image

We calculated the bubble velocity using Eq. (8) assuming (a) Leff = Lb0 and (b) Leff = Lb,dynamic, and the results for αinc = 13° for white oil are shown in Fig. 15. The values of bubble velocity calculated based on assumption (b) were remarkably greater that those obtained based on assumption (a), and assumption (b) seems to be more realistic based on the definition of effective length given earlier in Sect. 2. However, the calculated values for the bubble velocity with the assumption (a) were closer to the experimental values of velocity measured in this work. These results suggest that the bubbles moving in the porous medium saturated with white oil did not reach their terminal velocity during the time given in our experiments.

Fig. 15
figure 15

Comparison of calculated bubble velocity, ub, with two assumptions for effective length, Leff = Lb0 and Leff = Lb,dynamic (αinc = 13°; white oil)

Full size image

5.2 Numerical Simulation

The network size considered for the calculations is 9x101 the same as the pore network size used for the experimental studies. The bubble velocity was calculated for different bubble lengths. Values of the contact angles \(\theta_{\text{R}}\) and \(\theta_{\text{A}}\) are obtained by calculating the difference between the dynamic and equilibrium contact angles using the correlation \(\Delta \cos \theta = 2 \sqrt {N_{\text{ca}}}\) suggested by Rillaerts and Joos (1980), where \(N_{\text{ca}}\) is the capillary number expressed as \(N_{\text{ca}} = \mu u_{\text{b}} /\sigma\). Values of equilibrium contact angle were taken from Dong and Chatzis (2004) as listed in Table 1. Figure 16 shows the calculated values of the bubble velocity obtained from experiments and the simulation code as a function of the bubble length. As seen, the simulation results are generally closer to the experimental values at lower velocities and have values higher than the experiments’ with an increasing difference as bubble length grows. One of the reasons is that the numerical simulations represent the steady-state (terminal) bubble velocity while the experimental results are average values over a certain distance over which the bubble has not necessarily reached to a steady-state condition. Longer bubbles require longer distance to reach to the steady-state conditions, and thus, their average velocities over the same distance would be lower than the steady-state values.

Fig. 16
figure 16

Comparison between the calculated velocity of bubbles in Soltrol 170 for αinc = 10° from experiment and simulation for various grid sizes

Full size image

Another observation is that the bubble velocities calculated by the numerical model are lower than the experimental results for bubble lengths smaller than about 2 cm for Soltrol 170 and kerosene. This implies that the assumptions behind developing the numerical model do not hold for bubbles shorter than a critical length since the transient velocity cannot be higher than the steady-state velocity. One of the fundamental assumptions is that the bubble pushes the entire liquid inside the pores ahead of the bubble pore column out and into the surrounding pore and tube network. However, the buoyancy force created by small bubbles seems not enough to push all the liquid out of the bubble pore column and into the surrounding pore and tube network. Instead, some of the liquid seems to stay inside the bubble pore reducing the pore volume filled by the bubble. This can be seen by comparing the portion of the pore volume filled by the liquid at the tip of the bubble in Fig. 13a versus d, e. As a result, the bubble length is extended and becomes longer than what is assumed in the numerical simulations. Therefore, the experimental bubble velocities are higher than numerical values for bubble lengths shorter than a critical value. This needs further investigations.

The simulation results for bubbles rising in pore networks of different grid sizes showed that the bubble velocity was smaller for smaller domains due to interactions with sidewalls. By increasing the domain size, the effects of sidewall interactions became smaller and the bubble velocity increased up to a certain value, after which the velocity did not change significantly with further increase in the grid size. In real conditions, the domain affected by a rising bubble is limited by the territory of other bubbles or impervious solids which change the bubble velocity.

Figure 17 shows a comparison between two tube arrangements for bubbles of 2.5 cm length (Nb = 11) rising in pore networks of 21 × 31 grid size saturated with Soltrol 170 for αinc = 10°. The physical properties of the Soltrol 170 are taken from Table 1. In Fig. 17a, the diameters of horizontal tubes are 0.025 cm and those of vertical tubes are 0.055 cm. In Fig. 17b, the diameters of horizontal tubes have been increased to 0.035 cm, while those of vertical tubes have been remained constant. The results showed the higher bubble velocity for the bubbles traveling in the horizontal tubes with the larger diameter (Fig. 17b), also representing a stretched flow field in the horizontal direction. The reason for the increase in bubble velocity is that for larger horizontal tube diameters, the resistance to the liquid flow in the tubes due to the surface tension force is smaller, and consequently, the fraction of the flow that travels from top of the bubble to the side channels and then to the tail of the rising bubble is larger; thus, the bubble velocity is increased. Table 3 lists the calculated velocities for a bubble of 2.5 cm length (Nb = 11) for different tube arrangements when the vertical tube diameter remains constant and the horizontal tube diameter varies. As seen, the bubble rise velocity increases with increasing the horizontal tube diameter.

Fig. 17
figure 17

Calculated velocity, ub, for a bubble of 2.5 cm length (Nb = 11) for vertical and horizontal tube diameters of aDHorizontal = 0.025 cm and DVertical = 0.055 cm, and bDHorizontal = 0.035 cm and DVertical = 0.055 cm. αinc = 10° (Soltrol 170)

Full size image
Table 3 Calculated velocities for bubble of 2.5 cm length (Nb = 11) for various vertical and horizontal tube diameters for αinc = 10° and grid size 21 × 31 (Soltrol 170)
Full size table

6 Conclusions

The following conclusions can be drawn from the findings of this work:

  • The bubble migration velocity in a liquid-saturated porous medium is a function of the bubble length, inclination angle, the permeability of the medium, gas phase saturation, and the physical properties of the wetting liquid. The bubble velocity increases with increasing the bubble length and the medium inclination angle.

  • It was observed that rising bubbles stretched in length and the tail end of bubbles deformed in shape and became very narrow during the upward migration. This behavior was more significant for longer bubbles moving at high speeds and nearly nonexistent for bubbles moving at low speeds. The reason could be explained by the fact that some of the liquid displaced from the front of the bubble returns back to the rear of the bubble through the side passageways and accumulates in between the bubble and the pore walls. The deformation in the shape of the tail end to a narrower shape is to minimize the pressure difference within the gas phase and the fluid drag on the bubble.

  • An effective bubble length, Leff, for bubble flow is responsible for the liquid flow around the bubble during upward motion. Leff is a function of permeability, fluid properties, pore geometry and connectivity of porous medium. The value of Leff is usually larger than the apparent bubble length, particularly for small bubbles.

  • The results of numerical simulation of a rising bubble in a saturated porous medium showed that the velocity of a bubble is affected by the presence of boundaries around the pore network. It was found that the velocity of bubbles rising in pore networks increases when enlarging the domain of the bubble flow (i.e., the number of the pores in the vertical and horizontal dimensions) until it reaches a critical value at a particular domain size above which the velocity does not change with increasing the dimensions of the network. Also, the velocity of a bubble is proportionally affected by the diameters of the horizontal and vertical tubes in which it is traveling.