Stability of Penetrative Natural Convection in a Non-Newtonian Fluid-Saturated Vertical Porous Layer

Abstract

The stability of natural penetrative convection arising due to a uniform internal heat source in a vertical porous layer saturated with an Oldroyd-B fluid is investigated. The vertical walls of the porous layer are impermeable and maintained at different uniform temperatures. The energy stability analysis performed reveals that the system is unconditionally stable even in the presence of internal heating in the case of Newtonian fluids, while for viscoelastic fluids the base flow is found to be unstable. As the energy stability analysis of Gill type is unable to decide the stability of the system, the Galerkin method is used to solve the complex eigenvalue problem. The internal heating introduces asymmetry in the basic flow and amounts to the existence of different set of onset modes. The internal heating and stress relaxation parameter facilitates instability of the system while increasing strain retardation parameter discloses stabilizing effect on the system. Moreover, the critical Darcy–Rayleigh number, wave number and wave speed become invariant as Ns becomes large. The streamlines and isotherms presented herein demonstrate the development of complex dynamics at the critical state.

1 Introduction

Buoyancy-driven convection in a Newtonian fluid-saturated porous layer has been a subject of intensive research because of its relevance in many fields of applications including the design of packed bed reactors, geothermal systems, enhanced oil recovery methods, insulation engineering to mention a few. The stability aspects of natural convection in a differentially heated vertical porous slab in the framework of Darcy’s law was first studied by Gill (1969) and established that the system is always stable. Later, Rees (1988) considered the effect of a finite Prandtl–Darcy number on Gill’s problem and observed that the flow is linearly stable even in the presence of a time derivative of the velocity. Straughan (1988) showed that Gill’s proof of stability can be extended to the nonlinear domain of perturbations. By taking into account of the local thermal non-equilibrium (LTNE) effect, Rees (2011) and Scott and Straughan (2013) presented a new perspective on Gill’s problem by performing linear and nonlinear stability analyses, respectively, and observed that the basic state is stable. By assuming permeable boundaries of the vertical porous layer instead of impermeable walls, Barletta (2015) reconsidered the analysis carried out by Gill and found that the buoyant flow in the vertical porous slab exhibits a linear instability.

In various practical problems, unusual reactions to applied mechanical stresses are likely to occur, including time-independent viscosity, time-dependent viscosity and a combination of both time-dependent and time-independent viscosity. In these cases, the non-Newtonian rheology of fluids becomes important. There exist different kinds of non-Newtonian fluids whose behavior is different from one another. Most of the time, non-Newtonian viscous fluids modeled as viscoelastic ones with retardation and relaxation effects are used as working media. The flow of viscoelastic fluids has received significant attention of researchers because of their importance in superfluity of engineering applications including blood flow, catalytic polymerization, polymer processing, bio-processing, geology and many others. Such types of fluids are modeled more effectively by an Oldroyd-B constitutive equation. Alishaev and Mirzadjanzade (1975) and Khuzhayorov et al. (2000) formulated a modified Darcy’s law to be considered when the fluid saturating a porous medium has a viscoelastic behavior. Majority of the studies on this topic are concentrated on convective instability in a horizontal porous layer and the details can be found in the book by Nield and Bejan (2017). However, a limited number of studies have been dealt with the stability of natural convection in a non-Newtonian fluid-saturated vertical porous layer. Barletta and Alves (2014) investigated Gill’s stability problem for power-law fluids and observed that the system remains stable despite the presence of inflexion point at the mid-plane in the base flow. Recently, Shankar and Shivakumara (2017a, b) treated Gill’s problem for viscoelastic fluids of Oldroyd-B type and noticed that the system becomes unstable although the basic state is same as that of Newtonian fluid. In the latter case, the LTNE effect was considered in investigating the problem.

The occurrence of natural convection in a fluid-saturated porous medium with internal heat generation is of interest in many engineering problems and it is also a commonly occurring configuration in geophysics which has been studied extensively (Gasser and Kazimi 1976; Rhee et al. 1978; Khalili and Shivakumara 1998; Nouri-Borujerdi et al. 2007, 2008; Nield and Kuznetsov 2013, 2016; Kuznetsov and Nield 2013). Alves et al. (2014) discussed thermal convective instability of viscoelastic mixed convection flows in a horizontal porous layer in the presence of horizontal throughflow and viscous dissipation. It was shown that an ample description of the combined effects of viscoelasticity and viscous dissipation can be obtained with the large Peclet number approximation. The effect of internal heat generation on the instability of parallel buoyant Newtonian fluid flow in a vertical porous layer was investigated by Barletta and Celli (2017) considering the boundaries of the porous layer to be permeable and showed that the stationary flow is unstable.

Nonetheless, the study on the stability of natural penetrative convection arising due to a uniform internal heating in a vertical porous layer saturated by a viscoelastic fluid has not received any attention to the best of our knowledge. A modified Darcy’s law for an Oldroyd-B type of viscoelastic fluid is used to describe the flow in a porous medium. The basic state becomes non-uniform due to the presence of a uniform internal heat source and the eigenvalue problem is solved numerically using the Galerkin method.

2 Mathematical Formulation

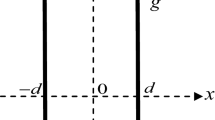
We consider a vertical porous layer heated uniformly internally and saturated by an Oldroyd-B fluid lying in the region $- \,d \le x \le d$ as shown in Fig. 1. The vertical boundaries of the porous layer are kept at constant but different temperatures $T_{1}$ and $T_{2} ( > T_{1} )$. The porous medium is considered to be homogeneous and isotropic with local thermal equilibrium between the fluid and the solid phases. Assuming that the Oberbeck–Boussinesq approximation is valid, the governing equations in the dimensionless form are (Alishaev and Mirzadjanzade 1975; Khuzhayorov et al. 2000; Shankar and Shivakumara 2017a)

$$ \nabla \cdot \vec{q} = 0 , $$

(1)

$$ \left( {1 + \Lambda_{1} \frac{\partial }{\partial t}} \right)\left( {\nabla P - R_{\text{D}} T\,\hat{k}} \right) = \left( {1 +\Lambda _{2} \frac{\partial }{\partial t}} \right)\vec{q} , $$

(2)

$$ \alpha \frac{\partial T}{\partial t} + (\vec{q} \cdot \nabla )T = \nabla^{2} T + {\text{Ns}} . $$

(3)

Fig. 1

Physical configuration

In these equations, $\vec{q} = (u,v,w)$ is the velocity vector, t is the time, P is the modified pressure, T is the temperature, α is the ratio of heat capacities. Here $R_{\text{D}} = {{\rho_{0} g\beta \Delta TKd} \mathord{\left/ {\vphantom {{\rho_{0} g\beta \Delta TKd} {\mu \kappa }}} \right. \kern-0pt} {\mu \kappa }}$ is the Darcy–Rayleigh number, $\Lambda_{1} = \lambda_{1} \kappa /d^{2}$ is the relaxation parameter, $\Lambda_{2} = \lambda_{2} \kappa /d^{2}$ is the retardation parameter and ${\text{Ns}} = Qd^{2} /\Delta T\kappa$ is the dimensionless heat source strength, while $\rho_{0}$, g, β, K, μ, κ, Q, λ₁ and λ₂ are the density at reference temperature T = T₀ (at the middle of the channel), gravitational acceleration, thermal expansion coefficient, permeability, viscosity of the fluid, effective thermal diffusivity, heat generated within the fluid per unit volume per unit time, stress relaxation and strain retardation time constants, respectively.

Taking curl on both sides of Eq. (2) to eliminate the pressure term and introducing the stream function $\psi (x,z,t)$ through

$$ (u,0,w) = \left( { - \frac{\partial \psi }{\partial z},0,\frac{\partial \psi }{\partial x}} \right) , $$

(4)

the governing Eqs. (2) and (3) become

$$ R_{\text{D}} \left( {1 + \Lambda_{1} \frac{\partial }{\partial t}} \right)\frac{\partial T}{\partial x} = \left( {1 + \Lambda_{2} \frac{\partial }{\partial t}} \right)\left( {\frac{{\partial^{2} \psi }}{{\partial x^{2} }} + \frac{{\partial^{2} \psi }}{{\partial z^{2} }}} \right) , $$

(5)

$$ \alpha \frac{\partial T}{\partial t} + \frac{\partial \psi }{\partial x}\frac{\partial T}{\partial z} - \frac{\partial \psi }{\partial z}\frac{\partial T}{\partial x} = \frac{{\partial^{2} T}}{{\partial x^{2} }} + \frac{{\partial^{2} T}}{{\partial z^{2} }} + {\text{Ns}} . $$

(6)

The boundaries are impermeable, and the appropriate boundary conditions are

$$ \psi = 0,\;T = - \,1,\;{\text{at}}\;x = - \,1,\;\psi = 0,\;T = 1\;{\text{at}}\;x = 1. $$

(7)

3 Base Flow

The basic flow is fully developed, unidirectional, steady and laminar. Under these circumstances, Eqs. (5) and (6) reduce to

$$ \frac{{{\text{d}}^{2} \psi_{\text{b}} }}{{{\text{d}}x^{2} }} = R_{\text{D}} \frac{{{\text{d}}T_{\text{b}} }}{{{\text{d}}x}} , $$

(8)

$$ \frac{{{\text{d}}^{2} T_{\text{b}} }}{{{\text{d}}x^{2} }} + {\text{Ns}} = 0 , $$

(9)

accompanied with the boundary conditions

$$ \begin{aligned} \psi_{\text{b}} &= 0\quad {\text{at}}\quad x = \pm \,1, \hfill \\ T_{\text{b}}& = \pm \,1\quad {\text{at}}\quad x = \pm \,1, \hfill \\ \end{aligned} $$

(10)

where the subscript b denotes the basic state.The basic state solution is found to be

$$ \begin{aligned} \psi_{\text{b}} (x) & = \frac{{R_{\text{D}} }}{6}\left\{ {3(x^{2} - 1) + {\text{Ns}}(x - x^{3} )} \right\}, \\ T_{\text{b}} (x) & = \frac{1}{2}\left[ {2x + {\text{Ns}}(1 - x^{2} )} \right]. \\ \end{aligned} $$

(11)

The scaled basic stream function ψ_b(x)/R_D and the temperature T_b(x) are plotted in Fig. 2a, b, respectively. From Fig. 2a, it can be seen that the flow near the hot wall increases as the strength of internal heating increases and as a consequence of this, flow near the cold wall reduces. Basic temperature field shows a parabolic distribution with the width of the layer due to the presence of a uniform distribution of internal heat sources (Fig. 2b). Increase in the value of Ns enhances the deviation of basic temperature profile and, otherwise, it is linear in the absence of internal heat generation.

Fig. 2

a Plots of the scaled basic stream function profile for different values of Ns. b Plots of the basic temperature profile for different values of Ns

4 Linear Stability Analysis

In linear stability analysis, infinitesimal disturbances are imposed on the base flow. Thus, the stream function and temperature fields can be written as

$$ \psi = \psi_{\text{b}} (x) + \psi^{\prime } ,\;T = T_{\text{b}} (x) + T^{\prime } , $$

(12)

where the primed quantities denote infinitesimal disturbances to the corresponding terms. By using normal mode analysis, the disturbances can be expressed by

$$ \left( {\psi^{\prime } ,T^{\prime } } \right) = \left[ {\Psi (x),\Theta (x)} \right]e^{i\,a\,\,(z - ct)} , $$

(13)

where a is the real-valued vertical wave number and c = c_r + ic_i is the complex wave speed. If c_i < 0 the system is stable, c_i > 0 the system is unstable and c_i = 0 the system is neutrally stable. Following the standard linear instability analysis, the governing linear equations for the infinitesimal disturbances can then be shown to be

$$ \left( {1 - ia\Lambda_{2} c} \right)(D^{2} - a^{2} )\Psi = \left( {1 - ia\Lambda_{1} c} \right)R_{\text{D}} D\Theta , $$

(14)

$$ (D^{2} - a^{2} )\Theta + ia\;\Psi (1 - {\text{Ns}}\;x) - \frac{{ia\,\Theta R_{\text{D}} }}{6}\;(6x + {\text{Ns}}(1 - 3\,x^{2} )) = - \,ia\,\alpha \,c\,\Theta . $$

(15)

The associated boundary conditions are:

$$ \Psi = \Theta = 0\;{\text{at}}\;x = \pm \,1. $$

(16)

5 Energy Stability Analysis

Following the method of Gill (1969) and Rees (2011), Eq. (15) is used to determine Ψ in terms of Θ, and substitute it into Eq. (14), to obtain

$$ \begin{aligned} & \Theta^{\prime \prime \prime \prime } - 2a^{2} \Theta^{\prime \prime } + a^{4} \Theta + iaR_{\text{D}} \left( {\frac{{1 - iac\Lambda_{1} }}{{1 - iac\Lambda_{2} }}} \right)\left( {1 - {\text{Ns}}\,x} \right)\Theta^{\prime } \\ & \quad - \frac{{iaR_{\text{D}} }}{6}\left\{ {6\left[ {(x\Theta )^{\prime \prime } - a^{2} x\Theta } \right] + {\text{Ns}}\left[ {\left( {\Theta^{\prime \prime } - a^{2} \Theta } \right) - 3\left( {\left( {x^{2} \Theta } \right)^{\prime \prime } - a^{2} x^{2} \Theta } \right)} \right]} \right\} = - ia\alpha c\left( {\Theta^{\prime \prime } - a^{2} \Theta } \right). \\ \end{aligned} $$

(17)

Given that Ψ and Θ are complex quantities, we now multiply Eqs. (17) by $\bar{\Theta }$, a complex conjugate of Θ, and integrate over the channel width to get the following expression,

$$ \begin{aligned} & \int\limits_{ - 1}^{1} {\left( {\left| {\Theta^{\prime \prime } } \right|^{2} + 2a^{2} \left| {\Theta^{\prime } } \right|^{2} + a^{4} \left| \Theta \right|^{2} } \right)} \,{\text{d}}x + iaR_{\text{D}} \left( {\frac{{1 - iac\Lambda_{1} }}{{1 - iac\Lambda_{2} }}} \right)\int\limits_{ - 1}^{1} {\left( {1 - {\text{Ns}}\,x} \right)\Theta^{\prime } \bar{\Theta }\;{\text{d}}x} \, \\ & \quad - \frac{{iaR_{\text{D}} }}{6}\left\{ {6\left[ {\int\limits_{ - 1}^{1} {\left( {x\Theta } \right)^{\prime \prime } \bar{\Theta }\;{\text{d}}x - a^{2} \int\limits_{ - 1}^{1} {x\left| \Theta \right|^{2} {\text{d}}x} } } \right] - {\text{Ns}}\left[ \begin{array}{l} \int\limits_{ - 1}^{1} {\left( {\left| {\Theta^{\prime } } \right|^{2} + a^{2} \left| \Theta \right|^{2} } \right)} \;{\text{d}}x \hfill \\ \quad+ \,3\left( {\int\limits_{ - 1}^{1} {\left( {x^{2} \Theta } \right)^{\prime \prime } } \bar{\Theta }\;{\text{d}}x - a^{2} \int\limits_{ - 1}^{1} {x^{2} \left| \Theta \right|^{2} \;{\text{d}}x} } \right) \hfill \\ \end{array} \right]} \right\} \\ & \quad = ia\alpha c\int\limits_{ - 1}^{1} {\left( {\left| {\Theta^{\prime } } \right|^{2} + a^{2} \left| \Theta \right|^{2} } \right)} \;{\text{d}}x. \\ \end{aligned} $$

(18)

If we take the real part of Eq. (18), we get

$$ \int\limits_{ - 1}^{1} {\left( {\left| {\Theta^{\prime \prime } - a^{2} \Theta } \right|^{2} } \right)} \;{\text{d}}x + a^{2} c_{r} R_{\text{D}} \left( {\frac{{\Lambda_{1} - \Lambda_{2} }}{{a^{2} c_{r}^{2} \Lambda_{2}^{2} + \left( {1 + ac_{i} \Lambda_{2} } \right)^{2} }}} \right)\int\limits_{ - 1}^{1} {\left( {1 - {\text{Ns}}\,x} \right)\Theta^{\prime } \bar{\Theta }\;{\text{d}}x} = - a\alpha c_{i} \int\limits_{ - 1}^{1} {\left( {\left| {\Theta^{\prime } } \right|^{2} + a^{2} \left| \Theta \right|^{2} } \right)} \;{\text{d}}x. $$

(19)

From Eq. (19), it is clear that c_i is always negative when Λ₁ = Λ₂ = 0 (Newtonian fluid case) indicating that all small-amplitude disturbances decay even in the presence of internal heat source, a result established by Gill (1969). However, the stability of the system cannot be ascertained for an Oldroyd-B fluid as the sign of c_i cannot be determined and hence Gill’s proof of stability becomes ineffective in the present case.

6 Method of Solution

Equations (14) and (15) together with the boundary conditions (16) constitute an eigenvalue problem and solved numerically using the Galerkin method. Accordingly, Ψ(x) and Θ(x) are expanded in terms of Legendre polynomials in the form

$$ \Psi (x) = \sum\limits_{n = 0}^{N} {a_{n} \xi_{n} (x)} ,\;\Theta (x) = \sum\limits_{n = 0}^{N} {b_{n} \xi_{n} (x)} , $$

(20)

with the corresponding base functions

$$ \xi_{n} (x) = (1 - x^{2} )P_{n} (x) , $$

(21)

where P_n(x) is the Legendre polynomial of degree n and a_n and b_n are constants. It may be noted that Ψ(x) and Θ(x) satisfy the boundary conditions. Equation (20) is substituted into Eqs. (14) and (15) and the resulting error is required to be orthogonal to ξ_m(x) for m = 0, 1, 2,…, N. This gives

$$ \begin{aligned} & \sum\limits_{n = 0}^{N} {a_{n} \int\limits_{ - 1}^{1} {\left( {\xi_{n}^{\prime } \xi_{m}^{\prime } + a^{2} \xi_{n} \xi_{m} } \right)} \;{\text{d}}x} + R_{\text{D}} \sum\limits_{n = 0}^{N} {b_{n} \int\limits_{ - 1}^{1} {\xi_{n}^{\prime } \xi_{m} } \;{\text{d}}x} \\ & \quad = iac\Lambda_{2} \sum\limits_{n = 0}^{N} {a_{n} \int\limits_{ - 1}^{1} {\left( {\xi_{n}^{\prime } \xi_{m}^{\prime } + a^{2} \xi_{n} \xi_{m} } \right)} \;{\text{d}}x + iac\Lambda_{1} } R_{D} \sum\limits_{n = 0}^{N} {b_{n} \int\limits_{ - 1}^{1} {\xi_{n}^{\prime } \xi_{m} } \;{\text{d}}x} , \\ \end{aligned} $$

(22)

$$ \begin{aligned} & ia\sum\limits_{n = 0}^{N} {a_{n} \int\limits_{ - 1}^{1} {\left( {1 - {\text{Ns}}\;x} \right)\xi_{n} \xi_{m} \;{\text{d}}x} } - \sum\limits_{n = 0}^{N} {b_{n} \int\limits_{ - 1}^{1} {\left( {\xi_{n}^{\prime } \xi_{m}^{\prime } + a^{2} \xi_{n} \xi_{m} } \right)\;{\text{d}}x} } \\ & \quad - \frac{{iaR_{\text{D}} }}{6}\sum\limits_{n = 0}^{N} {b_{n} \int\limits_{ - 1}^{1} {\left( {6x + {\text{Ns}}(1 - 3\,x^{2} )} \right)\xi_{n} \xi_{m} \;{\text{d}}x} } = - ia\alpha c\,\,\sum\limits_{n = 0}^{N} {b_{n} \int\limits_{ - 1}^{1} {\xi_{n} \xi_{m} \;{\text{d}}x} } , \\ \end{aligned} $$

(23)

in which the primed quantities denote differentiation with respect to x. The above equations form the following system of linear algebraic equations

$$ AX = cBX $$

(24)

where c is the eigenvalue, X is the discrete representation of the eigenfunction, A and B are complex matrices of order 2(N + 1). For fixed values of all dimensionless parameters present here, the values of c which make sure a non-trivial solution of Eq. (24) are achieved as the eigenvalue of the matrix B⁻¹A. Once the eigenvalues c are found then one of the parameters, say R_D, is varied until the imaginary part of c vanishes from one having the largest imaginary part among the eigenvalues. The zero crossing of c_r is accomplished by Newton’s method for a fixed point determination. The corresponding values of R_D and a are the critical conditions for neutral stability. The bisection method is built-in to locate the critical Darcy–Rayleigh number with respect to the wave number to the desired degree of accuracy. The real part of c corresponding to the critical Darcy–Rayleigh number with respect to the wave number gives the critical wave speed. This procedure is replicated for different values of physical parameters involved therein (Shankar et al. 2016). The convergence process of the Galerkin method is shown in Table 1. It is seen that as the order of polynomial (N) increased, the results remain consistent and accuracy up to five decimal points can be obtained by taking 10 terms in the Galerkin expansion and the results obtained for this order are presented.

Table 1 Process of convergence of the Galerkin method for some selected parametric values

7 Results and Discussion

The effect of penetrative convection occurring due to internal heat source is investigated on the stability of natural convection in an Oldroyd-B fluid-saturated vertical porous layer. The dimensionless parameters which are affecting the stability of the system are the Darcy–Rayleigh number R_D, the heat source strength Ns, the relaxation parameter Λ₁ and the retardation parameter Λ₂. The value of Λ₁ must be greater than Λ₂ (Bird et al. 2007; Hirata et al. 2015) and for the Newtonian fluid Λ₁ = Λ₂ = 0. The value of α is fixed at unity in all the calculations.

Figure 3a–c demonstrates the typical neutral stability curves in the (R_D, a)-plane for various values of Λ₁ (with Λ₂ = 0.1, Ns = 1), Λ₂ (with Λ₁ = .5, Ns = 1) and Ns (with Λ₁ = 0.5, Λ₂ = 0.4), respectively. The neutral stability curves show an upward concave shape exhibiting a single but different minima with respect to the wave number a, and the unstable region lies above each of the neutral stability curve. The effect of increasing Λ₁ (Fig. 3a) and Ns (Fig. 3c) is to reduce the region of stability as the minimum of the Darcy–Rayleigh number decreases, while an opposite trend could be seen with increasing Λ₂ (Fig. 3b). Besides, the minimum Darcy–Rayleigh number shifts toward the lower values of the wave number with increasing Λ₁, Λ₂ and Ns indicating their effect is to increase the cell width.

Fig. 3

Neutral stability curves

It is intriguing to note that the presence of internal heating leads to a break in the symmetry of the basic state which in turn breaks the symmetry between the upward-moving and the downward-moving disturbances. When Ns = 0, the solutions always correspond to c_c < 0, and hence the cells move up the layer. By the odd symmetry of the basic thermal state, one would expect identical cells moving down the layer and thus c_c > 0 with the same magnitude. However, when Ns increases from zero then the positive c_c will have a different magnitude from the negative c_c. To make the things more clear, the neutral stability curves for different values of Ns when Λ₁ = 0.2 and Λ₂ = 0.1 are presented in Fig. 4a–c for both c_c > 0 and c_c < 0. As expected, there exists a different set of onset modes and for the mode with c_c < 0 has the lower value of R_Dc for all the values of Ns considered. The same trend was noticed for other choices of parameters as well.

Fig. 4

Neutral stability curves for c_c < 0 and c_c > 0

Figure 5a–c illustrates the variation of critical Darcy–Rayleigh number R_Dc, the critical wave number a_c and the critical wave speed c_c, respectively, as a function of Ns for different values of Λ₁ when Λ₂ = 0.1. Figure 5a suggests that R_Dc is inversely proportional to Ns and it will tend to a constant value as Ns becomes large because of the increase in energy supply to the system. As the value of Λ₁ rises, the ordinate of the R_Dc curve alleviates indicating it has a destabilizing effect on the flow. This may be due to the fact that enlarging of relaxation stops the stickiness of the fluid and consequently the effect of friction will be smaller so that the convection sets in at lesser values of R_Dc. The variation of a_c versus Ns pursues a reverse trend with unique rise rates for every value of Λ₁ as shown in Fig. 5b but remains invariant with increasing values of Ns. The values of a_c are found to be high at lower values of Λ₁ but only up to a certain value of Ns. It is observed that increase in Λ₁ is to increase the size of convection cells till Ns = 1 and thereafter the trend gets reversed. Corresponding curves of c_c displayed in Fig. 5c for different values of Λ₁ show that the instability sets in only via oscillatory mode and the values of c_c tend to a constant value as Ns becomes large. It is also evident that increasing Λ₁ is to increase the critical wave speed.

Fig. 5

Critical value of a R_D, b a, c c versus Ns for various values of Λ₁ when Λ₂ = 0.1

A qualitative plot of the streamlines and isotherms of the perturbation modes at critical conditions is given in Figs. 6, 7, 8 and 9 for values of Ns = 1, 5, 10 and 50 and for different choices of viscoelastic parameters. These patterns are calculated from the sinusoidal change of ψ^′ and T^′ given by Eq. (13). No explicit orientation of the streamlines and isotherms is drawn in these figures but an alternate rotating and counter-rotating cells do in fact occur. Figure 6 shows that the unicellular cells in the streamlines for Ns = 1 are inclined and which get stretched with further increase in its value. As far as the isotherms are concerned, the unicellular cell elongates and the temperature field becomes double cells as Ns increases (Fig. 7). These facts together denote that the transfer of the disturbance temperature takes place more effectively, leading to a more unstable flow configuration. This can also be confirmed when the largest disturbance function and temperature are compared. Streamlines value fall drastically from 0.630 to 0.115 and at the same time isotherms increase from 0.104 to 0.525, when Ns increases from 1 to 50. Similar trend is observed with increasing Λ₁ and the same is shown in Figs. 8 and 9. It is also observed that the maximum disturbance temperature for Λ₁ = 0.4 and Λ₂ = 0.1 is higher than that for Λ₁ = 0.2 and Λ₂ = 0.1 indicating that the system has a destabilizing effect with increasing relaxation parameter.

Fig. 6

Disturbance streamlines for different values of Ns when Λ₁ = 0.2, Λ₂ = 0.1

Fig. 7

Disturbance isotherms for different values of Ns when Λ₁ = 0.2, Λ₂ = 0.1

Fig. 8

Disturbance streamlines for different values of Ns when Λ₁ = 0.4, Λ₂ = 0.1

Fig. 9

Disturbance isotherms for different values of Ns when Λ₁ = 0.4, Λ₂ = 0.1

The effect of Λ₂ on the stability characteristics of the system is presented in Fig. 10a–c as a function of Ns for Λ₁ = 0.5. From Fig. 10a, it is seen that the effect of increasing Λ₂ is to increase the value of R_Dc and thus it has a stabilizing effect on the system. This is because increase in Λ₂ amounts to increase in the time taken by the fluid element to react to the applied stress. That is, all through the enlargement of retardation parameter, the effect of friction will be higher and as a result higher values of R_Dc are needed to encourage instability of the system. To confirm the above fact, disturbance stream function and temperature are plotted for various values of Ns when Λ₁ = 0.5 and Λ₂ = 0.2 (Figs. 11, 12). By more closely examining the maximum values of Ψ and Θ, it is found that Ψ_max decreases from 0.650 to 0.113 and Θ_max increases from 0.113 to 0.580 as Ns increases. With increase in Λ₂, Ψ_max increases while Θ_max decreases (Figs. 13, 14). The plot of a_c against Ns illustrates unique characteristics for almost each value of Λ₂ (Fig. 10b). For lower value of Λ₂, the size of the convection cell becomes smaller as Ns increases. As Λ₂ increases, the cell width remains constant as dependence of a_c upon Ns is weak. Figure 10c shows that the value of c_c increases with decreasing Λ₂.

Fig. 10

Critical value of a R_D, b a, c c versus Ns for various values of Λ₂ when Λ₁ = 0.5

Fig. 11

Disturbance streamlines for different values of Ns when Λ₁ = 0.5, Λ₂ = 0.2

Fig. 12

Disturbance isotherms for different values of Ns when Λ₁ = 0.5, Λ₂ = 0.2

Fig. 13

Disturbance streamlines for different values of Ns when Λ₁ = 0.5, Λ₂ = 0.4

Fig. 14

Disturbance isotherms for different values of Ns when Λ₁ = 0.5, Λ₂ = 0.4

8 Conclusions

The effect of penetrative convection arising due to a uniform internal heating on the stability of natural convection in an Oldroyd-B fluid-saturated vertical porous layer is investigated. The following conclusions are drawn from the foregoing study:

• 1. The presence of internal heating is to deviate the basic temperature from linear to nonlinear with respect to the horizontal coordinate resulting in the asymmetry of the basic state.

• 2. The energy stability analysis is used to analyze the stability of the system. The system is stable to disturbances of all wave numbers for all values of the Darcy–Rayleigh number even in the presence of internal heat source only in the case of Newtonian fluid.

• 3. The energy stability analysis is ineffective in deciding the stability of the system when the viscoelastic effects are present and hence the eigenvalue problem is solved numerically using the Galerkin method. The system is found to be unstable in the case of viscoelastic fluids; a result which is qualitatively different from Newtonian fluids.

• 4. The asymmetry in the basic state due to the presence of internal heating amounts to the existence of different set of onset modes and observed that the mode with c_c < 0 has smaller R_Dc compared to the mode with c_c > 0 for all choices of physical parameters considered.

• 5. The instability occurs via only oscillatory motions and the effect of increasing Ns has a destabilizing effect on the fluid flow irrespective of the values of physical parameters. The critical values of Darcy–Rayleigh number, wave number and wave speed become invariant as Ns becomes large.

• 6. The viscoelastic parameters exhibit opposite contribution on the stability of the system; the relaxation and retardation parameters display destabilizing and stabilizing effects, respectively.

• 7. Increase in the strength of internal heating amounts to decrease in Ψ_max and an increase in Θ_max, irrespective of the values of viscoelastic parameters.