1 Introduction

Washburn (1921) invented the pore-scale network modeling approach when he assumed that the pore space could be simplified to a bundle of tubes. His model was later extended when researchers accounted for the interconnectivity of the pores (Fatt 1956). Implementing the interconnectivity allowed researchers to capture many transport properties such as two-phase permeability (Bryant and Blunt 1992), three-phase permeability (Piri and Blunt 2005; Piri and Karpyn 2007), and drainage and imbibition (Mason and Mellor 1995; Joekar-Niasar et al. 2008). Models with interconnectivity were also useful for understanding gelation in porous media (Thompson and Fogler 1997, 1998) and for modeling the non-Newtonian fluids (Balhoff and Thompson 2004, 2006).

In recent years, the advent of high-resolution images has produced major advances in the area of pore-scale modeling (Blunt et al. 2013). The small-scale images help us to better understand the topology of the void space (Spanne et al. 1994; Lindquist and Venkatarangan 1999; Wildenschild and Sheppard 2013). These images are used to reconstruct the pore space (Dong and Blunt 2009), which provides a basis for direct pore-scale simulation (Arns et al. 2002; Oren and Bakke 2002; Oren et al. 2007; Ovaysi and Piri 2010, 2011; Mostaghimi et al. 2012; Takbiri Borujeni et al. 2013) and for a pore-scale network modeling approach (Oren et al. 1998; Valvatne et al. 2005; Al-Raoush et al. 2003; Thompson et al. 2008; Piri and Blunt 2005). Researchers have adopted both approaches to analyze pore-scale physics of multiphase flow in porous media (Joekar-Niasar et al. 2008; Bijeljic et al. 2013). However, using high-resolution images for tight and ultra-tight formations remains difficult. It is not yet possible to build a model based on the high-resolution images whose size is comparable to the core size. This means that developing analytical pore-scale network models could be critical for investigating the transport properties of ultra-tight formations.

Like every other model, the pore-scale network model has its limitations and entails modification to be realistic for different formations. The network model was originally invented to represent the intergranular porosity of a porous medium (Washburn 1921). The intergranular porosity is the void space between grains of different shapes and sizes that have been randomly deposited by primary processes. This means that the pore throat size is randomly distributed on a network, which is useful for capturing the transport properties when the void space resides mainly between the grains (Oren et al. 1998). The pore-throat sizes associated with the intergranular porosity are randomly distributed because they are between grains, with different sizes being randomly deposited (Bryant et al. 1996).

There are formations with a significant fraction of the pore space positioned inside the grains; these include tight gas sandstones (Milliken 2001), carbonates (Al-Shalabi et al. 2014), and shales (Javadpour et al. 2007; Fathi and Akkutlu 2009; Sakhaee-Pour and Bryant 2012; Kethireddy et al. 2014; Heller and Zoback 2014; Saneifar et al. 2014; Yu and Sepehrnoori 2014). This type of porosity is considered intragranular, which implies that the spatial location of intragranular porosity is different from that of the intergranular porosity and the two types of porosity can take different structures.

A spatially random distribution of the pore-throat size on a well-connected network leads to a plateau-like trend of capillary pressure variation with wetting phase saturation (Sahimi 1994; Prodanovic et al. 2013; Sakhaee-Pour and Bryant 2015). The plateau-like trend, which is relevant to intergranular porosity, is absent in the capillary pressure measurements of tight gas sandstones (Byrnes et al. 2009; Shanley et al. 2014). Mousavi and Bryant (2012) pointed out that it is impossible to capture the mercury intrusion capillary pressure measurements of tight gas sandstones if we use only a spatially random distribution of the pore-throat size. This was because of the topology of the void space (its spatial distribution), and not the pore-throat sizes, as they picked the pore-throat sizes to be representative of the measurements. Mehmani and Prodanovic (2014) indicated that microporosity plays an important role in controlling such trends in tight gas sandstones based a network modeling approach. Recently, Sakhaee-Pour and Bryant (2014) have developed a multitype void model that captures intergranular porosity, intragranular porosity, and their interaction. The difference between the porosities was clarified, which is something that we will take into consideration in the present study.

It is crucial to predict the capillary pressure of a formation to model the multiphase flow behavior more accurately. Brown (1951) showed that the capillary pressures converge if scaled using nondimensional groups. For such convergence, we have to account for transport properties like permeability, porosity, and wetting phase saturation. We also have to account for the parameters concerned with the lithology of the formation, such as pore structure and wettability. The scaled capillary pressures are calculated using the J-function as follows (Leverett 1941):

$$\begin{aligned} J\left( {\varGamma ,S_\mathrm{w} } \right) =\frac{P_\mathrm{c} }{\gamma \cos {\theta }}\sqrt{\frac{k}{{\varphi }}} \end{aligned}$$
(1)

where J is the dimensionless function, often referred to as the J-function, \(\varGamma \) is representative of the pore structure, \( S_\mathrm{w} \) is the wetting phase saturation, \(P_\mathrm{c} \) is the capillary pressure, \( \gamma \) is the interfacial tension, \({\theta }\) is the contact angle, k is the permeability, and \({\varphi }\) is the porosity. The term relevant to the pore structure is often neglected in the J-function expression (Thomeer 1960; Brooks and Corey 1966; Thomas et al. 1968; Bentsen and Anli 1997; Alpak et al. 1999; Peters 2012; Buryakovsky et al. 2012).

There is no simple way to implement the effect of pore structure on the J-function, and the J-function is usually plotted only with respect to the wetting phase saturation. The motivation behind the present study is to evaluate the importance of such an effect for tight gas sandstones. We will decompose the J-function and determine the effective transport properties of two pore structures interpreted from mercury intrusion experiment and compare the results with those of the traditional approach.

2 Pore Structure Effect on Drainage

We begin by elaborating the effect of pore structure on the trend of capillary pressure with wetting phase saturation during drainage. During the drainage, a nonwetting phase is injected into a sample saturated by a wetting phase. Mercury is usually used for this purpose because it becomes the nonwetting phase for most rock samples, whereas air, or mercury vapor, is the wetting phase.

We consider a regular lattice model whose pore-throat size is randomly distributed on the network, which is realistic for intragranular porosity. During the drainage, we increase the capillary pressure gradually, which allows the nonwetting phase to invade the pore space (Fig. 1). The invasion starts when the capillary pressure is equal to the entry pressure of the sample. Pores accessible to the nonwetting phase with entry pressures less than or equal to the capillary pressures are invaded at each pressure. The nonwetting phase saturation, which is the fraction of the pore space taken by the nonwetting phase, increases when the nonwetting phase occupies the pores (\(\hbox {wetting phase saturation} = 1- \hbox {nonwetting phase saturation}\)). As a result, the wetting phase saturation decreases in this process.

When the spatial distribution of the pore-throat size on the network is random, the nonwetting phase enters a considerable number of pores at some capillary pressure (Fig. 1a2, a3). This leads to a significant decrease in the wetting phase saturation over a small range of capillary pressure (the plateau-like trend in Fig. 1b). Pores with lower entry pressures are invaded at a higher capillary pressure because the nonwetting phase has access to them only through pores with higher entry pressures. This means that the spatially random distribution of the pore-throat sizes is the main reason for the plateau-like trend observed in the capillary pressure measurements.

Fig. 1
figure 1

Schematic of the mercury intrusion experiment at four capillary pressures (a1)–(a4) where the nonwetting phase is indicated by solid red lines. The pore sizes, denoted by the thickness of the red lines, are randomly distributed, which is the reason for the plateau-like trend of capillary pressure with wetting phase saturation in b

Full size image

We now turn to the capillary pressure measurements available for tight gas sandstones (Byrnes et al. 2009; Sakhaee-Pour and Bryant 2014). We only consider measurements carried out by Byrnes et al. (2009) for this study because most measurements for tight gas sandstones (Sakhaee-Pour and Bryant 2014; Byrnes et al. 2009) exhibit similar trends. Figure 2 shows the measurements for three sets of samples that are acquired under confined boundary conditions (with confinement). We analyze only the data acquired under confined boundary conditions because they are more representative of in situ conditions. We presume that the microcracks created during recovery (Teufel 1983, 1989) are closed with confinement. The created microcracks can have major effects on transport properties when pores are small. The wetting phase saturation in these measurements is determined from mercury saturation (\(\hbox {wetting phase saturation} = 1- \hbox {mercury saturation}\)). Table 1 lists other transport properties of these samples.

Fig. 2
figure 2

Mercury intrusion capillary pressure measurements of tight gas sandstones for three sets of samples (data from Byrnes et al. 2009). The threshold wetting phase saturation \((S_\mathrm{w}^{*})\) used for calculating transport properties of the ordered pore structure is shown in red

Full size image
Table 1 Petrophysical properties of the samples whose drainage measurements are shown in Fig. 2 (data from Byrnes et al. 2009)
Full size table
Fig. 3
figure 3

a Dashed black lines show the random pore structure (\(\varGamma _\mathrm{r}\)), and solid gray lines show the ordered pore structure (\(\varGamma _\mathrm{o}\)), where the pore size is represented by the line thickness. The mercury intrusion experiment at five capillary pressures is shown in a–e, where the nonwetting phase is indicated by solid red lines. b The beginning of the drainage in the ordered pore structure where the random pore structure is fully invaded

Full size image

The variation of the capillary pressure with wetting phase saturation shows two trends. In the early stages of mercury intrusion (low capillary pressure and high wetting phase saturation), the variation of the capillary pressure with the wetting phase saturation exhibits a plateau-like trend. Later during the drainage, the variation of the capillary pressure with the wetting phase saturation becomes almost exponential.

The observed trends are relevant to different pore structures. The plateau-like trend takes place during the invasion of the pore structure whose pore-throat size is randomly distributed on a well-connected network. The corresponding pore space, shown by dashed black lines in Fig. 3a, has a random pore structure. Thus, the pore structures are indicative of the pore-throat size distribution on the network.

The exponential trend indicates that the invasion of the pore space is not delayed due to the limited accessibility of the nonwetting phase to the pores. Figure 3b depicts an example of such conditions, where the nonwetting phase, shown in red, has direct access to all the pores that are not invaded. Figure 3b–e shows the invasion of the pore space, represented by gray lines in Fig. 3b. This type of nonwetting accessibility to the pores is fundamentally different from that of the plateau-like trend shown in Fig. 1 or in Fig. 3a, which has a random pore structure. Thus, we consider the pore structure corresponding to the exponential trend an ordered pore structure.

We now define the pore structures mathematically by classifying them into two groups as follows:

$$\begin{aligned} \varGamma =\varGamma _\mathrm{r} \cup \varGamma _\mathrm{o} \end{aligned}$$
(2)

where \(\varGamma \) is the overall pore structure (the dashed black and solid gray lines in Fig. 3a), \(\varGamma _\mathrm{r}\) is the random pore structure (the dashed black lines in Fig. 3a), and \(\varGamma _\mathrm{o} \) is the ordered pore structure (the solid gray lines in Fig. 3a). This classification is more realistic for two-phase flow than for single-phase flow because it is based on the spatial distribution of the pore-throat size interpreted from two-phase displacement.

3 J-function Decomposition for Tight Gas Sandstones

We take into account the effect of the pore structure on the J-function here. We express the J-function, although it is not possible to calculate it yet, for each pore structure as follows:

$$\begin{aligned} J=J_\mathrm{r} \left( {\varGamma _\mathrm{r} , S_\mathrm{w} } \right) \cup J_\mathrm{o} \left( {\varGamma _\mathrm{o} , S_{\mathrm{w}\text {-}\mathrm{o}} } \right) \end{aligned}$$
(3)

where \(J_\mathrm{r} \left( {\varGamma _\mathrm{r},S_\mathrm{w}}\right) \) is the corresponding function for the random pore structure and \(J_\mathrm{o} \left( {\varGamma _\mathrm{o},S_{\mathrm{w}\text {-}\mathrm{o}}}\right) \) for the ordered pore structure. \(S_\mathrm{w}\) and \(S_{\mathrm{w}\text {-}\mathrm{o}}\) are the wetting phase saturations of the random and the ordered pore structures, respectively. We drop the pore structure term (\(\varGamma _\mathrm{r}\) and \(\varGamma _\mathrm{o}\)) from now on because each function represents only a single pore structure. These functions are exclusive, because the pore structures accessible to the nonwetting phase are separated where the trend of capillary pressure variation with wetting phase changes. The wetting phase saturation at which this exponential trend starts is the threshold value (\(S_\mathrm{w} =S_\mathrm{w}^{*} \)). This means we can decompose the J-function for the entire range of wetting phase saturation as follows:

$$\begin{aligned} \begin{array}{ll} J=J_\mathrm{r} \left( {S_\mathrm{w} } \right) =\frac{P_\mathrm{c} }{\gamma cos{\theta }}\sqrt{\frac{k_\mathrm{r} }{{\varphi }_\mathrm{r} }}&{}\quad S_\mathrm{w} >S_\mathrm{w}^{*}\\ J=J_\mathrm{o} \left( {S_{\mathrm{w}\text {-}\mathrm{o}} } \right) &{}\quad S_\mathrm{w} \le S_\mathrm{w}^{*}\\ \end{array} \end{aligned}$$
(4)

where \(J_{r}\) and \(J_{o}\) are the corresponding values of the J-function for random and ordered pores structures, respectively, \(S_\mathrm{w}\) is the wetting phase saturation obtained from mercury intrusion experiment, \(P_\mathrm{c}\) is the capillary pressure, \(\gamma \) is the interfacial tension, \(\theta \) is the contact angle, \(k_\mathrm{r} \) is the permeability of the random pore structure, \(\varphi _\mathrm{r}\) is the porosity of the random pore structure, and \(S_{\mathrm{w}\text {-}\mathrm{o}}\) is the wetting phase saturation of the ordered pore structure.

For the ordered pore structure, we present the corresponding function with respect to its wetting phase saturation (\(S_{\mathrm{w}\text {-}\mathrm{o}}\)) instead of \(S_\mathrm{w} \) as follows:

$$\begin{aligned} J=J_\mathrm{o} \left( {S_{\mathrm{w}\text {-}\mathrm{o}} } \right) =\frac{P_\mathrm{c} }{\gamma cos{\theta }}\sqrt{\frac{k_\mathrm{o} }{{\varphi }_\mathrm{o} }} \qquad 0\le S_{\mathrm{w}\text {-}\mathrm{o}} \le 1 \end{aligned}$$
(5)

where \(k_\mathrm{o}\) is the effective permeability of the ordered pore structure and \({\varphi }_\mathrm{o}\) is its porosity. We elaborate subsequently how the effective transport properties of the ordered pore structure are obtained.

3.1 Transport Properties of Random and Ordered Pore Structures

We determine the transport properties of the ordered pore structure such as permeability and porosity here. This will allow us to implement parameters that are more representative of the pore space invaded during the drainage. For the random pore structure, we will use laboratory measurements available for tight gas sandstones without modification. This is a common practice used for samples with significant intergranular porosity. These measurements give us an estimate of the overall properties that are plausible when the spatial distribution of the pore-throat size on the network is random.

We assume that mercury begins to enter the pore space with ordered pore structure when the wetting phase saturation becomes equal to the threshold value (\(S_\mathrm{w} =S_\mathrm{w}^{*}\)). Thus, the threshold wetting phase saturation is the ratio of the void space accessible to the mercury with ordered pore structure to the total void space as follows:

$$\begin{aligned} S_\mathrm{w}^{*} =\frac{V_{\mathrm{p}\text {-}\mathrm{o}}}{V_\mathrm{p} } \end{aligned}$$
(6)

where \(S_\mathrm{w}^{*}\) is the threshold wetting phase saturation, \(V_{\mathrm{p}\text {-}\mathrm{o}}\) is the pore volume of the ordered pore structure, and \(V_\mathrm{p}\) is the total pore volume. The pore volume of the ordered pore structure is represented by the gray lines in Fig. 3a and the total pore volume is represented by both the gray and the black lines in Fig. 3a. This relation enables us to calculate the effective porosity of the ordered pore space. Porosity, by definition, is the ratio of the void space to the bulk volume. Thus, we can calculate the effective porosity of the ordered pore space as follows:

$$\begin{aligned} {\varphi }_\mathrm{o} =\frac{V_{\mathrm{p}\text {-}\mathrm{o}} }{V_\mathrm{b} }=\frac{V_{\mathrm{p}\text {-}\mathrm{o}} }{V_\mathrm{p} }\times \frac{V_\mathrm{p} }{V_\mathrm{b} }=S_\mathrm{w}^{*} \times {\varphi } \end{aligned}$$
(7)

where \({\varphi }_\mathrm{o}\) is the effective porosity of the ordered pore structure, \(V_{\mathrm{p}\text {-}\mathrm{o}}\) is the pore volume of the ordered pore structure, \(V_\mathrm{b}\) is the bulk volume, \(V_\mathrm{p} \) is the total pore volume, \({\varphi }\) is the total porosity, and \(S_\mathrm{w}^{*}\) is the threshold value

Next, we turn to the calculation of the wetting saturation for the ordered pore structure that is required for plotting the results after scaling. The wetting phase saturation of the ordered pore structure is equal to the ratio of the wetting phase volume to the total pore volume of the ordered pore structure. For this purpose, we use the wetting phase saturation reported for each capillary pressure as follows:

$$\begin{aligned} S_{\mathrm{w}\text {-}\mathrm{o}} =\frac{V_\mathrm{w} }{V_{\mathrm{p}\text {-}\mathrm{o}} }=\frac{V_\mathrm{w} }{V_\mathrm{p} }\times \frac{V_\mathrm{p} }{V_{\mathrm{p}\text {-}\mathrm{o}} }=\frac{S_\mathrm{w} }{S_\mathrm{w}^{*}} \end{aligned}$$
(8)

where \(S_{\mathrm{w}\text {-}\mathrm{o}} \) is the wetting saturation of the ordered pore structure, \(V_\mathrm{w} \) is the wetting phase volume, \(V_{\mathrm{p}\text {-}\mathrm{o}} \) is the pore volume of the ordered pore structure, \(V_\mathrm{p} \) is the total pore volume, \(S_\mathrm{w}\) is the wetting phase saturation, and \(S_\mathrm{w}^{*}\) is the threshold wetting phase saturation. \( S_{\mathrm{w}\text {-}\mathrm{o}} \) is equal to unity, or 100 %, when the drainage in the ordered pore structure starts (Fig. 3b) and becomes equal to zero when the pore space is fully occupied by the nonwetting phase (Fig. 3e).

Next, we derive a relation for the effective permeability of the ordered pore structure by accounting for the spatial distribution of the pores, their characteristic sizes, and the effective porosity. For this purpose, we consider the pressure distribution of the pore space when mercury enters the ordered pore structure. The pressure is higher in the random pore model (\(P_\mathrm{h}\)) and lower in the ordered pore model (\(P_\mathrm{l}\)). Figure 4 shows the corresponding pressure distribution; black arrows indicate the flow directions. Considering the flow directions allows us to calculate the effective permeability of the ordered pore structure, in a manner similar to that of Purcell (1949), as follows:

$$\begin{aligned} k_{\mathrm{e}\text {-}\mathrm{o}}={\varphi }_\mathrm{o} \mathop \sum \limits _{S_{\mathrm{w}\text {-}\mathrm{o}} =1}^0 k_i \Delta S_{\mathrm{w}\text {-}\mathrm{o}} ={\varphi }_\mathrm{o} \mathop \sum \limits _{S_{\mathrm{w}\text {-}\mathrm{o}} =1}^0 \frac{r_i^2 }{8}\Delta S_{\mathrm{w}\text {-}\mathrm{o}} =\frac{{\varphi }_\mathrm{o}}{S_\mathrm{w}^{*} }\mathop \sum \limits _{S_\mathrm{w} =S_\mathrm{w}^{*}}^0 \frac{r_i^2 }{8}\Delta S_\mathrm{w} \end{aligned}$$
(9)

where \(k_{\mathrm{e}\text {-}\mathrm{o}}\) is the effective permeability of the ordered pore structure, \({\varphi }_\mathrm{o}\) is the effective porosity of the ordered pore structure, \(\Delta S_\mathrm{w}\) is the change in wetting phase saturation, and \(r_{i}\) is the characteristic size of the pores accessed at each capillary pressure, which is calculated using the Young–Laplace relation. In the present study, we determine the change in wetting phase saturation from the change in mercury saturation injected into the sample during the drainage experiment (\(\hbox {wetting phase saturation} = 1-\hbox {mercury saturation}\)).

Fig. 4
figure 4

Pressure distribution in tight gas sandstones when nonwetting phase flows from high pressure (\(P_\mathrm{h}\)) to low pressure (\(P_\mathrm{l}\)). Black arrows show the flow directions from random pore structure to the ordered pore structure, which are used for permeability calculation (Eq. 9)

Full size image

In the ordered pore structure, the accessibility of the nonwetting phase to the pores is not limited (Fig. 3b). This unlimited accessibility is the reason that the effective permeability of the ordered pore structure is equal to that of the bundle-of-tubes model (Purcell 1949). The ordered pore structure, as defined in this study, is not necessarily equivalent to the bundle-of-tubes model because the pores in the ordered pore structure do not necessarily form connected-through paths, unlike the bundle of tubes. Compare the flow paths indicated by the black arrows in Fig. 4 with the flow paths in the bundle of tubes.

4 Results

We evaluate the importance of pore structure effect for the J-function here. We first determine the J-function without modification, using the traditional approach, where the results are presented with wetting phase saturation. We then implement the pore structure effect by decomposing the J-function and compare the results of the two methods.

We begin by calculating the J-function using the traditional approach where the effect of pore structure is neglected. We use the drainage data shown in Fig. 2 for this calculation, and in Fig. 5 we present the results for three sets of samples. The scaled results converge at high wetting phase saturations where there is a minimum scatter in the scaled results, but there is a significant scatter at low wetting phase saturations. The ratios of the highest to lowest values are equal to 13, 5, and 8 for sets 1, 2, and 3, respectively. The pore structure is random at high wetting phase saturation and changes to ordered at low wetting phase saturations. This reveals that the J-function fails to capture the scaled capillary pressures at low wetting phase saturation when we do not account for the effects of pore structure.

Fig. 5
figure 5

J-function presentations of the drainage results shown in Fig. 2 without accounting for the effect of the pore structures. There is a significant scatter in the scaled results at low wetting phase saturation corresponding to the ordered pore structure

Full size image

Next, we implement the pore structure effect on the J-function. We first identify the threshold wetting phase saturation \((S_\mathrm{w}^{*} )\) at which the pore structure changes from random to ordered in drainage. At this threshold, the trend of capillary pressure variation with wetting phase saturation changes from plateau-like to exponential as the wetting phase saturation decreases. These threshold wetting phase saturations of different samples are listed in Table 2 and shown in blue in Fig. 2.

We should emphasize that the data used in this study are for real samples, and thus, the prefect exponential trend may not be observed. The samples were provided by different groups for measurement (Byrnes et al. 2009), presumably from different places, which is why they are listed as sets 1, 2, and 3 here. We do not sort them to improve the results and only analyze the measurements reported. We choose the threshold value that honors the exponential trend when the highest capillary pressure is included. Our main objective is to determine whether we can improve the results by using a threshold value and distinguishing the pore structures. Subsequently, we discuss the sensitivity of the results to the threshold value.

We also calculate the effective permeability and porosity of the ordered pore structure (Table 2) based on the transport properties listed in Table 1. In most cases, the effective permeability of the ordered pore structure (\(k_\mathrm{o}\) in Table 2) is significantly smaller than the measured value (k in Table 1). This means that the ordered pore structure contribution to the effective permeability is negligible. Thus, knowing transport properties of the ordered pore structure is important, not only because of its contribution to the effective permeability (Apourvari and Arns 2016), but also because it can constitute a significant fraction of the pore space. The pore space fraction associated with the ordered pore structure is equal to the threshold wetting phase saturation, when expressed in fraction. This fraction varies from 0.11 to 0.98 and its mathematical average is equal to 0.32. Knowing this fraction, when \(k_\mathrm{o} \) is significantly smaller, also helps us determine which part of the pore space dominates the effective permeability.

The effective permeability of the ordered pore structure is close the measured permeability in few cases and even larger in one case. This is because we do not include the tortuosity effect—often referred to as the formation or the lithology factor in the Purcell model (1949)—in the effective permeability. The tortuosity effect, if included, appears as a tuning factor in the denominator of Eq. 9 and lowers the permeability value. We do not include the tuning factor because our main objective in this study is to determine the pore structure effect on J-function, and we analyze the scatter in the results and not the absolute values. In reality, the effective permeability of the ordered pore structure should be smaller than the values estimated here because it may not form a connected-through path. We have access to the nonconnected-through pores because mercury (nonwetting phase) is injected into a sample which is filled with compressible fluid, like air or mercury vapor, during the drainage experiment. This is different from a condition where the in situ wetting phase, such as brine, is incompressible and may remain in the pore space as irreducible wetting phase saturation.

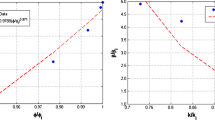
Table 2 Computed petrophysical properties of the ordered pore structure for the samples with petrophysical measurements listed in Table 1 and the drainage data shown in Fig. 2
Full size table

We now calculate the J-function for random and ordered pore structures of tight gas sandstones whose drainage data are shown in Fig. 2. We denote the corresponding functions by \(J_{r}\) and \(J_{o}\). Figures 6 and 7 present the results for random and ordered pore structures, respectively. We observe that there is a minimum scatter where the ratios of the highest to lowest values for the random pore structures are almost equal to unity for all formations. For the ordered pore structures, the ratios are equal to 2, 1, and 3 for sets 1, 2, and 3, respectively. This is a significant improvement over the traditional way of calculating J, in that the ratio of the highest to lowest value is 13. This reveals that the effect of pore structure on the J-function is significant, and we can collapse the data better if we account for that effect.

Fig. 6
figure 6

J-function presentation of tight gas sandstones with random pore structure for samples whose capillary pressure measurements are shown in Fig. 2. There is a minimum scatter in the scaled results

Full size image
Fig. 7
figure 7

J-function presentation of tight gas sandstones with ordered pore structure for samples whose capillary pressure measurements are shown in Fig. 2. The results are significantly improved compared to the traditional presentation of the J function shown in Fig. 3

Full size image

Next, we test the dependency of the results on the threshold value used for J-function calculation. For this, we randomly use different threshold values for the capillary pressures (\(P_{\mathrm{c}\text {-}\mathrm{threshold}}\)) for the samples in Set 2. The threshold capillary pressures are equal to 200, 1200, and 2600 psi, and the computed petrophysical properties are listed in Table 3. The ordered pore structure is invaded when the capillary pressure surpasses the threshold value.

Table 3 Computed petrophysical properties of the ordered pore structure when the threshold capillary pressures (\(P_{\mathrm{c}\text {-}\mathrm{threshold}}\)) are chosen randomly to be equal to 200, 1200, and 2600 psi for different samples in Set 2
Full size table

The threshold wetting phase saturation (\(S_\mathrm{w}^{*}\) in Table 3) decreases with the increase in threshold capillary pressure because a smaller fraction of the void space is uninvaded at a higher capillary pressure. This dependency also lowers the porosity of the ordered pore structure (Eq. 7), leading to higher threshold capillary pressures. We also observe that the permeability of the ordered pore structure (\(k_\mathrm{o}\)) is a function of the threshold capillary pressure. Higher capillary pressure corresponds to a narrower pore throat, based on the Young–Laplace equation, and this leads to a lower permeability. Thus, the petrophysical properties of the ordered pore structure depend on threshold value because they are representative of different fractions of the pore space depending on the adopted threshold value.

Now, we turn to the dependency of the J-function on the computed petrophysical properties. Figure 8 shows the results for different samples in Set 2. The J-function can capture the drainage data more accurately, where there is less scatter than the original case, especially when a high threshold capillary pressure is used (\(P_{\mathrm{c}\text {-}\mathrm{threshold}}\) = 1200 psi and 2600 psi). This suggests that the computed petrophysical properties are more representative of the ordered pore structure and that their performance improves when evaluated for a higher threshold capillary pressure.

Fig. 8
figure 8

J-function of tight gas sandstones with ordered pore structure for all samples of Set 2. The threshold capillary pressures are randomly chosen to be equal to 200, 1200, and 2600 psi

Full size image

The J-function decomposition enables us to differentiate the pore structures and characterize their transport properties more accurately. The transport properties of each pore structure are important because they dictate the overall transport properties of the formation. One example of this is the ultimate recovery from tight gas sandstone, which depends on the volume fraction and connectivity of the intragranular porosity (Sakhaee-Pour and Bryant 2014).

A better characterization of the pore structures can also have major applications for understanding multiphase flow rates of tight gas sandstones. The relative permeability of tight gas sandstones is a related example, which can be considered in future extensions of this study. We computed the petrophysical properties of the ordered pore structure here. At high capillary pressures, the computed properties are more representative of the ordered pore space than the original core-plug measurements because they explain the signature of the capillary pressure versus wetting phase saturation curve. Our model is different from network models that are based on high-resolution images, where a sub-core-scale volume is considered, because our model captures the core-scale measurements.

The tight gas sandstone samples analyzed in this study are water wet. Thus, brine (or water) first fills the ordered pore structure and gas occupies the random pore structure under capillary equilibrium conditions. The ordered pore structure is associated with narrower pore throats, and the random pore structure is accessible from wider pore throats. Hence, the transport properties of the wetting phase at the pore scale are controlled by the ordered pore structure, which can be estimated as described in the present study, whereas standard laboratory measurements seem realistic for the random pore structure.

5 Conclusions

In this study, we have for the first time decomposed the J-function to account for the effect of pore structure. The importance of pore structure for the J-function was mentioned in earlier studies, but was never evaluated systematically. To decompose the J-function, we interpreted the pore structures of connected pores in tight gas sandstones from mercury intrusion capillary pressure measurements (drainage) under confined boundary conditions. We then determined the effective transport properties (permeability, porosity, and wetting phase saturation) of the interpreted pore structures from laboratory measurements. In future works, it may become possible to test the interpreted pore structures by observing the three-dimensional pore space directly using experimental techniques such as nuclear magnetic resonance (NMR) imaging, X-ray computed tomography (XRCT), and focused ion beam and scanning electron microscopy (FIBSEM) imaging.

Implementing the effect of the pore structure on the J-function enabled us to capture the capillary pressures more accurately where there is a minimum scatter in the scaled results. We used the ratio of the highest to lowest values of the J-function to test the proposed method. With the traditional approach, the ratios are equal to 13, 5, and 8 for three tight formations. Those numbers reduce to 2, 1, and 3 when the effect of pore structure is implemented. This study provides a better way to collapse data from a set of measurements by accounting for the pore structure effect.