1 Introduction

The onset of convection, induced by applied thermal or salinity gradients, is commonly referred to as the Rayleigh-Bénard problem (for a fluid clear of solid material) or the Horton–Rogers–Lapwood problem (for a porous medium). The double-diffusive extension in each case has been extensively studied, and it is well known that oscillatory convection can generally result when the faster diffusing component (commonly heat) is destabilizing and the slower diffusing component (commonly salt) is stabilizing. It is also known that in the case when the perturbation concentrations of each component are subject to isoflux boundary conditions, the instability appears at zero wave number (Nield 1967, 1968). However, the authors are not aware of any detailed investigation of how the oscillatory instability is affected by the critical wave number being zero. The purpose of this note was to discuss this matter on the basis of an analytical investigation supplemented by numerical calculations.

2 Analysis and Discussion

With possible future extensions to multi-diffusive convection in mind, we formulate the problem in a general manner, based on the Brinkman model for a porous medium. The case of a Newtonian fluid clear of solid material can be dealt with as a special limiting case of the general scheme. Thus, our general conclusions apply to a clear fluid as well as to a porous medium. We confine ourselves to linear instability, and so the quadratic convective inertial terms in the momentum equation are irrelevant and so can be neglected from the start.

We denote dimensional quantities by asterisks. We adopt a Cartesian coordinate system with the \(z^{*}\)-axis oriented vertically upwards. The Darcy velocity is denoted by \(\mathbf{v}^{*}= (u^{*},v^{*},w^{*})\). The fluid is assumed to be incompressible and so the mass conservation equation is

$$\begin{aligned} \nabla ^{*}\cdot \mathbf{v}^{*}=0. \end{aligned}$$
(1)

We consider two diffusing solutal components (labeled in order of decreasing diffusivities) whose concentrations are \(C_{1}^{*}\) and \(C_{2}^{*}\). The Oberbeck-Boussinesq approximation is adopted, and the momentum equation is taken to be

$$\begin{aligned} \frac{\rho _0 }{\phi }\frac{\partial \mathbf{v}^{*}}{\partial t^{*}}=-\nabla ^{*}p^{*}+\mu _\mathrm{e} \nabla ^{*^{2}}\mathbf{v}^{*}-\frac{\mu }{K}{} \mathbf{v}^{*}+\rho _0 \left[ {1-\sum _{i=1}^2 {\beta _i (C_i^{*}-C_{i0} )} } \right] \mathbf{g} \end{aligned}$$
(2)

Here, the subscript 0 denotes a reference quantity (the value at the top of the layer); \(\phi \) and K are the porosity and permeability of the medium; \(t^{*}\) is the time; \(p^{*}\), \(\rho \), and \(\mu ^{*}\) are the fluid pressure, density, and viscosity, respectively; \(\mu _\mathrm{e}\) is an effective viscosity; the factors \(\beta _{i}\) are solutal expansion coefficients; and g denotes the gravitational acceleration. (Note that we have used the sign convention adopted in Nield and Bejan (2013), one for which the coefficients \(\beta _{i}\) have negative values in most practical situations. This allows solutal Rayleigh numbers to appear in a symmetric fashion with a thermal Rayleigh number in the following analysis. In each case, a positive Rayleigh number characterizes a destabilizing effect.)

The solutal mass conservation equations are

$$\begin{aligned} \phi \frac{\partial C^{*}_i }{\partial t^{*}}+\mathbf{v}^{*}\cdot \nabla ^{*}C_i^{*}=\kappa _i \nabla ^{{*}^{2}}C_i^{*},\quad i=1,2, \end{aligned}$$
(3)

where \(\kappa _{i}\) is the REV averaged diffusivity of the i-th component.

We study a layer of depth H, with bottom at \(z^{*} = 0\). We suppose that each boundary is rigid and impermeable. We examine the stability of a diffusive solution in which the concentrations at the boundaries are specified for the basic solution, but for the perturbations they are subject to isoflux boundary conditions. Hence, for the basic solution, we impose boundary conditions as follows.

At \(z^{*}=0\),

$$\begin{aligned} \mathbf{v}^{*}=0, C_i^{*}=C_{i0} +\Delta C_i ,\quad i=1,2; \end{aligned}$$
(4)

at \(z^{*} = H\),

$$\begin{aligned} \mathbf{v}^{*}=0, C_i^{*}=C_{i0},\quad i=1,2. \end{aligned}$$
(5)

We now put the equations in dimensionless form by introducing scalings as follows.

$$\begin{aligned} \mathbf{x}=\mathbf{x}^{*}/H, t=t^{*}\nu /H^{2}, \mathbf{v}=\mathbf{v}^{*}H/\nu , p=p^{*}K/(\mu \nu ) , C_i =\left( C_i^{*}-C_{i0} \right) /\Delta C_i . \end{aligned}$$
(6)

Here,

$$\begin{aligned} \nu = \mu /\rho _{0} \end{aligned}$$
(7)

is the kinematic viscosity. The differential equations become

$$\begin{aligned}&\displaystyle \nabla \cdot \mathbf{v}=0, \end{aligned}$$
(8)
$$\begin{aligned}&\displaystyle c_a \frac{\partial \mathbf{v}}{\partial t}=-\nabla \tilde{p}+{Da}\nabla ^{2}{} \mathbf{v}-\mathbf{v}+\sum _{i=1}^2 {\frac{Ra_i }{Sc_i }C_i \mathbf{e}_z } , \end{aligned}$$
(9)
$$\begin{aligned}&\displaystyle \phi \frac{\partial C_i }{\partial t}+\mathbf{v}\cdot \nabla C_i =\frac{1}{Sc_i }\nabla ^{2}C_i ,\quad i=1,2, \end{aligned}$$
(10)

where we have introduced an acceleration coefficient \(c_{a}\), a Darcy number Da, some solutal Rayleigh numbers \(Ra_{i}\), and some Schmidt numbers \(Sc_{i}\) defined by

$$\begin{aligned} c_{a} =\frac{K}{\phi H^{2}\nu },\, {Da}=\frac{\mu _\mathrm{e} K}{\mu H^{2}},\,{Ra}_i =\frac{\rho _0 g\beta _i KH\Delta C_i }{\mu \kappa _i },\hbox { Sc}_i =\frac{\nu }{\kappa _i }. \end{aligned}$$
(11)

The symbol \(\tilde{p}\) has been chosen to denote an excess pressure above a hydrostatic pressure relative to a suitably chosen reference value. (If the diffusing quantity is heat, then the usual term would be Prandtl number rather than Schmidt number.)

Note that \(c_{a} =\frac{\mu }{\phi \mu _\mathrm{e} }{Da}\approx {Da}\).

The equations are satisfied by the steady-state diffusive basic solution

$$\begin{aligned} \mathbf{v}_{b} =0,C_{i b} =-z,\quad i=1,2. \end{aligned}$$
(12)

We now perturb this solution and write

$$\begin{aligned} \mathbf{v}_b =\mathbf{v}_{b} +\mathbf{v}^{\prime },\tilde{p}=\tilde{p}_{b} +{\tilde{p}}^{\prime },\, C_{i b} =C_{i b} +{C}^{\prime }_i ,\quad i=1,2, \end{aligned}$$
(13)

where the primes denote small perturbation quantities. We substitute these expressions into Eqs. (8)–(10) and linearize the equations to obtain

$$\begin{aligned}&\displaystyle \nabla \cdot {\mathbf{v}}^{\prime }=0, \end{aligned}$$
(14)
$$\begin{aligned}&\displaystyle c_a \frac{\partial {\mathbf{v}}^{\prime }}{\partial t}=-\nabla {\tilde{p}}^{\prime }+{Da}\nabla ^{2}{\mathbf{v}}^{\prime }-{\mathbf{v}}^{\prime }+\sum _{i=1}^2 {\frac{Ra_i }{Sc_{{ i}} }{C}^{\prime }_i \mathbf{e}_z } , \end{aligned}$$
(15)
$$\begin{aligned}&\displaystyle \phi \frac{\partial {C}^{\prime }_i }{\partial t}+{\mathbf{v}}^{\prime }\cdot \nabla C_{i b} =\frac{1}{Sc_i }\nabla ^{2}{C}^{\prime }_i ,\quad i=1,2. \end{aligned}$$
(16)

We now eliminate the pressure by operating on Eq. (15) with curl curl and using the operator identity \(\hbox {curl curl }\equiv \hbox {grad div }-\nabla ^{2}\), using Eq. (14), and finally taking the z-component. The result is

$$\begin{aligned} c_{a} \frac{\partial \nabla ^{2}{w}^{\prime }}{\partial t}={Da}\nabla ^{2}\nabla ^{2}{w}^{\prime }-\nabla ^{2}{w}^{\prime }+\sum _{i=1}^2 {\frac{Ra_i }{Sc_i }\nabla _H^{2}{C}^{\prime }_i } , \end{aligned}$$
(17)

where \(\nabla _H^{2}\equiv \partial ^{2}/\partial x^{2}+\partial ^{2}/\partial y^{2}\).

At this stage, we introduce isoflux solutal perturbation boundary conditions. We suppose that Eqs. (16) and (17) are to be solved subject to

$$\begin{aligned} {w}^{\prime }=0,\quad \frac{\partial {w}^{\prime }}{\partial z}=\hbox {0, }\frac{\partial {C}^{\prime }_i }{\partial z}=0,\quad \hbox { at }z=\hbox {0 and at }z=1. \end{aligned}$$
(18)

The limiting case of a Darcy porous medium is obtained by setting \(Da = 0\) and \(c_{a}=0\). In this case, the second equality in Eq. (18) (incorporating a no-slip condition) needs to be dropped.

The limiting case of a fluid clear of solid material is obtained by replacing Ra by the product Da Ra, setting \(\mu _\mathrm{e} =\mu ,\phi =1\), and then letting Da tend to infinity.

For the linear stability problem, we write

$$\begin{aligned} \left( {w}^{\prime },{C}^{\prime }_i\right) =[W(z),\Gamma (z)]\hbox { exp}(st+ilx+imy). \end{aligned}$$
(19)

On substitution in Eqs. (16)–(19), we get

$$\begin{aligned}&c_{a} s(D^{2}-a^{2})W=Da(D^{2}-a^{2})^{2}W-(D^{2}-a^{2})W-\sum _{i=1}^2 {\frac{Ra_i }{Sc_i }a^{2}\Gamma _i } , \end{aligned}$$
(20)
$$\begin{aligned}&\phi s\Gamma _i -W=\frac{1}{Sc_i }(D^{2}-a^{2})\Gamma _i ,{\quad } i=1,2, \end{aligned}$$
(21)
$$\begin{aligned}&W=0, Da DW=0,D\Gamma _i =0,\quad \hbox { at }z=\hbox {0 and at }z=1. \end{aligned}$$
(22)

(The second condition in Eq. (22) is to be dropped when \(Da=0\).)

We now confine our attention to the Darcy model that is case where \(Da=0\) (and hence \(c_{a}=0\)). For a qualitative investigation, we use a single-term Galerkin approximation. The natural trial functions to use are the lowest order polynomials that satisfy the boundary conditions exactly. Accordingly, we introduce

$$\begin{aligned} W_T =z-z^{2},\Gamma _{1T} =1,\Gamma _{2T} =1. \end{aligned}$$
(23)

(A reviewer pointed out that this choice of velocity trial function is apt because the leading order shape of the disturbance velocity profile takes this quadratic form for the present problem.)

For the onset of oscillatory convection, the real part of s is zero, and so we write \(s=i\omega \). Accordingly, we obtain

$$\begin{aligned}&\displaystyle (D^{2}-a^{2})W_T +\sum _{i=1}^2 {\frac{Ra_i }{Sc_i }a^{2}\Gamma _{Ti} } =0, \end{aligned}$$
(24)
$$\begin{aligned}&\displaystyle i\omega \phi Sc_{{i}} \Gamma _{Ti} -Sc_{i} W_T =(D^{2}-a^{2})\Gamma _{Ti},\quad i=1,2. \end{aligned}$$
(25)

We now solve these approximately using the usual procedure (for details, see Section 9.1 of Nield and Bejan 2013), and we omit the details.

This leads to the eigenvalue equation

$$\begin{aligned}&Ra_{1} \left( {1-i\omega \frac{\phi Sc_{2} }{a^{2}}} \right) +Ra_{2} \left( {1-i\omega \frac{\phi Sc_{1} }{a^{2}}} \right) \nonumber \\&\quad =\frac{6}{5}\left( {10+a^{2}} \right) \left( {1-i\omega \frac{\phi Sc_{1} }{a^{2}}} \right) \left( {1-i\omega \frac{\phi Sc_{2} }{a^{2}}} \right) =0. \end{aligned}$$
(26)

The real and imaginary parts of this equation give

$$\begin{aligned}&\displaystyle Ra_{1} +Ra_{2} =\frac{6}{5}\left( {10+a^{2}} \right) \left( {1-\omega ^{2}\frac{\phi ^{2}Sc_{1} Sc_{2} }{a^{4}}} \right) , \end{aligned}$$
(27)
$$\begin{aligned}&\displaystyle i\omega \left\{ {Sc_{2} Ra_{1} +Sc_{1} Ra_{2} -\frac{6}{5}\left( {10+a^{2}} \right) (Sc_{1} +Sc_{2} )} \right\} =0. \end{aligned}$$
(28)

Hence, either \(\omega =0\) and

$$\begin{aligned}&Ra_{1} +Ra_{2} =\frac{6}{5}\left( {10+a^{2}} \right) \end{aligned}$$
(29)

or

$$\begin{aligned} Sc_{2} Ra_{1} +Sc_{1} Ra_{2} =\frac{6}{5}\left( {10+a^{2}} \right) (Sc_{1} +Sc_{2}). \end{aligned}$$
(30)

In either case, \(Ra_{1}\) is minimized when \(a = 0\). We conclude that for non-oscillatory instability, the critical wave number is zero and the stability boundary is given by

$$\begin{aligned} Ra_{1} +Ra_{2} =12\left( {1+\frac{a^{2}}{10}} \right) , \end{aligned}$$
(31)

while for oscillatory instability, the critical wave number is still zero and the stability boundary is given by

$$\begin{aligned} \frac{Sc_{2} }{Sc_{1} +Sc_{2} }Ra_{1} +\frac{Sc_{1} }{Sc_{1} +Sc_{2} }Ra_{2} =12\left( {1+\frac{a^{2}}{10}} \right) , \end{aligned}$$
(32)

with frequency \(\omega \) given by

$$\begin{aligned} \omega ^{2}\frac{\phi ^{2}Sc_{1} Sc_{2} }{a^{4}}=Ra_{1} +Ra_{2} -12, \end{aligned}$$
(33)

provided that the right-hand side of Eq. (33) is positive.

Thus, it appears that oscillatory convection is not ruled out. But what sort of convection is this in which the perturbation concentrations are arbitrary constants? For conservation of the diffusing components, these constants must be zero, and in this case, the perturbation velocity is zero. (A reviewer’s answer to the question is that the disturbances are formally proportional to exp(iax) and therefore have a spatial structure even though the limit as a tends to zero is being considered. He/she also remarked that Eq. (24) shows that the order of magnitude of W is O(\(a^{2})\).)

Given that the expected critical wave number is zero, an asymptotic expansion in terms of a small parameter a is appropriate. Accordingly, we return to Eqs. (20)–(22), and let

$$\begin{aligned} (W,\Gamma _1 ,\Gamma _2 )=(W_0 ,\Gamma _{10} ,\Gamma _{20} )+a^{2}(W_1 ,\Gamma _{11} ,\Gamma _{21} )+a^{2}(W_2 ,\Gamma _{12} ,\Gamma _{22} )+\ldots . \end{aligned}$$
(34)

At order zero, we then have

$$\begin{aligned}&\displaystyle Da D^{4}W_0 -D^{2}W_0 -c_{a} sD^{2}W_0 =0, \end{aligned}$$
(35)
$$\begin{aligned}&\displaystyle \frac{1}{Sc_{1} }D^{2}\Gamma _{10} -\phi s\Gamma _{10} +W_0 =0, \end{aligned}$$
(36)
$$\begin{aligned}&\displaystyle \frac{1}{Sc_{2} }D^{2}\Gamma _{20} -\phi s\Gamma _{20} +W_0 =0, \end{aligned}$$
(37)
$$\begin{aligned}&\displaystyle W_0 =0, Da DW_0 =0,D\Gamma _{10} =0,D\Gamma _{20}=0 \hbox { at } z=\hbox {0 and at }z=1. \end{aligned}$$
(38)

For the case \(Da = 0\), \(c_{a}=0\), Eq. (35) reduces to

$$\begin{aligned} D^{2}W_0 =0, \end{aligned}$$
(39)

and the solution satisfying the boundary conditions is \(W_{0} = 0\). Then, Eq. (36) reduces to

$$\begin{aligned} D^{2}\Gamma _{10} -\lambda _1^{2}\Gamma _{10} =0, \end{aligned}$$
(40)

where \(\lambda _1 =\sqrt{\phi Sc_{1} s}\). The general solution of Eq. (40) is of the form

$$\begin{aligned} \Gamma _{10} =E\cosh \lambda _1 z+F\sinh \lambda _1 z, \end{aligned}$$
(41)

where E and F are arbitrary constants. The boundary conditions require that \(F = 0\) and \(\sinh \lambda _1 =0\). Hence, \(\lambda _1 =0\), and so \(s =0\) and thus \(\omega =0\).

This implies that oscillatory instability is ruled out when \(Da = 0\).

In the case where Da is not zero, the general solution of Eq. (35) is

$$\begin{aligned} W_0 =A+Bz+C\cosh \lambda _0 z+D\sinh \lambda _0 z, \end{aligned}$$
(42)

where \(\lambda _0 =\left( {\frac{1+c_{a} s}{Da}} \right) ^{1/2}\).

After some algebra, one finds that satisfaction of the boundary conditions requires that \(\cosh \lambda _0 =1,\) and hence \(\lambda _0 =0\), a real quantity. Again, the implication is that \(\omega \) must be zero.

(This analysis suggests that there is also something singular about the non-oscillatory instability problem except when Da is infinite, the case of a fluid clear of solid material.)

For a further investigation, we introduce general solutal perturbation boundary conditions. We suppose that Eqs. (16) and (17) are to be solved subject to

$$\begin{aligned} {w}^{\prime }=0,\frac{\partial {w}^{\prime }}{\partial z}=\hbox {0, }\frac{\partial {C}^{\prime }_i }{\partial z}-B_{Li} {C}^{\prime }_i =0,\quad \hbox { at }z=\hbox {0}, \end{aligned}$$
(43)
$$\begin{aligned} {w}^{\prime }=0,\frac{\partial {w}^{\prime }}{\partial z}=\hbox {0, }\frac{\partial {C}^{\prime }_i }{\partial z}+B_{Ui} {C}^{\prime }_i =0,\quad \hbox { at }z=\hbox {1}. \end{aligned}$$
(44)

Here,

$$\begin{aligned}&B_{Li} =HA_{Li} \hbox { and }B_{Ui} =HA_{Ui} , \end{aligned}$$
(45)

where the \(A_{Li}\) and \(A_{Ui}\) are solutal flux coefficients at the lower and upper boundaries, respectively.

The parameters defined by Eq. (45) are commonly called Biot numbers in the case when the diffusing quantity is heat. They take the value zero for the case of constant flux and infinity for the case of constant concentration (or temperature). We will call all of them Biot numbers.

The boundary conditions given by Eq. (22) now generalize to

$$\begin{aligned}&W=0, Da DW=0,D\Gamma _i -B_{Li} \Gamma _i =0,\hbox { at }z=\hbox {0}, \end{aligned}$$
(46)
$$\begin{aligned}&W=0, Da DW=0,D\Gamma _{i} +B_{Ui} \Gamma _i =0,\hbox { at }z=\hbox {1}. \end{aligned}$$
(47)

For simplicity, in this paper we confine ourselves to the case where the four Biot numbers are equal, with value Bi. In this case, the critical wave numbers for oscillatory instability and non-oscillatory instability are the same and can be denoted by \(a_{cr}\). We are interested in the case where Bi is small and consequentially \(a_{cr}\) is also small. We now have the possibility of performing an asymptotic analysis in terms of Bi. To this end, it is convenient to introduce a new length scale so that Bi is moved from the boundary conditions to the differential equations. Accordingly, we now take H / Bi as the length scale and write

$$\begin{aligned} {\tilde{\mathbf{x}}}=Bi\mathbf{x}=Bi\mathbf{x}^{*}/H\hbox { and }\tilde{D}\equiv d/d\tilde{z}. \end{aligned}$$
(48)

The set of Eqs. (24), (25), (46), and (47) becomes

$$\begin{aligned}&\displaystyle c_a s(Bi^{2}\tilde{D}^{2}-a^{2})W=Da(Bi^{2}\tilde{D}^{2}-a^{2})^{2}W-(Bi^{2}\tilde{D}^{2}-a^{2})W-\sum _{i=1}^2 {\frac{Ra_i }{Sc_i }a^{2}\Gamma _i } ,\nonumber \\ \end{aligned}$$
(49)
$$\begin{aligned}&\displaystyle \phi s\Gamma _i -W=\frac{1}{Sc_i }(Bi^{2}\tilde{D}^{2}-a^{2})\Gamma _i ,{\quad } i=1,2, \end{aligned}$$
(50)
$$\begin{aligned}&\displaystyle W=0, Da \tilde{D}W=0,\tilde{D}\Gamma _i -{\Gamma }_i =0,\quad \hbox { at }z=\hbox {0}, \end{aligned}$$
(51)
$$\begin{aligned}&\displaystyle W=0, Da \tilde{D}W=0,\tilde{D}\Gamma _{i} +\Gamma _i =0,\quad \hbox { at }z=\hbox {1}. \end{aligned}$$
(52)

We immediately see that in Eqs. (49) and (50), the highest order derivatives are multiplied by the small parameter and so constitute a singular perturbation problem of sixth order. This is a non-trivial problem whose solution (something that involves boundary layers at both top and bottom surfaces) we are leaving for a future investigation. In the meantime, to attack the problem directly, we have made a numerical investigation.

3 Numerical Investigation and Discussion

For neutral stability, we set \(s=i\omega \), where \(\omega \) is the dimensionless frequency; \(\omega \) must be real and without loss of generality can be taken as nonnegative. We substituted this into Eqs. (20) and (21) and separated these equations into their real and imaginary components. We concentrated on the case \(N=2\). The path described in Straughan (2008), Rees and Bassom (2000), Barletta and Storesletten (2011), and Barletta et al. (2012) was followed. We treated \(Ra_{1}\) as an eigenvalue, and for numerical purposes, we treated \(Ra_{1}\) as a function of z. The statement that \(Ra_{1}\) is in fact a constant then gives the following:

$$\begin{aligned} D Ra_1 =0. \end{aligned}$$
(53)

For the case of \(Da = 0\), the resulting set of equation was solved subject to the following boundary conditions (which were also separated into their real and imaginary components):

$$\begin{aligned}&W=0,D\Gamma _1 -B_{L1} \Gamma _1 =0,D\Gamma _2 -B_{L2} \Gamma _2 =0,\Gamma _1 =1\quad \hbox { at }z=0, \end{aligned}$$
(54)
$$\begin{aligned}&W=0,D\Gamma _2 +B_{U2} \Gamma _2 =0\quad \hbox { at }z=1. \end{aligned}$$
(55)

The last equation in (54) is a normalization constraint for the eigenfunction \(\Gamma _1 \left( z \right) \).

In addition, the following boundary condition at \(z = 1\) was utilized:

$$\begin{aligned} D\hbox {Im}\left( {\Gamma _1 } \right) +B_{U1} \hbox {Im}\left( {\Gamma _1 } \right) =0\quad \hbox { at }z = 1. \end{aligned}$$
(56)

For given values of a and Ra, we solved the resulting boundary value problem by using the Chebfun V4 package (Driscoll et al. 2008; Driscoll 2010) written for MATLAB (MATLAB R2015a, MathWorks, Natick, MA, USA). We then iterated with respect to \(\omega \) (using the MATLAB routine fzero) until the following boundary condition was satisfied:

$$\begin{aligned} D \,\text {Re}\left( {\Gamma _1 } \right) +B_{U1} \,\text {Re} \left( {\Gamma _1 } \right) =0 \quad \hbox { at }z = 1. \end{aligned}$$
(57)

We then varied a until we found the smallest value of Ra. The MATLAB routine fminbnd was used to find the minimum. The values of \(Ra_{1 {cr}}\) and \(a_{cr}\) were thus obtained.

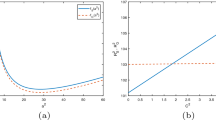
Unfortunately, we found that for the system of Eqs. (49)–(52), we were unable to obtain convergence for values of Bi less than 0.1. However, for the system (20), (21), (53)–(57), we were able deal with Bi as small as 0.000001. Calculations were made for the case \(Da = 0\), \(c_{a}=0\), \(Sc_{1} = 1\), \(Sc_{2} = 10\). Our results indicated that the non-oscillatory instability boundary is given by

$$\begin{aligned}&Ra_{1} +Ra_{2} =Ra_{0} , \end{aligned}$$
(58)

while the oscillatory instability boundary is given by

$$\begin{aligned} \frac{Sc_{2} }{Sc_{1} +Sc_{2} }Ra_{1} +\frac{Sc_{1} }{Sc_{1} +Sc_{2} }Ra_{2} =Ra_{0} , \end{aligned}$$
(59)

with frequency \(\omega \) given by

$$\begin{aligned} \omega ^{2}\frac{\phi ^{2} Sc_{1} Sc_{2} }{a_\mathrm{cr0}^{2}}=-\mu (Bi)\Delta R, \end{aligned}$$
(60)

provided that the right-hand side of Eq. (60) is positive. The general picture of the situation is given in Figure 9.2 of Nield and Bejan (2013).

Here, Ra and \(a_{cr0}\) are the critical Rayleigh number and critical wave number for the mono-diffusive case, with values given in Table 1 (which are more precise than the values presented graphically by Wilkes 1995), while

$$\begin{aligned} \Delta R=\frac{Sc_{1} }{Sc_{1} +Sc_{2} }Ra_{1} +\frac{Sc_{2} }{Sc_{1} +Sc_{2} }Ra_{2} \end{aligned}$$
(61)

and \(\mu (Bi)\) is a factor given approximately by

$$\begin{aligned} \mu =0.38 Bi^{{1/2}}. \end{aligned}$$
(62)

Further, approximately

$$\begin{aligned} a_{cr0} =2.13 Bi^{1/4}. \end{aligned}$$
(63)

Thus,

$$\begin{aligned} \omega \sim \mu ^{1/2}a_{cr0} \sim Bi^{1/2}. \end{aligned}$$
(64)
Table 1 Values of the mono-diffusive critical wave number and critical Rayleigh number for various values of the Biot number Bi
Full size table

4 Conclusions

The imposition of isoflux boundary conditions for the perturbation concentrations leads to a singular solution for the oscillatory instability problem. Formally, oscillatory instability can still occur as Bi tends to zero, but the frequency of oscillation tends to zero. Thus, in practical situations, it is likely that no oscillations will be observed. In this sense, isoflux boundary conditions do indeed inhibit oscillatory double-diffusive convection.