1 Introduction

1.1 Relative Permeability Hysteresis

Two-phase immiscible fluid flow in porous media is important in many applications such as enhanced oil recovery, groundwater management and \(\hbox {CO}_{2}\) sequestration. In these applications, an accurate modeling of the relative permeabilities, and hence the relative flow rates of the different fluid phases, is crucial. The relative permeability is a complicated function of local and nonlocal properties such as the pore-size distribution, pore-space topology (Arns et al. 2004) and flow rate (Nguyen et al. 2006). These dependencies make it difficult to formulate a universal relative permeability model. The relative permeability also depends, among other factors, on both the saturation path and history (Geffen et al. 1951), i.e., it is a hysteretic function of saturation.

The hysteretic behavior of relative permeability also depends on the type of porous medium. Naar et al. (1962) measured the hysteresis curves of nonwetting phase relative permeability versus saturation in consolidated sandstone and glass beads. In consolidated sandstone, they found the nonwetting phase relative permeability during primary drainage (\(k_\mathrm{rn}^{ PD }\)) to be greater than in imbibition (\(k_\mathrm{rn}^{I}\)) at a given saturation. In glass beads, they reported the opposite trend, with \(k_\mathrm{rn}^{I}\) being greater than \(k_\mathrm{rn}^{ PD }\). Similar experimental results were reported in the literature, e.g., Geffen et al. (1951), Raimondi and Torcaso (1964), Oak et al. (1990) for consolidated porous media and Hopkins and Ng (1986) for unconsolidated porous media (see also Jerauld and Salter 1990; Table 1). Interestingly, Colonna et al. (1972) reported a more complex pattern for hysteresis in Hassi R’Mel sandstone. They found that \(k_\mathrm{rn}^{I}\) is larger than \(k_\mathrm{rn}^{ PD }\) close to the turning point saturation (i.e., the saturation at which imbibition starts after primary drainage), but lower than \(k_\mathrm{rn}^{ PD }\) after a certain cross-over saturation.

Several authors have also investigated relative permeability hysteresis numerically using pore-network models. Here, the pore space is modeled by a network of pore bodies connected by pore throats with simplified shapes. Simplified two-phase flow equations in these networks are then solved. Pore-network models have evolved significantly since the pioneering work of Fatt et al. (1956) and recent models have predictive capabilities (Blunt et al. 2002). Jerauld and Salter (1990) investigated relative permeability hysteresis in networks of different aspect ratios (i.e., the pore-body to pore-throat radius ratio). High-aspect-ratio networks represented consolidated porous media, while low-aspect-ratio networks represented unconsolidated porous media. They reproduced qualitatively the relative permeability hysteresis trends observed experimentally in consolidated and unconsolidated porous media. Additionally, they were able to reproduce the complex trend for relative permeability hysteresis observed by Colonna et al. (1972) by employing a network representative of an intermediate aspect-ratio porous medium. In this paper, we aim to show that such complex trends can be better understood by considering the structure of the nonwetting subphases.

1.2 Fluid Subphases and Their Connection to the Relative Permeability

In two-phase flow in a porous medium, the wetting fluid, under strong wettability conditions, may be assumed to always be hydraulically connected due to the presence of wetting fluid films in the crevices of the pore space (Dullien et al. 1986). The nonwetting fluid on the other hand may be present in connected regions or as ganglia surrounded by the wetting fluid. Under the assumption of capillary dominated flow, the fluid in the ganglia does not move and is trapped. The connected nonwetting fluid can be subdivided into two subphases. One subphase occupies dendritic regions or so-called pseudo-dead ends, which are dead-end regions due to the presence of the wetting fluid and not directly due to the pore-space topology. In this paper, we refer to this as the nonwetting dendritic subphase. Under steady state flow conditions, fluid belonging to this subphase is stagnant and hence does not contribute to the relative permeability. The remaining part of the nonwetting connected fluid belongs to the flowing or backbone subphase (see Fig. 1).

Fig. 1
figure 1

a Conceptual illustration of the wetting phase (blue) and the nonwetting phase division into the backbone (red), dendritic (orange) and trapped (yellow) subphases. The gray regions are the solid matrix. b Illustration of the connected nonwetting subnetwork consisting of the backbone (red) and dendritic (orange) subphases. Note that only the backbone subphase contributes to the nonwetting phase flow

Full size image

There are a few experimental works in the literature dealing with the measurement of the backbone and dendritic nonwetting saturations. Raimondi and Torcaso (1964) calculated the backbone and dendritic nonwetting saturation by first establishing a steady state oil–water flow, with oil being the nonwetting phase, in consolidated sandstone cores at several injection ratios. This oil was then displaced by a solvent, miscible with the oil and having matching properties. The oil–solvent production history was then analyzed and used to determine indirectly the backbone, the dendritic and the trapped nonwetting saturations. Stalkup (1970) used a similar experimental setup to calculate the oil subphases. However, he analyzed the oil–solvent production history by using a capacitance–dispersion model, which included the backbone fraction as one of its parameters. The parameters of the model were then tuned to match the observed production history. Using a similar method, Salter et al. (1982) inferred the backbone and dendritic saturations for a wide range of fractional flows in primary drainage, primary imbibition and secondary drainage cycles. However, the aforementioned studies did not investigate backbone and dendritic saturations for drainage and imbibition scanning cycles.

Several existing relative permeability hysteresis models attribute the hysteresis only to nonwetting phase trapping during imbibition (Carlson 1981; Killough 1976) (see also Joekar-Niasar et al. 2013 for a recent review of trapping models). However, such models are not able to qualitatively capture the hysteretic behavior of relative permeability in unconsolidated porous media as they predict \(k_\mathrm{rn}^{I}<k_\mathrm{rn}^{ PD }\). They do not take into account the dendritic or backbone subphases, even though this is a crucial step in understanding the hysteretic relation between the relative permeability and phase saturation. Referring to the state of existing relative permeability models at the time, Larson et al. (1981) stated that “...isolated and dead-end saturations play important roles in the relative permeability story. Thus tortuous capillary tube models may yield useful empirical formulas, but it must be concluded that they contribute little to real understanding of two-phase flow in porous media.”

A nonhysteretic relation between the nonwetting backbone saturation and the relative permeability obtained from different 3D pore networks has been reported by Jerauld and Salter (1990). This suggests that a relative permeability hysteresis model based on the evolution of the backbone saturation can be formulated. Such a model has not been, to the knowledge of the authors, reported in the literature. It has to be mentioned that Larsen and Skauge (1998), and Van Kats and Duijn (2001) highlight the significance of the backbone saturation, but they did not use it for closure of their relative permeability hysteresis models.

1.3 Objectives and Structure

The main objective of this work is to model and gain insight into relative permeability hysteresis phenomena through a study of nonwetting subphase evolution. A macroscopic two-phase flow modeling framework is introduced in Sect. 2, which requires constitutive relations for the volume transfer between the nonwetting subphases. In order to motivate and derive these constitutive relations, experimental data are required. However, due to the difficulty in obtaining the required data experimentally, we employ a pore-network model which is briefly described in Sect. 3. In addition to networks similar to those used by Jerauld and Salter (1990), we employ a more realistic pore network representing a Berea sandstone to investigate the evolution of the nonwetting subphases. We emphasize that in this work we do not consider a comparison between measured and simulated pore-scale data, but we rely on the pore network simulations as a representative substitute for experiments. The results of pore-network simulations for imbibition and drainage scanning cycles are presented in Sect. 4. Next, in Sect. 5, insight gained from these simulations is then used to propose models for the volume transfer between the nonwetting subphases. The evolution of the nonwetting subphases can then be computed, making it possible to formulate the nonwetting relative permeability as a function of backbone saturation. The proposed models are calibrated and validated in Sect. 6.

2 Two-Phase Flow Framework

We consider incompressible immiscible two-phase flow in a rigid porous medium. A strongly wetted system is assumed with a contact angle of 0 for both drainage and imbibition. The capillary number is assumed to be sufficiently low such that the capillary forces dominate the viscous forces, and hence we do not consider rate effects. Let \(S_\mathrm{n}=S\) and \(S_\mathrm{w}=1-S\) denote the nonwetting and wetting phase saturations, respectively. Neglecting gravity and assuming that Darcy’s law for two-phase flow holds, the mass conservation equation of the wetting and nonwetting phases can be written as (Bear 2013)

$$\begin{aligned} \phi \frac{\partial S_{\alpha }}{\partial t}-\frac{\partial }{\partial x_{i}}\left( \frac{K}{\mu _{\alpha }}k_{r\alpha }\frac{\partial P_{\alpha }}{\partial x_{i}}\right) =0, \end{aligned}$$
(2.1)

where \(\alpha =n\) denotes the nonwetting and \(\alpha =w\) the wetting phase. Here, \(\phi \) is the porosity of the porous medium, K is the absolute permeability, and \(P_{\alpha }\), \(\mu _{\alpha }\) and \(k_{r\alpha }\) are the pressure, viscosity and relative permeability of phase \(\alpha \), respectively. For the macroscopic capillary pressure

$$\begin{aligned} P_\mathrm{c}(S)=P_\mathrm{n}-P_\mathrm{w}, \end{aligned}$$
(2.2)

a common algebraic relation can be employed; see, for example, (Parker and Lenhard 1987). In this paper, we will mainly focus on obtaining a model for \(k_\mathrm{rn}\) based on the evolution of the nonwetting subphases.

2.1 Fluid Subphases

In a previous theoretical work by Hilfer (2006), the nonwetting and wetting fluid phases were each divided into a continuous hydraulically connected subphase and a trapped nonpercolating subphase. In the framework proposed here, the nonwetting continuous subphase is further subdivided into a backbone and dendritic subphase (see Fig. 1), and the wetting phase is assumed to always form a continuous phase. In a given representative elementary volume (REV) (Bear 2013), the backbone subphase consists of the nonwetting fluid in all pores which can be connected to both inlet and outlet boundaries of the REV by at least two independent paths through the nonwetting fluid. The dendritic or “dead-end” subphase consists of all the stagnant nonwetting fluid which is connected to the rest of the backbone through only one independent nonwetting flow path and is blocked due to the presence of the wetting phase. The trapped subphase consists of all nonwetting fluid completely surrounded by the wetting fluid. Note that we do not consider nonwetting ganglion dynamics here although they may contribute to the net transport of the nonwetting phase even at low capillary numbers. Rücker et al. (2015) imaged pore-scale displacements of oil and brine during imbibition in a sandstone rock using X-ray computed microtomography. They showed that snap-off events can trigger nonwetting filling events due to induced local pressure gradients. However, they were not able to quantify the contribution of the resultant ganglia mobilization to the net nonwetting phase flow.

The wetting fluid, under strong wettability conditions, is assumed to always form a continuous phase at all saturation values. Nevertheless, the wetting fluid may also be divided into three separate subphases: a backbone subphase which contributes the most to the hydraulic conductance; a “film flow” subphase which occupies the crevices of pores occupied by the nonwetting phase; and a dendritic subphase which connects the film and the backbone subphase regions. However, we will not consider this problem any further here.

The total nonwetting phase saturation can be written as

$$\begin{aligned} S_\mathrm{n}=S=S_\mathrm{b}+S_\mathrm{d}+S_\mathrm{t}, \end{aligned}$$
(2.3)

where \(S_\mathrm{b}\), \(S_\mathrm{d}\) and \(S_\mathrm{t}\) are the backbone, dendritic and trapped subphase saturations, respectively. The connected nonwetting saturation is given by

$$\begin{aligned} S_\mathrm{c}=S_\mathrm{b}+S_\mathrm{d}. \end{aligned}$$
(2.4)

A few comments on the size of the REV are in order. We have implicitly assumed the existence of an REV, the size of which satisfies both a lower and an upper bound. The lower bound is required to ensure that the REV is sufficiently large such that the subphase saturations are independent of the size of REV. In particular, what might appear to be part of the connected subphase at a particular REV size may be part of the trapped subphase for a larger REV. Results from percolation theory (see eg. Stauffer and Aharony 1994) predict that the error made in computing the residual trapped nonwetting subphase in a finite, as opposed to an infinite, window scales with \(L^{-(1+\beta )/\nu }\) (Wilkinson 1986) where \(\beta \) and \(\nu \) are percolation exponents and L is the REV size. Assuming the values \(\beta =0.43\) and \(\nu =0.88\) (Sahimi 1988) are universal for three dimensional systems, the trapped saturation error scales as \(S_\mathrm{t}^{\varepsilon }\sim L^{-1.625}\), and the chosen lower bound for the REV should be such that this error is negligible. On the other hand, an upper bound for the REV size is required such that the macroscale capillary pressure \(\overline{Ca}\) and macroscopic gravillary number \(\overline{Gl}\) (Hilfer and Øren 1996) are negligibly small. This ensures that the viscous pressure drop and gravitational pressure drop across the REV are negligible compared to the capillary pressure, and hence capillary equilibrium within the REV can be assumed.

Fig. 2
figure 2

Conceptual illustration of the evolution of the wetting phase (blue) and the backbone (red), dendritic (orange) and trapped (yellow) nonwetting subphases during drainage. The dashed ellipses highlight changes in the fluid–fluid interface. The flow direction is from bottom to top. a Hypothetical scenario at the beginning of drainage. b Direct increase in the dendritic subphase saturation due to increase in nonwetting phase saturation. c Direct increase in the backbone subphase saturation due to increase in nonwetting phase saturation. d Transfer of dendritic subphase volume to backbone subphase volume. e Transfer of trapped subphase volume to dendritic subphase volume. f Transfer of dendritic subphase volume to backbone subphase volume. The previously trapped region shown in d is now part of the backbone subphase

Full size image

2.2 Nonwetting Subphase Evolution

During drainage, the nonwetting saturation increases and its constituent subphase saturations evolve with volume being transferred between the subphases. An increase in the nonwetting saturation can result in a direct increase in both the dendritic (see Fig. 2a, b) and the backbone (see Fig. 2b, c) subphase saturations. By ’direct’ we mean that the volume previously occupied by the wetting phase is transferred to a particular nonwetting subphase without initially being transferred to another nonwetting subphase. Additionally, a small increase in the nonwetting phase volume may cause a transfer of a larger volume from the dendritic to the backbone subphase (see Fig. 2c, d). Moreover, previously trapped nonwetting ganglia can get untrapped (see Fig. 2d, e). If we assume that only one pore-scale event may occur instantaneously, a volume of trapped nonwetting phase is transferred to the dendritic subphase first, and can only become part of the backbone subphase when another fluid path is established after further drainage (see Fig. 2e, f).

Similarly, during imbibition, the nonwetting phase decreases, which can cause a decrease in the dendritic subphase and backbone subphase saturations, transfer of backbone subphase volume to the dendritic subphase, and trapping of connected nonwetting phase volume due to either piston-type displacements or snap-off. The evolution of the nonwetting subphases may be described by the following equations:

$$\begin{aligned}&\displaystyle \phi \frac{\partial S_\mathrm{b}}{\partial t} = \lambda \phi \frac{\partial S}{\partial t}+Q_{\mathrm{d}-\mathrm{b}}, \end{aligned}$$
(2.5)
$$\begin{aligned}&\displaystyle \phi \frac{\partial S_\mathrm{d}}{\partial t} = \left( 1-{\lambda }\right) \phi \frac{\partial S}{\partial t}-Q_{\mathrm{d}-\mathrm{t}}-Q_{\mathrm{d}-\mathrm{b},} \end{aligned}$$
(2.6)
$$\begin{aligned}&\displaystyle \hbox {and}\,\,\,\,\phi \frac{\partial S_\mathrm{t}}{\partial t} = Q_{\mathrm{d}-\mathrm{t}} \end{aligned}$$
(2.7)

for the nonwetting subphase saturations. Note that any one of these equations is redundant due to Eq. (2.3). Here, the function \(\lambda \) is the fraction of the nonwetting saturation change due to a direct change in backbone subphase saturation, and \(Q_{\beta _{1}-\beta _{2}}\) is the rate of volume transfer from subphase \(\beta _{1}\) to subphase \(\beta _{2}\), e.g., \(Q_{\mathrm{d}-\mathrm{t}}\) is the rate of volume transfer from the dendritic to the trapped subphase (see Fig. 3). These equations are solved together with Eq. (2.1), from which we obtain the saturation rate \(\frac{\partial S}{\partial t}\). If, in addition to the phase relative permeabilities \(k_{r\alpha }\) and the macroscopic capillary pressure \(P_\mathrm{c}\), the source terms \(Q_{\beta _{1}-\beta _{2}}\) and the function \(\lambda \) are provided, one obtains a closed system.

Fig. 3
figure 3

Redistribution of mass among the three subphases. \(Q_{\beta _{1}-\beta _{2}}\) is the volume transfer rate from subphase \(\beta _{1}\) to subphase \(\beta _{2}\)

Full size image

3 Network Modeling

In order to study the evolution of the nonwetting backbone, dendritic and trapped subphases during imbibition and drainage cycles, a pore-network simulator was implemented. It was used here as a proxy for experiments, i.e., we assumed that the results are representative for real porous media. In this section, we briefly describe the pore networks employed in this work and the algorithm used to simulate drainage and imbibition cycles. We also describe the methods used to extract the subphase saturations and relative permeabilities.

3.1 Network Geometry and Topology

Pore networks are composed of two types of pore elements, i.e., pore bodies and pore throats. In this work, the pore elements were assumed to have an angular cross section, which can be characterized by the shape factor (Mason and Morrow 1991)

$$\begin{aligned} G=\frac{A_\mathrm{tot}}{{P}^{2}}, \end{aligned}$$
(3.1)

where P and \(A_\mathrm{tot}\) are the effective perimeter and the cross-sectional area, respectively. A pore element can be completely occupied by either the wetting phase or contain nonwetting fluid in the center with wetting layers at the corners (see Fig. 5).

Three different pore networks were used. The first two, networks A and B, are structured pore networks with a coordination number of 6 representing consolidated and unconsolidated porous media, respectively. Note that consolidated media, as opposed to unconsolidated media, are characterized by large ratios of average pore-body to pore-throat radii. Following (Jerauld and Salter 1990), the inscribed pore-body and pore-throat radii of networks A and B were sampled from a beta distribution

$$\begin{aligned} f(x)=\frac{x^{a-1}(1-x)^{b-1}}{B(a,b)}, \end{aligned}$$
(3.2)

where a and b are shape parameters and B is a normalization constant. The inscribed radii were then scaled to have a minimum radius of \(r_\mathrm{min}\) and maximum radius of \(r_\mathrm{max}\). The parameters used for networks A and B are shown in Table 1. The pore elements of networks A and B were chosen to be square cross sections, with \(G=1/16\). A fixed pore-to-pore distance of \(160\,\upmu \hbox {m}\) was used. Both networks A and B consist of \(160\times 80\times 80\) pore bodies (160 pore bodies along the general flow direction).

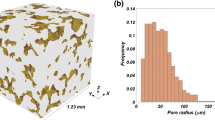
Table 1 Parameters of beta distribution, Eq. (3.2), used to generate the pore elements for the structured pore networks (Jerauld and Salter 1990)
Full size table

In addition to networks A and B, we also employed a pore network, which is more representative of real porous media. A stochastic pore network generator, described in Idowu and Blunt (2010), was used to generate an unstructured pore network representing a Berea sandstone, which we denote here as network C (see Fig. 4). Unlike networks A and B, network C has a distribution of pore-body coordination numbers and pore element shape factors. The statistics of network C are shown in Table 2.

Fig. 4
figure 4

Pore network representative of Berea sandstone produced by the stochastic pore-network generator described in Idowu and Blunt (2010)

Full size image

3.2 Invasion Mechanisms

We simulated drainage–imbibition cycles using a standard invasion percolation algorithm (Wilkinson and Willemsen 1983), which was modified to include snap-off and cooperative pore-filling events during imbibition. During simulation of drainage, the capillary pressure \(P_\mathrm{c}\) is increased. Pore-filling events occur in the order of their increasing threshold capillary pressure. Piston displacement in a pore element, with the nonwetting phase displacing the wetting phase, occurs when the capillary pressure \(P_\mathrm{c}\) exceeds the entry capillary pressure \(P_\mathrm{c}^{e}\) of a given pore element (Øren et al. 1998):

$$\begin{aligned} P_\mathrm{c}>P_\mathrm{c}^{e}=\gamma \frac{1+2\sqrt{\pi G}}{r}. \end{aligned}$$
(3.3)

Here, r is the inscribed radius of a pore element and \(\gamma \) is the interfacial tension between the nonwetting and wetting phases. Note that once a pore throat is occupied, the nonwetting phase can immediately enter the neighboring pore body, since it has a lower entry capillary pressure.

Fig. 5
figure 5

Cross section of a pore element

Full size image
Table 2 Pore-size statistics of network C, generated by the stochastic pore-network generator described in (Idowu and Blunt 2010)
Full size table

During simulation of imbibition, the capillary pressure decreases. The pore-level events occur in order of decreasing threshold capillary pressure. The criterion for the wetting phase to displace the nonwetting phase in a pore throat is

$$\begin{aligned} P_\mathrm{c}<P_\mathrm{c}^{e}. \end{aligned}$$
(3.4)

The criterion for snap-off, i.e., the collapse of the interface in a pore throat, for zero contact angle is given by Øren et al. (1998)

$$\begin{aligned} P_\mathrm{c}<P_\mathrm{c}^{\mathrm{snapoff}}=\frac{\gamma }{r_\mathrm{t}}, \end{aligned}$$
(3.5)

where \(r_\mathrm{t}\) is the inscribed radius of pore throat. Note that snap-off in a pore throat only occurs if piston displacement is not possible as \(P_\mathrm{c}^{\mathrm{snapoff}}<P_\mathrm{c}^{e}\) for a pore throat. The threshold capillary pressure, at which the wetting phase can enter a given pore body through several pore throats (cooperative pore filling) depends on the number of neighboring throats filled with nonwetting fluid (Lenormand et al. 1983). A cooperative pore-filling mechanism of type \(I_{z}\) occurs when z neighboring throats are filled with the nonwetting phase. Following Jerauld and Salter (1990), a simple capillary pressure threshold for the \(I_{z}\) displacement mechanism in a pore body of radius \(r_\mathrm{b}\) is used:

$$\begin{aligned} P_\mathrm{c}<\gamma \frac{1+2\sqrt{\pi G}}{zr_\mathrm{b}}. \end{aligned}$$
(3.6)

3.3 Conductances

In order to compute the relative permeability of a fluid phase, a phase conductance has to be assigned to each pore element. This is calculated following (Bakke and Øren 1997) and the relations are summarized here.

3.3.1 Single-Phase Flow in a Pore Element

When a pore element is completely filled with wetting fluid (single-phase condition), the conductance can be computed as

$$\begin{aligned} g_\mathrm{w}=\frac{r_{H}^{2}A_\mathrm{tot}}{8\mu _\mathrm{w}l}, \end{aligned}$$
(3.7)

where l the length of the pore element and

$$\begin{aligned} r_{H}=\frac{1}{2}\left( r+\sqrt{\frac{A_\mathrm{tot}}{\pi }}\right) \end{aligned}$$
(3.8)

the mean hydraulic radius.

3.3.2 Two-Phase Flow in a Pore Element

When a pore element is filled with both nonwetting and wetting fluid, the wetting and nonwetting cross-sectional areas are

$$\begin{aligned} A_\mathrm{w}=r_\mathrm{w}^{2}\left( \frac{1}{4G}-\pi \right) , \end{aligned}$$
(3.9)

and

$$\begin{aligned} A_\mathrm{n}=A_\mathrm{tot}-A_\mathrm{w}, \end{aligned}$$
(3.10)

respectively. Here, the radius \(r_\mathrm{w}\) quantifies the curvature of the phase interface in the corners, which is given by the Young–Laplace equation

$$\begin{aligned} r_\mathrm{w}=\frac{\gamma }{P_\mathrm{c}}. \end{aligned}$$
(3.11)

Similar as for the wetting phase, the hydraulic conductance of nonwetting fluid in a pore element is given by

$$\begin{aligned} g_\mathrm{n}=\frac{r_{H}^{2}A_\mathrm{n}}{8\mu _\mathrm{n}l}. \end{aligned}$$
(3.12)

The hydraulic conductance of the wetting fluid through the corners of the cross section is

$$\begin{aligned} g_\mathrm{w}=\frac{r_\mathrm{w}^{2}A_\mathrm{w}}{8B\mu _\mathrm{w}l}, \end{aligned}$$
(3.13)

where \(B=5.3\) is a dimensionless resistance factor [see Ransohoff and Radke (1988) for details]. The effective conductance \(g_{\alpha ,ij}\) of phase \(\alpha \) between the centers of pore i and pore j can be computed by the harmonic average

$$\begin{aligned} \frac{1}{g_{\alpha ,ij}}=\frac{1}{g_{\alpha ,k}}+\frac{1}{2}\left( \frac{1}{g_{\alpha ,i}}+\frac{1}{g_{\alpha ,j}}\right) , \end{aligned}$$
(3.14)

where \(g_{\alpha ,k}\) is the conductance of the throat connecting pore i and pore j.

3.4 Computing Relative Permeabilities

To compute the relative permeability in a pore network, we first compute its absolute permeability. A unit pressure difference between inlet and outlet boundaries of a pore network, filled with the wetting phase, is imposed and the resulting mass flux

$$\begin{aligned} Q_\mathrm{tot}=\sum _{i\in {\mathbb {P}}_\mathrm{inlet}}\,\sum _{j\in {\mathbb {P}}_{\mathrm{nghs}(i)}}g_{w,ij}(p_{w,i}-p_{w,j}) \end{aligned}$$
(3.15)

at the inlet is computed. Here, \({\mathbb {P}}_\mathrm{inlet}\) is the set of all pore indices at the inlet and \({\mathbb {P}}_{\mathrm{nghs}(i)}\) are the neighboring pore indices of pore i. To obtain the pressure values \(p_{w,i}\), a linear set of equations for the mass conservation at each pore body, i.e.,

$$\begin{aligned} \sum _{j\in {\mathbb {P}}}g_{w,ij}(p_{w,i}-p_{w,j})=0\quad \forall \,i, \end{aligned}$$
(3.16)

where \({\mathbb {P}}\) is the set of all pore indices, is solved with appropriate Dirichlet boundary conditions. The absolute permeability is then given by (assuming unit pressure difference)

$$\begin{aligned} K=\frac{Q_\mathrm{tot}\mu _\mathrm{w}L_\mathrm{net}}{A_\mathrm{net}}, \end{aligned}$$
(3.17)

where \(A_\mathrm{net}\) is the cross-sectional area of the pore network and \(L_\mathrm{net}\) is its length.

Next, we compute the effective and relative permeability of each phase. From drainage or imbibition simulations, we obtain two-phase configurations in a pore network at several saturation intervals. In order to compute the effective permeabilities for a given two-phase configuration, it is assumed that the interface between the two fluids in the network is frozen. This is justified here as we are considering capillary dominated flow, where the pressure drop in a pore network within each of the two phases can be assumed to be negligible compared to the capillary pressure (Blunt et al. 2002). Each phase \(\alpha \) then forms a separate fixed subnetwork in which the corresponding mass flux \(Q_\mathrm{tot}^{\alpha }\) is computed similarly to the case of single-phase flow. The effective permeability \(K_\mathrm{eff}^{\alpha }\) for phase \(\alpha \) can be obtained from an expression analogous to Eq. (3.17), and relative permeability is then simply

$$\begin{aligned} k_{r\alpha }=\frac{K_{\mathrm{eff}}^{\alpha }}{K}. \end{aligned}$$
(3.18)

3.5 Extracting the Subphase Saturations

The pore network can be represented by a graph \(G=(V,E)\) with vertices V and edges E representing pore bodies and throats, respectively. This allows us to use standard graph-theory algorithms to compute \(S_\mathrm{b}\), \(S_\mathrm{d}\) and \(S_\mathrm{t}\). For this purpose, we have employed the igraph library (Csardi and Nepusz 2006). In the following, we describe how to obtain the subphase saturations.

First, we construct a graph \(G_\mathrm{n}=(V_\mathrm{n},E_\mathrm{n})\) consisting of vertices \(V_\mathrm{n}\) and edges \(E_\mathrm{n}\), which are occupied by the nonwetting phase. This graph may contain several components. A subgraph of \(G_\mathrm{n}\) consisting only of those components which contain inlet vertices, \(G_\mathrm{c}=(V_\mathrm{c},E_\mathrm{c})\), is then obtained by using a cluster algorithm. As a result, we obtain \(\mathbb {P}_\mathrm{c}\) and \({\mathbb {T}}_\mathrm{c}\), the corresponding set of indices of the pore bodies and throats, respectively. The set of trapped pore-body and pore-throat indices is then given by \(\mathbb {P}_\mathrm{t}=\mathbb {P}{\setminus }\mathbb {P}_\mathrm{c}\) and \({\mathbb {T}}_\mathrm{t}={\mathbb {T}}{\setminus }{\mathbb {T}}_\mathrm{c}\), respectively.

Secondly, we obtain \(\mathbb {P}_\mathrm{b}\) and \({\mathbb {T}}_\mathrm{b}\), the set of indices of the pore bodies and throats occupied by the nonwetting backbone subphase. For this purpose, an additional dummy vertex is added to \(G_\mathrm{c}\). Next, edges connecting this dummy vertex to all inlet and outlet boundary vertices contained in \(G_\mathrm{c}\) are added. The backbone can then be obtained by finding the largest bi-connected component of the resulting graph (Kirpatrick 1978). Finally, the set of dendritic pore body and throat indices can be easily obtained by the relations \(\mathbb {P}_\mathrm{d}=\mathbb {P_\mathrm{c}}{\setminus }\mathbb {P}_\mathrm{b}\) and \({\mathbb {T}}_\mathrm{d}={\mathbb {T_\mathrm{c}}}{\setminus }{\mathbb {T}}_\mathrm{b}\), respectively.

At this point, the nonwetting subphase saturations \(S_{\beta }\), \(\beta \in \left\{ b,d,t\right\} \) can be easily obtained. The local nonwetting saturation of each pore body and pore throat is computed by

$$\begin{aligned} S_{i}^{\mathrm{loc}}=\frac{A_{n,i}}{A_{\mathrm{tot},i}}, \end{aligned}$$
(3.19)

where the subscript i denotes the index of a pore body or pore throat and \(A_{n,i}\) is given by Eq. (3.10). The saturation of subphase \(\beta \) is then given by

$$\begin{aligned} S_{\beta }=\frac{1}{v_\mathrm{tot}}\left( \sum _{i\in {{\mathbb {P}}}_{\beta }}S_{i}^{\mathrm{loc}}v_{i} +\sum _{i\in {{\mathbb {T}}}_{\beta }}S_{i}^{\mathrm{loc}}v_{i}\right) , \end{aligned}$$
(3.20)

where \(v_{i}\) is the volume of a pore element and \(v_\mathrm{tot}\) is the total volume of the pore elements in the pore network. In order to reduce boundary effects, a post-processing window extending over 50 % in flow direction around the domain center was considered when computing the relative permeabilities and subphase saturations.

4 Pore-Network Results and Discussion

In this section, pore-network simulation results of several drainage and imbibition scanning cycles are presented. The evolution of the backbone and dendritic nonwetting subphase saturations is first discussed. Next, the evolution of the trapped subphase and its relation with the backbone subphase is considered. A visualization of the subphase evolution is shown in Fig. 6. The nonwetting relative permeability and its hysteretic behavior when plotted against the nonwetting connected and the backbone subphase saturations is then discussed.

Fig. 6
figure 6

Snapshots of the backbone (left column), dendritic (middle column) and trapped (right column) nonwetting subphases during pore-network simulation of a primary drainage–imbibition cycle for network C at three different saturations: a \(S=0.4\) during drainage. b \(S=0.7\) during imbibition. c \(S=0.25\) during imbibition

Full size image

4.1 Connected Subphases

The primary drainage and imbibition curves of the subphase saturations \(S_\mathrm{b}\) and \(S_\mathrm{d}\) for networks A, B and C are shown in Fig. 7. Also shown, in Fig. 8, are the drainage and imbibition scanning curves for \(S_\mathrm{b}\) and \(S_\mathrm{d}\) in network C. As can be observed, the nonwetting dendritic saturation is greater during primary drainage (\(S_\mathrm{d}^\mathrm{max}\)) than during primary imbibition (\(S_\mathrm{d}^\mathrm{min}\)) for a given value of \(S_\mathrm{c}\). This behavior can be explained in terms of the pore-scale invasion mechanisms under the assumptions of capillary dominated flows and fully connected wetting fluid.

Fig. 7
figure 7

Pore-network simulation results: primary drainage and primary imbibition curves of the backbone (solid lines) and dendritic (dashed lines) nonwetting saturations for network A (left), network B (center) and network C (right) versus the nonwetting connected saturation. \(S_\mathrm{d}^{\mathrm{max}}\) and \(S_\mathrm{d}^{\mathrm{min}}\) denote the primary drainage and primary imbibition curves, respectively, for the dendritic nonwetting saturation

Full size image
Fig. 8
figure 8

Pore-network simulation results: drainage (left column) and imbibition (right column) scanning curves of backbone (top row) and dendritic (bottom row) nonwetting subphases for network C. Labels (1–2) and (3–4) denote segments of drainage scanning cycles on saturation reversal

Full size image

During drainage, piston displacements by nonwetting fluid may result in an increase in \(S_\mathrm{d}\), either via reconnection of previously trapped nonwetting fluid or via the direct transfer of volume previously occupied by the wetting phase. On the other hand, piston displacements by nonwetting fluid may also cause the formation of nonwetting connections between two dendritic nonwetting fingers, leading to an increase in \(S_\mathrm{b}\) and decrease in \(S_\mathrm{d}\). The latter event is more likely as \(S_\mathrm{c}\) increases. During imbibition, the wetting fluid can invade nonwetting occupied pore space by three mechanisms: snap-off and piston displacement in pore throats, and cooperative pore displacement in pore bodies (Lenormand et al. 1983). The cooperative pore-filling mechanism of type \(I_{1}\) is the most favorable invasion mechanism in pore bodies (having the highest threshold capillary pressure), while piston displacement is the most favorable invasion mechanism in pore throats. These two mechanisms can only result in a decrease in \(S_\mathrm{d}\). The other less favorable invasion mechanisms which can cause an increase in \(S_\mathrm{d}\), i.e., mechanism \(I_{z}\) with \(z>1\) or snap-off, occur only when the previously two mentioned mechanisms are not topologically possible. This behavior, which is discussed in more detail in Wardlaw and Yu (1988), explains the observed hysteresis of \(S_\mathrm{d}\).

4.2 Trapped Subphase

Figure 9a–c shows imbibition scanning \(S-S_\mathrm{t}\) curves for networks A, B and C. Each scanning cycle starts at a different turning point saturation \(S^{*}\). The maximum trapped saturation increases with \(S^{*}\). Note that a hysteretic \(S-S_\mathrm{t}\) cycle exists for each \(S^{*}\). On the other hand, for any given turning point backbone saturation \(S_\mathrm{b}^{*}\), only very weak hysteretic effects can be observed in the \(S_\mathrm{b}-S_\mathrm{t}\) curves of Fig. 9d–f. Furthermore, when the points on the \(S_\mathrm{b}-S_\mathrm{t}\) curves are normalized by their turning point backbone saturation \(S_\mathrm{b}^{*}\) and their corresponding maximum trapped saturation \(S_\mathrm{t}^{*}\), they appear to collapse on a single curve as shown in Fig. 10.

Fig. 9
figure 9

Pore-network simulation results: imbibition scanning curves showing the dependence of trapped nonwetting saturation on the total (top row) and backbone (bottom row) nonwetting saturations for network A (left column), network B (center column) and network C (right column)

Full size image
Fig. 10
figure 10

Pore-network simulation results: normalized trapped nonwetting saturation \(\hat{S}_\mathrm{t}=\frac{S_\mathrm{t}}{S_\mathrm{t}^{*}}\) versus the normalized backbone nonwetting saturation \(\hat{S}_\mathrm{b}=\frac{S_\mathrm{b}}{S_\mathrm{b}^{*}}\) for network A (left column), network B (center column) and network C (right column). The symbols correspond to scanning cycles starting from \(S^{*}=0.4\) (inverted triangle), \(S^{*}=0.5\) (circle), \(S^{*}=0.6\) (triangle), \(S^{*}=0.7\) (open square), \(S^{*}=0.8\) (cross), and \(S^{*}=0.9\) (right pointing triangle)

Full size image

4.3 Relative Permeability

Shown in Fig. 11 are imbibition scanning curves of \(k_\mathrm{rn}\) versus S, \(S_\mathrm{c}\) and \(S_\mathrm{b}\). The relation between \(k_\mathrm{rn}\) and S for different drainage–imbibition cycles in networks A, B and C is shown in Fig. 11a, d and g, respectively. Significant hysteretic behavior can be observed, and thus it is difficult to find a general constitutive relation for \(k_\mathrm{rn}\) in terms of S. The complexity of the hysteretic behavior is reduced when \(k_\mathrm{rn}\) is plotted against \(S_\mathrm{c}\). As observed in Fig. 11b, \(k_\mathrm{rn}\) can be considered a nonhysteretic function of \(S_\mathrm{c}\) for network A. This is not the case for network B and network C as shown in Figs. 11e and 11h. However, for both of these networks the value of \(k_\mathrm{rn}\) is bounded by the primary drainage and primary imbibition curves.

Fig. 11
figure 11

Pore-network simulation results: imbibition scanning curves showing the dependence of nonwetting relative permeability on total, connected and backbone nonwetting saturations for network A (top row), network B (middle row) and network C (bottom row)

Full size image

Figure 11f shows that, for network B, \(k_\mathrm{rn}\) can be approximated as a nonhysteretic function of \(S_\mathrm{b}\). This is in agreement with results by Jerauld and Salter (1990). For network C, \(k_\mathrm{rn}(S_\mathrm{b})\) is hysteretic as can be seen in Fig. 11i. However, according to the presented results, the error that would be made in assuming that \(k_\mathrm{rn}(S_\mathrm{b})\) is a nonhysteretic function is less than the one made in assuming that \(k_\mathrm{rn}(S_\mathrm{c})\) is a nonhysteretic function, particularly for lower saturations.

It can be seen that, for network C, \(k_\mathrm{rn}(S_\mathrm{b})\) is larger during drainage than during imbibition. Although there is no significant hysteresis, the same trend for \(k_\mathrm{rn}(S_\mathrm{b})\) is observed in Fig. 11c for network A. This may be explained to be due to the higher capillary pressure during drainage than during imbibition. The capillary pressure, according to the network model employed, determines the cross-section area of the wetting and nonwetting fluid in a pore element [see Eqs. (3.9) and (3.10)] and hence the phase conductance. Due to their smaller cross sections, the nonwetting phase conductance and saturation in pore throats are more sensitive to a change in capillary pressure than they are in pore bodies. Furthermore, pore throats in a network have a larger effect on the relative permeability than pore bodies, but contribute less to the total pore volume. Hence increasing the capillary pressure (while maintaining the same phase occupancy in the pore elements) can result in an increase in relative permeability without an appreciable increase in saturation. While we have not considered contact angle hysteresis in this work, it is expected by the same reasoning to contribute to relative permeability hysteresis. As a check, simulations were performed in which the wetting cross-sectional area \(A_\mathrm{w}\) of all nonwetting occupied pore elements was kept constant, resulting in a nonhysteretic \(k_\mathrm{rn}(S_\mathrm{b})\) for network C (results not shown here).

5 Modeling of Volumetric Transfer Rates

In this section, we will propose models for the volume transfer rates between the subphases \(Q_{\alpha -\beta }\) and function \(\lambda \) which were introduced in Sect. 2. Results of pore-network simulations presented in Sect. 4 will be used to motivate these models.

5.1 Volume Transfer Rate \(Q_{\mathrm{d}-\mathrm{t}}\) Between Dendritic and Trapped Subphases

Here, a model for the volume transfer rate \(Q_{\mathrm{d}-\mathrm{t}}\) is proposed. The basic idea relies on a strong correlation between \(\phi \frac{\partial S_\mathrm{t}}{\partial t}=Q_{\mathrm{d}-\mathrm{t}}\) and \(\phi \frac{\partial S_\mathrm{b}}{\partial t}\), which is supported by the fact that the mechanisms responsible for transition between dendritic and trapped subphases, and those which cause a change in the backbone subphase are of similar nature. This can be understood as follows: During imbibition, both trapping and creation of dendritic fingers occur due to either cooperative pore-filling mechanisms of type \(I_{z}\), \(z>1\) or snap-off. Similarly, during drainage, the reconnection of trapped fluid as well as increase in backbone fluid (either directly or by transfer of dendritic fingers to the backbone) occurs due to piston displacement mechanisms where wetting fluid between two pore regions occupied by nonwetting fluid gets displaced. Note that this correlation between \(Q_{\mathrm{d}-\mathrm{t}}\) and \(\frac{\partial S_\mathrm{b}}{\partial t}\) may not hold for pore systems of mixed wettability, where both phases may be present as films and the displacement mechanisms are more complex than those which are assumed here (see eg. Ryazanov et al. 2014).

Based on the arguments given above, it is hypothesized that

$$\begin{aligned} Q_{\mathrm{d}-\mathrm{t}}=-f_{\mathrm{d}-\mathrm{t}}(S_\mathrm{b})\phi \frac{\partial S_\mathrm{b}}{\partial t}. \end{aligned}$$
(5.1)

This is supported by pore-network simulations (see Fig. 9 in Sect. 4.2). For a functional form of \(f_{\mathrm{d}-\mathrm{t}}\), we assume self-similarity of the different \(S_\mathrm{t}-S_\mathrm{b}\) curves for a given maximum turning point backbone saturation \(S_\mathrm{b}^{*}\) and the corresponding maximum trapped saturation \(S_\mathrm{t}^{*}=S_\mathrm{t}^{*}(S_\mathrm{b}^{*})\) as suggested by pore-network results (see Fig. 10). A functional relation

$$\begin{aligned} \frac{S_\mathrm{t}}{S_\mathrm{t}^{*}}=1-\left( \frac{S_\mathrm{b}}{S_\mathrm{b}^{*}}\right) ^{\delta _{1}} \end{aligned}$$
(5.2)

is assumed for the similarity solutions. Differentiating both sides of this relation with respect to t and noting that \(Q_{\mathrm{d}-\mathrm{t}}=\phi \frac{\partial S_\mathrm{t}}{\partial t}\), we arrive at

$$\begin{aligned} f_{\mathrm{d}-\mathrm{t}}(S_\mathrm{b})=\frac{\delta _{1}S_\mathrm{t}^{*}}{\left( S_\mathrm{b}^{*}\right) ^{\delta _{1}}}S_\mathrm{b}^{\delta _{1}-1}, \end{aligned}$$
(5.3)

with \(\delta _{1}\) being a fitting parameter. A relation between \(S_\mathrm{b}^{*}\) and \(S_\mathrm{t}^{*}\) is now required. For this, we employ the following relation

$$\begin{aligned} S_\mathrm{t}^{*}(S_\mathrm{b}^{*})=S_{tr}S_\mathrm{b}^{*\delta _{2}}, \end{aligned}$$
(5.4)

where \(S_{tr}\) is the maximum residual saturation corresponding to \(S_\mathrm{b}^{*}=1\) and \(\delta _{2}\) is a constant.

Using Eq. (5.1), we can now rewrite the subphase evolution equations (2.5)–(2.7) along with the nonwetting saturation equation as

$$\begin{aligned} \phi \frac{\partial S_\mathrm{b}}{\partial t}= & {} \lambda \phi \frac{\partial S}{\partial t}+Q_{\mathrm{d}-\mathrm{b}}, \end{aligned}$$
(5.5)
$$\begin{aligned} \phi \frac{\partial S_\mathrm{d}}{\partial t}= & {} (1-\lambda )\phi \frac{\partial S}{\partial t}+f_{\mathrm{d}-\mathrm{t}}(S_\mathrm{b})\phi \frac{\partial S_\mathrm{b}}{\partial t}-Q_{\mathrm{d}-\mathrm{b}}, \end{aligned}$$
(5.6)
$$\begin{aligned} \phi \frac{\partial S_\mathrm{t}}{\partial t}= & {} -f_{\mathrm{d}-\mathrm{t}}(S_\mathrm{b})\phi \frac{\partial S_\mathrm{b}}{\partial t}, \end{aligned}$$
(5.7)
$$\begin{aligned} \hbox {and} \; \phi \frac{\partial S}{\partial t}= & {} \frac{\partial }{\partial x_{i}}\left( \frac{K}{\mu _\mathrm{n}}k_\mathrm{rn}\frac{\partial P_\mathrm{n}}{\partial x_{i}}\right) . \end{aligned}$$
(5.8)

Note that by adding Eqs. 5.5 and 5.6, one gets \(\phi \frac{\partial S_\mathrm{c}}{\partial t}=\phi \frac{\partial S}{\partial t}+f_{\mathrm{d}-\mathrm{t}}(S_\mathrm{b})\phi \frac{\partial S_\mathrm{b}}{\partial t}\), and Eq. (5.6) can be rewritten as

$$\begin{aligned} \phi \frac{\partial S_\mathrm{d}}{\partial t}=\phi \frac{\partial S_\mathrm{c}}{\partial t}-\lambda \phi \frac{\partial S}{\partial t}-Q_{\mathrm{d}-\mathrm{b}}. \end{aligned}$$
(5.9)

For a given nonwetting pressure field (flow problem), the remaining unclosed terms are \(\lambda \), \(Q_{\mathrm{d}-\mathrm{b}}\) and \(k_\mathrm{rn}\). The latter can be expressed as a unique function of \(S_\mathrm{b}\), which has been mentioned earlier and will further be discussed in Sect. 5.3. Note that in order to compute the nonwetting pressure field, closures for the wetting phase relative permeability \(k_{rw}\) and macroscopic capillary pressure \(P_\mathrm{c}\) are also required [see Eqs. (2.1) and (2.2)].

5.2 Backbone Saturation Rate \(\frac{\partial S_\mathrm{b}}{\partial t}\)

The backbone saturation rate \(\frac{\partial S_\mathrm{b}}{\partial t}\), Eq. (5.5), is now considered, the value of which consists of two contributions: one from the exchange of volume between the backbone and dendritic subphases, and another from the direct change in \(S_\mathrm{b}\) due to a change in S.

During drainage, regions of the pore space occupied with the dendritic phase coalesce. This coalescence causes a subset of the dendritic subphase to transfer to the backbone subphase. On the other hand, during imbibition there is volume transfer from the backbone subphase to the dendritic subphase due to nonwetting paths being broken by the invading wetting phase. The volume transfer rate \(Q_{\mathrm{d}-\mathrm{b}}\) is a function of both \(S_\mathrm{b}\) and \(S_\mathrm{d}\). As stated earlier, here only quasi-static flow is considered, i.e., \(\mathrm{d}S_\mathrm{b}/\mathrm{d}S_\mathrm{c}\) is independent of the magnitude of the saturation \(\mathrm{d}S_\mathrm{c}/\mathrm{d}t\). As a direct consequence, one can state that \(Q_{\mathrm{d}-\mathrm{b}}\propto \mathrm{d}S_\mathrm{c}/\mathrm{d}t\). In general, volume transfer between the backbone and dendritic subphases is not reversible due to differences in pore-scale invasion mechanisms and sequences between drainage and imbibition, i.e., the volume transfer depends on \(sgn\left( \frac{\mathrm{d}S_\mathrm{c}}{\mathrm{d}t}\right) \). We thus have

$$\begin{aligned} Q_{\mathrm{d}-\mathrm{b}}=f_{\mathrm{d}-\mathrm{b}}\left( S_\mathrm{b},S_\mathrm{d},sgn\left( \frac{\partial S_\mathrm{c}}{\partial t}\right) \right) \phi \frac{\partial S_\mathrm{c}}{\partial t}, \end{aligned}$$
(5.10)

where \(f_{\mathrm{d}-\mathrm{b}}\) is a function which needs to be modeled.

In order to model the fraction \(\lambda \), we introduce an additional requirement here that the backbone subphase saturation rate \(\frac{\partial S_\mathrm{b}}{\partial t}\) depends directly only on \(S_\mathrm{b}\) and \(S_\mathrm{d}\), and not on \(S_\mathrm{t}\). In order to satisfy this requirement for the first rhs. term in Eq. (5.5), the fraction \(\lambda \) is has the form

$$\begin{aligned} \lambda =f_{\lambda }\left( S_\mathrm{b},S_\mathrm{d},sgn\left( \frac{\partial S_\mathrm{c}}{\partial t}\right) \right) \frac{\mathrm{d}S_\mathrm{c}}{\mathrm{d}S}. \end{aligned}$$
(5.11)

Substituting Eqs. (5.10) and (5.11) into Eq. (2.5), we obtain

$$\begin{aligned} \phi \frac{\partial S_\mathrm{b}}{\partial t}=\phi f_{\lambda }\left( S_\mathrm{b},S_\mathrm{d},sgn\left( \frac{\partial S_\mathrm{c}}{\partial t}\right) \right) \frac{\partial S_\mathrm{c}}{\partial t}+\phi f_{\mathrm{d}-\mathrm{b}}\left( S_\mathrm{b},S_\mathrm{d},sgn\left( \frac{\partial S_\mathrm{c}}{\partial t}\right) \right) \frac{\partial S_\mathrm{c}}{\partial t}, \end{aligned}$$
(5.12)

In order to devise models for \(f_{\mathrm{d}-\mathrm{b}}\) and \(f_{\lambda }\), two constraints can be stated. First, if one assumes that the pore space itself has no dead ends, one arrives at \({\lim }_{S_\mathrm{c}\rightarrow 1} S_\mathrm{d}=0\). In addition, \({\lim }_{S_\mathrm{c}\rightarrow 1} S_\mathrm{t}=0\). This implies \(\int _{0}^{1}\mathrm{d}S_\mathrm{b}=1\). By integrating Eq. 5.12, we obtain the first constraint for \(f_{\mathrm{d}-\mathrm{b}}\) and \(f_{\lambda }\):

$$\begin{aligned} \int _{0}^{1}\mathrm{d}S_\mathrm{b}=\int _{0}^{1}f_{\mathrm{d}-\mathrm{b}}^{*}\mathrm{d}S_\mathrm{c}=1, \end{aligned}$$
(5.13)

where we have introduced \(f_{\mathrm{d}-\mathrm{b}}^{*}=f_{\lambda }+f_{\mathrm{d}-\mathrm{b}}\). Second, one can assume that \({\lim }_{S_\mathrm{c}\rightarrow 1}\frac{\mathrm{d}S_\mathrm{b}}{\mathrm{d}S_\mathrm{c}}=1\), since for an almost fully drained porous medium, all the nonwetting phase is connected and no dendritic fingers exist. Hence, we have

$$\begin{aligned} f_{\mathrm{d}-\mathrm{b}}^{*}\left( S_\mathrm{b}=1,\,S_\mathrm{d}=0,\,sgn\left( \frac{\mathrm{d}S_\mathrm{c}}{\mathrm{d}t}\right) \right) =1. \end{aligned}$$
(5.14)

Functions for \(f_{\lambda }\) and \(f_{\mathrm{d}-\mathrm{b}}\) are now proposed, which satisfy these constraints. For drainage, i.e., for \(sgn\left( \frac{\mathrm{d}S_\mathrm{c}}{\mathrm{d}t}\right) =1\), we have

$$\begin{aligned} f_{\mathrm{d}-\mathrm{b}}^{dr}= & {} \left( S_\mathrm{d}\right) ^{\alpha _{1}^{dr}}\left( S_\mathrm{b}\right) ^{\alpha _{2}^{dr}}A^{dr}, \end{aligned}$$
(5.15)
$$\begin{aligned} f_{\lambda }^{dr}= & {} \left( S_\mathrm{c}\right) ^{\alpha _{3}^{dr}}, \end{aligned}$$
(5.16)

where \(A^{dr}\), \(\alpha _{1}^{dr}\), \(\alpha _{2}^{dr}\) and \(\alpha _{3}^{dr}\) are coefficients which have to be fitted to the primary drainage \(S_\mathrm{b}-S_\mathrm{c}\) curve from, e.g., pore-network simulations. Note that only 3 of the 4 coefficients are independent due to constraint (5.13), while the constraint (5.14) is trivially satisfied, since \({\lim }_{{S_\mathrm{c}\rightarrow 1}}f_{\mathrm{d}-\mathrm{b}}^{dr}=0\) and \({\lim }_{{S_\mathrm{c}\rightarrow 1}} f_{\lambda }=1\). A similar expression is used for imbibition, i.e.,

$$\begin{aligned} f_{\mathrm{d}-\mathrm{b}}^{imb}= & {} \left( S_\mathrm{d}\right) ^{\alpha _{1}^{imb}}\left( S_\mathrm{b}\right) ^{\alpha _{2}^{imb}}A^{imb}, \end{aligned}$$
(5.17)
$$\begin{aligned} f_{\lambda }^{imb}= & {} \left( S_\mathrm{c}\right) ^{\alpha _{3}^{imb}}. \end{aligned}$$
(5.18)

Equations (5.15–5.16) and (5.17–5.18) are valid only for primary drainage (along the saturation path starting at \(S_\mathrm{c}=0\)) and primary imbibition (along the saturation path starting at \(S_\mathrm{c}=1\)), respectively. Hysteretic effects during saturation path reversals for \(0<S_\mathrm{c}<1\) have yet to be taken into account.

As shown in Sect. 4.1, pore-network simulation results suggest that, for any particular \(S_\mathrm{c}\), the dendritic saturation \(S_\mathrm{d}\) is always larger during drainage than during imbibition. We denote \(S_\mathrm{max}^{d}(S_\mathrm{c})\) and \(S_\mathrm{min}^{d}(S_\mathrm{c})\) as the maximum and minimum dendritic saturations attainable for a given \(S_\mathrm{c}\) (see Fig. 7b). Based on our pore-network simulation results, we make the approximation that on transition from drainage to imbibition and on transition from imbibition to drainage, initially \(\mathrm{d}S_\mathrm{b}=0\) while \(\mathrm{d}S_\mathrm{d}=\mathrm{d}S_\mathrm{c}\), until \(S_\mathrm{d}(S_\mathrm{c})=S_\mathrm{min}^{d}(S_\mathrm{c})\) or \(S_\mathrm{d}(S_\mathrm{c})=S_\mathrm{max}^{d}(S_\mathrm{c})\), respectively; (see, e.g., segments 1–2 and 3–4 in Fig. 8a, c). A more accurate closure can certainly be made for these interior scanning curves, but this simple play-type model (see Visintin 1994) is sufficient for our purposes. Hence the final model for \(\frac{\partial S_\mathrm{b}}{\partial t}\) can be written as

$$\begin{aligned} \phi \frac{\partial S_\mathrm{b}}{\partial t}={\left\{ \begin{array}{ll} \left[ 1-H\left( S_\mathrm{d}-S_\mathrm{d}^\mathrm{max}\right) \right] \phi \frac{\partial S_\mathrm{c}}{\partial t}+H\left( S_\mathrm{d}-S_\mathrm{d}^\mathrm{max}\right) f_{\mathrm{d}-\mathrm{b}}^{*dr}\phi \frac{\partial S_\mathrm{c}}{\partial t}, &{} \,\frac{\partial S_\mathrm{c}}{\partial t}>0\\ \left[ 1-H\left( S_\mathrm{d}^\mathrm{min}-S_\mathrm{d}\right) \right] \phi \frac{\partial S_\mathrm{c}}{\partial t}+H\left( S_\mathrm{d}^\mathrm{min}-S_\mathrm{d}\right) f_{\mathrm{d}-\mathrm{b}}^{*imb}\phi \frac{\partial S_\mathrm{c}}{\partial t}, &{} \,\frac{\partial S_\mathrm{c}}{\partial t}<0\\ 0, &{} \,\frac{\partial S_\mathrm{c}}{\partial t}=0 \end{array}\right. }, \end{aligned}$$
(5.19)

where

$$\begin{aligned} H(x)={\left\{ \begin{array}{ll} 0, &{} x<0\\ 1, &{} x\ge 0 \end{array}\right. } \end{aligned}$$

is the Heaviside step function, \(f_{\mathrm{d}-\mathrm{b}}^{*dr}=f_{\lambda }^{dr}+f_{\mathrm{d}-\mathrm{b}}^{dr}\), and \(f_{\mathrm{d}-\mathrm{b}}^{*imb}=f_{\lambda }^{imb}+f_{\mathrm{d}-\mathrm{b}}^{imb}\).

5.3 Relative Permeability

As shown in Sect. 4.3, it is justified to consider the nonwetting relative permeability \(k_\mathrm{rn}\) to be a one-to-one function of the backbone saturation \(S_\mathrm{b}\). Here, for the functional form of \(k_\mathrm{rn}\), a van Genuchten-type equation (Van Genuchten 1980),

$$\begin{aligned} k_\mathrm{rn}=\left( S_\mathrm{b}\right) ^{0.5}\left[ 1-\left( 1-\left( S_\mathrm{b}\right) ^{1/m}\right) ^{m}\right] ^{2}, \end{aligned}$$
(5.20)

is assumed with m being a fitting parameter.

6 Model Calibration and Validation

The models proposed in Sect. 5 for use in the subphase framework require the calibration of ten independent parameters: one for \(f_{\mathrm{d}-\mathrm{t}}\) [Eq. (5.3)], two for \(S_\mathrm{t}^{*}(S_\mathrm{b}^{*})\) [Eq. (5.4)], six for \(f_{\mathrm{d}-\mathrm{b}}^{*}=f_{\lambda }+f_{\mathrm{d}-\mathrm{b}}\) [Eqs. (5.15)–(5.18)] and one for \(k_\mathrm{rn}\left( S_\mathrm{b}\right) \) [Eq. (5.20)]. Note that in this paper we have not considered wetting relative permeability and the macroscopic capillary pressure, models of which would add additional parameters.

The model parameters of the functions \(f_{\mathrm{d}-\mathrm{b}}^{*dr}\) and \(f_{\mathrm{d}-\mathrm{b}}^{*imb}\) were calibrated by least square fitting to the pore-network simulation results of primary drainage and primary imbibition. As shown in Fig. 12, the assumed form of \(f_{\mathrm{d}-\mathrm{b}}^{*dr}\) and \(f_{\mathrm{d}-\mathrm{b}}^{*imb}\) is flexible enough to fit the pore-network simulation data for networks A, B and C.

Fig. 12
figure 12

The function \(f_{\mathrm{d}-\mathrm{b}}^{*dr}\) obtained from pore-network simulations (circles) and from the calibrated model Eqs. (5.15) and (5.16) (solid lines) is shown together with \(f_{\mathrm{d}-\mathrm{b}}^{*imb}\) obtained from pore-network simulations (crosses) and from the calibrated model Eqs. (5.17) and (5.18) (dashed lines). The values of \(S_\mathrm{b}\) and \(S_\mathrm{d}\) used here are obtained from three pore-network simulations. a For an artificial consolidated porous medium. The calibrated parameters used in Eqs. (5.15) and (5.17) are \(A^{dr}=5.3\), \(\alpha _{1}^{dr}=0.243\), \(\alpha _{2}^{dr}=1.84\), \(\alpha _{3}^{dr}=0.929\), \(A^{imb}=5.73\), \(\alpha _{1}^{imb}=0.332\), \(\alpha _{2}^{imb}=1.82\) and \(\alpha _{3}^{imb}=0.854\). b For an artificial unconsolidated porous medium. The calibrated parameters used in Eqs. (5.15) and (5.17) are \(A^{dr}=8.74\), \(\alpha _{1}^{dr}=0.48\), \(\alpha _{2}^{dr}=1.90\), \(\alpha _{3}^{dr}=0.842\), \(A^{imb}=2.68\), \(\alpha _{1}^{imb}=0.308\), \(\alpha _{2}^{imb}=1.67\) and \(\alpha _{3}^{imb}=0.364\). c For a network representative of Berea sandstone. The calibrated parameters used in Eqs. (5.15) and (5.17) are \(A^{dr}=1.89\), \(\alpha _{1}^{dr}=0.231\), \(\alpha _{2}^{dr}=0.962\), \(\alpha _{3}^{dr}=0.662\), \(A^{imb}=3.66\), \(\alpha _{1}^{imb}=0.518\), \(\alpha _{2}^{imb}=1.73\) and \(\alpha _{3}^{imb}=0.313\)

Full size image

After the functions \(f_{\mathrm{d}-\mathrm{b}}^{*dr}\) and \(f_{\mathrm{d}-\mathrm{b}}^{*imb}\) were calibrated, Eq. (5.9) was used to numerically compute the \(S_\mathrm{b}\) versus \(S_\mathrm{c}\) and the \(S_\mathrm{d}\) versus \(S_\mathrm{c}\) scanning curves for a 0-d (homogeneous) case. Figure 13 shows \(S_\mathrm{b}\) and \(S_\mathrm{d}\) imbibition scanning curves generated by pore-network simulations and by the calibrated model for networks B and C. As can be observed, the model results for the bounding primary curves are in good agreement with the pore-network simulation data. However, there is a discrepancy for the values between the bounding primary curves for network C. This is due to the play-type model for the interior scanning curves [see Eq. (5.19)]. A more elaborate model with more parameters can readily be used to rectify this discrepancy. However, the current model is sufficient for the purpose of demonstrating the subphase framework.

Fig. 13
figure 13

Comparison of imbibition scanning curves for backbone (left) and dendritic (right) nonwetting subphases, as computed by Eqs. (5.5)–(5.8) (solid lines) and by pore-network simulations (circles) for network B (top) and network C (bottom). Model parameters are the same as in Fig. 12

Full size image

In order to compute the evolution of the trapped nonwetting saturation, the parameters in the model for the volume transfer term \(Q_{\mathrm{d}-\mathrm{t}}\) [Eqs. (5.1)–(5.4)] were calibrated. Figure 14 shows the \(S_\mathrm{t}^{*}\) versus \(S_\mathrm{b}^{*}\) relation as obtained from pore-network simulation data and by the calibrated model Eq. (5.4) for networks A, B and C. With the calibrated \(S_\mathrm{t}^{*}(S_\mathrm{b}^{*})\) model, the imbibition scanning curves for \(S_\mathrm{t}\) versus \(S_\mathrm{b}\) and \(S_\mathrm{t}\) versus S in network C can be computed by Eq. (5.7), and are shown in Fig. 15. As can be observed in Fig. 15b, there is a reasonable quantitative agreement between the model results and the pore-network simulation data. The differences observed can be mainly attributed to the employment of a play-type model in Eq. (5.19) for the interior scanning curves of the backbone saturation \(S_\mathrm{b}\).

Fig. 14
figure 14

The function \(S_\mathrm{t}^{*}(S_\mathrm{b}^{*})\) obtained from pore-network simulations (crosses) and from the calibrated model Eq. (5.4) (solid lines). a For an artificial consolidated porous medium. The calibrated parameters used in Eq. (5.4) are \(S_{tr}=0.85\), \(\delta _{2}=0.3\). b For an artificial unconsolidated porous medium. The calibrated parameters used in Eq. (5.4) are \(S_{tr}=0.45\), \(\delta _{2}=0.3\). c For a network representative of Berea sandstone. The calibrated parameters used in Eq. (5.4) are \(S_{tr}=0.47\), \(\delta _{2}=0.38\)

Full size image
Fig. 15
figure 15

Comparison of imbibition scanning curves for the trapped saturation plotted against the backbone saturation (left) and the nonwetting saturation (right) as computed by Eq. (5.7) (solid lines) and by pore-network simulations (dashed lines) for network C. The calibrated parameters used are \(\delta _{1}=0.41\), \(\delta _{2}=0.38\) and \(S_{tr}=0.47\)

Full size image

The relative permeability relation (5.20) was then calibrated by least square fitting using pore-network simulation data. As can be observed in Fig. 16, the van Genuchten-type relation in Eq. (5.20) is adequate in matching the pore-network simulation results.

Fig. 16
figure 16

Nonwetting relative permeability \(k_\mathrm{rn}\) obtained from pore-network simulations (crosses) and from the calibrated van Genuchten-type Eq. (5.20) (solid line) for network A (left), network B (center) and network C (right). The calibrated parameter used in Eq. (5.20) is \(m=1.04\) for network A, \(m=0.89\) for network B and \(m=2.02\) for network C

Full size image

Having calibrated the model equations, the capability of the proposed framework in capturing complex hysteresis trends in \(k_{r}\) can now be demonstrated. Shown in Fig. 17 are the \(k_{r}\) versus S imbibition scanning curves obtained by pore-network simulations in network C and by our proposed subphase framework with the calibrated models described in Sect. 5. Additionally, shown in Fig. 17c is a \(k_{r}\) versus S curve computed using a hysteresis model based on Land’s formulation (Land 1968) . The basis of this formulation is that the imbibition relative permeability at a given saturation \(k_\mathrm{rn}^{I}(S)\) can be computed from the primary drainage relative permeability curve \(k_\mathrm{rn}^{D}(S)\) by replacing S with \(S_\mathrm{c}\), i.e.,

$$\begin{aligned} k_\mathrm{rn}^{I}(S)=k_\mathrm{rn}^{D}(S_\mathrm{c}). \end{aligned}$$

It is trivial to show that under this assumption the inequality \(k_\mathrm{rn}^{I}(S)\le k_\mathrm{rn}^{D}(S)\) holds for any saturation. On the other hand, using the proposed framework to model relative permeability hysteresis, we are able to capture the complex relative permeability hysteresis trends.

Fig. 17
figure 17

Model results: imbibition scanning curves for the backbone saturation plotted against the nonwetting saturation for network C. a Pore-network simulation results. b 0-d simulations using the subphase modeling framework. c 0-d simulations using Land’s relative permeability hysteresis model (best case scenario)

Full size image

We conclude this section with a few remarks regarding the possibility of calibrating the model from experiments as opposed to from pore-network simulations, as has been done here. Different experiments have been previously conducted in order to measure nonwetting relative permeability and nonwetting residual saturation (see Krevor et al. 2012 and references within). This information is not sufficient to calibrate the parameters of the devised subphase-based model. In particular, the difficulty lies in determining the parameter m for the \(k_\mathrm{rn}-S_\mathrm{b}\) relation [Eq. (5.20)] and the parameters \(\delta _{1}\) and \(\delta _{2}\) for the \(S_\mathrm{t}-S_\mathrm{b}\) relation [Eqs. (5.2) and (5.4)]. If these three parameters are known, along with the relative permeability and residual saturation data, the remaining parameters may be obtained through standard curve-fitting procedures. However, the experimental measurement of the backbone and trapped subphase saturations required for these parameters is not straight forward. These quantities have been inferred, but not directly measured, in the works of Raimondi and Torcaso (1964), Stalkup (1970) and Salter et al. (1982).

More recently, X-ray computed microtomography has been used to study the nonwetting fluid topology in rock samples (eg. Herring et al. 2013; Rücker et al. 2015) as well as in bead packs (eg. Krummel et al. 2013). Existing data from these and similar experiments can be used to extract the nonwetting subphase saturations and study the relation of the backbone subphase with both the trapped subphase and the nonwetting relative permeability. To the knowledge of the authors, such a study has not been conducted yet.

7 Concluding Remarks

We have presented a framework for immiscible two-phase flow in porous media, which can account for nonwetting relative permeability hysteresis in both consolidated and unconsolidated porous media. The central idea of the framework is the subdivision of the nonwetting phase into three subphases: backbone, dendritic and trapped subphases. The formulation of the models for the rate of volume transfer between the subphases, required in this framework, was based on observations from pore-network simulation results. Using these models, it is possible to capture complex relative permeability hysteresis behavior where the nonwetting phase relative permeability is greater during imbibition than during drainage. This is not possible using the widely employed Land’s model.

The closure models presented in this paper only deal with low capillary number flows. Further pore-network studies of flow-rate effects on the nonwetting subphase saturations are needed in order to extend the models for more general flow scenarios. In order to devise models applicable to a range of capillary numbers, additional parameters describing the topology of the fluid subphases may be crucial. The topology of a fluid subphase can be described by the Euler characteristic, which has been used previously by Herring et al. (2015) to study the 3D topology of the nonwetting fluid phase and its effect on nonwetting phase trapping. They found that for high capillary numbers, the nonwetting phase Euler number plays an important role on the residual nonwetting saturation.

The pore-network results in this work were limited to two lattice networks and a network representing Berea sandstone. Further investigations are required in order to test whether a nonhysteretic \(k_\mathrm{rn}-S_\mathrm{b}\) and \(S_\mathrm{b}-S_\mathrm{t}\) relations hold for other more complex porous media, e.g., for those with bimodal pore-size distributions.