Dispersion in Porous Media with Heterogeneous Nonlinear Reactions

Abstract

The upscaling of mass transport in porous media with a heterogeneous reaction at the fluid–solid interface, typical of dissolution problems, is carried out with the method of volume averaging, starting from a pore-scale transport problem involving thermodynamic equilibrium or nonlinear reactive boundary conditions. A general expression to describe the macro-scale mass transport is obtained involving several effective parameters which are given by specific closure problems. For representative unit cell with a simple stratified geometry, the effective parameters are obtained analytically and numerically, while for those with complicated geometries, the effective parameters are only obtained numerically by solving the corresponding closure problems. The impact on the effective parameters of the fluid properties, in terms of pore-scale Péclet number Pe, and the process chemical properties, in terms of pore-scale Damköhler number Da and reaction order (n), is studied for periodic stratified and 3D unit cells. It is found that the tortuosity effects play an important role on the longitudinal dispersion coefficient in the 3D case, while it is negligible for the stratified geometry. When Da is very small, the effective reaction rate coefficient is nearly identical to the pore-scale one, while when Da is very large, the reactive condition turns out to be equivalent to pore-scale thermodynamic equilibrium, and the macro-scale mass exchange term is consequently given in a different form from the reactive case. An example of the application of the macro-scale model is presented with the emphasis on the potential impact of additional, non-traditional effective parameters appearing in the theoretical development on the improvement of the accuracy of the macro-scale model.

1 Introduction

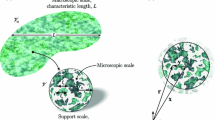
The main focus of our work is on porous media dissolution, which can be found in many fields, such as the formation of karstic structures, acid injection in petroleum engineering, groundwater protection, $\mathrm {CO}_{2}$ storage, etc, (Waele et al. 2009; Golfier et al. 2002; Nordbotten and Celia 2011). Mass and momentum transport during dissolution processes in porous media happen in a hierarchical, multi-scale system, as schematically depicted in Fig.1. The porous medium under consideration consists of three phases at pore-scale: two solid phases, one being soluble, denoted s, the other insoluble, denoted i, and a liquid phase (in general water + dissolved species), denoted l. The corresponding micro-scale (pore-scale) characteristic lengths are defined as $l_\mathrm{s}$, $l_\mathrm{i}$ and $l{}_\mathrm{l}$ respectively, and the macro-scale characteristic length is denoted L. In addition, a third length scale, the radius of the averaging volume $r_{0}$ is also considered. The three length scales conform to the separation of scale assumption $l_\mathrm{s},l_\mathrm{i},l_\mathrm{l}\ll r_{0}\ll L$.

Fig. 1

An example of the multiple scales associated with dissolution in a porous medium

To describe the dissolution of the soluble medium contained in such a porous medium, it is often not practical, even if this is the more secure way of handling the geometry evolution (Békri et al. 1995), to take into account all the pore-scale details (corresponding to $l_\mathrm{i}$, $l_\mathrm{s}$ and $l_\mathrm{l}$) by direct numerical modeling in a L-scale problem. Consequently, attempts have been made to filter the pore-scale information through the use of upscaling techniques. Macro-scale models were developed for passive dispersion, i.e., with no exchange at the liquid–solid interface, starting with the well-known work of Taylor (1953, 1954) and Aris (1956) for dispersion in tubes. In the general case, a macro-scale dispersion theory was proposed following various upscaling techniques: Brenner (1980) using a method of moment, Eidsath et al. (1983) using the method of volume averaging, Mauri (1991) using the method of homogenization, etc. All methods bring some theoretical support for the classical dispersion equation and also provide closure problems which can be used to directly calculate the dispersion tensor components for various representative unit cells. These theoretical methods have been used also to investigate the case of active dispersion, i.e., with thermodynamic equilibrium or reactive conditions at the fluid–solid interface.

The case of thermodynamic equilibrium at the interface leads, when local-equilibrium is considered, to a simple model stating that the macro-scale concentration is equal to the pore-scale surface equilibrium concentration. Non-equilibrium models have been obtained through the volume averaging method, neglecting contributions of the interface velocity in the closure problems and at several points in the averaging process, leading to the introduction of a linear exchange term in the macro-scale equation (Quintard and Whitaker 1994, 1999; Ahmadi et al. 2001; Golfier et al. 2002). These results have been extended to the case of mass exchange controlled by partitioning expressions (Raoult’s law, Henry’s law, etc.) in Coutelieris et al. (2006) and Soulaine et al. (2011), the additional terms associated with the interface recession velocity being taken into account in this latter paper. Non-traditional convective terms appear in the macro-scale equations, which are often discarded in practical implementations of the macro-scale models. However, it was shown in Golfier et al. (2002) that they must be taken into account, at least for simple unit cells like tubes.

The case of heterogeneous reaction with a linear reaction has been investigated by a large amount of studies using the above mentioned various upscaling techniques (Whitaker 1986; Shapiro and Brenner 1988; Whitaker 1991; Mauri 1991; Edwards et al. 1993; Valdés-Parada et al. 2011; Varloteaux et al. 2013). The major feature of the resulting macro-scale models is the notion of effective reaction rate, which depends highly on the pore-scale Damköhler number, as well as the pore-scale medium geometry. In particular, the form and value of the reaction rate is in theory affected by the coupling between reaction and transport. In addition, contrary to most engineering practice, these upscaling studies show also that the resulting dispersion tensor is affected by the heterogeneous reaction, i.e., dispersion curves depend on the Damköhler number.

To our knowledge, few works have been published concerning macro-scale models developed from pore-scale problem with nonlinear reactions. Wood et al. (2007) reported on the development of an effective macro-scale reaction rate using the method of volume averaging for a Michaelis–Menton reaction in the biotransformation problems and discussed the dependence of the effective macro-scale reaction rate on the closure variable, the Damköhler and the Péclet numbers, respectively. Heße et al. (2009) studied the upscaling of a Monod reaction at the interface of polluted water and biofilm through a simple averaging scheme based on direct numerical simulations. Interestingly, the results show that the macro-scale reaction rate does not follow the Monod type in the transition zone between the reaction-limited regime and the diffusion-limited regime. This is also consistent with the findings of Orgogozo et al. (2010) about reactive transport in porous media with biofilms. In Lichtner and Tartakovsky (2003), Tartakovsky et al. (2009), the authors derived probability density functions for both linear and nonlinear heterogeneous chemical reactions involving an aqueous solution reacting with a solid phase, which were used to quantify the uncertainty related to the spatially varying reaction rate coefficient. Effective transport equations were obtained for the average concentration, starting from the governing equation of the probability density function, with time-dependent effective reaction rate coefficients generated. This adds to the motivation of developing a more comprehensive averaging scheme. While the general framework developed in this paper can be applied to different mathematical forms of nonlinear reaction rates, the development is presented for a nonlinear heterogeneous reaction at the dissolving interface expressed under the form

$$\begin{aligned} R_\mathrm{diss}=k_\mathrm{s}\left( 1-\frac{c_\mathrm{s}}{c_\mathrm{eq}}\right) ^{n}, \end{aligned}$$

(1)

which is often used for dissolution problems and that has been documented for instance for limestone and gypsum dissolution (Eisenlohr et al. 1999; Svensson and Dreybrodt 1992; Gabrovšek and Dreybrodt 2001; Lasaga and Luttge 2001), where $c_\mathrm{s}$ is the concentration of the dissolved species at the surface, $c_\mathrm{eq}$ is the related equilibrium concentration, $k_\mathrm{s}$ is the surface reaction rate constant and n is the chemical reaction order. It was obtained by Jeschke et al. (2001) for gypsum dissolution that when the concentration of the dissolved species is close to thermodynamic equilibrium, the reaction becomes highly nonlinear, with $n\thickapprox 4.5$ and $k_\mathrm{s}$ in the order of $10\,\hbox {mmol\,cm}^{-2}\,\hbox {s}^{-1}\pm 15\,\%$. Given this research survey, the objective of this study is to develop a general form of the macro-scale model, starting from pore-scale problems with thermodynamic equilibrium or nonlinear reactive boundary conditions, taking into account as much as possible the role of the interface velocity in the upscaling process.

The paper is organized as follows. Sect. 2 contains the pore-scale model. In Sect. 3, the method of volume averaging is used to develop a non-equilibrium macro-scale model, as well as the corresponding closure problems from which the effective parameters are obtained. Some limiting cases in terms of Da are also discussed in order to connect our results to the literature. In Sect. 4, closure problems are resolved for stratified and 3D representative unit cells with nonlinear reaction rates, and the properties of the generated effective parameters are studied. In the last section, an example of the use of this macro-scale model is presented in order to investigate the importance of the non-traditional effective parameters.

The main new features taken into account in this paper are: (i) a more general form of the reaction rate, (ii) the introduction of the soluble material,¹ (iii) a full coupling of the two closure variables in the closure problems, (iv) an investigation on the potential implications of non-traditional terms. The development is presented in a simplified manner with the emphasis on the original and specific points of our study. The reader are referred to the cited literature for more thorough developments on the classical aspects of the upscaling method.

2 Pore-Scale Model

In the case under consideration, several assumptions have been adopted. First, it is assumed that the activity of the solute in the liquid phase is not modified near the solid surface of the insoluble material, so no solute deposition occurs since the bulk concentration is below the equilibrium concentration. There are many experiments with various salts and passive solid surfaces, for instance, that are compatible with this assumption (a common situation indeed in laboratory experiments aimed at measuring dissolution rates). Even if initially a layer of salt covers the insoluble material, a case which is covered by the model, the thin layer is likely to dissolve more rapidly than the salt grains and leads to a situation in which both soluble and insoluble surfaces are present. Second, solid dissolution can be described by the dissolution of a single pseudo-component. In practice, most soluble materials have a complex chemistry, which implies that dissolution brings several chemical species in the liquid. The water composition will be affected by geochemistry and by segregation due to different transport properties. For instance, gypsum ($\text {CaSO}{}_{4} \cdot 2\text {H}_{2}\text {O}$) dissolution will produce several water components, which will require in principle to follow at least: $\text {H}^{+}$, $\text {OH}^{-}$, $\text {SO}_{4}^{2-}$, $\text {HSO}_{4}^{-}$, $\text {HSO}_{4}^{-}$, $\text {H}_{2}\text {SO}_{4}$, $\text {Ca}^{2+}$, $\text {CaSO}_{4}$ and finally $\text {H}_{2}\text {O}$! The presence of other dissolving species, calcium carbonates for instance, may affect the water composition. In addition, differences in the diffusion coefficients will produce a separation of the gypsum dissolved components, which must be taken into account in the transport model. However, differences in the water diffusion coefficients for gypsum dissolved components are small (Li and Gregory 1974), which favors the treatment of gypsum as a single pseudo-component, with the assumption that geochemistry plays a minor role for instance if gypsum is the only dissolving species in the problem under consideration. In that case, the mass balance problem can be written as a total mass balance equation plus a single balance equation for one of the component, or the pseudo-component. This assumption can be made for many other situations involving a dissolving material different from gypsum. A notation is adopted below which corresponds to a mass balance equation for one ion, let us say $\text {Ca}^{2+}$ in our gypsum illustration, which is denoted Ca. Third, the fluid density $\rho _\mathrm{l}$ and viscosity $\mu _\mathrm{l}$ are assumed constant. Similarly, the diffusion coefficient is supposed constant. One may consult (Quintard et al. 2006) for an example of introduction of nonlinear diffusion coefficients within the averaging scheme.

The pore-scale liquid mass transfer problem is described by the following equations

$$\begin{aligned}&\displaystyle \frac{\partial \rho _\mathrm{l}}{\partial t}+\nabla \cdot \left( \rho _\mathrm{l}\mathbf {v}_\mathrm{l}\right) =0\qquad \text { in }V_\mathrm{l}, \end{aligned}$$

(2)

$$\begin{aligned}&\displaystyle \frac{\partial \rho _\mathrm{l}\omega _\mathrm{l}}{\partial t}+\nabla \cdot \left( \rho _\mathrm{l}\omega _\mathrm{l}\mathbf {v}_\mathrm{l}\right) =\nabla \cdot \left( \rho _\mathrm{l}D_\mathrm{l}\nabla \omega _\mathrm{l}\right) \qquad \text { in }V_\mathrm{l}, \end{aligned}$$

(3)

where $\mathbf {v}_\mathrm{l}$ is the liquid velocity, $V_\mathrm{l}$ is the volume of the liquid phase, $\omega _\mathrm{l}$ is the mass fraction of the followed component in the liquid phase, and $D_\mathrm{l}$ is the molecular diffusion coefficient.

The boundary conditions for the mass balance of $\mathrm {Ca}$ at the interface with the solid phase may be written as a kinetic condition following

$$\begin{aligned} \mathbf {n}_\mathrm{ls}\cdot \left( \rho _\mathrm{l}\omega _\mathrm{l}\left( \mathbf {v}_\mathrm{l}-\mathbf {w}_\mathrm{sl}\right) -\rho _\mathrm{l}D_\mathrm{l}\nabla \omega _\mathrm{l}\right)= & {} -M_\mathrm{Ca}k_\mathrm{s}\left( 1-\frac{\omega _\mathrm{l}}{\omega _\mathrm{eq}}\right) ^{n}\nonumber \\= & {} \mathbf {n}_\mathrm{ls}\cdot \left( \rho _\mathrm{s}\omega _\mathrm{s}\left( \mathbf {v}_\mathrm{s}-\mathbf {w}_\mathrm{sl}\right) \right) \quad \text { at }A_\mathrm{ls}, \end{aligned}$$

(4)

where $k_\mathrm{s}$ and n can be taken as discussed in Sect. 1. In this equation, $\rho _\mathrm{s}$ is the solid density, $\omega _\mathrm{s}$ is the mass fraction of $\mathrm {Ca}$ in the soluble solid phase, $M_\mathrm{Ca}$ is the molar weight of $\mathrm {Ca}$, $\omega _\mathrm{eq}$ is the thermodynamic equilibrium mass fraction of Ca, $\mathbf {v}_\mathrm{s}$ is the solid velocity, $\mathbf {w}_\mathrm{sl}$ is the interface velocity, and $A_\mathrm{ls}$ is the interfacial area between the liquid phase and the soluble material.

The mass balance for the solid phase gives the following boundary condition

$$\begin{aligned} \mathbf {n}_\mathrm{ls}\cdot \left( \rho _\mathrm{s}\left( \mathbf {v}_\mathrm{s}-\mathbf {w}_\mathrm{sl}\right) \right)= & {} \nu _\mathrm{s}\mathbf {n}_\mathrm{ls}\cdot \left( \rho _\mathrm{l}\omega _\mathrm{l}\left( \mathbf {v}_\mathrm{l}-\mathbf {w}_\mathrm{sl}\right) -\rho _\mathrm{l}D_\mathrm{l}\nabla \omega _\mathrm{l}\right) \nonumber \\ {}= & {} -\nu _\mathrm{s}M_\mathrm{Ca}k_\mathrm{s}\left( 1-\frac{\omega _\mathrm{l}}{\omega _\mathrm{eq}}\right) ^{n}\,\quad \quad \text { at }A_\mathrm{ls}, \end{aligned}$$

(5)

where $\nu _\mathrm{s}=M_\mathrm{g}/M_\mathrm{Ca}$ and $M_\mathrm{g}$ is the molar weight of the dissolving species. The total mass balance boundary condition may be written formally as

$$\begin{aligned} \mathbf {n}_\mathrm{ls}\cdot \left( \rho _\mathrm{l}\left( \mathbf {v}_\mathrm{l}-\mathbf {w}_\mathrm{sl}\right) \right) =\mathbf {n}_\mathrm{ls}\cdot \left( \rho _\mathrm{s}\left( \mathbf {v}_\mathrm{s}-\mathbf {w}_\mathrm{sl}\right) \right) \qquad \text { at }A_\mathrm{ls}. \end{aligned}$$

(6)

In this paper, it is assumed that the solid phase is immobile, i.e., $\mathbf {v}_\mathrm{s}=0$; therefore, $\mathbf {v}_\mathrm{s}$ will not appear anymore in the expressions for the boundary conditions. With this assumption, Eqs. 5 and 6 can be rewritten as the following two equations

$$\begin{aligned}&\displaystyle \mathbf {n}_\mathrm{ls}\cdot \mathbf {w}_\mathrm{sl}= \rho _\mathrm{s}^{-1}M_\mathrm{g}k_\mathrm{s}\left( 1-\frac{\omega _\mathrm{l}}{\omega _\mathrm{eq}}\right) ^{n}\qquad \text { at }A_\mathrm{ls}, \end{aligned}$$

(7)

$$\begin{aligned}&\displaystyle \mathbf {n}_\mathrm{ls}\cdot \rho _\mathrm{l}\mathbf {v}_\mathrm{l}=\mathbf {n}_\mathrm{ls}\cdot \left( \rho _\mathrm{l}-\rho _\mathrm{s}\right) \mathbf {w}_\mathrm{sl}=-\left( 1-\frac{\rho _\mathrm{l}}{\rho _\mathrm{s}}\right) M_\mathrm{g}k_\mathrm{s}\left( 1-\frac{\omega _\mathrm{l}}{\omega _\mathrm{eq}}\right) ^{n}\qquad \text { at }A_\mathrm{ls}, \end{aligned}$$

(8)

which can be used to calculate the interface velocity and liquid velocity respectively. Eqs. 5 and 6 can be combined to provide a different expression for the calculation of the interface velocity, which is more convenient in the case of an equilibrium condition. This leads to

$$\begin{aligned} \mathbf {n}_\mathrm{ls}\cdot \mathbf {w}_\mathrm{sl}=\frac{\nu _\mathrm{s}}{\rho _\mathrm{s}\left( 1-\nu _\mathrm{s}\omega _\mathrm{l}\right) }\mathbf {n}_\mathrm{ls}\cdot \left( \rho _\mathrm{l}D_\mathrm{l}\nabla \omega _\mathrm{l}\right) \qquad \text { at }A_\mathrm{ls}. \end{aligned}$$

(9)

How large is the interface velocity? As an example, it can be estimated as

$$\begin{aligned} \left| \mathbf {n}_\mathrm{ls}\cdot \mathbf {w}_\mathrm{sl}\right| \approx \rho _\mathrm{s}^{-1}M_\mathrm{g}k_\mathrm{s}=\frac{172.17\times 1.3\times 10^{-7}}{2.310}=9.69\times 10^{-6}\mathrm {cm/s}\,\text { at }A_\mathrm{ls}, \end{aligned}$$

(10)

for gypsum when $\omega _\mathrm{l}=0$ and it is even lower for carbonate calcium.

Together with the mass balance of the solid phase in $V_\mathrm{s}$, and boundary conditions at the interface between the liquid phase and the insoluble material, $A_\mathrm{li}$, the pore-scale problem can be finally written as

$$\begin{aligned}&\displaystyle \frac{\partial \rho _\mathrm{l}}{\partial t}+\nabla \cdot \left( \rho _\mathrm{l}\mathbf {v}_\mathrm{l}\right) =0\qquad \text { in }V_\mathrm{l}, \end{aligned}$$

(11)

$$\begin{aligned}&\displaystyle \frac{\partial \rho _\mathrm{l}\omega _\mathrm{l}}{\partial t}+\nabla \cdot \left( \rho _\mathrm{l}\omega _\mathrm{l}\mathbf {v}_\mathrm{l}\right) =\nabla \cdot \left( \rho _\mathrm{l}D_\mathrm{l}\nabla \omega _\mathrm{l}\right) \qquad \text { in }V_\mathrm{l}, \end{aligned}$$

(12)

$$\begin{aligned}&\displaystyle \text {B.C. I}\,\,\,\mathbf {n}_\mathrm{ls}\cdot \left( \rho _\mathrm{l}\omega _\mathrm{l} \left( \mathbf {v}_\mathrm{l}-\mathbf {w}_\mathrm{sl}\right) -\rho _\mathrm{l}D_\mathrm{l}\nabla \omega _\mathrm{l}\right) =-M_\mathrm{Ca}k_\mathrm{s}\left( 1-\frac{\omega _\mathrm{l}}{\omega _\mathrm{eq}}\right) ^{n}\,\text { at }A_\mathrm{ls}, \end{aligned}$$

(13)

$$\begin{aligned}&\displaystyle \text {B.C. II}\qquad \mathbf {n}_\mathrm{ls}\cdot \left( -\rho _\mathrm{s}\mathbf {w}_\mathrm{sl}\right) =\mathbf {n}_\mathrm{ls}\cdot \left( \rho _\mathrm{l}\left( \mathbf {v}_\mathrm{l}-\mathbf {w}_\mathrm{sl}\right) \right) \nonumber \\&\displaystyle =\nu _\mathrm{s}\mathbf {n}_\mathrm{ls}\cdot \left( \rho _\mathrm{l}\omega _\mathrm{l}\left( \mathbf {v}_\mathrm{l}-\mathbf {w}_\mathrm{sl}\right) -\rho _\mathrm{l}D_\mathrm{l}\nabla \omega _\mathrm{l}\right) \nonumber \\&\displaystyle =- M_\mathrm{g}k_\mathrm{s}\left( 1-\frac{\omega _\mathrm{l}}{\omega _\mathrm{eq}}\right) ^{n}\qquad \text { at }A_\mathrm{ls}, \end{aligned}$$

(14)

$$\begin{aligned}&\displaystyle \frac{\partial \rho _\mathrm{s}}{\partial t}=0\text { in }V_\mathrm{s}, \end{aligned}$$

(15)

$$\begin{aligned}&\displaystyle \text {B.C. III}\qquad \mathbf {n}_\mathrm{li}\cdot \left( \rho _\mathrm{l}\omega _\mathrm{l}\mathbf {v}_\mathrm{l}-\rho _\mathrm{l}D_\mathrm{l}\nabla \omega _\mathrm{l}\right) =0\qquad \text { at }A_\mathrm{li}, \end{aligned}$$

(16)

$$\begin{aligned}&\displaystyle \text {B.C. IV}\qquad \mathbf {n}_\mathrm{li}\cdot \mathbf {v}_\mathrm{l}=0\qquad \text { at }A_\mathrm{li}. \end{aligned}$$

(17)

The problem has to be completed with momentum balance equations, Navier–Stokes equations for instance. When the velocity of dissolution is small compared to the relaxation time of the viscous flow,² and considering constant $\rho _\mathrm{l}$ and $\mu _\mathrm{l}$, the problem for the momentum balance equations is independent of the concentration field and therefore can be treated independently. Consequently, the focus below is on the transport problem assuming that $\mathbf {v}_\mathrm{l}$ and its average value are known fields.

3 Upscaling

As mentioned in the introduction, several upscaling methods can be adopted (Cushman et al. 2002), for instance, volume averaging (Whitaker 1999), ensemble averaging (Dagan 1989; Cushman and Ginn 1993), moments matching (Brenner 1980; Shapiro and Brenner 1988) and multi-scale asymptotic (Bensoussan et al. 1978). In this present study, the developments of a macro-scale model are based on the method of volume averaging. The general framework has been developed over several decades and a comprehensive presentation can be found in Whitaker (1999). Our present work extends the contribution of Quintard and Whitaker (1994), Soulaine et al. (2011), Valdés-Parada et al. (2011). Therefore, the focus of this paper is on the original contribution, while the classical steps are presented at a minimum necessary for reader’s comprehension.

3.1 Averages and Averaged Equations

Averages are defined in the traditional manner as

$$\begin{aligned} \left\langle \mathbf {v}_\mathrm{l}\right\rangle =\frac{1}{V}\int _{V_\mathrm{l}}\mathbf {v}_\mathrm{l}{\text {d}}V={\varepsilon }_\mathrm{l}\left\langle \mathbf {v}_\mathrm{l}\right\rangle ^{l},\,{\varepsilon }_\mathrm{l}=\frac{1}{V}\int _{V_\mathrm{l}}{\text {d}}V\,\text { and}\quad \left\langle \omega _\mathrm{l}\right\rangle ^{l}=\frac{1}{V_\mathrm{l}}\int _{V_\mathrm{l}}\omega _\mathrm{l}{\text {d}}V, \end{aligned}$$

(18)

where $\left\langle \mathbf {v}_\mathrm{l}\right\rangle$ and $\left\langle \mathbf {v}_\mathrm{l}\right\rangle ^{l}$ denote the superficial and intrinsic average of the pore-scale liquid velocity, respectively, V denotes the volume of the representative unit cell, ${\varepsilon }_\mathrm{l}$ denotes the porosity and $\left\langle \omega _\mathrm{l}\right\rangle ^{l}$ denotes the intrinsic average of the mass fraction of Ca in the liquid phase. The following deviation fields are introduced

$$\begin{aligned} \omega _\mathrm{l}=\left\langle \omega _\mathrm{l}\right\rangle ^{l}+\tilde{\omega }_\mathrm{l}\quad \text {and}\quad \mathbf {v}_\mathrm{l}=\left\langle \mathbf {v}_\mathrm{l}\right\rangle ^{l}+\tilde{\mathbf {v}}_\mathrm{l}, \end{aligned}$$

(19)

with $\tilde{\omega }_\mathrm{l}$ and $\tilde{\mathbf {v}}_\mathrm{l}$ denoting the deviation of mass fraction and liquid velocity, respectively.

The average of Eq. 11 gives simply

$$\begin{aligned} \frac{\partial {\varepsilon }_\mathrm{l}\rho _\mathrm{l}}{\partial t}+\nabla \cdot \left( \rho _\mathrm{l}\left\langle \mathbf {v}_\mathrm{l}\right\rangle \right) =-K, \end{aligned}$$

(20)

with the mass exchange term corresponding to $K=\frac{1}{V}\int _{A_\mathrm{ls}}\mathbf {n}_\mathrm{ls}\cdot \rho _\mathrm{l}\left( \mathbf {v}_\mathrm{l}-\mathbf {w}_\mathrm{sl}\right) {\text {d}}A$.

The average of the solid mass balance equation gives

$$\begin{aligned} \frac{\partial {\varepsilon }_\mathrm{s}\rho _\mathrm{s}}{\partial t}=K, \end{aligned}$$

(21)

where Eq. 14 has been used to obtain

$$\begin{aligned} K= & {} \frac{1}{V}\int _{A_\mathrm{ls}}\mathbf {n}_\mathrm{ls}\cdot \left( -\rho _\mathrm{s}\mathbf {w}_\mathrm{sl}\right) {\text {d}}A=\frac{1}{V}\int _{A_\mathrm{ls}}\mathbf {n}_\mathrm{ls}\cdot \rho _\mathrm{l}\left( \mathbf {v}_\mathrm{l}-\mathbf {w}_\mathrm{sl}\right) {\text {d}}A\nonumber \\= & {} -a_\mathrm{vl}M_\mathrm{g}k_\mathrm{s}\left\langle \left( 1-\frac{\omega _\mathrm{l}}{\omega _\mathrm{eq}}\right) ^{n}\right\rangle _\mathrm{ls}, \end{aligned}$$

(22)

with the definition of the surface average and specific area as $\left\langle \cdot \right\rangle _\mathrm{ls}=\frac{1}{A_\mathrm{ls}}\int _{A_\mathrm{ls}}\cdot {\text {d}}A$ and $a_\mathrm{vl}=\frac{1}{V}\int _{A_\mathrm{ls}}{\text {d}}A$, respectively.

Finally, the mass balance equation for the Ca component yields

$$\begin{aligned}&\frac{\partial {\varepsilon }_\mathrm{l}\rho _\mathrm{l}\left\langle \omega _\mathrm{l}\right\rangle ^{l}}{\partial t}+\nabla \cdot \left( {\varepsilon }_\mathrm{l}\rho _\mathrm{l}\left\langle \omega _\mathrm{l}\right\rangle ^{l}\left\langle \mathbf {v}_\mathrm{l}\right\rangle ^{l}\right) +\underset{\text {dispersion}}{\underbrace{\nabla \cdot \left( \rho _\mathrm{l}\left\langle \tilde{\omega }_\mathrm{l}\tilde{\mathbf {v}}_\mathrm{l}\right\rangle \right) }}\nonumber \\&\quad =\nabla \cdot \left( {\varepsilon }_\mathrm{l}\rho _\mathrm{l}D_\mathrm{l}\nabla \left\langle \omega _\mathrm{l}\right\rangle ^{l}+\underset{\text {tortuosity}}{\underbrace{\frac{1}{V}\int _{A_\mathrm{ls}}\mathbf {n}_\mathrm{ls}\rho _\mathrm{l}D_\mathrm{l}\tilde{\omega }_\mathrm{l}{\text {d}}A+\frac{1}{V}\int _{A_\mathrm{li}}\mathbf {n}_\mathrm{li}\rho _\mathrm{l}D_\mathrm{l}\tilde{\omega }_\mathrm{l}{\text {d}}A}}\right) -K_\mathrm{l}. \end{aligned}$$

(23)

The total mass exchange term is related to $K_\mathrm{l}$ by

$$\begin{aligned} K_\mathrm{l}=\frac{M_\mathrm{Ca}}{M_\mathrm{g}}K=-a_\mathrm{vl}M_\mathrm{Ca}k_\mathrm{s}\left\langle \left( 1-\frac{\omega _\mathrm{l}}{\omega _\mathrm{eq}}\right) ^{n}\right\rangle _\mathrm{ls}. \end{aligned}$$

(24)

Using Eq. 20, Eq. 23 can be written as

$$\begin{aligned}&{\varepsilon }_\mathrm{l}\rho _\mathrm{l}\frac{\partial \left\langle \omega _\mathrm{l}\right\rangle ^{l}}{\partial t}+{\varepsilon }_\mathrm{l}\rho _\mathrm{l}\left\langle \mathbf {v}_\mathrm{l}\right\rangle ^{l}\cdot \nabla \left\langle \omega _\mathrm{l}\right\rangle ^{l}+\underset{\text {dispersion}}{\underbrace{\nabla \cdot \left( \rho _\mathrm{l}\left\langle \tilde{\omega }_\mathrm{l}\tilde{\mathbf {v}}_\mathrm{l}\right\rangle \right) }}=-K_\mathrm{l}+K\left\langle \omega _\mathrm{l}\right\rangle ^{l}\nonumber \\&\qquad +\nabla \cdot \left( {\varepsilon }_\mathrm{l}\rho _\mathrm{l}D_\mathrm{l}\nabla \left\langle \omega _\mathrm{l}\right\rangle ^{l}+\underset{\text {tortuosity}}{\underbrace{\frac{1}{V}\int _{A_\mathrm{ls}}\mathbf {n}_\mathrm{ls}\rho _\mathrm{l}D_\mathrm{l}\tilde{\omega }_\mathrm{l}{\text {d}}A+\frac{1}{V}\int _{A_\mathrm{li}}\mathbf {n}_\mathrm{li}\rho _\mathrm{l}D_\mathrm{l}\tilde{\omega }_\mathrm{l}{\text {d}}A}}\right) . \end{aligned}$$

(25)

3.2 Deviation Equations and Closure

At this point, an estimate for the concentration deviations has to be found. The governing equations are obtained by substituting Eq. 19 into the pore-scale mass balance equations, then subtracting the averaged equation (Eq. 25) divided by ${\varepsilon }_\mathrm{l}$ (neglecting spatial variations of the volume fraction and liquid density over the representative elementary volume). Using the following intermediate results

$$\begin{aligned}&\nabla \cdot \left( \rho _\mathrm{l}\omega _\mathrm{l}\mathbf {v}_\mathrm{l}\right) =\rho _\mathrm{l}\omega _\mathrm{l}\nabla \cdot \mathbf {v}_\mathrm{l}+\rho _\mathrm{l}\mathbf {v}_\mathrm{l}\cdot \nabla \omega _\mathrm{l}=\rho _\mathrm{l}\mathbf {v}_\mathrm{l}\cdot \nabla \left\langle \omega _\mathrm{l}\right\rangle ^{l}+\rho _\mathrm{l}\mathbf {v}_\mathrm{l}\cdot \nabla \tilde{\omega }_\mathrm{l}, \end{aligned}$$

(26)

$$\begin{aligned}&\quad -{\varepsilon }_\mathrm{l}^{-1}\nabla \cdot \left( {\varepsilon }_\mathrm{l}\rho _\mathrm{l}D_\mathrm{l}\nabla \left\langle \omega _\mathrm{l}\right\rangle ^{l}+\frac{1}{V}\int _{A_\mathrm{ls}}\mathbf {n}_\mathrm{ls}\rho _\mathrm{l}D_\mathrm{l}\tilde{\omega }_\mathrm{l}{\text {d}}A+\frac{1}{V}\int _{A_\mathrm{li}}\mathbf {n}_\mathrm{li}\rho _\mathrm{l}D_\mathrm{l}\tilde{\omega }_\mathrm{l}{\text {d}}A\right) \approx \nonumber \\&\quad -\nabla \cdot \left( \rho _\mathrm{l}D_\mathrm{l}\nabla \left\langle \omega _\mathrm{l}\right\rangle ^{l}+\frac{{\varepsilon }_\mathrm{l}^{-1}}{V}\int _{A_\mathrm{ls}}\mathbf {n}_\mathrm{ls}\rho _\mathrm{l}D_\mathrm{l}\tilde{\omega }_\mathrm{l}{\text {d}}A+\frac{{\varepsilon }_\mathrm{l}^{-1}}{V}\int _{A_\mathrm{li}}\mathbf {n}_\mathrm{li}\rho _\mathrm{l}D_\mathrm{l}\tilde{\omega }_\mathrm{l}{\text {d}}A\right) , \end{aligned}$$

(27)

$$\begin{aligned}&\quad {\varepsilon }_\mathrm{l}^{-1}K_\mathrm{l}-{\varepsilon }_\mathrm{l}^{-1}K\left\langle \omega _\mathrm{l}\right\rangle ^{l}={\varepsilon }_\mathrm{l}^{-1}\frac{1}{V}\int _{A_\mathrm{ls}}\mathbf {n}_\mathrm{ls}\cdot \left( \rho _\mathrm{l}\tilde{\omega }_\mathrm{l}\left( \mathbf {v}_\mathrm{l}-\mathbf {w}_\mathrm{sl}\right) -\rho _\mathrm{l}D_\mathrm{l}\nabla \tilde{\omega }_\mathrm{l}\right) {\text {d}}A\nonumber \\&\quad -\rho _\mathrm{l}D_\mathrm{l}{\varepsilon }_\mathrm{l}^{-1}\frac{1}{V}\int _{A_\mathrm{ls}}\mathbf {n}_\mathrm{ls}{\text {d}}A\cdot \nabla \left\langle \omega _\mathrm{l}\right\rangle ^{l},\end{aligned}$$

(28)

$$\begin{aligned}&\quad \nabla \cdot \left( \frac{{\varepsilon }_\mathrm{l}^{-1}}{V}\int _{A_\mathrm{ls}}\mathbf {n}_\mathrm{ls}\rho _\mathrm{l}D_\mathrm{l}\tilde{\omega }_\mathrm{l}{\text {d}}A+\frac{{\varepsilon }_\mathrm{l}^{-1}}{V}\int _{A_\mathrm{li}}\mathbf {n}_\mathrm{li}\rho _\mathrm{l}D_\mathrm{l}\tilde{\omega }_\mathrm{l}{\text {d}}A\right) \ll \nabla \cdot \left( \rho _\mathrm{l}D_\mathrm{l}\nabla \tilde{\omega }_\mathrm{l}\right) , \end{aligned}$$

(29)

which make use of classical algebra and approximations about averages that are discussed at length in the averaging literature, in particular (Quintard and Whitaker 1994, 1994, 1994, 1994, 1994; Whitaker 1999), one obtains

$$\begin{aligned}&\rho _\mathrm{l}\frac{\partial \tilde{\omega }_\mathrm{l}}{\partial t}+\rho _\mathrm{l}\mathbf {v}_\mathrm{l}\cdot \nabla \tilde{\omega }_\mathrm{l}+\rho _\mathrm{l}{\tilde{\mathbf v}}_\mathrm{l}\cdot \nabla \left\langle \omega _\mathrm{l}\right\rangle ^{l}-{\varepsilon }_\mathrm{l}^{-1}\nabla \cdot \left( \rho _\mathrm{l}\left\langle \tilde{\omega }_\mathrm{l}{\tilde{\mathbf v}}_\mathrm{l}\right\rangle \right) \nonumber \\&\quad =\nabla \cdot \left( \rho _\mathrm{l}D_\mathrm{l}\nabla \tilde{\omega }_\mathrm{l}\right) +\frac{{\varepsilon }_\mathrm{l}^{-1}}{V}\int _{A_\mathrm{ls}}\mathbf {n}_\mathrm{ls}\cdot \rho _\mathrm{l}\tilde{\omega }_\mathrm{l}\left( \mathbf {v}_\mathrm{l}-\mathbf {w}_\mathrm{sl}\right) {\text {d}}A\nonumber \\&\quad \quad -\frac{{\varepsilon }_\mathrm{l}^{-1}}{V}\int _{A_\mathrm{ls}}\mathbf {n}_\mathrm{ls}\cdot \rho _\mathrm{l}D_\mathrm{l}\nabla \tilde{\omega }_\mathrm{l}{\text {d}}A-\rho _\mathrm{l}D_\mathrm{l}{\varepsilon }_\mathrm{l}^{-1}\frac{1}{V}\int _{A_\mathrm{ls}}\mathbf {n}_\mathrm{ls}{\text {d}}A\cdot \nabla \left\langle \omega _\mathrm{l}\right\rangle ^{l}. \end{aligned}$$

(30)

Using Eq. 13, the boundary condition for the deviation may be written

$$\begin{aligned}&\mathbf {n}_\mathrm{ls}\cdot \left( \rho _\mathrm{l}\left\langle \omega _\mathrm{l}\right\rangle ^{l}\left( \mathbf {v}_\mathrm{l}-\mathbf {w}_\mathrm{sl}\right) \right) +\mathbf {n}_\mathrm{ls}\cdot \left( \rho _\mathrm{l}\tilde{\omega }_\mathrm{l}\left( \mathbf {v}_\mathrm{l}-\mathbf {w}_\mathrm{sl}\right) \right) +\mathbf {n}_\mathrm{ls}\cdot \left( -\rho _\mathrm{l}D_\mathrm{l}\nabla \tilde{\omega }_\mathrm{l}\right) \nonumber \\&\quad +\mathbf {n}_\mathrm{ls}\cdot \left( -\rho _\mathrm{l}D_\mathrm{l}\nabla \left\langle \omega _\mathrm{l}\right\rangle ^{l}\right) =-M_\mathrm{Ca}k_\mathrm{s}\left( 1-\frac{\left\langle \omega _\mathrm{l}\right\rangle ^{l}+\tilde{\omega }_\mathrm{l}}{\omega _\mathrm{eq}}\right) ^{n}\qquad \text { at }A_\mathrm{ls}. \end{aligned}$$

(31)

The crucial assumption now, which will be tested quantitatively against direct numerical simulations in Sect. 5, is the approximation of the nonlinear reaction rate by a first-order Taylor’s expansion, i.e.,

$$\begin{aligned}&\mathbf {n}_\mathrm{ls}\cdot \left( \rho _\mathrm{l}\left\langle \omega _\mathrm{l}\right\rangle ^{l}\left( \mathbf {v}_\mathrm{l}-\mathbf {w}_\mathrm{sl}\right) \right) +\mathbf {n}_\mathrm{ls}\cdot \left( \rho _\mathrm{l}\tilde{\omega }_\mathrm{l}\left( \mathbf {v}_\mathrm{l}-\mathbf {w}_\mathrm{sl}\right) \right) +\mathbf {n}_\mathrm{ls}\cdot \left( -\rho _\mathrm{l}D_\mathrm{l}\nabla \tilde{\omega }_\mathrm{l}\right) \nonumber \\&\quad +\mathbf {n}_\mathrm{ls}\cdot \left( -\rho _\mathrm{l}D_\mathrm{l}\nabla \left\langle \omega _\mathrm{l}\right\rangle ^{l}\right) =-\frac{M_\mathrm{Ca}k_\mathrm{s}}{\omega _\mathrm{eq}}\left( 1-\frac{\left\langle \omega _\mathrm{l}\right\rangle ^{l}}{\omega _\mathrm{eq}}\right) ^{n-1}\left( \omega _\mathrm{eq}-\left\langle \omega _\mathrm{l}\right\rangle ^{l}-n\tilde{\omega }_\mathrm{l}\right) . \end{aligned}$$

(32)

Similarly, with Eq. 17 taken into account, Eq. 16 can be rewritten as

$$\begin{aligned} \mathbf {n}_\mathrm{li}\cdot \left( -\rho _\mathrm{l}D_\mathrm{l}\nabla \tilde{\omega }_\mathrm{l}\right) +\mathbf {n}_\mathrm{li}\cdot \left( -\rho _\mathrm{l}D_\mathrm{l}\nabla \left\langle \omega _\mathrm{l}\right\rangle ^{l}\right) =0\qquad \text { at }A_\mathrm{li}. \end{aligned}$$

(33)

Following the developments described in the literature (Valdés-Parada et al. 2011; Soulaine et al. 2011; Quintard and Whitaker 1994), $\left( \left\langle \omega _\mathrm{l}\right\rangle ^{l}-\omega _\mathrm{eq}\right)$ and $\nabla \left\langle \omega _\mathrm{l}\right\rangle ^{l}$ may be viewed as source terms in the above coupled macro-scale and micro-scale governing equations since they may act as generators of the deviation terms. Given the mathematical structure of these coupled equations, an approximate solution can be built based on an expansion involving the source terms and their higher derivatives under the following form

$$\begin{aligned} \tilde{\omega }_\mathrm{l}=s_\mathrm{l}\,\left( \left\langle \omega _\mathrm{l}\right\rangle ^{l}-\omega _\mathrm{eq}\right) +\mathbf {b}_\mathrm{l}\cdot \nabla \left\langle \omega _\mathrm{l}\right\rangle ^{l}+\cdots , \end{aligned}$$

(34)

which gives for the first-order derivatives

$$\begin{aligned} \nabla \tilde{\omega }_\mathrm{l}=\nabla s_\mathrm{l}\,\left( \left\langle \omega _\mathrm{l}\right\rangle ^{l}-\omega _\mathrm{eq}\right) +\left( \nabla \mathbf {b}_\mathrm{l}+s_\mathrm{l}\mathbf {I}\right) \cdot \nabla \left\langle \omega _\mathrm{l}\right\rangle ^{l}+\cdots \end{aligned}$$

(35)

According to the length scale constraints $l_\mathrm{s},l_\mathrm{i},l_\mathrm{l}\ll r_{0}\ll L$, terms involving higher order derivatives than $\nabla \left\langle \omega _\mathrm{l}\right\rangle ^{l}$ in Eq. 35 can be neglected. Substituting Eqs. 34 and 35 into Eq. 30, collecting terms for $\left( \left\langle \omega _\mathrm{l}\right\rangle ^{l}-\omega _\mathrm{eq}\right)$ and $\nabla \left\langle \omega _\mathrm{l}\right\rangle ^{l}$ and then applying the fundamental lemma stated in Quintard and Whitaker (1994), the following two “closure problems” were obtained, which depend on the macro-scale concentration $\left\langle \omega _\mathrm{l}\right\rangle ^{l}$ as a parameter. This latter result is entirely a consequence of the Taylor’s expansion approximation.

Problem I:

$$\begin{aligned}&\displaystyle \rho _\mathrm{l}\frac{\partial s_\mathrm{l}}{\partial t}+\rho _\mathrm{l}\mathbf {v}_\mathrm{l}\cdot \nabla s_\mathrm{l}=\nabla \cdot \left( \rho _\mathrm{l}D_\mathrm{l}\nabla s_\mathrm{l}\right) +{\varepsilon }_\mathrm{l}^{-1}\rho _\mathrm{l}X_\mathrm{l}\,\,\,\,\,\ \text { in }V_\mathrm{l}, \end{aligned}$$

(36)

$$\begin{aligned}&\displaystyle \text {B.C. I}\,\,\,\,\,\,\mathbf {n}_\mathrm{ls}\cdot \frac{\left\langle \omega _\mathrm{l}\right\rangle ^{l}}{\left\langle \omega _\mathrm{l}\right\rangle ^{l}-\omega _\mathrm{eq}}\rho _\mathrm{l}\left( \mathbf {v}_\mathrm{l}-\mathbf {w}_\mathrm{sl}\right) +\mathbf {n}_\mathrm{ls}\cdot \left( \rho _\mathrm{l}s_\mathrm{l}\left( \mathbf {v}_\mathrm{l}-\mathbf {w}_\mathrm{sl}\right) -\rho _\mathrm{l}D_\mathrm{l}\mathbf {\nabla }s_\mathrm{l}\right) \nonumber \\&\displaystyle \qquad =\frac{M_\mathrm{Ca}k_\mathrm{s}}{\omega _\mathrm{eq}}\left( 1-\frac{\left\langle \omega _\mathrm{l}\right\rangle ^{l}}{\omega _\mathrm{eq}}\right) ^{n-1}\left( 1+n\, s_\mathrm{l}\right) \qquad \text { at }A_\mathrm{ls}(t), \end{aligned}$$

(37)

$$\begin{aligned}&\displaystyle \text {B.C. II}\,\,\,\,\,\,\mathbf {n}_\mathrm{li}\cdot \left( -\rho _\mathrm{l}D_\mathrm{l}\mathbf {\nabla }s_\mathrm{l}\right) =0\,\,\,\,\,\ \text {at }A_\mathrm{li},\end{aligned}$$

(38)

$$\begin{aligned}&\displaystyle \left\langle s_\mathrm{l}\right\rangle =0\,\,\,\,\,\ \text {in }V_\mathrm{l}, \end{aligned}$$

(39)

$$\begin{aligned}&\displaystyle s_\mathrm{l}\left( \mathbf {x}+\mathbf {l}_\mathrm{i}\right) =s_\mathrm{l}\left( \mathbf {x}\right) , \end{aligned}$$

(40)

where the notation $A_\mathrm{ls}(t)$ was used to remind of the geometry evolution. In the above set of closure problem, the following notation has been used

$$\begin{aligned} \rho _\mathrm{l}X_\mathrm{l}= & {} \frac{1}{V}\int _{A_\mathrm{ls}}\mathbf {n}_\mathrm{ls}\cdot \rho _\mathrm{l}s_\mathrm{l}\left( \mathbf {v}_\mathrm{l}-\mathbf {w}_\mathrm{sl}\right) {\text {d}}A-\frac{1}{V}\int _{A_\mathrm{ls}}\mathbf {n}_\mathrm{ls}\cdot \rho _\mathrm{l}D_\mathrm{l}\nabla s_\mathrm{l}{\text {d}}A\nonumber \\&-\frac{1}{V}\int _{A_\mathrm{li}}\mathbf {n}_\mathrm{li}\cdot \rho _\mathrm{l}D_\mathrm{l}\nabla s_\mathrm{l}{\text {d}}A. \end{aligned}$$

(41)

Taking the average of Eq. 36 and the fact that $\rho _\mathrm{l}\left\langle \mathbf {v}_\mathrm{l}\cdot \nabla s_\mathrm{l}\right\rangle =\rho _\mathrm{l}\nabla \cdot \left\langle \mathbf {v}_\mathrm{l}s_\mathrm{l}\right\rangle =0$ because of the periodicity conditions leads to the equation

$$\begin{aligned} \rho _\mathrm{l}\frac{\partial \left\langle s_\mathrm{l}\right\rangle }{\partial t}= & {} -\frac{1}{V}\int _{A_\mathrm{ls}}\mathbf {n}_\mathrm{ls}\cdot \rho _\mathrm{l}s_\mathrm{l}\left( \mathbf {v}_\mathrm{l}-\mathbf {w}_\mathrm{sl}\right) {\text {d}}A+\frac{1}{V}\int _{A_\mathrm{ls}}\mathbf {n}_\mathrm{ls}\cdot \rho _\mathrm{l}D_\mathrm{l}\nabla s_\mathrm{l}{\text {d}}A\nonumber \\&+\frac{1}{V}\int _{A_\mathrm{li}}\mathbf {n}_\mathrm{li}\cdot \rho _\mathrm{l}D_\mathrm{l}\nabla s_\mathrm{l}{\text {d}}A+\rho _\mathrm{l}X_\mathrm{l}\equiv 0, \end{aligned}$$

(42)

which confirms the consistency of the proposed closure problem.

Problem II:

$$\begin{aligned}&\displaystyle \rho _\mathrm{l}\frac{\partial \mathbf {b}_\mathrm{l}}{\partial t}+\rho _\mathrm{l}\mathbf {v}_\mathrm{l}\cdot \left( \nabla \mathbf {b}_\mathrm{l}+s_\mathrm{l}\mathbf {I}\right) +\rho _\mathrm{l}\tilde{\mathbf {v}}_\mathrm{l}-{\varepsilon }_\mathrm{l}^{-1}\rho _\mathrm{l}\left\langle {\tilde{\mathbf v}}_\mathrm{l}s_\mathrm{l}\right\rangle \nonumber \\&\displaystyle \quad = \nabla \cdot \left( \rho _\mathrm{l}D_\mathrm{l}\left( \nabla \mathbf {b}_\mathrm{l}+s_\mathrm{l}\mathbf {I}\right) \right) +{\varepsilon }_\mathrm{l}^{-1}\rho _\mathrm{l}\mathbf {u}_\mathrm{l}\,\text { in }V_\mathrm{l}, \end{aligned}$$

(43)

$$\begin{aligned}&\displaystyle \text {B.C. I}\mathbf {n}_\mathrm{ls}\cdot \left( \rho _\mathrm{l}\left( \mathbf {v}_\mathrm{l}-\mathbf {w}_\mathrm{sl}\right) \mathbf {b}_\mathrm{l}-\rho _\mathrm{l}D_\mathrm{l}\left( \nabla \mathbf {b}_\mathrm{l}+s_\mathrm{l}\mathbf {I}\right) \right) -\rho _\mathrm{l}D_\mathrm{l}\mathbf {n}_\mathrm{ls}\nonumber \\&\displaystyle \quad =n\frac{M_\mathrm{Ca}k_\mathrm{s}}{\omega _\mathrm{eq}}\left( 1-\frac{\left\langle \omega _\mathrm{l}\right\rangle ^{l}}{\omega _\mathrm{eq}}\right) ^{n-1}\mathbf {b}_\mathrm{l}\ \qquad \text {at }A_\mathrm{ls}(t), \end{aligned}$$

(44)

$$\begin{aligned}&\displaystyle \text {B.C. II}\,\,\,\,\,\,\mathbf {n}_\mathrm{li}\cdot \left( -\rho _\mathrm{l}D_\mathrm{l}\left( \nabla \mathbf {b}_\mathrm{l}+s_\mathrm{l}\mathbf {I}\right) \right) =\rho _\mathrm{l}D_\mathrm{l}\mathbf {n}_\mathrm{li}\,\,\,\,\,\ \text {at }A_\mathrm{li}, \end{aligned}$$

(45)

$$\begin{aligned}&\displaystyle \left\langle \mathbf {b}_\mathrm{l}\right\rangle =0\,\,\,\,\,\ \text { in }V_\mathrm{l}, \end{aligned}$$

(46)

$$\begin{aligned}&\displaystyle \mathbf {b}_\mathrm{l}\left( \mathbf {x}+\mathbf {l}_\mathrm{i}\right) =\mathbf {b}_\mathrm{l}\left( \mathbf {x}\right) , \end{aligned}$$

(47)

in which

$$\begin{aligned} \rho _\mathrm{l}\mathbf {u}_\mathrm{l}= & {} \frac{1}{V}\int _{A_\mathrm{ls}} \mathbf {n}_\mathrm{ls}\cdot \rho _\mathrm{l}\left( \mathbf {v}_\mathrm{l}- \mathbf {w}_\mathrm{sl}\right) \mathbf {b}_\mathrm{l}{\text {d}}A-\frac{1}{V}\int _{A_\mathrm{ls}} \mathbf {n}_\mathrm{ls}\cdot \rho _\mathrm{l}D_\mathrm{l}\left( \nabla \mathbf {b}_\mathrm{l}+s_\mathrm{l} \mathbf {I}\right) {\text {d}}A\qquad \nonumber \\&-\frac{1}{V}\int _{A_\mathrm{li}}\mathbf {n}_\mathrm{li}\cdot \rho _\mathrm{l}D_\mathrm{l} \left( \nabla \mathbf {b}_\mathrm{l}+s_\mathrm{l}\mathbf {I}\right) {\text {d}}A, \end{aligned}$$

(48)

which can be used to check the consistency relationship $\rho _\mathrm{l}\frac{\partial \left\langle \mathbf {b}_\mathrm{l}\right\rangle }{\partial t}\equiv 0$.

In both closure problems, the zero average conditions on the mapping fields $s_\mathrm{l}$ and $\mathbf {b}_\mathrm{l}$ ensure that the concentration deviation is zero. The initial conditions that must be added to the two sets of equations in order to get a complete problem remain unspecified. They depend on the specific problem to be solved in the transient case. Since only the steady-state behavior is considered in the next sections, this discussion is not pushed further here.

Here one sees that a complete coupling between Problem I and II has been kept according to terms involving $s_\mathrm{l}$ in Problem II. While this coupling is often discarded in many contributions, it has been shown in Golfier et al. (2002) that such a coupling may be necessary to get an accurate estimate of the exchanged flux, depending on the pore-scale geometry. So far the interface velocity has not been discarded at any step, which provides a very consistent theory in the mass balance equations. In order to solve these problems, however, the interface position and velocity as well as the macro-scale concentration must be known properties because of the reaction nonlinearity. The classical geochemistry problem faced here is that in principle, the coupled pore-scale (here the closure problems) and macro-scale equations must be solved at each time step in order to compute the interface evolution and $\left\langle \omega _\mathrm{l}\right\rangle ^{l}$. In geochemistry (or other problems involving changing geometries), it is often assumed a given interface evolution and the closure problems are solved for each realization, which in turn yields effective properties depending on, for instance, the medium porosity. In turn, these effective properties can be used in a macro-scale simulation without the need of a coupled micro-scale/macro-scale solution. Of course, it is well known that some history effects are lost in this process (Békri et al. 1995), but it has the advantage that this is far more practical than solving the coupled problem.

Assuming that mass fluxes near the interface are triggered by the diffusive flux, which is acceptable in most dissolution problems, approximate closure problems may be developed as done in Sect. 4.

3.3 Macro-Scale Equation and Effective Properties

Introducing the deviation expression Eq. 34 in the averaged equation Eq. 23 leads to

(49)

with $K_\mathrm{l}$ defined by Eq. 24.

It is convenient to write Eq. 49 under the form of a generalized dispersion equation such as

$$\begin{aligned}&\frac{\partial {\varepsilon }_\mathrm{l}\rho _\mathrm{l}\left\langle \omega _\mathrm{l}\right\rangle ^{l}}{\partial t}+\nabla \cdot \left( {\varepsilon }_\mathrm{l}\rho _\mathrm{l}\left\langle \omega _\mathrm{l}\right\rangle ^{l}\left\langle \mathbf {v}_\mathrm{l}\right\rangle ^{l}+{\varepsilon }_\mathrm{l}\rho _\mathrm{l}\left( \left\langle \omega _\mathrm{l}\right\rangle ^{l}-\omega _\mathrm{eq}\right) \mathbf {U}_\mathrm{l}^{*}\right) \nonumber \\&\quad =\nabla \cdot \left( {\varepsilon }_\mathrm{l}\rho _\mathrm{l}\mathbf {D}_\mathrm{l}^{*}\cdot \nabla \left\langle \omega _\mathrm{l}\right\rangle ^{l}\right) -K_\mathrm{l}, \end{aligned}$$

(50)

with the dispersion tensor given by

$$\begin{aligned} \mathbf {D}_\mathrm{l}^{*}=D_\mathrm{l}\left( \mathbf {I}+\frac{1}{V_\mathrm{l}}\int _{A_\mathrm{ls}}\mathbf {n}_\mathrm{ls}\mathbf {b}_\mathrm{l}{\text {d}}A+\frac{1}{V_\mathrm{l}}\int _{A_\mathrm{li}}\mathbf {n}_\mathrm{li}\mathbf {b}_\mathrm{l}{\text {d}}A\right) -\left\langle \tilde{\mathbf {v}}_\mathrm{l}\mathbf {b}_\mathrm{l}\right\rangle ^{l}, \end{aligned}$$

(51)

and the non-traditional effective velocity given by

$$\begin{aligned} \mathbf {U}_\mathrm{l}^{*}=\left\langle \tilde{\mathbf {v}}_\mathrm{l}s_\mathrm{l}\right\rangle ^{l}-\frac{1}{V_\mathrm{l}}\int _{A_\mathrm{ls}}\mathbf {n}_\mathrm{ls}D_\mathrm{l}s_\mathrm{l}{\text {d}}A-\frac{1}{V_\mathrm{l}}\int _{A_\mathrm{li}}\mathbf {n}_\mathrm{li}D_\mathrm{l}s_\mathrm{l}{\text {d}}A. \end{aligned}$$

(52)

The mass exchange term can be calculated as (neglecting higher order derivatives than $\nabla \left\langle \omega _\mathrm{l}\right\rangle ^{l}$)

$$\begin{aligned} K_\mathrm{l}= & {} \left\langle \omega _\mathrm{l}\right\rangle _\mathrm{ls}K+\left( \left\langle \omega _\mathrm{l}\right\rangle ^{l}-\omega _\mathrm{eq}\right) \frac{1}{V}\int _{A_\mathrm{ls}}\mathbf {n}_\mathrm{ls}\cdot \left( \rho _\mathrm{l}s_\mathrm{l}\left( \mathbf {v}_\mathrm{l}-\mathbf {w}_\mathrm{sl}\right) -\rho _\mathrm{l}D_\mathrm{l}\nabla s_\mathrm{l}\right) {\text {d}}A\nonumber \\&+\left( \frac{1}{V}\int _{A_\mathrm{ls}}\mathbf {n}_\mathrm{ls}\cdot \left( \rho _\mathrm{l}\left( \mathbf {v}_\mathrm{l}-\mathbf {w}_\mathrm{sl}\right) \mathbf {b}_\mathrm{l}-\rho _\mathrm{l}D_\mathrm{l}\left( \nabla \mathbf {b}_\mathrm{l}+s_\mathrm{l}\mathbf {I}\right) \right) {\text {d}}A\right) \cdot \nabla \left\langle \omega _\mathrm{l}\right\rangle ^{l}\nonumber \\&-\rho _\mathrm{l}D_\mathrm{l}\left( \frac{1}{V}\int _{A_\mathrm{ls}}\mathbf {n}_\mathrm{ls}{\text {d}}A\right) \cdot \nabla \left\langle \omega _\mathrm{l}\right\rangle ^{l}. \end{aligned}$$

(53)

This formula is useful in the sense that it emphasizes the structure of the mass exchange term regardless of the chosen expression used for the reaction rate (it could be also an equilibrium boundary condition). In particular it shows that the mass exchange term is not only depending on the averaged concentration but also on its gradient. Of course, it is also useful to relate this term to the reaction rate expression by a direct averaging of Eq. 24, which gives

$$\begin{aligned} K_\mathrm{l}=-a_\mathrm{vl}M_\mathrm{Ca}k_\mathrm{s}\left\langle \left( 1-\frac{\left\langle \omega _\mathrm{l}\right\rangle ^{l}+s_\mathrm{l}\,\left( \left\langle \omega _\mathrm{l}\right\rangle ^{l}-\omega _\mathrm{eq}\right) +\mathbf {b}_\mathrm{l}\cdot \nabla \left\langle \omega _\mathrm{l}\right\rangle ^{l}}{\omega _\mathrm{eq}}\right) ^{n}\right\rangle _\mathrm{ls}. \end{aligned}$$

(54)

The linearized version, as in Eq. 32, would lead to

$$\begin{aligned} K_\mathrm{l}=-a_\mathrm{vl}M_\mathrm{Ca}\left( 1-\frac{\left\langle \omega _\mathrm{l}\right\rangle ^{l}}{\omega _\mathrm{eq}}\right) ^{n}k_\mathrm{s,eff}+a_\mathrm{vl}M_\mathrm{Ca}\left( 1-\frac{\left\langle \omega _\mathrm{l}\right\rangle ^{l}}{\omega _\mathrm{eq}}\right) ^{n-1}\mathbf {h}_\mathrm{l}^{*}\cdot \nabla \left\langle \omega _\mathrm{l}\right\rangle ^{l}. \end{aligned}$$

(55)

where the effective reaction rate coefficient is given by

$$\begin{aligned} k_\mathrm{s,eff}=k_\mathrm{s}\left( 1+n\left\langle s_\mathrm{l}\right\rangle _\mathrm{ls}\right) , \end{aligned}$$

(56)

in a similar form as in Wood et al. (2007) for the first-order reaction case. The additional gradient term coefficient is

$$\begin{aligned} \mathbf {h}_\mathrm{l}^{*}=n\frac{k_\mathrm{s}}{\omega _\mathrm{eq}}\left\langle \mathbf {b}_\mathrm{l}\right\rangle _\mathrm{ls}. \end{aligned}$$

(57)

One must remember that the macro-scale problem involves also the following averaged equations

$$\begin{aligned} \frac{\partial {\varepsilon }_\mathrm{l}\rho _\mathrm{l}}{\partial t}+\nabla \cdot \left( \rho _\mathrm{l}\left\langle \mathbf {v}_\mathrm{l}\right\rangle \right) =-K,\quad \frac{\partial {\varepsilon }_\mathrm{s}\rho _\mathrm{s}}{\partial t}=K. \end{aligned}$$

(58)

The resulting macro-scale model is a generalization to nonlinear reaction rates of non-equilibrium models previously published. Such models are useful in many circumstances, for instance as diffuse interface models for modeling the dissolution of cavities (Luo et al. 2012, 2014) or for studying instability of dissolution fronts (Golfier et al. 2002).

3.4 Reactive Limiting Cases and Thermodynamic Equilibrium

It is useful to rewrite the above developed closure problems into a dimensionless form as presented in “Appendix”, where two dimensionless numbers were generated therein with the following definitions

$$\begin{aligned} (\mathrm {a})\quad Pe=\frac{U_\mathrm{r}l_\mathrm{r}}{D_\mathrm{l}},\quad (\mathrm {b})\quad Da=\frac{M_\mathrm{Ca}}{\rho _\mathrm{l}\omega _\mathrm{eq}}\frac{l_\mathrm{r}k_\mathrm{s}}{D_\mathrm{l}}\left( 1-\frac{\left\langle \omega _\mathrm{l}\right\rangle ^{l}}{\omega _\mathrm{eq}}\right) ^{n-1}, \end{aligned}$$

(59)

where Da is the second Damköhler number since the reaction takes place at the solid–liquid surface. The first limiting case of interest is obtained when Da is very small, which leads to

• 1. the mapping variable $s_\mathrm{l}$ is zero,

• 2. one recovers for $\mathbf {b}_\mathrm{l}$ the closure problem for passive dispersion.

As a consequence, the mass exchange rate from Eq. 54 can be written as

$$\begin{aligned} K_\mathrm{l}=-a_\mathrm{vl}M_\mathrm{Ca}k_\mathrm{s}\left\langle \left( 1-\frac{\left\langle \omega _\mathrm{l}\right\rangle ^{l}}{\omega _\mathrm{eq}}\right) ^{n}\right\rangle _\mathrm{ls}, \end{aligned}$$

(60)

where the estimate $\mathbf {b}_\mathrm{l}\cdot \nabla \left\langle \omega _\mathrm{l}\right\rangle ^{l}\approx \mathcal {O}\left( \frac{l_\mathrm{l}}{L}\left\langle \omega _\mathrm{l}\right\rangle ^{l}\right)$ has been used to discard this term in front of $\left\langle \omega _\mathrm{l}\right\rangle ^{l}$.

The second limiting case of interest is obtained when Da is very large, then Eq. 13 may be replaced by

$$\begin{aligned} \text {B.C. I}\qquad \omega _\mathrm{l}=\omega _\mathrm{eq}\qquad \text { at }A_\mathrm{ls}, \end{aligned}$$

(61)

and thermodynamic equilibrium is recovered at the dissolving interface at pore-scale. With the definition of Da by Eq. 59b, this may be obtained under the following two conditions:

• 1. the physical parameters must be such that $\frac{M_\mathrm{Ca}}{\rho _\mathrm{l}\omega _\mathrm{eq}}\frac{l_\mathrm{r}k_\mathrm{s}}{D_\mathrm{l}}\gg 1$,

• 2. $n=1$ (since $\left\langle \omega _\mathrm{l}\right\rangle ^{l}$ has a tendency to grow up to $\omega _\mathrm{eq}$), which excludes nonlinear reaction rates!

As a consequence of Eq. 61, it is recovered that

$$\begin{aligned} s_\mathrm{l}=-1\quad \text {and}\quad \mathbf {b}_\mathrm{l}=0\qquad \text {at }A_\mathrm{ls}(t), \end{aligned}$$

(62)

when $Da\gg 1$.

In the case of thermodynamic equilibrium at pore-scale, the macro-scale equations are the same as before obtained for the reactive case (Eqs. 49 to 52 and 58), but for a different expression of the mass exchange term which can be rewritten from Eq. 53 (one cannot use Eq. 55 because of the undetermined limit at large $k_\mathrm{s}$), since $\left\langle \omega _\mathrm{l}\right\rangle _\mathrm{ls}=\omega _\mathrm{eq}$, as

$$\begin{aligned} K_\mathrm{l}= & {} \omega _\mathrm{eq}K+\left( \left\langle \omega _\mathrm{l}\right\rangle ^{l}-\omega _\mathrm{eq}\right) \frac{1}{V}\int _{A_\mathrm{ls}}\mathbf {n}_\mathrm{ls}\cdot \left( -\rho _\mathrm{l}D_\mathrm{l}\nabla s_\mathrm{l}\right) {\text {d}}A\nonumber \\&+\left( \frac{1}{V}\int _{A_\mathrm{ls}}\mathbf {n}_\mathrm{ls}\cdot \left( -\rho _\mathrm{l}D_\mathrm{l}\nabla \mathbf {b}_\mathrm{l}\right) {\text {d}}A\right) \cdot \nabla \left\langle \omega _\mathrm{l}\right\rangle ^{l}, \end{aligned}$$

(63)

which can be formally written as

$$\begin{aligned} K_\mathrm{l}=\omega _\mathrm{eq}K+\rho _\mathrm{l}\alpha _\mathrm{l}\left( \left\langle \omega _\mathrm{l}\right\rangle ^{l}-\omega _\mathrm{eq}\right) +\rho _\mathrm{l}\mathbf {h}_\mathrm{l}\cdot \nabla \left\langle \omega _\mathrm{l}\right\rangle ^{l}, \end{aligned}$$

(64)

where the following notations for the mass exchange coefficient

$$\begin{aligned} \alpha _\mathrm{l}=\frac{1}{V}\int _{A_\mathrm{ls}}\mathbf {n}_\mathrm{ls}\cdot \left( -D_\mathrm{l}\nabla s_\mathrm{l}\right) {\text {d}}A, \end{aligned}$$

(65)

and the additional gradient term

$$\begin{aligned} \mathbf {h}_\mathrm{l}=\left( \frac{1}{V}\int _{A_\mathrm{ls}}\mathbf {n}_\mathrm{ls}\cdot \left( -D_\mathrm{l}\nabla \mathbf {b}_\mathrm{l}\right) {\text {d}}A\right) , \end{aligned}$$

(66)

have been adopted. One should note that the mass exchange term is often reduced in the literature to the single term $\rho _\mathrm{l}\alpha _\mathrm{l}\left( \left\langle \omega _\mathrm{l}\right\rangle ^{l}-\omega _\mathrm{eq}\right)$.

When assuming that terms involving the interface velocity are small, the two closure problems are reminiscent of the closure problems encountered in NAPL dissolution and studied in Quintard and Whitaker (1994). One limiting case of this transport model is the local-equilibrium model, obtained when $\alpha _\mathrm{l}$ is very large and that will impose

$$\begin{aligned} \left\langle \omega _\mathrm{l}\right\rangle ^{l}=\omega _\mathrm{eq}, \end{aligned}$$

(67)

as soon as the liquid is in contact with a zone containing the dissolving material. In that case, $\left\langle \omega _\mathrm{l}\right\rangle ^{l}=\omega _\mathrm{eq}$ is put in Eq. 50 to calculate K in Eq. 58.

Of special interest is the case of a linear reaction rate, i.e., $n=1$, for which the mass exchange term can be written as

$$\begin{aligned} \frac{\omega _\mathrm{eq}}{M_\mathrm{Ca}}K_\mathrm{l}=-a_\mathrm{vl}k_\mathrm{s,eff}\left( \omega _\mathrm{eq}-\left\langle \omega _\mathrm{l}\right\rangle ^{l}\right) +a_\mathrm{vl}k_\mathrm{s}\left\langle \mathbf {b}_\mathrm{l}\right\rangle _\mathrm{ls}\cdot \nabla \left\langle \omega _\mathrm{l}\right\rangle ^{l}, \end{aligned}$$

(68)

where an effective reaction rate coefficient, $k_\mathrm{s,eff}$, has been introduced such as

$$\begin{aligned} \frac{k_\mathrm{s,eff}}{k_\mathrm{s}}\mid _{n=1}=\left( 1+\left\langle s_\mathrm{l}\right\rangle _\mathrm{ls}\right) . \end{aligned}$$

(69)

The two limiting cases with respect to Da lead to

• 1. $Da\rightarrow 0$: $s_\mathrm{l}=0$ and hence $\frac{k_\mathrm{s,eff}}{k_\mathrm{s}}\mid _{n=1}=1$;

• 2. $Da\rightarrow \infty$: the effective reaction rate becomes independent of Da and is only controlled by the transport problem.

Neglecting the additional coupling terms and the terms involving the interface velocity, the theoretical results presented in Valdés-Parada et al. (2011) are recovered.

4 Effective Parameters for the Nonlinear Reactive Case

In this section, the steady-state form of the closure equations in “Appendix” is solved for a stratified and two 3D representative unit cells. Both unit cells in Fig. 2a, b are composed of a soluble solid (s), an insoluble solid (i) and a liquid (l) phase. For the 3D geometry, a second case is tested with all the solid phase soluble (cf. Fig. 2c). The dependency of the macro-scale effective parameters on the flow properties and chemical features in terms of local Péclet (Pe) and Damköhler (Da) numbers defined by Eq. 59, as well as on the reaction nonlinearity, are investigated. In the dimensionless problems, the height of the stratified geometry ($l_\mathrm{i}+l_\mathrm{l}+l_\mathrm{s}$), and the diameter of the spheres, $d_{0}$ in the 3D geometries, are used as the characteristic length, $l_\mathrm{r}$. The characteristic velocity $U_\mathrm{r}$ is defined as the x-component of the intrinsic average velocity $\left\langle u_\mathrm{l}\right\rangle ^{l}$. For the stratified unit cell, the flow is of Poiseuille type given by the following expression

$$\begin{aligned} u_\mathrm{l}=\frac{3}{2}\left\langle u_\mathrm{l}\right\rangle ^{l}\left( 1-\frac{(y-R_{0})^{2}}{\left( \frac{l_\mathrm{l}}{4}\right) ^{2}}\right) , \end{aligned}$$

(70)

with $R_{0}=\pm \left( l_\mathrm{i}/2+l_\mathrm{l}/4\right)$, positive in the upper part and negative in the lower part of the domain, while the velocity field is obtained numerically for the 3D flow problem, by solving dimensionless Navier–Stokes equations with $Re=\frac{\rho U_\mathrm{r}l_\mathrm{r}}{\mu _\mathrm{l}}=10^{-6}$, i.e., negligible inertia effects.

Fig. 2

Unit cells. a Stratified (1D) unit cell. b 3D unit cell with insoluble material. c 3D unit cell without insoluble material

4.1 Analytical Solutions for the Stratified Unit Cell

Solving the dimensionless form of the simplified closure problems in “Appendix” for the stratified unit cell presented in Fig. 2a, the analytical solutions for the effective parameters generated in Sect. 3 were obtained, with

$$\begin{aligned}&\displaystyle \frac{\left( {\mathbf {D}}_\mathrm{l}^{*}\right) _{xx}}{D_\mathrm{l}}=1+\frac{\mathrm {Pe^{2}}{\varepsilon }_\mathrm{l}^{2} \left( \mathrm {11Da^{2}}{\varepsilon }_\mathrm{l}^{2}n^{2}- \mathrm {3Da^{2}}{\varepsilon }_\mathrm{l}^{2}n+\mathrm {146Da} {\varepsilon }_\mathrm{l}n+\mathrm {16Da}{\varepsilon }_\mathrm{l}+480\right) }{11200\left( Da{\varepsilon }_\mathrm{l}n+6\right) ^{2}}, \qquad \quad \end{aligned}$$

(71)

$$\begin{aligned}&\displaystyle \frac{\left( {\mathbf {D}}_\mathrm{l}^{*}\right) _{xy}}{D_\mathrm{l}} =\frac{PeDa{\varepsilon }_\mathrm{l}^{2} \left( \mathrm {4Da}{\varepsilon }_\mathrm{l}n^{2}+3Da {\varepsilon }_\mathrm{l}n+24n+24\right) }{320\left( Da {\varepsilon }_\mathrm{l}n+6\right) ^{2}}, \end{aligned}$$

(72)

$$\begin{aligned}&\displaystyle \frac{\left( {\mathbf {D}}_\mathrm{l}^{*}\right) _{yx}}{D_\mathrm{l}}=-\frac{PeDa{\varepsilon }_\mathrm{l}^{2}\left( \mathrm {7Da}{\varepsilon }_\mathrm{l}n^{2}-4Da{\varepsilon }_\mathrm{l}n+42n-126\right) }{560\left( Da{\varepsilon }_\mathrm{l}n+6\right) ^{2}},\end{aligned}$$

(73)

$$\begin{aligned}&\displaystyle \frac{\left( {\mathbf {D}}_\mathrm{l}^{*}\right) _{yy}}{D_\mathrm{l}}=\frac{3Da{\varepsilon }_\mathrm{l}n\left( 4Da{\varepsilon }_\mathrm{l}n-Da{\varepsilon }_\mathrm{l}+24\right) }{16\left( Da{\varepsilon }_\mathrm{l}n+6\right) ^{2}}, \end{aligned}$$

(74)

$$\begin{aligned}&\displaystyle (\mathrm {a})\quad \frac{\left( \mathbf {U}_\mathrm{l}^{*}\right) _{x}}{U_\mathrm{r}}=\frac{Da{\varepsilon }_\mathrm{l}}{20\left( Da{\varepsilon }_\mathrm{l}n+6\right) },\quad (\mathrm {b})\quad \frac{\left( \mathbf {U}_\mathrm{l}^{*}\right) _{y}}{U_\mathrm{r}}=\frac{3Da}{\left( Da{\varepsilon }_\mathrm{l}n+6\right) Pe}, \end{aligned}$$

(75)

$$\begin{aligned}&\displaystyle \frac{k_\mathrm{s,eff}}{k_\mathrm{s}}=\frac{6}{Da{\varepsilon }_\mathrm{l}n+6},\end{aligned}$$

(76)

$$\begin{aligned}&\displaystyle \frac{\left( \mathbf {h}_\mathrm{l}^{*}\right) _{x}}{l_\mathrm{r}}=\frac{n\, k_\mathrm{s}Pe{\varepsilon }_\mathrm{l}^{2}\left( 7Da{\varepsilon }_\mathrm{l}n+17Da{\varepsilon }_\mathrm{l}+42\right) }{280\omega _\mathrm{eq}\left( Da{\varepsilon }_\mathrm{l}n+6\right) ^{2}}, \end{aligned}$$

(77)

$$\begin{aligned}&\displaystyle \frac{\left( \mathbf {h}_\mathrm{l}^{*}\right) _{y}}{l_\mathrm{r}}=-\frac{3n\, k_\mathrm{s}{\varepsilon }_\mathrm{l}\left( 4Da{\varepsilon }_\mathrm{l}n-Da{\varepsilon }_\mathrm{l}+24\right) }{8\omega _\mathrm{eq}\left( Da{\varepsilon }_\mathrm{l}n+6\right) ^{2}}. \end{aligned}$$

(78)

Regarding the impact of flow properties, the longitudinal dispersion coefficient $\left( {\mathbf {D}}_\mathrm{l}^{*}\right) _{xx}/D_\mathrm{l}$ has a classical square dependence on the local Péclet number (Pe) typical of Taylor’s dispersion. $\left( {\mathbf {D}}_\mathrm{l}^{*}\right) _{xy}/D_\mathrm{l}$, $\left( {\mathbf {D}}_\mathrm{l}^{*}\right) _{yx}/D_\mathrm{l}$ and $\left( \mathbf {h}_\mathrm{l}^{*}\right) _{x}/l_\mathrm{r}$ are linear functions of Pe. $\left( {\mathbf {D}}_\mathrm{l}^{*}\right) _{yy}/D_\mathrm{l},$ $\left( \mathbf {U}_\mathrm{l}^{*}\right) _{x}/U_\mathrm{r}$, $k_\mathrm{s,eff}/k_\mathrm{s}$ and $\left( \mathbf {h}_\mathrm{l}^{*}\right) _{y}/l_\mathrm{r}$ are independent of Pe, while $\left( \mathbf {U}_\mathrm{l}^{*}\right) _{y}/U_\mathrm{r}$ is inversely proportional to Pe. It must be understood that these results, because of the periodicity condition, correspond to a fully developed concentration field, i.e., at some distance of the entrance region (cf. Golfier et al. 2002). If one wants to take into account precisely the entrance region effect (i.e., dissolution at the beginning of the front), one has to develop a non-local closure in which the distance from the front beginning will play a role.

When $Da=0$, the classical passive dispersion case is recovered, with the transport properties given by

$$\begin{aligned} \mathbf {U}_\mathrm{l}^{*}=0,\quad \frac{\left( {\mathbf {D}}_\mathrm{l}^{*}\right) _{xx}}{D_\mathrm{l}}=1+\frac{\mathrm {Pe^{2}{\varepsilon }_\mathrm{l}^{2}}}{840},\quad \frac{\left( {\mathbf {D}}_\mathrm{l}^{*}\right) _{xy}}{D_\mathrm{l}}=\frac{\left( {\mathbf {D}}_\mathrm{l}^{*}\right) _{yx}}{D_\mathrm{l}}=\frac{\left( {\mathbf {D}}_\mathrm{l}^{*}\right) _{yy}}{D_\mathrm{l}}=0. \end{aligned}$$

(79)

The effective reaction rate coefficient turns to be

$$\begin{aligned} \frac{k_\mathrm{s,eff}}{k_\mathrm{s}}=1 \hbox { in the limit}\;Da \rightarrow 0 \quad \text { and } \quad \frac{k_\mathrm{s,eff}}{k_\mathrm{s}}=0\, \hbox { in the limit}\;Da \rightarrow \infty . \end{aligned}$$

(80)

As stated previously, the condition of large Da can be obtained only in the linear reactive case with $n=1$, with the analytical solution of the mass exchange coefficient at large Da calculated as

$$\begin{aligned} \frac{\alpha _\mathrm{l}l_\mathrm{r}^{2}}{D_\mathrm{l}}=-\frac{1}{V^{\prime }}\int _{A_\mathrm{ls}^{\prime }}\mathbf {n}_\mathrm{ls}\cdot \nabla ^{\prime }s_\mathrm{l}{\text {d}}A^{\prime }=\frac{12}{{\varepsilon }_\mathrm{l}}, \end{aligned}$$

(81)

for the tube case.

The impact of the heterogeneous reaction is clearly seen, for instance when comparing the passive and active dispersion coefficient. It is interesting to notice that the coefficient of nonlinearity, n, plays also an important role and this is discussed in the following subsection.

4.2 Numerical Calculations

Special procedures have been devised to solve easily for the integro-differential equations involved in the closure problems for $s_\mathrm{l}$ and $\mathbf {b}_\mathrm{l}^{\prime }$ which are presented in “Appendix”. Following Quintard and Whitaker (1994), the decompositions

$$\begin{aligned} s_\mathrm{l}=-\frac{1}{n}+X_\mathrm{l}^{\prime }\psi _\mathrm{s}\quad \text {and}\quad \mathbf {b}_\mathrm{l}^{\prime }= \mathbf {b}_{0}^{\prime }+\psi _\mathrm{b}\mathbf {u}_\mathrm{l}^{\prime }. \end{aligned}$$

(82)

were introduced. The closure problems can be rewritten consequently for $\psi _\mathrm{s}$, $\mathbf {b}_{0}^{\prime }$ and $\psi _\mathrm{b}$, respectively, without integro-differential terms. One may notice that the closure problems for $\psi _\mathrm{s}$ and $\psi _\mathrm{b}$ are identical; therefore, the closure problems can be subsequently simplified by solving only one of them. The numerical simulations were performed with $\mathrm {COMSOL}{}^{\textregistered }$ with proper choices of the mesh size and other numerical parameters to ensure convergence. For instance for the 3D case, the mean element volume ratio, the element number and the number of degree of freedom (DOF) were equal to $5\times 10^{-4}$, $7\times 10^{4}$ and 176968 (plus 20634 internal DOFs), respectively. The porosity is taken at a value of 0.36 for the two geometries, and the soluble and insoluble materials have the same volume fraction. As introduced in Jeschke et al. (2001) for gypsum dissolution, the reaction order may range from 1 to 4.5 at different stages, so in the following numerical simulations $n=1,\,3,\,5$ were chosen as examples of the nonlinear reaction orders. The effective parameters under investigation were the longitudinal dispersion coefficient $\left( {\mathbf {D}}_\mathrm{l}^{*}\right) _{xx}/D_\mathrm{l}$, the ratio of the effective and surface reaction rate coefficient $k_\mathrm{s,eff}/k_\mathrm{s}$, the x-component of the dimensionless effective velocity $\left( \mathbf {U}_\mathrm{l}^{*}\right) _{x}/U_\mathrm{r}$ and the x-component of additional gradient term coefficient in the form of $\left( \mathbf {h}_\mathrm{l}^{\text {*}}\right) _{x}\omega _\mathrm{eq}/\left( k_\mathrm{s}l_\mathrm{r}\right)$. For all these four parameters, the analytical solutions developed above for the stratified unit cell were verified by the numerical results. As illustrated in Figs. 3, 5, 7 and 9, one observes that the analytical solutions agree very well with the corresponding numerical results for the studied effective parameters.

Fig. 3

$\left( {\mathbf {D}}_\mathrm{l}^{*}\right) _{xx}/D_\mathrm{l}$ as a function of Da with $Pe=100$

The results of $\left( {\mathbf {D}}_\mathrm{l}^{*}\right) _{xx}/D_\mathrm{l}$ as a function of Da with $\mathrm {Pe=100}$ (cf. Fig. 3) are discussed firstly, i.e., a case with important dispersion effects. One sees that when $Da\rightarrow 0$, i.e., in the passive case, dispersion reaches two different values for the 1D and 3D geometries, respectively, regardless of n, since a different value of n does not affect the limit of $\text {Da}$. In the limit for $Da\rightarrow \infty$, $\left( {\mathbf {D}}_\mathrm{l}^{*}\right) _{xx}/D_\mathrm{l}$ reaches constant values again which are dependent on the geometry, the proportion of the insoluble material and n. The decrease of $\left( {\mathbf {D}}_\mathrm{l}^{*}\right) _{xx}/D_\mathrm{l}$ in the active case when Pe is large illustrated in both Figs. 3 and 4 has been also observed previously (Quintard and Whitaker 1994; Valdés-Parada et al. 2011). It is attributed to the fact that a large Da makes the concentration field around the surface more uniform than the zero flux condition, which in turn produces less “tortuosity,” which also translates into an increase of $\big (\mathbf{D}^*_1\big )_{xx}/D_1$ in the diffusive regime. The word tortuosity in this paper is not used in the classical geometrical sense, i.e., path length, but rather as an indication of the decrease in the apparent diffusion coefficient in the macro-scale equation, which depends on the tortuous character of the geometry but also on transport properties, in particular the boundary conditions at the liquid–solid interface as made clear by the closure problems. Results show that nonlinearity has a significant impact, dependent upon the topological properties of the unit cell: monotonous for the 3D unit cells under consideration, with a transition at intermediate Da for the stratified unit cell. It is interesting to note that the nonlinearity of the reaction rate, quantified through n, makes the effect of Da more dramatic for the 3D unit cell than for the stratified unit cell. The influences of Da and n are, as one would expect, stronger for the 3D case with only soluble solid than for the one with insoluble material.

Fig. 4

$\left( {\mathbf {D}}_\mathrm{l}^{*}\right) _{xx}/D_\mathrm{l}$ as a function of Pe

Effective reaction rate The second parameter under consideration is the effective reaction rate coefficient, in the form of $k_\mathrm{s,eff}/k_\mathrm{s}$. Regarding the impact of Pe on $k_\mathrm{s,eff}/k_\mathrm{s}$, it is seen from Eq. 76 that $k_\mathrm{s,eff}/k_\mathrm{s}$ is independent of Pe for the stratified unit cell, which must be attributed to the fact that periodicity conditions are corresponding to a fully developed regime. According to our numerical calculations, when increasing Pe from 0.1 to 1000, $k_\mathrm{s,eff}/k_\mathrm{s}$ increases 2.0, 5.5 and 8.4 % for $n=1,\,3\,\mathrm {and}\,5$ respectively, for the 3D unit cell with insoluble material and $Da=1$. In summary, the Pe number is not important for the linear reactive case, while it has larger impacts in the nonlinear reactive cases.

The results of $k_\mathrm{s,eff}/k_\mathrm{s}$ versus Da are presented in Fig. 5 for the three unit cells and for different values of n. One observes the classical behavior for the ratio $k_\mathrm{s,eff}/k_\mathrm{s}$, which is equal to one at small Da and tends to zero at large Da. Similar results were also reported in Wood et al. (2007), Valdés-Parada et al. (2011) for different geometries with heterogeneous reactions. Nonlinearity in the reaction rate and the presence of insoluble material tend to decrease $k_\mathrm{s,eff}/k_\mathrm{s}$, in a limited manner, for a given value of Da.

Fig. 5

$k_\mathrm{s,eff}/k_\mathrm{s}$ as a function of Da

One should notice that, the increase in Da is also equivalent to an increase in $k_\mathrm{s}$. Therefore, looking at the limit of $k_\mathrm{s,eff}/k_\mathrm{s}$ at large Da number is not informative. Instead, results for an effective Damköhler number defined by $Da_\mathrm{eff}=\frac{k_\mathrm{s,eff}}{k_\mathrm{s}}Da$ are plotted in Fig. 6. One sees that $k_\mathrm{s,eff}$ reaches a constant at large Da, i.e., in transport limited situations. The constant decreases with n and the proportion of insoluble material. One should also remember that in the case of large Da with $n=1$, the boundary condition will become the one of the thermodynamic equilibrium, and the mass exchange coefficient should be predicted by Eq. 65 instead of Eq. 56, as already discussed.

Fig. 6

$Da_\mathrm{eff}$ as a function of Da for $Pe=1$

Non-classical terms The first non-classical term of interest is the x-component of the effective velocity, $\left( \mathbf {U}_\mathrm{l}^{*}\right) _{x}$. In Fig. 7, the results of $\left( \mathbf {U}_\mathrm{l}^{*}\right) _{x}/U_\mathrm{r}$ versus Da are plotted for the three unit cells. One sees that $\left( \mathbf {U}_\mathrm{l}^{*}\right) _{x}/U_\mathrm{r}$ can be estimated as a linear function of Da when $Da<1$, and in this range the reaction order does not play a role. With further increase in Da, the growth of $\left( \mathbf {U}_\mathrm{l}^{*}\right) _{x}/U_\mathrm{r}$ becomes slower and finally reaches an asymptote which decreases with increasing n. The asymptotic value decreases also when decreasing the amount of soluble material in the unit cell. These results are a reminder of the discussion in Golfier et al. (2002) about the potential increase in the apparent advection velocity by the non-conventional terms. This effect may be up to $30\,\%$ in the linear case for the 3D geometry without insoluble material and for large Da.

Fig. 7

$\left( \mathbf {U}_\mathrm{l}^{*}\right) _{x}/U_\mathrm{r}$ as function of Da

From Eq. 75a, one observes that the ratio $\left( \mathbf {U}_\mathrm{l}^{*}\right) _{x}/U_\mathrm{r}$ is independent of Pe for the stratified unit cell. The evolution of $\left( \mathbf {U}_\mathrm{l}^{*}\right) _{x}/U_\mathrm{r}$ as a function of Pe is illustrated in Fig. 8 for the 3D geometries. The common features of all the curves are two folds: the ratio $\left( \mathbf {U}_\mathrm{l}^{*}\right) _{x}/U_\mathrm{r}$ is constant for small and large Pe numbers. There is a transition regime at intermediate Pe numbers, with non-monotonous behavior when passive surfaces are present within the unit cell. The curves for $Da=1$ show very small variations with Pe, and a negligible impact of n. The curves for ${Da=100}$ undergo complex and significant variations, with marked minimums at intermediate Pe for the case with insoluble materials. A higher reaction order decreases significantly $\left( \mathbf {U}_\mathrm{l}^{*}\right) _{x}/U_\mathrm{r}$.

Fig. 8

$\left( \mathbf {U}_\mathrm{l}^{*}\right) _{x}/U_\mathrm{r}$ as a function of Pe for the 3D unit cells, with $Da=100$ (curves indicated) and $Da=1$ (other curves)

The second non-classical parameter to be studied is the x-component of the additional gradient term coefficient in the form of $\left( \mathbf {h}_\mathrm{l}^{\text {*}}\right) _{x}\omega _\mathrm{eq}/\left( k_\mathrm{s}l_\mathrm{r}\right)$, which contributes to the macro-scale mass exchange. According to analytical solution Eq. for the stratified unit cell and our numerical results for the 3D geometries, $\left( \mathbf {h}_\mathrm{l}^{\text {*}}\right) _{x}\omega _\mathrm{eq}/\left( k_\mathrm{s}l_\mathrm{r}\right)$ can be represented as a linear function of Pe. The results of $\left( \mathbf {h}_\mathrm{l}^{\text {*}}\right) _{x}\omega _\mathrm{eq}/\left( k_\mathrm{s}l_\mathrm{r}\right)$ as a function of Da with $\mathrm {Pe=1}$ are plotted in Fig. 9. It is shown that $\left( \mathbf {h}_\mathrm{l}^{\text {*}}\right) _{x}\omega _\mathrm{eq}/\left( k_\mathrm{s}l_\mathrm{r}\right)$ is almost a constant for small Da up to $\text {Da}\approx 1$. The reaction order is important at this stage, and the linear reactive case leads to smaller $\left( \mathbf {h}_\mathrm{l}^{\text {*}}\right) _{x}\omega _\mathrm{eq}/\left( k_\mathrm{s}l_\mathrm{r}\right)$ for all the geometries. After a transition zone, the values of $\left( \mathbf {h}_\mathrm{l}^{\text {*}}\right) _{x}\omega _\mathrm{eq}/\left( Pek_\mathrm{s}l_\mathrm{r}\right)$ become linear functions of Da. Moreover, the presence of insoluble medium has a tendency to increase $\left( \mathbf {h}_\mathrm{l}^{\text {*}}\right) _{x}\omega _\mathrm{eq}/\left( Pek_\mathrm{s}l_\mathrm{r}\right)$ for the 3D cases.

Fig. 9

$\left( \mathbf {h}_\mathrm{l}^{\text {*}}\right) _{x} \omega _\mathrm{eq}/\left( k_\mathrm{s}l_\mathrm{r}\right)$ as a function of Da with $Pe=1$

So far the impact of the flow properties and chemical features on the four effective parameters has been presented. The results for $\left( {\mathbf {D}}_\mathrm{l}^{*}\right) _{xx}/D_\mathrm{l}$ and $k_\mathrm{s,eff}/k_\mathrm{s}$ agree well with the previous works which considered the first-order reactive case. Nonlinearity plays a significant role, however, similar to Da. Concerning the non-traditional items, $\left( \mathbf {U}_\mathrm{l}^{*}\right) _{x}/U_\mathrm{r}$ and $\left( \mathbf {h}_\mathrm{l}^{\text {*}}\right) _{x}\omega _\mathrm{eq}/\left( k_\mathrm{s}l_\mathrm{r}\right)$, it is clear that they are important with respect to the classical terms only under some conditions and neglecting their contributions may lead to errors when applying the macro-scale model. This point is further discussed in the next section where the macro-scale model is tested against a reference obtained from direct numerical simulations.

5 Example of Application to a Macro-Scale Problem

In this section, the potential importance of the additional terms is further discussed based on a 1D macro-scale example. The corresponding macro-scale steady-state problem may be written in dimensionless form as

$$\begin{aligned}&{Pe^{*}}\varepsilon _\mathrm{l}\left( U_\mathrm{l}^{\prime }+U_\mathrm{l}^{*\prime }\left( \left\langle \omega _\mathrm{l}^{\prime }\right\rangle ^{l}\right) \right) \frac{\partial \left\langle \omega _\mathrm{l}^{\prime }\right\rangle ^{l}}{\partial x^{\prime }}+{Pe^{*}}\varepsilon _\mathrm{l}\left( \left\langle \omega _\mathrm{l}^{\prime }\right\rangle ^{l}- \omega _\mathrm{eq}^{\prime }\right) \frac{{\partial } U_\mathrm{l}^{*\prime }\left( \left\langle \omega _\mathrm{l}^{\prime }\right\rangle ^{l}\right) }{\partial x^{\prime }}\nonumber \\&\quad =-\left( -\frac{k_\mathrm{s,eff}\left( \left\langle \omega _\mathrm{l}^{\prime }\right\rangle ^{l}\right) }{k_{s}}\left( 1-\frac{\left\langle \omega _\mathrm{l}^{\prime }\right\rangle ^{l}}{\omega _\mathrm{eq}^{\prime }}\right) +h_\mathrm{l}^{*\prime }\left( \left\langle \omega _\mathrm{l}^{\prime }\right\rangle ^{l}\right) \frac{\partial \left\langle \omega _\mathrm{l}^{\prime }\right\rangle ^{l}}{\partial x^{\prime }}\right) {Da^{*}\left( \left\langle \omega _{ l }^{\prime }\right\rangle ^{ l }\right) }\nonumber \\&\qquad +\,\varepsilon _\mathrm{l}\frac{\partial }{\partial x^{\prime }}\left( \frac{D_\mathrm{l}^{*}\left( \left\langle \omega _\mathrm{l}^{\prime }\right\rangle ^{l}\right) }{D_{r}}\frac{\partial \left\langle \omega _\mathrm{l}^{\prime }\right\rangle ^{l}}{\partial x^{\prime }}\right) , \end{aligned}$$

(83)

with the dimensionless numbers defined as

$$\begin{aligned}&Pe^{*}=\frac{U_\mathrm{r}L_\mathrm{r}}{D_\mathrm{r}}\mathrm {\text { , }}U_\mathrm{l}^{\prime }=\frac{U_\mathrm{l}}{U_\mathrm{r}}\text { , }U_\mathrm{l}^{*\prime }\left( \left\langle \omega _\mathrm{l}^{\prime }\right\rangle ^{l}\right) =\frac{U_\mathrm{l}^{*}}{U_\mathrm{r}}, \left\langle \omega _\mathrm{l}^{\prime }\right\rangle ^{l}=\frac{\left\langle \omega _\mathrm{l}\right\rangle ^{l}}{\omega _\mathrm{eq}}\text { , } \omega _\mathrm{eq}^{\prime }=\frac{\omega _\mathrm{eq}}{\omega _\mathrm{eq}}=1,\nonumber \\&\quad x^{\prime }=\frac{x}{L_\mathrm{r}},\text { }h_\mathrm{l}^{*\prime }\left( \left\langle \omega _\mathrm{l}^{\prime }\right\rangle ^{l}\right) =\frac{h_\mathrm{l}^{*}\omega _\mathrm{eq}}{L_\mathrm{r}k_\mathrm{s}}\text {, }Da^{*}\left( \left\langle \omega _\mathrm{l}^{\prime }\right\rangle ^{l}\right) =\frac{a_\mathrm{vl}^{\prime }M_\mathrm{Ca}}{\rho _\mathrm{l}\omega _\mathrm{eq}}\frac{L_\mathrm{r}k_\mathrm{s}}{D_\mathrm{r}}\left( 1-\frac{\left\langle \omega _\mathrm{l}^{\prime }\right\rangle ^{l}}{\omega _\mathrm{eq}^{\prime }}\right) ^{n-1} \end{aligned}$$

(84)

where $L_\mathrm{r}$ is the macro-scale characteristic length and $D_\mathrm{r}$ can be the molecular diffusion coefficient or alternatively the maximum dispersion coefficient, depending on the problem of interest. It must be emphasized that $Da^{*}\left( \left\langle \omega _\mathrm{l}^{\prime }\right\rangle ^{l}\right)$ is not a constant in the nonlinear reactive cases and is dependent on the mass fraction distribution. Since closure problems depend on parameter Da, the effective parameters $D_\mathrm{l}^{*}\left( \left\langle \omega _\mathrm{l}^{\prime }\right\rangle ^{l}\right)$, $U_\mathrm{l}^{*\prime }\left( \left\langle \omega _\mathrm{l}^{\prime }\right\rangle ^{l}\right)$, $k_\mathrm{s,eff}\left( \left\langle \omega _\mathrm{l}^{\prime }\right\rangle ^{l}\right)$ and $\text { }h_\mathrm{l}^{*\prime }\left( \left\langle \omega _\mathrm{l}^{\prime }\right\rangle ^{l}\right)$ are also dependent on the distribution of mass fraction accordingly in the nonlinear reactive cases.

When taking $D_\mathrm{r}=max\left( D_\mathrm{l}^{*}\left( \left\langle \omega _\mathrm{l}^{\prime }\right\rangle ^{l}\right) \right)$ and $U_\mathrm{r}=\left\langle u_\mathrm{l}\right\rangle ^{l}$, the mass transport by dispersion is small compared to that by convection in the case of large $Pe^{*}$. Therefore, Eq. 83 can be simplified into

$$\begin{aligned} {Pe^{*}}\varepsilon _\mathrm{l}\frac{\partial \left\langle \omega _\mathrm{l}^{\prime }\right\rangle ^{l}}{\partial x^{\prime }}\thickapprox \underset{\text {apparent reactive term}}{\underbrace{\frac{\frac{k_\mathrm{s,eff}\left( \left\langle \omega _\mathrm{l}^{\prime }\right\rangle ^{l}\right) }{k_{s}}{Da^{*}\left( \left\langle \omega _{ l }^{\prime }\right\rangle ^{ l }\right) }}{\left( 1+U_\mathrm{l}^{*\prime }\left( \left\langle \omega _\mathrm{l}^{\prime }\right\rangle ^{l}\right) +\frac{ h _\mathrm{l}^{*\prime }\left( \left\langle \omega _\mathrm{l}^{\prime }\right\rangle ^{l}\right) {Da^{*}\left( \left\langle \omega _{ l }^{\prime }\right\rangle ^{ l }\right) }}{{Pe^{*}}\varepsilon _\mathrm{l}}\right) }}}\left( 1-\frac{\left\langle \omega _\mathrm{l}^{\prime }\right\rangle ^{l}}{\omega _\mathrm{eq}^{\prime }}\right) . \end{aligned}$$

(85)

Even though the full Eq. 83 was employed in the actual computations, this simplified form is interesting since it shows that additional terms may be incorporated in an apparent reactive term, as suggested in Golfier et al. (2002). Let us introduce $H\left( \left\langle \omega _\mathrm{l}^{\prime }\right\rangle ^{l}\right) =h_\mathrm{l}^{*^{\prime }}\left( \left\langle \omega _\mathrm{l}^{\prime }\right\rangle ^{l}\right) Da^{*}\left( \left\langle \omega _{ l }^{\prime }\right\rangle ^{ l }\right) /\left( {Pe}^{*}{\varepsilon }_\mathrm{l}\right)$. To investigate the contributions of the non-traditional terms $U_\mathrm{l}^{*\prime }\left( \left\langle \omega _\mathrm{l}^{\prime }\right\rangle ^{l}\right)$ and $H\left( \left\langle \omega _\mathrm{l}^{\prime }\right\rangle ^{l}\right)$ to the apparent reactive term, the closure problems were solved for a 2D representative unit cell which contains only the l and s phases (cf. Fig. 10a), as well as for the 3D representative unit cell containing the three phases as illustrated in Fig. 2b. The location in the (Pe, Da) plane of points having the property $U_\mathrm{l}^{*\prime }\left( \left\langle \omega _\mathrm{l}^{\prime }\right\rangle ^{l}\right) =0.05$ and $H\left( \left\langle \omega _\mathrm{l}^{\prime }\right\rangle ^{l}\right) =0.05$ are plotted in Figs. 11a, b for the 2D and 3D geometries, respectively, and for different reaction orders. In the regions above the curves, here at large Pe and Da, the magnitudes of $U_\mathrm{l}^{*\prime }\left( \left\langle \omega _\mathrm{l}^{\prime }\right\rangle ^{l}\right)$ and $H\left( \left\langle \omega _\mathrm{l}^{\prime }\right\rangle ^{l}\right)$ are larger than 0.05. Therefore, this map can be used to estimate regions for which the additional terms may play a role. All the curves arrive at a plateau when Pe is relatively large, and the values of $U_\mathrm{l}^{*\prime }\left( \left\langle \omega _\mathrm{l}^{\prime }\right\rangle ^{l}\right)$ and $H\left( \left\langle \omega _\mathrm{l}^{\prime }\right\rangle ^{l}\right)$ are mainly determined by Da and n under such circumstances. The curves for $U_\mathrm{l}^{*\prime }\left( \left\langle \omega _\mathrm{l}^{\prime }\right\rangle ^{l}\right)$ with $n=5$ are not present because $U_\mathrm{l}^{*\prime }\left( \left\langle \omega _\mathrm{l}^{\prime }\right\rangle ^{l}\right)$ is always smaller than 0.05 in the studied range. Typically, the additional coefficients may be important for relatively large Pe and small Da and have a strong impact on the apparent nonlinear reaction rate coefficient. This impact is much stronger for the 3D geometry than for the 2D geometry in the case of small Da, as observed in Fig. 11a, b.

Fig. 10

2D geometries for the DNS: a without insoluble material; b with insoluble material

Fig. 11

Pe–Da diagram for $U_\mathrm{l}^{*\prime }\left( \left\langle \omega _\mathrm{l}^{\prime }\right\rangle ^{l}\right) =0.05$ (curves 4 and 5) and $H\left( \left\langle \omega _\mathrm{l}^{\prime }\right\rangle ^{l}\right) =0.05$ (curves 1, 2 and 3): a for the 2D unit cell without insoluble case; b for the 3D unit cell with insoluble material

To test these ideas, the pore-scale equations (later referred to as DNS) were solved for case I illustrated by Fig. 10a, composed of 65 periodic elements arranged along the x-direction with all the solid phase soluble, and in case II corresponding to the geometry depicted in Fig. 10b, containing insoluble materials. The pore-scale problem introduced in Sect. 2 was transformed into dimensionless form, with the diameter of the circles as the characteristic length. The corresponding boundary conditions at the entrance and the exit were $\omega _\mathrm{l}^{\prime }=0$ and convective conditions, respectively. The Navier–Stokes equations were solved with low Reynolds number to get a periodic velocity field of constant average velocity. The corresponding macro-scale problem is 1D, i.e., a line along the x-direction with the same length as the 2D geometry, $L_\mathrm{r}$. For case I, a significant impact of the additional terms with $n=3$ was observed successfully. In the nonlinear reactive case, since Da is a function of the mass fraction, its value decreased quickly along the x-direction due to the mass fraction distribution. For case II it was difficult to keep a relatively large Da to see the impact of the additional non-classical terms and hence the linear reactive case was chosen as an example. Since the mass fraction disappears in the definition of Da for a linear reactive case, $H\left( \left\langle \omega _\mathrm{l}^{\prime }\right\rangle ^{l}\right)$ and $U_\mathrm{l}^{*\prime }\left( \left\langle \omega _\mathrm{l}^{\prime }\right\rangle ^{l}\right)$ become constant independent of $\left\langle \omega _\mathrm{l}^{\prime }\right\rangle ^{l}$ and are denoted as H and $U_\mathrm{l}^{*\prime }$, respectively. A large Pe and a proper Da were used to study the impact of the non-classical terms, avoiding too large Da, because in such circumstances the pore-scale boundary condition would be close to the one of the thermodynamic equilibrium. Numerical simulations for both the DNS and the macro-scale model were performed with COMSOL$^{\circledR }$.

Let us estimate a reactive coefficient for the DNS results using the following definition

$$\begin{aligned} \alpha _\mathrm{DNS}=\frac{\frac{1}{V^{\prime }}\int _\mathrm{ls}\mathbf {n}_\mathrm{ls}\cdot \rho _\mathrm{l}^{\prime }D_\mathrm{l}^{\prime }\nabla ^{\prime }\omega _\mathrm{l}^{\prime }{\text {d}}A^{\prime }}{\left( 1-\frac{\left\langle \omega _\mathrm{l}^{\prime }\right\rangle ^{l}}{\omega _\mathrm{eq}^{\prime }}\right) }, \end{aligned}$$

(86)

and computed at the centroid of each unit cell. The fact of not using very large Da ensured that $1-\frac{\left\langle \omega _\mathrm{l}^{\prime }\right\rangle ^{l}}{\omega _\mathrm{eq}^{\prime }}\ne 0$ to avoid any numerical problem in estimating $\alpha _\mathrm{DNS}$. The results of $\alpha _\mathrm{DNS}$ were compared with the apparent reactive term estimated in Eq. 85 for the macro-scale model. Four cases were tested with different non-traditional effective parameters taken into account: The apparent reactive term $\alpha _{L1}$ was obtained by solving the macro-scale equation with both $H\left( \left\langle \omega _\mathrm{l}^{\prime }\right\rangle ^{l}\right)$ and $U_\mathrm{l}^{*\prime }\left( \left\langle \omega _\mathrm{l}^{\prime }\right\rangle ^{l}\right)$, $\alpha _{L2}$ without $H\left( \left\langle \omega _\mathrm{l}^{\prime }\right\rangle ^{l}\right)$, $\alpha _{L3}$ without $U_\mathrm{l}^{*\prime }\left( \left\langle \omega _\mathrm{l}^{\prime }\right\rangle ^{l}\right)$ and $\alpha _{L4}$ without $H\left( \left\langle \omega _\mathrm{l}^{\prime }\right\rangle ^{l}\right)$ and $U_\mathrm{l}^{*\prime }\left( \left\langle \omega _\mathrm{l}^{\prime }\right\rangle ^{l}\right)$. For case I, the results are only presented for regions far from the entrance region, as illustrated in Fig. 12a. The reactive coefficients decrease along the x-axis because they are dependent on the mass fraction field. Considering the non-traditional effective properties improved the results and the best results were obtained by considering all the effective properties, including $H\left( \left\langle \omega _\mathrm{l}^{\prime }\right\rangle ^{l}\right)$ and $U_\mathrm{l}^{*\prime }\left( \left\langle \omega _\mathrm{l}^{\prime }\right\rangle ^{l}\right)$. It must be pointed out that, in this nonlinear case, two errors are accumulated. First, dispersion terms are not entirely controlled by the assigned value of the Pe number because of nonlinearities in the effective dispersion tensor. In our case, they induce a minor but visible effect of about a few percent over the estimated DNS reaction rate. Furthermore, because of the entrance region effect, the macro-scale concentration field lags a little bit behind the DNS value, which in turn impacts the estimation of the effective exchange rate. Improving the solution would require the introduction of a non-local theory taking care of the entrance region effect. From the results presented in Fig. 12b for case II, one observes a relatively large discrepancy in the entrance region, which may be attributed to the fact that the periodic assumption for the upscaling breaks down in this area. This would call for a specific non-local treatment, which is beyond the scope of this paper. But in the regions with an established regime, materialized by a constant $\alpha _\mathrm{DNS}$, the relative errors become very small and, among the four choices, $\alpha _{L4}$ gives the worst results, while the results are improved by taking into consideration the non-traditional parameters. Nevertheless, our results emphasize the importance of the additional terms in order to recover the correct mass exchange in the established regime, as was emphasized in Golfier et al. (2002) for a simpler flow problem and the case of thermodynamic equilibrium.

Fig. 12

Comparison of apparent reactive term between DNS and the macro-scale model: a for case I (nonlinear reactive order $n=3$ without insoluble material) with Pe =1000 and $Da|_{\left\langle \omega _\mathrm{l}^{\prime }\right\rangle ^{l}=0}=80$; b for case II (linear reactive case with insoluble material) with $Pe=1000$ and $Da=10$

6 Conclusion

The upscaling of a mass transport problem involving a nonlinear heterogeneous reaction typical of dissolution problems has been carried out using a first-order Taylor’s expansion for the reaction rate when developing the equations for the concentration deviation. A full model including all couplings and the interface velocity has been obtained. Several limiting cases have been developed emphasizing the coherence of the proposed theory with results available in the literature for these limiting cases, the only difference being due to some additional coupling terms, which, however, may correct the estimated effective reaction rate by tenths of percent.

The closure problems providing the effective properties have been solved analytically for a stratified unit cell and numerically for both stratified and 3D unit cells in a quasi-steady approximation. Effects of the pore-scale Damköhler and Péclet number were investigated, as well as the impact of the coefficient n appearing in the nonlinear reaction rate. The influence of the proportion of insoluble material was studied by comparing the 3D cases with the solid phase completely soluble or partially insoluble. Results for the classical effective properties such as dispersion coefficient and effective reaction rates are compatible with previous findings on active dispersion. In particular, tortuosity and dispersion effects become smaller when the Damköhler number increases, due to the homogenization of concentration at the interface. The nonlinear reaction rate coefficient tends to increase the impact of Da. The behavior of the non-traditional terms that appear in the development has been investigated based on comparisons between DNS of the pore-scale equations and macro-scale results. It was shown that they may play a role for large Pe and small Da, at least for the simple unit cells considered in this paper. This latter aspect deserves more investigation in terms of parameter range, complexity of the representative unit cell, form of the nonlinear reaction rate, etc.

The framework developed in this study is applicable to simulate dissolution process in various research areas, for instance in the evolution of karstic structures, $\mathrm {CO}_{2}$ storage and in the application of acid injection in petroleum wells to improve oil recovery. The development was based on a bundle of assumptions, such as constant fluid parameters, negligible interface velocity and pseudo-component for the dissolved material. Also, the calculations of effective parameters in the applications provided were not based on an actual dissolved pore-scale geometry. Real conditions are much more complicated so great attention should be paid where such assumptions may break down. For example, the dissolution of the porous matrix may lead to significant variation of porosity and consequently permeability and other effective parameters. In addition, the dissolving front may become unstable and may lead to the development of wormhole structures. Under some circumstances, hydrodynamic instabilities may also be induced by density change, such as in the case of salt dissolution in water. It is beyond the scope of this conclusion to review all the perspectives associated with these questions. Concerning the coupling with the pore-scale geometry evolution, if one is not satisfied with the geochemistry assumption, i.e., dependence of the effective parameters on the porosity, our developments offer a framework for a coupled solution between the macro-scale equation, on the one hand, and the pore-scale closure problems under the full version including the transient aspects, on the other hand.

More coupling and nonlinear effects can be introduced in the development, such as variation of fluid properties and reaction rate with concentration, more complicated geochemistry, etc. We believe that the idea of first-order corrections at the closure level can be extended to such cases, of course at the expense of some additional complexity.

Appendix: Simplified Dimensionless Closure Problems

Based on the discussion in Sect. 2, the interface velocity is assumed negligible and hence the closure problems can be simplified by discarding the terms involving interface velocity. With the following dimensionless quantities

$$\begin{aligned} \nabla ^{\prime }=l_\mathrm{r}\nabla ,\,\mathbf {\,\, b}_\mathrm{l}^{\prime }=\mathbf {b}_\mathrm{l}/l_\mathrm{r},\,\,\,\mathbf {v}_\mathrm{l}^{\prime }=\mathbf {v}_\mathrm{l}/U_\mathrm{r},\,\,\, t^{\prime }=\frac{D_\mathrm{l}}{l_\mathrm{r}^{2}}t, \end{aligned}$$

(87)

the dimensionless form of the simplified closure problems in Sect. 3.2 may be written as

Problem I:

$$\begin{aligned}&\displaystyle \frac{\partial s_\mathrm{l}}{\partial t^{\prime }}+Pe\,\mathbf {v}_\mathrm{l}^{\prime }\cdot \nabla ^{\prime }s_\mathrm{l}=\nabla ^{\prime }\cdot \left( \nabla ^{\prime }s_\mathrm{l}\right) +{\varepsilon }_\mathrm{l}^{-1}X_\mathrm{l}^{\prime }\,\,\,\,\,\ \text {in }V_\mathrm{l}, \end{aligned}$$

(88)

$$\begin{aligned}&\displaystyle \text {B.C. I}\,\,\,\,\,\,\mathbf {n}_\mathrm{ls}\cdot \mathbf {\nabla ^{\prime }}s_\mathrm{l}=\mathrm {-Da}\,\left( 1+n\, s_\mathrm{l}\right) \qquad \text {at }A_\mathrm{ls}(t^{\prime }), \end{aligned}$$

(89)

$$\begin{aligned}&\displaystyle \text {B.C. II}\,\,\,\,\,\,\mathbf {n}_\mathrm{li}\cdot \mathbf {\nabla ^{\prime }}s_\mathrm{l}=0\,\,\,\,\,\ \text {at }A_\mathrm{li}, \end{aligned}$$

(90)

$$\begin{aligned}&\displaystyle \left\langle s_\mathrm{l}\right\rangle ^{\prime }=0\,\,\,\,\,\ \text {in }V_\mathrm{l},\end{aligned}$$

(91)

$$\begin{aligned}&\displaystyle s_\mathrm{l}\left( \mathbf {x}^{\prime }+\mathbf {l}_\mathrm{i}^{\prime }\right) =s_\mathrm{l}\left( \mathbf {x}^{\prime }\right) , \end{aligned}$$

(92)

in which

$$\begin{aligned} X_\mathrm{l}^{\prime }=-\frac{1}{V^{\prime }}\int _{A_\mathrm{ls}^{\prime }} \mathbf {n}_\mathrm{ls}\cdot \nabla ^{\prime }s_\mathrm{l}{\text {d}}A^{\prime }=\frac{l_\mathrm{r}^{2}}{D_\mathrm{l}}X_\mathrm{l}. \end{aligned}$$

(93)

Problem II:

$$\begin{aligned}&\displaystyle \frac{\partial \mathbf {b}_\mathrm{l}^{\prime }}{\partial t^{\prime }}+Pe\,\mathbf {v}_\mathrm{l}^{\prime }\cdot \left( \nabla ^{\prime }\mathbf {b}_\mathrm{l}^{\prime }+s_\mathrm{l}\mathbf {I}\right) +Pe\,\tilde{\mathbf {v}}_\mathrm{l}^{\prime }-{\varepsilon }_\mathrm{l}^{-1}Pe\,\left\langle {\tilde{\mathbf v}}_\mathrm{l}^{\prime }s_\mathrm{l}\right\rangle ^{\prime }=\nabla ^{\prime }\cdot \left( \nabla ^{\prime }\mathbf {b}_\mathrm{l}^{\prime }+s_\mathrm{l}\mathbf {I}\right) +{\varepsilon }_\mathrm{l}^{-1}\mathbf {u}_\mathrm{l}^{\prime }\,\,\,\,\,\ \text {in }V_\mathrm{l}, \nonumber \\\end{aligned}$$

(94)

$$\begin{aligned}&\displaystyle \text {B.C. I}\,\,\,\,\,\,\mathbf {n}_\mathrm{ls}\cdot \left( \nabla ^{\prime }\mathbf {b}_\mathrm{l}^{\prime }+s_\mathrm{l}\mathbf {I}\right) +\mathbf {n}_\mathrm{ls}=-n\,Da\,\mathbf {b}_\mathrm{l}^{\prime }\,\,\,\,\,\ \text {at }A_\mathrm{ls}(t^{\prime }), \end{aligned}$$

(95)

$$\begin{aligned}&\displaystyle \text {B.C. II}\,\,\,\,\,\,\mathbf {n}_\mathrm{li}\cdot \left( -\left( \nabla ^{\prime }\mathbf {b}_\mathrm{l}^{\prime }+s_\mathrm{l}\mathbf {I}\right) \right) =\mathbf {n}_\mathrm{li}\,\,\,\,\,\ \text {at }A_\mathrm{li}, \end{aligned}$$

(96)

$$\begin{aligned}&\displaystyle \left\langle \mathbf {b}_\mathrm{l}^{\prime }\right\rangle ^{\prime }=0\,\,\,\,\,\ \text {in }V_\mathrm{l}, \end{aligned}$$

(97)

$$\begin{aligned}&\displaystyle \mathbf {b}_\mathrm{l}^{\prime }\left( \mathbf {x}^{\prime }+\mathbf {l}_\mathrm{i}^{\prime }\right) =\mathbf {b}_\mathrm{l}^{\prime }\left( \mathbf {x}^{\prime }\right) , \end{aligned}$$

(98)

in which

$$\begin{aligned} \mathbf {u}_\mathrm{l}^{\prime }=-\frac{1}{V^{\prime }}\int _{A_\mathrm{ls}^{\prime }}\mathbf {n}_\mathrm{ls}\cdot \left( \nabla ^{\prime }\mathbf {b}_\mathrm{l}^{\prime }+s_\mathrm{l}\mathbf {I}\right) {\text {d}}A^{\prime }-\frac{1}{V^{\prime }}\int _{A_\mathrm{li}^{\prime }}\mathbf {n}_\mathrm{li}\cdot \left( \nabla ^{\prime }\mathbf {b}_\mathrm{l}^{\prime }+s_\mathrm{l}\mathbf {I}\right) {\text {d}}A^{\prime }=\frac{l_\mathrm{r}^{2}}{D_\mathrm{l}}\mathbf {u}_\mathrm{l}. \end{aligned}$$

(99)

While the interface velocity does not appear anymore in the equations, it must be reminded that the evolving geometry is still there and this is emphasized by the introduction of the notation $A_\mathrm{ls}(t^{\prime })$.