1 Introduction

The theory of two-phase immiscible or partly miscible flows in porous media is used in a variety of applications, first of all, in waterflooding or another immiscible fluid displacement during the development of petroleum reservoirs (Barenblatt et al. 1990; Bedrikovetsky 1993). Other important applications include spreading of immiscible contaminants, like LNAPL and DNAPL in the ground (Yadav and Hassanizadeh 2011); unsaturated ground flow (Bear and Cheng 2010); and carbon dioxide injection for sequestration in aquifers (Pau et al. 2010).

The standard description of two-phase incompressible flows in porous media (often called the Buckley–Leverett scheme) is based on two assumptions: (1) that each liquid phase flows in its own part of the porous space; and (2) the boundary between these parts is determined by the value of water saturation (in more general versions of the theory, by the geometry of the clusters occupied by the phases). For example, it is widely accepted in the percolation approaches to displacement (Seljakov and Kadet 1997; Bedrikovetsky 1993; Hunt and Ewing 2009) that the wetting phase occupies thinner capillaries. Then, a boundary between parts of the porous space occupied by the wetting and the non-wetting fluid is determined by the value of saturation and by the pore size distribution.

Several approaches have been proposed to enhance the simplified physical picture of the traditional Buckley–Leverett model. Works of (Marle 1982; Panfilov and Panfilova 2005; Dinariev and Mikhailov 2008) consider (each in its own way) the contact surface with portions of the adjacent bulk phases as a special phase, whose motion is described either in terms of general linear non-equilibrium thermodynamics, or of the capillary “Washburn” force (after the Washburn model of displacement in a capillary, Washburn 1921). In other works, it is proposed to introduce an additional free parameter, e.g., specific interfacial area, responsible for the hysteresis under different flow conditions (Hassanizadeh and Gray 1990, 1993; Joekar-Niasar and Hassanizadeh 2011). An alternative approach consisting in treating the capillary pressure as an independent dynamic variable was developed in works of (Hilfer 2006; Hilfer and Doster 2010). In papers of (Bedrikovetsky 2003; Plohr et al. 2001), hysteresis was explained as a result of entrapment of the ganglia when the saturation changes non-monotonously. A model proposed by (Barenblatt 1971) and further developed in a number of publications (see overview in Barenblatt et al. 2003; Amaziane et al. 2012) accounts for the difference between the equilibrium and the non-equilibrium saturation, and includes, as an additional evolution equation, a relaxation equation with empirical relaxation time, a parameter to be found from microlevel considerations. Extensions of the classical Bukingham–Darcy–Richards approach have also been discussed in the area of unsaturated ground flow (Cueto-Felgueroso and Juanes 2009; DiCarlo 2010).

In the papers of Shvidler (1961), Kurbanov (1968), Raats and Klute (1968), Kalaydjian (1990), Kalaydjian et al. (1989), Rose (1991) (see also references therein), concepts of the linear non-equilibrium thermodynamics were applied on the macroscopic level, resulting in the phenomenological coupling cross terms in the Darcy expressions for the water and oil fluxes. This approach is probably the most general under steady-state flow conditions, where phase saturations do not vary with time. While many models listed above are strongly non-equivalent for unsteady flows, for the steady states they are reduced either to the standard Buckley–Leverett model, or to the non-equilibrium thermodynamic model with coupling. Coupling may either appear directly, or via common moving interface (see the discussion below).

The phase Darcy laws with coupling have the form of

$$\begin{aligned} U_{w}&= -\lambda _{ww} \nabla P_{w} -\lambda _{wo} \nabla P_{o} \nonumber \\ U_{o}&= -\lambda _{ow} \nabla P_{w} -\lambda _{oo} \nabla P_{o} \end{aligned}$$
(1)

Here, \(U_i \) are phenomenological (superficial) phase velocities; \(P_i \) are phase pressures; \(\lambda _{ij} \) are phenomenological Onsager coefficients forming 2 \({\times }\) 2 matrix \(\Lambda (i,j=o,w)\) .

There is a discussion in the literature about the actual form of the coefficients forming matrix \(\Lambda \). They are necessary to know for practical applications of the theory. However, even the Onsager property of symmetry of matrix \(\Lambda \) (equality of non-diagonal coefficients) may be doubted, since any derivation of Eq. (1) would involve additional averaging of the highly nonlinear processes happening during two-phase flows in multiple pores. Usual concepts of entropy and approaching equilibrium should be reinterpreted on this scale (Shapiro 1996). Another question is whether the diagonal coefficients in the matrix \(\Lambda \) may be expressed by usual Buckley–Leverett expressions \(k_i /\mu _i \), as in Ayub and Bentsen (1999), Dullien and Dong (1996). In other words, it may be questioned whether the cross coefficients \(\lambda _{wo}\) and \(\lambda _{ow}\) may be factorized in the same way as the transport coefficients in the classical Backley–Leverett theory, so that the relative permeabilities \(k_i \) are determined by the geometry of the flowing phases (ideally, by saturation), while the transport properties of these phases are expressed by individual phase viscosities. We will show that a different choice may be more reasonable, and that apparent relative permeabilities \(k_i \) may depend on phase viscosity ratio.

Experimental determination of coefficients \(\Lambda _{ij} \) may also be complicated. The reason is in a difficulty to organize the different and independent pressure gradients in both phases, since phase pressures are connected via capillary pressure (Ayub and Bentsen 1999; Dullien and Dong 1996). Hence, more detailed a priori information about these coefficients is needed prior to their experimental determination.

In this work, we develop an approach to the two-phase immiscible flows based on the Maxwell–Stefan formalism. The Maxwell–Stefan (MS) theory is based on the axiom that the flows of the fluids in the different media are described by the balance of the driving and friction forces (Wesselingh and Krishna 1990, 2000). The driving forces are usually determined by the gradients of the proper potential functions driving the flow, like pressures, temperature, or chemical potentials. The friction forces are proportional to the differences in the individual velocities and are introduced for each pair of components or phases, as well as between them and the containing medium. It may be shown that the MS theory is a particular representation of the formalism of the non-equilibrium thermodynamics. However, its great advantage is that it considers flow phenomena in the way allowing direct physical interpretation. This makes it possible, for many cases, to make plausible assumptions about the structure of the phenomenological coefficients in a particular MS model.

We discuss the two MS approaches to the two-phase flow in porous media. The general approach (Sect. 2.1) expresses the friction force between the phases in terms of the common friction coefficient. This approach makes it possible to investigate symmetry of the phenomenological coefficients. A more detailed physical picture of the flow may be obtained if, similarly to previous works (Hassanizadeh and Gray 1993; Panfilov and Panfilova 2005; Dinariev and Mikhailov 2008), we will not consider directly the friction between the flowing phases, but will introduce a moving interface between them, as described in Sect. 2.2. Under conditions of the steady-state flow, such an interface moves along itself and parallel to the flow, so that its position does not vary. It acts on the phases as the moving boundary in the Newton viscosity experiment. The Maxwell–Stefan interaction coefficients between each phase and the interface are specific for individual phases, unlike the common friction coefficient between phases. This approach makes it possible to split the transport and coupling coefficients into the functions of the flow geometries and phase viscosities.

Further, in Sect. 3, we present mesoscopic description of the two-phase flow in a porous medium. This description involves the interaction between the pore clusters occupied by the phases. The flows inside the clusters are described by the second-order equations, like Stokes or Brinkmann ones. The boundary conditions are formulated on the moving boundaries between the phases. It is shown that the Maxwell–Stefan equations with moving interface may be obtained by averaging this mesoscopic flow equations. Further, we propose a relatively simple geometric flow model that makes it possible to evaluate the phenomenological friction coefficients (Sect. 4). The model is based on the representation of the branches of the clusters formed by the phases as interacting “jets.” Exact expressions for the MS coefficients are obtained for the cylindrical flow geometry (the detailed derivation is presented in Appendix).

Thus, the developed approach results in a closed formalism where the transport coefficients in a theoretically grounded scheme may be computed analytically, within a number of parameters having a clear physical meaning. They may further be transformed into coefficients \(\lambda _i \) from Eq. (1). To the best of our knowledge, the previous works where such coefficients were produced were based on the Poiseuille flow in a cylindrical geometry (like film flow in a capillary), which is a rather restrictive assumption (Rose 1990). An alternative might be given by the percolation theory (Hunt and Ewing 2009; Bedrikovetsky 1993; Seljakov and Kadet 1997), which is also based on rather restrictive assumptions about the structure of the porous medium and the character of the flow and, to the best of our knowledge, has not been involved the effect of viscous coupling. In the framework of the developed model, it becomes possible to evaluate apparent relative permeabilities produced in the steady-state experiments. They may be studied analytically and compared to the available experimental data. In this respect, our model is as useful as the previously proposed empirical models for relative permeabilities (see an overview in Siddiqui et al. 1999). However, it is more theoretically grounded and, hence, more universal. Additionally, it involves the effect of viscous coupling, which, to the best of our knowledge, has not been accounted for in the empirical models.

Sample calculations presented in Sect. 5 confirm these statements. Their goal was to study the behavior of the relative permeabilities and fractional flow functions for the stationary co-current flows of the two phases. One of the observed effects is significant dependence of the apparent relative permeabilities on the phase viscosity ratio, unlike in the traditional Buckley–Leverett scheme. The behavior of the fractional flow function is determined by a dimensional parameter expressing the characteristic size ratio of a cluster branch and of a single pore. Finally, qualitative and quantitative comparison of the developed approach to the available steady-state relative permeability data is discussed.

1.1 Assumptions

In this paper, the derivations are carried out in the simplest possible assumptions, in order to demonstrate the physical origin and implications of the formalism. Some generalizations are straightforward, some other will require separate studies.

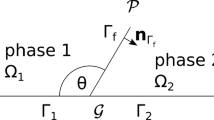
We consider a steady one-dimensional flow of the two immiscible liquids (phases). The phases will be denoted by subscripts w (white) and o (orange) in order to stress relevance to the petroleum applications, but, simultaneously, to mark a wider applicability of the formalism. Another interpretation is w for Wetting and o for nOn-wetting, although this property is not directly assumed. The medium is supposed to be macroporous, so that the pore sizes much exceed molecular sizes, and the Stokes flow equation may be applied in each region containing single phase.

A porous medium, where the flow occurs, is a cylinder of the cross section \(A\) and of the extent \(L\) in the flow direction. On the macroscale, the phase flows are co-directed, leaving out countercurrent flows or more complex cases (with nonzero angles between the flows). The flow direction is parallel to \(x\)-coordinate, while orthogonal coordinates are \(y,z\). The porous medium is assumed to be homogeneous on the macroscale, so that porosity \(\phi \) and single-phase permeability \(k\) are constants. We will also consider the flow on the mesoscale (considerably larger than the pore sizes, but much smaller than the sample size). On this scale, the porous medium is assumed to be statistically homogeneous, as discussed in more detail in Sect. 3.

2 The Maxwell–Stefan Flow Description

2.1 The General Form

As stated in the Introduction, the general MS approach for inertia-less flows is based on the balance of the driving and friction forces. We apply symbol \(G\) for the forces, since letter \(F\) is reserved for fractional flow.

For the two-phase flow in the cylindrical porous volume described above, the driving forces \(G_{id} \;(i=o,w)\) are the pressure forces acting on the phases in the cylinder

$$\begin{aligned} G_{wd} =(\Delta P_w )\phi As_w ,\quad G_{od} =\Delta P_o \phi As_o \end{aligned}$$

Here, \(\Delta P_i =P_{i,1} -P_{i,2} \approx -\frac{\partial P_i }{\partial x}L\) are the pressure differences (where subscripts 1 and 2 are used for entrance and exit pressures of a selected volume); \(s_i \) are phase saturations. Designation \(s\) is traditionally used for \(s_w \), while \(s_o =1-s\). The value \(\phi \, As_i \) represents the actual cross-sectional area open to flowing liquid (\(i=o,w)\).

In the Buckley–Leverett paradigm, the friction forces \(G_{ws},\;G_{os} \) between the flowing phases and the solid are proportional to superficial phase velocities and to the total porous volume accessible for the phases

$$\begin{aligned} G_{ws} =-\phi ALs_w \frac{\mu _w }{k_w }U_w ,\quad G_{os} =-\phi ALs_o \frac{\mu _o }{k_o }U_o \end{aligned}$$
(2)

Proportionality of the forces \(G_{is} \) to the phase porous volumes \(\phi ALs_i \) is introduced in order to make the definition of individual phase permeabilities \(k_i \) as close to the standard Buckley–Leverett definition as possible.

According to the standards of the MS approach, the friction force \(G_{wo} \) between the flowing phases may be defined to be proportional to the difference in the interstitial velocities

$$\begin{aligned} G_{wo} =\phi ALs_w s_o \alpha _{wo} \left( {\frac{U_o }{\beta _o }-\frac{U_w }{\beta _w }} \right) \end{aligned}$$
(3)

Here, \(\beta _i \) are multipliers transforming superficial flow rates \(U_i \) from interstitial (hydrodynamic) velocities \(u_i \):

$$\begin{aligned} u_{o,w} =U_{o,w}\big /\beta _{o,w} \end{aligned}$$

It is usually assumed that \(\beta _i =\phi s_i \). However, this is not the general case. The values of \(U_i /\phi s_i \) represent average components of the phase velocities in \(x\)-direction. Meanwhile, friction may be proportional to the difference in the absolute local values of the phase velocities. This may be accounted by introducing the tortuosity coefficients \(\tau _i \):

$$\begin{aligned} \beta _i =\frac{\phi s_i }{\tau _i } \end{aligned}$$
(4)

The force balances for the inertia-less flow have the form of

$$\begin{aligned} G_{wd} +G_{ws} +G_{wo}&= 0\\ G_{od} +G_{os} -G_{wo}&= 0 \end{aligned}$$

Combining the expressions above and reduction to the unit volume gives:

$$\begin{aligned} -\frac{\partial P_w }{\partial x}-\frac{\mu _w }{k_w }U_w +s_o \alpha _{wo} \left( {\frac{U_o }{\beta _o }-\frac{U_w }{\beta _w }} \right)&= 0; \nonumber \\ -\frac{\partial P_o }{\partial x}-\frac{\mu _o }{k_o }U_o -s_w \alpha _{wo} \left( {\frac{U_o }{\beta _o }-\frac{U_w }{\beta _w }} \right)&= 0 \end{aligned}$$
(5)

This system of equations has the form of \(\mathbf{D}=\kappa \mathbf{U}\) where \(\mathbf{D}\) is the vector of pressure gradients and \(\mathbf{U}\) is the vector of phase velocities. The proportionality matrix \(\kappa \) is inverse to matrix \(\Lambda \) from eq. (1):

$$\begin{aligned} \kappa =\left[ {{\begin{array}{l@{\quad }l} {-\left( \frac{\mu _w }{k_w }+\frac{s_o \alpha _{wo} }{\beta _w }\right) }&{} {\frac{s_o \alpha _{wo} }{\beta _o }} \\ {\frac{s_w \alpha _{wo} }{\beta _w }}&{} {-\left( \frac{\mu _o }{k_o }+\frac{s_w \alpha _{wo} }{\beta _o }\right) } \\ \end{array} }} \right] \end{aligned}$$

This matrix is symmetric if \(s_w /\beta _w =s_o /\beta _o \), that is, if tortuosities of the two phases are equal. The same should be valid for matrix \(\Lambda \) of the reciprocal coefficients. Thus, for this case, symmetry of the reciprocal matrix is a non-trivial property, which may not be obeyed, at least, for some flow models. This matrix has the form of

$$\begin{aligned} \Lambda&= \frac{1}{\beta _o \beta _w +\alpha _{wo} \left( \beta _w s_w \frac{k_o }{\mu _o }+\beta _o s_o \frac{k_w }{\mu _w }\right) }\nonumber \\&\quad \left[ {{\begin{array}{l@{\quad }l} {\beta _o \beta _w \frac{k_w }{\mu _w }+s_w \beta _w \alpha _{wo} \frac{k_w }{\mu _w }\frac{k_o }{\mu _o }}&{} {\alpha _{wo} \beta _w s_o \frac{k_w }{\mu _w }\frac{k_o }{\mu _o }}\\ {\alpha _{wo} \beta _o s_w \frac{k_w }{\mu _w }\frac{k_o }{\mu _o }}&{} {\beta _o \beta _w \frac{k_o }{\mu _o }+s_o \beta _o \alpha _{wo} \frac{k_w }{\mu _w }\frac{k_o }{\mu _o }} \end{array} }} \right] \end{aligned}$$
(6)

If the coupling coefficient \(\alpha _{wo} \) becomes zero, matrix \(\Lambda \) is expectedly reduced to the common diagonal Buckley–Leverett matrix. Otherwise, the presence of coupling has the two consequences. First, there are non-diagonal coefficients in \(\Lambda \) indicating the dependence of the flow rate of one phase on velocity of another phase. Second, apparent individual phase permeabilities depend on the viscosities of both phases. For example, the apparent permeability for water will be different depending whether the second flowing phase will be oil or gas, unlike in the traditional Buckley–Leverett scheme.

2.2 The MS Equations With Moving Interface

The Maxwell–Stefan equations have initially been developed for component diffusion in single-phase mixtures. The components in these mixtures are mixed up to molecular scale, and the friction forces reflect interactions at this scale.

On the contrary, the flowing phases in a macroporous medium usually form the interacting networks of pores or capillaries. There is an entangled interface that moves between the phases and together with them. Each phase “feels” the presence of another liquid not directly, but via this interface. With regard to the individual phases, this surface works as a “dragging” surface in the classical Newton imaginary experiment on the determination of viscosity.

For a stationary flow, position of the interface should remain invariable. Hence, its velocity should be tangent to the interface itself, so that it moves “along itself.” The \(x\)-component of this velocity will be denoted by \(V\). Then, \(\tau V\) is the average absolute value of the velocity, where \(\tau \) is the tortuosity of the surface.

A moving surface affects viscous liquid in such a way that liquid sticks to the surface and its local velocity becomes equal to the velocity of the surface. Velocities in other points in the liquid are correspondingly adjusted. On average, this adjustment may be described by introducing a friction force proportional to the difference between the surface velocity \(\tau V\) and liquid velocities \(U_i /\beta _i \), or, equivalently (with a different coefficient) between \(V\) and \(U_i /\tau \beta _i \). A more detailed substantiation of this assumption will be given later.

A modified set of the MS equations, assuming interactions between phases and their moving interface, may be represented in the form of

$$\begin{aligned} -\frac{\partial P_w }{\partial x}-\frac{\mu _w }{k_w }U_w +\frac{\mu _w }{k_{wV} }\left( V-\frac{U_w }{\tau \beta _w }\right)&= 0\end{aligned}$$
(7)
$$\begin{aligned} -\frac{\partial P_o }{\partial x}-\frac{\mu _o }{k_o }U_o +\frac{\mu _o }{k_{oV} }\left( V-\frac{U_o }{\tau \beta _o }\right)&= 0 \end{aligned}$$
(8)

The fact that the apparent friction should be dependent on the extent and configuration of the phase interface is reflected in the new set of phase permeabilities \(k_{wV} ,\;k_{oV} \). Unlike coefficient \(\alpha _{wo} \), which is determined by the properties of both phases, these permeabilities are single-phase properties. This is the advantage of the new approach; for example, while the friction coefficient \(\alpha _{wo} \) depends on the properties (let us say, viscosities) of both phases, and this dependence is unknown, coefficients \(k_{iV} \) may ideally be regarded as viscosity-independent.

Comparison to the general MS, Eq. (5) results in

$$\begin{aligned} s_w \frac{\mu _w }{k_{wV} }\left( V-\frac{U_w }{\tau \beta _w }\right) =-s_o \frac{\mu _o }{k_{oV} }\left( V-\frac{U_o }{\tau \beta _o }\right) =s_w s_o \alpha _{wo} \left( \frac{U_o }{\beta _o }-\frac{U_w }{\beta _w }\right) \end{aligned}$$
(9)

The first two equations in (9) represent the force balance for the surface. It is interpreted as the balance of the friction forces acting on the interface from the moving phases. Other possible forces (pressure force or friction of the interface with solid surface) are assumed to be negligible for this interface.

A consequence of (9) is the following equation for the surface velocity \(V\):

$$\begin{aligned} V=\frac{s_w \frac{\mu _w }{k_{wV} }\frac{U_w }{\tau \beta _w }+s_o \frac{\mu _o }{k_{oV} }\frac{U_o }{\tau \beta _o }}{s_w \frac{\mu _w }{k_{wV} }+s_o \frac{\mu _o }{k_{oV} }} \end{aligned}$$
(10)

Back-substitution of Eq. (10) into Eq. (9) results in the following expression for the friction coefficient \(\alpha _{wo} \) in terms of \(k_{Vi} \)

$$\begin{aligned} \alpha _{wo} =\frac{1}{\tau }\frac{1}{s_w \frac{k_{oV} }{\mu _o }+s_o \frac{k_{wV} }{\mu _w }} \end{aligned}$$
(11)

The computations will be simplified if we will assume that individual phase tortuosities \(\tau _i \) are equal to each other and the tortuosity \(\tau \) of the separating surface. In this case, matrices \(\kappa ,\;\Lambda \) of the reciprocal coefficients become symmetric (cf. Eqs. 4, 6). Equation (10) is simplified to

$$\begin{aligned} V=\frac{1}{\phi }\frac{\frac{\mu _w }{k_{wV} }U_w +\frac{\mu _o }{k_{oV} }U_o }{s_w \frac{\mu _w }{k_{wV} }+s_o \frac{\mu _o }{k_{oV} }} \end{aligned}$$
(12)

Other relations above remain valid.

3 Mesoscopic Description of the Flow

The phenomenological formalism presented above produces a set of equations describing the flow, but cannot be used for the determination of the coefficients in these equations. Meanwhile, these coefficients may be rather complex functions of saturation responsible for important peculiarities of the physical behavior of the system. The goal of the following two sections was to develop a model making it possible to compute coefficients \(k_{wV} ,\;k_{wV} \), at least, in some simplifying assumptions.

3.1 Assumptions

The two-phase flow in porous media is possible within a range of saturations, which boundaries are traditionally denoted by \(s_{wi} \) and \(1-s_{or} \). Within this range, both phases may flow. For \(s<s_{wi} \), the white phase cannot flow, while the orange phase becomes immobile if \(s>1-s_{or} \).

Mobility of the phases is usually related to their connectivity (Barenblatt et al. 1990). While a mobile phase, or, at least, a part of it is connected throughout the whole porous medium, an immobile phase is split into isolated “spots” that are kept from flowing by the capillary forces that are prevailing on the small scales. In terms of the percolation theory (Hunt and Ewing 2009; Seljakov and Kadet 1997), the phases forming infinite clusters may flow, while finite clusters remain trapped.

On the macroscopic level, for which the previous MS equations have been derived, each elementary representative volume (r.e.v.) contains both water and oil, which are supposed to be well mixed. In order to avoid discussing a problem that the phase pressure gradients may not always be parallel, we neglect the capillary pressure difference: \(P_w =P_o =P\). This assumption is not important for steady-state co-current flows, since under steady-state conditions, capillary pressure becomes the function of the saturation and its gradient is equal to zero, apart, probably, from the end effect zone. The capillary pressure becomes important for the countercurrent flows (Kalaydjian et al. 1989; Bourblaux and Kalaydjian 1990; Eastwood and Spanos 1991). For unsteady flows, capillary pressure may play an important role, especially, on the laboratory scale or in inhomogeneous porous media (Bedrikovetsky 1993). The picture may be different for the models with dynamic capillary pressures (Hassanizadeh and Gray 1990, 1993; Joekar-Niasar and Hassanizadeh 2011; Hilfer 2006; Hilfer and Doster 2010); however, this difference is not important for steady-state flows.

Under the assumption about zero or constancy of the capillary pressure, the pressure gradient \(P_x =\partial P/\partial x\) becomes common for both phases. Then, for an isotropic medium, the velocities are directed along it. Since \(x\) is the flow direction, the \(x\)-components of velocities \(U_o ,\;U_w \) are the same as the absolute values of these velocities.

Our goal was to describe flow on the mesoscopic scale. It is determined as such a scale where each r.e.v. belongs totally to a single o- or w-cluster, although it may still contain multiple pores. In cases where phases are so well mixed, that they flow together in each pore, r.e.v. may be a part of a pore.

Velocities \(\mathbf{U}_i \;(i=o,w)\) are defined as averages of the mesoscopic velocities \(\mathbf{W}_i \) over a sufficiently large cross section \(y,z\). The averages are defined as in Eq. (21) below. For the present approach, this is more convenient than averaging over representative volumes. For a large cross section, the \(y\)- and \(z\)-components of velocities \(\mathbf{W}_i \) become zero under averaging, due to assumed statistical homogeneity of the medium. Thus,

$$\begin{aligned} U_i =\phi s_i \left\langle {W_{i,x} } \right\rangle ;\quad \left\langle {W_{i,y} } \right\rangle =\left\langle {W_{i,z} } \right\rangle =0 \end{aligned}$$
(13)

In the following, we omit subscript \(x\), denoting \(W_i =W_{i,x} \;(i=o,w)\). This value is assumed to obey an operator equation in the form of

$$\begin{aligned} P_x =-\mu _i Z_i (W_i )\;(i=o,w) \end{aligned}$$
(14)

Let us discuss the possible forms of operator \(Z_i \).

The classical Buckley–Leverett theory is based on an inherent assumption that each phase moves “in its own porous medium,” which geometry is only dependent on the phase saturations, and that there is no interaction between the w- and the o-phases. This is true if flow at the cluster scale obeys the ordinary Darcy law

$$\begin{aligned} P_x =-\frac{\mu _i }{K_i }W_i ,\;\;Z_i (W)=W\big /K_i \;(i=o,w) \end{aligned}$$
(15)

Since the flow equation is linear, its averaging over a single cluster, taking the interphase boundary as impermeable, results in a linear equation of the Darcy type

$$\begin{aligned} P_x =-\frac{\mu _i }{k_i (s)}U_i \end{aligned}$$

In this case, the phase flows are not affected by each other, and matrix \(\mathbf{K}\) in Eq. (1) becomes diagonal.

The Darcy law (15) is not the real “microscopic” law, but is already a result of averaging by a smaller r.e.v. It may be obtained by averaging steady-state linearized Stokes flow equations over a volume or a section, which should be sufficiently large (contain many pores or capillaries) (Dullien 1992; Shapiro and Stenby 2000). In order for this law to be valid at the mesoscopic scale, a branch of a region occupied by one phase should still contain significant number of capillaries. This looks unlikely for many flows in porous media where the two phases are strongly “mixed,” like, for example, for the film flow structure (in terminology of Panfilov and Panfilova 2005). If the meniscus flow structure is realized, the phase clusters are usually highly branched and are also well mixed. In such cases, application of the Darcy approximation to describe flow inside separate phase regions becomes inadequate. It becomes also important to account for interaction between w- and o-clusters. This interaction may be reflected in the flow continuity condition on the boundary \(\Gamma _V \) between the clusters. For the steady-state flow, this continuity condition is reduced to the continuity of the velocity over the boundary, equal to the tangential velocity of the boundary itself. This boundary condition is not applicable to the Darcy operator (15), but it is necessary for the second-order operators \(Z_i \) of the Stokes or Brinkman type

$$\begin{aligned}&\displaystyle P_x =\mu _i \Delta W_i ,\quad Z_i =-\Delta \;(i=o,w)\,\, (\hbox {Stokes}), \,\,\hbox {or} \end{aligned}$$
(16)
$$\begin{aligned}&\displaystyle P_x =-\frac{\mu _i }{K_i }W_i +\mu _{ei} \Delta W_i ,\quad Z_i =\frac{1}{K_i }\mathbf{I}-\gamma _i \Delta \;(i=o,w)\,\, (\hbox {Brinkman}) \end{aligned}$$
(17)

Here, \(\gamma _i \) are the ratios between effective Brinkman viscosity \(\mu _{ei}\) and true viscosity \(\mu _i\). Permeabilities \(K_i \) differ from the ”true” permeability \(k\) even for one phase, since they involve mesoscale tortuosity \(\tau \) (recalling that \(W_i \) is the \(x\)-component of the velocity). Designation \(P_x \) is interpreted as \(\partial P/\partial x\).

The Stokes Eq. (16) is valid for the same r.e.v. as in the traditional hydrodynamics. It may be applied if both phases are present within most of the single pores (like in the situation of corner flows). Such flows should be considered if the internal surface of the porous medium is homogeneous and is strongly preferentially wet by one of the phases. In many cases, the porous rock is composed on different minerals, and the internal porous surface is heterogeneous on the microscale, making the porous medium fractional- or mixed-wet (Skauge and Ottesen 2002). In such porous media, different pores are occupied by the different fluids, and the branches of the clusters occupied by the different phases may be several capillaries thick. The r.e.v. in mixed-wet media may contain several pores, but not that many as needed for the validity of the Darcy law. Then, the Brinkman approximation (17), which is intermediate between the Darcy and the Stokes equations, becomes reasonable (see detailed substantiation in Valdes-Parada et al. 2007).

The flow continuity boundary condition for the second-order operators in Eqs. (16), (17) may formally be formulated as

$$\begin{aligned} W_i =V\quad \hbox {at}\,\,\Gamma _V \end{aligned}$$
(18)

Velocity \(V\) remains unknown until the flow equations are solved for both clusters, and then, it is calculated on the basis of the solution (cf. Eq. 9).

Another condition on the immobile boundary \(\Gamma _0 \) (the solid surface) might be necessary, as especially relevant for the Stokes flow model

$$\begin{aligned} W_i =0\quad \hbox {at}\,\,\Gamma _0 \end{aligned}$$
(19)

In the following, we will apply a simplifying assumption that the system possesses a translational invariance in \(x\)-direction, or that it is somehow averaged in this direction, so that pressure gradient \(P_x \) is independent of \(x\). Then, it becomes possible to look for a solution for velocities \(W_i ,\;V\) that is independent of \(x\). Correspondingly, operators \(Z_i \) in Eqs. (16), (17) become two-dimensional

$$\begin{aligned} \Delta =\Delta _2 =\frac{\partial ^{2}}{\partial y^{2}}+\frac{\partial ^{2}}{\partial z^{2}} \end{aligned}$$

3.2 Averaging

In this section, we demonstrate that averaging of the mesoscopic equations results in the MS equations with mobile surface described in Sect. 2.2.

Consider the general Eq. (14) with a general second-order linear differential operator \(Z_i \) of the type of (16) or (17), and boundary conditions (18), (19). In view of the linearity of the problem, its solution may be represented as a sum of the terms reflecting the influence of the pressure gradient and of the boundary condition

$$\begin{aligned} W_i =-\frac{1}{\mu _i }P_x \omega _{iP} +V\omega _{iV} \end{aligned}$$
(20)

Here, functions \(\omega _{iP} ,\;\omega _{iV}\) describe the reactions of the system, separately, to a unit pressure gradient and unit drag velocity

$$\begin{aligned} Z_i (\omega _{iP} )&= 1; \\ \omega _{iP}&= 0 \quad \hbox {at}\,\,\Gamma _V \cup \Gamma _0 \\ Z_i (\omega _{iV} )&= 0; \\ \omega _{iV}&= 1\,\,\hbox { at }\,\,\Gamma _V ;\quad \omega _{iV} =0\,\,\hbox { at }\,\,\Gamma _0 \end{aligned}$$

Functions \(\omega _{iP} ,\;\omega _{iV}\) are invariantly determined by the geometry of the region where the solution is considered, that is, of the w- or o-region. It should be noticed that these functions have different dimensions than \(W_i \) and than each other.

In order to demonstrate (20), consider solution \(W^{\prime }\) of the boundary problem (14) to (19) for \(V=0\), that is, solution of Eq. (14) with zero boundary conditions. Obviously, this solution is proportional to \(P_x /\mu _i \), that is, may be represented in the form \(W^{\prime }=P_x \omega _{iP} /\mu _i \). Now, let \(W_i \) be a solution of the full problem (14) to (19) and consider function \(W^{\prime \prime }=W_i -W^{\prime }=W_i +\frac{1}{\mu _i }P_x \omega _{iP} \). Substitution of this form into linear Eq. (14) results in equation \(Z_i (W^{\prime \prime })=0\) with full boundary conditions (18), (19). In view of linearity, \(W^{\prime \prime }\) is proportional to \(V\), that is, equal to \(V\omega _{iV}\).

For averaging of Eq. (20), consider a sufficiently large cross section \(A\). Part \(A_i =\phi s_i A\) of the cross section belongs to phase \(i\) (with some arbitrariness in designations, we denote both the cross section and its area by the same letter).

The macroscopic flow rate of phase \(i=o,w\) is defined as

$$\begin{aligned} U_i =\frac{\phi s_i }{A_i }\int _{A_i } {W_i \textit{dA}} =\frac{1}{A}\int _{A_i } {W_i \textit{dA}} \end{aligned}$$
(21)

Applying this integration to Eq. (20), we obtain

$$\begin{aligned} U_i&= -\frac{l_i }{\mu _i }P_x +\phi s_i l_\textit{iV} V;\nonumber \\ l_i&= \frac{1}{A}\int _{A_i } {\omega _{iP} \textit{dA}} ;\;l_\textit{iV} =\frac{1}{A_i }\int _{A_i }{\omega _{iV} \textit{dA}} \end{aligned}$$
(22)

Coefficients \(l_i \), \(l_{iV} \) depend only on the geometry of the w- and o-regions (and have different dimensions). In the Buckley–Leverett scheme, this geometry is uniquely characterized by the saturation. More complex assumptions (e.g., involving hysteresis) may also be considered.

Equation (22) may further be transformed to the form of MS Eqs. (7), (8):

$$\begin{aligned} P_x =-\frac{\mu _i }{k_i }U_i +\frac{\mu _i l_{iV} \phi s_i }{k_i (1-l_{iV} )}\left( V-\frac{U_i }{\phi s_i }\right) \end{aligned}$$
(23)

Here, values \(k_i =l_i /(1-l_{iV} )\) may be interpreted as phase permeabilities. Comparison to Eqs. (7), (8) shows also that

$$\begin{aligned} k_{iV} =\frac{k_i (1-l_{iV} )}{l_{iV} \phi s_i } \end{aligned}$$
(24)

The last formula is meaningful if \(0<l_{iV} <1\), otherwise the friction coefficients become negative. We cannot provide a general proof of this inequality, but will show later that it is valid for the considered model examples. Under this condition, validity of the MS equations with a flowing interface in the framework of the mesoscopic description has been demonstrated.

We will also apply an equivalent but different form of Eq. (23)

$$\begin{aligned} U_i =-(1-l_{iV} )\frac{k_i }{\mu _i }P_x +l_{iV} \phi s_i V \end{aligned}$$
(25)

4 Computation of the Phenomenological Coefficients

If the Buckley–Leverett permeabilities \(k_i \) are assumed to be known (for example, given by the Corey expressions), the problem of determining transport coefficients is reduced to coefficients \(l_{iV} \). This section describes the computation of \(l_{iV} \) under some geometrical assumptions, which will be called “the jet model.”

4.1 Geometrical Representation

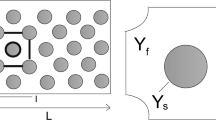
Consider in more detail the distribution of the two flowing phases in the cross-section orthogonal to the flow. As saturation varies, this distribution may undergo qualitative changes, different from the changes that will be observed in three dimensions. Combination of the two- and three-dimensional pictures forms the qualitative basis for the jet model.

Distribution of the two phases in the cross section consists of the w- and the o-“spots.” There is a significant qualitative distinction of the phase distribution in two dimensions, compared to the three-dimensional case. In three dimensions, both phases form continuous clusters if \(s_{wi} <s<s_{or} \), and one of the phases becomes discontinuous outside these limits. Meanwhile, in two dimensions, only one phase may be connected in all the directions, while another phase is necessarily discontinuous. It may happens that both phases are discontinuous (for example, they form interchanging “strips”). If the phase distribution is statistically homogeneous and isotropic, as assumed here, then at any given saturation, only one of the phases will be continuous, while another phase will form isolated spots.

Apparently, the higher saturation, the more probable is that the w-phase will be connected. Then, there is a threshold saturation \(s^{*}\) below which the orange phase and above which the white phase are connected in the cross section. In percolation theory, this saturation corresponds to the percolation probability of 0.5 (Hunt and Ewing 2009); however, this will not be used in the following. For definiteness, we will concentrate on the case \(s<s^{*}\) (connected o-phase). Computations under \(s>s^{*}\) are similar.

Although most of the orange phase is connected under \(s<s^{*}\), there may still be disconnected orange “spots.” These “spots” become negligible and disappear at some distance from the threshold saturation. For simplicity, we will neglect them. Thus, in each two-dimensional cross section, at \(s<s^{*}\), there are isolated clusters of the white phase surrounded by continuous orange phase (Fig. 1a). At \(s>s^{*}\), there are, inversely, clusters of the orange phase surrounded by continuous white phase (Fig. 1b).

Fig. 1
figure 1

Distribution of w- and o-clusters in the cross section: a for \(s<s^{*}\); b for \(s>s^{*}\); c the jet model (for \(s<s^{*})\)

Full size image

The described picture is a cut of the three-dimensional phase distribution. In three dimensions, a phase may flow if it forms an infinite cluster, while finite clusters remain immobile due to capillary effects. Both phases form connected infinite clusters for saturations \(s_{wi} <s<1-s_{or} \), while only orange phase flows at \(s<s_{wi} \). As assumed above, at the saturation interval \(s_{wi} <s<s^{*}\). the orange phase fully belongs to an infinite cluster, while the white phase may form both one infinite and multiple finite clusters. Hence, in the cross section. some white “spots” belong to the moving infinite cluster, and some to immobile finite clusters.

We introduce fraction \(I_P \) of the spots belonging to the immobile phase. This value is a function of \(s\), tending to unity when \(s\) approaches \(s_{wi}\), and becoming (almost) zero at \(s^{*}\).

Although all the spots may be of irregular shapes, we approximate them by a series of equal cylindrical “jets,” with the outer jet radius \(R\) and inner radius \(r_j \) (Fig. 1c). The value of \(R\) may be treated as effective “hydraulic radius,” expressing the characteristic dispersion size of the system.

Such a representation is a rough approximation of the real (branched and tortous) picture of the clusters. For example, the described configuration either cannot provide full coverage of the plane, or some jets must intersect (or both). It is difficult to evaluate the accuracy of the jet approximation. However, this error does not seem to influence the physics of the system or to change the values of the phenomenological coefficients by an order of magnitude. An advantage of this approach is that it makes it possible to derive analytical expressions for the phenomenological coefficients, within few constants allowing for direct physical interpretation. This may be useful for engineering computations. More complex geometries may only be studied numerically.

The main simplifications of the jet model, compared to real phase geometry, are that the tortuosity of the jets is taken into account in a very simplified way, via the only parameter \(\tau \); and that the complex shapes, size distributions, and multiconnectivity of the o- and w-clusters are not accounted for. Distribution of the jets by sizes might be introduced as the next approximation to reality. It will not be considered here.

If \(s<s^{*}\), the outer space of a jet is filled by o-phase, and the inner by w-phase, so that

$$\begin{aligned} r_j^2 /R^{2}=s \end{aligned}$$
(26)

If \(s>s^{*}\), the configuration is inverse.

Relation (26) does not determine the actual size of a jet, only the relative sizes of its inner and outer parts. Hence, the dispersion radius \(R\) may be considered as a free parameter determining the flow regime. Another free parameter is \(I_P \) determining the fraction of jets in inner part of which the flow occurs. The last parameter is important for relative permeabilities \(k_i \); for example, the residual saturation points correspond to \(I_P =0\). However, it may be shown that contribution of \(I_P \) into coefficients \(l_{iV} \) does not affect their behavior qualitatively.

4.2 Flow in the Inner and Outer Parts of a Jet

The problem of flow in a jet possesses radial symmetry. Axis \(x\) is directed along the jet, while radial coordinate \(r\) measures the distance to its center line. We assume that the flow in the inner and in the outer parts of a jet is described by the Brinkman Eq. (17). Considerations based on the Stokes equation are fully similar (Rose 1990). In radial coordinates, we obtain the second-order ordinary equation with regard to \(W_i \)

$$\begin{aligned} P_x =-\frac{\mu _i }{K_i }W_i +\frac{\mu _{ei} }{r}\frac{d}{dr}\left( r\frac{dW_i }{dr}\right) ,\quad (i=o,w) \end{aligned}$$
(27)

We will distinguish between inner jets (\(0<r<r_j )\) and outer jets (\(r_j <r<R)\). They are filled by the different phases, and the phase distribution changes when saturation \(s\) crosses the value of \(s^{*}\). If \(s<s^{*}\), the inner part of the jet is occupied by w-phase, while the outer part contains o-phase. The interface \(\Gamma _V \) is at \(r=r_j \). Correspondingly, the two boundary conditions for the considered problem are

$$\begin{aligned} W_w |_{r_j } =W_o |_{r_j } =V \end{aligned}$$

For the w-phase, the problem is solved for \(r_j \le r\le R\). The second boundary condition at outer boundary of the jet \(r=R\) is impermeability condition

$$\begin{aligned} \frac{\partial W_o }{\partial r}\Big |_R =0 \end{aligned}$$

The problem for \(W_w \) is solved inside the tube of radius \(r_j \quad (-r_j \le r\le r_j )\), with a boundary condition

$$\begin{aligned} W_w |_{r_j } =W_w {|_{-r_j }} =V \end{aligned}$$
(28)

The solutions of the stated problems and the subsequent averaging of the velocities according to Eq. (21) are discussed in Appendix. The result is described by Eqs. (23) and (25). The expressions for coefficients at \(s<s^{*}\) have the form of

$$\begin{aligned} l_{oV}&= \frac{\sqrt{k_{ro} \gamma _o }\Delta _1 }{\xi \Delta }\sqrt{\frac{s}{(1-s)^{3}}}; \nonumber \\ \Delta&= \hbox {K}_0 \left( \frac{\xi }{\sqrt{k_{ro} \gamma _o }}\sqrt{s(1-s)}\right) \hbox {I}_1 \left( \frac{\xi }{\sqrt{k_{ro} \gamma _o }}\sqrt{1-s}\right) \nonumber \\&+\,\hbox {K}_1 \left( \frac{\xi }{\sqrt{k_{ro} \gamma _o }}\sqrt{1-s}\right) \hbox {I}_0 \left( \frac{\xi }{\sqrt{k_{ro} \gamma _o }}\sqrt{s(1-s)}\right) \nonumber \\ \Delta _1&= \hbox {I}_1 \left( \frac{\xi }{\sqrt{k_{ro} \gamma _o }}\sqrt{1-s}\right) \hbox {K}_1 \left( \frac{\xi }{\sqrt{k_{ro} \gamma _o }}\sqrt{s(1-s)}\right) \nonumber \\&-\hbox {K}_1 \left( \frac{\xi }{\sqrt{k_{ro} \gamma _o }}\sqrt{1-s}\right) \hbox {I}_1 \left( \frac{\xi }{\sqrt{k_{ro} \gamma _o }}\sqrt{s(1-s)}\right) \nonumber \\ l_{wV}&= \frac{2\sqrt{k_{rw} \gamma _w }}{\xi s}\hbox {I}_1 \left( \frac{\xi }{\sqrt{k_{rw} \gamma _w }}s\right) \Big /\hbox {I}_0 \left( \frac{\xi }{\sqrt{k_{rw} \gamma _w }}s\right) \end{aligned}$$
(29)

At \(s>s^{*}\)

$$\begin{aligned} l_{oV}&= \frac{2\sqrt{k_{ro} \gamma _o }}{(1-s)\xi }\hbox {I}_1 \left( \frac{\xi }{\sqrt{k_{ro} \gamma _o }}(1-s)\right) \Big /\hbox {I}_0 \left( \frac{\xi }{\sqrt{k_{ro} \gamma _o }}(1-s)\right) \nonumber \\ l_{wV}&= \frac{2\sqrt{k_{rw} \gamma _w }\Delta _1 }{\xi \Delta }\sqrt{\frac{1-s}{s^{3}}}; \nonumber \\ \Delta&= \hbox {K}_0 \left( \frac{\xi }{\sqrt{k_{rw} \gamma _w }}\sqrt{s(1-s)}\right) \hbox {I}_1 \left( \frac{\xi }{\sqrt{k_{rw} \gamma _w }}\sqrt{s}\right) \nonumber \\&+\,\hbox {K}_1 \left( \frac{\xi }{\sqrt{k_{rw} \gamma _w }}\sqrt{s}\right) \hbox {I}_0 \left( \frac{\xi }{\sqrt{k_{rw} \gamma _w }}\sqrt{s(1-s)}\right) \nonumber \\ \Delta _1&= \hbox {I}_1 \left( \frac{\xi }{\sqrt{k_{rw} \gamma _w }}\sqrt{s}\right) \hbox {K}_1 \left( \frac{\xi }{\sqrt{k_{rw} \gamma _w }}\sqrt{s(1-s)}\right) \nonumber \\&-\hbox {K}_1 \left( \frac{\xi }{\sqrt{k_{rw} \gamma _w }}\sqrt{s}\right) \hbox {I}_1 \left( \frac{\xi }{\sqrt{k_{rw} \gamma _w }}\sqrt{s(1-s)}\right) \end{aligned}$$
(30)

Here, \(\xi =R/\sqrt{k/\phi }\) is a characteristic scale of the cluster heterogeneity, expressed in characteristic pore sizes \(\sqrt{k/\phi }\) . Similar expressions for permeabilities \(k_i \) may, in principle, also be obtained, but they will not be considered in the present paper.

Plots of the coefficients \(l_{iV} \) versus saturation are shown in Fig. 2. The data for computation are collected in Table 1. It may be seen that the coefficients are non-monotonous, and that they become zero at the corresponding residual saturations. The values of coefficients are between zero and unity, as required by Eq. (24). As expected, they decrease with increase in the ratio \(\xi \) of the characteristic number of pores in a cluster branch. The thicker are the branches, the less pronounced is the mutual influence of the water and oil clusters.

Fig. 2
figure 2

Coefficients \(l_{iV} (i=w,\hbox {o})\). Dashed lines: \(l_{oV} \); continuous lines: \(l_{wV} \). Blue lines: \(\xi =3\); black lines: \(\xi =30\).

Full size image
Table 1 Characteristic values for numerical computations
Full size table

Another characteristic peculiarity of the plots is discontinuity around the critical saturation \(s^{*}\). Formally, this discontinuity arises from the different expressions (29), (30) for the coefficients \(l_{iV} \), under saturations above or below the threshold saturation \(s^{*}\). Close to this saturation, the system exhibits a critical transition in a cross section, as infinite cluster becomes thinner, finite clusters grow to infinity, and the assumptions of the jet model become invalid (Hunt and Ewing 2009). A different model for coefficients \(l_{iV} \) should be developed close to the percolation transition (for example, a “mixture” of the inner w- and inner o-jets).

The expressions above are provided without account for passive jets (\(I_p =0)\). It may be shown (see Appendix) that in their presence, all the coefficients above should be multiplied by \(1-I_p \). This multiplier changes the values, but does not change the expressions for \(l_{iV} \).

Individual phase permeabilities \(k_i \) may also be computed within the jet model and depend strongly on \(I_P \). In this work, for simplicity, we will use the standard Corey (power-type) expressions for \(k_i \), assuming that dependence on \(I_p \) is somehow reflected in these expressions.

5 Computational Examples

5.1 Relative Permeabilities and Fractional Flow Function

There has been a discussion in the literature how reciprocal coefficients may be determined experimentally (Ayub and Bentsen 1999; Dullien and Dong 1996 and references therein). A common approach is related to the analysis of the combination of the co-current and countercurrent flows. This may be a difficult experimental task, since the phase pressures are connected via the capillary pressure, while phases flow along the pressure gradients. A more usual experimental procedure (although not as wide spread as the standard JBN test, Johnson et al. 1959) makes it possible to determine apparent relative permeabilities by the analysis of the co-current steady-state flow. Indeed, under steady-state flow conditions, saturation is constant and may be determined by mass balance. Constancy of the saturation means constancy of the capillary pressure and, hence, equality of the pressure gradients in both phases. The fractional flow may be measured directly, while the measurement of the pressure difference makes it possible to determine the overall phase mobility. Then, the individual relative permeabilities may be calculated by the use of the fractional flow and overall mobility, similarly to the JBN method.

In this paper, we will concentrate on the analysis of the contribution of the viscous coupling to the apparent relative permeabilities, fractional flow function, and overall mobility of the phases. The expressions for these dependences are given below.

The apparent relative permeabilities \(k_{ri} \;(i=o,w)\) may be found from basic equations (1), in which coefficients \(K_{ij} \) are given by Eq. (6). If the capillary pressure may be neglected \((P_o =P_w =P)\), these equations are reduced to

$$\begin{aligned} U_w&= -\frac{\beta _o \beta _w \frac{k_w }{\mu _w }+\beta _w \alpha _{wo} \frac{k_w }{\mu _w }\frac{k_o }{\mu _o }}{\beta _o \beta _w +\alpha _{wo} \left( \beta _w s_w \frac{k_o }{\mu _o }+\beta _o s_o \frac{k_w }{\mu _w }\right) }\frac{\partial P}{\partial x}; \\ U_o&= -\frac{\beta _o \beta _w \frac{k_o }{\mu _o }+\beta _o \alpha _{wo} \frac{k_w }{\mu _w }\frac{k_o }{\mu _o }}{\beta _o \beta _w +\alpha _{wo} \left( \beta _w s_w \frac{k_o }{\mu _o }+\beta _o s_o \frac{k_w }{\mu _w }\right) }\frac{\partial P}{\partial x} \end{aligned}$$

Hence, the relative permeabilities are equal to

$$\begin{aligned} k_{rw}&= \frac{1}{k}\frac{\beta _o \beta _w k_w +\beta _w \alpha _{wo} k_w \frac{k_o }{\mu _o }}{\beta _o \beta _w +\alpha _{wo} \left( \beta _w s_w \frac{k_o }{\mu _o }+\beta _o s_o \frac{k_w }{\mu _w }\right) };\\ k_{ro}&= \frac{1}{k}\frac{\beta _o \beta _w k_o +\beta _o \alpha _{wo} k_o \frac{k_w }{\mu _w }}{\beta _o \beta _w +\alpha _{wo} \left( \beta _w s_w \frac{k_o }{\mu _o }+\beta _o s_o \frac{k_w }{\mu _w }\right) } \end{aligned}$$

The fractional flow function becomes correspondingly

$$\begin{aligned} F=\frac{\frac{k_w }{\mu _w }+\frac{\alpha _{wo} }{\beta _o }\frac{k_w }{\mu _w }\frac{k_o }{\mu _o }}{\frac{k_w }{\mu _w }+\frac{k_o }{\mu _o }+\alpha _{wo} \left( \frac{1}{\beta _w }+\frac{1}{\beta _o }\right) \frac{k_w }{\mu _w }\frac{k_o }{\mu _o }} \end{aligned}$$
(31)

In these expressions, individual phase permeabilities \(k_w k_o \) are such as in the Maxwell–Stefan Eq. (5). They may be defined as phase permeabilities for the case where the phase interaction does not exist. This justifies the application of the Corey dependences for their calculation

$$\begin{aligned} k_w&= kk_{rw0} (s);\quad k_o =kk_{ro0} (s);\nonumber \\ k_{rw0} (s)&= k_{rwor} \left( {\frac{s-s_{wi} }{1-s_{wi} -s_{or} }} \right) ^{\alpha _w };\quad k_{ro0} (s)=k_{rowi} \left( {\frac{1-s_{or} -s}{1-s_{wi} -s_{or} }} \right) ^{\alpha _o } \end{aligned}$$
(32)

The “standard” fractional flow function, in the absence of flow coupling, is defined as

$$\begin{aligned} F_0 =\frac{k_w /\mu _w }{k_w /\mu _w +k_o /\mu _o }=\frac{k_{rw0} }{k_{rw0} +k_{ro0} /\mu }\;\;(\mu =\mu _o /\mu _w ) \end{aligned}$$
(33)

The difference between the two functions is proportional to the coupling coefficient \(\alpha _{wo} \)

$$\begin{aligned} F-F_0 =\frac{k_w }{\mu _w }\frac{k_o }{\mu _o }\alpha _{wo} \frac{\frac{1}{\beta _o }\frac{k_o }{\mu _o }-\frac{1}{\beta _w }\frac{k_w }{\mu _w }}{\left[ {\frac{k_w }{\mu _w }+\frac{k_o }{\mu _o }+\frac{k_w }{\mu _w }\frac{k_o }{\mu _o }\alpha _{wo} \left( {\frac{1}{\beta _o }+\frac{1}{\beta _w }} \right) } \right] \left[ {\frac{k_w }{\mu _w }+\frac{k_o }{\mu _o }} \right] } \end{aligned}$$

We will consider the case of flow with a moving surface, where all the tortuosities are equal. The coefficient \(\alpha _{wo} \) is then found from Eq. (11), where values of \(k_{iV} \) are further substituted by expressions (24). After long but obvious transformations, it may be obtained that

$$\begin{aligned} k_{rw}&= \frac{k_{rw0} \left( s_w^2 \frac{k_{ro0} (1-l_{oV} )}{l_{oV} }+s_o^2 \mu \frac{k_{rw0} (1-l_{wV} )}{l_{wV} }\right) +s_w k_{rw0} k_{ro0} }{s_w^2 \frac{k_{ro0} }{l_{oV} }+s_o^2 \mu \frac{k_{rw0} }{l_{wV} }}\end{aligned}$$
(34)
$$\begin{aligned} k_{ro}&= \frac{k_{ro0} \left( s_w^2 \frac{k_{ro0} (1-l_{oV} )}{l_{oV} }+s_o^2 \mu \frac{k_{rw0} (1-l_{wV} )}{l_{wV} }\right) +s_o \mu k_{ro0} k_{rw0} }{s_w^2 \frac{k_{ro0} }{l_{oV} }+s_o^2 \mu \frac{k_{rw0} }{l_{wV} }}\end{aligned}$$
(35)
$$\begin{aligned} F&= \frac{k_{rw0} +s_w \frac{k_{rw0} k_{ro0} }{s_w^2 \frac{k_{ro0} (1-l_{oV} )}{l_{oV} }\,+\, s_o^2 \mu \frac{k_{rw0} (1-l_{wV} )}{l_{wV} }}}{k_{rw0} +\frac{k_{ro0} }{\mu }+\frac{k_{rw0} k_{ro0} }{s_w^2 \frac{k_{ro0} (1-l_{oV} )}{l_{oV} }\, +\, s_o^2 \mu \frac{k_{rw0} (1-l_{wV} )}{l_{wV} }}} \end{aligned}$$
(36)

Equations (34), (35), and (36) will be applied for sample computations presented in the next chapter. The coefficients \(l_{iV} \) in them are given by Eqs. (29) and (30), while the phase permeabilities by Eq. (32). Both relative permeabilities and fractional flow function are independent of tortuosities, provided that it is the same for both phases. More precisely, this dependence is “hidden” in the value of absolute permeability (which disappears from the final answer) and in the shapes of the diagonal relative permeabilities (which in this work are approximated by the Corey expressions).

5.2 Sample Calculations

A series of sample computations has been carried out, with the parameters listed in Table 1. Ratios \(\gamma _{w,o} \) of effective Brinkman to real liquid viscosities were selected to be unity, following Valdes-Parada et al. (2007). Other parameters are typical for reservoir simulations.

Comparison of the fractional flow curves: one calculated with these parameters, and one without viscous coupling, is presented in Fig. 3. An obvious effect of coupling is that the fractional flow curve becomes straighter. The difference between phase mobilities decreases, and the flow picture becomes closer to single phase (although residual saturations are still there). If this fractional flow curve might be applied to non-stationary flows in the standard Buckley–Leverett scheme, as in Rose (1988), one would conclude that in the presence of coupling the displacement of one phase by another would become more piston-like.

Fig. 3
figure 3

Fractional flow curves without phase interactions (the dashed line) and with phase interactions (basic case-solid line)

Full size image

The fractional flow curves in Fig. 3 look continuous, in spite of the discontinuities of the involved coefficients \(l_{iV}\) at the threshold saturation \(s^{*}\). In fact, the discontinuity of \(F\) at this saturation does not exceed 0.001. This jump increases if the threshold saturation moves away from the value of 0.5. A near-extreme case, with the value of \(s^{*}\) equal to 0.65, is depicted in Fig. 4. The jump in the value of the fractional flow function is 0.01. Such a discontinuity cannot significantly influence important flow characteristics.

Fig. 4
figure 4

Behavior of the fractional flow curve in a neighborhood of the discontinuity

Full size image

Variation in the fractional flow function with the ratio \(\xi \) of the cluster branch thickness to pore size is shown in Fig. 5. For \(\xi =10\), curve \(F\) is very close to the fractional flow curve without coupling. The two curves become practically indistinguishable for \(\xi \ge 15\). If the size of the jet is over 10 times larger than the size of a single pore, then, on average, only one of the 50 pores contains a flowing surface (50 comes from the ratio of the cylinder surface to volume). The interaction of the flowing phases with solid becomes much larger than the interaction between the flowing phases. The last interaction may be neglected, and the model is reduced to the classical Buckley–Leverett theory.

Fig. 5
figure 5

Fractional flow curve at the different cluster branch-to-pore ratios \(\xi \). Dashed line: \(\xi =10\). Dotted line: \(\xi =3\) (basic case). Solid line: \(\xi =1.2\)

Full size image

On the contrary, for the values of \(\xi \) below two, the flowing phases become very well mixed, and the interactions between them become dominating. Correspondingly, the fractional flow curve changes its shape, as shown for the extreme example of \(\xi =1.2\). If applied to a displacement problem, such a curve would produce two displacement fronts. Qualitatively, such a picture was observed in the capillary network simulations (Panfilov and Panfilova 2005). For the present example, the two displacement fronts would move almost with the same rate, as seen from the inclination of the tangents (Bedrikovetsky 1993). The displacement would be nearly piston-like. This is an expected effect, since strong coupling facilitates the disappearance of the difference between velocities of the flowing phases.

The phase relative permeabilities with and without coupling are compared in Fig. 6. It may be seen that they vary even more dramatically than the fractional flow curves. The largest changes are observed around the endpoint saturations: it may be shown that, compared to the case of no coupling, the endpoint relative permeabilities are multiplied by \(1-l_{wV}\) or \(1-l_{oV}\), correspondingly. The overall mobility of the two phases also decreases. The dimensionless mobility \(M\), defined as \(k_{rw} +k_{ro} /\mu \), is shown in Fig. 7. The mobility decreases more at lower factors \(\xi \). Interaction between the branches of water and oil clusters tends to delay the total flow, and this delay is higher for stronger interaction. The decrease in mobility is more pronounced close to the endpoint saturations, where one of the phases becomes almost immobile and slows down another phase.

Fig. 6
figure 6

Relative permeability curves without phase interactions (dashed lines) and for the basic case (solid lines). Black: relative permeabilities for oil, blue: relative permeabilities for water

Full size image
Fig. 7
figure 7

Dimensionless total phase mobility \(M\) as dependent on the cluster size. Dashed line: the case without phase interactions. Dotted line: the case with cluster branch-to-pore ratio \(\xi =6\). Solid line: the basic case (\(\xi =3)\)

Full size image

Figure 8 presents the behavior of the apparent relative permeabilities. While the endpoint permeabilities always decrease, the intermediate values of permeabilities are strongly dependent on the viscosity ratio. The apparent relative permeabilities may change from concave to convex and may even become non-monotonous under high viscosity ratios, as for the shown example of the oil relative permeability at \(\mu =10\).

Fig. 8
figure 8

Relative permeabilities for the different viscosity ratios \(\mu \). Dashed lines: relative permeabilities without phase interactions. Dotted lines: \(\mu =1\). Dot-dashed lines: \(\mu =3\) (basic case). Solid lines: \(\mu =10\). Black: oil relative permeabilities. Blue: water relative permeabilities

Full size image

Such behavior, although complex, seems to be well interpretable within the described physics of the flow. The endpoint relative permeabilities decrease, because a flowing phase is slowed down by the second immobile phase, apart from friction with the immobile porous medium. For intermediate values of saturations, the “fast” w-phase may drag the o-phase, which otherwise would be slowed down by its high viscosity. This explains the non-monotonous behavior of the relative permeability.

5.3 Comparison to Experimental Data

The apparent relative permeabilities are often determined experimentally. The traditional Buckley–Leverett theory presumes that these relative permeabilities are independent of the viscosities of the fluids. At least, if the temperature changes within reasonable limits, it is only oil or water viscosity that should be affected, but not the relative permeability curves (Bedrikovetsky 1993).

On the contrary, the developed theory predicts that the apparent relative permeabilities should be dependent on fluid viscosity ratio (oil to water) (Fig. 8). The oil relative permeability should increase with the viscosity ratio, while the water relative permeability decreases with it. This prediction is conditioned, however, by the limitations of the model. It is true within the model assumptions, the most important of which are the steady-state flow, and the fact that, while the viscosities vary, other parameters do not change, and, in particular, the fluid distribution on the microscale roughly expressed by parameter \(\xi \). The last condition is especially difficult to maintain or to verify in experiments. The first condition requires usage of the data from steady-state experiments only, which strongly restricts the data available for verification of the model.

Probably, the first experimental evidence on dependence of the relative permeabilities on viscosities was reported by Odeh (1959). The experimental data from this work indicate that relative permeability for oil increases with viscosity ratio, in a qualitative agreement with the prediction of the developed model. The relative permeability for water remains (almost) invariable (in our computations, it varies to a lesser extent than the relative permeability for oil). A model, by which Odeh explained his experimental results, was strongly criticized (Baker 1960). However, the work by Yuster (1951) corrects the errors of the Odeh model approach, with qualitatively similar dependencies of the relative permeabilities on the viscosity ratio (see also Rose 1991, and references therein).

Other sources predict very different behavior of the relative permeabilities depending on the viscosity ratio (see cf. ex. Downie and Crane 1961; Siddiqui et al. 1999; Wang et al. 2006). The main reason for such difference is, in our opinion, that change in the viscosity ratios is achieved by the selection of different fluids, while other properties like wettability and capillary pressure are not taken care of. Change in the capillary number may result in qualitatively different distribution of the phases in the pore space and, as a result, to the different flow behavior (Avraam and Payatakes 1995). Hysteresis of the relative permeabilities may also contribute to the results (Eleri et al. 1995). It is difficult to separate the different mechanisms, and analysis of their interaction requires much more sophisticated approaches and more detailed considerations than the one presented here. In terms of the proposed model, the endpoint relative permeabilities, the Corey exponents and the value of \(\xi \) may vary from one to another experiment.

In the Fulcher et al. (1985) experiment, the care was taken, at least, about the surface tension between the phases. Fulcher et al. demonstrated that the relative permeabilities should not be considered as functions of the capillary number as a whole, but of its different constituents separately. In the particular set of the experiments to be discussed here, the viscosity ratio varied, while surface tension remained invariable. This is not sufficient: the authors remarked that the wettability could not be controlled. The viscosity of brine or its substitutes varied in wide limits, but was always high compared to viscosity of the oil. The viscosity ratios, as recalculated from the paper, were equal to 0.17, 0.018, and 0.0024, correspondingly. The data show that the oil relative permeabilities increase, and the brine relative permeabilities decrease with the viscosity ratio. This is in full qualitative agreement with predictions of our model.

For quantitative comparison with the experiments of Fulcher et al., their data for drainage were used, so that \(s_{or} =0\) and \(k_{rwor} =1\). In agreement with the experimental data, the value of \(s_{wi} \) was taken to be 0.32.

Based on several trials, the adjustable parameters in the model were divided into the two groups. The values of \(\xi \), \(s^{*}\), and the Corey exponent for oil \(\alpha _o \), Eq. (32), were taken to be the same for all the three viscosity ratios investigated. The values of \(k_{rowi} \) and \(\alpha _w \) were taken to be individual for the different viscosity ratios. Unfortunately, application of the same set of parameters for all the data points has turned out to be impossible. Analysis of Eq. (35) indicates that at small viscosity ratios (as in the experiment), the relative permeability for oil is almost equal to \(k_{r0} (1-l_{oV} )\). It is impossible to produce experimentally observed large variation in \(k_{ro} \) without variation in the parameters in the Corey expression (32). This probably indicates that in experiments of Fulcher et al., the geometry of phase distribution varied with the change in the wetting phase, although the surface tension was the same. It should also be remarked that in our model, the value of \(k_{rowi} \) in Eq. (32) does not have a meaning of actual residual permeability, but is only an effective parameter. The actual relative permeability is equal to \(k_{rowi} (1-l_{oV} )\). That is why the values of \(k_{rowi} \) were sometimes allowed to be larger than unity in our simulations.

The result of model adjustment to experimental data is shown in Fig. 9. The reproduction of the data is rather satisfactory, both qualitatively and quantitatively. The average deviation of the predicted relative permeabilities from the experimental values is 0.023. Such an accurate description of the experimental data could not be achieved with the traditional Corey model.

Fig. 9
figure 9

Testing the theory with experimental data of Fuhler et al. (1985). Relative permeabilities for a water, b oil for different viscosity ratios \(\mu \). Stars/dotted lines: \(\mu =0.17\). Circles/dashed lines: \(\mu =0.018\). Crosses/solid lines: \(\mu =0.0025\)

Full size image

The value of \(\xi \) was found to be 3.16. This low value indicates a small size of a jet and high interaction of the water and oil. Attempts to fit \(\xi \) to individual curves resulted in the values in the range from 2.1 to 4.1, which are also law. This illustrates a stability of the conclusion about strong water–oil interaction.

The value of threshold saturation \(s^{*}\) was found to be 0.77 and varied from 0.71 to 0.78 in the individual fits. The jumps of the relative permeabilities at \(s^{*}\) are rather pronounced, which shows that the model is imperfect at this region. Probably, continuous transition from w-jets to o-jets should be introduced in the future instead of the abrupt transition used in the present version of the model.

A more straightforward test could be the comparison of the results of cocurrent and countercurrent flow experiments (Bourblaux and Kalaydjian 1990; Eastwood and Spanos 1991). However, such flows require a separate analysis.

6 Conclusions

We have developed the Maxwell–Stefan approach to two-phase immiscible flows in porous media. This approach makes it possible to account for viscous coupling between the flowing phases and introduce the transport coefficients possessing a clear physical significance.

The approach has been developed in the two forms: the general form, and the form with moving interface between flowing phases. The last form is advantageous, since it reduces the interphase interactions to the interactions between a phase and an interface, which makes it possible to express the phenomenological coefficients of the model in terms of the properties of a single phase.

The coefficients in the model have further been determined from the analysis of the system behavior on the mesoscale. The flow in the infinite oil and water clusters was described by the Brinkman equation with a moving boundary, in the framework of a simplified geometrical model. This has made it possible to find explicit expressions for the phenomenological transport coefficients. The key parameter \(\xi \) in the expressions for them is the characteristic ratio of the thickness of a cluster branch to the pore size. Thus, the model may distinguish between the different degrees of “mixing” between the phases.

Sample computations show a non-trivial dependence of the fractional flow function and apparent relative permeabilities on the parameter \(\xi \) and on the viscosity ratio. Coupling between the flows transforms the fractional flow function toward the dependence corresponding to (more) piston-like displacement (although it should be remarked that the developed formalism is strictly valid only for the steady-state flows). Apparent relative permeabilities are dependent on the viscosity ratio. For large viscosity ratios, they may exhibit non-monotonous behavior. The endpoint relative permeabilities, as well as the overall phase mobility, decrease compared to the case of no coupling. This decrease is especially pronounced close to the end points, where one of the phases becomes immobile and slows down another phase.

Comparison with experimental data on steady-state determination of the apparent relative permeabilities indicates that the developed model is in qualitative agreement with their dependence on viscosity ratio in cases where other conditions of the model are obeyed. It is capable of reproducing the shapes of relative permeabilities. It has been possible to adjust the parameters of the model to the experimental data of Fulcher et al. (1985) in such a way that the measured relative permeabilities and their dependence on the viscosity ratio were reproduced with a high degree of accuracy.