End-to-end latency characterization of task communication models for automotive systems

Abstract

Different communication models have been historically adopted in the automotive domain for allowing concurrent tasks to coordinate, interact and synchronize on a shared memory system for implementing complex functions, while ensuring data consistency and/or time determinism. To this extent, most automotive OSs provide inter-task communication and synchronization mechanisms based upon memory-sharing paradigms, where variables modified by one task may be concurrently accessed also by other tasks. A so-called “effect chain” is created when the effect of an initial event is propagated to an actuation signal through sequences of tasks writing/reading shared variables. The responsiveness, performance and stability of the control algorithms of an automotive application typically depend on the propagation delays of selected effect chains. Depending on the communication model adopted, the propagation delay of an effect chain may significantly vary, as may be the resulting overhead and memory footprint. In this paper, we explore the trade-offs between three communication models that are widely adopted for industrial automotive systems, namely, Explicit, Implicit, and Logical Execution Time (LET). A timing and schedulability analysis is provided for tasks scheduled following a mixed preemptive configuration, as specified in the AUTOSAR model. An end-to-end latency characterization is then proposed, deriving different latency metrics for effect chains under each one of the considered models. The results are compared against an industrial case study consisting of an automotive engine control system.

1 Introduction

In recent years, the amount of electronics in automotive vehicles has risen dramatically, representing a significant share of the overall cost of the vehicle. The technological reason behind such a trend in the automotive industry lies in the increased number of safety and control functionalities that are being integrated in modern cars, as well as in the replacement of older hydraulic and mechanical direct actuation systems with modern by-wire counterparts, leading to an increased safety and comfort at a reduced unit cost. Well-known examples are anti-lock braking system (ASB), electronic stability program (ESP), active suspension, etc.

With the evolution of processors, several industries are facing a transition from single-core to multi-core systems. This kind of platforms allows application providers to counter the thermal and power-related limitations to the Moore law demand for computing power without incurring thermal and power problems. In the automotive domain, multi-core platforms bring major improvements for some applications requiring high performance such as high-end engine controllers, electric and hybrid powertrains, advanced driver assistance systems, etc. Moreover, the increased computational power of multi-core platforms allows integrating into a single controller multiple functionalities that were spread around different electronic control units (ECUs), reducing the number of computing units as well as communication overhead.

However, task-core distribution may have a significant impact over the control performance of a given application, due to the concurrency of multiple tasks mapped onto different cores that communicate through shared variables, aka shared labels. With regard to this type of intertask communication, in the automotive domain we should distinguish between three different models: Explicit, Implicit and Logical Execution Time. Each of these communication models has a different impact over the communication latencies experienced by tasks accessing the same shared variable. In particular, automotive applications are especially concerned with optimizing end-to-end propagation latencies of input events that trigger a chain of computations leading to a control action or final actuation.

In this paper, we analyze in detail the propagation latencies of event chains composed of multiple tasks under different models of the above-mentioned intertask communication. We propose and characterize meaningful latency metrics to evaluate the control performance of selected event chains. For each considered communication model, we characterize worst-case scenarios that lead to the largest latency of the event chain, deriving analytical upper bounds of the worst-case propagation time of an input event. We also provide valid upper bounds of the response time of tasks scheduled either under the preemptive or the cooperative scheduling policy supported in AUTOSAR. To our knowledge, this is the first work that provides such an analytical characterization and comparison of end-to-end latencies under different industrial-grade communication models, for task systems compliant with the AUTOSAR scheduling model.

Organisation of the paper. The following section introduces the related work and the AUTOSAR standard. Section 3 presents the adopted scheduling model and the related response-time analyses for AUTOSAR tasks scheduled with preemptive and/or cooperative algorithms. Section 4 describes the considered communication models, discussing the additional memory and communication overhead implied by each model. Section 5 derives analytical upper bounds of meaningful end-to-end latencies for each considered communication model. The analytical bounds are then instantiated in Sect. 6 by means of an automotive industrial case study, consisting of an engine control system provided by Robert Bosch GmbH in Hamann et al. (2017b), based on concurrent AUTOSAR tasks partitioned onto a multi-core system. Finally, Sect. 7 presents our conclusions and directions for future works.

2 Background and related work

2.1 AUTOSAR

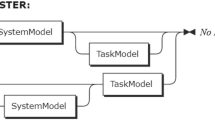
To better understand the background where the considered communication models have been proposed, we hereafter provide a short summary of the AUTomotive Open System ARchitecture (AUTOSAR¹). AUTOSAR is an open standard for automotive system development whose main goals are: software independence from hardware, modularity, scalability, functions reusability, and flexible maintenance. AUTOSAR looks at the different functionalities in a car network, combines them into logical clusters (Software Compositions), and finds functional atomic units (Software Components) that compose these clusters. AUTOSAR establishes a uniform development methodology for automotive control software, providing a standard interface between the different software layers and a hierarchical organization of the software/hardware components deployed in the vehicle. The AUTOSAR architecture is composed of three main layers: (i) Application Software (ASW), (ii) Run-Time Environment (RTE), and (iii) Basic Software (BSW), as detailed in Fig. 1a.

Fig. 1

AUTOSAR architecture (a); BSW sublayers (b)

• 1. The ASW consists of interconnected Software Components (SWCs) with well-defined interfaces, described and standardized within AUTOSAR, that are provided to communicate with other SWCs.

• 2. The communication between SWCs is enabled by the RTE. This layer makes SWCs independent from the mapping to a specific ECU and provides different communication paradigms between SWCs, such as sender–receiver, client–server, etc. In this paper, we focus on the sender–receiver communication paradigm, that is the memory sharing mechanism allowing tasks to communicate by means of labels. For this sort of communication, the RTE supports two modes, namely Explicit and Implicit.

• 3. The BSW provides the infrastructural functionality for an ECU and is composed of the following sub-layers (see Fig. 1b): the Microcontroller Abstraction layer (MCAL) which provides hardware drivers making upper software layers independent from the microcontroller; the ECU abstraction layer which provides APIs to access peripherals making upper software layers independent from the ECU hardware layout; and the Service Layer that provides operating system functionalities, memory services, diagnostic services, etc. Drivers that are not specified in AUTOSAR are to be found in the Complex Drivers layer.

The characterization of end-to-end timing latencies of effect chains between communicating AUTOSAR tasks is an important problem for many automotive applications with tight real-time requirements.

2.2 Related work

2.2.1 Task chains

A task chain is a sequence of communicating tasks in which every task receives data from its predecessor Kloda et al. (2018). Depending on the activation model, the literature distinguishes between two types of task chains: periodic chains and event-driven chains Vincentelli et al. (2007). In the periodic case, each task is activated independently at a given rate, and communicates with its successor by means of shared variables. In the event-driven paradigm, instead, task executions are triggered by an event issued from a preceding task. Periodic-activated chains are also known as effect chains Hamann et al. (2017a), cause-effect chains Becker et al. (2017) or data chains Kloda et al. (2018), and are usually found in automotive systems Feiertag et al. (2009). Event-driven activation is instead found in other domains, like avionics and aerospace Girault et al. (2018).

2.2.2 End-to-end latency

In Davare et al. (2007), the authors provided upper bounds on the end-to-end latency of effect chains that are composed of tasks mapped onto different Electronic Control Units (ECUs), as well as messages transmitted via CAN bus. They proposed a mixed-integer geometric programming (MIGP) optimization approach that assigns periods to tasks and messages at design stage so that deadlines across ECUs and buses can be met. In Vincentelli et al. (2007), the trade-offs between periodic and event-driven activations of task chains are explored, showing that a purely periodic or event-driven activation model might not always meet the deadline constraints of a given distributed automotive system. Thus, the authors proposed an algorithm based on a mixed activation model that can meet the latency requirements of the aforementioned inter-ECU communication.

An analysis of worst-case latencies along functional chains in critical avionic distributed systems is presented in Lauer et al. (2014), proposing a mixed integer linear programming (MILP) formulation focusing on two end-to-end requirements, namely, latency and temporal consistency. In Kloda et al. (2018), a method is presented to reduce the pessimism of upper bounds on the end-to-end latency of effect chains consisting of periodic tasks scheduled by a partitioned fixed-priority preemptive policy on a multi-core platform. In Schlatow et al. (2018), the authors addressed the latency analysis of multi-rate distributed effect chains considering static-priority preemptive scheduling of offset-synchronized periodic tasks, proposing a Mixed Integer Linear Program-based optimization in order to select design parameters, such as priorities, task-to-processor mapping, and offsets, that minimize data age. In Girault et al. (2018), tighter upper bounds are presented on the end-to-end latency of synchronous and asynchronous event-driven activated chains on a single core platform. Lower bounds on these latencies are also computed to evaluate the tightness of the derived bounds.

2.2.3 Task communication models

In the automotive domain, multiple communication models have been proposed, affecting the resulting end-to-end latencies of event chains in different ways. Beside the Explicit and Implicit communication models, the Logical Execution Time (LET) paradigm has been proposed within the time-triggered programming language Giotto Henzinger et al. (2001, 2003). This communication model allows determining the time it takes from reading program input to writing program output regardless of the actual execution time of a real-time program. As stated in Kirsch and Sokolova (2012), LET evolved from a highly controversial idea to a well-understood principle of real-time programming, motivated by the observation that the relevant behavior of real-time programs is determined by when inputs are read and outputs are written. This concept has been adopted by the automotive industry as a way to introduce a more deterministic behavior of concurrent applications.

To address the migration problem of automotive applications from single- to multi-core platforms, Kehr et al. (2015) presented an AUTOSAR compliant communication mechanism named Timed Implicit Communication (TIC) that allows legacy applications to run in parallel, making them platform-independent. This adaptation of the Implicit communication model relies on time stamps and somewhat resembles the LET communication model. In Hamann et al. (2017a), the authors provided an overview of the different communication models used in the automotive domain, highlighting the importance of the end-to-end latencies of effect chains in an engine management system. Moreover, a method is presented to transform LET and implicit communication into their corresponding direct communication analogues. The impact on end-to-end latencies and communication overheads in terms of temporal determinism and data consistency is shown using the SymTA/S tool.²

In Becker et al. (2016), a holistic end-to-end timing latency analysis for effect chains with specified age-constraints is presented. The analysis is based on deriving all possible data propagation paths. These paths are used to compute minimum and maximum end-to-end latencies of effect chains. Later, in Becker et al. (2017), the same authors extended the analysis in order to include the Implicit and LET communication models, providing techniques for deriving the maximum data age of effect chains. In Martinez et al. (2018), the authors presented a formal analysis of the LET communication model for real-time applications composed of periodic tasks with harmonic and non-harmonic periods, and computed their exact end-to-end latencies. They also showed that by introducing tasks offsets, the real-time performance of non-harmonic tasks may improve, getting closer to the constant end-to-end latency experienced in the harmonic case. To that end, they proposed a heuristic algorithm to obtain a set of offsets that might reduce end-to-end latencies, improving the determinism of the LET communication model.

To the best of our knowledge, our work is the first complete study that combines three communication models: explicit,implicit, and LET, with a concise mathematical end-to-end latency timing analysis that encompasses two end-to-end timing semantics of paramount importance for automotive systems, namely, Age and Reaction latency. To that end, we present a novel tight schedulability and timing analysis of a mixed preemptive-cooperative task system, that will enable us to provide upper bounds on the end-to-end latency of effect chains in an automotive setting. Detailed considerations are provided concerning the implementation and mathematical models of the aforementioned communication paradigms, comparing the resulting latencies of the different semantics against an industrial case study.

3 System model, terminology and notation

This section describes the terminology and notation adopted throughout the paper. The smallest functional entity in AUTOSAR is called runnable. A SWC is made up of one or more runnables. Runnables having the same functional period are grouped into the same task. In the simplest case, one functionality is realized by means of a single runnable. However, more complex functionalities are typically accomplished using several communicating runnables, possibly distributed over multiple tasks.

The model is assumed to be comprised of m identical cores, with periodic tasks and runnables statically partitioned to the cores, and no migration support. Each task $\tau _i$ is specified by a tuple ($C_i, D_i, T_i, P_i, PT_i$), where $C_i$ stands for the worst-case execution time (WCET), $D_i$ is the relative deadline, $T_i$ is the period, $P_i$ is the priority, and $PT_i$ defines the type of preemption. Every period $T_i$, each task releases a job composed of $\gamma _i$ subsequent runnables, where $\tau _i^r$ represents the rth runnable of $\tau _i$, with $1\le r \le \gamma _i$. The worst-case execution time of $\tau _i^r$ is denoted as $C_i^r$. Therefore,

$$\begin{aligned} C_i = \sum _{k\in [1,\gamma _i]} C_i^k. \end{aligned}$$

(1)

We also denote as ${\overline{C}}_i^r$ the cumulative execution time of runnables $\tau _i^1,\ldots ,\tau _i^r$, i.e.,

$$\begin{aligned} {\overline{C}}_i^r = \sum _{k\in [1,r]} C_i^k. \end{aligned}$$

(2)

Tasks are scheduled by the operating system based on the assigned (fixed) priorities. The scheduling policy may be either preemptive or cooperative, as specified by $PT_i$. Preemptive tasks always preempt lower priority tasks, while cooperative tasks preempt a lower priority one only at runnable boundaries. Preemptive tasks are assumed to always have a higher priority than that of any cooperative task. The mixed cooperative-preemptive nature allows modeling automotive systems where hard real-time tasks co-exist with soft and firm real-time tasks, providing a proper balance between preemption latency and context switch overhead according to the needs of each task.

Tasks communicate through shared labels in such a fashion that they abstract a message-passing communication mechanism implemented with a shared memory. Regarding the type of access, a task can be either a sender or a receiver of a label. A sender is a task that writes a label. We assume there is only one sender per label, while there may be multiple receiving tasks reading one label. Even though the typical multicore architecture used in the automotive field, i.e. TriCore AURIX,³ allows more than one instruction-per-cycle (IPC), the complexity of automotive software can make the actual average value less than that. For the sake of simplicity, we consider $IPC=1$. The execution time of a runnable $\tau _i^r$, without taking memory computation into account, can then be computed as $C_i^r=E_i^r/f$, where $E_i^r$ is an upper bound on the number of instructions for the considered runnable, and f is the core frequency.

The overall worst-case execution time $C_i^r$ of runnable $\tau _i^r$ can then be derived by also taking into account the access time of each label $\ell$ of $\tau _i^r$,

$$\begin{aligned} C_i^r=\frac{E_i^r}{f}+\sum _{\ell \in \tau _i^r}\left\{ F^r_{i,\ell }\cdot \xi _\ell \right\} \end{aligned}$$

(3)

where $F^r_{i,\ell }$ represents the number of times the label $\ell$ is accessed by runnable $\tau _i^r$, and $\xi _\ell$ is the time it takes to access $\ell$.

In the same way, we can also obtain the best-case execution time (BCET) of runnable $\tau _i^r$, $b_i^r$, by taking into consideration the minimum number of instructions $e_i^r$:

$$\begin{aligned} b_i^r=\frac{e_i^r}{f}+\sum _{\ell \in \tau _i^r}\left\{ F^r_{i,\ell }\cdot \xi _\ell \right\} \end{aligned}$$

(4)

Thus the best-case start time of runnable $\tau _i^r$, $s_i^r$ can be computed as the sum of the BCETs of the preceding runnables:

$$\begin{aligned} s_i^r = \sum _{k\in [1,r-1]} b_i^k. \end{aligned}$$

(5)

3.1 Analysis for preemptive tasks

According to the considered system model, preemptive runnables can only be preempted by higher priority preemptive runnables, and they can always preempt any lower priority task. Therefore, a preemptive task will never experience any blocking delay due to lower priority (preemptive or cooperative) tasks. Hence, the response time for preemptive tasks can be computed adapting the classic response time analysis for arbitrary deadlines presented in Lehoczky (1990). The arbitrary deadline model is used instead of the simpler analysis for constrained deadlines because there are configurations where the response time $R_i$ of a task $\tau _i$ may be later than the activation of the subsequent job of the same task, i.e., $R_i > T_i$. Under these conditions, the maximum response time of a task is not necessarily given by the first instance released after the synchronous arrival of all higher priority tasks (also called critical instant), but may be due to later jobs.

For each task $\tau _i$, the analysis requires checking multiple jobs until the end of the level-i busy period, i.e., the maximum consecutive amount of time for which a processor is continuously executing tasks of priority $P_i$ or higher. The longest Level-i active period ($L_i$) can be calculated by fixed-point iteration of the following relation, starting with $L_i=C_i$:

$$\begin{aligned} L_i = \sum _{j: P_j \ge P_i} \left\lceil \frac{L_i}{T_j} \right\rceil C_j. \end{aligned}$$

(6)

The number of $\tau _i$’s instances to check is therefore $K_i = \left\lceil \frac{L_i}{T_i} \right\rceil$. The finishing time of the k-th instance ($k\in [1,K_i]$) of runnable $\tau _i^r$ in the level-i busy period can be iteratively computed as

$$\begin{aligned} f_i^{r,k} = \sum _{j:P_j>P_i}\left\lceil \frac{f_i^{r,k}}{T_j}\right\rceil C_{j} + (k-1)C_i + {\overline{C}}_i^r, \end{aligned}$$

(7)

where the first term in the sum accounts for the higher priority interference, the second term accounts for the $(k-1)$ preceding jobs of $\tau _i$, and the last term considers the contribution of the k-th job limited to $\tau _i^r$ and its preceding runnables. The response time of the k-th instance of $\tau _i^r$ can then be easily found subtracting its arrival time:

$$\begin{aligned} R_i^{r,k}=f_i^{r,k}-(k-1)T_i . \end{aligned}$$

(8)

The worst-case response time (WCRT) of runnable $\tau _i^r$ can be found by taking the maximum among all $K_i$ jobs in the level-i busy period:

$$\begin{aligned} R_i^r=\max _{k\in [1,K_i]} \{R_i^{r,k}\}. \end{aligned}$$

(9)

Finally, the worst-case response time of task $\tau _i$ is computed in the following way:

$$\begin{aligned} R_i = R_i^{\gamma _i}. \end{aligned}$$

(10)

3.2 Analysis for cooperative tasks

While the main advantage of preemptive scheduling is real-time response, cooperative scheduling limits the number of preemptions between cooperative tasks, reducing the kernel overheads and simplifying re-entrance problems. Moreover, in classic automotive platforms based on single core technologies, cooperative scheduling was a way to provide implicit data consistency at runnable level, avoiding the need for mutual exclusion primitives.

The analysis for cooperative tasks is somewhat more complicated, since it needs to take into account (i) the blocking delays due to lower priority cooperative tasks that can be preempted only at runnable boundaries; (ii) the interference due to higher priority cooperative tasks that can preempt the considered task only at runnable boundaries; (iii) the interference of preemptive tasks that may preempt even within a runnable. To tackle this problem, we will modify and merge the analysis for limited-preemption systems with Fixed Preemption Points (FPP) and for Preemption Threshold Scheduling (PTS), both summarized in Buttazzo et al. (2013). The outcome will be a necessary and sufficient response-time analysis for the considered mixed preemptive-cooperative task model.

Under this model, a preemption threshold is assigned to cooperative tasks. This priority is higher than that of any cooperative task, but lower than that of any preemptive tasks. When a cooperative task $\tau _i$ is executing one of its runnables, its nominal priority $P_i$ is raised to the threshold $\theta _i$, so that cooperative tasks cannot preempt it. The nominal priority is restored when the runnable is completed, allowing cooperative preemptions from higher priority tasks.

As with preemptive tasks, it is also necessary to consider multiple jobs within a busy period. However, the busy period must also include the blocking due to lower priority tasks. The longest Level-i active period can be calculated adding a blocking factor to the recurring relation of Eq. (6):

$$\begin{aligned} L_i = B_i + \sum _{j: P_j \ge P_i} \left\lceil \frac{L_i}{T_j} \right\rceil C_j. \end{aligned}$$

(11)

Since a task can only be blocked once by lower priority instances, $B_i$ corresponds to the largest execution time among lower priority runnables:⁴

$$\begin{aligned} B_i = \max \limits _{j,r: P_j<P_i} \{ C_j^r \}. \end{aligned}$$

(12)

The starting time ${\hat{s}}_i^{r,k}$ of the k-th instance of runnable $\tau _i^r$ can be iteratively computed by taking into consideration the blocking time $B_i$, the interference produced by higher priority tasks before $\tau _{i,r}$ can start, the preceding (k−1) instances of $\tau _i$, and the execution time of the preceding runnables of $\tau _{i,r}$:

$$\begin{aligned} {\hat{s}}_i^{r,k} = B_i + \sum _{j: P_j > P_i} \left( \left\lfloor \frac{\hat{s_i}^{r,k}}{T_j}\right\rfloor + 1 \right) C_j + (k-1) C_i + {\overline{C}}_i^{r-1}. \end{aligned}$$

(13)

The worst-case finishing time $f_i^{r,k}$ is calculated by adding to the worst-case starting time ${\hat{s}}_i^{r,k}$, the execution time of the considered runnable $C_i^r$, along with the interference of the tasks that can preempt $\tau _i^r$, i.e., the preemptive tasks which have a nominal priority higher than the preemption threshold of any cooperative task. To compute this last interfering term, we compute the higher priority instances that arrive from the critical instant until the finishing time, and subtract those that arrived before the starting time:

$$\begin{aligned} f_i^{r,k} = {\hat{s}}_i^{r,k} + C_i^r \!+\!\! \sum _{j: P_j > \theta _i}\!\! \left( \left\lceil \frac{f_i^{r,k}}{T_j}\right\rceil \!- \left( \left\lfloor \frac{{\hat{s}}_i^{r,k}}{T_j}\right\rfloor \!\!+\! 1 \right) \right) C_j. \end{aligned}$$

(14)

Equations  (8),  (9) and  (10) can then be identically used to compute the worst-case response time of the considered runnable and task, respectively.

4 Inter-task communication

In line with the multi-core complexity trend, automotive applications are evolving towards more complicated task and runnable settings. As tasks communicate across the memory hierarchy, data consistency problems may arise. On the other hand, as control algorithms need deterministic timing, non-deterministic behavior, such as task jitter, might cause different levels of control performance degradation that might even lead to system instability. Thus, in the automotive domain distinct communication models have been proposed in order to provide different levels of determinism and consistency: (i) Explicit, (ii) Implicit and (iii) Logical Execution Time (LET).

• 1. Explicit communication means that a runnable makes an explicit RTE API call in order to directly write or read labels, i.e., a runnable or a task may have unrestricted access to variables at any point during its execution. To avoid data inconsistency issues, accesses must be protected through explicit synchronization or locking constructs. A memory-aware analysis of Explicit communication is proposed in Sañudo et al. (2016).

• 2. Implicit communication aims at data consistency and defines two kinds of operations: Implicit Read and Implicit Write. The former implies that if a runnable reads a label, a copy of this label, instead of the original, should become available for the runnable at the latest when its execution starts. The RTE ensures that this copy does not change during the execution of the runnable. Implicit write means that a label modified by a runnable should be made available to other runnables at the earliest when the runnable execution is over. The RTE makes sure that this update is done by means of a copy mechanism. One way to implement this is that tasks accessing shared labels work on task-local copies instead of the original labels. To avoid data inconsistency, each task instance gets a copy of the required labels at the beginning of its execution. After working on local copies in an exclusive way, it then publishes its results at the end of its execution. Consistency between variables, i.e. data coherency, is not covered in this journal. If needed, extra buffers or locking support might be used. The latter is only required at the beginning of a reading task, and at the end of a writing task, which signifies a much lighter synchronization overhead than in the explicit model.

• 3. As mentioned above, the Logical Execution Time (LET) is a hard real-time programming abstraction that was introduced by the Giotto programming model. As the relevant behavior of real-time tasks is determined by when inputs are read and outputs are written, the LET semantics requires that inputs and outputs be logically updated at the beginning and at the end of the so called Logical Execution Time. Henceforth, we assumed that the LET of a task equals its period. This allows deterministically fixing the time it takes from reading an input to writing an output regardless of the actual response time of the involved communicating tasks.

The LET implementation we consider in this paper adopts a lock-free paradigm that tries to closely resemble the above-mentioned ideal behavior at the cost of a slightly higher use of local buffers, as will be shown in Sect. 4.2. An implementation of the Implicit communication model that tries to duplicate its behavior is presented in the following section.

4.1 Implicit communication

Let $I_i$ and $O_i$ be the set of all shared labels read and written by task $\tau _i$, respectively. $I_i$ and $O_i$ therefore represent the inputs and outputs of the considered task. Our implementation for Implicit communication assumes that any task $\tau _i$ accessing a shared label works on a copy instead of the original label. Copies are created, statically allocated to the task-local memory and inserted in runnables at compile time. Furthermore, two task-specific runnables $\tau _i^0$ and $\tau _i^{(\gamma _i+1)}$ (also called $\tau _i^{last}$ for simplicity) are to be inserted at the beginning and at the end of the task. Runnable $\tau _i^0$ is responsible of reading shared labels to the local copies, while $\tau _i^{last}$ will write the local copies to the corresponding shared variables. If ${\dot{I}}_i$ and ${\dot{O}}_i$ represent the set of $\tau _i$-local copies of the labels contained in $I_i$ and $O_i$, respectively, runnable $\tau _i^0$ updates ${\dot{I}}_i$, whereas runnable $\tau _i^{last}$ publishes its updates by writing ${\dot{O}}_i$ to the corresponding shared variables in $O_i$. See Fig. 2. Observe that if a task writes and reads the same label, only one copy is created.

Fig. 2

Implicit communication implementation

For example, suppose a task $\tau _i$ reads shared label $L_1$ and writes shared label $L_2$. Let $L_{i,1}$ and $L_{i,2}$ represent the $\tau _i$-local copies of $L_1$ and $L_2$ respectively. This model dictates that $L_{i,1}$ is to be updated by runnable $\tau _i^0$ at the beginning of task $\tau _i$. After that, $\tau _i$ reads $L_{i,1}$ and writes $L_{i,2}$, never accessing the original labels $L_1$ and $L_2$. In the end, runnable $\tau _i^{last}$ writes the latest value of $L_{i,2}$ to $L_2$. It does not need to publish $L_1$, since it did not modify it. See Fig. 3.

Fig. 3

Implicit communication implementation example

An upper bound on the overhead introduced by the copy-in ($\tau _i^0$) and copy-out ($\tau _i^{last}$) runnables can be easily computed as

$$\begin{aligned} C_i^0 = \sum _{\ell \in I_i} \xi _\ell , \end{aligned}$$

(15)

and

$$\begin{aligned} C_i^{last} = \sum _{\ell \in O_i} \xi _\ell , \end{aligned}$$

(16)

where the sum is extended over all shared labels read (resp. written) by the considered task $\tau _i$. The total execution time of $\tau _i$ is computed as

$$\begin{aligned} C_i = C_i^0+C_i^{last} +\sum _{r\in [1,\gamma _i]} C_i^r, \end{aligned}$$

(17)

The additional memory occupancy in the Implicit model is given by the local copies created for shared labels, i.e., all labels in $I_i \cup O_i$ for all tasks $\tau _i$.

4.2 LET communication

Differently from the Implicit case, LET enforces task communication at deterministic times, corresponding to task activation times. In our implementation, each reader creates one or more local copies of the shared label. Since the considered model allows just one writer task for each label, the writer task is allowed to directly modify the original label, updating the readers copies at well-determined times.

For instance, let us consider the communication between the writer with period $T_W=2$ and one of the readers with period $T_R=5$, as in Fig. 4a: while $\tau _W$ may repeatedly write the considered label, these updates are not visible to the concurrently executing reader, until a publishing point$P_{W,R}^n$, where the value is updated for the next reader instance. This point corresponds to the first upcoming writer release that directly precedes a reader release, i.e., where no other write release appears before the arrival of the following reader instance. We call publishing instance the writing instance that updates the shared value for the next reading instance, i.e., the writer’s job that directly precedes a publishing point. Note that not all writing instances are publishing instances. See Fig. 4, where publishing instances are marked in bold red.

It is also convenient to define reading points$Q_{R,W}^n$, which correspond to the arrival of the reading instance that will first use the new data published in the preceding publishing point $P_{R,W}^n$. Figure 4b shows publishing and reading points for a case where $T_W=5$ and $T_R=2$. If we define the hyperperiod of two communicating tasks as the least common multiple ($LCM$) of their periods, the next theorem shows how publishing and reading points of two communicating tasks can be computed.

Fig. 4

Publishing and reading points when the reader has a larger (a) or smaller (b) period than the writer

Theorem 1

Given two communicating tasks$\tau _W$and$\tau _R$, the publishing and the reading points can be computed as

$$\begin{aligned} P_{W,R}^n= & {} \left\lfloor \dfrac{n T_{\max }}{T_W}\right\rfloor T_W \end{aligned}$$

(18)

$$\begin{aligned} Q_{W,R}^n= & {} \left\lceil \dfrac{n T_{\max }}{T_R}\right\rceil T_R \end{aligned}$$

(19)

where$T_{\max }=\max (T_W,T_R)$.

Proof

If the writer $\tau _W$ has a smaller or equal period than the reader $\tau _R$, i.e., $T_W\le T_R$ as in Fig. 4a, there is one publishing and one reading point for each reading instance. Reading points trivially correspond to each reading task release, i.e.,

$$\begin{aligned} Q_{W,R}^n = n T_R, \end{aligned}$$

while publishing points correspond to the last writer release before such a reading instance, i.e.,

$$\begin{aligned} P_{W,R}^n = \left\lfloor {\dfrac{n T_R}{T_W}}\right\rfloor T_W. \end{aligned}$$

Otherwise, when the writer $\tau _W$ has a larger period than the reader $\tau _R$, i.e., $T_W\ge T_R$ as in Fig. 4b, there is one publishing and one reading point for each writing instance. Publishing points trivially correspond to each writing task release, i.e.,

$$\begin{aligned} P_{W,R}^n = n T_W \end{aligned}$$

while reading points correspond to the last reader release before such a writing instance, i.e.,

$$\begin{aligned} Q_{W,R}^n = \left\lceil \dfrac{n T_W}{T_R}\right\rceil T_R. \end{aligned}$$

It is easy to see that, in both cases $T_W\le T_R$ and $T_W\ge T_R$, the formula for $P_{W,R}^n$ and $Q_{W,R}^n$ are generalized by Eqs. (18) and (19). Note that, when $T_W = T_R$, $P_{W,R}^n = Q_{W,R}^n = n T_W$. $\square$

Let $I_{W,R}$ denote the set of labels written by $\tau _W$ and read by $\tau _R$. For each of these labels, the reading task $\tau _R$ creates a local copy to which it has exclusive access. Let ${\dot{I}}_{W,R}$ denote the set of $\tau _R$-local copies of the labels contained in $I_{W,R}$. Depending on the harmonicity of $T_W$ and $T_R$, ${\dot{I}}_{W,R}$ is to be updated either by $\tau _W$ or $\tau _R$ as shown in the next section.

4.2.1 Harmonic synchronous communication (HSC)

Two communicating tasks $\tau _W$ and $\tau _R$ have harmonic periods if the period of one of them is an integer multiple of the other. When a harmonic synchronous communication (HSC) is established, the following relations hold: $LCM(T_W,T_R)=T_{\max }$, and $P_{W,R}^n=Q_{W,R}^n=nT_{\max }$, i.e., publishing and reading points are integer multiples of the largest period of the communicating tasks.

Consider the example in Fig. 5, where two tasks $\tau _l$ and $\tau _s$, with $T_l=2T_s$, both read shared labels $L_1$ and $L_2$. Moreover, $\tau _l$ writes $L_1$, while $\tau _s$ writes $L_2$. The proposal suggests that $\tau _s$ and $\tau _l$ are to read $L_{s,1}$ and $L_{l,2}$ instead of the original labels. Notice that $\tau _l$ and $\tau _s$ directly modify $L_1$ and $L_2$, respectively, instead of working with local copies. These copies are to be updated by a communication-specific runnable, either $\tau _s^{last}$ or $\tau _l^{last}$, depending on whichever job finishes last before the next publishing point. In other words, the responsibility to update the copies is given either to the reader or to the writer, depending on which one completes last in the communication. The first reader instance after the publishing point is the first one that accesses the updated value. Such a value will be used by all reading instances until the next reading point. Unlike the Implicit communication, only one task pays the overhead for maintaining the determinism in the communication.

Fig. 5

LET harmonic communication

4.2.2 Non-harmonic synchronous communication (NHSC)

When two communicating tasks do not have harmonic periods, a non-harmonic synchronous communication (NHSC) is established. The general formulas of Sect. 4.2 apply.

Like in the HSC case, the reading task of a shared label accesses a local copy instead of the original label. However, due to the misaligned activations of the communicating tasks, at least two copies of the same shared label are needed. A task-specific runnable is to be inserted at the end of the writer in order to update the copies of $I_{W,R}$ before the publishing point. If only one copy was used, a task could be writing it while the reader is reading it, leading to an inconsistent state. With two copies, instead, a reader reads a local copy, while the writer may freely write a new value for the next reading instance in a different buffer.

For example, consider a reading task $\tau _R$ and a writing task $\tau _W$ communicating through a shared variable $L_2$, with $2T_R = 5T_W$ as in Fig. 6. There are two $\tau _R$-local copies, $L_{R,2,1}$ and $L_{R,2,2}$, of the shared label $L_2$. The reading task $\tau _R$ reads from one of these copies instead of the original label. These copies are to be updated by the last runnable $\tau _W^{last}$ of the writing task. Note that $\tau _W$ directly writes to $L_2$ instead of a local copy.

Fig. 6

Non harmonic (NHSC): $2T_R = 5T_W$

There might also be cases where three copies per labels are needed in order to fulfill the required determinism. Consider Fig. 7 where $5T_R = 2T_W$. Note that $\tau _W$ may directly access $L_1$, while $\tau _R$ reads from one of the three copies $L_{R,1,1}$, $L_{R,1,2}$ or $L_{R,1,3}$, which are to be updated by runnable $\tau _W^{last}$. An extra copy of $L_1$ is needed because the value computed by the second writing instance may be available either before or after the next reading point $Q_{R,W}^1$, depending on the response time of $\tau _W$. If the second instance of $\tau _W$ finishes before (resp. after) $Q_{R,W}^1$, the reading instance after $Q_{R,W}^1$ would read the data of the second (resp. first) writing instance. Therefore, the value read at $Q_{R,W}^1$ is not deterministic, as it might correspond either to the first or to the second writing instance. Introducing a third buffer allows obtaining a deterministic behavior, where the values published by the first and second writing instances are always read at $Q_{R,W}^1$ and $Q_{R,W}^2$, respectively.

Fig. 7

Non harmonic (NHSC): $5T_R = 2T_W$

In general, this happens when a publishing instance has a best-case finishing time that precedes the next reading point. Let us define $w_{W,R}^n$ as the window of time between a publishing point $P_{W,R}^n$ and the next reading point $Q_{W,R}^n$. Then, using Eqs. (18) and (19),

$$\begin{aligned} w_{W,R}^n = Q_{W,R}^n -P_{W,R}^n = \left\lceil \dfrac{n T_{\max }}{T_R}\right\rceil T_R - \left\lfloor \dfrac{n T_{\max }}{T_W}\right\rfloor T_W. \end{aligned}$$

(20)

It is worth pointing out that if a HSC is established, then $w_{W,R}^n = 0$. Furthermore, if the best-case response time of a publishing instance is smaller than the corresponding $w_{W,R}^n$, a third buffer is needed to store the new value.

As the type of LET communication is defined by the periods of the communicating task pair, a given tasks $T_i$ can establish a HSC with one task and a NHSC with another. Thus, depending on the type(s) of estabished communication, the additional memory occupancy is given by the total number of local copies created for each label in $I_i$ .

5 End-to-end latency characterization

In this section, we propose a method for computing the end-to-end propagation delay of effect chains taking into consideration different communication models.

An effect chain, EC, is a producer/consumer relationship between runnables working on shared labels. Effects chains are assumed to be triggered by an event or a task release. The first task in the chain produces an output (i.e., writes to a shared label) for another task following in the event chain. This second task reads the shared label to write an output to a different shared label, which may be then read by a third task, and so on. When the last task produces its final output, the event chain is over.

Depending on the application requirements, different end-to-end delay metrics can be of interest. Control systems driving external actuators are interested in the “age” of an input data, i.e., for how long a given sensor data will be used to take actuation decisions. For example, how long a radar or camera frame will be used as a valid reference by a localization or object detection system to perceive the environment: the older the frame, the less precise is the system. Similar considerations are valid for an engine control or a fuel injection system, where correct actuation decisions depend on the “freshness” of sensed data. Another metric of interest is the “reaction” latency to a change of the input, i.e., how long it takes for the system to react to a new sensed data. Multiple body and chassis automotive applications are concerned with this metric. For example, for a door locking system, it is important to know the time it takes to effectively lock or unlock the doors after receiving the corresponding signal.

To more formally characterize age and reaction latencies, consider Fig. 8a, showing an event chain triggered by a periodic sensor (incoming green arrows). The upper task reads the sensor data, elaborates it, and shares the result with the next task. And so on, until the end of the event chain. Green arrows denote when an input is propagated to the next task. In this case, we call it a valid input. Red arrows correspond to elaborations that are not propagated, also called invalid inputs, because they are overwritten before being read by the next task in the chain.

The age latency is defined as the delay between a valid sensor input until the last output related to this input in the event chain. This data age metric is particularly important for control applications, such as, fuel injection control. The reaction latency is defined as the delay between a valid sensor input until the first output of the event chain that reflects such an input. It measures how much time it takes for a new event to propagate to the end of the event chain. This metric allows estimating the reactivity to new inputs and has great importance for the automotive body domain, where the first reaction is paramount. Depending on tasks alignments, the reaction latency may significantly vary. In Fig. 8b, the first sensor input arrives just a bit after the runnable that is responsible of elaborating it (marked as a green dot in the first job of $\tau _i$). This causes the reaction latency to increase substantially, as the output task $\tau _k$ will continue working with an older input for three further jobs (marked as A, B and C in the figure). In Feiertag et al. (2009), age and reaction latencies are also referred to as last-to-last (L2L) and first-to-first (F2F) delay, respectively.

Fig. 8

Age and reaction latency

Before proceeding to compute end-to-end age and reaction latencies of an effect chain, we first compute an upper bound on the delay $\phi _i^r$ between two operations on the same variable executed by two consecutive instances of the same runnable $\tau _i^r$. Assuming the first and the second runnable instance access the shared label at the beginning and at the end of their execution respectively, see Fig. 9, $\phi _i^r$ is derived as a function of the best-case start time $s_i^r$ and the worst-case response time $R_i^r$ of runnable $\tau _i^r$:

$$\begin{aligned} \phi _i^r = T_i - s_i^r + R_i^r. \end{aligned}$$

(21)

Fig. 9

Calculation of $\phi _i^r$

In the following, we first examine the Explicit communication in detail, since it establishes the basis for the latency characterization of its Implicit counterpart.

5.1 Explicit communication

Consider an effect sub-chain, where a runnable $\tau _W^i$ with $\phi _W^i$ writes a label, which is in turn read by another runnable $\tau _R^j$ with $\phi _R^j$. We hereafter compute an upper bound on the worst-case sub-chain age latency $\alpha _{W,R}^{i,j}$ and worst-case sub-chain reaction latency $\delta _{W,R}^{i,j}$. To do this, we consider different worst-case settings where the following conditions hold:

C1.:

$\tau _W^i$ updates L right after $\tau _R^j$ started loading it.

C2.:

Two subsequent read operations are $\phi _R^j$ time-units apart.

C3.:

Two subsequent write operations are $\phi _W^i$ time-units apart.

Theorem 2

An upper bound on the worst-case sub-chain age latency of two communicating tasks $\tau _W$ and $\tau _R$ is

$$\begin{aligned} \alpha _{W,R}^{i,j} = \phi _W^i \end{aligned}$$

(22)

Proof

To compute the age latency $\alpha _{W,R}^{i,j}$, we separately consider the cases with $\phi _R^j \ge \phi _W^i$ and $\phi _R^j < \phi _W^i$. When $\phi _R^j \ge \phi _W^i$, the worst-case situation is that of Fig. 10a, where $\alpha _{W,R}^{i,j} = \phi _W^i$. Shifting the reading instance of $\tau _R$ earlier would cause a proportional decrement in the age latency, while postponing it right after the second update of $\tau _W$ would cause a sudden drop of the age latency to zero, as the read would refer to the new writing update. When instead $\phi _R^j < \phi _W^i$, the worst-case scenario is that of Fig. 10b, where the latest instance of $\tau _R$ reads just before the next update of $\tau _W$. In this case, an upper bound on the age latency is $\phi _W^i$. Shifting the reading instance to the left would proportionally decrement the age latency, whereas postponing it right after the update would decrease the age latency by one reading period.

In both considered cases, an upper bound on the age latency is $\alpha _{W,R}^{i,j} = \phi _W^i$, proving the theorem. $\square$

Theorem 3

An upper bound on the worst-case sub-chain reaction latency of two communicating tasks$\tau _W$ i $\tau _R$is

$$\begin{aligned} \delta _{W,R}^{i,j} = \phi _R^j \end{aligned}$$

(23)

Proof

To compute the reaction latency $\delta _{W,R}^{i,j}$, we again separately consider the cases with $\phi _R^j \ge \phi _W^i$ and $\phi _R^j < \phi _W^i$. When $\phi _R^j \ge \phi _W^i$, the worst-case situation is shown in Fig. 11a, where an upper bound on the reaction latency is equal to $\phi _R^j$. Shifting earlier the reading instance would cause a proportional decrease of the reaction latency, while moving it later would make it refer to the last write update, leading to a null reaction latency. Note that earlier writing instances within the considered window do not need to be considered for the reaction latency because they are overwritten, i.e., they do not cause any “reaction” in the system. When instead $\phi _R^j < \phi _W^i$, the worst-case scenario is that of Fig. 11b, where $\delta _{W,R}^{i,j} = \phi _R^j$. Shifting the writing instance to the right would cause a proportional decrement in the reaction latency, while moving it a bit earlier would cause a sudden drop of the reaction latency to zero.

In both considered cases, an upper bound on the reaction latency is $\delta _{W,R}^{i,j} = \phi _R^j$, proving the theorem. $\square$

Fig. 10

Upper bound on the worst-case sub-chain age latency $\alpha _{W,R}^{i,j}$ when $\phi _R^j \ge \phi _W^i$ (a) and $\phi _R^j < \phi _W^i$ (b)

Fig. 11

Upper bound on the worst case sub-chain reaction latency $\delta _{W,R}^{i,j}$ when $\phi _R^j \ge \phi _W^i$ (a) and $\phi _R^j < \phi _W^i$ (b)

For simplicity, we will drop the apexes of $\delta _{W,R}^{i,j}$, $\alpha _{W,R}^{i,j}$, $\phi _W^i$ and $\phi _R^j$ when we do not need to explicitly refer to the communicating tasks. An upper bound on the overall end-to-end age latency of an effect chain $\alpha (EC)$ can therefore be computed as

$$\begin{aligned} \alpha (EC) =\sum _{h=1}^{\eta -1} \alpha _{h,h+1} = \sum _{h=1}^{\eta -1} \phi _h, \end{aligned}$$

(24)

where $\eta$ is the number of tasks constituting the effect chain EC.

Similarly, if we assume that the first task in the EC misses the event that triggers the chain, then an upper bound on the overall end-to-end reaction latency of an effect chain $\delta (EC)$ can be computed as:

$$\begin{aligned} \delta (EC) = \phi _1 + \sum _{h=1}^{\eta -1} \delta _{h,h+1} =\phi _1 + \sum _{h=1}^{\eta -1} \phi _{h+1} =\phi _1 + \sum _{h=2}^{\eta } \phi _h = \sum _{h=1}^{\eta } \phi _h. \end{aligned}$$

(25)

5.2 Implicit communication

As explained in Sect. 4.1, our Implicit communication model introduces two extras runnables at task boundaries in charge of reading and publishing the shared labels. From an end-to-end latency perspective, the Implicit communication can be considered as a particular case of its Explicit counterpart, considering $\tau _W^{last}$ and $\tau _R^0$ as writing and reading runnables, respectively. For instance, an upper bound on the worst-case sub-chain propagation delay $\delta _{W,R}^{i,j}$ for any pair of communicating runnables $\tau _W^{i}$ and $\tau _R^j$ is equal to $\delta _{W,R}^{last,0}$, plus an extra delay $\varDelta _R$ due to the fact that $\tau _R$ publishes all its shared labels at the end of its execution. For any task $\tau _i$, $\phi _i^0$ and $\phi _i^{last}$ can be calculated as $\phi _i^0 = T_i + R_i^0$ and $\phi _i^{last} = T_i - s_i^{last} + R_i$.

Fig. 12

Upper bound on the worst-case sub-chain reaction latency ($\phi _R^0 < \phi _W^{last}$) for the Implicit communication

Figure 12 shows an upper bound on the worst-case sub-chain reaction latency with $\phi _R^0 < \phi _W^{last}$. It is easy to see that $\varDelta _R = R_R - R_R^0$. A similar situation has been verified to happen in all other possible settings. Upper bounds on sub-chain age and reaction latencies for the Implicit model can then be simply computed adding $\varDelta _R$ to the corresponding explicit counterparts given by Eqs. (22) and (23). Thus, $\alpha _{W,R}^{i,j} = \alpha _{W,R}^{last,0}+\varDelta _R = \phi _W^{last} + \varDelta _R$ and $\delta _{W,R}^{i,j} = \delta _{W,R}^{last,0}+\varDelta _R = \phi _R^{0} + \varDelta _R$.

An upper bound on the overall end-to-end age and reaction latency can then be computed as

$$\begin{aligned} \alpha (EC)= & {} \sum _{h=1}^{\eta -1} \alpha _{h,h+1} = \sum _{h=1}^{\eta -1} (\phi _h^{last} + \varDelta _{h+1}) \end{aligned}$$

(26)

$$\begin{aligned} \delta (EC)= & {} \phi _1 + \sum _{h=1}^{\eta -1} \delta _{h,h+1} = \sum _{h=1}^{\eta } (\phi _h^{0} + \varDelta _{h}). \end{aligned}$$

(27)

5.3 LET communication

If we define the hyperperiod $H_{EC}$ of an EC as the LCM of the periods of the tasks composing the chain, i.e., $H_{EC} = LCM_{i=1}^\eta (T_i)$, then there is a fixed number of possible communication paths in a hyperperiod, starting from the end of the period of the first task and finishing with the release of the last one in the EC. We call these chains basic paths. For example, in the EC of Fig. 13a, there are two basic paths in the highlighted hyperperiod $H_{EC}=10$ : [30,36] and [34,40]. Note that if all tasks in the EC have harmonic periods then there is only one basic path.

Let us define ${\dot{P}}_{W,R}^n$ (resp. ${\dot{Q}}_{W,R}^n$) as the publishing (resp. reading) point between two tasks $\tau _W$ and $\tau _R$ in the n-th basic path of an EC. Then, the n-th basic path in the EC starts at ${\dot{P}}_{1,2}^n$ and ends at ${\dot{Q}}_{\eta -1,\eta }^{n}$. See Fig. 13a. Note that ${\dot{P}}_{W,R}^n$ and ${\dot{Q}}_{W,R}^n$ are not necessarily equal to $P_{W,R}^n$ and $Q_{W,R}^n$.

Fig. 13

End-To-End latency characterization of the LET communication: Age latency (a) Reaction latency (b)

$$\begin{aligned} \delta (EC) = \max _{\forall n \in H_{EC}}{\delta ^n}. \end{aligned}$$

(28)

Algorithm 1 returns the publishing point ${\dot{P}}_{i,j}^{n}$ that corresponds to a given reading point ${\dot{Q}}_{i,j}^{n}$. Similarly, Algorithm 2 returns the reading point ${\dot{Q}}_{i,j}^{n}$ and its corresponding publishing point ${\dot{P}}_{i,j}^{n}$ that precedes a given publishing point, ${\dot{P}}_{j,k}^{n}$. By applying Algorithm 1 to the last pair in the EC, and Algorithm 2 to every other pair of consecutive tasks composing the EC, the boundaries ${\dot{P}}_{1,2}^{n}$ and ${\dot{Q}}_{\eta -1,\eta }^{n}$ of the n-th basic path of an EC can be obtained. The length $\theta _{EC}^n$ of the n-th basic path of the EC can then be computed as $\theta _{EC}^n = {\dot{Q}}_{\eta -1,\eta }^{n} - {\dot{P}}_{1,2}^{n}$. Paths starting with the same publishing point ${\dot{P}}_{1,2}^{n}$ of a previous path are not to be considered.

If we assume the EC is triggered by the release of the first task in the chain, the age latency $\alpha ^n$ associated to the n-th basic path can then be computed by adding to the basic path length (i) the period $T_1$ of the first task in the EC, and (ii) the distance to the end of the next $(n+1)$-th basic path, where the output of the EC will eventually reflect a new input signal. That is,

$$\begin{aligned} \alpha ^n = T_1 + \theta _{EC}^n + {\dot{Q}}_{\eta -1,\eta }^{n+1} - {\dot{Q}}_{\eta -1,\eta }^n . \end{aligned}$$

(29)

The worst-case age latency $\alpha (EC)$ of the EC is then given by the maximum $\alpha ^n$ over all basic paths in a hyperperiod of the EC.

$$\begin{aligned} \alpha (EC) = \max _{\forall n \in H_{EC}}{\alpha ^n}. \end{aligned}$$

(30)

In the example of Fig. 13a, $\alpha ^1=12$ and $\alpha ^2 =14$. Therefore, $\alpha (EC)=14$.

With regard to the reaction latency $\delta ^n$ associated to the n-th basic path, the worst-case scenario occurs when the event that triggers the EC arrives right after the release of the first task $\tau _1$ in the EC as shown in Fig. 13b. Thus, $\delta ^n$ can be computed by appending the period $T_\eta$ of the last task in the EC to the corresponding $\alpha ^n$, i.e., $\delta ^n = \alpha ^n + T_\eta$. In the example of Fig. 13b, $\delta ^1=14$ and $\delta ^2 =16$. The worst-case end-to-end reaction latency, $\delta (EC)$ of the EC is then given by the maximum $\delta ^n$ over all basic paths in a hyperperiod of the EC.

6 End-to-end latency analysis

In this section, we apply our end-to-end worst-case latency analysis to a representative automotive application taken from a real industrial use case presented in Hamann et al. (2016, 2017b) (Refer to Table 1). The application represented in Fig. 15 was formalized using the AMALTHEA⁵ model, an open-source XML-based document format for modeling multi-core applications, supporting the AUTOSAR standard. The hardware described in the given AMALTHEA model consists of 4 cores, running at 300 MHz, 4 core-local RAMs, and one global DRAM. Non-local RAMs and the GRAM are accessible via a cross-bar interconnection network. Tasks are distributed among the four cores with different preemption schemes and types of activations. Notice that all cooperative tasks (Task_20, Task_50, Task_100, Task_200 and Task_100) run on the same core. See Fig. 14.

Fig. 14

Hardware model with tasks already partitioned

Table 1 FMTV industrial use case, system description (cooperative tasks are highlighted in bold)

The first effect chain under analysis (EC1 in Fig. 15) is composed of three runnables mapped onto three ($\eta =3$) different tasks $\tau _1$, $\tau _2$ and $\tau _3$ with the following harmonic periods: 100 ms, 10 ms, and 2 ms, respectively. The second effect chain (EC2 in Fig. 15) is also composed of three runnables mapped onto three tasks. However, while the last two tasks have periods of 2 ms and 50 ms, respectively, the first task is sporadic with an inter-arrival time between 700 and 800 ${\upmu }$s. In the following we characterize the end-to-end latency of the first effect chain for the three communication patterns discussed in this article. Note that there exists previous work (Gemlau and Schlatow 2017; Boniol and Forget 2017; Rivas and Gutiérrez 2017; Biondi and Pazzaglia 2017; Martinez and Sañudo 2017) that deals with the aforementioned industrial use case; however, either they do not take the cooperative scheduling into consideration or they assume that the EC is triggered by the release of the first task in the chain for the age and reaction semantics.

Fig. 15

Proposed ECs. In the figure the subindex of each runnable uses the task_runnable notation. For instance, $r_{100 ms\_7}$ denotes runnable number 7 of the 100 ms task

6.1 Explicit communication

Since no sensor information is given, we assume that the EC starts at the release time of the task that initiates the chain. Therefore, we append the best-case start time of the runnable that initiates the effect chain EC, $s_{1}^{I}$, to (24) and (25). From (5), (9), (10), and (24),

$$\alpha (EC) = s_{1}^{I} + \phi _{1}^{{r_{{100ms\_7}} }} + \phi _{2}^{{r_{{10ms\_19}} }} = 70,333\;{\upmu }{\text{s}} + \phi _{1}^{{r_{{100ms\_7}} }} + \phi _{2}^{{r_{{10ms\_19}} }} .$$

From (21),

$$\begin{aligned} \phi _1^{r_{100 ms\_7}}= & {} T_1-s_1^{r_{100 ms\_7}}+R_1^{r_{100 ms\_7}}= 100000\, {\upmu }{\text{s}}-70,333 \,{\upmu }{\text{s}}\\&+13294,876\, {\upmu }{\text{s}}=113225\, {\upmu }{\text{s}}, \hbox { and } \phi _2^{r_{10 ms\_19}}=T_2-s_2^{r_{10 ms\_19}}\\&+R_2^{r_{10 ms\_19}}= 10000 \,{\upmu }{\text{s}}-196,366 \,{\upmu }{\text{s}}+619,43\, {\upmu }{\text{s}}=10423\, {\upmu }{\text{s}}. \end{aligned}$$

Thus,

$$\begin{aligned} \alpha (EC)=70,333 \,{\upmu }{\text{s}}+113225 \,{\upmu }{\text{s}}+10423 \,{\upmu }{\text{s}}={\mathbf{123,718 ms }}. \end{aligned}$$

Similarly, from (25), we obtain

$$\begin{aligned} \delta (EC) =\phi _1^{r_{100 ms\_7}}+\phi _2^{r_{10 ms\_19}}+\phi _3^{r_{2 ms\_8}}= 123648\, {\upmu }{\text{s}}+\phi _3^{r_{2 ms\_8}}. \end{aligned}$$

From (21),

$$\begin{aligned} \phi _3^{r_{2 ms\_8}}=T_3-s_3^{r_{2 ms\_8}}+R_3^{r_{2 ms\_8}}=2000\, {\upmu }{\text{s}}-36, 053 \,{\upmu }{\text{s}}+99 \,{\upmu }{\text{s}}=2062 \,{\upmu }{\text{s}}. \end{aligned}$$

Then,

$$\begin{aligned} \delta (EC)={\mathbf{125,710 ms }} \end{aligned}$$

6.2 Implicit communication

As the sensor information is unknown, we likewise add the best-case start time of the copy-out runnable, $s_1^{last}$, to (26) and (27).

Thus, from (5), (9), (10), (26) and (27),

$$\begin{aligned} \alpha (EC)=s_{1}^{last}+\phi _1^{last}+\varDelta _2+\phi _2^{last}+\varDelta _3. \end{aligned}$$

Moreover,

$$\begin{gathered} s_{1}^{{last}} = 2191,530{\mkern 1mu} \;{\upmu }{\text{s}}, \hfill \\ \phi _{1}^{{last}} = T_{1} - s_{1}^{{last}} + R_{1} = 100000{\mkern 1mu} \;{\upmu }{\text{s}} - 2191,530\;{\mkern 1mu} {\upmu }{\text{s}} + 31556,579{\mkern 1mu} \;{\upmu }{\text{s}} = 129365,049\;{\upmu }{\text{s}}, \hfill \\ \Delta _{2} = R_{2} - R_{2}^{0} = 8019,393{\mkern 1mu} \;{\upmu }{\text{s}} - 73,523{\mkern 1mu} \;{\upmu }{\text{s}} = 7945,87\;{\upmu }{\text{s}},\;\phi _{2}^{{last}} = T_{2} - s_{2}^{{last}} + R_{2} = \hfill \\ 10000\;{\mkern 1mu} \mu s - 2812,369\;{\mkern 1mu} {\upmu }{\text{s}} + 8019,393\;{\mkern 1mu} {\upmu }{\text{s}} = 15207,024{\mkern 1mu} \;{\upmu }{\text{s}}, \hfill \\ \end{gathered}$$

and

$$\begin{aligned} \varDelta _3=R_3-R_3^0=279,596 \,{\upmu }{\text{s}}-0,3 \,{\upmu }{\text{s}}=279,296 \,{\upmu }{\text{s}}. \end{aligned}$$

Then,

$$\begin{aligned} \alpha (EC)= & {} 2191,530 \,{\upmu }{\text{s}}+129365,049 \,{\upmu }{\text{s}}+7945,87 \,{\upmu }{\text{s}}+15207,024 \,{\upmu }{\text{s}}\\&+279,296 \,{\upmu }{\text{s}}={\mathbf{154,988 ms }}. \end{aligned}$$

In a similar way,

$$\begin{aligned} \phi _1^{0}= & {} T_1+R_1^0=100000 \,{\upmu }{\text{s}}+13043,313 \,{\upmu }{\text{s}}=113043,313 \,{\upmu }{\text{s}}, \\ \phi _2^{0}= & {} T_2+R_2^0=10000 \,{\upmu }{\text{s}}+73,523 \,{\upmu }{\text{s}}=10073,523 \,{\upmu }{\text{s}}, \\ \phi _3^{0}= & {} T_3+R_3^0=2000 \,{\upmu }{\text{s}}+0,3 \,{\upmu }{\text{s}}=2000,3 \,{\upmu }{\text{s}} \end{aligned}$$

and

$$\begin{aligned} \varDelta _1=R_1-R_1^0=31556,579 \,{\upmu }{\text{s}}-13043,313 \,{\upmu }{\text{s}}=18513,266 \,{\upmu }{\text{s}}. \end{aligned}$$

Finally,

$$\begin{aligned} \delta (EC)= & {} \phi _1^{0}+\varDelta _1+\phi _2^{0}+\varDelta _2+\phi _3^{0}+ \varDelta _3=113043,313 \,{\upmu }{\text{s}}+18513,266 \,{\upmu }{\text{s}}\\&+10073,523 \,{\upmu }{\text{s}}+7945,87 \,{\upmu }{\text{s}} +2000,3 \,{\upmu }{\text{s}}+279,296 \,{\upmu }{\text{s}}={\mathbf{151,855 ms }} \end{aligned}$$

6.3 LET communication

Again, due to the lack of sensor information, we assume $P_{1,2}^1=0 ms$. Since the three tasks composing the EC have harmonic periods, then there is only one basic path. Since

$$\theta _{{EC}}^{1} = Q_{{2,3}}^{1} - P_{{1,2}}^{1} = 10\;{\text{ms}} - 0\;{\text{ms}} = 10\;{\text{ms}},$$

using Algorithm 1 and Algorithm 2 in conjunction with  (29), yields

$$\begin{aligned} \alpha (EC) =T_1 + \theta _{EC}^1 + {\dot{Q}}_{2,3}^2 - {\dot{Q}}_{2,3}^1= 100 \,{\text{ms}} +10 \,{\text{ms}} +110-10= {\mathbf{210 ms }} \end{aligned}$$

and

$$\begin{aligned} \delta (EC) = \alpha (EC) + T_3 = 210 \,{\text{ms}} + 2 \,{\text{ms}} = {\mathbf{212 ms }}. \end{aligned}$$

Even though the characterization of EC2 is similar to that of the other EC, it is worth mentioning that the worst-case scenario for the Explicit and Implicit communication model occurs when the sporadic task releases jobs that are spaced 800 ${\upmu }$s apart, as this value maximizes the delays computed through Eqs. (24),  (25), (26) and (27). For the LET communication, instead, the effect chain length computed with (30) is maximized for 799 ${\upmu }$s. Results of the characterization of both ECs are summarized in Table 2.

As expected, the end-to-end latencies with the implicit model are somewhat larger than those of its explicit counterpart, due to the copy-related overhead introduced to guarantee data consistency. Moreover, age and reaction latencies may significantly differ, depending on the parameters of the tasks building the effect chain. The LET paradigm introduces much larger latencies, especially when tasks have non-harmonic periods, as is the case with EC2. It is also worth pointing out that there are studies, like the ones by Bradatsch et al. (2016) and Martinez et al. (2018), that aim at reducing the latency introduced by the LET model.

Table 2 End-to-End latency characterization of EC1 and EC2

Fig. 16

Normalized End-To-End latencies: Age latency (a) Reaction latency (b)

The FMTV challenge presented only three effect chains. Therefore, in order to obtain a better characterization of the latency introduced by the communication models on a much larger number of chains, we synthetically created additional effect chains based on the considered AMALTHEA model. To this extent, we considered all producer/consumer relationships between runnables in the FMTV task set, leading to a set of more than 1000 ECs spanning between 2 and 6 tasks. While the considered ECs may not correspond to functional effect chains of the original AMALTHEA application, they are however representative of the latencies introduced with typical producer/consumer communication in a realistic automotive task set. We therefore computed the age and reaction latencies for each considered EC, using the formulas derived for each communication model. The results are summarized in Fig. 16a, b for each group of ECs with a given number of communicating tasks. Box plots show the minimum, $25\%$ percentile, average, $75\%$ percentile, and worst-case age and reaction latencies within each considered group of tasks. Results are normalized with respect to the worst-case latency, which is always given by the maximum latency in the LET case.

The latencies for the LET case are about twice those found in the explicit and implicit cases. The latencies of the last two communication models are also comparable, with the implicit case providing only a slightly higher latency than the explicit case, in most considered chains. Absolute values are not shown, but, as a general rule, the longer the chain, the longer the latency. It is interesting to notice that the relative performance of the different semantics are rather independent from the number of tasks building the chain.

It is worth reminding that race conditions arise when two or more tasks may concurrently modify the same label. In the automotive domain, this so-called multiple-writer scenario is often discouraged, since data consistency cannot be guaranteed through copies. In this case, a lock-based Explicit communication model is more suited to guarantee data consistency. This latter has typically a shorter end-to-end latency and it does not introduce extra memory footprint due to copies. However, it requires properly protecting the access to shared resources via explicit synchronization constructs.

Another important factor to consider is the variation of the end-to-end latency of an effect chain throughout the execution. As shown in Marti et al. (2001) and Lampke et al. (2015), a deterministic and stable effect chain latency may be very important for control algorithms. The improved latency determinism is the biggest advantage of the LET communication, especially in the HSC case where the end-to-end latency is always constant. Moreover, since task communication takes place at deterministic points in time, there is no need to use locks to guarantee data consistency. The price to pay for these valuable features is however a significantly larger age and reaction latency than those of the implicit and explicit counterparts, as shown in Fig. 16a, b. In Fig. 17, we show the end-to-end jitter for each of the presented communication paradigms. We computed the end-to-end jitter as the difference between the best- and worst-case end-to-end latency for a given effect chain. As it can be observed, the end-to-end jitter of the LET model is significantly smaller than that of the other two communication models. This result highlights the ability of LET for improving the predictability of control processes depending on effect chains of tasks concurrently executing on the same platform.

Fig. 17

Mean end-to-end jitter

7 Conclusion

This paper presented a study motivated by the industrial need to characterize the end-to-end latencies of effect chains of automotive real-time tasks communicating through shared variables in a multi-core system. A tight schedulability analysis for cooperative and preemptive tasks that are concurrently scheduled on the same partitioned platform was presented. Moreover, different communication models adopted to ensure a consistent task communication were analyzed from a memory and timing perspective, characterizing the overhead introduced. Then, a formal implementation was proposed for two of them, namely Implicit and LET, analyzing the impact introduced in terms of memory footprint and communication delay. Furthermore, an analytical characterization was presented to compute valid upper bounds of end-to-end propagation delays of age and reaction latencies for all the considered communication models. Pros and cons of explicit, implicit and LET semantics were discussed in order to assess which paradigm may suit best the need of an automotive application. A detailed experimental characterization was also provided based on an automotive industrial use case composed of multiple real-time tasks partitioned on a four-core setting.

As a future work, we plan to extend the presented analysis to deal with real-time applications that require not only periodic but also aperiodic task sets. Moreover, we plan to propose task-to-core partitioning strategies to improve, i.e., reduce, the latency metrics of selected effect chains.