Static probabilistic timing analysis for real-time systems using random replacement caches

Abstract

In this paper, we investigate static probabilistic timing analysis (SPTA) for single processor real-time systems that use a cache with an evict-on-miss random replacement policy. We show that previously published formulae for the probability of a cache hit can produce results that are optimistic and unsound when used to compute probabilistic worst-case execution time (pWCET) distributions. We investigate the correctness, optimality, and precision of different approaches to SPTA for random replacement caches. We prove that one of the previously published formulae for the probability of a cache hit is optimal with respect to the limited information (reuse distance and cache associativity) that it uses. We derive an alternative formulation that makes use of additional information in the form of the number of distinct memory blocks accessed (the stack distance). This provides a complementary lower bound that can be used together with previously published formula to obtain more accurate analysis. We improve upon this joint approach by using extra information about cache contention. To investigate the precision of various approaches to SPTA, we introduce a simple exhaustive method that computes a precise pWCET distribution, albeit at the cost of exponential complexity. We integrate this precise approach, applied to small numbers of frequently accessed memory blocks, with imprecise analysis of other memory blocks, to form a combined approach that improves precision, without significantly increasing complexity. The performance of the various approaches are compared on benchmark programs. We also make comparisons against deterministic analysis of the least recently used replacement policy.

1 Extended version

This paper builds upon, and significantly extends the 6 page paper (Altmeyer and Davis 2014) published in Design Automation and Test in Europe (DATE) 2014. The main extensions are as follows:

• Derivation of an alternative method of computing a lower bound on the probability of a cache hit, based on the concept of stack distance (Sect. 4).

• Correcting an omission in the basic approach to cache contention given by Altmeyer and Davis (2014), and introducing a more effective cache contention approach (Sect. 5).

• Integration of the cache contention approaches with exhaustive analysis of a limited number of relevant memory blocks, and the introduction of an additional heuristic to select relevant memory blocks in a given trace (Sect. 7).

• Extended evaluation on significantly larger real-life examples, with comparisons against deterministic analysis of the least recently used (LRU) replacement policy (Sect. 8).

2 Introduction

Real-time systems such as those deployed in space, aerospace, automotive and railway applications require guarantees that the probability of the system failing to meet its timing constraints is below an acceptable threshold (e.g. a failure rate of less than $10^{-9}$ per hour for some aerospace and automotive applications). Advances in hardware technology and the large gap between processor and memory speeds, bridged by the use of cache, make it difficult to provide such guarantees without significant over-provision of hardware resources. The use of deterministic cache replacement policies means that pathological worst-case behaviours need to be accounted for, even when in practice they may have a vanishingly small probability of actually occurring. The use of cache with random replacement policies facilitate upper bounding the probability of pathological worst-cases behaviours to quantifiably extremely low levels for example well below the maximum permissible failure rate (e.g. $10^{-9}$ per hour) for the system. This allows the extreme worst-case behaviours to be safely ignored, and hence provides the potential to increase guaranteed performance in hard real-time systems.

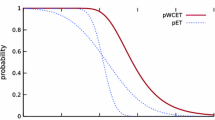
The timing behaviour of programs running on a processor with a random cache replacement policy can be determined using static probabilistic timing analysis (SPTA). SPTA computes an upper bound on the probabilistic worst-case execution time (pWCET) in terms of an exceedance function [1-cumulative distribution function (CDF)]. This exceedance function gives the probability, as a function of all possible values for an execution time budget $x$, that the execution time of the program will not exceed that budget on any single run. The reader is referred to Davis et al. (2013) for examples of pWCET distributions, and Cucu-Grosjean (2013) for a detailed discussion of what is meant by a pWCET distribution and the important difference between that and a probabilistic execution time (pET) distribution.

Simple forms of SPTA comprise two main steps (Davis et al. 2013): First, a probability function is required to compute an estimate of the probability of a cache hit for each memory access. This probability function is valid if it provides a lower bound on the probability of a cache hit. Typical probability functions used in SPTA are a function of the cache associativity and the reuse distance, defined as the number of intervening memory accesses that could cause an eviction, since the memory block was last accessed. The probability function is used to obtain a pWCET distribution for each instruction. Second, the pWCET distribution for a sequence of instructions is computed by convolving the distributions obtained for individual instructions. For the basic form of convolution to give correct results, the pWCET distributions obtained for the different instructions must be independent. By independent, we mean that the estimate of the probability of a cache hit for a given memory access remains a valid lower bound irrespective of the behaviour of other memory accesses. We note that the precise probability of a cache hit for a given memory access is rarely independent, it typically depends strongly on the history of previous accesses (i.e. whether or not they were cache hits). Thus care needs to be taken in the derivation of suitable probability functions to ensure that independence is obtained.

SPTA has been developed for single processor systems assuming evict-on-miss (Quiñones et al. 2009; Kosmidis et al. 2013), and evict-on-access (Cucu-Grosjean et al. 2012; Cazorla et al. 2013) random replacement policies. This initial work assumed single path programs and no pre-emption. Subsequently, Davis et al. (2013) provided analysis for both evict-on-miss and evict-on-access policies for single and multi-path programs, along with a method of accounting for cache related pre-emption delays. As the evict-on-miss policy dominates evict-on-access we focus on the former in this paper.

Despite the intensive research in this area over the past few years, it remains an open problem (Davis 2013) how to accurately and efficiently compute the pWCET distributions for individual instructions and sequences of them. In particular, prior approaches gave little information about the correctness and precision of the pWCET distributions obtained.

2.1 Related work

In the previous section, we covered specific related work on SPTA for random replacement caches. A detailed review of these methods is given in Sect. 2. We now set the work on SPTA in context with respect to related work on both probabilistic hard real-time systems and cache analysis for deterministic replacement policies.

The methods introduced in this paper belong to the realm of analyses that estimate bounds on the execution time of a program. These bounds may be classified as either a worst-case value (WCET), or a worst-case probability distribution (pWCET).

The first class is a mature area of research and the interested reader may refer to Wilhelm et al. (2008) for an overview of these methods. A specific overview of cache analysis for deterministic replacement policies together with comparison between deterministic and random cache replacement policies is provided at the end of this section.

The second class is a more recent research area with the first work on providing bounds described by probability distributions published by Burns and Edgar (2000), and Edgar and Burns (2001). The methods for obtaining such distributions can be categorised into three different families: measurement-based probabilistic timing analyses, static probabilistic timing analyses, and hybrid probabilistic timing analyses.

Measurement-based probabilistic timing analyses provide a pWCET distribution for a program from a set of execution time observations obtained by running the program on the target hardware. This distribution is obtained by applying Extreme Value Theory as originally proposed by Edgar and Burns (2001). Several works have improved upon this first use of the Extreme Value Theory in hard real-time systems by including block maxima reasoning (Hansen et al. 2009), and via the treatment of execution time observations such that the conditions of the basic version of Extreme Value Theory are fulfilled (Yue et al. 2011). Extreme Value Theory may underestimate the pWCET of a program as shown by Griffin and Burns (2010). The work of Cucu-Grosjean et al. (2012) overcomes this limitation and also introduces the appropriate statistical tests required to treat worst-case execution times as rare events.

Static probabilistic timing analyses provide a pWCET distribution for a program by analysing the structure of the program and modeling the behaviour of the hardware it runs on. Here, each instruction of the program may have a probability distribution associated with it; by combining these distributions, static probabilistic timing analysis provides a pWCET for the entire program. Existing work is primarily focussed on randomized architectures containing caches with random replacement policies. Initial results for the evict-on-miss (Quiñones et al. 2009; Kosmidis et al. 2013) and evict-on-access (Cucu-Grosjean et al. 2012; Cazorla et al. 2013) policies were derived for single-path programs. These results were superseded by later work that also included extensions to multi-path programs and took account of cache related preemption delays (Davis et al. 2013). Static probabilistic timing analyses have also been developed taking into account faults (Hardy and Puaut 2013). The work described in this paper belongs to this family of static probabilistic timing analyses. It extends the work of Altmeyer and Davis (2014) as described in the next section. Static probabilistic timing analyses may have complexity problems to solve related to their heavy use of convolution; however, techniques exist that are effective in addressing this issue without making the pWCET estimation unsound (Refaat and Hladik 2010; Maxim et al. 2012).

Hybrid probabilistic timing analyses are methods that apply measurement-based methods at the level of sub-programs or blocks of code and then operations such as convolution to combine these bounds to obtain a pWCET for the entire program. The main principles of hybrid analysis were introduced by Bernat et al. (2002; 2003) with execution time probability distributions estimated at the level of sub-programs. Here, dependencies may exist among the probability distributions of the sub-programs and copulas are used to describe them (Bernat et al. 2005).

Static timing analysis for deterministic caches (Wilhelm et al. 2008) relies on a two step approach with a low-level analysis to classify the cache accesses into hits and misses (Theiling et al. 2000) and a high-level analysis to determine the length of the worst-case path (Li and Malik 2006). The most common deterministic replacement policies are least-recently used (LRU), first-in first-out (FIFO) and pseudo-LRU (PLRU). Due to the high-predictability of the LRU policy, academic research typically focusses on LRU caches—with a well-established LRU cache analysis based on abstract interpretation (Ferdinand et al. 1999; Theiling et al. 2000). Only recently, analyses for FIFO (Grund and Reineke 2010a) and PLRU (Grund and Reineke 2010b) have been proposed, both with a higher complexity and lower precision than the LRU analysis due to specific features of the replacement policies. Despite the focus on LRU caches and its analysability, FIFO and PLRU are often preferred in processor designs due to the lower implementation costs which enable higher associativities.

Recent work by Abella et al. (2014) and Reineke (2014) compares static analysis of caches using LRU with prior work on SPTA (Davis et al. 2013) for evict-on-miss random replacement policies, and also makes comparisons with measurement-based analysis (Cucu-Grosjean et al. 2012). We discuss the findings of Reineke (2014) in further detail in Sect. 8.3.

2.2 Contributions

In this paper, we re-visit the probability functions that form the fundamental building blocks of SPTA. We show that convolution of the probability functions given by Kosmidis et al. (2013) and Quiñones et al. (2009) is unsound (optimistic), as these probability functions do not provide lower bounds on the probability of a cache hit that are independent of the behaviour of previous memory accesses. By contrast, we show that the probability function derived by Davis et al. (2013) provides a valid lower bound that is independent of the behaviour of previous memory accesses, enabling the calculation of sound pWCET distributions via convolution. We prove that this probability function is optimal with respect to the limited information (reuse distances and the cache associativity) that it employs, in the sense that no further improvement is possible without considering additional information.

As well as correctness and optimality, we also investigate the precision of SPTA. Despite claims to the contrary in the conclusions of Cucu-Grosjean et al. (2012), SPTA does not provide a precise pWCET distribution for a sequence of instructions when based on the convolution of simple pWCET distributions for each instruction. Instead, precise analysis requires that the probabilities of all possible sequences of cache hits and cache misses are considered leading to exponential complexity. Previous work (Cazorla et al. 2013; Cucu-Grosjean et al. 2012; Kosmidis et al. 2013; Quiñones et al. 2009) provides little indication of the precision of existing SPTA techniques, while Davis et al. (2013) provide some comparisons with simulation.

In this paper, we improve the precision and efficiency of SPTA for single-path programs in a number of ways. First, we present an alternative formulation giving a lower bound on the probability of a cache hit, based on the stack distance, i.e. the number of distinct memory blocks accessed within the reuse distance. This formulation is incomparable with that given by Davis et al. (2013). Since neither formula dominates the other and both are valid lower bounds, we may take the maximum of them to provide an improved lower bound. Second, we refine the probability function given by Davis et al. (2013) using the concept of cache contention. Third, we describe a simple approach that exhaustively enumerates all cache states that may occur for a given sequence of memory accesses. This provides precise analysis at the cost of complexity that is exponential in the number of pairwise distinct memory blocks. Nevertheless, this approach enables us to quantify the precision of various approaches to SPTA for small programs. Finally, we introduce a combined approach which integrates precise analysis of the most important memory accesses (those made most frequently), with imprecise analysis of the remaining memory accesses, using simple probability functions. We show that this combined technique is effective in improving the accuracy of SPTA while avoiding the exponential increase in complexity that exhaustive analysis brings.

While the focus of this paper is on the fundamentals of analysis for single path programs we note that the methods presented are extendable to multipath programs. Such extension is the subject of further work by the authors.

3 System model and prior approaches

3.1 Random cache replacement

A cache with the evict-on-miss random replacement policy operates as follows: whenever a memory block is requested and is not found in the cache, then a randomly chosen cache line is evicted and the requested block is loaded into the evicted location. We assume an $N$-way fully associative cache,¹ and so the probability of any cache line being evicted on a miss is $1/N$. We also assume pessimistically that random caches do not replace free or invalid cache lines first, which means that cache evictions can occur even when less than $N$ elements are cached.

Prior work considered mostly instruction cache only and no data cache; however, this restriction is unnecessary for the theoretical foundations of our analysis as we assume that access traces are given. We therefore define traces as sequences of memory blocks directly (independent of the content of the memory blocks) instead of sequences of instructions as was done by Davis et al. (2013). Further, the restriction to a fully-associative cache can be easily lifted, as a set-associative cache with $s$ cache sets can be analysed as $s$ parallel and independent fully-associative caches. In the context of random cache replacement, the cache-hit and cache-miss delays are assumed to be constant and hence the processor architecture is assumed to not exhibit timing anomalies. For data caches, accesses to unknown memory blocks are possible when the effective memory address cannot be statically determined. In such cases, we use a unique memory block identifier for each unidentified access which guarantees that it is considered a cache miss.

3.2 Traces and reuse distance

A trace $T$ of size $n$ is an ordered sequence of $n$ memory blocks $[e_1,\ldots , e_n]$. The set of all traces is denoted by $\mathbb {T}$, while $\mathbb {E}$ denotes the set of all elements, where an element is an access to a memory block. The reuse distance ${\text{ rd }}(e)$ of an element $e$ is the maximum possible number of evictions since the last access to the same memory block, with reuse distance $\infty$ in the case that there is no prior access to that memory block.

$$\begin{aligned} rd:\mathbb {E} \times \mathbb {T} \rightarrow \mathbb {N} \cup \{ \infty \} \end{aligned}$$

$$\begin{aligned} rd\left( e_l,\left[ e_1, \ldots e_{l-1}\right] \right) = \left\{ \begin{array}{ll} l-j-1 &{}\quad \hbox {if } \exists e_j:e_j = e_l \wedge \forall _{j < i < l}:e_l \ne e_i\\ \infty &{}\quad \hbox {otherwise} \end{array} \right. \end{aligned}$$

(1)

We typically represent the reuse distance $k$ using a superscript and omit all infinite reuse distances. For example,

$$\begin{aligned} a, b, a^1, c, d, b^3, c^2, f, a^5, c^5 \end{aligned}$$

We denote the event of a cache hit at memory block $e_i$ as $e_i^\mathrm{{hit}}$ and $P(e_i^\mathrm{{hit}})$ the corresponding probability, with $e_i^\mathrm{{miss}}$ and $P(e_i^\mathrm{{miss}})$ being the equivalent for a cache miss. Further, we use $\hat{P}$ to denote approximations to distinguish them from the precise probability values.

Successive accesses to the same memory block will always lead to cache hits in a random cache with the evict-on-miss replacement policy. We therefore collapse the traces and remove all successive accesses. For instance, the trace

$$\begin{aligned} a, b, b, c, c, b, c, c, a, a, c \end{aligned}$$

is collapsed to

$$\begin{aligned} a, b, c, b, c, a, c \end{aligned}$$

and successive accesses to the same element do not count towards the reuse distance. We note that this step does not influence the number of cache misses.

3.3 Review of prior approaches

In this section, we present the different approaches that have been proposed to compute the probability of cache hits and misses and thus the pWCET distribution.

Zhou (2010) proposed using the reuse-distance to compute the probability $P(e^\mathrm{{hit}})$ of a cache hit at access $e$ with reuse distance $k$:

$$\begin{aligned} \hat{P}^Z(k) = \left( \frac{N-1}{N}\right) ^k \end{aligned}$$

(2)

where $N$ is the associativity of the cache. To simplify the notation, we write $\hat{P}^Z(e_l^\mathrm{{hit}})$ as a short form of $\hat{P}^Z(rd\left( e_l,\left[ e_1, \ldots e_{l-1}\right] \right)$).

The rationale behind (2) is that the second access to $e$ can only be a hit, if all intermediate cache misses evict cache lines other than the one that element $e$ occupies. Equation (2) is not precise, but a lower bound on the individual probability of a cache hit for that specific access. Recall that the reuse distance is defined as the maximum number of evictions, and not the actual number. Therefore $\hat{P}^Z(e^\mathrm{{hit}}) < P(e^\mathrm{{hit}})$ holds for some access sequences.

Quiñones et al. (2009) proposed deriving the pWCET distribution of a single path program via convolution of the pWCET distributions of individual accesses obtained from (2). However, (2) is only valid if considered in isolation and the convolution for independent events cannot be used due to a dependency stemming from the finite size of the cache (Davis et al. 2013). To correct (2), Davis et al. (2013) proved an independent lower bound on the probability of a cache hit:

$$\begin{aligned} \hat{P}^D(k) = \left\{ \begin{array}{ll}\left( \frac{N-1}{N}\right) ^{k}&{}\quad N>k \\ 0 &{}\quad \hbox {otherwise} \end{array} \right. \end{aligned}$$

(3)

We use $\hat{P}^D(e_l^\mathrm{{hit}})$ as a short form of $\hat{P}^D(rd\left( e_l,\left[ e_1, \ldots , e_{l-1}\right] \right)$).

The drawback of (3) is that all accesses with reuse distance higher than the associativity of the cache are considered to be cache misses. Kosmidis et al. (2013) proposed the following formula:

$$\begin{aligned} \hat{P}^K(e^\mathrm{{hit}}) = \left( \frac{N-1}{N}\right) ^{\sum P\left( e_j^{\mathrm{miss}}\right) } \end{aligned}$$

(4)

where the summation in the exponent is over the probabilities of misses of the intervening memory accesses. (We note that a similar formula was given by Zhou (2010) as an approximation). Equation (4) may over-estimate the actual probability of a cache hit as noted by Davis (2013), and thus lead to a pWCET distribution that is optimistic.

Using one of the above estimates of the probability of a cache hit, the Probability Mass Function (PMF) $\mathcal {I}_i$ of element $e_i$ is defined as follows:

$$\begin{aligned} \mathcal {I}_i = \begin{pmatrix} \hbox {hit-delay} &{}\quad \hbox {miss-delay} \\ P(e^\mathrm{{hit}}) &{}\quad P(e^\mathrm{{miss}}) \end{pmatrix} \end{aligned}$$

(5)

with $P(e^\mathrm{{miss}}) = 1 - P(e^\mathrm{{hit}})$ and hit-delay (miss-delay) denoting the execution time for a cache hit (cache miss). The probability mass function thus gives the probability distribution for a discrete random variable that describes the possible execution times of the memory access. The $pWCET$ distribution is then derived by computing the convolution $\otimes$ of the probability mass function of every memory access $e_i$ in the original (uncollapsed) trace:

$$\begin{aligned} pWCET = \mathcal {I}_1 \otimes \mathcal {I}_2 \otimes \ldots \mathcal {I}_n \end{aligned}$$

(6)

where convolution provides the sum ${\mathcal Z}$ of two independent random variables ${\mathcal X}_1$ and ${\mathcal X}_2$:

$$\begin{aligned} {\mathcal Z}= {\mathcal X}_1 \otimes {\mathcal X}_2 \end{aligned}$$

For discrete random variables:

$$\begin{aligned} P\{{\mathcal Z}=z\}=\sum _{k=-\infty }^{+\infty }P\{{\mathcal X}_1=k\}P\{{\mathcal X}_2=z-k\} \end{aligned}$$

Note that convolution is commutative and associative.

Under the assumption of constant hit- and miss-delays, computing the distribution of cache-hits and cache-misses is sufficient to derive the pWCET distribution. We will therefore concentrate only on the former, the latter can be obtained by multiplying the constant delays by the number of hits and misses.

4 Correctness conditions and optimality

As stated by Davis et al. (2013), the probability that a single access is a cache hit/miss is not independent of prior events. This means that in general, the convolution for independent events cannot be soundly applied, as it is only valid for independent events. What can be done instead; however, is to provide a lower bound approximation $\hat{P}$ to the actual probability of a cache hit for which we can soundly apply the basic convolution for independent events. Sound in this context means that for any sequence of cache accesses $[e_1,\ldots , e_n]$, the approximation $\hat{P}$ complies with two constraints: (C1) it does not over-estimate the probability of a cache hit, and (C2) the value obtained from convolution of the approximated probabilities for any subset of accesses on a trace $T$ describing the probability that all elements in the subset are a hit, is at most the precise probability of such an event occurring:

• C1 $\forall e \in \{e_1,\ldots , e_n\} :P(e^\mathrm{{hit}}) \ge \hat{P}(e^\mathrm{{hit}})$,

• C2 $\forall E \subseteq \{e_1,\ldots , e_n\}:P \left( \bigwedge _{e \in E} e^\mathrm{{hit}}\right) \ge \prod _{e \in E} \hat{P}(e^\mathrm{{hit}})$.

We note that C2 can be instantiated to C1; however, we define two separate constraints as each one covers a distinct property of a correct approximation $\hat{P}$.

4.1 Counterexamples to Eqs. (2) and (4)

Of the different approaches presented in Sect. 1, only (3) provides a valid and sound lower-bound. Equation (2) does not fulfil C2 and (4) fulfils neither C1 nor C2 as shown below.

To show that (4) over-estimates the probability of an individual cache hit (i.e. contradicts constraint C1), we use the access sequence

$$\begin{aligned} a,b,c,d,a^3,b^3 \end{aligned}$$

and a cache with associativity $2$.

Equation (4) computes the probability of a cache hit for the second access to $a$ as

$$\begin{aligned} (1/2)^3 = 0.125 \end{aligned}$$

which is correct and precise. For the second access to $b$, however, (4) results in

$$\begin{aligned} (1/2)^{2+0.875} \ge 0.1363 \end{aligned}$$

which is optimistic as the correct probability of a cache hit is in this case

$$\begin{aligned} (1/2)^3 = 0.125 \end{aligned}$$

This can be seen by enumerating all the possible cache states that could exist after the second access to $a$; out of 16 possibilities each with probability 0.0625, only two contain $b$.

To show that C2 does not hold using (4) we use an example from Davis (2013), we assume the access sequence

$$\begin{aligned} a,b,a^1,b^1 \end{aligned}$$

and a cache with associativity of $4$. Further, we assume that the latency of a cache hit is $1$ and the latency of a cache miss is $10$. The first two accesses are certain misses, so using (4), the probability distributions for the first three instructions are as follows:

$$\begin{aligned} \begin{pmatrix} 1 &{}\quad 10 \\ 0 &{}\quad 1 \end{pmatrix} , \begin{pmatrix} 1 &{}\quad 10 \\ 0 &{}\quad 1 \end{pmatrix} , \begin{pmatrix} 1 &{}\quad 10 \\ 0.75 &{}\quad 0.25 \end{pmatrix} \end{aligned}$$

(7)

According to (4), the probability of the 4th access being a cache hit is then: $\hat{P}^K(e^\mathrm{{hit}}) = {0.75}^{0.25} = 0.9306$. (Note this value is rounded down slightly, which is a safe assumption). So the overall $pWCET$ is

$$\begin{aligned}&\begin{pmatrix} 10 \\ 1 \end{pmatrix} \otimes \begin{pmatrix} 10 \\ 1 \end{pmatrix} \otimes \begin{pmatrix} 1 &{}\quad 10 \\ 0.75 &{}\quad 0.25 \end{pmatrix} \otimes \begin{pmatrix} 1 &{}\quad 10 \\ 0.9306 &{}\quad 0.0694 \end{pmatrix}\nonumber \\&\quad = \begin{pmatrix} 22 &{}\quad 31 &{}\quad 40 \\ 0.69795 &{}\quad 0.0.2847 &{}\quad 0.01735 \end{pmatrix} \end{aligned}$$

(8)

However, the correct $pWCET$ is

$$\begin{aligned} \begin{pmatrix} 22 &{}\quad 31 &{}\quad 40 \\ 0.75 &{}\quad 0.1875 &{}\quad 0.0625 \end{pmatrix} \end{aligned}$$

(9)

This can be seen by considering the scenarios that result in a total of two and four cache misses respectively. (The first accesses to $a$ and $b$ are certain to be cache misses). If the first access to $b$ does not evict $a$ (probability 0.75), then the second access to $a$ can only be a cache hit, which in itself does not evict $b$, and so in this scenario, which has a probability of occurring of 0.75, there are two cache misses in total. Alternatively, if the first access to $b$ evicts $a$ (probability 0.25), then the second access to $a$ is certain to be a cache miss, which in turn has a probability of 0.25 of evicting $b$ and so making the second access to $b$ a cache miss. Hence the only scenario with four cache misses in total has a probability of occurring of $0.0625$.

In this example, using (4) results in a pWCET distribution that significantly under-estimates the probability of obtaining four cache misses and hence an execution time of 40. This is an optimistic and unsound result. We note that if the same example is repeated for a larger cache associativity then the discrepancy becomes more marked with (4) resulting in a pWCET distribution that under-estimates the probability of obtaining four cache misses by more than two orders of magnitude for an associativity of 128 (e.g. a small fully-associative cache).

To show that (2) also contradicts constraint C2, we assume an associativity of $2$ and the access sequence:

$$\begin{aligned} a,b,c,b^1,a^3 \end{aligned}$$

Using (2), the overall $pWCET$ is computed as follows:

$$\begin{aligned}&\begin{pmatrix} 10 \\ 1 \end{pmatrix} \otimes \begin{pmatrix} 10 \\ 1 \end{pmatrix} \otimes \begin{pmatrix} 10 \\ 1 \end{pmatrix} \otimes \begin{pmatrix} 1 &{}\quad 10 \\ 0.5 &{}\quad 0.5 \end{pmatrix} \otimes \begin{pmatrix} 1 &{}\quad 10 \\ 0.125 &{}\quad 0.875 \end{pmatrix}\nonumber \\&\quad = \begin{pmatrix} 32 &{}\quad 41 &{}\quad 50 \\ 0.0625 &{}\quad 0.5 &{}\quad 0.4375 \end{pmatrix} \end{aligned}$$

(10)

However, the correct $pWCET$ is:

$$\begin{aligned} \begin{pmatrix} 41 &{}\quad 50 \\ 0.625 &{}\quad 0.375 \end{pmatrix} \end{aligned}$$

(11)

This can be seen by considering the scenarios that result in one and two cache misses for the last two accesses in the sequence. (The first accesses to $a$, $b$, and $c$ are certain to be cache misses). If the access to $c$ does not evict $b$ (which occurs with a probability of 0.5), then the second access to $b$ is certain to be a hit; however, as the cache then contains both $b$ and $c$ and the associativity is two, the final access to $a$ is certain to be a miss. Alternatively, if the access to $c$ evicts $b$ (which also occurs with a probability of 0.5), then the second access to $b$ is certain to be a miss. In this case, since $c$ evicted $b$, it did not evict $a$, and so the final access to $a$ has a conditional probability of 0.25 of surviving the two accesses to $b$ both of which are misses. Hence the overall probabilities of a cache hit for the final accesses to $a$ and $b$ are 0.125 and 0.5 respectively. We note that these are the values given by (2); however, these two events (cache hits for the final accesses to $a$, and $b$) are not independent, they are instead mutually exclusive; either the last access to $a$ is a hit, or the last access to $b$ is a hit, but both cannot be hits, hence the values in the correct $pWCET$ (11).

As a further example, we assume an associativity of $4$ and the access sequence:

$$\begin{aligned} a,b,c,d,f,a^4,b^4,c^4,d^4,f^4 \end{aligned}$$

Using (2) then by construction, all probabilities of a cache hit $\hat{P}^Z(e^\mathrm{{hit}})$ for the last five accesses are non-zero. Hence, the combined probability of five hits is also non-zero, which contradicts with the fact that at most $4$ elements can be stored simultaneously in the cache.

Note that the counter examples we have given in this section are for small associativity (i.e. 2 or 4) as found in typical set-associative caches. The associativity and the sequences chosen are simply used to highlight the issues, and to make the calculations easy to comprehend; however, the reader should be in no doubt that these issues persist for finite values of associativity ($\ge$2), and for access sequences of arbitrary lengths.

4.2 Correctness of Eq. (3)

In this section, we prove that Equation (3) is correct in the sense that it fulfils both constraints (C1) and (C2) and therefore can be used for static probabilistic timing analysis. Recall that we use $\hat{P}^D(e_l^\mathrm{{hit}})$ as a short form of $\hat{P}^D(rd\left( e_l,\left[ e_1, \ldots e_{l-1}\right] \right)$).

Theorem 1

The function $\hat{P}^D(e^\mathrm{{hit}})$ does not over-estimate the probability of a cache hit and therefore provides a valid lower bound on the exact probability of a cache hit for any single element in a trace. (C1)

$$\begin{aligned} \forall e \in \{e_1,\ldots , e_n\} :P(e^\mathrm{{hit}}) \ge \hat{P}^D(e^\mathrm{{hit}}) \end{aligned}$$

Proof

(Theorem 1) Let $e$ be an arbitrary element on a trace $T$ with reuse distance $k$. We prove Theorem 1 using a case distinction over $k$:

• Case $k \ge N$: If the reuse distance $k$ is equal to or larger than the associativity $N$, the value $\hat{P}^D(k)$ is equal to zero and $\hat{P}^D(k) \le P(e^\mathrm{{hit}})$ holds.

• Case $k < N$: By definition of the reuse distance, we know that exactly $k$ elements have been accessed in between the last and the current access to the memory block of $e$. Each of these accesses is either a cache hit, which means that the state of the cache does not change (and the memory block accessed may potentially reside in the cache for all of the reuse distance of $e$), or a cache-miss, which means that the memory block of element $e$ is evicted with probability $1/N$. The worst-case situation is given by $k$ misses (as shown by Theorem 4 in the appendix of Davis et al. (2013), and discussed further in Sect. 5) and hence, the probability of a cache hit at $e$ is given by $\left( \frac{N-1}{N}\right) ^{k}$ and thus $\hat{P}^D(k) \le P(e^\mathrm{{hit}})$ holds, as any access to an intermediate element $e'$ resulting in a cache hit will only improve the hit-probability of the remaining elements. $\square$

Theorem 2

The value obtained from the product of the approximated probabilities $\hat{P}^D(k)$ for any subset of accesses $E$ on any trace $T$ describing the probability that all elements in the subset are a hit, is at most the precise probability of such an event occurring. (C2)

$$\begin{aligned} \forall E \subseteq \{e_1,\ldots , e_n\}:P \left( \bigwedge _{e \in E} e^\mathrm{{hit}}\right) \ge \prod _{e \in E} \hat{P}^D(e^\mathrm{{hit}}) \end{aligned}$$

Proof

(Theorem 2) We prove Theorem 2 by induction over the set of accesses $E$.

Base case: For a set $E$ with cardinality one ($\vert E \vert = 1$) there is only one element and $\left( \bigwedge _{e \in E} e^\mathrm{{hit}}\right) \ge \prod _{e \in E} \hat{P}^D(e^\mathrm{{hit}})$ holds by Theorem 1.

Induction step: assuming that $\left( \bigwedge _{e \in E} e^\mathrm{{hit}}\right) \ge \prod _{e \in E} \hat{P}^D(e^\mathrm{{hit}})$ holds for a set of elements $E$ with cardinality $i$, we show that $\left( \bigwedge _{e \in E'} e^\mathrm{{hit}}\right) \ge \prod _{e \in E'} \hat{P}^D(e^\mathrm{{hit}})$ holds for $E'$ with $E' = E \cup \{e'\}$ and cardinality $i+1$. Note, we assume without loss of generality that $e'$ occurs later in the trace than any element of $E$.

Let $k$ be the reuse distance of element $e'$. We can conclude that the induction hypothesis trivially holds for $E'$, if (i) $k \ge N$, or (ii) $\prod _{e \in E} \hat{P}^D(e^\mathrm{{hit}}) = 0$, since in both these cases, $\prod _{e \in E'} \hat{P}^D(e^\mathrm{{hit}}) = 0$. We therefore only need to show the correctness of the theorem assuming that $k < N$ and $\prod _{e \in E} \hat{P}^D(e^\mathrm{{hit}}) > 0$.

We note that the reuse distance of each element $e \in E$ is independent of the selection of $e'$ and that since $k < N$ and $\prod _{e \in E} \hat{P}^D(e^\mathrm{{hit}}) > 0$ the reuse distance of each element in $E'$ is less than $N$. If we assume a cache-state evolution in which elements are evicted in Least-Recently Used (LRU) order (note any specific order including LRU is possible for a random replacement cache), then all accesses in $E'$ can result in cache hits during the same sequence of accesses (this is the case because an element is only evicted in an LRU cache if the reuse-distance is greater than or equal to $N$), and hence $\left( \bigwedge _{e \in E'} e^\mathrm{{hit}}\right) > 0$ holds. Further, since Theorem 1 also holds for element $e'$, we know that $\hat{P}^D(k) \le P(e'^\mathrm{{hit}})$ where $k$ is the reuse distance of element $e'$. As $\hat{P}^D(k)$ lower bounds the probability of a hit for $e'$ for any pattern of hits or misses prior to access $e'$ then it follows that $\left( \bigwedge _{e \in E'} e^\mathrm{{hit}}\right) \ge \left( \bigwedge _{e \in E} e^\mathrm{{hit}}\right) \cdot \hat{P}^D(k)$. Since $\left( \bigwedge _{e \in E} e^\mathrm{{hit}}\right) \ge \prod _{e \in E} \hat{P}^D(e^\mathrm{{hit}})$ it follows that $\left( \bigwedge _{e \in E'} e^\mathrm{{hit}}\right) \ge \prod _{e \in E'} \hat{P}^D(e^\mathrm{{hit}})$. $\square$

4.3 Optimality of Eq. (3)

We can derive an estimate of the probability of a cache hit that is more precise than (3) as we can simply enumerate all possible cache states and the associated probabilities; however, this solution is computationally intractable, as we will explain in Sect. 6. If we aim at an estimate using only the reuse distances and on which we can apply the convolution for independent events, then (3) is optimal in the sense that there is no function of only $k$ and $N$ that is valid and returns any larger value.

Theorem 3

The lower bound on the probability of a cache hit $\hat{P}^D(k)$ is optimal for the information it uses, i.e., the reuse distance $k$ and the associativity $N$.

Proof

(Theorem 3) We assume that $\hat{P}'(k)$ is a probability function such that $\hat{P}'(k)$ is more precise than $\hat{P}^D(k)$. Hence:

$$\begin{aligned} \exists k:\hat{P}'(k) = \hat{P}^D(k) + \epsilon \end{aligned}$$

(12)

for some $\epsilon > 0$. We assume that the only input to $\hat{P}^D$ and $\hat{P}'$ is the reuse distance $k$ which must be valid for any sequence of accesses $[e_1,\ldots , e_n]$, and the associativity $N$. We make a case distinction on $k$:

• Case $k < N$: Assume the following ordered sequence with accesses to $k$ pairwise distinct elements

  $$\begin{aligned}{}[e_x, e_1, e_2, e_3, \ldots e_{k-1}, e_k, e_x] \end{aligned}$$

  and an initially empty cache. The reuse distance of the second access to $e_x$ is $k$. Each access to any of the other elements results in a cache miss, the probability of a cache hit $P(e_x^\mathrm{{hit}})$ is exactly $\hat{P}^D(k)$ and the assumption that $\epsilon > 0$ contradicts C1.

• Case $k \ge N$: Assume the access pattern to $k+1$ memory blocks repeated twice:

  $$\begin{aligned}{}[e_1, e_2, e_3, \ldots e_{k}, e_{k+1}, e_1, e_2, e_3, \ldots e_{k}, e_{k+1}] \end{aligned}$$

  for each second access to $e_i$, the reuse distance is $k$. Since the cache can store at most $N$ elements and $k+1>N$, we know that the probability of $k+1$ hits is $0$, i.e, $P \left( \bigwedge _{e_i} e_i^\mathrm{{hit}}\right) = 0$. However, since $\epsilon > 0$ and $\hat{P}^D(k) \ge 0$, we can conclude that $\prod _{e \in E} \hat{P}'(e^\mathrm{{hit}}) > 0$, which contradicts C2.

Hence, we can construct for any $k$ and any $N$, an access sequence where $\hat{P}^D(k)$ is optimal in the sense that it provides the largest valid value of any function relying only on the reuse distance and the associativity. $\square$

5 Stack distance

In the previous section, we showed that $\hat{P}^D(k)$ i.e. (3) is optimal in the sense that there is no function of the reuse distance $k$ and the associativity $N$ that is valid and returns any larger value. In this section, we show how additional information can be used to obtain an alternate formula for the probability of a cache hit.

We note that $\hat{P}^D(k)$ can be pessimistic in the commonly observed case of sequences with repeated accesses (e.g. loops). For example, the trace $a, b, c, d, c^1, d^1, c^1, d^1,$ $a^7, b^7$ repeats the accesses $c, d$ three times within the reuse distance of the final accesses to $a$ and $b$. Assuming an associativity of 4, then $\hat{P}^D(k)$ gives zero probability of a cache hit for these accesses, since their reuse distance exceeds the associativity of the cache. However, it is possible for the cache to contain all four distinct memory blocks $a, b, c, d$ accessed in this sequence, and so a zero value for the probability of a cache hit for the final accesses to $a$ and $b$ is pessimistic.

In this section we derive a simple, alternative formula $\hat{P}^A(\Delta ,k)$ that is effective in such cases. Let $\Delta$ be the stack distance ² of element $e_l$, i.e., the total number of pair-wise distinct memory blocks that are accessed within the reuse distance $k$ of element $e_l$. The maximum number of distinct cache locations loaded during the reuse distance of $e_l$ is upper bounded by $\Delta$ (proved below), hence it follows that a lower bound on the probability that $e_l$ will survive all of the loads and remain in the cache is given by:

$$\begin{aligned} \hat{P}^A(\Delta ,k) = \left\{ \begin{array}{ll} \left( \frac{N-\Delta }{N}\right) &{}\quad (N>\Delta ) \wedge (k \ne \infty ) \\ 0 &{}\quad \hbox {otherwise} \end{array} \right. \end{aligned}$$

(13)

Observe that the lower bound probability is zero if the reuse distance is infinite (i.e. $e_l$ was never previously loaded into the cache) or if the stack distance is larger than or equal to the associativity ($\Delta \ge N$), i.e., the number of distinct memory blocks that may be loaded into the cache within the reuse distance of $e_l$ is sufficient to fill the cache.

Theorem 4

The total number of distinct cache locations loaded with memory blocks during the reuse distance of element $e_l$, is no greater than the stack distance.

Proof

(Theorem 4) The proof of Theorem 4 can be obtained by induction. Let $r = l - rd(e_l)$ be the index of the element immediately following the previous access to the same memory block as $e_l$. (Note if $rd(e_l) = \infty$ then $r=0$ and $e_r$ identifies the first element in the trace). Let $X_i$ be the set of distinct cache locations that are loaded with memory blocks due to accesses $e_r \ldots e_i$ inclusive (where $r \le i < l$). Further let $M_i$ be the set of distinct memory blocks cached in the locations given by $X_i$ after element $e_i$ has been accessed.

We show that independent of the access history, $\forall e_i \in [e_r,\ldots , e_{l-1}] :\big \vert X_i \big \vert \le \Delta$.

Base case: initially, we have $X_i = \emptyset$ and $M_i = \emptyset$, hence $\big \vert X_i \big \vert = 0 \le \Delta$ prior to access $e_r$.

Inductive step: assuming that $\big \vert X_i \big \vert \le \Delta$, we show that $\big \vert X_{i+1} \big \vert \le \Delta$. There are three cases to consider:

• (i) $e_{i+1}$ is in the cache. In this case, no eviction takes place and no new memory block is loaded, hence $\big \vert X_{i+1} \big \vert = \big \vert X_{i} \big \vert \le \Delta$.

• (ii) $e_{i+1}$ is not in the cache and the eviction and load of a memory block takes place in a location that is not in $X_i$. In this case, $\big \vert X_{i+1} \big \vert = \big \vert X_{i} \big \vert +1$ and $M_{i+1} = M_i \cup e_{i+1}$. Note that $\big \vert X_{i+1} \big \vert = \big \vert M_{i+1} \big \vert$ and since $M_{i+1}$ can contain only unique memory blocks, then $\big \vert X_{i+1} \big \vert \le \Delta$.

• (iii) $e_{i+1}$ is not in the cache and the eviction and load of a memory block takes place in a location that is in $X_i$. In this case, $\big \vert X_{i+1} \big \vert = \big \vert X_{i} \big \vert \le \Delta$. Further, $M_{i+1} = (M_i \setminus e_{ev}) \cup e_{i+1}$ where $e_{ev}$ is the unique memory block evicted from the location into which $e_{i+1}$ is loaded. Note that $\big \vert X_{i+1} \big \vert = \big \vert M_{i+1} \big \vert$.

Induction over $e_i \in [e_r,\ldots , e_{l-1}]$ is sufficient to prove that $\forall e_i \in [e_r,\ldots , e_{l-1}] :$ $\big \vert X_i \big \vert \le \Delta$. $\square$

Theorem 5

The lower bound on the probability of a cache hit $\hat{P}^A(\Delta ,k)$ is incomparable with the lower bound on the probability of a cache hit $\hat{P}^D(k)$ derived by Davis et al. (2013).

Proof

(Theorem 5) Theorem 5 can be proven by considering two extremes.

Firstly when the reuse distance is large ($k>N$) then $\hat{P}^D(k) = 0$; however, in this case, the stack distance may be small. As an example, consider the final accesses to $a$ and $b$ in the sequence $a, b, c, d, c^1, d^1, c^1, d^1, a^7, b^7$ with an associativity of $N=4$. Here, we have $\hat{P}^D(k) = 0$ since $N=4$ and $k=7$, yet $\hat{P}^A(\Delta ,k) = 1/4$ since there are only three distinct memory blocks accessed within the reuse distance.

Secondly, consider the case where $1<k<N$ and all of the accesses within the reuse distance are to different memory blocks. In this case, $\Delta = k$ and we have:

$$\begin{aligned} \hat{P}^A(\Delta ,k) = \left( \frac{N-k}{N}\right) < \left( \frac{N-1}{N}\right) ^k = \hat{P}^D(k) \end{aligned}$$

(14)

The correctness of (14) can be shown by induction over values of $i$ from $1$ to $k$.

Base case: for $i = k = \Delta = 1$ then trivially, $\hat{P}^A(i,i) = \hat{P}^D(i)$. Inductive step: assuming that $\hat{P}^A(i,i) \le \hat{P}^D(i)$, then for $0 < i < N-1$, we have:

$$\begin{aligned} \hat{P}^A(i+1,i+1) = \hat{P}^A(i,i) \left( \frac{N-(i+1)}{N-i}\right) \end{aligned}$$

(15)

$$\begin{aligned} \hat{P}^D(i+1) = \hat{P}^D(i) \left( \frac{N-1}{N}\right) \end{aligned}$$

(16)

Since $\left( \frac{N-(i+1)}{N-i}\right) < \left( \frac{N-1}{N}\right)$ holds for $0 < i < N-1$ then $\hat{P}^A(i+1,i+1) < \hat{P}^D(i+1)$

Induction over all integer values of $i$ from 1 to $k$ suffices to prove (14). $\square$

As $\hat{P}^A(\Delta ,k)$ and $\hat{P}^D(k)$ are incomparable, yet both give valid lower bounds on the probability of a cache hit, then, we may use the maximum of them to compute an improved lower bound that dominates each individually.

6 Cache contention

Equation (14) shows that $\hat{P}^D(k)$ i.e. (3) can often give a larger lower bound for the probability of a cache hit compared to $\hat{P}^A(\Delta ,k)$ i.e. (13). Indeed, the value at which $\hat{P}^D(k)$ is forced to zero to ensure correctness with respect to constraint C2 is $\left( \frac{N-1}{N}\right) ^N$ which tends to $1/e \approx 0.367$ for large $N$, (where $e$ is Euler’s number). This illustrates the significant loss of precision that can potentially result from the simple approach taken to ensuring the validity of the formula. While (3) provides a lower bound on the probability of a cache hit, it is thus imprecise even for simple access sequences. If we consider a cache with associativity $4$ and the following access sequence,

$$\begin{aligned} a, b, c, d, f, a^4, b^4, c^4, d^4, f^4 \end{aligned}$$

all accesses are considered cache misses. The reason for this is that for each of the last five accesses, the probability of a cache hit is set to $0$ to ensure correctness with respect to constraint C2, i.e, that the probability of the last five accesses all being hits is zero.

The proof that Davis et al. (2013) give for the correctness of (3) is based on modelling the set of intervening accesses (i.e. within the reuse distance $k$ of an element $e_l$ in the trace) as all having the possibility of either being hits or misses. Misses are assumed to result in evictions which reduce the probability of element $e_l$ remaining in the cache. By contrast, hits are assumed not to cause evictions, but instead to reduce the number of cache locations available to $e_l$, since a hit could imply that a memory block is present in the cache for the entire reuse distance. If there are $h \ge N$ such memory blocks, then there can be no locations available for $e_l$, and hence the only safe assumption is that the probability of a cache hit is zero. Otherwise, for $h<N$, the probability of a cache hit for $e_l$ is lower bounded by:

$$\begin{aligned} \hat{P}^h(k) = \left( \frac{N-h-1}{N-h}\right) ^{k-h} \end{aligned}$$

(17)

Davis et al. (2013) showed that $\hat{P}^h(k)$ takes its smallest value for $h=0$. Equation (3) then follows from the safe assumption that $h$ could take any value from 0 to $k$.

We now build on this previous work, refining the limit on the number of contending memory blocks that need to be considered (Davis et al. 2013 assume this could be as high as $k$). To this end, we define the concept of the cache contention ($con(e_l,T)$) of an access $e_l$ which denotes the number of accesses within the reuse distance of $e_l$ in trace $T$ that could potentially contend with $e_l$ for locations in the cache.

We only need to set the probability of a cache hit for an access $e_l$ to zero when the cache contention is greater than or equal to the associativity $N$.

$$\begin{aligned} \hat{P}^N(e^\mathrm{{hit}}_l) = \left\{ \begin{array}{ll} 0 &{}\quad con(e_l,T) \ge N \\ \max \left( \hat{P}^A(\Delta ,k), \left( \frac{N-1}{N}\right) ^{k}\right) &{}\quad \hbox {otherwise} \end{array} \right. \end{aligned}$$

(18)

The cache contention and the probability $\hat{P}^N$ are mutually dependent; but the cache contention of an element $e_l$ depends only on the probability of a cache hit for the preceding elements, which enables the cache contention and the probability $\hat{P}^N$ to be computed efficiently.

We present two different methods of computing cache contention, first a basic approach, and second an improved one that uses a form of cache simulation.

6.1 Basic cache contention

The basic approach to cache contention models each of the accesses within the reuse distance of $e_l$ that have been assigned non-zero probability of being a hit as requiring its own separate location in the cache. Further, it is also assumed that the first element $e_r$ within the reuse distance of $e_l$ (i.e. where $r = l - rd(e_l,[e_1,\ldots , e_{l-1}])$ also requires a separate location in the cache regardless of its assigned probability.

$$\begin{aligned} con:\mathbb {E} \times \mathbb {T} \rightarrow \mathbb {N} \end{aligned}$$

$$\begin{aligned} con\left( e_l, \left[ e_1, e_2, \ldots , e_{l-1}\right] \right) = \left\{ \begin{array}{ll} \infty &{}\quad rd(e_l,[e_1,\ldots , e_{l-1}]) = \infty \\ \Bigl \vert conS \Bigr \vert &{}\quad \hbox {otherwise} \end{array} \right. \end{aligned}$$

(19)

with

$$\begin{aligned}&conS = \left\{ e_i \in [e_1, \ldots , e_{l-1}] ~\big \vert \left( l - rd(e_l,[e_1,\ldots , e_{l-1}]) < i \wedge \hat{P}(e_i^\mathrm{{hit}}) \ne 0\right) \right\} \\&\quad \cup \left\{ e_r \in [e_1, \ldots , e_{l-1}] ~\big \vert \left( l - rd(e_l,[e_1,\ldots , e_{l-1}]\right) = r\right\} \end{aligned}$$

Table 1 presents the probability $\hat{P}^N$ for the elements of the example sequence

$$\begin{aligned} a, b, c, d, f, a, b, c, d, f \end{aligned}$$

In contrast to (3), only one of the five elements with finite reuse distance is assumed to have zero probability of being a cache hit.

Table 1 Probabilities $\hat{P}^N$, $\hat{P}^D$, and $\hat{P}^A$ for the access sequence $a, b, c, d, f, a, b, c, d, f$, with reuse distances ($rd$) and cache contentions ($con$)

Theorem 6

The cache contention defined in Equation (19) eliminates all combinations of cache hits that are infeasible due to the finite associativity of the cache.

Proof

(Theorem 6) To prove Theorem 6, we must show that there is an evolution of the cache state for the entire trace $T$ that permits all accesses assigned a non-zero probability to all be hits. (It follows trivially that any subset of these accesses could also all be hits). To do so, we consider the evolution of the set $Z$ which contains the subset of the cache state that is necessary to support cache hits for all of the accesses assigned non-zero probabilities. Let $Z_i$ be this subset of the cache state, immediately following access $e_i$.

We construct the set $Z$ as follows:

$$\begin{aligned} Z_{1} = \{e_1\} \end{aligned}$$

$$\begin{aligned} Z_i = \left\{ \begin{array}{ll} \left( Z_{i-1} \setminus \{e_{i-1}\} \right) \cup \{e_i\} &{}\quad \hbox {if } con(e_{n_{i-1}},T) \ge N \\ \left( Z_{i-1} \cup \{e_i\} \right) &{}\quad \hbox {if } con(e_{n_{i-1}},T) < N \\ \end{array} \right. \end{aligned}$$

(20)

where $e_{n_{i-1}}$ denotes the next access to element $e_{i-1}$. (Note if there is no such next access, then we assume that $con(e_{n_{i-1}},T) = \infty$). We now prove that the set $Z$ is always a subset of a feasible cache behaviour. Specifically, (i) it always contains the least recently accessed element, (ii) all elements in $Z_i$ have been accessed prior to element $e_i$ and (iii) the set always contains at most $N$ elements:

• (i) $\forall i:e_i \in Z_i$,

• (ii) $\forall i:\forall e_j\in Z_i :\exists l \le i :e_j = e_l$, and

• (iii) $\forall i:\vert Z_i \vert \le N$.

Conditions (i) and (ii) hold by construction. Further, each element $e_j \in Z_i$ where $e_j \ne e_i$ must have a non-zero probability of being a hit at its next reuse and thus a cache contention smaller than $N$, otherwise it would have been removed from $Z_i$ thus:

$$\begin{aligned} \forall e_j \in Z_i:e_j \ne e_i \Rightarrow con(e_{n_{j}},T) < N \end{aligned}$$

(21)

We now prove condition (iii) by contradiction. We assume (for contradiction) that $i$ is the smallest index such that $\vert Z_i \vert > N$ holds. It follows that $\vert Z_{i-1} \vert = N$ and $\vert Z_i \vert = N +1$, since at most one element can be added to $Z_{i-1}$ to form $Z_i$ (see (20)). As $\vert Z_{i-1} \vert < \vert Z_i \vert$, then from (20), $e_{i-1}$ must be a member of $Z_i$ with $e_i \ne e_{i-1}$. It must also be the case that $con(e_{n_{i-1}},T) < N$, otherwise $e_{i-1}$ would have been removed and we would instead have $\vert Z_{i-1} \vert = \vert Z_i \vert$.

As $con(e_{n_{i-1}},T) < N$, it follows that $Z_{i-1}$ contains $N$ elements, all of which have a non-zero probability of being a hit at their next reuse. Further, we know that $e_i$ is not one of these elements, since otherwise we would again have $\vert Z_i \vert = \vert Z_{i-1} \vert$.

Let $e_j \in Z_i$ be the element with the highest index $n_j$ for its next reuse of all those elements in $Z_i$ with a non-zero probability at their next reuse.

(Recall that the next access to the same memory block as $e_j$ is denoted by $e_{n_j}$). Since $Z_{i-1}$ contains $N$ elements all of which have a non-zero probability of being a hit on their next reuse, but does not contain $e_i$, then we conclude that there must be at least $N-1$ accesses between $e_i$ and $e_{n_j}$ that are assigned non-zero probabilities.

There are two cases to consider:

Case 1: $j = i$. In this case, we know that $e_i \notin Z_{i-1}$ and that all $N$ elements of $Z_{i-1}$ have non-zero probabilities on their next reuse, it must therefore be the case that there are $N$ accesses between $e_j$ and $e_{n_j}$ with non-zero probabilities. Hence the cache contention of $e_{n_j}$ is at least $N$ which contradicts the assumption that $e_{n_j}$ has a non-zero probability of being a cache hit. Hence it cannot be the case that $j = i$.

Case 2: $j < i$. In this case, we know that $e_j \in Z_{i-1}$, $e_j \ne e_i$, and that there must be at least $N-1$ accesses between $e_i$ and $e_{n_j}$ that are assigned non-zero probabilities and so contribute to the cache contention of $e_{n_j}$. Further, there is also the access $e_{j+1}$ immediately following $e_j$ (where $j+1 \le i$), which also contributes 1 to the cache contention of $e_{n_j}$ irrespective of the probability assigned to it. Hence the cache contention of $e_{n_j}$ is at least $N$ which contradicts (21).

Both cases lead to contradictions, hence the assumption that $\exists i :\vert Z_i \vert = N +1$ is wrong, and thus condition (iii) $\forall i:\vert Z_i \vert \le N$ holds. $\square$

The cache contention embodied in (19) is therefore sufficient to ensure that there is a feasible evolution of the cache state, following the construction rules given in (20) that permits all accesses assigned a non-zero probability to be cache hits.

6.2 Improved cache contention

The cache contention as defined in Eq. (19) is pessimistic in that it assumes that each access with a non-zero probability of being a cache hit, within the reuse distance of $e_l$ contends separately with $e_l$ for space in the cache; however, this may not necessarily be the case. Consider the trace $a, b, c, d, f, d, f, g, h, g, h, a, b$ and a cache with an associativity of 4. Here blocks $d$ and $f$ need to remain in the cache for two accesses, as do blocks $g$ and $h$, but $g$ and $h$ could potentially replace $d$ and $f$ leaving the possibility that the last two accesses, to $a$ and $b$, are also hits. This potential reuse of cache space is not captured by the basic method of determining cache contention given in the previous section.

Table 2 illustrates this pessimism. The second accesses to $d$, $f$, $g$, $h$, $a$ and $b$ could all potentially be hits within the trace $a, b, c, d, f, d, f, g, h, g, h, a, b$ and could therefore be assigned non-zero probabilities; however this is not captured by $\hat{P}^N$.

Table 2 Probabilities $\hat{P}^N$ for the access sequence $a, b, c, d, f, d, f, g, h, g, h, a, b$, with reuse distances ($rd$) and cache contentions ($con$)

To overcome this pessimism, as well as pessimism due to repeated accesses to the same set of memory blocks, we propose an alternative cache contention based on a simulation of a feasible cache behaviour. We conceptually simulate one valid cache behaviour to check which elements may be cached simultaneously, and thus, for which accesses we can assign non-zero probabilities of being a cache hit. In the case of an eviction, we assume that the element with the maximum reuse distance at its next reuse will be evicted. By doing so, we aim to have the smallest possible impact on the overall cache hit/miss distribution, and thus the least pessimism. We note that this is a heuristic and we do not claim optimality.

We use the term forward reuse-distance ${\text{ rd }}^{\rightarrow }(e)$ to denote the reuse distance of an element at its next reuse, with a forward reuse-distance of $\infty$ in the case that there is no next access to that memory block.

$$\begin{aligned} rd^{\rightarrow }:\mathbb {E} \times \mathbb {T} \times \mathbb {N} \rightarrow \mathbb {N} \cup \{ \infty \} \end{aligned}$$

$$\begin{aligned}&rd^{\rightarrow }\left( e,\left[ e_{1}, \ldots e_{n}\right] ,i\right) \nonumber \\&\quad = \left\{ \begin{array}{ll} rd\left( e_l,\left[ e_{1}, \ldots e_{l-1}\right] \right) &{}\quad \hbox {if } \exists e_l :e = e_l \wedge l> i\wedge \forall _{i < j < l}:e \ne e_j\\ \infty &{}\quad \hbox {otherwise} \end{array} \right. \end{aligned}$$

(22)

Let $S_i$ be the set of potentially cached elements immediately before the access to $e_i$. We define the set $S_i$ recursively and start with an initially empty cache:

$$\begin{aligned} S_0 = \emptyset \end{aligned}$$

(23)

$$\begin{aligned} S_{i+1} = \left\{ \begin{array}{ll} S_{i} &{}\quad \hbox {if } e_i \in S_{i} \\ S_{i} \cup \{e_i\} &{}\quad \hbox {if } \vert S_{i} \vert < N\\ S_{i} \setminus \Big (\underset{e \in S_{i}}{\hbox {arg max}}\big (rd^{\rightarrow }\big (e,T,i\big )\big )\Big ) \cup \{e_i\} &{}\quad \hbox {if } \vert S_{i} \vert = N \end{array} \right. \end{aligned}$$

(24)

The three different cases in (24)) are as follows: First case: if we access an element $e_i$ that is currently cached, i.e, $e_i \in S_{i}$, then we do not need to update the cache contents. Second case: if the set $S_{i}$ contains less then $N$ elements at the previous access, we only need add the currently accessed element $e_i$. Third case: if the set $S_{i}$ contains $N$ elements at the previous access, we first remove the element with the largest forward reuse-distance from the set $S_{i}$ and then add element $e_i$. (For completeness, we break ties deterministically by assuming that the memory block with the lowest address is evicted). By construction, $\forall _i :\vert S_i\vert \le N$ holds. Hence $S_i$ represents a feasible evolution of the cache state for $i=1$ to $n$ (i.e. over the entire trace).

Using the definition of the potentially cached elements, we can safely set the probability of a cache hit for an access $e_i$ to $\max \left( \hat{P}^A(\Delta ,k), \left( \frac{N-1}{N}\right) ^{k}\right)$ when the accessed element is contained in $S_{i}$

$$\begin{aligned} \hat{P}^C(e^\mathrm{{hit}}_i) = \left\{ \begin{array}{ll} \max \left( \hat{P}^A(\Delta ,k), \left( \frac{N-1}{N}\right) ^{k}\right) &{}\quad \hbox { if}~e_i \in S_i \\ 0 &{}\quad \hbox { if}~e_i \notin S_i \end{array} \right. \end{aligned}$$

(25)

Theorem 7

The improved cache contention as defined in Eq. (25) eliminates all combinations of cache hits that are infeasible due to the limited associativity of the cache.

Proof

(Theorem 7) Proof of Theorem 7 is trivial as $S_i$ represents a feasible evolution of the cache state over the entire trace. $\square$

Table 3 shows the probabilities of a cache hit according to (25) for the access sequence $a, b, c, d, f, d, f, g, h, g, h, a, b$ for a cache with an associativity of 4. The evolution of $S_i$ is as follows $S_5 = \{a,b,f,d\}$, since $f$ replaces $c$ which has an infinite forward reuse distance. $S_9 = \{a,b,g,h\}$, since $g$ and $h$ replace $d$ and $f$ which have an infinite forward reuse distance by the time $g$ is first accessed. Hence the second accesses to $d$, $f$, $g$, $h$, and $a$ and $b$ are all assigned a non-zero probability of being a cache hit.

Table 3 Probabilities $\hat{P}^C$ and $\hat{P}^N$ for the access sequence $a, b, c, d, f, d, f, g, h, g, h, a, b$

7 Exhaustive state-enumeration

We now describe a simple analysis that computes the exact probability distribution of cache hits. This analysis is different from the approaches presented in previous sections. Here, we exhaustively enumerate all cache states that may occur during the execution of a given trace.

The domain of the analysis is a set of cache states defined as follows: A cache state $CS$ is a triple $(E,P,D)$ consisting of a set of memory blocks $E\subseteq \mathbb {E}$, a probability $P \in \mathbb {R}$

and a distribution of cache misses $D:(\mathbb {N} \rightarrow \mathbb {R})$. A cache state $CS = (E,P,D)$ has the following meaning: the cache contains exactly the elements $E$ with probability $P$, and $D$ denotes the distribution of cache misses when the cache is in this state. The set of all cache states is denoted by $\mathbb {CS}$. Note that we model a distribution by the function $\mathbb {N} \rightarrow \mathbb {R}$ which assigns each possible number of cache hits a probability. We start with an initially empty cache, i.e. $CS_\mathrm{{init}} = (\emptyset ,1,D)$ with

$$\begin{aligned} D(x) = \left\{ \begin{array}{ll} 1 &{}\quad \hbox {if } x = 0 \\ 0 &{}\quad \hbox {otherwise} \end{array} \right. \end{aligned}$$

Hence, our initial state space is the set containing the initially empty cache: $\{CS_\mathrm{{init}}\}$.

The update function $u$ describes the cache update when accessing element $e$ for a single cache state as follows:

$$\begin{aligned} u:\mathbb {CS} \times \mathbb {E} \rightarrow 2^\mathbb {CS} \end{aligned}$$

$$\begin{aligned} u\left( \left( E,P,D\right) ,e\right) = \left\{ \begin{array}{ll} \left\{ \left( E,P,D\right) \right\} &{}\quad \hbox {if } e \in E \\ {\hbox {miss}}((E,P,D), e) &{}\quad \hbox { otherwise} \\ \end{array} \right. \end{aligned}$$

(26)

If the accessed element $e$ is a cache hit, then the cache state remains unchanged, and the output is the set containing the input cache state. However, if the accessed element $e$ is a cache miss, then the update function generates a set of possible cache states as follows:

$$\begin{aligned}&{\text{ miss }}((E,P,D),e) = \left\{ (E\setminus e' \cup \{e\},P\cdot 1/N,D') \vert e' \in E\right\} \nonumber \\&\quad \cup \left\{ (E \cup \{e\},P\cdot (N-|E|)/N,D') \vert \text{ if } |E |< N\right\} \end{aligned}$$

(27)

with $D'(0) = 0$ and $\forall x > 0:D'(x) = D(x-1)$.

Each element $e'$ from the set $E$ may be evicted from the cache with probability $1/N$ and the element $e$, which is now cached, is added to $E$. In the case that the set $E$ is smaller than the associativity of the cache, an empty cache line or a cache line with unknown content will be evicted with probability $(N-|E|)/N$. In either case, the miss-distribution will be shifted by one to account for the additional cache miss.

In order to reduce the state space, we merge two cache states if they contain exactly the same memory blocks. We thus define the merge operation $\uplus$ for cache states as follows:

$$\begin{aligned} \uplus :\mathbb {CS} \times \mathbb {CS} \rightarrow 2^\mathbb {CS} \end{aligned}$$

$$\begin{aligned}&(E_1,P_1,D_1) \uplus (E_2,P_2,D_2) \nonumber \\&\quad =\left\{ \begin{array}{ll} \left\{ (E_1,P_1+P_2, ( \frac{P_1}{P_1+P_2} \cdot D_1) \oplus (\frac{P_2}{P_1+P_2}\cdot D_2))\right\} &{}\quad \hbox {if } E_1 = E_2 \\ \left\{ (E_1,P_1,D_1),(E_2,P_2,D_2)\right\} &{}\quad \hbox { otherwise} \\ \end{array} \right. \end{aligned}$$

(28)

where $\oplus$ denotes the summation of two distributions (i.e. $D_1 \oplus D_2 := \lambda x.D_1(x) + D_2(x)$) and $p\cdot D$ denotes the multiplication of each element in $D$ by $p$ (i.e. $p\cdot D := \lambda x.p\cdot D(x)$). This step is necessary to weight each distribution by its probability.

We can lift the update function $u$ from single cache states to a set of cache states as follows:

$$\begin{aligned} U:2^\mathbb {CS} \times \mathbb {E} \rightarrow 2^\mathbb {CS} \end{aligned}$$

$$\begin{aligned} U(S,e) = \biguplus \left\{ u(CS,e) \vert CS \in S\right\} \end{aligned}$$

(29)

By construction of the update function, the sum of the probabilities of the indiviual cache states $(E,P,D)$ within the set of cache states $S$ holds:

$$\begin{aligned} \sum _{(E_i,P_i,D_i) \in S} P_i = 1 \end{aligned}$$

(30)

The set of cache states $S_\mathrm{{res}}$ generated by a trace $T = [e_1,\ldots , e_n]$ executed on the initial cache state $CS_\mathrm{{init}}$ is thus given by the composition of $U$:

$$\begin{aligned} S_\mathrm{{res}} := U(\ldots (U(U(CS_\mathrm{{init}},e_1),e_2),\ldots ,e_n) \end{aligned}$$

(31)

The final distribution of all cache states in $S_\mathrm{{res}}$ is then given by the summation of all individual distributions of each cache state weighted by their probabilities:

$$\begin{aligned} D_\mathrm{{res}} = \bigoplus \left\{ D\cdot P \vert (E,P,D) \in S_\mathrm{{res}} \right\} \end{aligned}$$

(32)

See Fig. 1 for an example of the exhaustive enumeration of all cache states, for a cache with associativity 4. Here, we assume an initially empty cache. The access to block $a$ leads with probability $1$ to the next cache state (where only $a$ is cached). The next access to $b$ evicts memory block $a$ with probability $1/4$ or is stored in a different cache line to $a$ with probability $3/4$, and so on.

Fig. 1

The first four steps of exhaustive enumeration of all cache states for the access sequence $a, b, a, c, d, b, c, f, a, c$ The dotted arrows show the evolution of the different cache states, annotated with the corresponding probability

The presented method computes all possible behaviours of the random cache with the associated probabilities. It is thus correct by construction as it simply enumerates all states exhaustively.

Unfortunately, a complete enumeration of all possible cache states is computationally intractable. Due to the behaviour of the random replacement policy, each element that was cached once, may still be cached. Thus the number of different cache states grows exponentially.

8 Combined approach

So far, we presented a precise but computationally intractable approach, and two imprecise yet efficient approaches based on cache contention and cache simulation.

In this section, we show how these approaches can be combined to form a new approach with scalable precision. The idea is to use the precise approach for a small subset of relevant memory blocks, while using one of the imprecise approaches for the remaining blocks. So, instead of enumerating all possible cache states, we abstract the set of cache states and focus only on the $m$ most important memory blocks, where $m$ can be chosen to control both the precision and the runtime of the analysis. In this way, we effectively reduce the complexity of the precise component of the analysis for a trace with $l$ distinct elements from $2^l$ to $2^m$ (typically with $m \ll l$).

8.1 Heuristic to select relevant memory blocks

We use the number of occurrences of a memory block $e$ within a trace $T$ as a simple heuristic indicating relevance. We therefore order the memory blocks within a trace $T$ by the number of occurrences and select the $m$ blocks with the highest frequency. Let $R \subseteq \mathbb {E}$ be the set of these $m$ blocks. For the access sequence

$$\begin{aligned} a, b, a, c, d, b, c, f, a, c \end{aligned}$$

and $m=2$,

$R = \{a,c\}$. Thus, the state exploration conceptually computes a precise probability distribution for the sequence

$$\begin{aligned} a, \_, a, c, \_, \_, c, \_, a, c \end{aligned}$$

while the imprecise calculation is used to compute the probability of cache hits for the sequence

$$\begin{aligned} \_, b, \_, \_, d, b, \_, f, \_, \_ \end{aligned}$$

8.2 Update function for the combined approach

We have to change the update function of the precise analysis (see (26)) such that only elements from the set $R$ are represented explicitly, i.e. $\forall (E,P,D) \in \mathbb {CS}:E \subseteq R$. Each access to a memory block $e$ which is not contained in the set $R$ will be considered a cache miss; however, $e$ will not be added to the set $E$ (to ensure that $E \subseteq R$). Further, as we use (18) to compute the probability of a hit for access $e$, and include the distribution for $e$ via convolution, we do not increase the miss counts of the cache states in respect of $e$, i.e., we do not update the miss-distributions $D$ of a cache state $(E,P,D)$.

$$\begin{aligned} u:\mathbb {CS} \times \mathbb {E} \rightarrow 2^\mathbb {CS} \end{aligned}$$

$$\begin{aligned} u((E,P,D),e) = \left\{ \begin{array}{ll} \left\{ (E,P,D)\right\} &{}\quad \hbox {if } e \in E \\ miss((E,P,D),e) &{}\quad \hbox {if } e \notin E \wedge e \in R\\ miss'((E,P,D)) &{}\quad \hbox {if } e \notin R\\ \end{array} \right. \end{aligned}$$

(33)

with

$$\begin{aligned}&miss'((E,P,D)) = \left\{ (E\setminus e',P\cdot 1/N,D) \vert e' \in E\right\} \nonumber \\&\qquad \cup \left\{ (E,P\cdot (N-|E|)/N,D) \vert \text{ if } |E |< N\right\} \end{aligned}$$

(34)

The function $miss'$ computes the resulting set of cache states in the case of a miss, without inserting the accessed element $e$ as it is not an element of $R$. Figure 2 shows the reduced cache state exploration on the example sequence with $R = \{a,c\}$.

Fig. 2

The first five steps of the reduced cache state enumeration for the access sequence $a, b, a, c, d, b, c, f, a, c$ with $R=\{a,c\}$. The dotted arrows show the evolution of the different cache states, annotated with the corresponding probability. The access to memory block $b$ is considered as cache miss, but this block is not added to the cache states, since $b\notin R$

We also have to update the definition of cache contention (19) to consider all memory blocks of $R$ as potentially cached:

$$\begin{aligned} con:\mathbb {E} \times \mathbb {T} \rightarrow \mathbb {N} \end{aligned}$$

$$\begin{aligned} {con}\left( e_l, \left[ e_1, e_2, \ldots , e_{l-1}\right] \right) = \quad \quad \left\{ \begin{array}{ll} \infty &{}\quad rd(e_l,[e_1,\ldots , e_{l-1}]) = \infty \\ \Bigl \vert conS \Bigr \vert + \big \vert R \big \vert &{}\quad \hbox {otherwise} \end{array} \right. \end{aligned}$$

(35)

with

$$\begin{aligned}&{conS} = \left\{ e_i \in [e_1, \ldots , e_{l-1}] ~\big \vert \left( l - rd(e_l,[e_1,\ldots , e_{l-1}]) < i \wedge \hat{P}(e_i^\mathrm{{hit}}) \ne 0 \wedge e_i \notin R \right) \right\} \\&\quad \cup \left\{ e_r \in [e_1, \ldots , e_{l-1}] ~\big \vert \left( l - rd(e_l,[e_1,\ldots , e_{l-1}]\right) = r \wedge e_r \notin R \right\} \end{aligned}$$

And also the cache simulation (24) accordingly:

$$\begin{aligned} S'_{i+1} = \left\{ \begin{array}{ll} S'_{i} &{}\quad \hbox {if } e_i \in S'_{i} \\ S'_{i} \cup \{e_i\} &{}\quad \hbox {if } \vert S'_{i} \vert + \vert R \vert < N\\ S'_{i} \setminus \Big (\underset{e \in S'_{i}}{\hbox {arg max}}\big (rd^{\rightarrow }\big (e,T,i\big )\big )\Big ) \cup \{e_i\} &{}\quad \hbox {if } \vert S'_{i} \vert + \vert R \vert = N \end{array} \right. \end{aligned}$$

(36)

Furthermore, we must assume that each relevant memory block $e_i \in R$ constantly uses a cache location and thus add the number of relevant blocks to the stack distance $\Delta$:

$$\begin{aligned} \Delta ' = \Delta + \vert R \vert \end{aligned}$$

(37)

Table 4 presents the probability $\hat{P}^N$ for the elements of the example sequence, assuming $N=4$.

Table 4 Probabilities $\hat{P}^N$ for the access sequence $a, b, a, c, d, b, c, f, a, c$ and $R=\{a,c\}$, with reuse distances ($rd$) and cache contentions ($con$)

In the last step, we convolve the resulting distributions of both approaches to obtain the final distribution of cache misses.

8.3 Alternative heuristic

Instead of defining one fixed set of relevant blocks for the complete trace, we can define the set of relevant blocks depending on the position within the trace. We first determine all reused memory blocks in the complete trace, and the points at which they are last used. Then starting from the beginning of the trace, we greedily collect the reused memory blocks until we have a set of $q$ relevant blocks. When we encounter the last reuse of a block, that block is removed from the set of relevant blocks. Further, whenever the set of relevant blocks contains fewer than $q$ relevant blocks, the next reused block encountered is added to the set. This heuristic accounts for memory blocks with a high locality that occur frequently in one sub-trace and infrequently in others. By construction, at most $q$ memory blocks are relevant at any point in the trace, limiting the number of different cache states to $2^q$. (We note that the number of relevant blocks is often significantly lower than $q$ for some sub-traces). Table 5 shows the set of relevant memory blocks on an example trace for the trace-based and the occurrence-based heuristic.

Table 5 Sets of relevant memory blocks on trace $a, b, a, b, a, c , d , b f, c, d, f$ for the occurrence-based ($H^{{\mathrm{Occ}}}$) and trace-based heuristic ($H^{{\mathrm{Trace}}}$). The first line of the table indicates whether or not a memory block will be reused

We note that the set of relevant memory blocks is not fixed in the case of the alternative heuristic, but depends on the position in the trace. We therefore replace the global set $R$ with the local set of relevant memory blocks per access in (35) as follows: in the second line we have $e_i \notin R_i$ and in the third line $e_r \notin R_r$, while still adding the maximum number of relevant memory blocks $\big \vert R \big \vert$.

9 Evaluation

This section presents an evaluation of the precision and performance of the analyses for random replacement caches described in this paper based on two different sets of benchmarks. We also made comparisons against analysis for an LRU cache of the same associativity, using the stack distance³. The first set of benchmarks are those used in a previous publication (Davis et al. 2013) and are based on hand-crafted access sequences, which are limited in size. The second set of traces were automatically generated using the gem5 simulator (Binkert et al. 2011) and are significantly larger.

9.1 Mälardalen benchmarks

We first present results for all four Mälardalen benchmarks considered by Davis et al. (2013): binary search, fibonacci calculation, faculty computation and insertion sort. The execution traces for these benchmarks were manually extracted using the libFirm compiler framework⁴ and only contain memory blocks compiled from the source files (i.e. not including any library or operating system calls).

Our experiments assumed a fully-associative instruction-only cache with a block-size of $8$ and an associativity of (i) $8$ and (ii) $16$. (Note, we selected a small block size to compensate for the limited size of the available benchmarks). The results are shown in Figs. 3, 4, 5, 6, 7, 8, 9, and 10. The y-axis denotes the absolute number of misses and the x-axis the exceedance probability To derive an approximation to the actual performance of the cache, and thus a baseline for our experiments, we performed $10^9$ simulations of the cache behaviour for each benchmark (red line). The other lines on the graphs are the imprecise approach using only the reuse distance (3) (light blue line), only the stack distance (13) (orange line), the cache-contention approach (18) (black line), the improved cache-contention (25) (grey line), and the combined approach (with cache simulation (36)) using $4$, $8$ and $12$ relevant memory blocks (green, dark blue and pink lines respectively). The vertical green line depicts the performance of the LRU cache.

Fig. 3

Binary search. $132$ memory accesses in total, $25$ distinct memory blocks. (Associativity $=8$)

Fig. 4

Binary search. $132$ memory accesses in total, $25$ distinct memory blocks. (Associativity $=16$)

Fig. 5

Faculty computation. $99$ memory accesses in total, $25$ distinct memory blocks. (Associativity $=8$)

Fig. 6

Faculty computation. $99$ memory accesses in total, $25$ distinct memory blocks. (Associativity $=16$)

Fig. 7

Insertion sort. $707$ memory accesses in total, $21$ distinct memory blocks. (Associativity $=8$)

Fig. 8

Insertion sort. $707$ memory accesses in total, $21$ distinct memory blocks. (Associativity $=16$)

Fig. 9

Fibonacci calculation. $340$ memory accesses in total, $15$ distinct memory blocks. (Associativity $=8$)

Fig. 10

Fibonacci calculation. $340$ memory accesses in total, $15$ distinct memory blocks. (Associativity $=16$)

When the number of pairwise distinct memory blocks exceeds the associativity of the cache as is the case with binary search (see Figs. 3 and 4) and faculty computation (see Figs. 5 and 6), then the cache-contention approaches significantly improve upon the imprecise approaches that use only the reuse distance or only the stack distance. The improved cache contention does not improve upon the basic cache contention and the stack distance approach does not improve upon the reuse distance. Note for these benchmarks, the latter approaches predict hardly any cache hits.

For the other two benchmarks: insertion sort (see Figs. 7 and 8) and fibonacci calculation (see Figs. 9 and 10), the number of distinct memory blocks accessed within a loop is smaller than $16$. In these case, the cache-contention approaches result in no improvement or only a slight improvement over the reuse distance approach. The combined approach; however, with $8$ relevant memory blocks reduces the over-approximation by 40–60 $\%$, and with $12$ relevant memory blocks results in exact or nearly exact results. The difference between the two cache contention approaches is limited in these cases, while the approach using the stack distance performs considerably worse than the approach using the reuse distance.

The relative performance of the LRU replacement policy in these experiments strongly depends on the number of distinct memory blocks and the cache associativity. If the number of distinct memory blocks is below the associativity, LRU outperforms random cache replacement (see Fig. 10), whereas random replacement outperforms LRU if the number of distinct memory blocks exceeds the associativity (see Fig. 9).

Figure 11 shows how the runtime of the combined analysis varies with the number of relevant cache blocks. (Note the logarithmic scale on the graph). The experiments were run on a $4$-core $64$-bit $1.2$GHz CPU. The graph shows that the runtime of the analysis is exponential in the number of relevant blocks. This indicates that a complete analysis, i.e. where all blocks are considered relevant, is computationally infeasible: Even for the small number of distinct memory blocks and the short access traces, a precise analysis for the binary search and faculty computation benchmarks requires several hours of computation, and so an approximation is necessary.

Fig. 11

Runtime evaluation for the benchmarks fibonacci calculation, insertion sort, faculty computation and binary search

Observe that the runtime of the combined analysis for the insertion sort benchmark remains constant for 14 or more relevant blocks as the total number of reused memory blocks is 13 in this case. Hence, increasing the number of relevant blocks does not affect the precision or the runtime of the analysis. The same holds for the fibonacci benchmark and 13 blocks. Here, the flattening of the runtime between 8 and 10 relevant blocks is caused by the specific structure of this benchmark. The 9th and 10th most-frequent used memory blocks only occur in the final tenth of the access trace, which means that the exponential growth of the number of states does not fully affect the runtime when increasing the number of relevant blocks from 8 to 10.

9.2 Precision and performance on larger traces

In addition to the benchmarks used by Davis et al. (2013), we generated cache access traces for the four largest Mälardalen benchmarks (Gustafsson et al. 2010) using the gem5 simulator (Binkert et al. 2011) assuming an ARM7 processor⁵. Even though the benchmarks are not single-path, the C-Code is provided with example inputs, which results in well-defined traces and guarantee one single execution path. In contrast to the other benchmarks, the gem5-traces contain library and operating-system calls and are thus significantly larger. We assumed the same cache configuration: a fully-associative instruction-only cache with an associativity of (i) $8$ and (ii) $16$ and a block-size of $8$. The results are shown in Figs. 12, 13, 14, 15, 16, 17, 18, and 19. For these larger traces, we used the alternative heuristic to select the relevant memory blocks as described in Sect. 7.3.

Fig. 12

Finite impulse response filter (fir). 3,419 memory accesses in total, $393$ distinct memory blocks. (Associativity $=8$)

Fig. 13

Finite impulse response filter (fir). 3,419 memory accesses in total, $393$ distinct memory blocks. (Associativity $=16$)

Fig. 14

Discrete-cosine transformation on a $8 \times 8$ pixel block (jfdctint). 2,185 memory accesses in total, $347$ distinct memory blocks. (Associativity $=8$)

Fig. 15

Discrete-cosine transformation on a $8 \times 8$ pixel block (jfdctint). $2185$ memory accesses in total, $347$ distinct memory blocks. (Associativity $=16$)

Fig. 16

Automatically generated code (statemate). 1,831 memory accesses in total, $394$ distinct memory blocks. (Associativity $=8$)

Fig. 17

Automatically generated code (statemate). 1,831 memory accesses in total, $394$ distinct memory blocks. (Associativity $=16$)

Fig. 18

Simulation of an extended Petri Net (nsichneu). 5,202 memory accesses in total, $454$ distinct memory blocks. (Associativity $=8$)

Fig. 19

Simulation of an extended Petri Net (nsichneu). 5,202 memory accesses in total, $454$ distinct memory blocks. (Associativity $=16$)

In this set of experiments, the cache contention approaches always improved upon the approaches that use only the reuse distance or only the stack distance: in the case of the finite impulse filter benchmark (see Fig. 13), the over-approximation compared to using reuse distance only is reduced by around 3 $\%$, whereas in the case of the petri-net simulation (see Fig. 19) the improvement is around 21 $\%$.

The approach using the stack distance improves upon the approach using the reuse distance in all examples except for statemate (see Fig. 17), where the situation is reversed. The evaluation clearly shows that both approaches are incomparable.

In the case of an associativity of $16$, the combined approach with $12$ relevant blocks provides highly accurate results, with an over-approximation of at most 6 $\%$ (Fig. 15) and a near-optimal estimate for the petri-net simulation (see Fig. 17). Similarly, in the case of an associativity of $8$, using $8$ or $12$ relevant blocks also provides accurate results (see Figs. 14 and 16). We note however, that in some cases, using a number of relevant blocks that is equal to or higher than the associativity could be detrimental to the precision of the results, this is because when the number of relevant blocks is equal to associativity, the imprecise approach is unable to predict any cache-hits, as it has to assume that associativity-many blocks are already cached.

By construction, the combined approach is very precise if the number of relevant memory blocks is close to or larger than the number of distinct memory blocks (see Figs. 3, 4, 5, 6, 7, 8, 9, and 10). But even the if the number of distinct memory blocks strongly exceeds the number of relevant blocks, the combined approach is typically able to provide precise results. See for instance the evaluation of the petri-net simulation (Fig. 19). Despite a total of $454$ distinct memory blocks, only a subset of these blocks are simultaneously in the working set of the task.

In the case of the more complex benchmarks, the LRU replacement policy outperforms random replacement. Due to the complex structure of the larger traces, there are significantly fewer sub-traces in which the number of distinct memory blocks accessed within a loop marginally exceeds the cache associativity and hence, no cases overall where random replacement outperforms LRU.

Figure 20 shows the runtime of the combined analysis for different numbers of relevant memory blocks for each of the second set of benchmark traces. We note again the exponential growth in runtime with an increasing number of relevant blocks; however, here the runtime of the analysis is significantly higher due to the larger traces. The alternative heuristic conceptually splits the traces into sub-traces enabling different sets of relevant blocks to be defined per sub-trace, while damping the exponential growth in runtime. Since the number of pairwise distinct memory blocks significantly exceeds the number of relevant blocks, we could not reach any saturation, in terms of relevant blocks, for any of these benchmarks within a reasonable time (unlike the insertion sort and fibonacci benchmarks in Fig. 11).

Fig. 20

Runtime evaluation for the benchmarks fir, jfdctint, statemate and nsichneu

Figure 21 shows the runtime of the combined approach with 4, 8 and 12 relevant blocks and the runtime of convolution using the reuse-distance for randomly generated traces of different length. Each trace consists of random accesses to 32 distinct memory blocks and the associativity is 16. The number of relevant blocks is the dominant factor, with the runtime increasing exponentially with an increase in this parameter. However, conversely our experiments on the benchmarks have shown that limiting the number of relevant blocks to 8 or 12 provides effective performance while limiting the growth in the runtime of the analysis. The length of the trace has a slightly super-linear influence on the runtime caused by two different factors: the convolution operation is quadratic in the number of accesses, while the exhaustive state-space exploration grows linearly. We note that the quadratic growth in runtime due to the convolution operation can be addressed via the use of re-sampling techniques (Maxim et al. 2012) enabling the analysis of much larger traces.

Fig. 21

Runtime evaluation depending on the length of the trace

Figures 22 and 23 show how the precision of the analyses depend on the associativity of the cache and on the block-size . In both cases, we have used the largest of our benchmarks, i.e, the simulation of an extended Petri Net (nsichneu). With increasing associativity, the precision of the convolution-based approaches (using re-use distance, stack distance and cache contention) increases as the lower bounds on the cache-hit probabilities are less likely to be zero. By contrast, the precision of the combined approaches using exhaustive state enumeration decreases slightly with increasing associativity. This is because the number of relevant blocks remains constant, and hence a smaller share of the complete cache is modelled explicitly. The block-size mostly influences the overall length of the trace and affects all approaches in a similar fashion.

Fig. 22

Influence of the associativity on the precision of the various analyses

Fig. 23

Influence of the block-size on the precision of the various analyses

The evaluation indicates that the precision is very high if the number of relevant blocks is close to or larger than the associativity of the cache. We note that in practice, this will often be the case, since the associativity is typically lower than $16$ for most cache designs.

9.3 Comparison with LRU caches—synthetic benchmarks

As discussed in Sect. 1.1 Reineke (2014) compared simple probabilistic analyses (Davis et al. 2013) for evict-on-miss random replacement (referred to by Reineke as Random) with analysis for LRU replacement. Reineke makes a number of interesting observations and conclusions as follows:

Observation R.1: With the same information about an access sequence, i.e. (only) upper bounds on the reuse distances of accesses, the hit probabilities for LRU are always greater than or equal to the hit probabilities for Random.

Observation R.2: In case of LRU, and in contrast to Random, current cache analyses can profit from bounding stack distances, which can be arbitrarily lower than reuse distances.

Conclusion R.1: With simple, state-of-the-art analysis methods, LRU replacement is preferable over Random replacement in static (probabilistic) timing analysis.

Reineke (2014) also describes so called “payroll sequences” which are loops where the number of accesses exceeds the cache associativity. For such sequences Reineke notes that LRU incurs only cache misses, and so will be outperformed by Random with a very high probability; however to profit from Random replacement in such cases, more sophisticated analysis techniques are required.

We agree with these observations and conclusions. Regarding Observation R.2 in this paper we have described new analysis for random replacement caches based on stack distance. We note that the following modification to observation R.1 applies to that analysis.

Observation R.1b. With the same information about an access sequence, i.e. (only) upper bounds on the stack distances of accesses, the hit probabilities for LRU are always greater than or equal to the hit probabilities for Random.

The validity of Observations R.1 and R.1b are demonstrated by our previous results where the number of misses computed for random replacement using the reuse distance and stack distance analyses are never below the number of misses obtained assuming the LRU replacement policy.

In this paper, we also derived combined analysis techniques that do not dependent entirely on convolving probability distributions for individual accesses. For these analyses, our experiments show that in the case of benchmarks that contain accesses with stack distances greater than the associativity of the cache, then random replacement can sometimes provably exceed the performance of LRU replacement. We note that there are also many cases when LRU outperforms random replacement, hence the two policies and their more sophisticated analyses are incomparable.

In this section, we specifically investigate the different performance of LRU and random replacement policies using synthetic benchmarks.

The first synthetic benchmark Random Sequence aims to be representative of straight-line code. It consists of traces of $1000$ random accesses to $x$ distinct memory blocks where we have varied $x$ from 4 to 64. The results are shown in Fig. 24. Note, we assume a cache associativity of 16. For all values of $x$, LRU outperforms random replacement on the Random Sequence benchmark, with the relative performance difference between the two remaining largely constant.

Fig. 24

Influence of the number of distinct blocks on the precision of the various analyses

The second synthetic benchmark LoopK was used to fevaluate the influence of the size of a loop body on the relative performance of LRU and random replacement. To this end, we generated 5 traces with 512 accesses each. These 512 accesses are within a loop body of size 4, 8, 16, 32 and 64 respectively. The number of loop iterations was varied to keep the total number of accesses constant (i.e. the loop with size 4 was repeated 128 times, while the loop with size 64 was repeated only 8 times). We again assumed an associativity of 16. The results are shown in Fig. 25. On the LoopK benchmark, LRU outperforms random replacement when the size of the loop body is less than or equal to the associativity, whereas random replacement outperforms LRU as soon as the size of the loop body exceeds the associativity.

Fig. 25

Influence of the size of the loop body on the precision of the various analyses

We also modified the LoopK benchmark to iterate a constant number of times ($10$) and presented the results in a different way in Fig. 26. This figure shows execution time estimates with an exceedance probability of $10^{-9}$ depending on the loop body size assuming an associativity of $8$ and $16$. Here, we can see a smooth progression in the performance of the random replacement policy which is in stark contrast the LRU replacement policy, where the performance rapidly degrades when the loop body size exceeds the associativity.

Fig. 26

Number of misses with exceedance probability $10^{-9}$ with varying loop-body size. $10$ iterations of the loop

10 Conclusion and future work

In this paper, we investigated the correctness, optimality and precision of Static Probabilistic Timing Analysis (SPTA) for systems that use a cache with an evict-on-miss random replacement policy.

The main contributions of this paper are:

• 1. Showing that the formula for the probability of a cache hit previously published in DATE (Kosmidis et al. 2013) is not sound for use in SPTA, since it can produce results in the form of pWCET distributions that are optimistic by orders of magnitude and thus unsafe.

• 2. Proving the optimality of the probability function given by Davis et al. (2013) with respect to the limited information (reuse distance and associativity) that it uses.

• 3. Deriving an alternative probability function based on the stack distance (the number of pair-wise distinct memory blocks accessed within the reuse distance). This approach is incomparable to that of Davis et al. (2013).

• 4. Providing two new cache contention methods; a basic method, and an improved one based on a conceptual cache simulation, that can be used to improve upon the previous analyses that use reuse distance and stack distance. The basic cache contention presented in this paper corrects an omission in the formulation given by Altmeyer and Davis (2014). Both approaches are proven correct by showing that there exists a feasible evolution of the cache state that supports cache hits for all accesses where the cache contention is less than the associativity.

• 5. Introducing an approach with scalable precision, combining precise analysis for frequently used memory blocks with imprecise analysis for those memory blocks that are used less often.

• 6. An evaluation on a set of benchmark programs, showing the performance of the different approaches, and in particular that the scalable approach is highly effective in reducing pessimism in SPTA without the problems of exponential complexity inherent in an exhaustive cache state exploration.

• 7. A comparison between the LRU replacement policy and the Evict-on-Miss random replacement policy, showing that when the sophisticated combined analysis for random replacement (introduced in this paper) is used, the two are incomparable, with random replacement having provably better hard real-time performance when the number of distinct memory blocks in a loop exceeds the associativity, and LRU having better performance otherwise.

The SPTA methods described in this paper, including the scalable combined approach, are extendable to multipath programs. Such extension is the subject of further work by the authors.